Jordan-Type Inequalities and Stratification
Abstract
1. Introduction
2. Preliminaries
3. Main Results
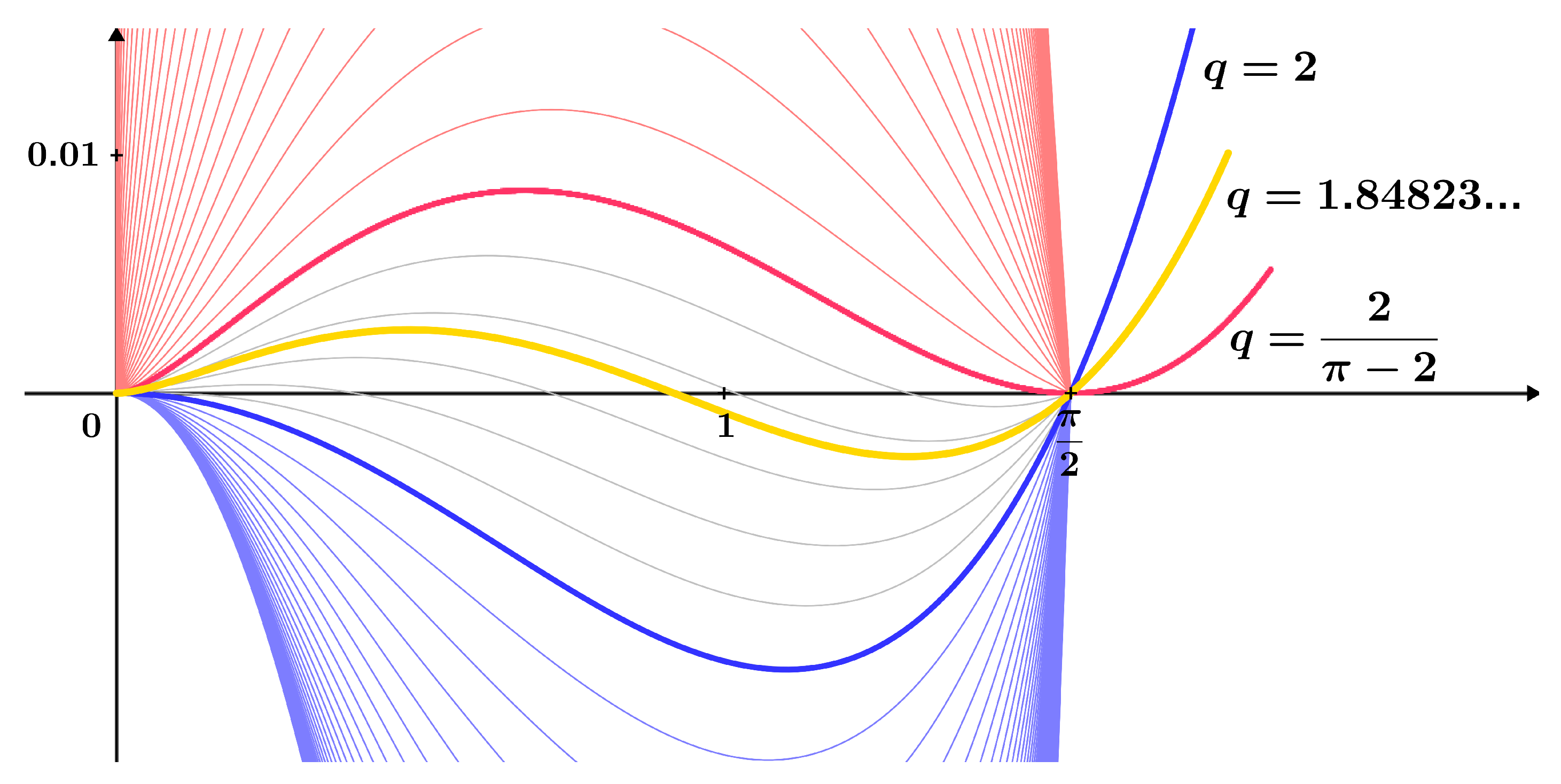
- (i) The family of functionsis decreasingly stratified with respect to the parameter on the interval .
- (ii) The family of functionsis increasingly stratified with respect to the parameter on the interval .
- (ii) Since , we obtain the one-parameter family of functions:
- (i) If , then the lower bounds of the function are given by
- (ii) If , then the equality
- (iii) If , then the upper bounds of the function are given by
- (iv) Each function from the family , for , has exactly one maximum and exactly one minimum at certain points , respectively, on the interval . Additionally, it holds that . The function , for , has exactly one maximum on , and for has exactly one minimum on .
- (v) The equality
- (ii) It is easily seen that and . In part of this proof, it will be shown that each function , for , has exactly one maximum and exactly one minimum on the interval , respectively. Hence, the stated inequalities follow.
- (iii) The assertion is equivalent to for and . Continuing from part of this proof, using multiple applications of L’Hôpital’s rule, it can be shown that
- (iv) Let us examine the monotonicity of functions from the family for on . The fourth derivative of with respect to x is
- By analyzing the monotonicity of the functions , , , , and for and for , in a similar manner, it can be concluded that the function , for , has exactly one maximum on , while the function , for , has exactly one minimum on .
- Note that the infimum of the error , for , exists and is attained when
- (i) If , then the upper bounds of the function are given byand the constant is the best possible.
- (ii) If , then the equality
- (iii) If , then the lower bounds of the function are given by
- (iv) Each function from the family , for , has exactly one maximum at a point on the interval .
- (v) The equality
- (ii) Continuing from the previous part of the proof, , using multiple applications of L’Hôpital’s rule, it can be shown that
- (iii) The assertion is equivalent to for and . Let us notice that for , where . In Statement 1, it has already been proven that for on the interval . Given that the family of functions is increasingly stratified with respect to the parameter q based on Lemma 3, for , it will also hold that
- (iv) It has been established in part of the proof for . Similarly, the proof holds for .
- (v) Note that the infimum of the error , for , exists and is attained when
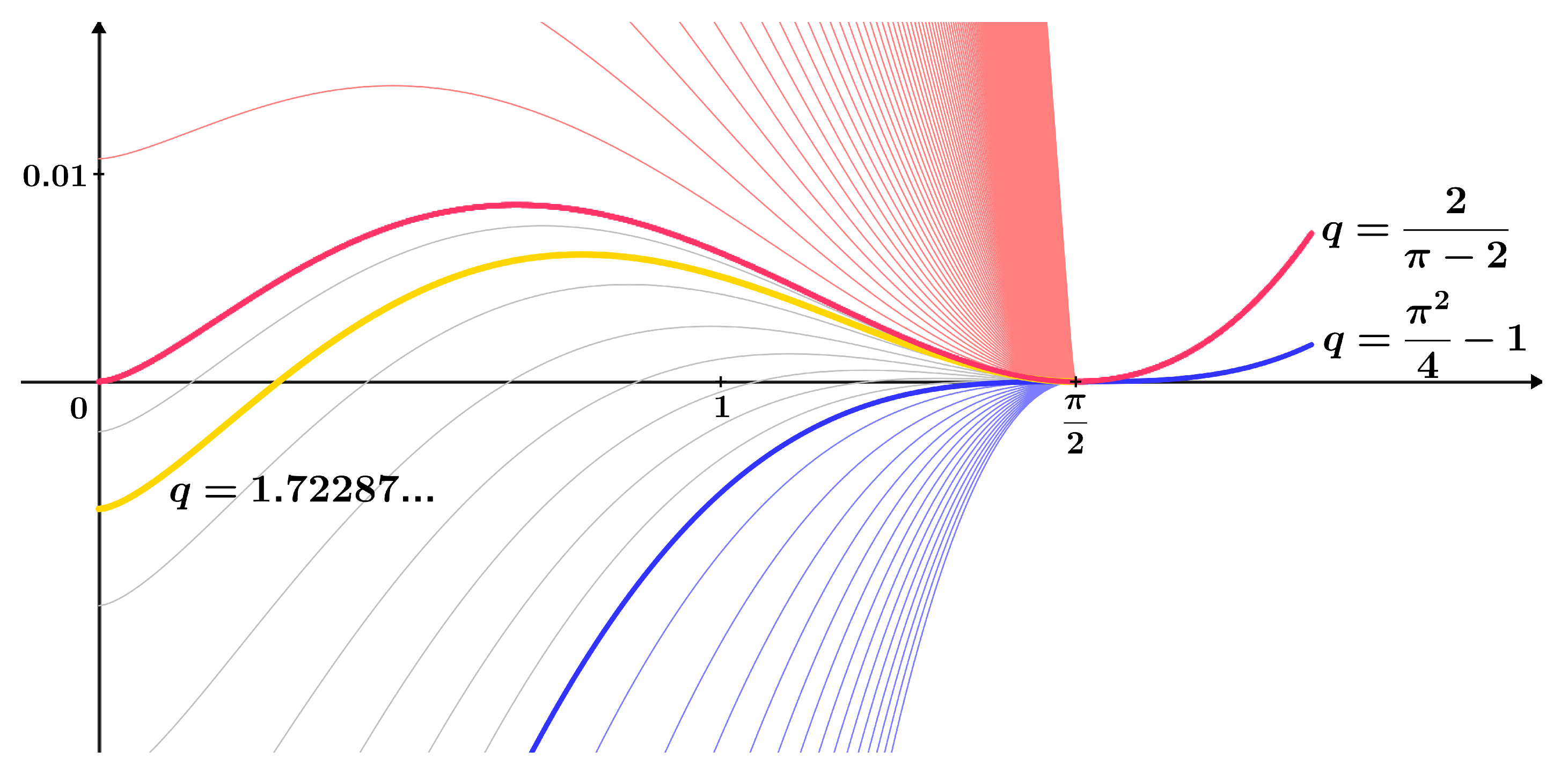
- (i) For and , it holds that
- (ii) For and , it holds that
4. Applications
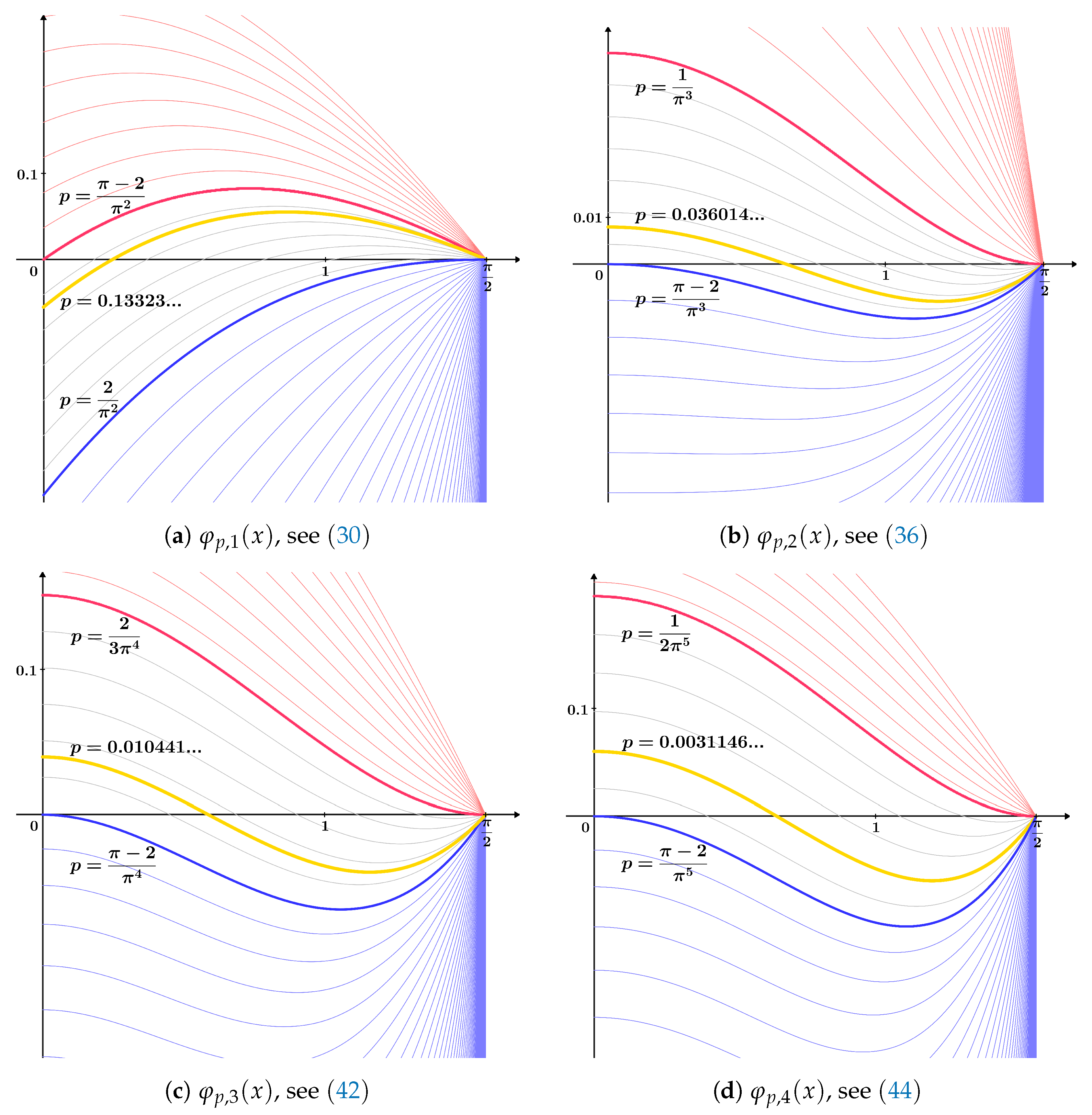
4.1. Improvements of Theorems 2–5
- (i) If , then
- (ii) If , then the equality
- (iii) If , then
- (iv) Each function from the family , for , has exactly one maximum at a point on the interval .
- (v) The equality
- (ii) Let us examine the monotonicity of functions for on the interval in a similar manner as in the proof of Statement 1. The second derivative of with respect to x is
- (iii) The claim follows directly from Statement 2 and based on the stratification. Namely, for , it holds that .
- (iv) It has been proven within proof .
- (v) Note that the infimum of the error , for , exists and is attained when
- (i) If , then
- (ii) If , then the equality
- (iii) If , then
- (iv) Each function from the family , for , has exactly one minimum at a point on the interval .
- (v) The equality
- (ii) Let us examine the monotonicity of functions for on the interval in a similar manner as in the proof of Statement 1. The third derivative of with respect to x is
- (iii) The claim follows directly from Statement 1 and based on the stratification. Namely, for , it holds that .
- (iv) It has been proven within proof .
- (v) Note that the infimum of the error , for , exists and is attained when
- (i) If , then
- (ii) If , then the equality
- (iii) If , then
- (iv) Each function from the family , for , has exactly one minimum at a point on the interval .
- (v) The equality
- (i) If , then
- (ii) If , then the equality
- (iii) If , then
- (iv) Each function from the family , for , has exactly one minimum at a point on the interval .
- (v) The equality
4.2. Approximations of the Function
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MTP | Mixed Trigonometric Polynomial |
References
- Mitrinović, D. Analytic Inequalities; Springer: Berlin, Germany, 1970. [Google Scholar]
- Qi, F.; Guo, B.-N. On generalizations of Jordan’s inequality. Coal High. Educ. 1993, 32–33. (In Chinese) [Google Scholar]
- Qi, F. Extensions and sharpenings of Jordan’s and Kober’s inequality. J. Math. Technol. 1996, 12, 98–102. (In Chinese) [Google Scholar]
- Deng, K. The noted Jordan’s inequality and its extensions. J. Xiangtan Min. Inst. 1995, 10, 60–63. (In Chinese) [Google Scholar]
- Jiang, W.D.; Yun, H. Sharpening of Jordan’s inequality and its applications. J. Inequal. Pure Appl. Math. 2006, 7, 4. [Google Scholar]
- Li, J.-L.; Li, Y.-L. On the Strengthened Jordan’s Inequality. J. Inequal. Appl. 2008, 2007, 74328. [Google Scholar] [CrossRef][Green Version]
- Qi, F.; Niu, D.-W.; Guo, B.-N. Refinements, Generalizations, and Applications of Jordan’s Inequality and Related Problems. J. Inequal. Appl. 2009, 2009, 271923. [Google Scholar] [CrossRef]
- Özban, A.Y. A new refined form of Jordan’s inequality and its applications. Appl. Math. Lett. 2006, 19, 155–160. [Google Scholar] [CrossRef]
- Li, J.-L. An identity related to Jordan’s inequality. Int. J. Math. Math. Sci. 2006, 2006, 76782. [Google Scholar] [CrossRef]
- Zhu, L. Sharpening Jordan’s inequality and the Yang Le inequality. Appl. Math. Lett. 2006, 19, 240–243. [Google Scholar] [CrossRef]
- Zhu, L. Sharpening Jordan’s inequality and the Yang Le inequality, II. Appl. Math. Lett. 2006, 19, 990–994. [Google Scholar] [CrossRef]
- Zhu, L. A general refinement of Jordan-type inequality. Comput. Math. Appl. 2008, 55, 2498–2505. [Google Scholar] [CrossRef][Green Version]
- Niu, D.-W.; Huo, Z.-H.; Cao, J.; Qi, F. A general refinement of Jordan’s inequality and a refinement of L. Yang’s inequality. Integral Transform. Spec. Funct. 2008, 19, 157–164. [Google Scholar] [CrossRef]
- Chen, C.-P.; Debnath, L. Sharpness and generalization of Jordan’s inequality and its application. Appl. Math. Lett. 2012, 25, 594–599. [Google Scholar] [CrossRef]
- Barbu, C.; Pişcoran, L.-I. Jordan type inequalities using monotony of functions. J. Math. Inequal. 2014, 8, 83–89. [Google Scholar] [CrossRef]
- Aharonov, D.; Elias, U. More Jordan type inequalities. Math. Inequal. Appl. 2014, 17, 1563–1577. [Google Scholar] [CrossRef]
- Alzer, H.; Kwong, M.K. On Jordan’s inequality. Period. Math. Hung. 2018, 77, 191–200. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, X. New Refinements and Improvements of Jordan’s Inequality. Mathematics 2018, 6, 284. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, X. New Polynomial Bounds for Jordan’s and Kober’s Inequalities Based on the Interpolation and Approximation Method. Mathematics 2019, 7, 746. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, C.-P. Sharpness and generalization of Jordan, Becker-Stark and Papenfuss inequalities with an application. J. Math. Inequal. 2019, 13, 1209–1234. [Google Scholar] [CrossRef]
- Haque, N. A Short Calculus Proof of Jordan’s Inequality. Camb. Open Engag. 2020. [Google Scholar] [CrossRef]
- Popa, E.C. A note on Jordan’s inequality. Gen. Math. 2020, 28, 97–102. [Google Scholar] [CrossRef]
- Malešević, B.; Mihailović, B. A minimax approximant in the theory of analytic inequalities. Appl. Anal. Discret. Math. 2021, 15, 486–509. [Google Scholar] [CrossRef]
- Malešević, B.; Mićović, M. Exponential Polynomials and Stratification in the Theory of Analytic Inequalities. J. Sci. Arts 2023, 23, 659–670. [Google Scholar] [CrossRef]
- Malešević, B.; Jovanović, D. Frame’s Types of Inequalities and Stratification. CUBO Math. J. 2024, 26, 1–19. [Google Scholar] [CrossRef]
- Chen, S.; Ge, X. A solution to an open problem for Wilker-type inequalities. J. Math. Inequal. 2021, 15, 59–65. [Google Scholar] [CrossRef]
- Malešević, B.; Mihailović, B.; Nenezić Jović, M.; Milinković, L. Some minimax approximants of D’Aurizio trigonometric inequalities. HAL 2022, hal-03550277. [Google Scholar]
- Chen, C.-P.; Mortici, C. The relationship between Huygens’ and Wilker’s inequalities and further remarks. Appl. Anal. Discret. Math. 2023, 17, 92–100. [Google Scholar] [CrossRef]
- Sándor, J. On D’Aurizio’s trigonometric inequality. J. Math. Inequal. 2016, 10, 885–888. [Google Scholar] [CrossRef]
- Sándor, J. Extensions of D’Aurizio’s trigonometric inequality. Notes Number Theory Discret. Math. 2017, 23, 81–83. [Google Scholar]
- Hung, L.-C.; Li, P.-Y. On generalization of D’Aurizio-Sándor inequalities involving a parameter. J. Math. Inequal. 2018, 12, 853–860. [Google Scholar] [CrossRef]
- Malešević, B.; Makragić, M. A method for proving some inequalities on mixed trigonometric polynomial functions. J. Math. Inequal. 2016, 10, 849–876. [Google Scholar] [CrossRef]
- Pinelis, I. L’Hospital type rules for monotonicity, with applications. J. Inequal. Pure Appl. Math. 2002, 3, 5. [Google Scholar]
- Estrada, R.; Pavlović, M. L’Hôpital’s monotone rule, Gromov’s theorem, and operations that preserve the monotonicity of quotients. Publ. Inst. Math. 2017, 101, 11–24. [Google Scholar] [CrossRef]
- Cutland, N. Computalibity: An Introduction to Recursive Funtion Theory; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
| Upper Bound of the Function on the Interval | Maximum Deviation from the Function on the Interval |
|---|---|
| Lower Bound of the Function on the Interval | Maximum Deviation from the Function on the Interval |
|---|---|
| Minimax Approximation of the Function on the Interval | Maximum Deviation from the Function on the Interval |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mićović, M.; Malešević, B. Jordan-Type Inequalities and Stratification. Axioms 2024, 13, 262. https://doi.org/10.3390/axioms13040262
Mićović M, Malešević B. Jordan-Type Inequalities and Stratification. Axioms. 2024; 13(4):262. https://doi.org/10.3390/axioms13040262
Chicago/Turabian StyleMićović, Miloš, and Branko Malešević. 2024. "Jordan-Type Inequalities and Stratification" Axioms 13, no. 4: 262. https://doi.org/10.3390/axioms13040262
APA StyleMićović, M., & Malešević, B. (2024). Jordan-Type Inequalities and Stratification. Axioms, 13(4), 262. https://doi.org/10.3390/axioms13040262






