Dynamic Simulation of Cracked Spiral Bevel Gear Pair Considering Assembly Errors
Abstract
:1. Introduction
2. FE Model Description
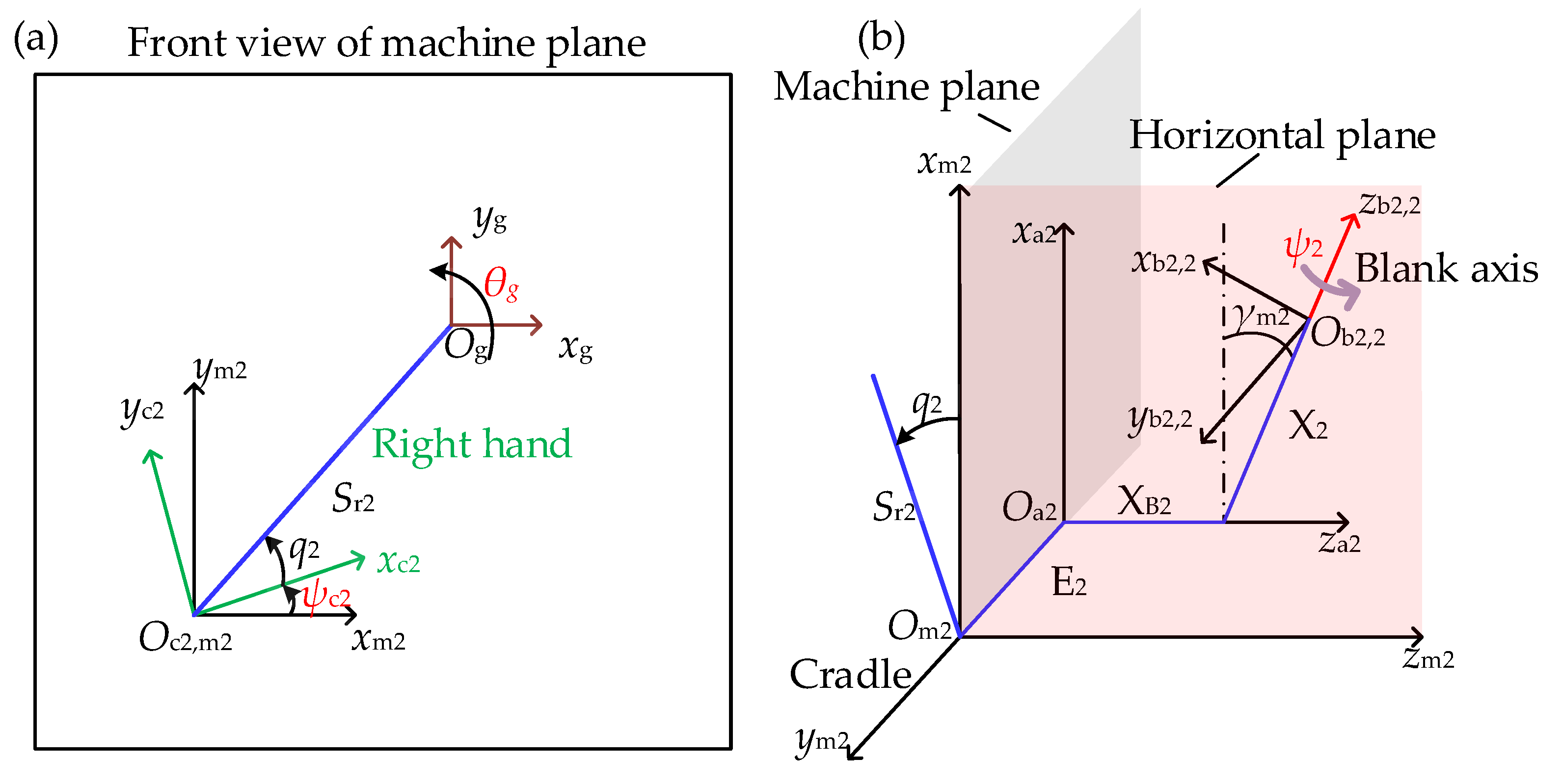
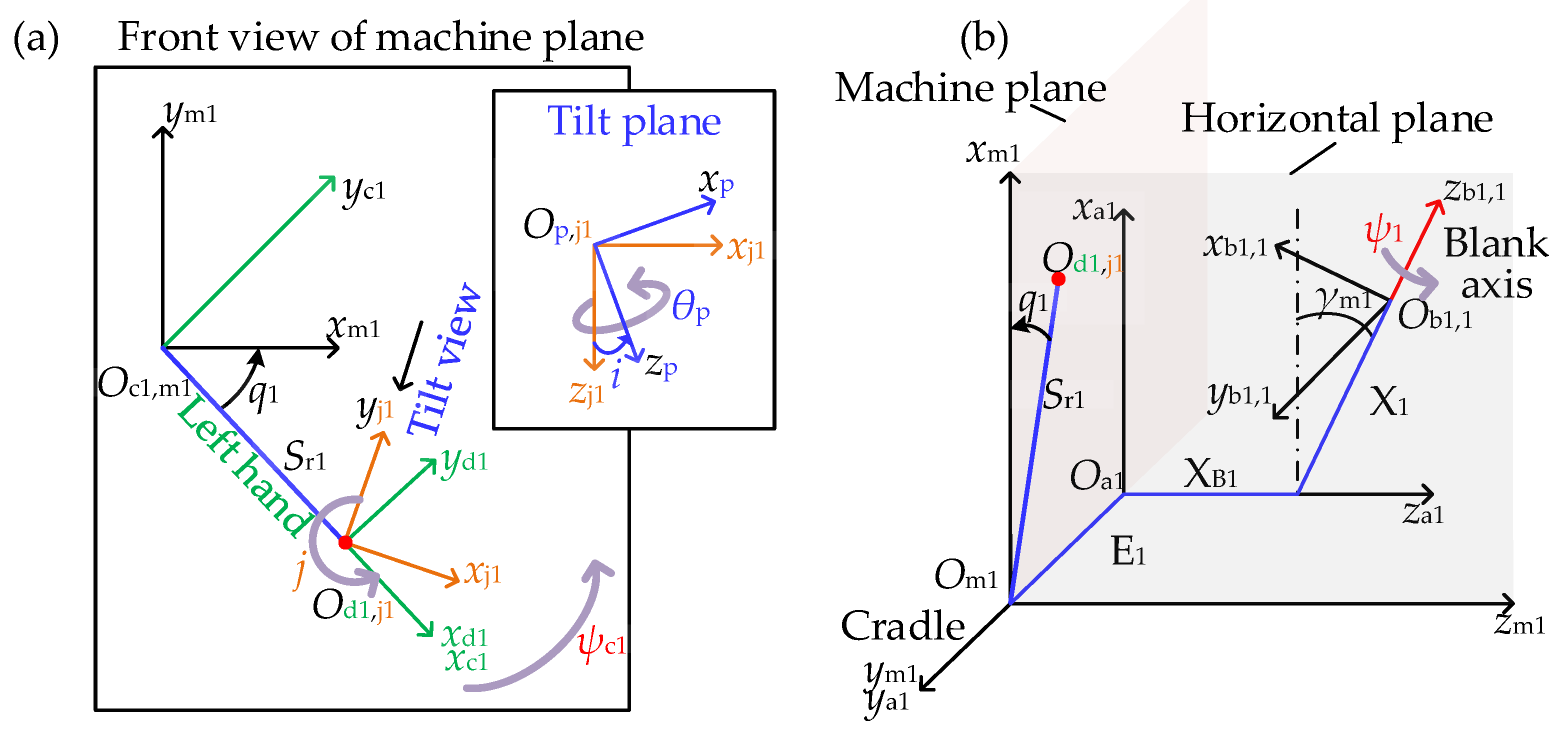
2.1. Tooth Contact Analysis Considering the Assembly Error
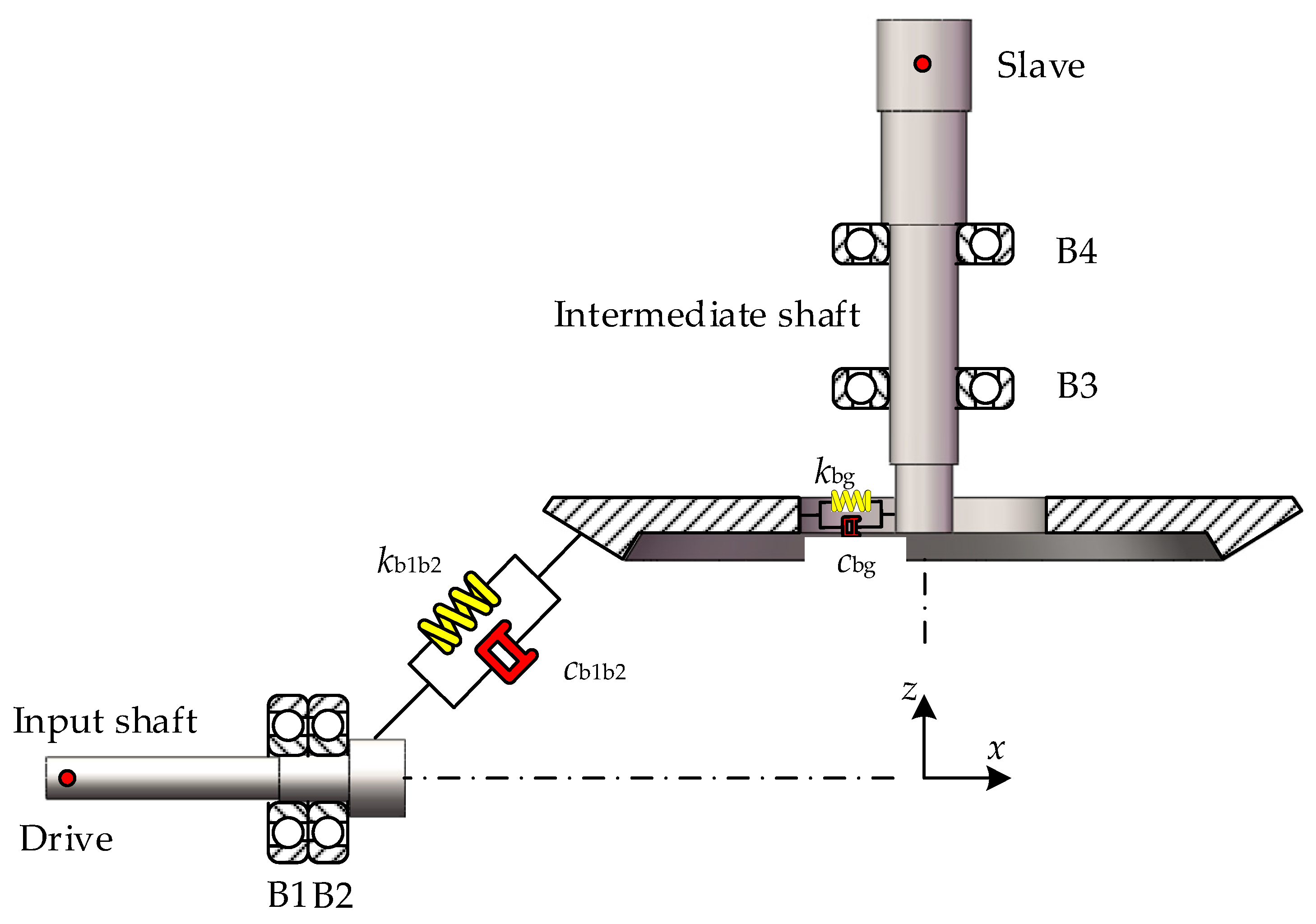
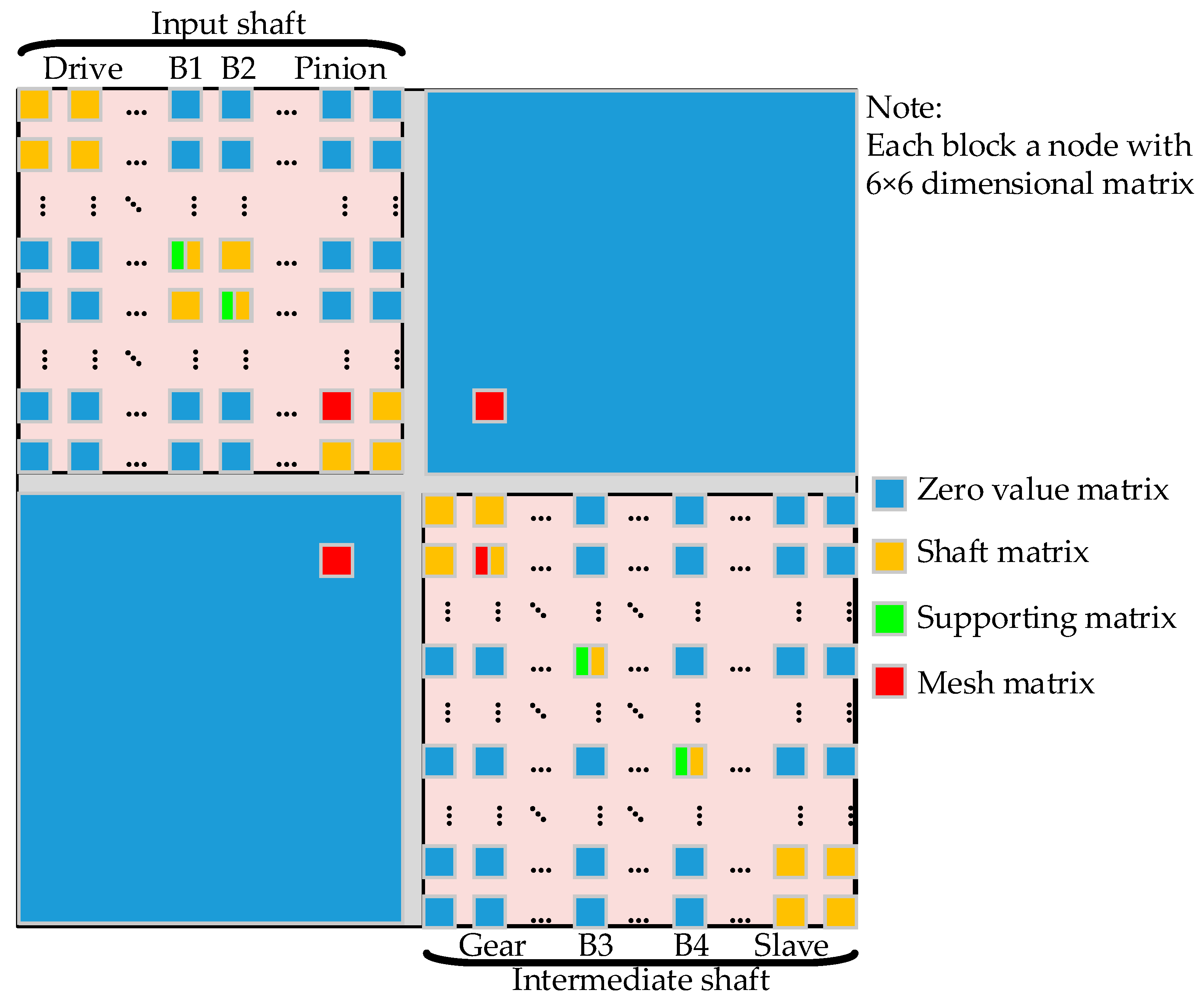
2.2. FE Modelling of the SBGP
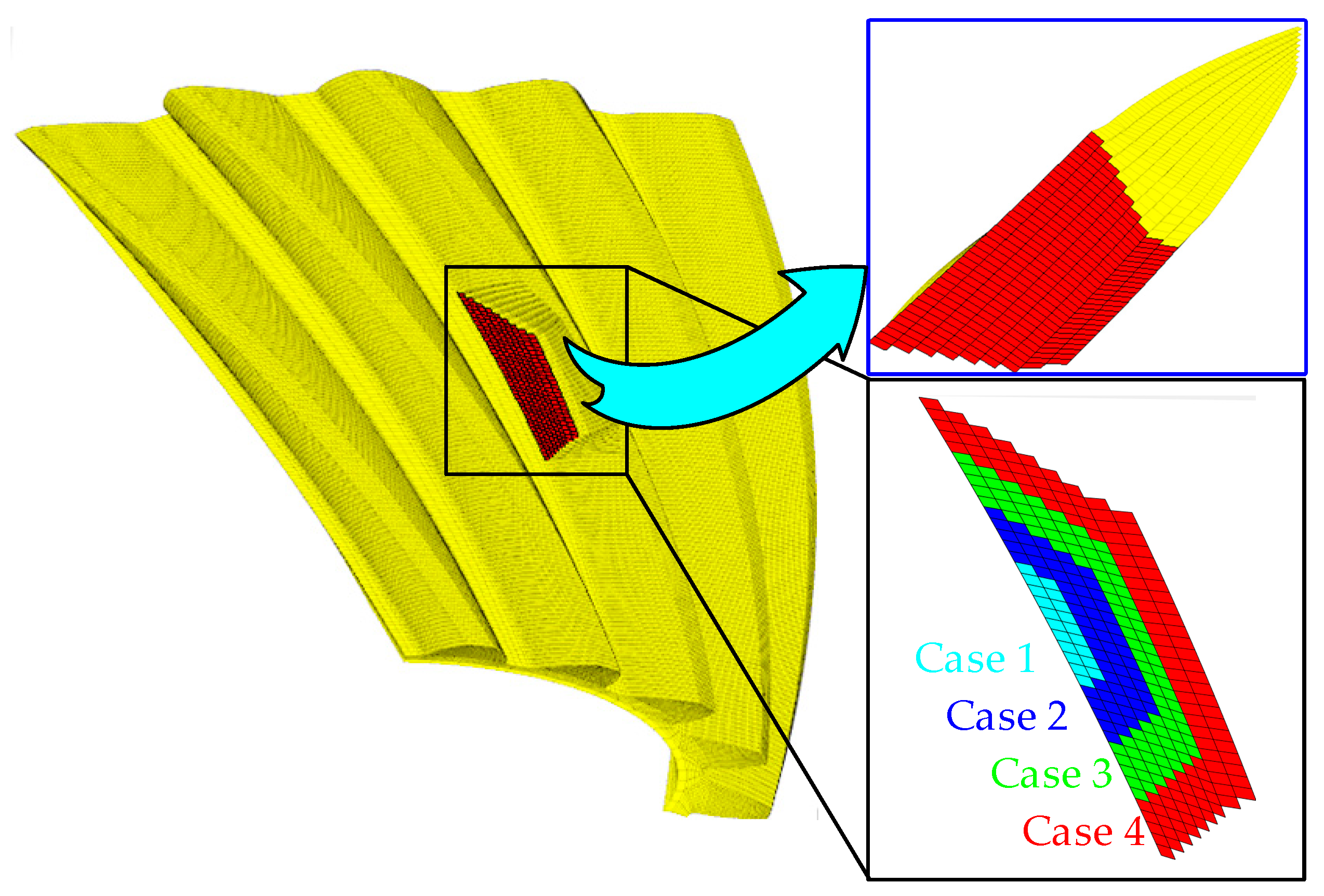
2.3. Tooth Root Crack Fault Simulation
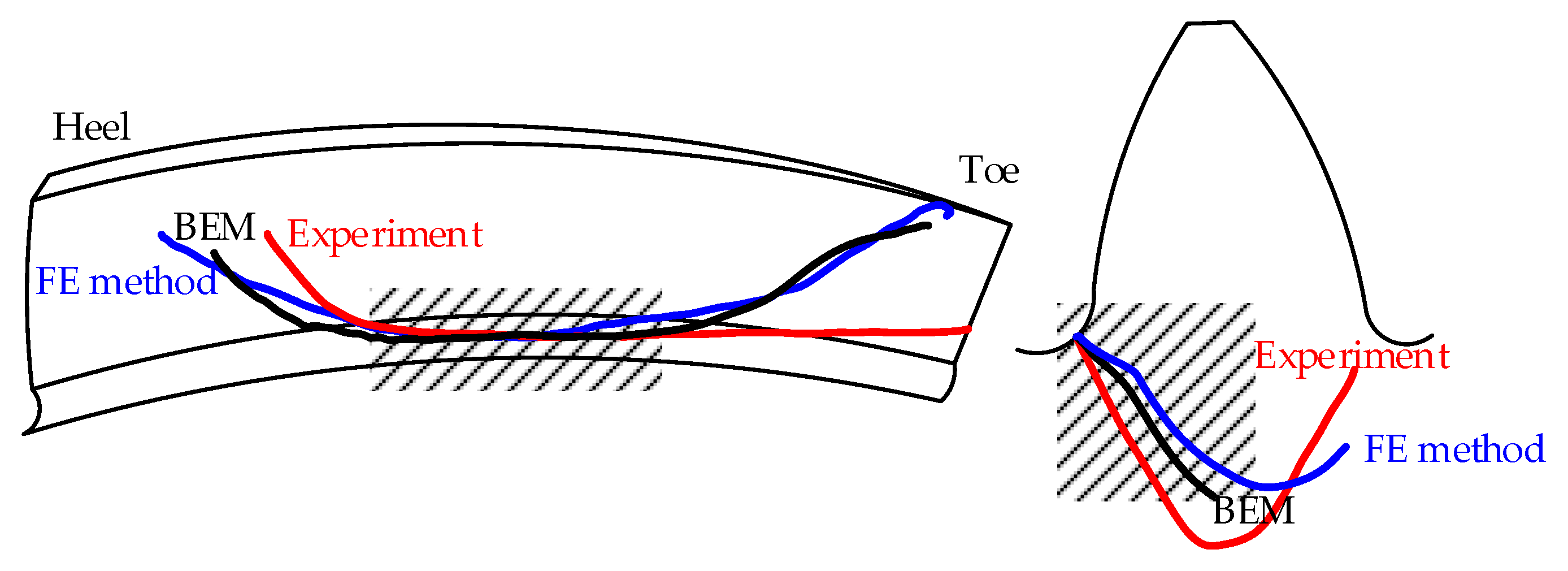
3. Results and Discussion
3.1. Influence of the Assembly Errors on the Tooth Root Stress Distribution
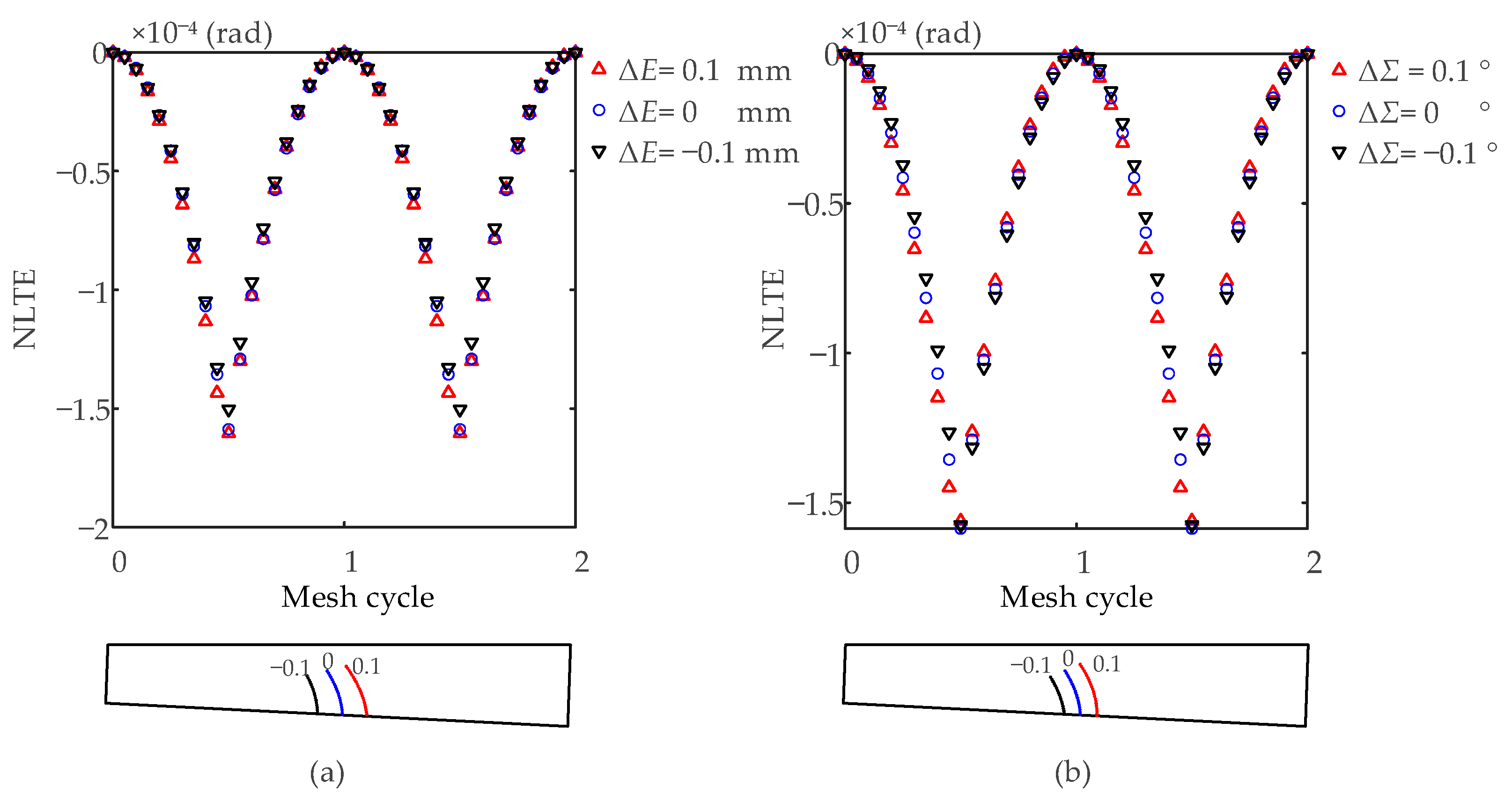
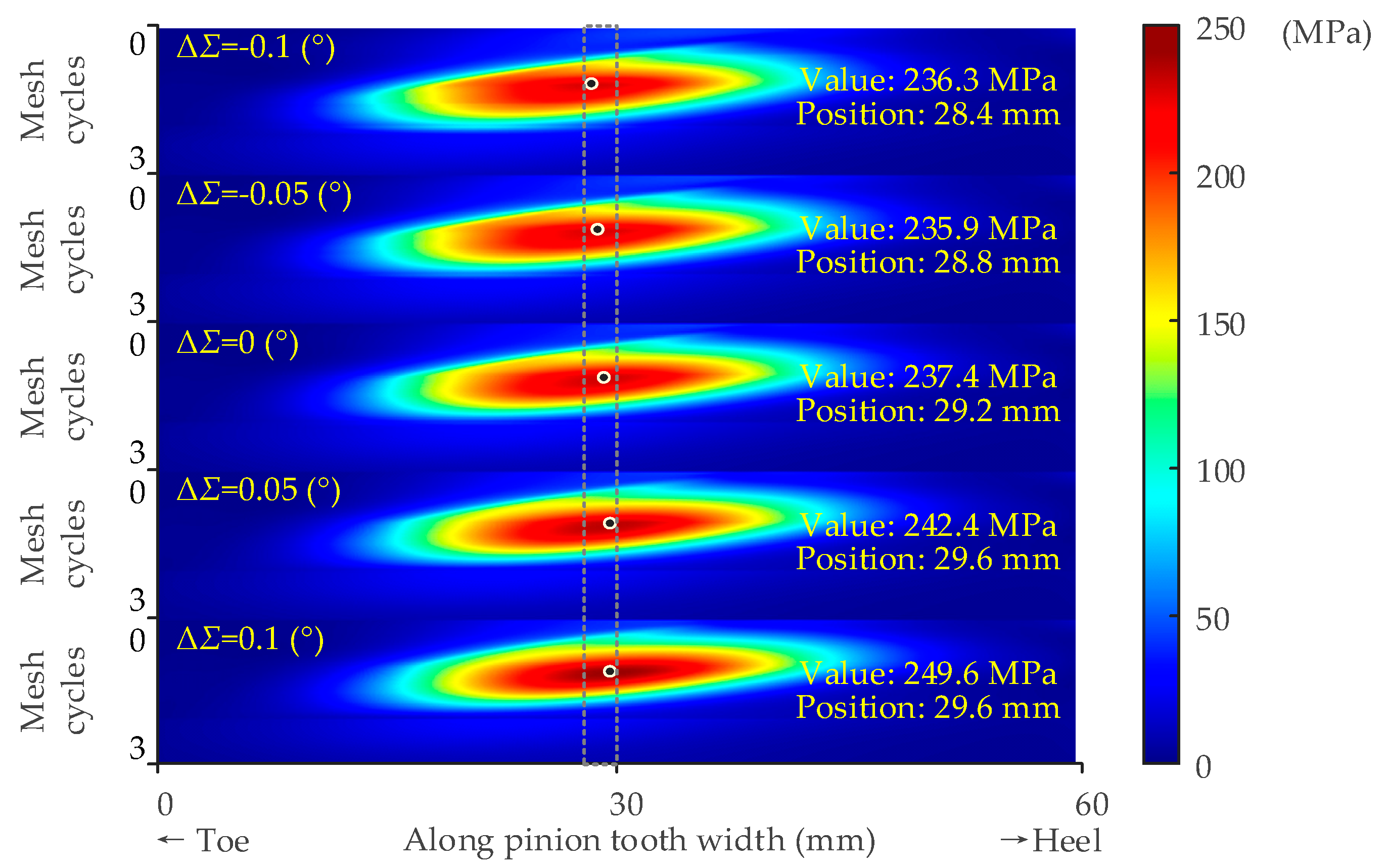
3.1.1. Offset Error
3.1.2. Shaft Angle Error
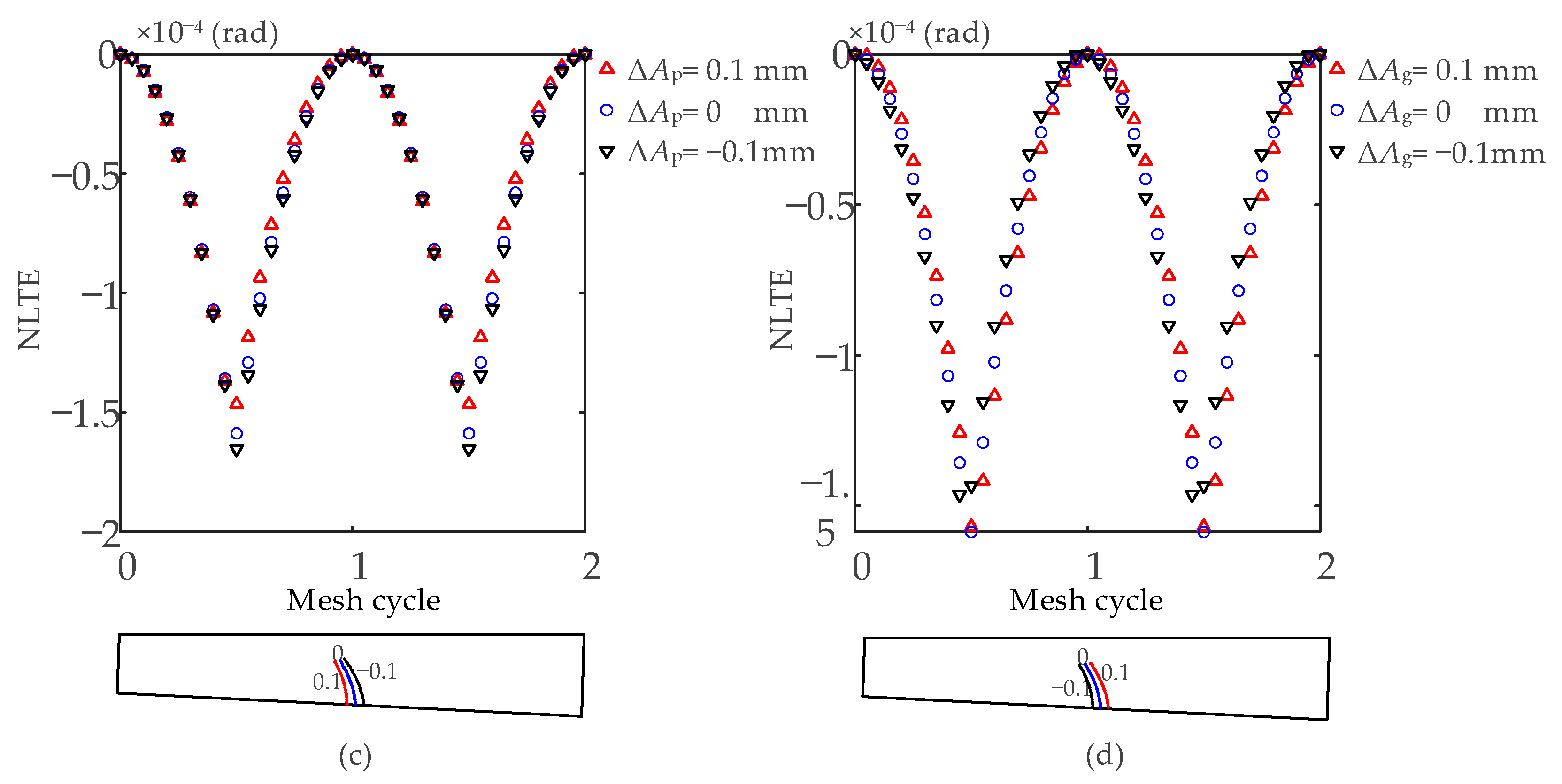
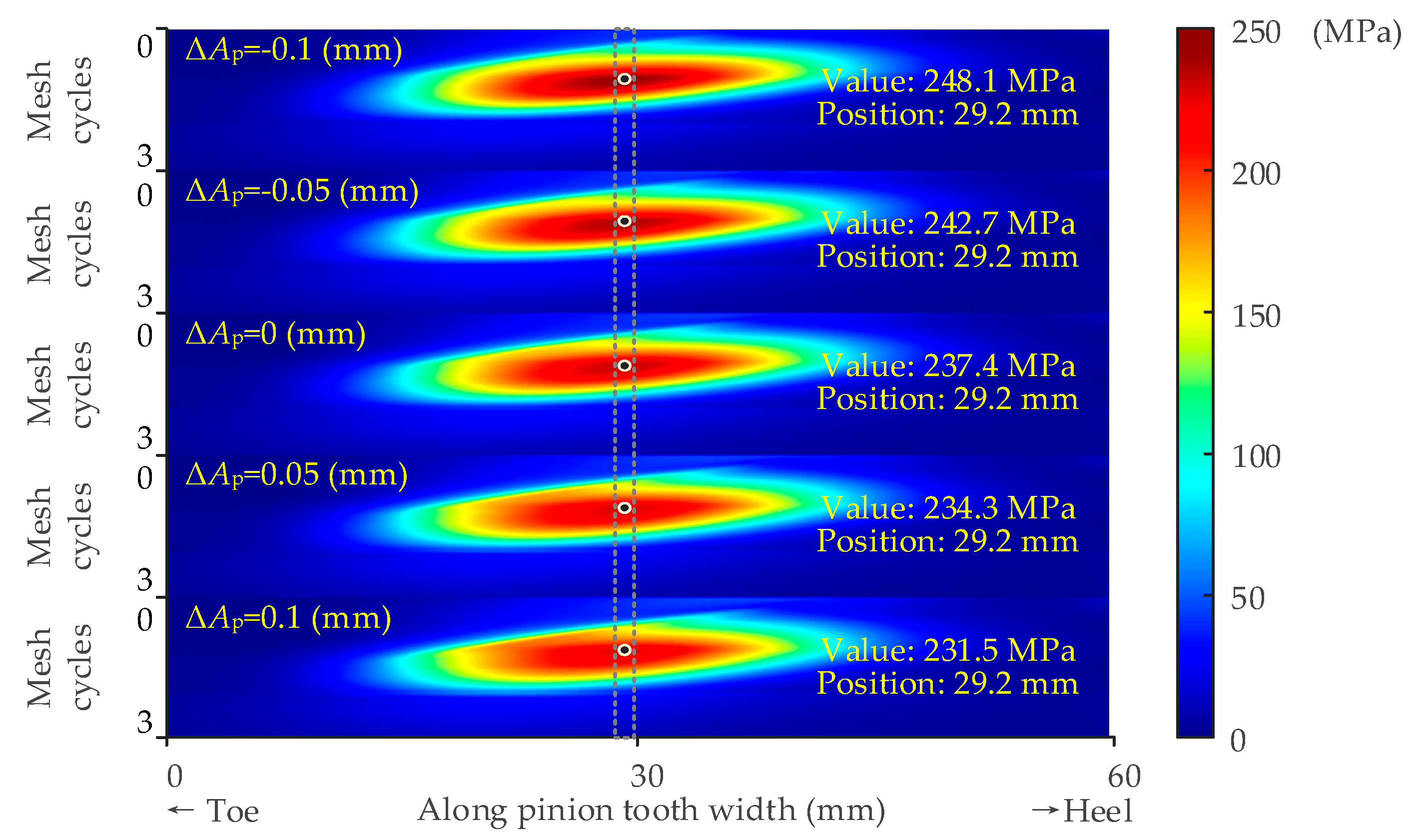
3.1.3. Pinion Axial Error
3.1.4. Gear Axial Error
3.2. Crack Fault Analysis of the SBGP
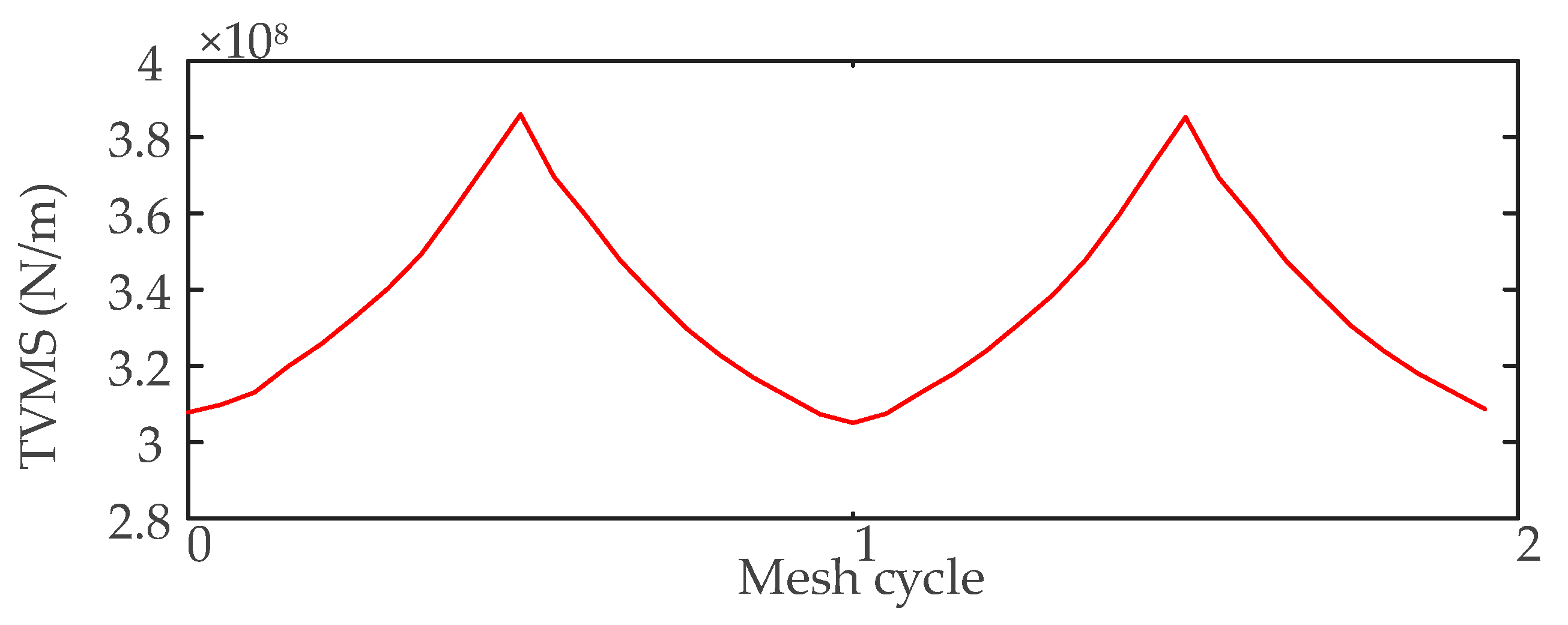
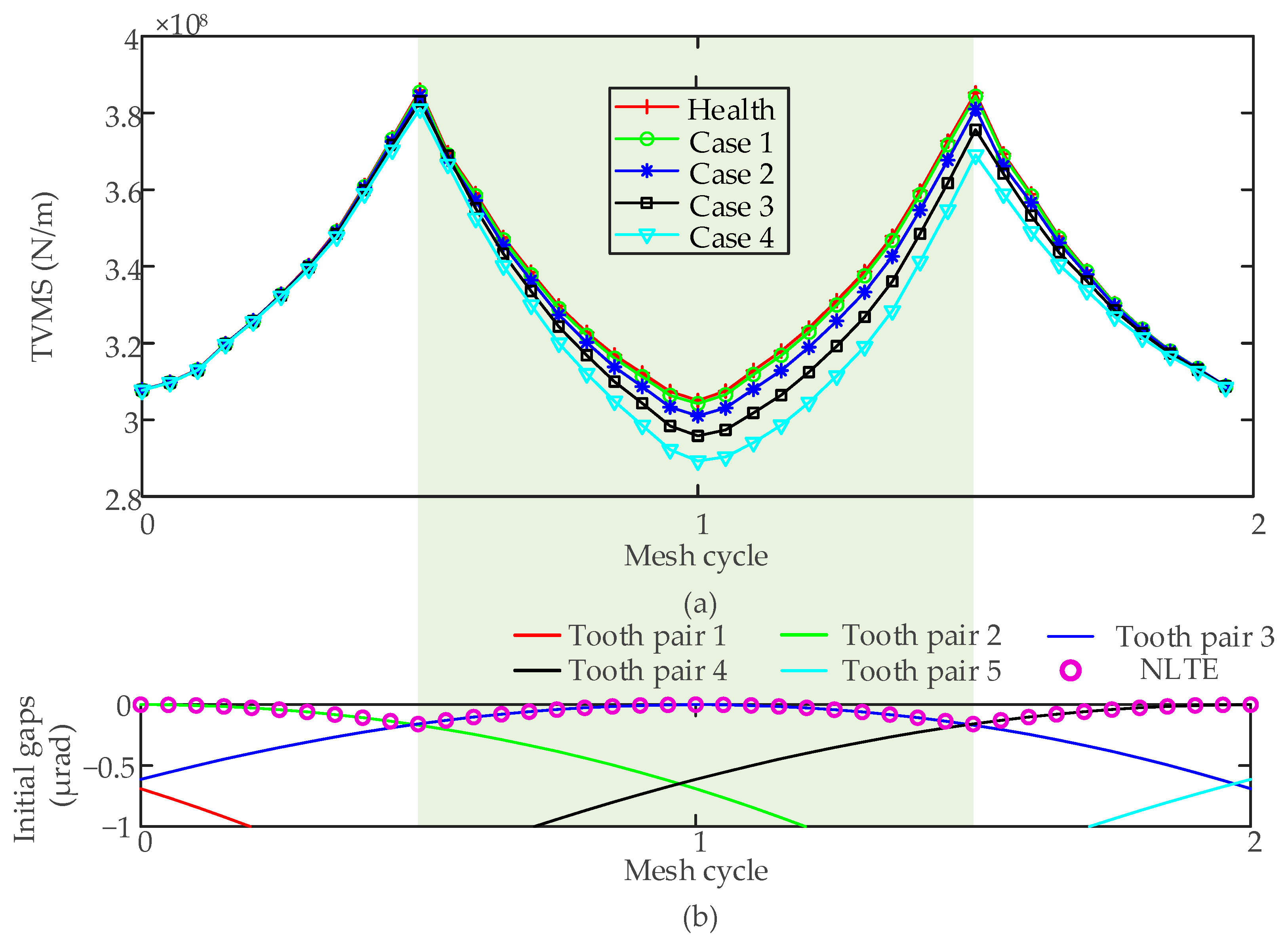
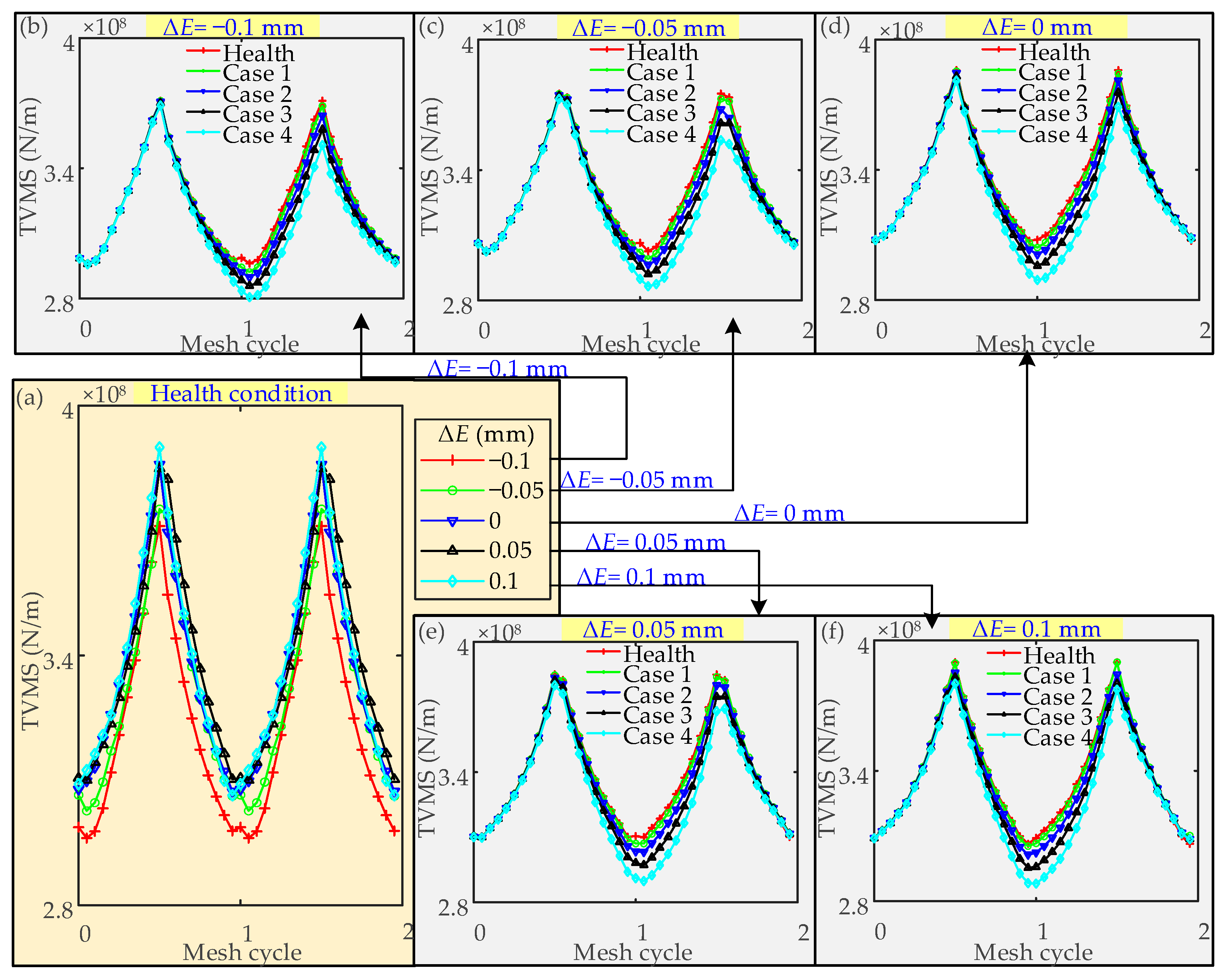
3.2.1. TVMS Due to the Crack Fault
3.2.2. Dynamic Simulation
3.2.3. Response Analysis Due to the Crack Fault of the SBGP
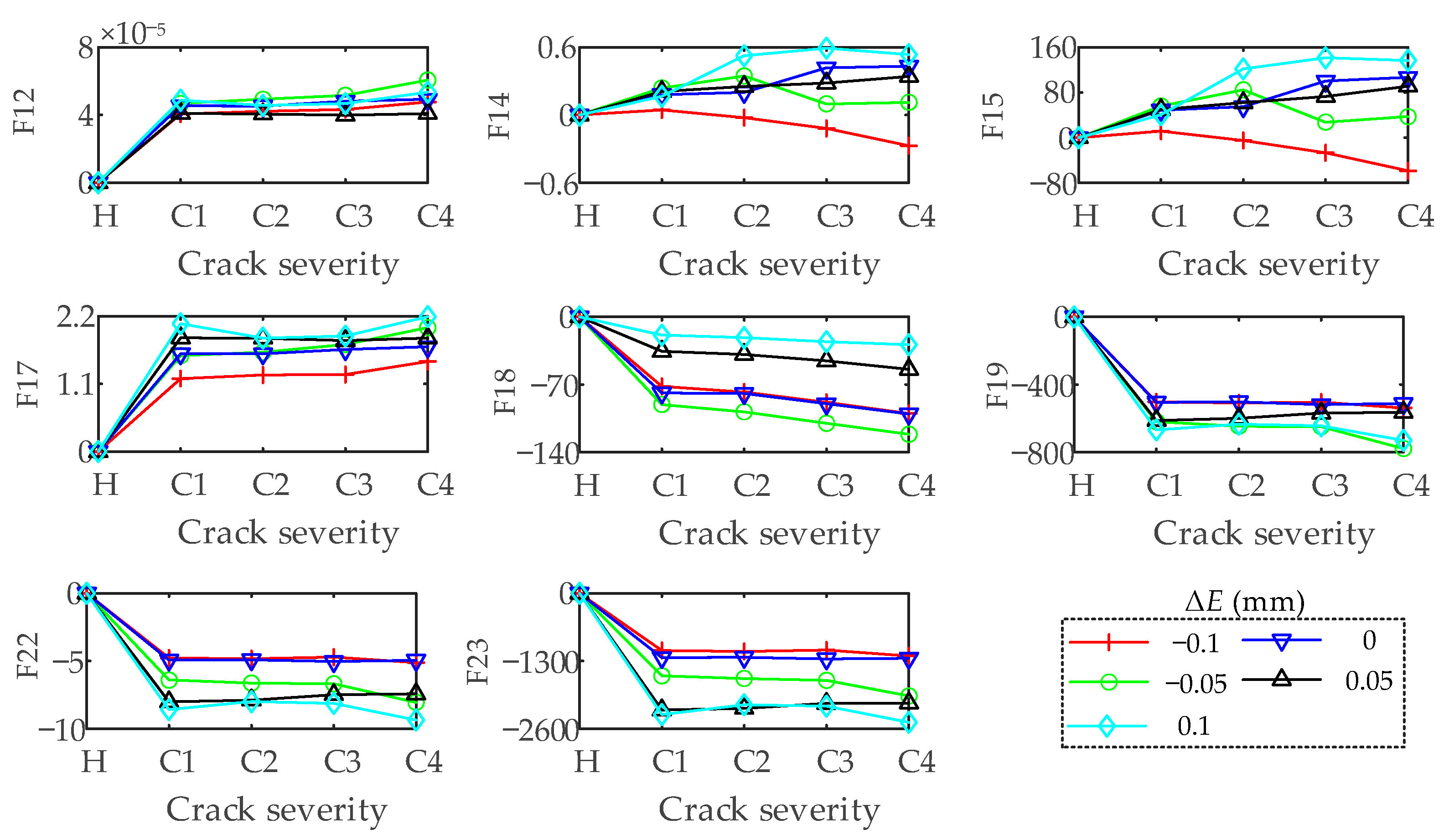
3.2.4. Sensitivity Analysis of Statistical Indicators under Healthy Condition
3.2.5. Crack Fault Detection under the Influence of the Offset Errors
4. Conclusions
- (1)
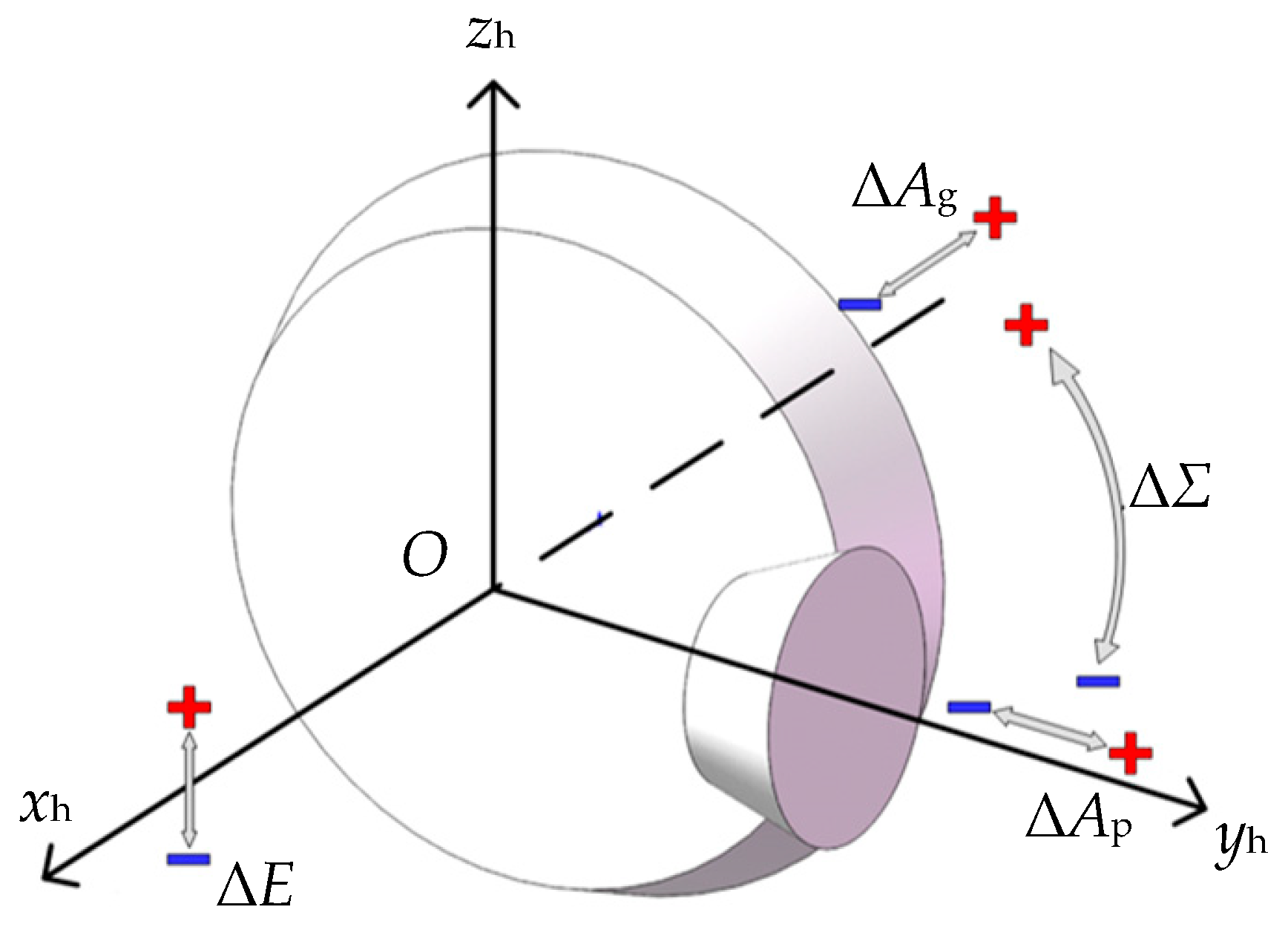
- Through static analysis, the value of the maximum tooth root stress and its position is discussed considering the assembly errors. It is found that the position of the maximum tooth root stress appears in the middle of the tooth width. The value is influenced by the assembly errors. To avoid excessive tooth root stress of the pinion, the changes in errors ΔE, ΔΣ and ΔAp should be strictly controlled. A smaller ΔE, ΔΣ, and a larger ΔAp are preferred to ease the pinion tooth root stress.
- (2)
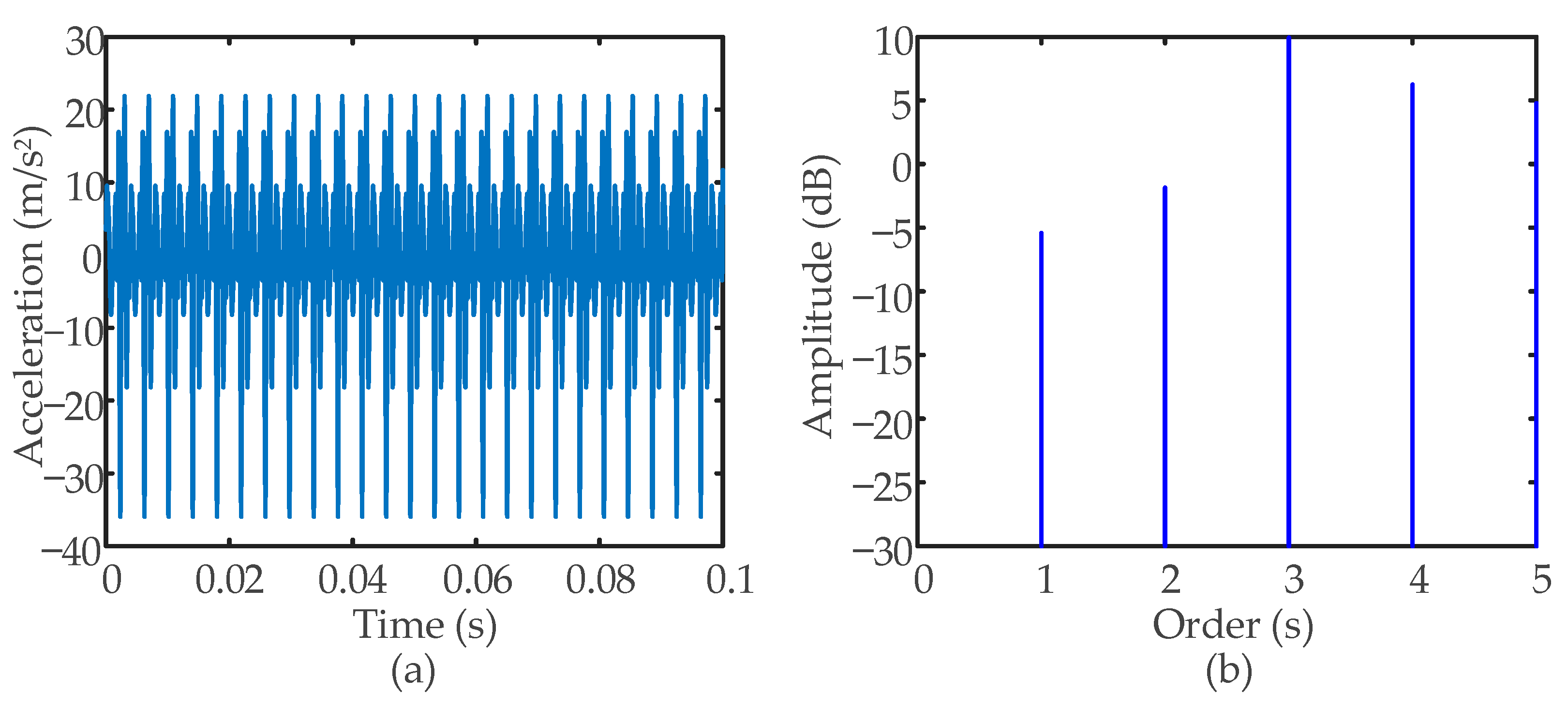
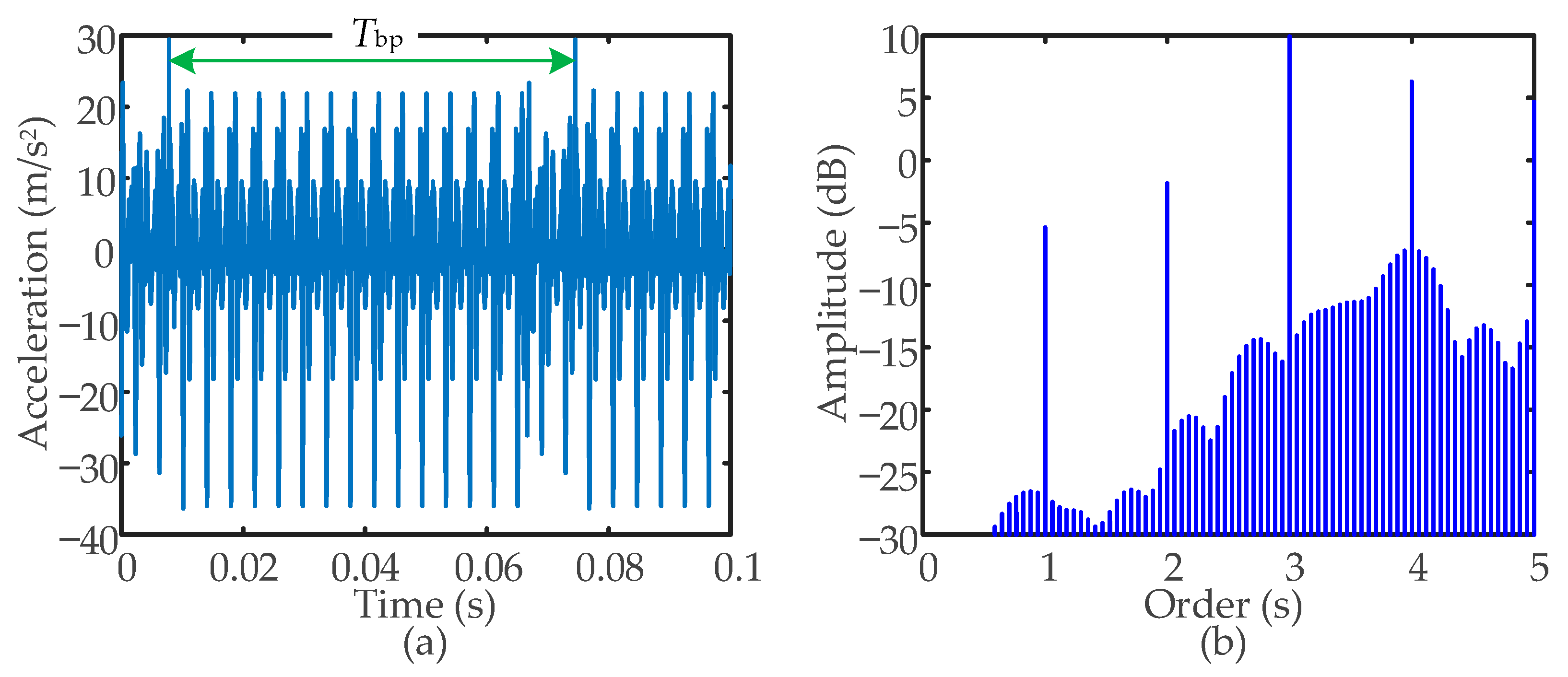
- The dynamic response of the SBGP with the pinion tooth root crack fault is obtained by introducing the faulty TVMS curve as the excitation. When a crack fault occurs on the pinion, every time the pinion revolves one cycle, the faulty tooth participates in meshing for two meshing periods. There are fluctuations at intervals of the pinion rotation period in the time-domain waveform. Each time the faulty tooth participates in meshing, there are three meshing cycle mutations in the time-domain waveform. In the faulty amplitude spectrum, under the influence of the crack fault, sidebands with the rotation frequency of the pinion as the interval appear on both sides of the meshing frequency and its harmonics.
- (3)
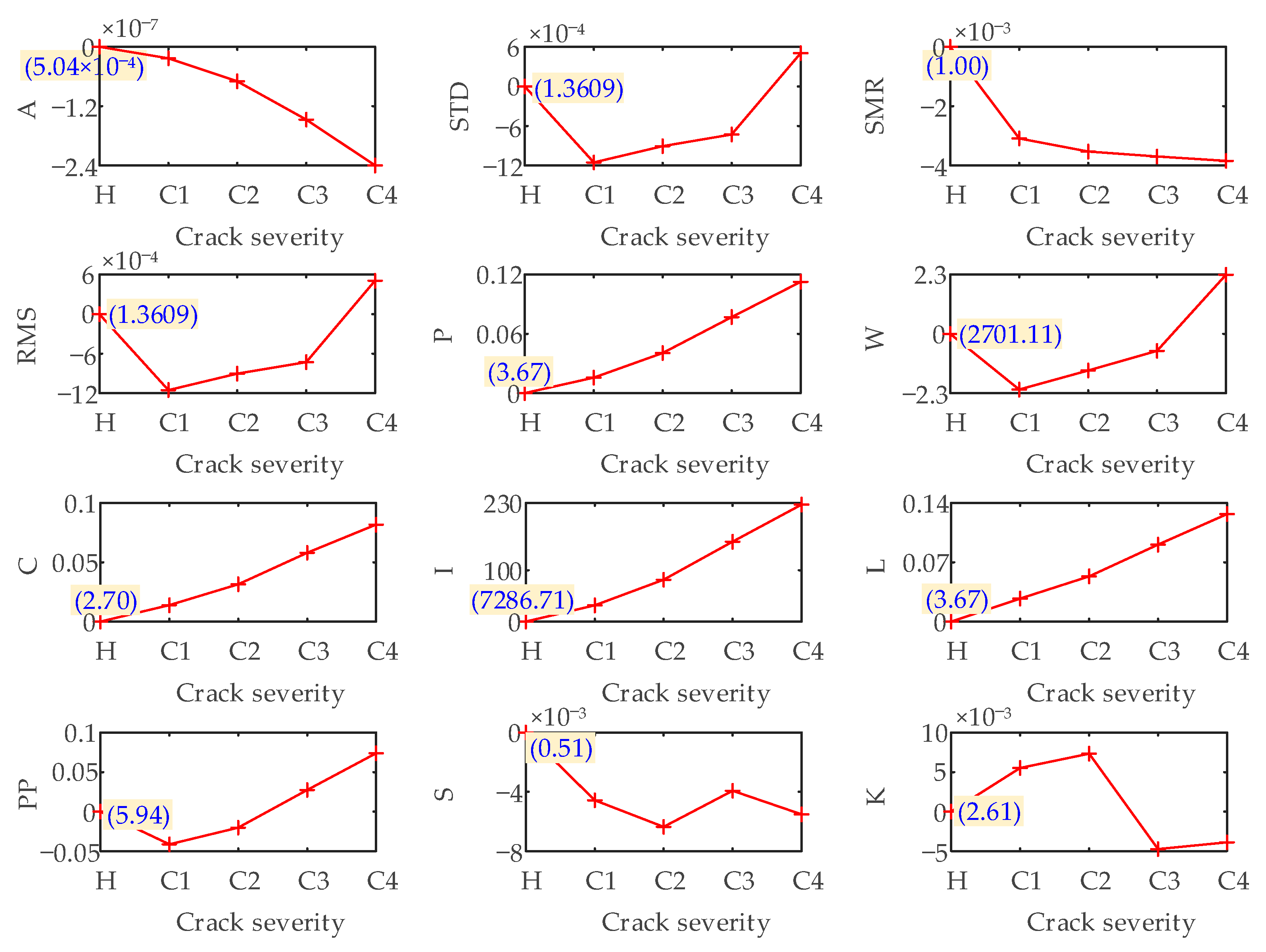
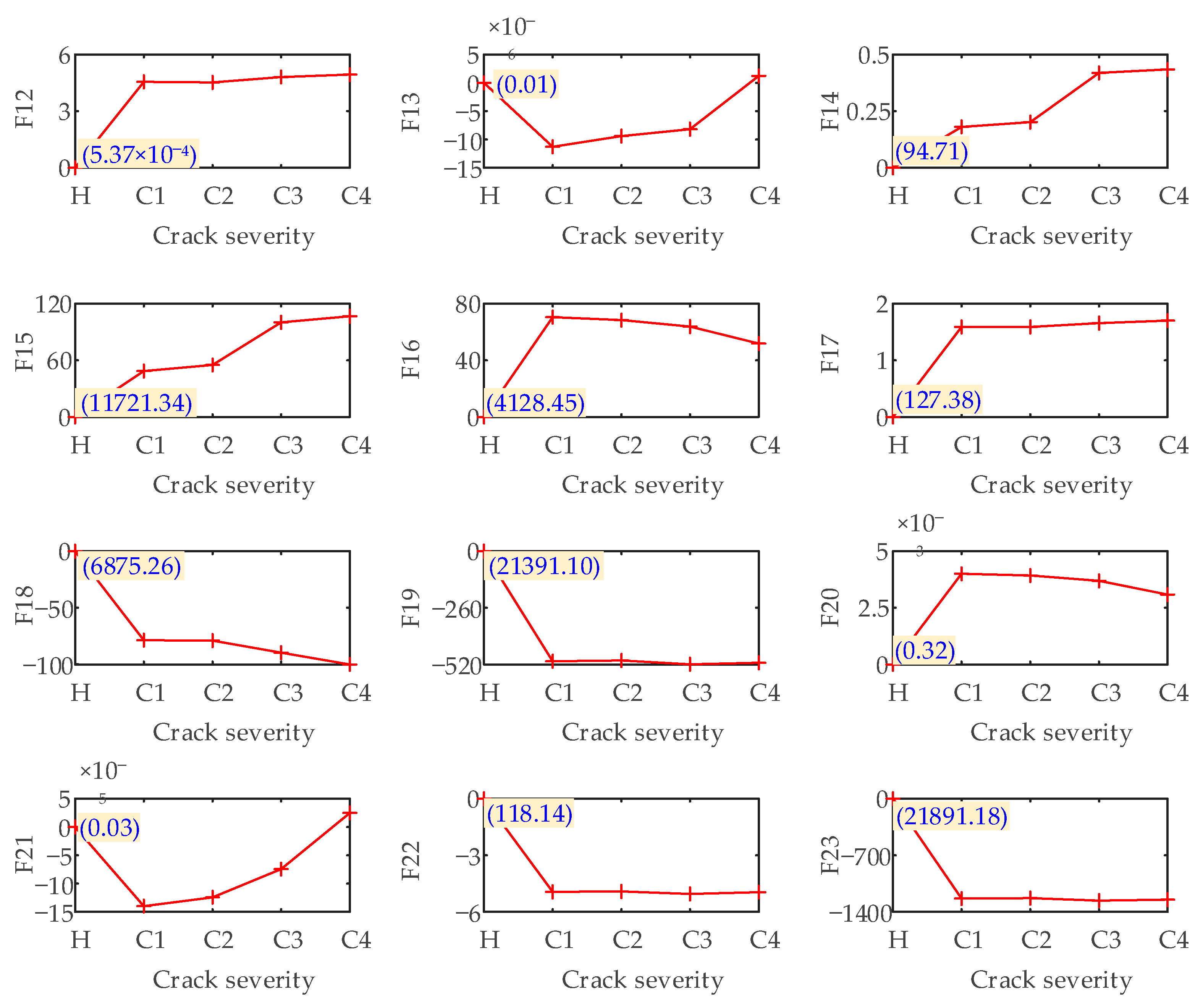
- Through the analysis of statistical indicators. The sensitive indicators for identifying the root crack of the pinion are obtained. They are the A, P, SMR, C, I, and L in the time-domain, and F12, F14, F16, F17, F18, F19, F20, F21, F22 and F23 in the frequency-domain. These indicators can be used to monitor and diagnose crack faults in the SBGP system under the assembly error free condition. Moreover, under the interference of offset error, the time-domain indicators A, P, C, I and L, and the frequency-domain indicators F12, F18 and F19 still maintain a good judgment threshold for fault information, so these indicators can be used as the indicators for diagnosing crack faults in the presence of offset errors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Kim, D.H.; Kim, J.H.; Kim, G.G.; Lee, Y.S. Random fatigue analysis of automotive bevel gear. Key Eng. Mater. 2006, 326–328, 987–990. [Google Scholar] [CrossRef]
- Park, M. Failure analysis of an accessory bevel gear installed on a J69 turbojet engine. Eng. Fail. Anal. 2003, 10, 371–382. [Google Scholar] [CrossRef]
- Spievak, L.E.; Wawrzynek, P.A.; Ingraffea, A.R.; Lewicki, D.G. Simulating fatigue crack growth in spiral bevel gears. Eng. Fract. Mech. 2001, 68, 53–76. [Google Scholar] [CrossRef] [Green Version]
- Lewicki, D.G.; Handschuh, R.F.; Spievak, L.E.; Wawrzynek, P.A.; Ingraffea, A.R. Consideration of moving tooth load in gear crack propagation predictions. J. Mech. Des. 2000, 123, 118–124. [Google Scholar] [CrossRef]
- Vukelic, G.; Pastorcic, D.; Vizentin, G.; Bozic, Z. Failure investigation of a crane gear damage. Eng. Fail. Anal. 2020, 115, 104613. [Google Scholar] [CrossRef]
- Ural, A.; Heber, G.; Wawrzynek, P.A.; Ingraffea, A.R.; Lewicki, D.G.; Neto, J.B.C. Three-dimensional, parallel, finite element simulation of fatigue crack growth in a spiral bevel pinion gear. Eng. Fract. Mech. 2005, 72, 1148–1170. [Google Scholar] [CrossRef]
- Böhme, S.A.; Vinogradov, A.; Papuga, J.; Berto, F. A novel predictive model for multiaxial fatigue in carburized bevel gears. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2033–2053. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Y.; Han, H.; Ma, H.; Wang, H.; Li, Z. Meshing Characteristics of Spur Gears Considering Three-Dimensional Fractal Rough Surface under Elastohydrodynamic Lubrication. Machines 2022, 10, 705. [Google Scholar] [CrossRef]
- Chen, K.; Huangfu, Y.; Ma, H.; Xu, Z.; Li, X.; Wen, B. Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech. Syst. Signal Process. 2019, 130, 273–292. [Google Scholar] [CrossRef]
- Huangfu, Y.; Chen, K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. Meshing and dynamic characteristics analysis of spalled gear systems: A theoretical and experimental study. Mech. Syst. Signal Process. 2020, 139, 106640. [Google Scholar] [CrossRef]
- Liu, Z.; Huangfu, Y.; Ma, H.; Peng, Z.; Zhu, J.; Wang, H.; Li, Z. Traveling wave resonance analysis of flexible spur gear system with angular misalignment. Int. J. Mech. Sci. 2022, 232, 107617. [Google Scholar] [CrossRef]
- Zhao, Z.; Han, H.; Wang, P.; Ma, H.; Zhang, S.; Yang, Y. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar] [CrossRef]
- Mu, Y.; Li, W.; Fang, Z.; Zhang, X. A novel tooth surface modification method for spiral bevel gears with higher-order transmission error. Mech. Mach. Theory 2018, 126, 49–60. [Google Scholar] [CrossRef]
- Mu, Y.; He, X. Design and dynamic performance analysis of high-contact-ratio spiral bevel gear based on the higher-order tooth surface modification. Mech. Mach. Theory 2021, 161, 104312. [Google Scholar] [CrossRef]
- Ding, H.; Tang, J.; Zhou, Y.; Zhong, J.; Wan, G. A multi-objective correction of machine settings considering loaded tooth contact performance in spiral bevel gears by nonlinear interval number optimization. Mech. Mach. Theory 2017, 113, 85–108. [Google Scholar] [CrossRef]
- Ding, H.; Tang, J.; Zhong, J. An accurate model of high-performance manufacturing spiral bevel and hypoid gears based on machine setting modification. J. Manuf. Syst. 2016, 41, 111–119. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations. J. Mech. Des. 2009, 132, 245–254. [Google Scholar]
- Hu, Z.; Ding, H.; Peng, S.; Tang, Y.; Tang, J. Numerical determination to loaded tooth contact performances in consideration of misalignment for the spiral bevel gears. Int. J. Mech. Sci. 2019, 151, 343–355. [Google Scholar] [CrossRef]
- Peng, S.; Ding, H.; Zhang, G.; Tang, J.; Tang, Y. New determination to loaded transmission error of the spiral bevel gear considering multiple elastic deformation evaluations under different bearing supports. Mech. Mach. Theory 2019, 137, 37–52. [Google Scholar] [CrossRef]
- Bibel, G.D.; Kumar, A.; Reddy, S.; Handschuh, R. Contact stress analysis of spiral bevel gears using finite element analysis. J. Mech. Des. 1995, 117, 235–240. [Google Scholar] [CrossRef]
- Argyris, J.; Fuentes, A.; Litvin, F.L. Computerized integrated approach for design and stress analysis of spiral bevel gears. Comput. Methods Appl. Mech. Eng. 2002, 191, 1057–1095. [Google Scholar] [CrossRef]
- Gonzalez-Perez, I.; Fuentes-Aznar, A. Reverse engineering of spiral bevel gear drives reconstructed from point clouds. Mech. Mach. Theory 2022, 170, 104694. [Google Scholar] [CrossRef]
- Hou, X.; Fang, Z.; Zhang, X. Static contact analysis of spiral bevel gear based on modified VFIFE (vector form intrinsic finite element) method. Appl. Math. Model. 2018, 60, 192–207. [Google Scholar] [CrossRef]
- Gan, L.; Xiao, K.; Wang, J.; Pu, W.; Cao, W. A numerical method to investigate the temperature behavior of spiral bevel gears under mixed lubrication condition. Appl. Ther. Eng. 2019, 147, 866–875. [Google Scholar] [CrossRef]
- Fu, Y.; Zhuo, Y.; Zhou, X.; Wan, B.; Lv, H.; Wang, Z. Theoretical and experimental study on contact characteristics of spiral bevel gears under quasi-static and large loading conditions. Appl. Sci. 2020, 10, 5109. [Google Scholar] [CrossRef]
- Hou, X.; Fang, Z.; Fu, X.; Zhang, X. Meshing performance of spiral bevel gear with different loads and modules considering edge contact by finite element method. Trans. Can. Soc. Mech. Eng. 2019, 43, 322–332. [Google Scholar] [CrossRef]
- Wang, P.-Y.; Fan, S.-C.; Huang, Z.-G. Spiral bevel gear dynamic contact and tooth impact analysis. J. Mech. Des. 2011, 133, 084501. [Google Scholar] [CrossRef]
- Guo, W.; Mao, S.; Yang, Y.; Kuang, Y. Optimization of cutter blade profile for face-hobbed spiral bevel gears. Int. J. Adv. Manuf. Technol. 2015, 85, 209–216. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, W.; Chen, Y.; Wang, T.; Li, G.; Ball, A.D. Investigation into the meshing friction heat generation and transient thermal characteristics of spiral bevel gears. Appl. Ther. Eng. 2017, 119, 245–253. [Google Scholar] [CrossRef]
- Yang, D.; Chen, L.; Jiang, L.; Wang, P.; Tao, J. Research on the influence of time-varying excitation on vibration characteristics of the spiral bevel geared transmission system with broken teeth. Shock Vib. 2021, 2021, 8880851. [Google Scholar] [CrossRef]
- Ding, H.; Tang, J.; Zhong, J.; Zhou, Z. A hybrid modification approach of machine-tool setting considering high tooth contact performance in spiral bevel and hypoid gears. J. Manuf. Syst. 2016, 41, 228–238. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Han, H.; Zhang, S.; Yang, Y.; Ma, H.; Jiang, L. Modulation sidebands analysis of coupled bevel gear pair and planetary gear train system. Mech. Mach. Theory 2022, 176, 104979. [Google Scholar] [CrossRef]
- Tayyab, S.M.; Chatterton, S.; Pennacchi, P. Fault Detection and Severity Level Identification of Spiral Bevel Gears under Different Operating Conditions Using Artificial Intelligence Techniques. Machines 2021, 9, 173. [Google Scholar] [CrossRef]

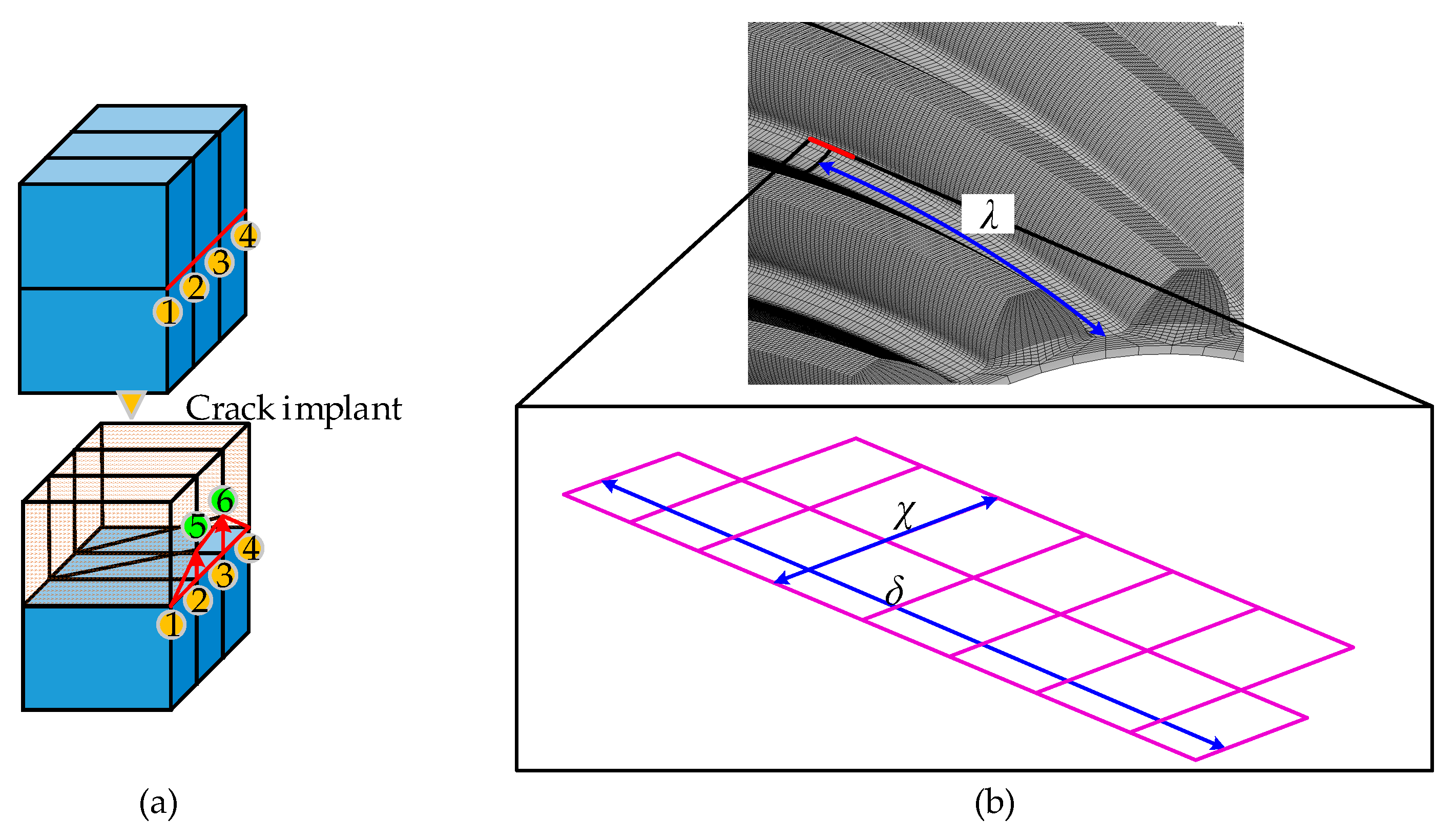

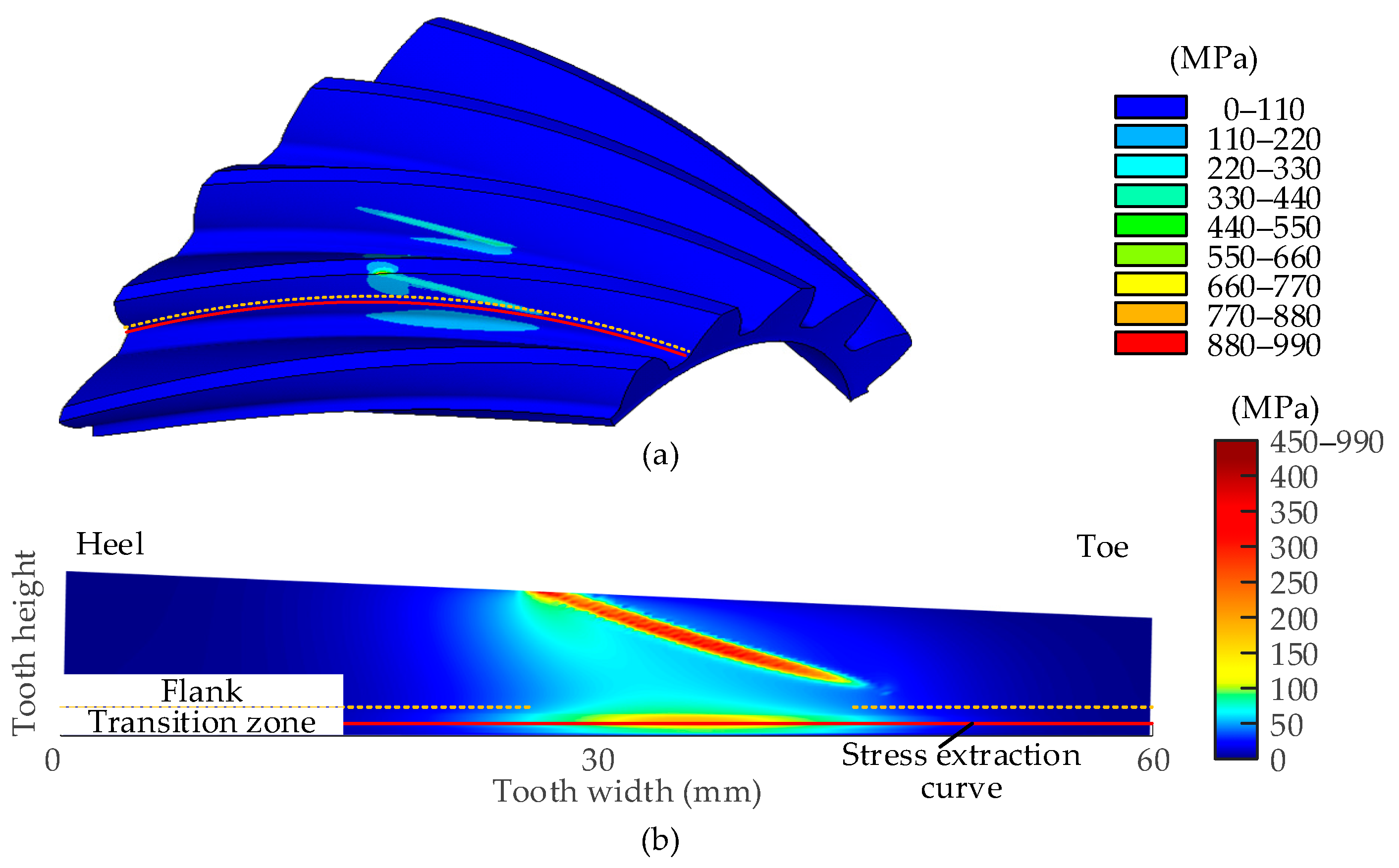



| Parameter | Bevel Pinion | Bevel Gear |
|---|---|---|
| Tooth number z1/z2 | 17 | 81 |
| Modulus m (mm)/Shaft angle Σ (°)/Mean spiral angle β (°) | 5.6/90/35 | |
| Direction of rotation | Left-handed | Right-handed |
| Face width b (mm) | 60 | |
| Mean cone distance R (mm) | 201.741 | |
| Pitch angle δ (°) | 11.8530 | 78.1470 |
| Root angle δf (°) | 10.9321 | 76.1944 |
| Face angle δa (°) | 13.8056 | 79.0679 |
| Addendum height ha (mm) | 6.8480 | 2.6720 |
| Dedendum height hf (mm) | 3.7250 | 7.9010 |
| Parameter | Concave | Convex |
|---|---|---|
| Cutter point radius r01 (mm) | 226.47 | 230.86 |
| Pressure angle α01 (°) | −18.75 | 21.25 |
| Root fillet radius ρ01 (mm) | 1 | 1 |
| Machine center to back X1 (mm) | −5.237 | 8.545 |
| Sliding base XB1 (mm) | 15.217 | 13.183 |
| Blank offset E1 (mm) | 3 | 3.5 |
| Radial distance Sr1 (mm) | 197.762 | 209.634 |
| Machine root angle γm1 (°) | 7.7936 | 10.05 |
| Cradle angle q1 (°) | 71.6258 | 67.3267 |
| Tilt Angle i (°) | 2.7343 | 3 |
| Swivel angle j (°) | 286.2802 | 227.2839 |
| Velocity ratio i1 | 4.6799 | 5.2574 |
| Parameter | Value |
|---|---|
| Cutter point radius r02 (mm) | 229.975(concave)/227.225(convex) |
| Pressure angle α02 (°) | −19(concave)/21(convex) |
| Root fillet radius ρ02 (mm) | 1.6 |
| Machine center to back X2 (mm) | 0 |
| Sliding base XB2 (mm) | 0 |
| Blank offset E2 (mm) | 0 |
| Radial distance Sr2 (mm) | 200.091 |
| Machine root angle γm2 (°) | 76.1944 |
| Cradle angle q2 (°) | 69.3682 |
| Velocity ratio i2 | 1.0212 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| λ (mm) | 29.2 | 29.2 | 29.2 | 29.2 |
| δ (mm) | 4.43 | 8.46 | 12.48 | 16.51 |
| χ (mm) | 1.78 | 4.45 | 6.23 | 8.02 |
| Name | Equation | Name | Equation |
|---|---|---|---|
| Average (A) | Crest (C) | ||
| Standard deviation (STD) | Impulse (I) | ||
| Square mean root (SMR) | Clearance (L) | ||
| Root mean square (RMS) | Peak-to-peak (PP) | ||
| Peak (P) | Skewness (S) | ||
| Waveform (W) | Kurtosis (K) |
| Name | Equation | Name | Equation |
|---|---|---|---|
| F12 | F18 | ||
| F13 | F19 | ||
| F14 | F20 | ||
| F15 | F21 | ||
| F16 | F22 | ||
| F17 | F23 |
| ΔE = −0.1 mm | ΔE = −0.05 mm | ΔE = 0 mm | ΔE = 0.05 mm | ΔE = 0.1 mm | |
|---|---|---|---|---|---|
| λ (mm) | 27.2 | 28.0 | 29.2 | 30.4 | 30.8 |
| ΔE = −0.1 mm | ΔE = −0.05 mm | ΔE = 0 mm | ΔE = 0.05 mm | ΔE = 0.1 mm | |
|---|---|---|---|---|---|
| Relative Error Max/Min (%) | |||||
| Case 1 | 0.02/1.31 | 0.03/1.20 | 0.03/1.02 | 0.07/0.95 | 0.09/1.34 |
| Case 2 | 0.14/2.13 | 0.18/2.06 | 0.35/2.06 | 0.40/2.22 | 1.23/1.63 |
| Case 3 | 0.30/3.46 | 0.31/3.50 | 0.75/3.75 | 0.71/4.14 | 1.79/3.60 |
| Case 4 | 0.60/5.23 | 0.65/5.34 | 1.25/5.89 | 1.29/6.52 | 2.53/5.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Ma, H.; Wang, H.; Zhu, J.; Li, Z.; Liu, Z. Dynamic Simulation of Cracked Spiral Bevel Gear Pair Considering Assembly Errors. Machines 2022, 10, 929. https://doi.org/10.3390/machines10100929
Han H, Ma H, Wang H, Zhu J, Li Z, Liu Z. Dynamic Simulation of Cracked Spiral Bevel Gear Pair Considering Assembly Errors. Machines. 2022; 10(10):929. https://doi.org/10.3390/machines10100929
Chicago/Turabian StyleHan, Hongzheng, Hui Ma, Haixu Wang, Jiazan Zhu, Zhanwei Li, and Zimeng Liu. 2022. "Dynamic Simulation of Cracked Spiral Bevel Gear Pair Considering Assembly Errors" Machines 10, no. 10: 929. https://doi.org/10.3390/machines10100929








