Research on Stiffness Identification Method for Complex Joints Based on Modal Correlation Analysis
Abstract
:1. Introduction
2. Materials and Methods
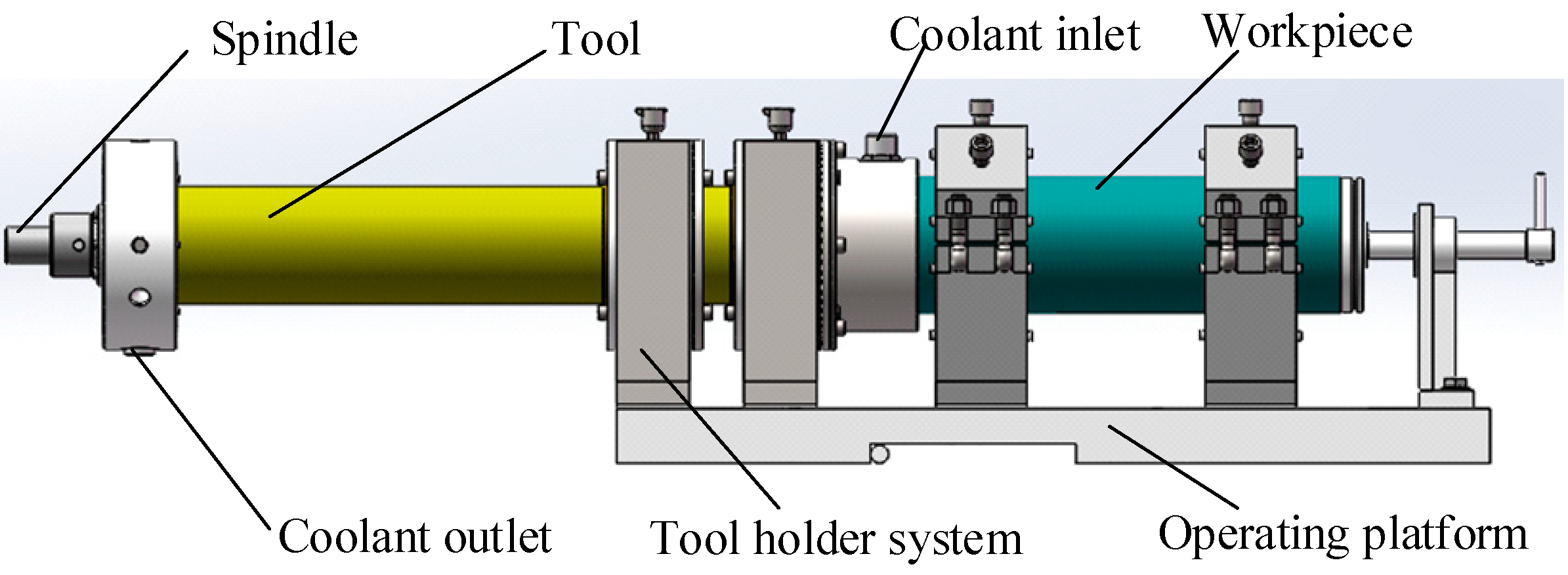
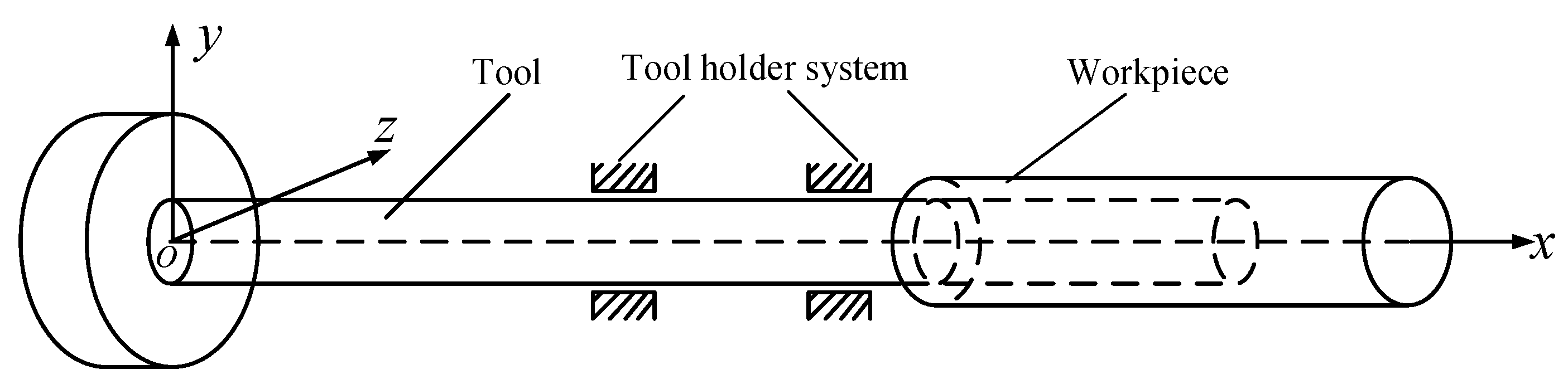
2.1. Model Profile
2.2. Modal Correlation Theory
- Frequency correlation: The natural frequency is the basic attribute of the modal parameters of the structure, and it is easier to measure accurately than the modal shape, so the frequency correlation is more widely used. The correlation is usually expressed as:where: is the coefficient of correlation, is the calculated mode frequency, is the experimental mode frequency.
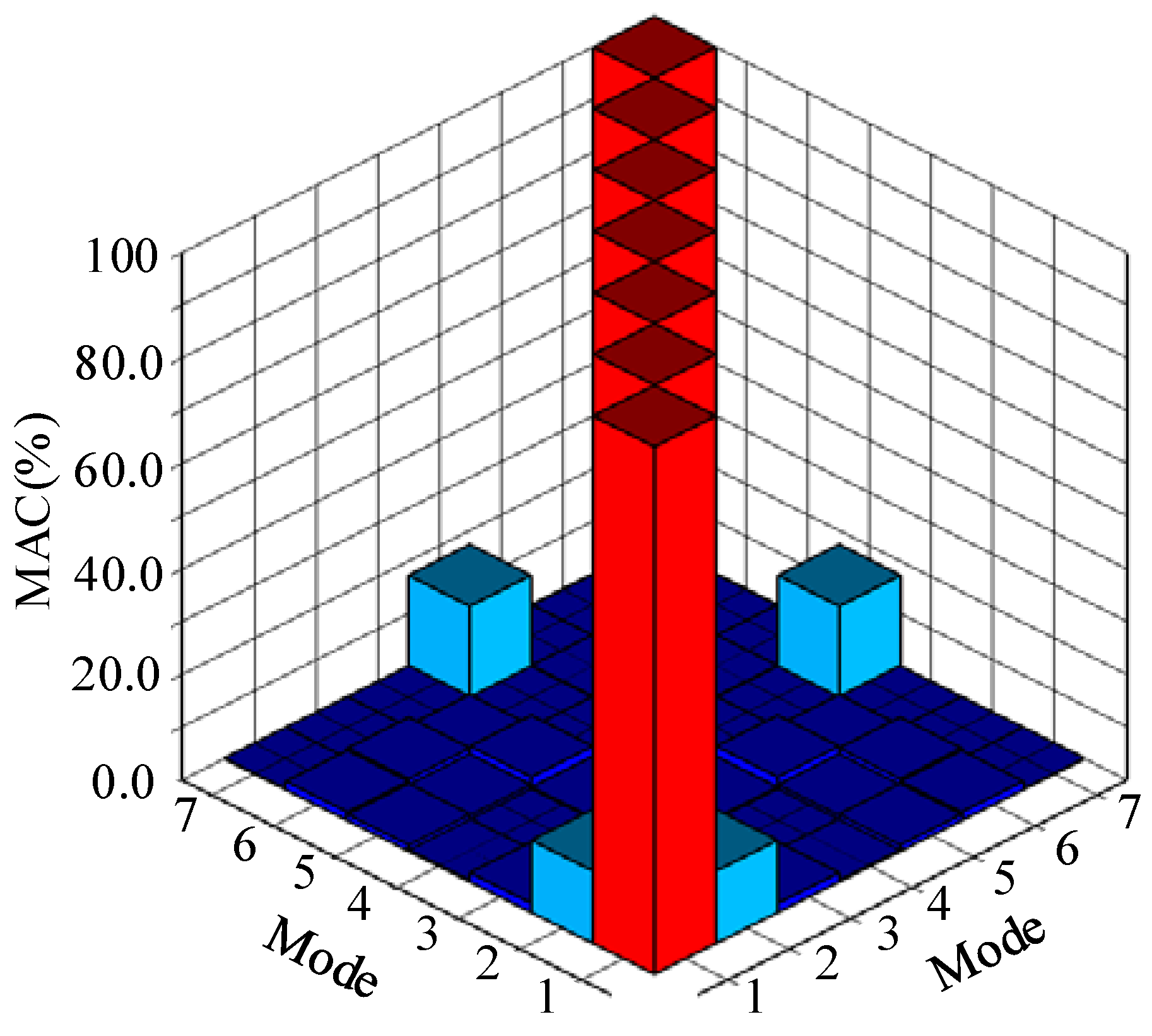
- Vibration mode correlation: While the modal shape is a description of structural vibration displacement in space, modal frequency is a description of structural vibration characteristics in time. Only by combining them can a complete description of structural vibration be achieved and the accuracy of the model correction be improved. The modal assurance criterion (MAC) value between the experimental and finite element modal vectors can be obtained by the following equation:where: is the modal vector of a EMA modal shape; is the transpose of ; is the modal vector of a FEA modal shape; is the transpose of .
3. Results
3.1. Experimental Modal Analysis (EMA)
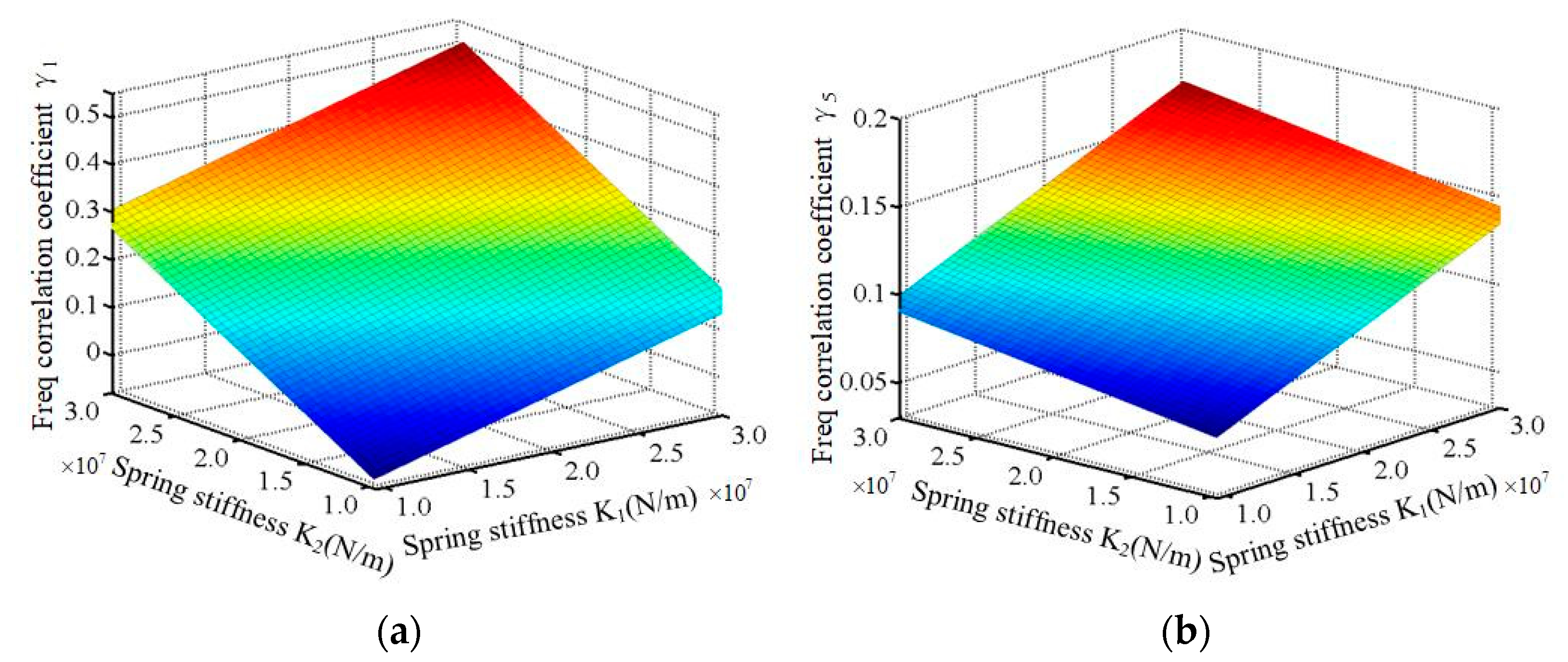
3.2. Frequency Correlation Analysis
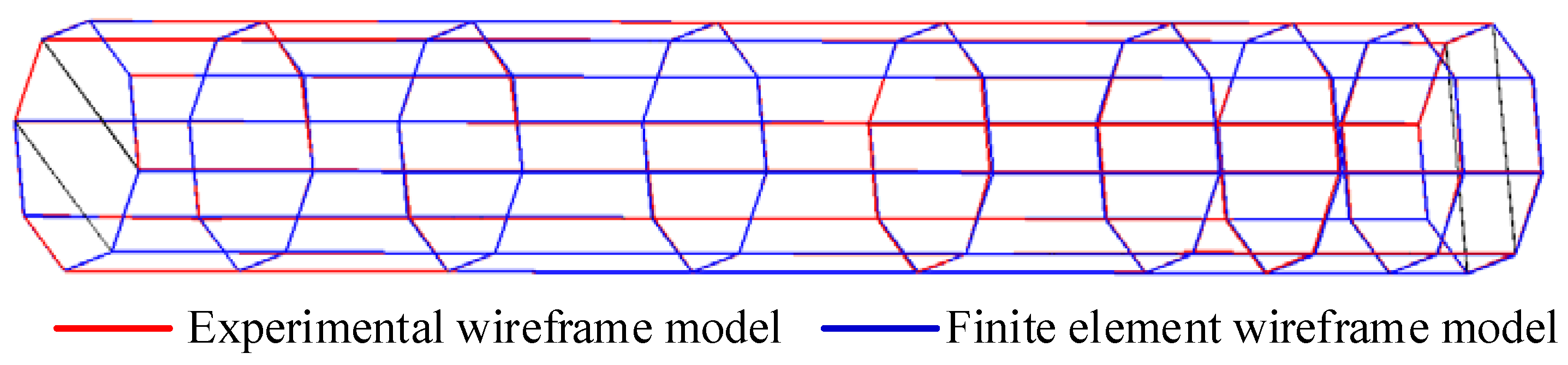
3.3. Modal Shape Correlation Analysis
4. Discussion
5. Conclusions
- (1)
- Compared with the current research on the identification of joint parameters, which focuses on the equivalent distribution of spring units or the parameter setting of virtual material physical properties for a typical, single joint, this paper focuses on the three contact surfaces formed by four components and their influence on the structural system as a whole, simplifying the connection relationship between the three joints and the specific situation of individual joints. At the same time, in the selection of experimental objects, all components forming the joint, are not taken as the experimental objects, but the components significantly affected by the parameters of the joint are taken as the experimental objects. The method is quite convenient to use in engineering. It can effectively avoid the errors caused by too many harsh assumptions in analytical modeling, especially since the advantages of parameter identification for complex and multiple joints are more pronounced and the errors meet the requirements of engineering use.
- (2)
- When the position of the radial spring unit is determined, the magnitude of its stiffness affects the overall mode of the trepanning drill tool, while the local mode of the tool is only affected by the position of the radial spring unit, independent of its size.
- (3)
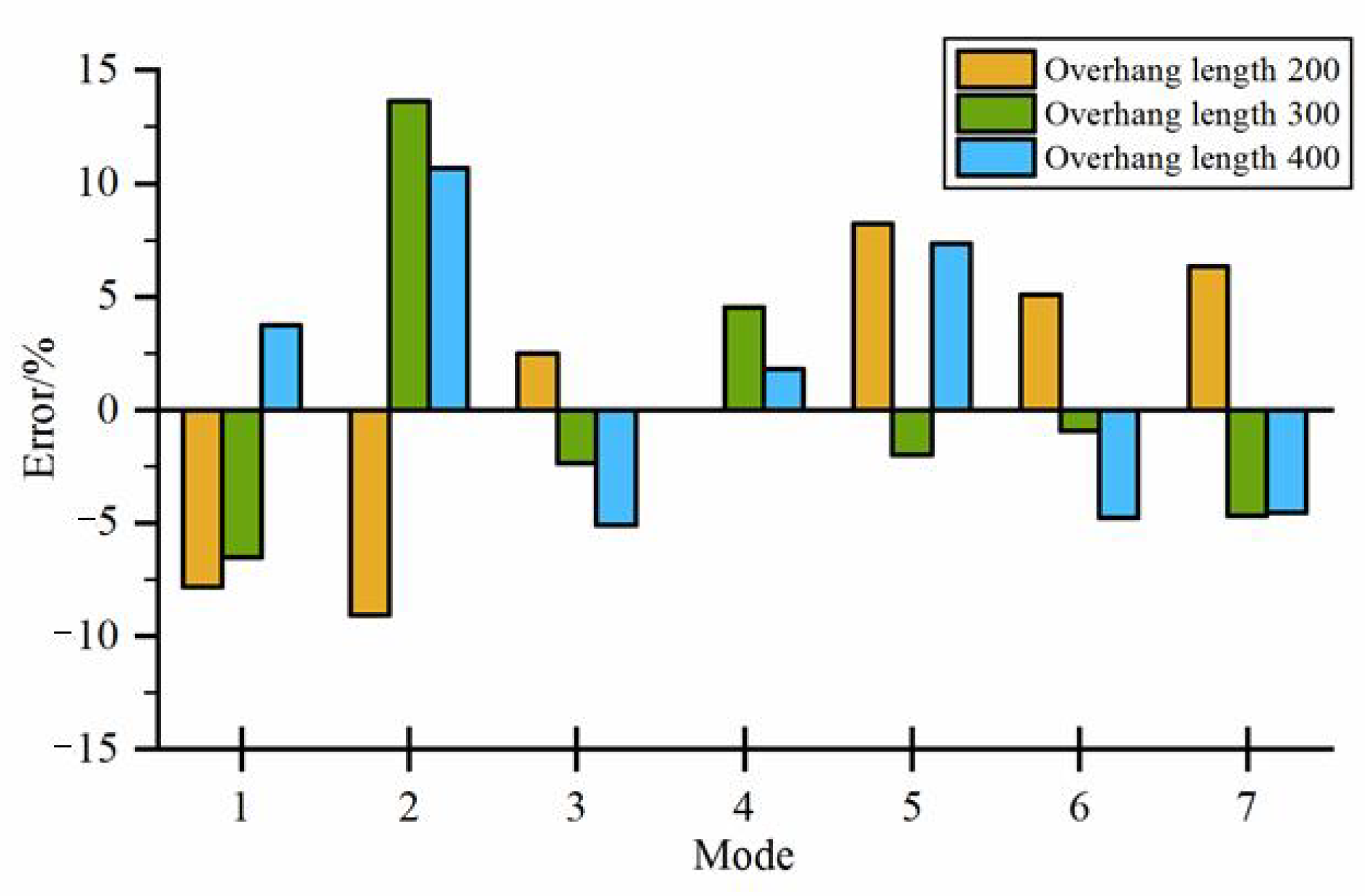
- The error analysis results show that, except for the second mode, the natural frequency errors of other modes are less than 10%. In Figure 2, it can be seen that there are many gaps on the tool head and the thickness of the teeth is slightly thicker than the tool body, which is extremely unfavorable to the finite element modeling and it is impossible to realize the modal experiment on this part. Therefore, this part is simplified in the finite element modeling and modal experiments. This simplification only changes the structural form of the tool head and does not change the overall structural form of the tool. It does not affect the accuracy of the model on other parts of the tool. In Table 5, the structural deformation of the second-order mode occurs precisely in the tool head. Therefore, the larger error in the second-order natural frequency is a normal situation due to the local simplification of the tool head in both finite element modeling and the modal experiments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ibrahim, R.A.; Pettit, C.L. Uncertainties and dynamic problems of bolted joints and other fasteners. J. Sound Vib. 2005, 279, 857–936. [Google Scholar] [CrossRef]
- Zaman, I.; Khalid, A.; Manshoor, B.; Araby, S.; Ghazali, M.I. The effects of bolted joints on dynamic response of structures. IOP Conf. Ser. Mater. Sci. Eng. 2013, 50, 012018. [Google Scholar] [CrossRef] [Green Version]
- Adel, F.; Shokrollahi, S.; Jamal-Omidi, M.; Ahmadian, H. A model updating method for hybrid composite/aluminum bolted joints using modal test data. J. Sound Vib. 2017, 396, 172–185. [Google Scholar] [CrossRef]
- Shamine, D.M.; Hong, S.W.; Shin, Y.C. Experimental Identification of Dynamic Parameters of Rolling Element Bearings in Machine Tools. J. Dyn. Syst. Meas. Control 2000, 122, 95–101. [Google Scholar] [CrossRef]
- Zhang, G.P.; Huang, Y.M.; Shi, W.H.; Fu, W.P. Predicting dynamic behaviours of a whole machine tool structure based on computer-aided engineering. Int. J. Mach. Tools Manuf. 2003, 43, 699–706. [Google Scholar] [CrossRef]
- Li, L.; Etsion, I.; Ovcharenko, A.; Talke, F.E. The Onset of Plastic Yielding in a Spherical Shell Compressed by a Rigid Flat. J. Appl. Mech. 2011, 78, 011016. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. Int. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-Plastic Contact Between Rough Surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Nobari, A.S.; Robb, D.A.; Ewins, D.J. A new approach to modal-based structural dynamic model updating and joint identification. Mech. Syst. Signal Process. 1995, 9, 85–100. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Sanati, M.; Park, S.S. Identification of joint dynamics in 3D structures through the inverse receptance coupling method. Int. J. Mech. Sci. 2016, 105, 135–145. [Google Scholar] [CrossRef]
- Fritzen, C.-P. Identification of Mass, Damping, and Stiffness Matrices of Mechanical Systems. J. Vib. Acoust. Stress Reliab. Des. 1986, 108, 9–16. [Google Scholar] [CrossRef]
- Wang, M.; Wang, D.; Zheng, G. Joint dynamic properties identification with partially measured frequency response function. Mech. Syst. Signal Process. 2012, 27, 499–512. [Google Scholar] [CrossRef]
- Ahmadian, H.; Jalali, H. Identification of bolted lap joints parameters in assembled structures. Mech. Syst. Signal Process. 2007, 21, 1041–1050. [Google Scholar] [CrossRef]
- Hu, J.W.; Leon, R.T.; Park, T. Mechanical modeling of bolted T-stub connections under cyclic loads Part I: Stiffness modeling. J. Constr. Steel Res. 2011, 67, 1710–1718. [Google Scholar] [CrossRef]
- Kim, S.-M.; Ha, J.-H.; Jeong, S.-H.; Lee, S.-K. Effect of joint conditions on the dynamic behavior of a grinding wheel spindle. Int. J. Mach. Tools Manuf. 2001, 41, 1749–1761. [Google Scholar] [CrossRef]
- Iranzad, M.; Ahmadian, H. Identification of nonlinear bolted lap joint models. Comput. Struct. 2012, 96–97, 1–8. [Google Scholar] [CrossRef]
- Ahmadian, H.; Mottershead, J.E.; James, S.; Friswell, M.I.; Reece, C.A. Modelling and updating of large surface-to-surface joints in the AWE-MACE structure. Mech. Syst. Signal Process. 2006, 20, 868–880. [Google Scholar] [CrossRef]
- Ahmadian, H.; Jalali, H.; Mottershead, J.; Friswell, M. Dynamic modeling of spot welds using thin layer interface theory. In Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweden, 7–10 July 2003; pp. 7–10. [Google Scholar]
- Ahmadian, H.; Ebrahimi, M.; Mottershead, J.E.; Friswell, M.I. Identification of bolted-joint interface models. Proc. ISMA 2002, 4, 1741–1747. [Google Scholar]
- Ye, H.; Huang, Y.; Li, P.; Li, Y.; Bai, L. Virtual material parameter acquisition based on the basic characteristics of the bolt joint interfaces. Tribol. Int. 2016, 95, 109–117. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, J.; Feng, P.; Wu, Z.; Yu, D. A virtual material-based static modeling and parameter identification method for a BT40 spindle–holder taper joint. Int. J. Adv. Manuf. Technol. 2015, 81, 307–314. [Google Scholar] [CrossRef]
- Ouisse, M.; Foltête, E. Model correlation and identification of experimental reduced models in vibroacoustical modal analysis. J. Sound Vib. 2015, 342, 200–217. [Google Scholar] [CrossRef] [Green Version]
- Magalhães, F.; Caetano, E.; Cunha, Á. Operational modal analysis and finite element model correlation of the Braga Stadium suspended roof. Eng. Struct. 2008, 30, 1688–1698. [Google Scholar] [CrossRef]
- Allemang, R.J. The Modal Assurance Criterion (MAC): Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]


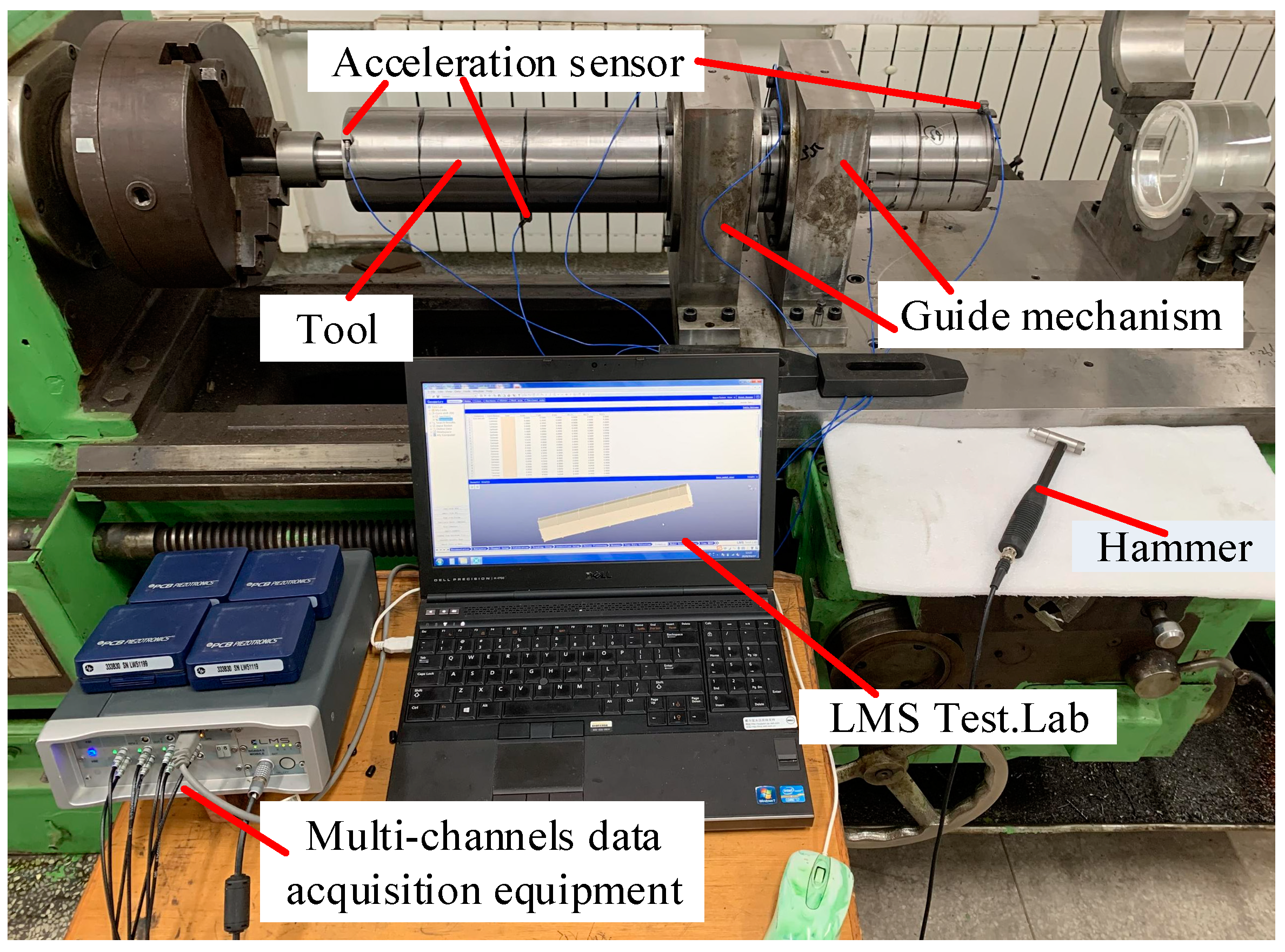
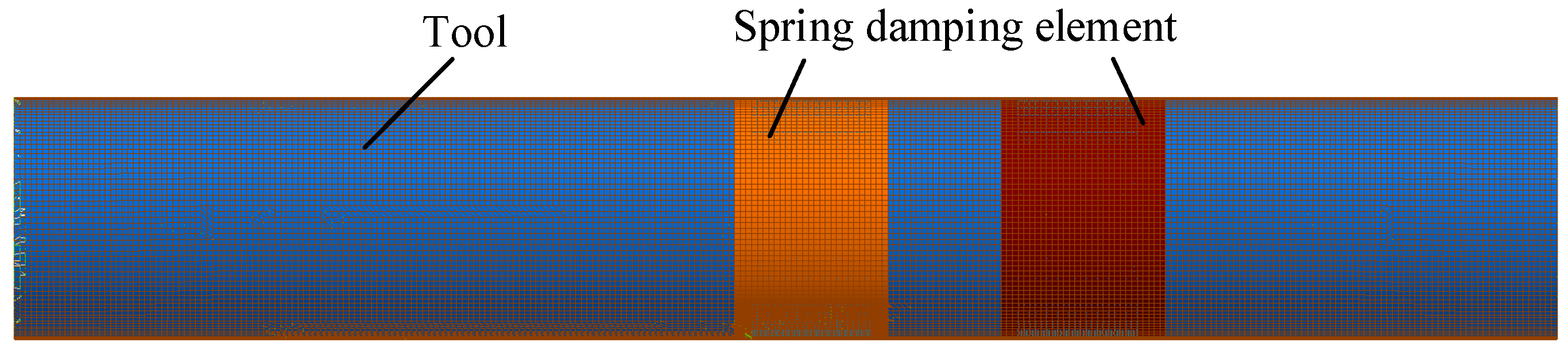




| Device | Model | Intent |
|---|---|---|
| Force hammer | PCB 086C03 | Generates the shock force signal |
| Acceleration sensor | PCB 333B30 | Obtains the force response signal |
| Multichannel data collector | LMS SCM09 | Collects data |
| Test analysis software | LMS Test.Lab | Data analysis and identification of modal parameters |
| Order | Frequency (Hz) | Vibration type |
|---|---|---|
| 1 | 380.3 |  |
| 2 | 462.5 |  |
| 3 | 788.5 |  |
| 4 | 926.4 |  |
| 5 | 1039.5 |  |
| 6 | 1430.0 |  |
| 7 | 1526.5 |  |
| Serial Number | K1/107 (N/m) | K2/107 (N/m) | γ1 | γ2 | γ3 | γ4 | γ5 | γ6 | γ7 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.03 | 2.26 | 0.268 | 0.091 | 0.026 | 0.001 | 0.120 | 0.038 | 0.064 |
| 2 | 2.30 | 1.30 | 0.140 | 0.091 | 0.026 | 0.001 | 0.117 | 0.038 | 0.064 |
| 3 | 2.50 | 1.03 | 0.113 | 0.091 | 0.026 | 0.001 | 0.120 | 0.038 | 0.064 |
| 4 | 2.15 | 2.72 | 0.342 | 0.091 | 0.026 | 0.001 | 0.130 | 0.038 | 0.064 |
| 5 | 1.70 | 2.63 | 0.296 | 0.091 | 0.026 | 0.001 | 0.113 | 0.038 | 0.064 |
| 6 | 2.62 | 1.87 | 0.259 | 0.091 | 0.026 | 0.001 | 0.135 | 0.038 | 0.064 |
| 7 | 1.35 | 2.97 | 0.316 | 0.091 | 0.026 | 0.001 | 0.106 | 0.038 | 0.064 |
| 8 | 2.74 | 2.13 | 0.304 | 0.091 | 0.026 | 0.001 | 0.143 | 0.038 | 0.064 |
| 9 | 2.99 | 2.76 | 0.401 | 0.091 | 0.026 | 0.001 | 0.160 | 0.038 | 0.064 |
| 10 | 1.02 | 2.41 | 0.202 | 0.091 | 0.026 | 0.001 | 0.087 | 0.038 | 0.064 |
| 11 | 2.08 | 1.68 | 0.182 | 0.091 | 0.026 | 0.001 | 0.114 | 0.038 | 0.064 |
| 12 | 1.52 | 1.59 | 0.107 | 0.091 | 0.026 | 0.001 | 0.094 | 0.038 | 0.064 |
| 13 | 1.75 | 1.12 | 0.043 | 0.091 | 0.026 | 0.001 | 0.096 | 0.038 | 0.064 |
| 14 | 1.40 | 1.23 | 0.022 | 0.091 | 0.026 | 0.001 | 0.086 | 0.038 | 0.064 |
| 15 | 1.92 | 2.92 | 0.352 | 0.091 | 0.026 | 0.001 | 0.125 | 0.038 | 0.064 |
| 16 | 1.24 | 1.98 | 0.149 | 0.091 | 0.026 | 0.001 | 0.090 | 0.038 | 0.064 |
| 17 | 1.31 | 2.40 | 0.226 | 0.091 | 0.026 | 0.001 | 0.097 | 0.038 | 0.064 |
| 18 | 1.13 | 1.62 | 0.067 | 0.091 | 0.026 | 0.001 | 0.082 | 0.038 | 0.064 |
| 19 | 1.62 | 1.81 | 0.157 | 0.091 | 0.026 | 0.001 | 0.100 | 0.038 | 0.064 |
| 20 | 2.44 | 2.17 | 0.287 | 0.091 | 0.026 | 0.001 | 0.133 | 0.038 | 0.064 |
| 21 | 1.56 | 1.39 | 0.074 | 0.091 | 0.026 | 0.001 | 0.093 | 0.038 | 0.064 |
| 22 | 2.86 | 1.76 | 0.263 | 0.091 | 0.026 | 0.001 | 0.142 | 0.038 | 0.064 |
| 23 | 2.40 | 2.85 | 0.376 | 0.091 | 0.026 | 0.001 | 0.141 | 0.038 | 0.064 |
| 24 | 1.98 | 2.05 | 0.232 | 0.091 | 0.026 | 0.001 | 0.116 | 0.038 | 0.064 |
| 25 | 1.17 | 1.16 | −0.027 | 0.091 | 0.026 | 0.001 | 0.077 | 0.038 | 0.064 |
| 26 | 2.68 | 1.43 | 0.197 | 0.091 | 0.026 | 0.001 | 0.131 | 0.038 | 0.064 |
| 27 | 1.87 | 2.51 | 0.291 | 0.091 | 0.026 | 0.001 | 0.118 | 0.038 | 0.064 |
| 28 | 2.89 | 1.50 | 0.226 | 0.091 | 0.026 | 0.001 | 0.139 | 0.038 | 0.064 |
| 29 | 2.59 | 2.32 | 0.319 | 0.091 | 0.026 | 0.001 | 0.140 | 0.038 | 0.064 |
| 30 | 2.23 | 2.59 | 0.330 | 0.091 | 0.026 | 0.001 | 0.131 | 0.038 | 0.064 |
| Spring Unit | Correlation | γ1 | γ2 | γ3 | γ4 | γ5 | γ6 | γ7 |
|---|---|---|---|---|---|---|---|---|
| K1 | Coefficient | 0.528 | - | - | - | 0.937 | - | - |
| Sig. | 0.003 | 0 | ||||||
| K2 | Coefficient | 0.869 | - | - | - | 0.395 | - | - |
| Sig. | 0 | 0.031 |
| Mode | EMA Modal Shape | FEA Modal Shape |
|---|---|---|
| 1 |  |  |
| 2 |  |  |
| 3 |  |  |
| 4 |  |  |
| 5 |  |  |
| 6 |  |  |
| 7 |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, R.; Li, S.; Liang, L.; Liu, F.; Wang, K. Research on Stiffness Identification Method for Complex Joints Based on Modal Correlation Analysis. Machines 2022, 10, 993. https://doi.org/10.3390/machines10110993
Yu R, Li S, Liang L, Liu F, Wang K. Research on Stiffness Identification Method for Complex Joints Based on Modal Correlation Analysis. Machines. 2022; 10(11):993. https://doi.org/10.3390/machines10110993
Chicago/Turabian StyleYu, Ruijiang, Shujuan Li, Lie Liang, Feilong Liu, and Kaixuan Wang. 2022. "Research on Stiffness Identification Method for Complex Joints Based on Modal Correlation Analysis" Machines 10, no. 11: 993. https://doi.org/10.3390/machines10110993





