Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines
Abstract
:1. Introduction
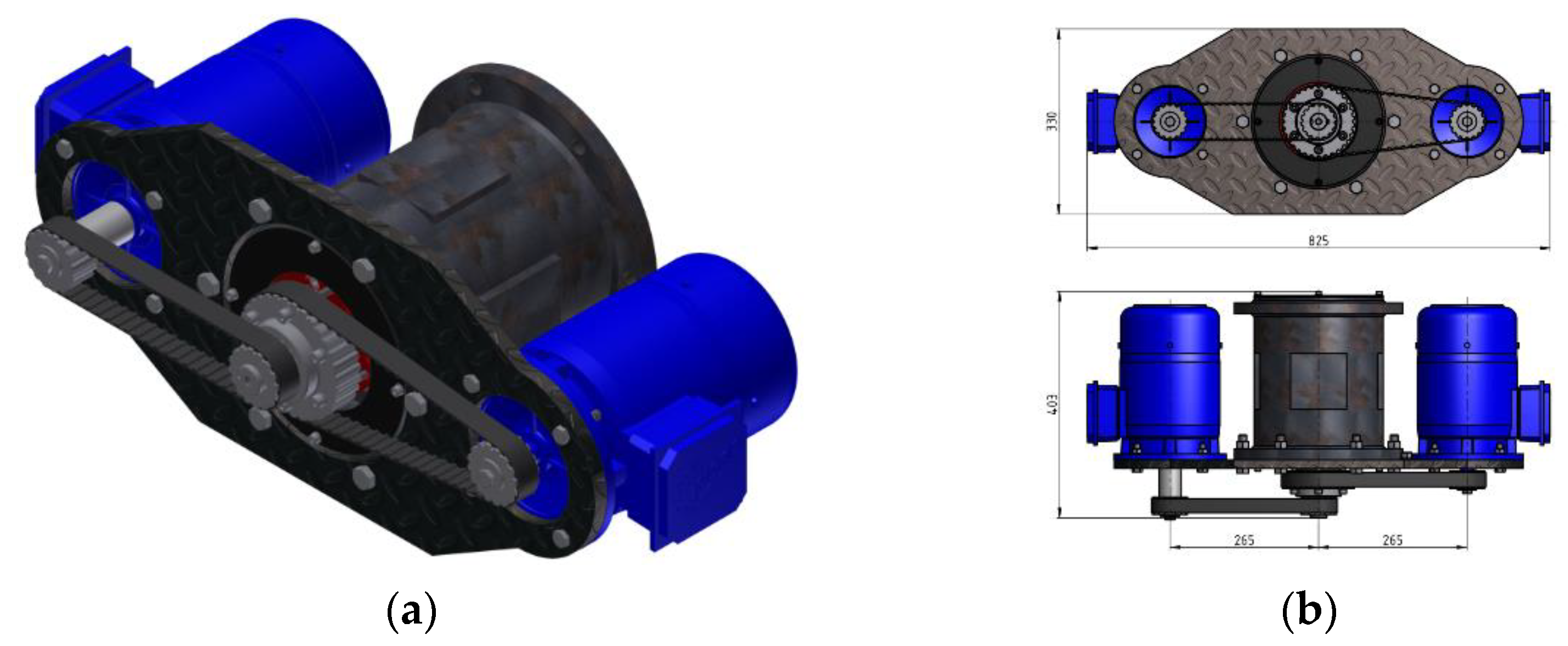
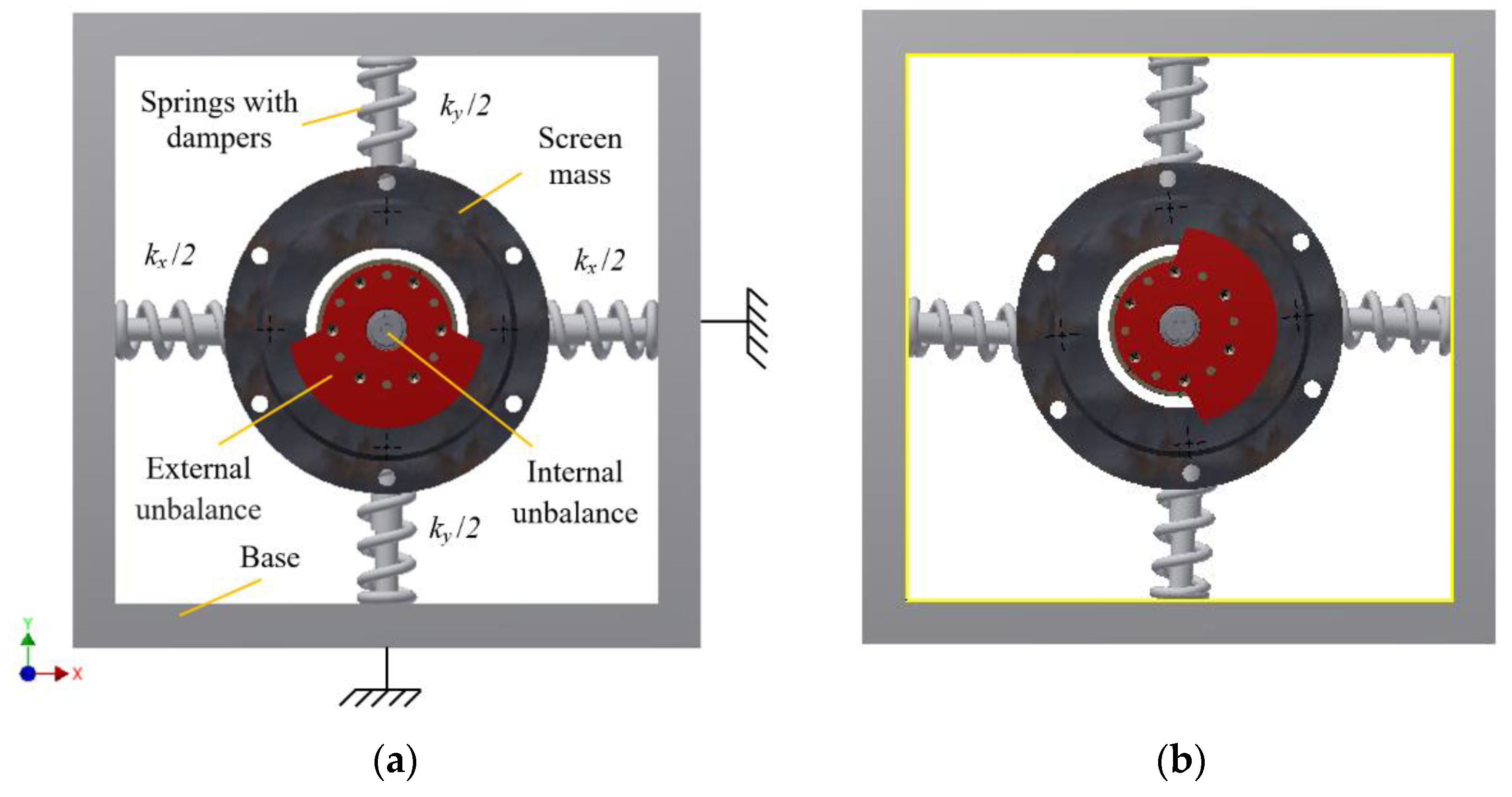
2. The Design of Vibrator
3. Results of Dynamic Analysis
3.1. Synthesis of Vibrators Parameters
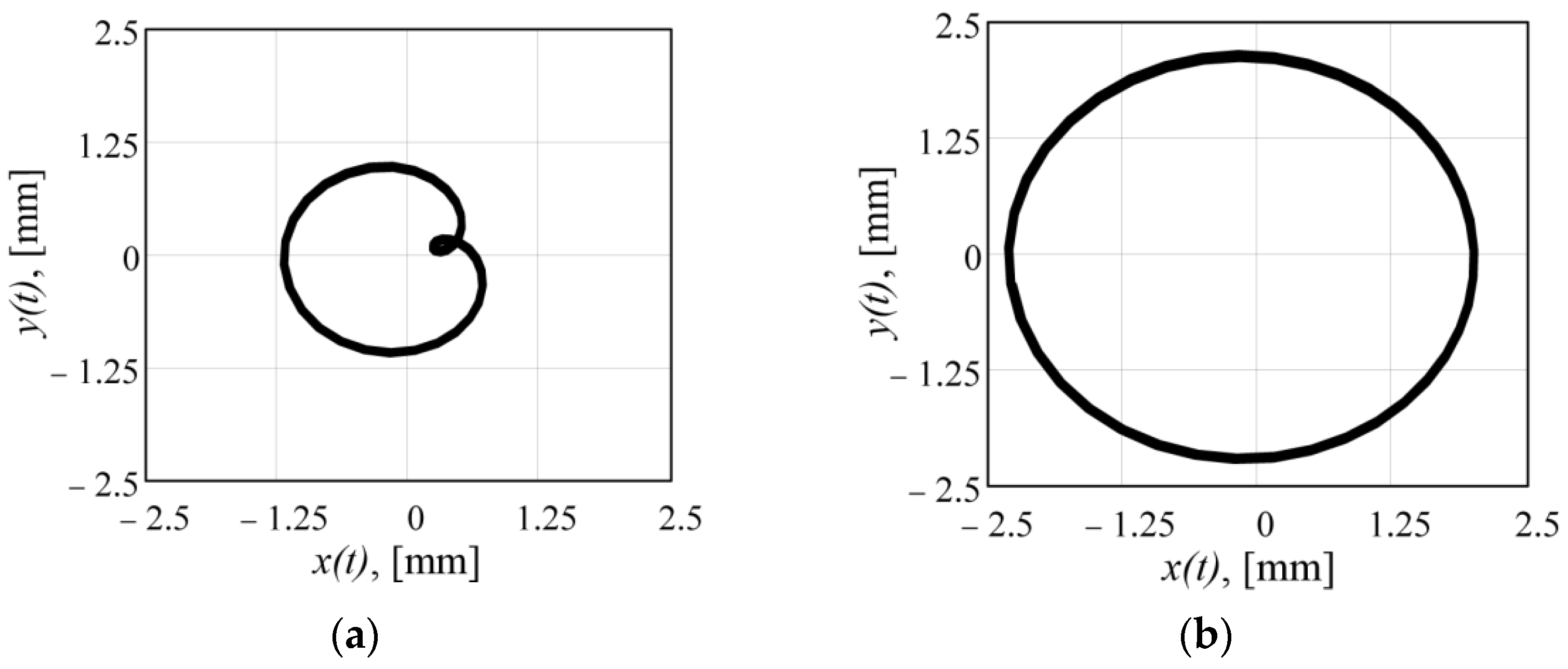
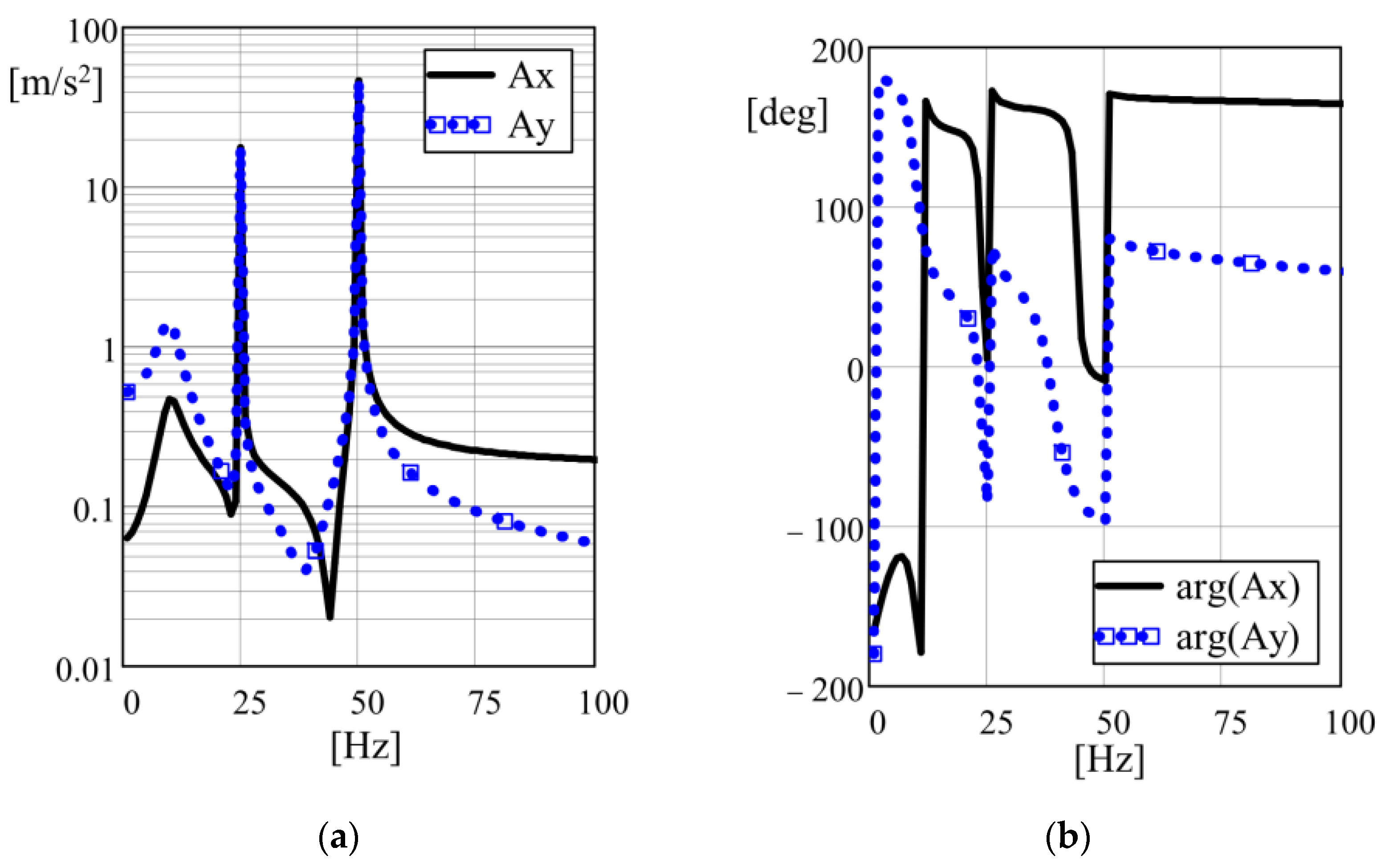
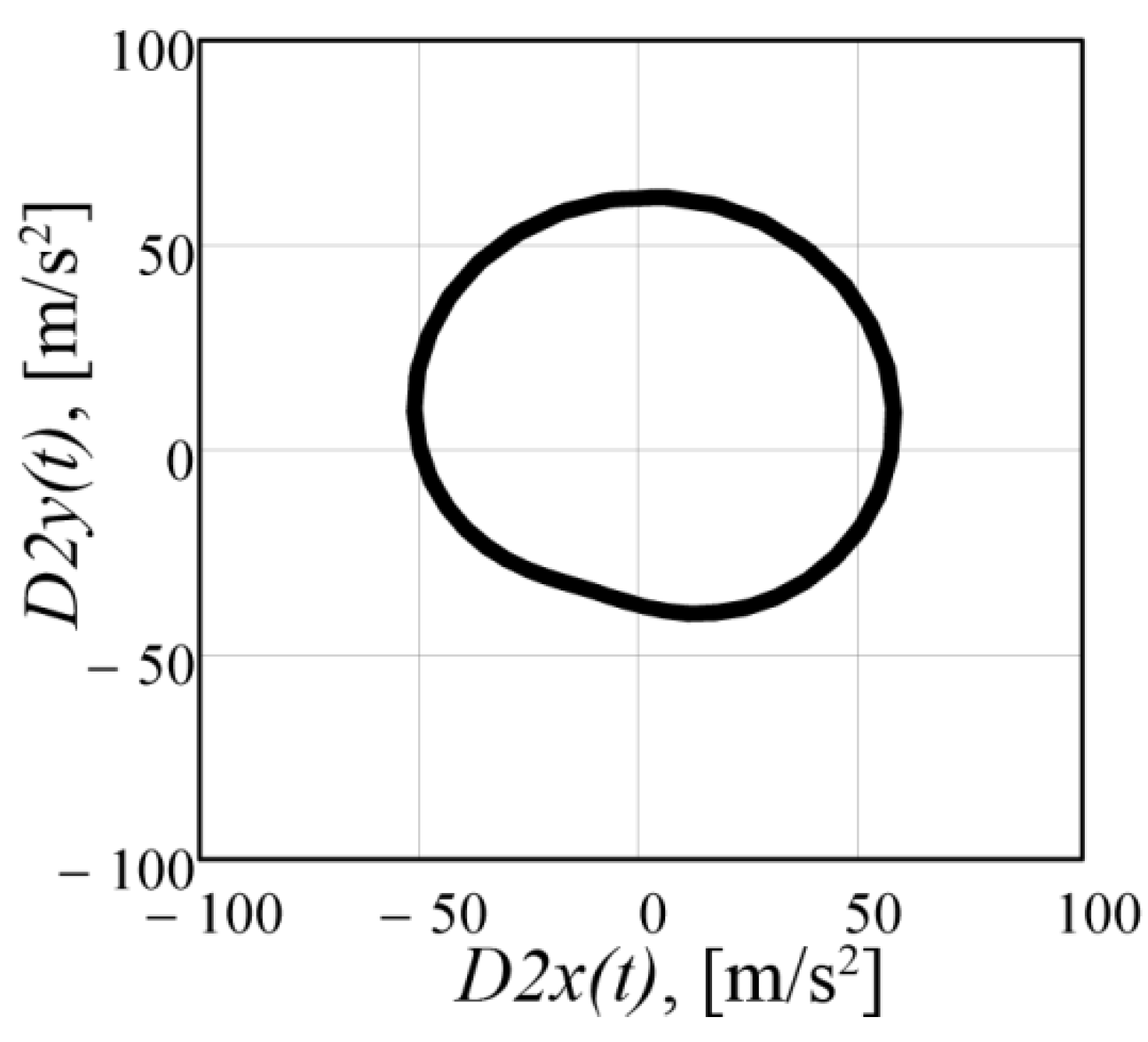
3.2. Dynamic Analysis of Vibrating Screen with Exciter of Enhanced Design
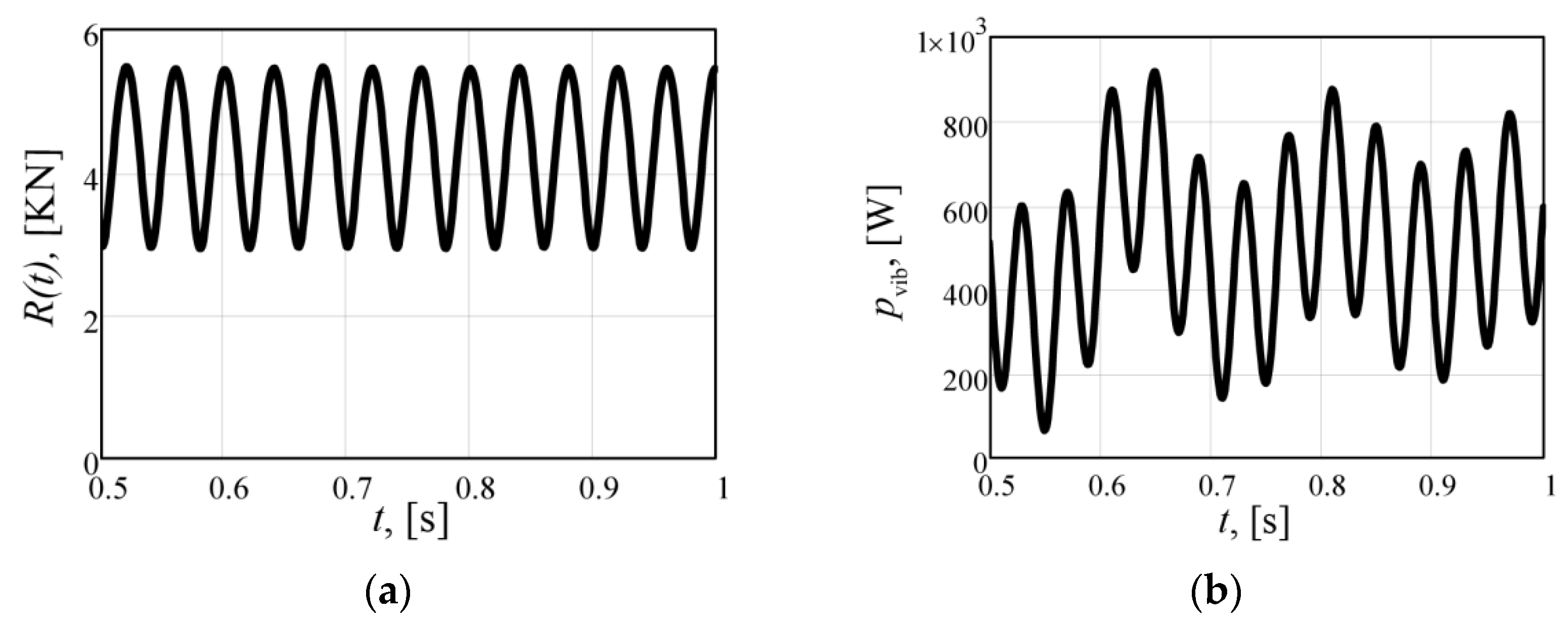
3.3. Power of the Designed Exciter
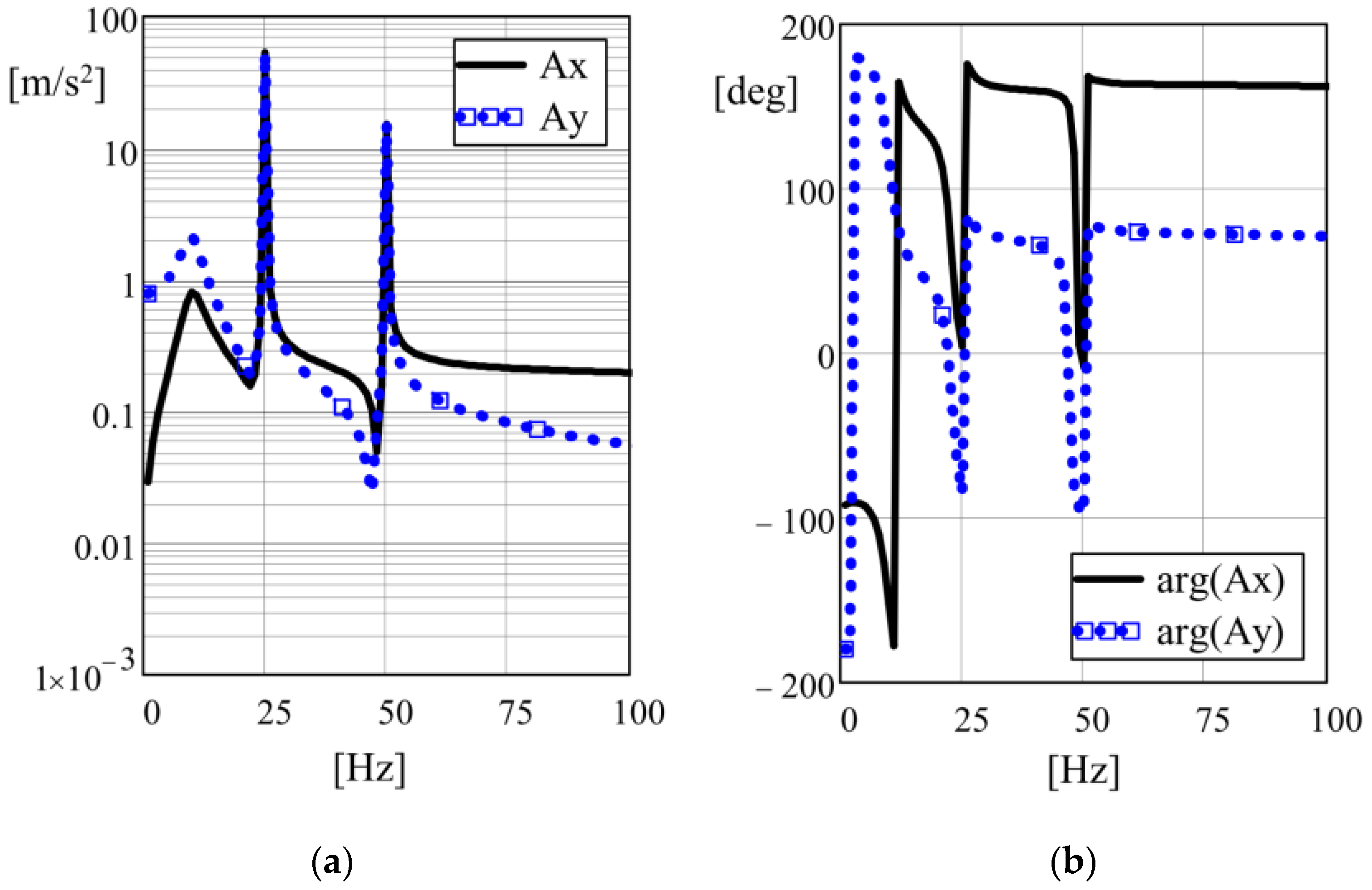
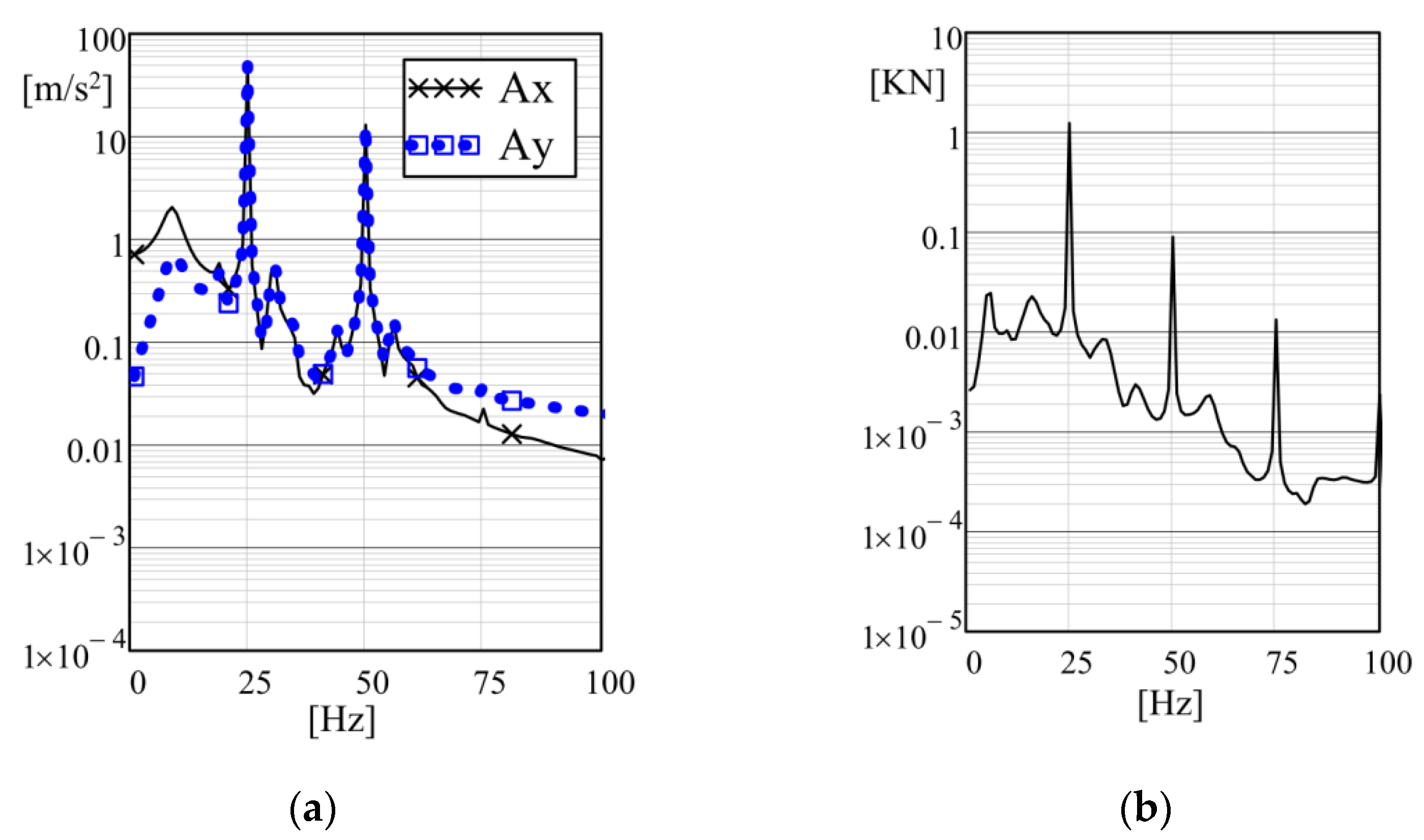
4. Simulation of the 3D Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Czubak, P. Vibratory conveyor of the controlled transport velocity with the possibility of the reversal operations. J. Vibroeng. 2016, 18, 3539–3547. [Google Scholar] [CrossRef] [Green Version]
- Majewski, T. Vibratory forces and synchronization in physical systems. Ing. Mec. Tecnol. Desarro. 2013, 4, 119–128. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-73812013000100002&lng=es&tlng=en (accessed on 22 December 2021).
- Zhang, X.; Hu, W.; Gao, Z.; Liu, Y.; Wen, B.-C. Composite synchronization on two pairs of vibrators in a far super-resonant vibrating system with the single rigid frame. J. Low Freq. Noise Vib. Act. Control 2021, 40, 2064–2076. [Google Scholar] [CrossRef]
- Hou, Y.; Du, M.; Wang, L. Investigation for synchronization of two co-rotating rotors installed with nonlinear springs in a non-resonance system. Adv. Mech. Eng. 2019, 11, 1687814019834110. [Google Scholar] [CrossRef] [Green Version]
- Blekhman, I.I.; Semenov, Y.A.; Yaroshevych, M.P. On the possibility of designing adaptive vibration machinery using self-synchronizing exciters. Mech. Mach. Sci. 2020, 80, 231–236. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Gu, D.; Jia, L.; Wen, B. Synchronization of a dual-mass vibrating system with two exciters. Shock Vib. 2020, 2020, 9345652. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, D.; Yue, H.; Li, M.; Wen, B. Synchronization and stability of a far-resonant vibrating system with three rollers driven by two vibrators. Appl. Math. Model. 2021, 91, 261–279. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Yu, C.; Liu, S.; Zhou, J.; Zhu, G. Research on static and dynamic characteristics of shear spring of the vibrating flip-flow screen. Symmetry 2020, 12, 1644. [Google Scholar] [CrossRef]
- Michalak, A.; Wodecki, J.; Drozda, M.; Wyłomańska, A.; Zimroz, R. Model of the vibration signal of the vibrating sieving screen suspension for condition monitoring purposes. Sensors 2021, 21, 213. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Wyłomańska, A.; Zimroz, R. Influence of non-Gaussian noise on the effectiveness of cyclostationary analysis—Simulations and real data analysis. Measurement 2021, 171, 108814. [Google Scholar] [CrossRef]
- Musschoot, A. Vibratory Conveyor. Patent US5131525A, 21 July 1992. Available online: https://patents.google.com/patent/US5131525A/en (accessed on 22 December 2021).
- Fuchigami, M. Variable-Force Vibrator. Patent US4108009A, 22 August 1978. Available online: https://patents.google.com/patent/us4108009a/en (accessed on 22 December 2021).
- Braun, G. Unbalance Vibration Generator. Patent US4058019A, 15 November 1977. Available online: https://patents.google.com/patent/EP0730792B1/en (accessed on 22 December 2021).
- Hanggi, G.J. Constant Force Variable Speed Vibrator. Patent US2989869A, 27 June 1961. Available online: https://patents.google.com/patent/US2989869 (accessed on 22 December 2021).
- Chen, B.; Yan, J.; Yin, Z.; Tamma, K. A new study on dynamic adjustment of vibration direction angle for dual-motor-driven vibrating screen. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2020, 235, 186–196. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Li, L. Dynamics of the vibration system driven by three homodromy eccentric rotors using control synchronization. Appl. Sci. 2021, 11, 7691. [Google Scholar] [CrossRef]
- Jia, L.; Kong, X.; Zhang, J.; Liu, Y.; Wen, B. Multiple-frequency controlled synchronization of two homodromy eccentric rotors in a vibratory system. Shock Vib. 2018, 2018, 4941357. [Google Scholar] [CrossRef]
- Modrzewski, R.; Wodziński, P. Oscillating motion of a double-frequency screen. Gór. Geoinżynieria 2009, 33, 209–219. [Google Scholar]
- Krot, P.; Zimroz, R. Methods of springs failures diagnostics in ore processing vibrating screens. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012147. [Google Scholar] [CrossRef]
- Krot, P.; Zimroz, R.; Michalak, A.; Wodecki, J.; Ogonowski, S.; Drozda, M.; Jach, M. Development and verification of the diagnostic model of the sieving screen. Shock Vib. 2020, 2020, 8015465. [Google Scholar] [CrossRef]
- Sorokin, V. Vibrations of a nonlinear stochastic system with a varying mass under near resonant excitation. J. Vib. Control 2019, 26, 1435–1444. [Google Scholar] [CrossRef]
- Yaroshevich, N.; Yaroshevych, O.; Lyshuk, V. Drive dynamics of vibratory machines with inertia excitation. Mech. Mach. Sci. 2021, 95, 37–47. [Google Scholar] [CrossRef]
- Gursky, V.; Krot, P.; Dilay, I.; Zimroz, R. Optimization of the vibrating machines with adjustable frequency characteristics. In Nonstationary Systems: Theory and Applications. WNSTA 2021. Appl. Cond. Monit. 2022, 18, 352–363. [Google Scholar] [CrossRef]
- Cieplok, G. Amplituda drgań symetrycznie posadowionej maszyny wibracyjnej podczas rezonansu przejściowego (Vibration amplitude of a symmetrically mounted vibrating machine during transient resonance). Czas. Tech. Mech. 2008, 105, 37–45. [Google Scholar]
- Czubak, P.; Surówka, W. Influence of the excitation frequency on operations of the vibratory conveyor allowing for a sudden stopping of the transport. Vib. Phys. Syst. 2020, 31, 1–12. [Google Scholar] [CrossRef]
- Yatsun, V.; Filimonikhin, G.; Dumenko, K.; Nevdakha, A. Search for two-frequency motion modes of single-mass vibratory machine with vibration exciter in the form of passive auto-balancer. East.-Eur. J. Enterp. Technol. 2017, 6, 1729–4061. [Google Scholar] [CrossRef] [Green Version]
- Lanets, O.; Kachur, O.; Korendiy, V.; Lozynskyy, V. Controllable crank mechanism for exciting oscillations of vibratory equipment. In DSMIE 2021: Advances in Design, Simulation and Manufacturing IV, Proceedings of the 4th International Conference on Design, Simulation, Manufacturing, Lviv, Ukraine, 8–11 June 2021; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2021; pp. 43–52. [Google Scholar] [CrossRef]
- Gursky, V.; Kuzio, I.; Krot, P.; Zimroz, R. Energy-Saving Inertial Drive for Dual-Frequency Excitation of Vibrating Machines. Energies 2021, 14, 71. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Xu, H. Dynamic characteristics analysis of a dual-rotor system with inter-shaft bearing. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 095441001774896. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Zhang, K.; Yue, G. Optimization and experiment of mass compensation strategy for built-in mechanical on-line dynamic balancing system. Appl. Sci. 2020, 10, 1464. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Zhou, H.; Liu, J.; Kang, C. Modeling and dynamic characteristic analysis of dual rotor-casing coupling system with rubbing fault. J. Low Freq. Noise Vib. Act. Control 2021, 14613484211039322. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Luo, Z. High dimensional nonlinear spring characteristic modelling and vibration analyses of subharmonic resonance of a dual-rotor system based on energy tracks. Appl. Math. Model. 2021, 91, 390–411. [Google Scholar] [CrossRef]
- Kroger, D. Unbalanced Mass Vibration Generator. Patent US5850110A, 15 December 1998. Available online: https://patents.google.com/patent/US5850110 (accessed on 22 December 2021).
- Nazarenko, I.; Gaidaichuk, V.; Dedov, O.; Diachenko, O. Investigation of vibration machine movement with a multimode oscillation spectrum. East.-Eur. J. Enterp. Technol. 2017, 6, 28–36. [Google Scholar] [CrossRef] [Green Version]
- Kuzo, I.V.; Lanets, O.V.; Gursky, V.M. Substantiation of technological efficiency of two-frequency resonant vibration machines with pulse electromagnetic disturbance. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2013, 3, 71–77. [Google Scholar]
- Gursky, V.M.; Kuzio, I.V.; Lanets, O.S.; Kisała, P.; Tolegenova, A.; Syzdykpayeva, A. Implementation of dual-frequency resonant vibratory machines with pulsed electromagnetic drive (Implementacja systemów rezonansowych o dwóch częstotliwościach z wieloma częstotliwościami drgań własnych). Prz. Elektrotech. 2019, 95, 41–46. [Google Scholar] [CrossRef]
- Gursky, V.; Kuzio, I. Strength and durability analysis of a flat spring at vibro-impact loadings. East.-Eur. J. Enterp. Technol. 2016, 5, 4–10. [Google Scholar] [CrossRef]
- Krot, P.V. Dynamical processes in a multi-motor gear drive of heavy slabbing mill. J. Vibroeng. 2019, 21, 2064–2081. [Google Scholar] [CrossRef] [Green Version]
- Angeles, J. Dynamic Response of Linear Mechanical Systems: Modeling, Analysis and Simulation; Springer: Boston, MA, USA, 2012; 560p. [Google Scholar] [CrossRef]

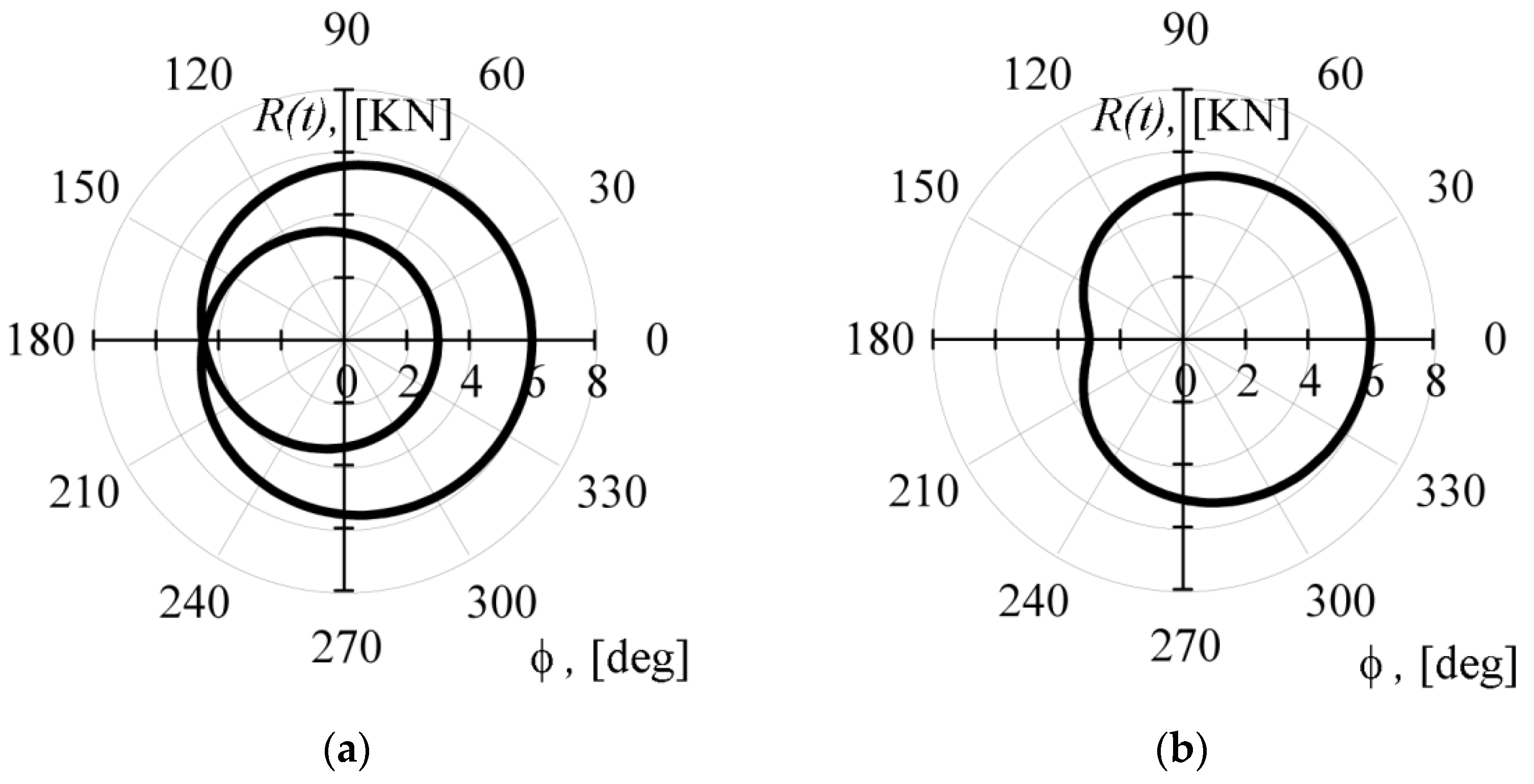
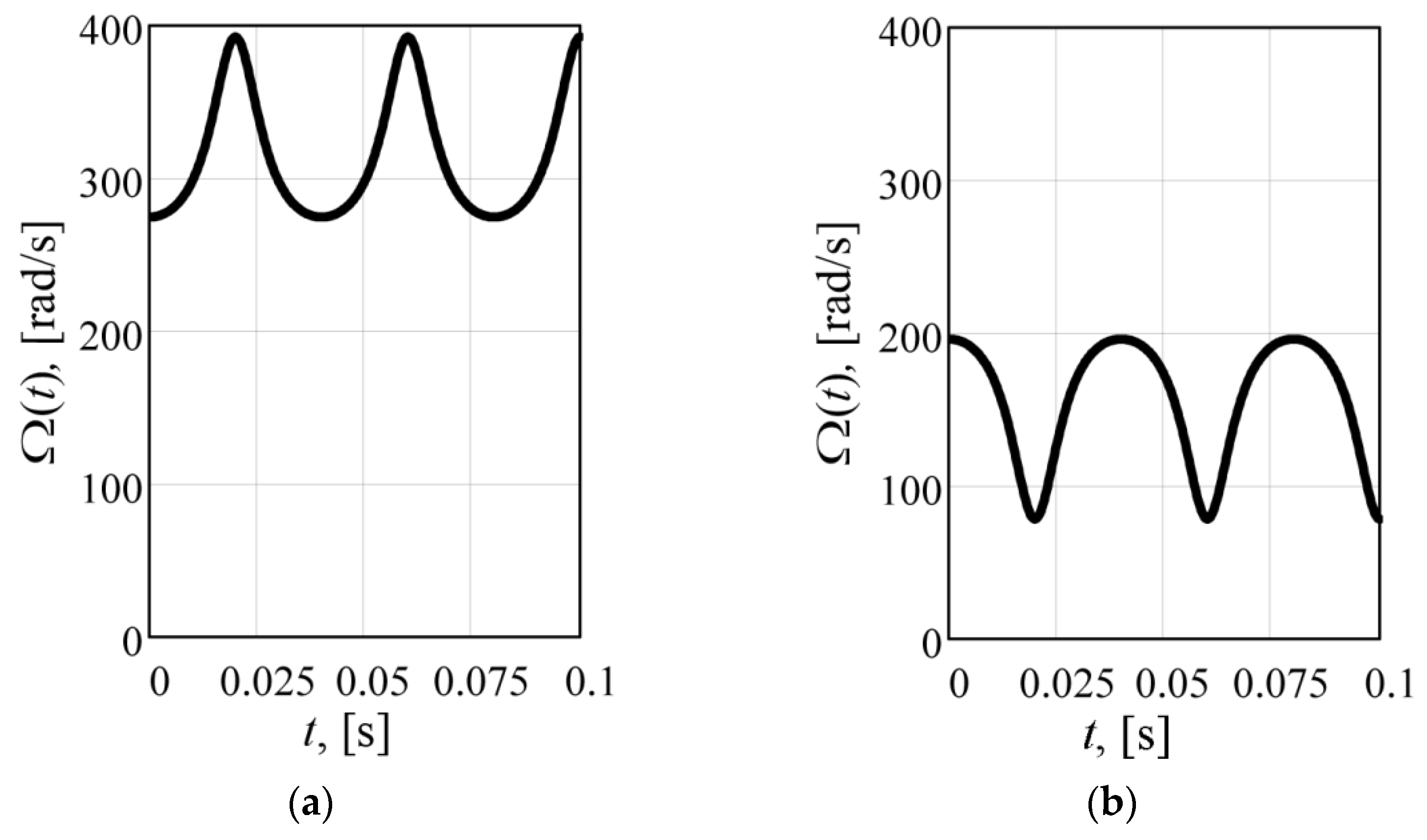
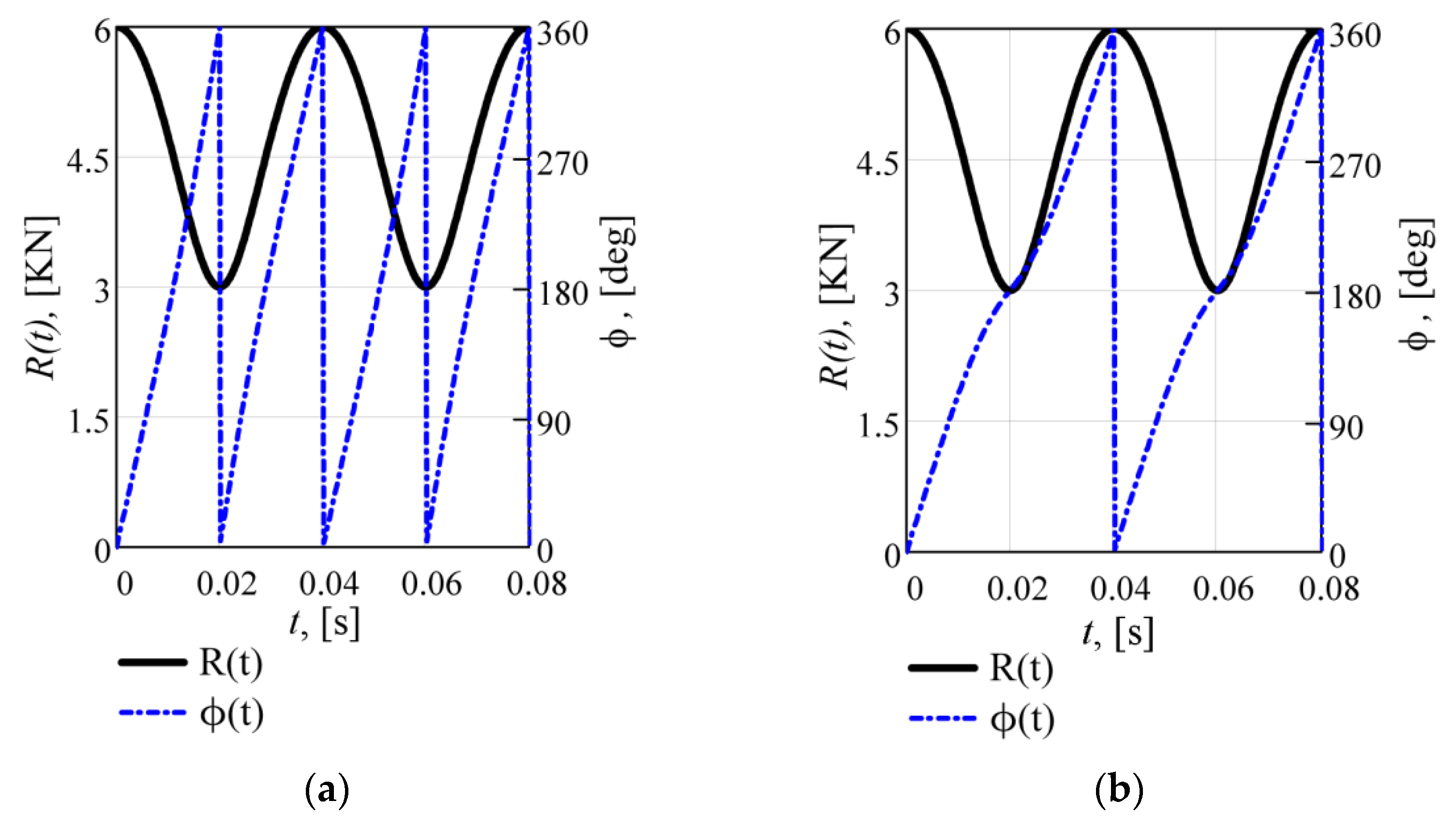
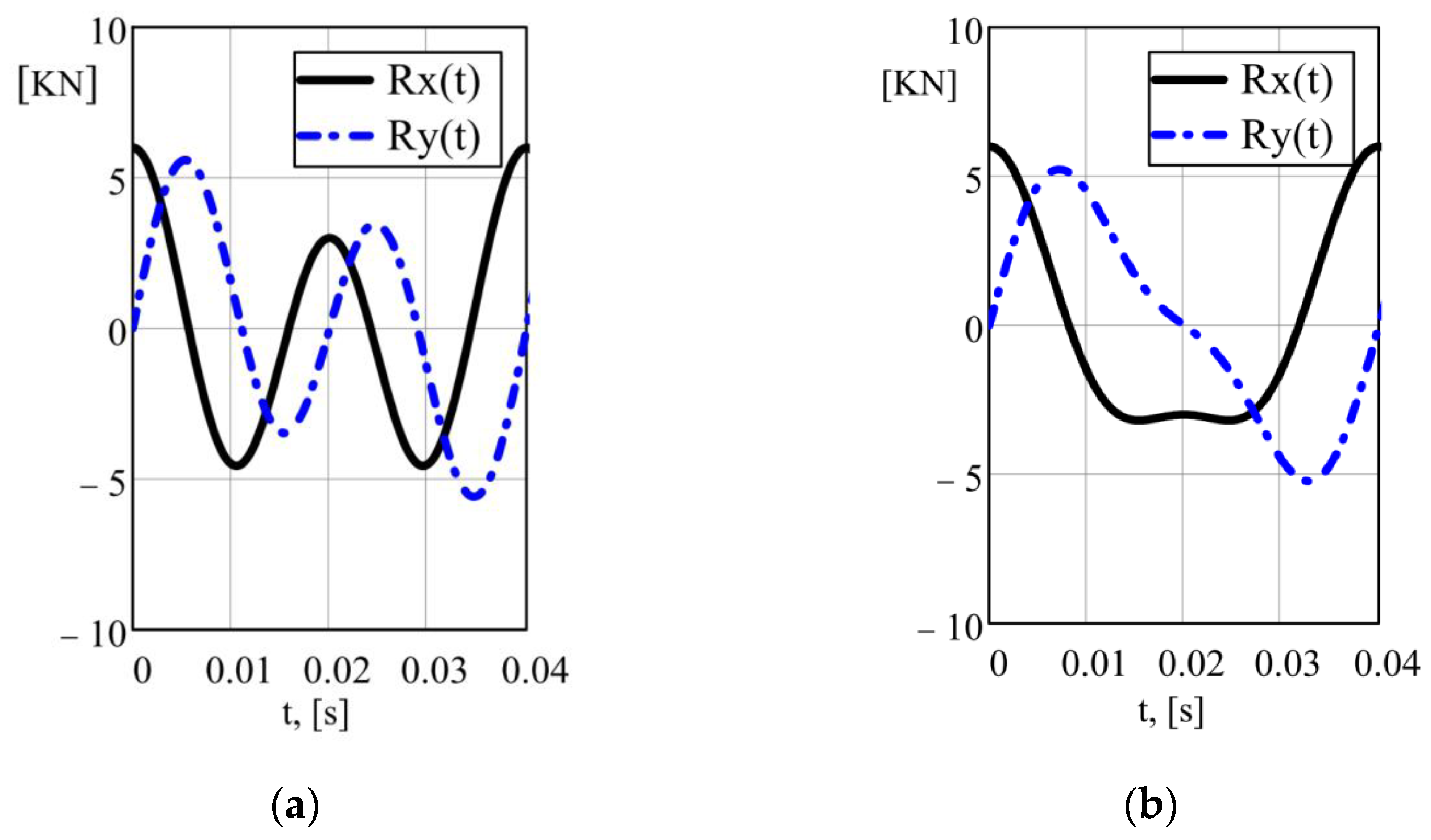





| Parameters | Kω = 0.5 | Kω = 2 | Kω = 1 | Kω = 1 |
|---|---|---|---|---|
| Static moment of unbalances 1/2, kg · m | 0.061/0.046 | 0.015/0.183 | 0.061/0 | 0.243/0 |
| Angular velocity 1/2, rad/s | 157/314 | 314/157 | 314/0 | 157/0 |
| Perturbation force, KN | 3–6 | 3–6 | 6 | 6 |
| Total oscillating mass, kg | 100 | 100 | 100 | 100 |
| Maximum amplitude, mm | 1.2 | 2.3 | 0.65 | 2.9 |
| Harmonics amplitude 25/50 Hz, m/s2 | 17.6/46.3 | 52.7/15.3 | 0/61.8 | 70.3/0 |
| Dynamic power of the vibrator, W | 229 | 142–494 | 120 | 276 |
| Parameters | Modeling | Error, % | |
|---|---|---|---|
| Analytical | 3D Model | ||
| Perturbation force, KN | 3–6 | 2.9–5.7 | 3-5 |
| Maximum amplitude, mm | 2.3 | 2.1 | 10 |
| Harmonics amplitude 25/50 Hz, m/s2 | 52.7/15.3 | 49.1/13 | 7–15 |
| Dynamic power of the vibrator, W | 172.7 | 190 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gursky, V.; Krot, P.; Korendiy, V.; Zimroz, R. Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines. Machines 2022, 10, 130. https://doi.org/10.3390/machines10020130
Gursky V, Krot P, Korendiy V, Zimroz R. Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines. Machines. 2022; 10(2):130. https://doi.org/10.3390/machines10020130
Chicago/Turabian StyleGursky, Volodymyr, Pavlo Krot, Vitaliy Korendiy, and Radosław Zimroz. 2022. "Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines" Machines 10, no. 2: 130. https://doi.org/10.3390/machines10020130









