Dynamic Analysis of a High-Contact-Ratio Spur Gear System with Localized Spalling and Experimental Validation
Abstract
:1. Introduction
- (1)
- Modeling of the mesh stiffness of the high-contact-ratio gear system with localized ellipsoid spalling.
- (2)
- Bifurcation characteristic of the high-contact-ratio gear system with localized ellipsoid tooth spalling fault is discussed.
- (3)
- Experiments are carried out for vibration measurement to validate the proposed dynamic model.
2. Mesh Stiffness Computation
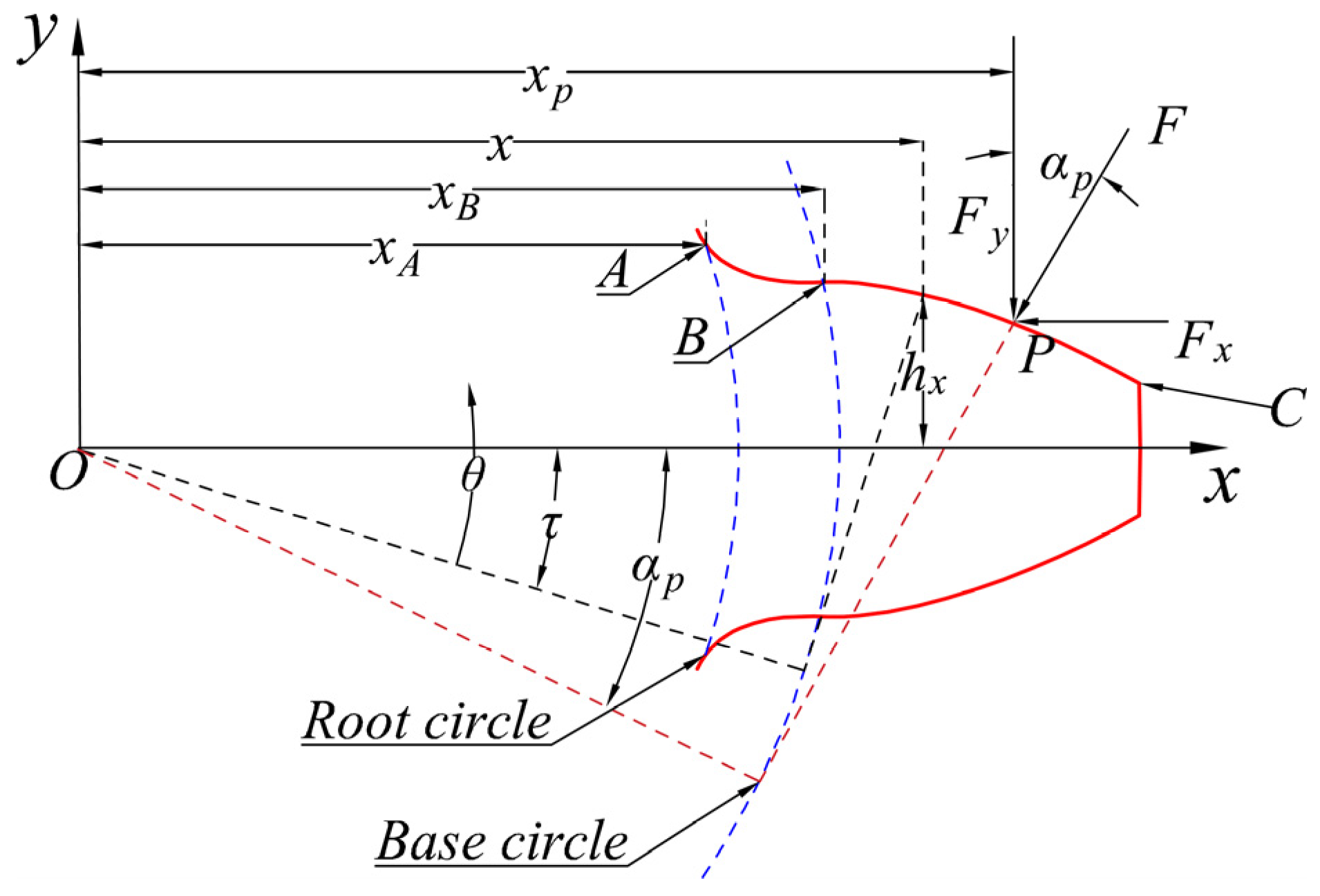
2.1. Accurate Tooth Profile Equation
2.2. Analytical Model of Meshing Stiffness
3. Dynamic Model of System
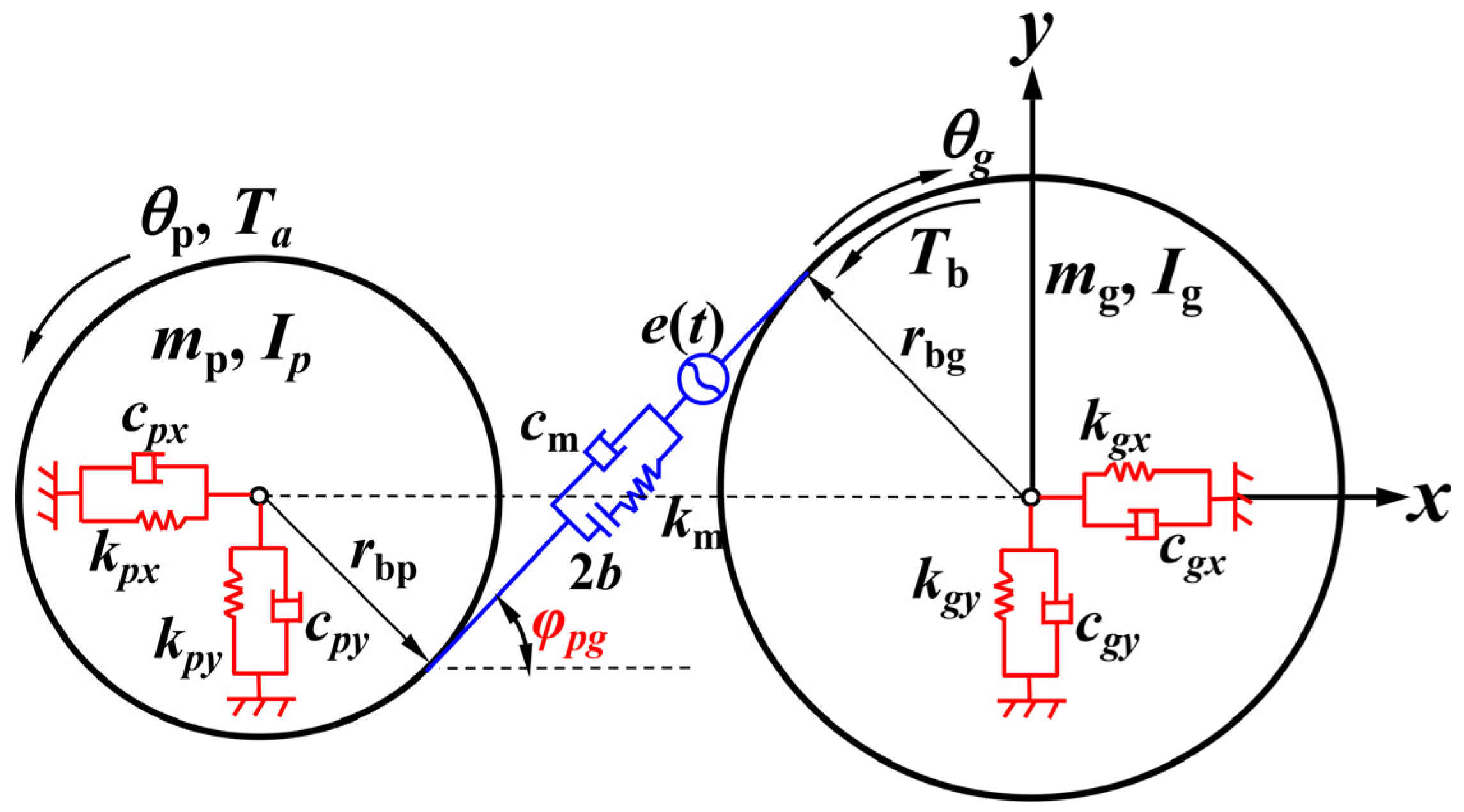
3.1. Gear-Bearing System
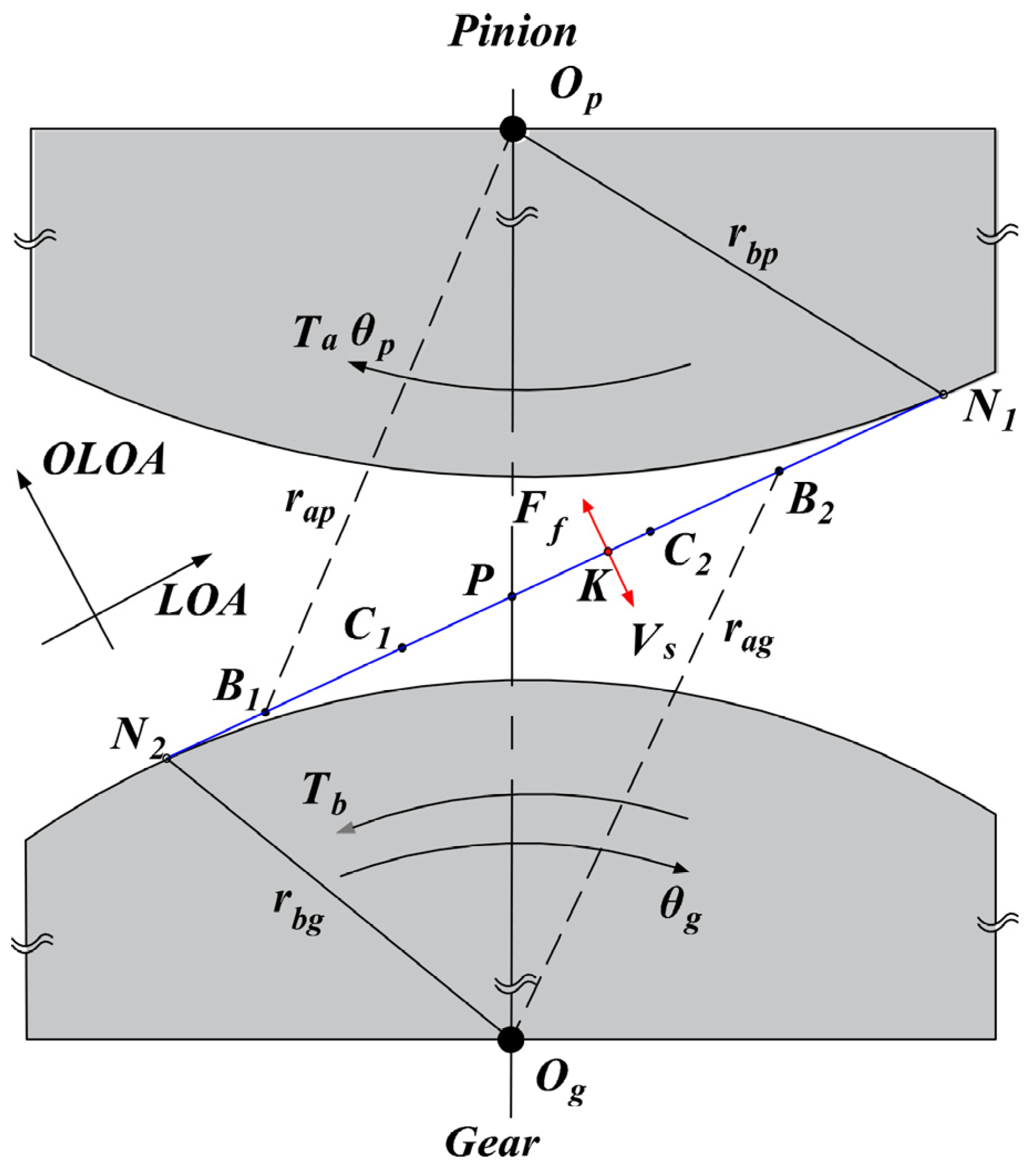
3.2. Dynamic Meshing Force and Frictional Force
3.3. Differential Equations of Motion
4. Numerical Simulation and Discussion
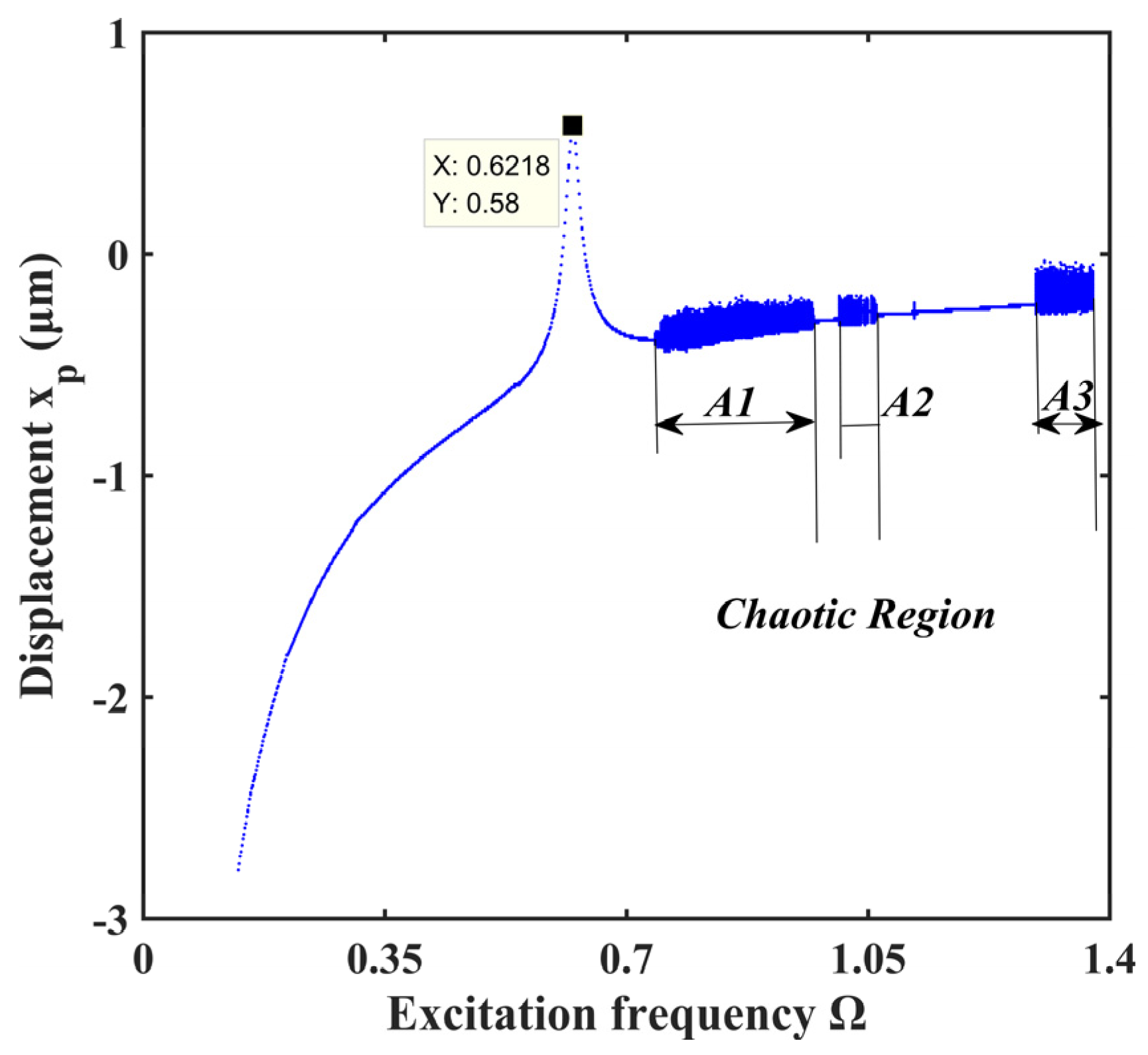
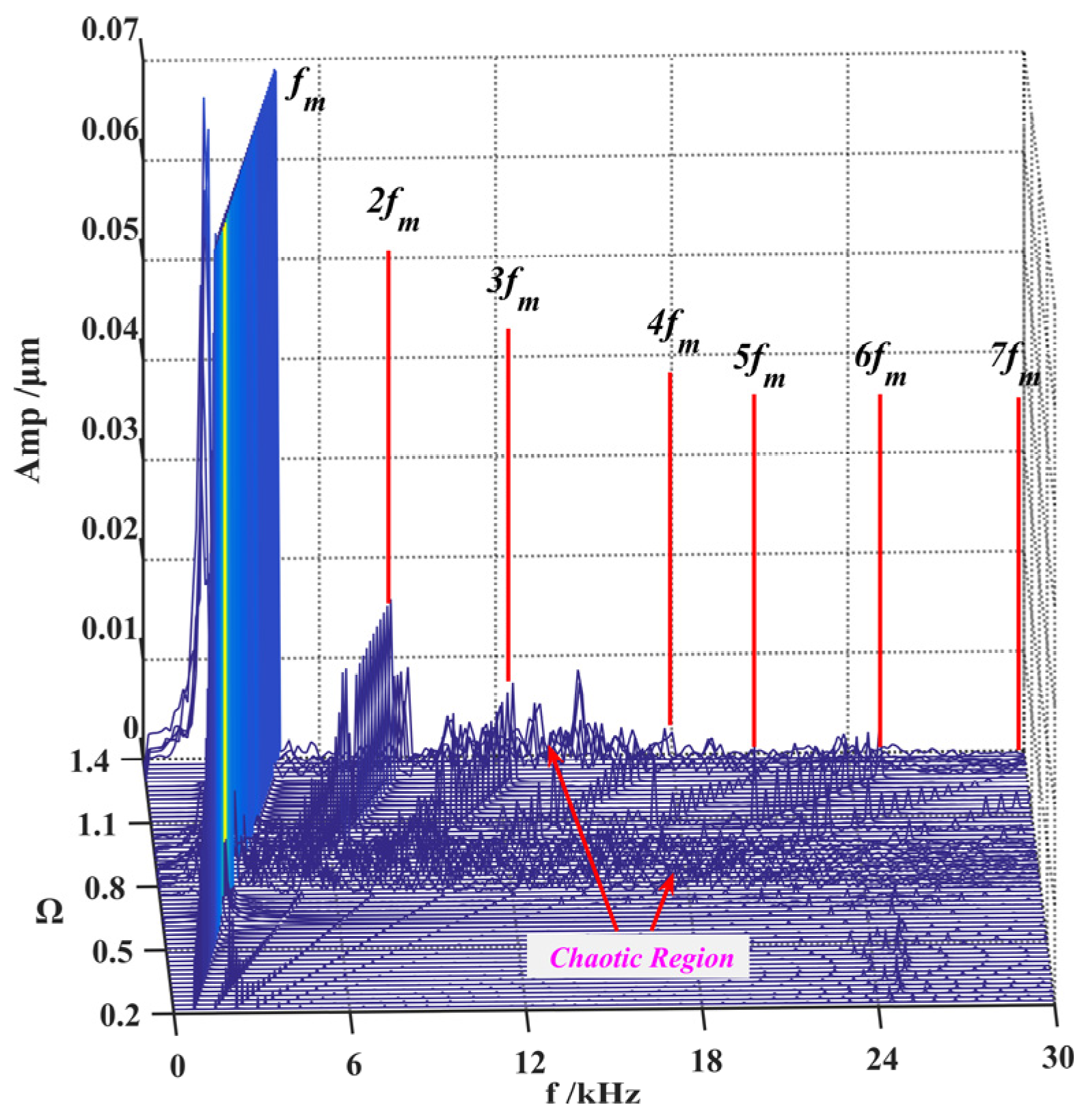
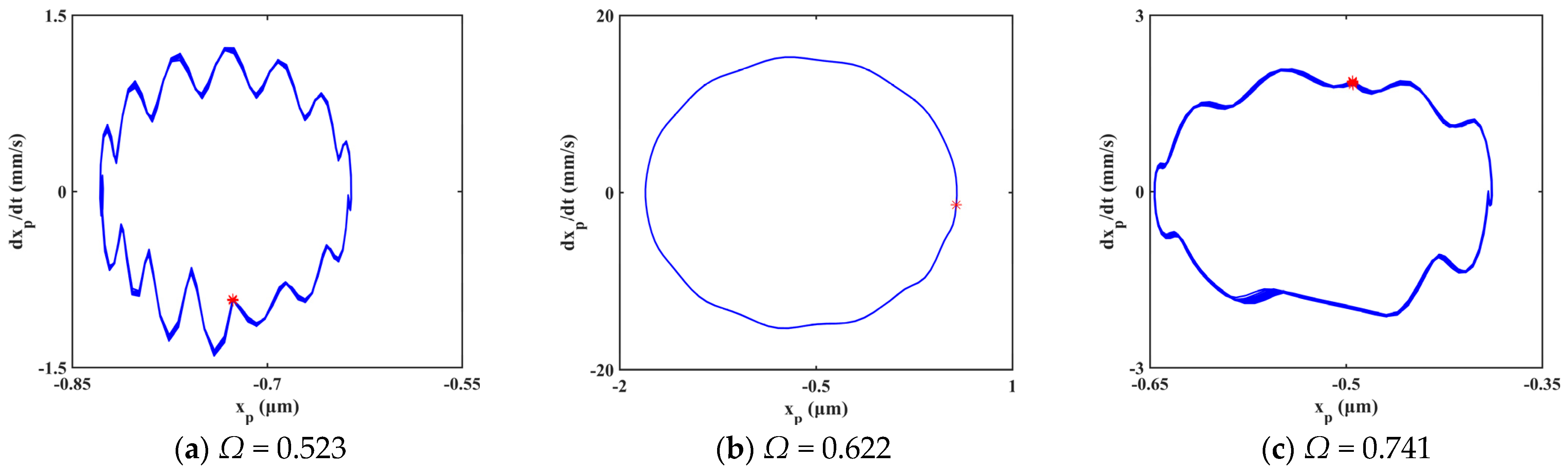
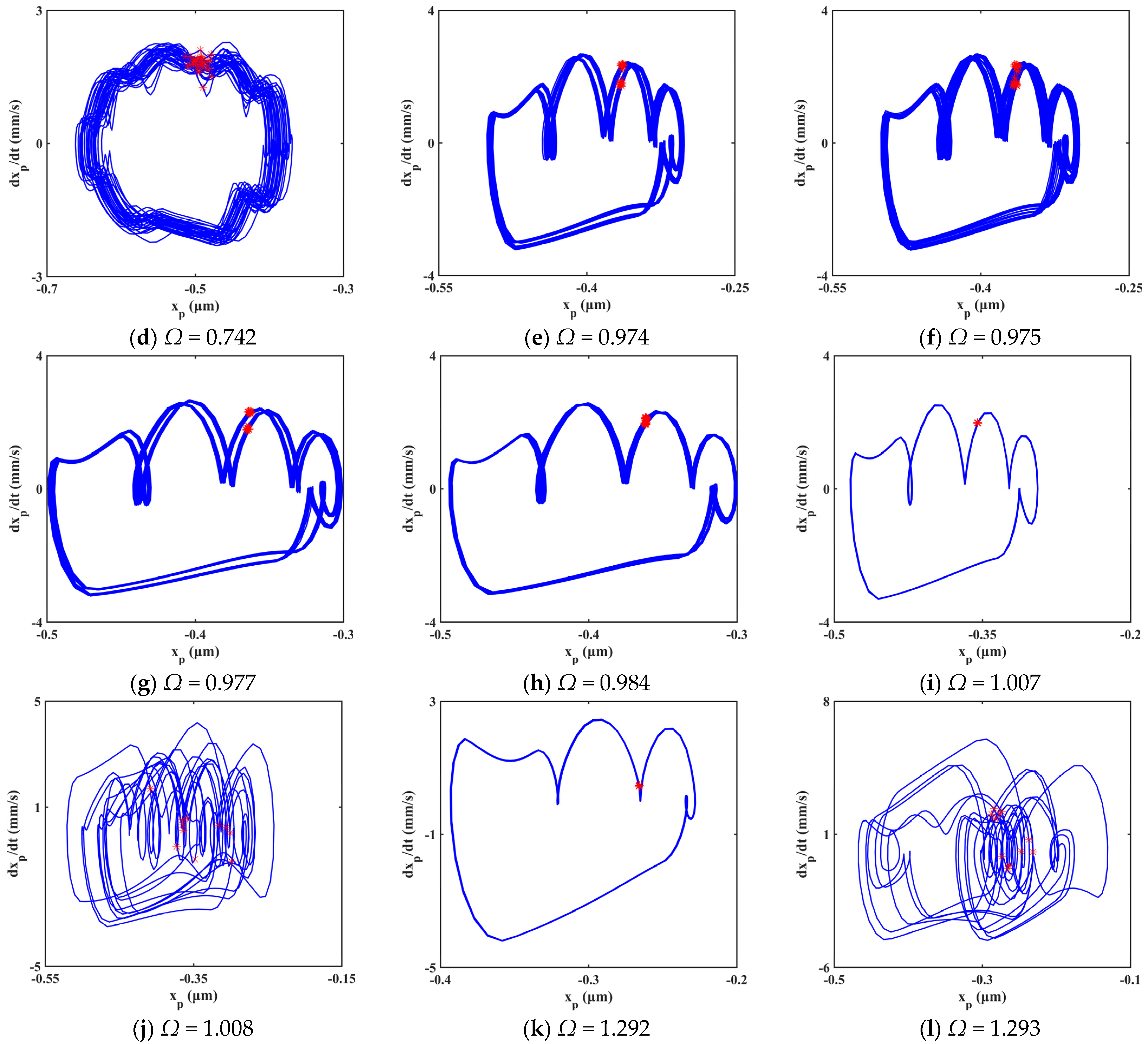
4.1. Effect of Excitation Frequency
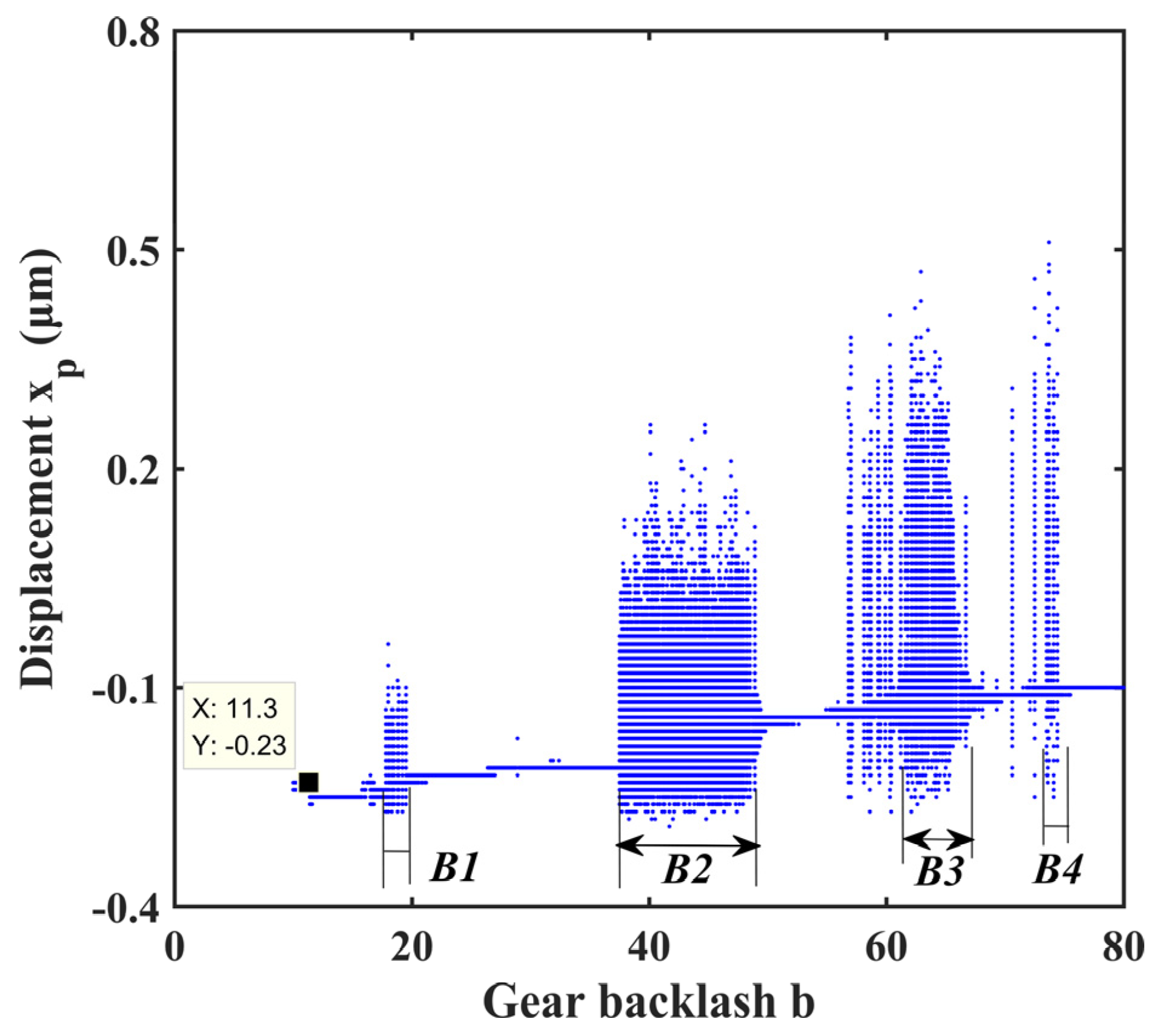
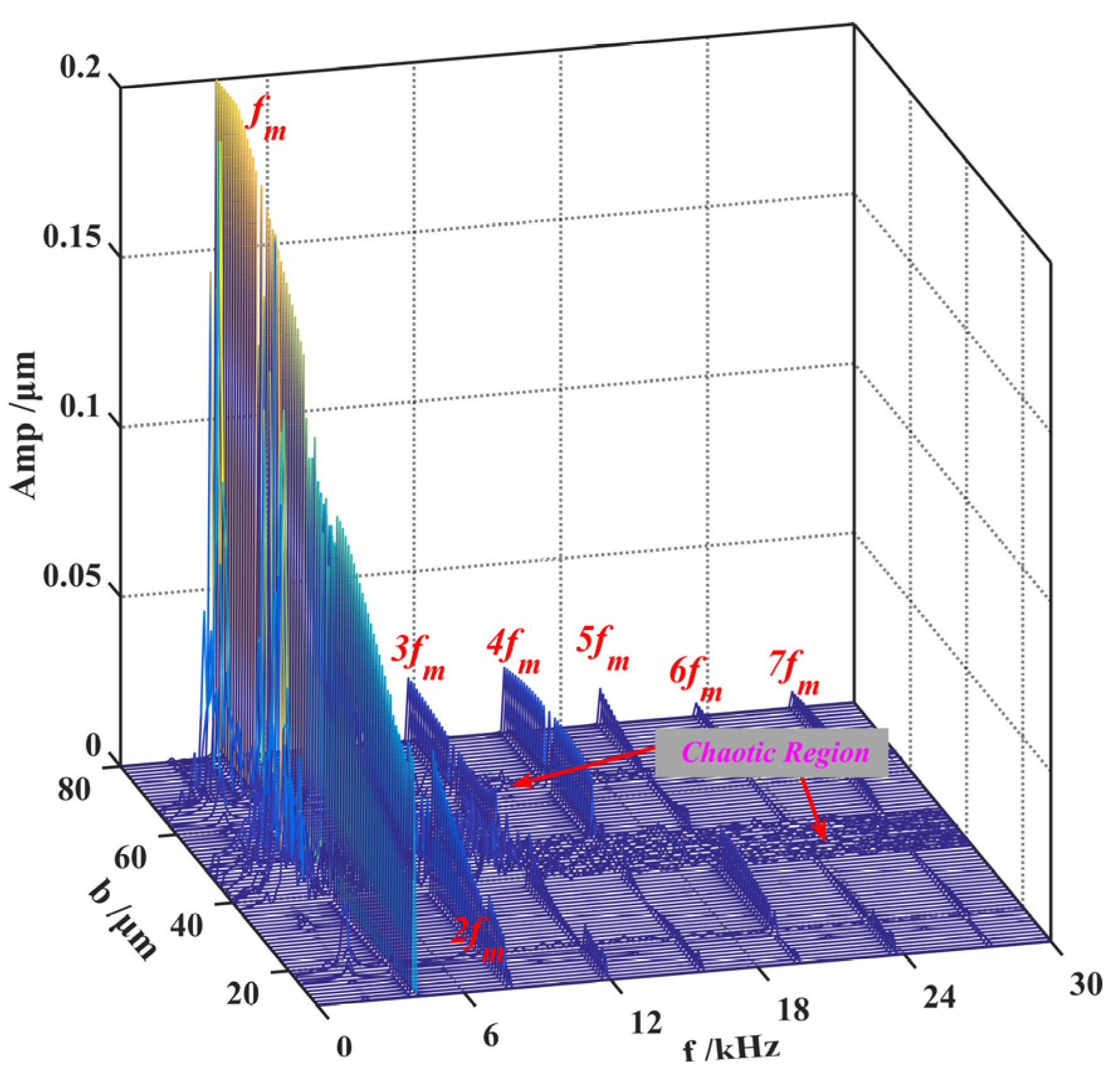
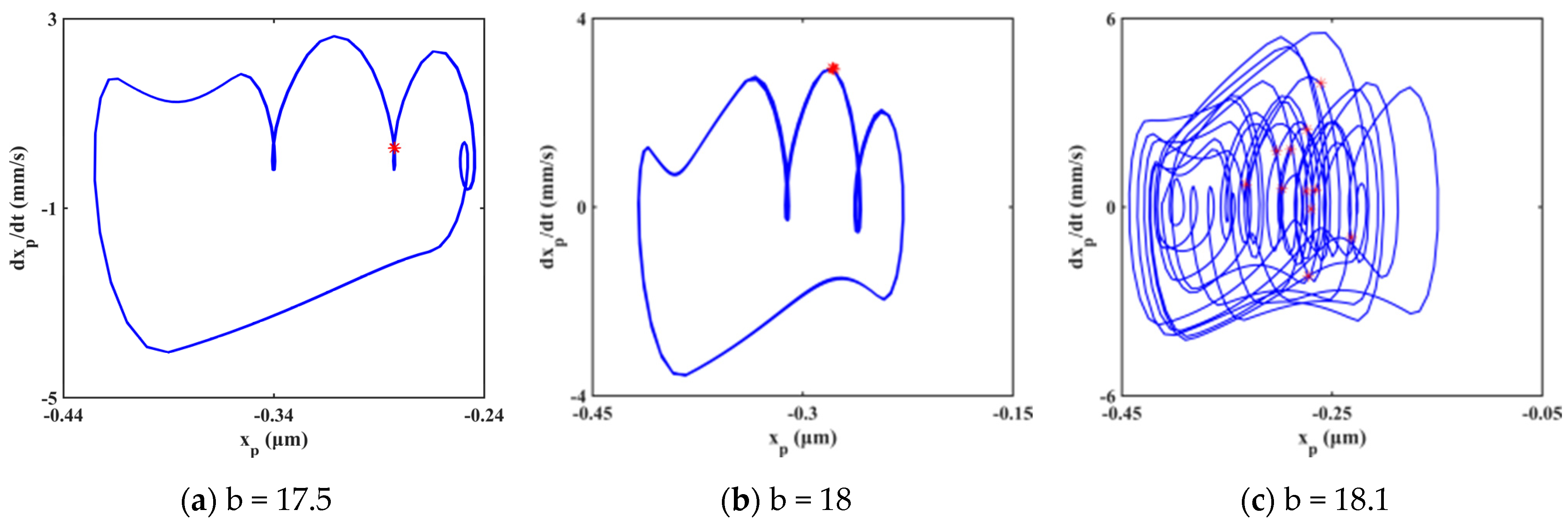
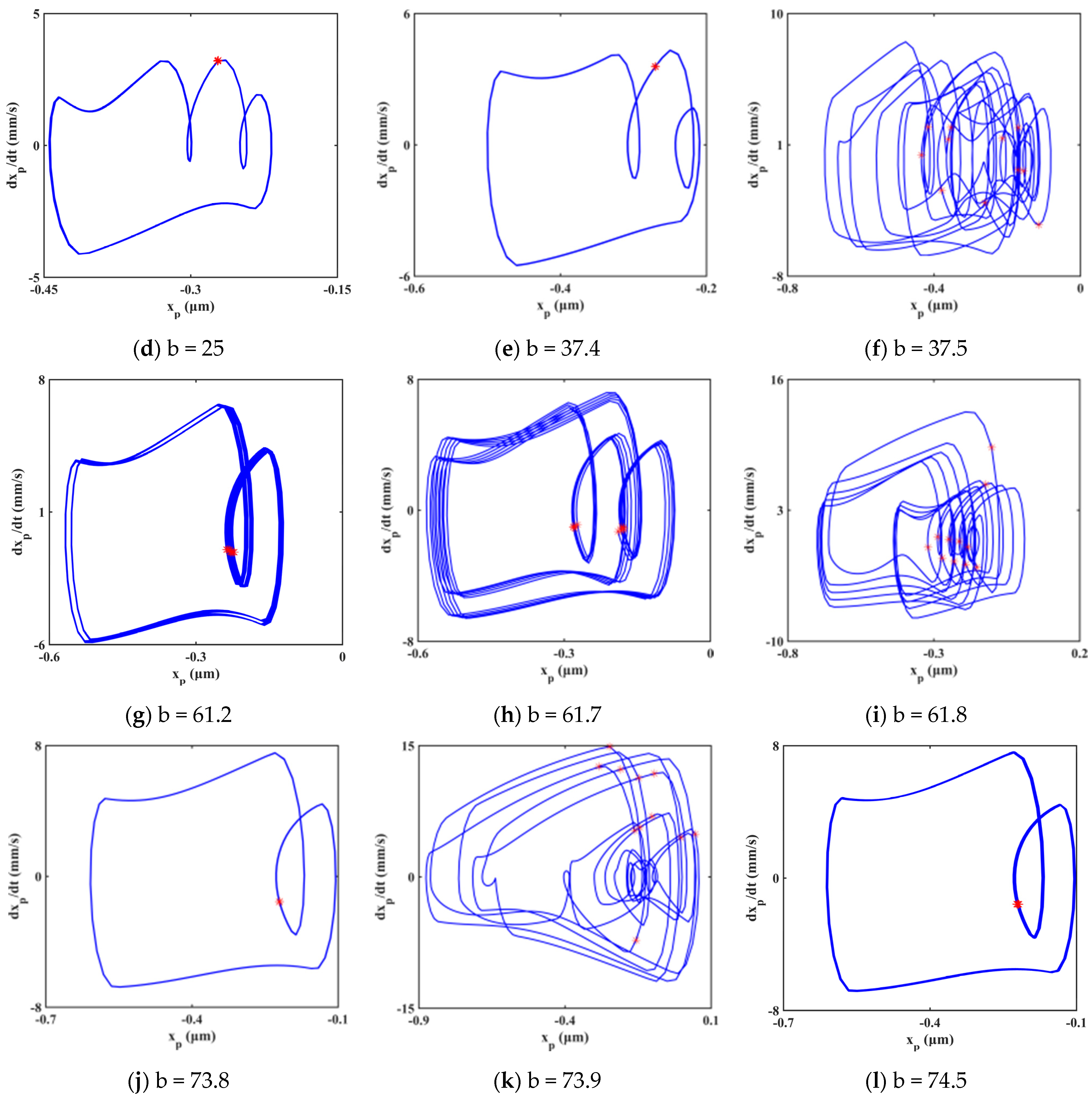
4.2. Effect of Gear Backlash
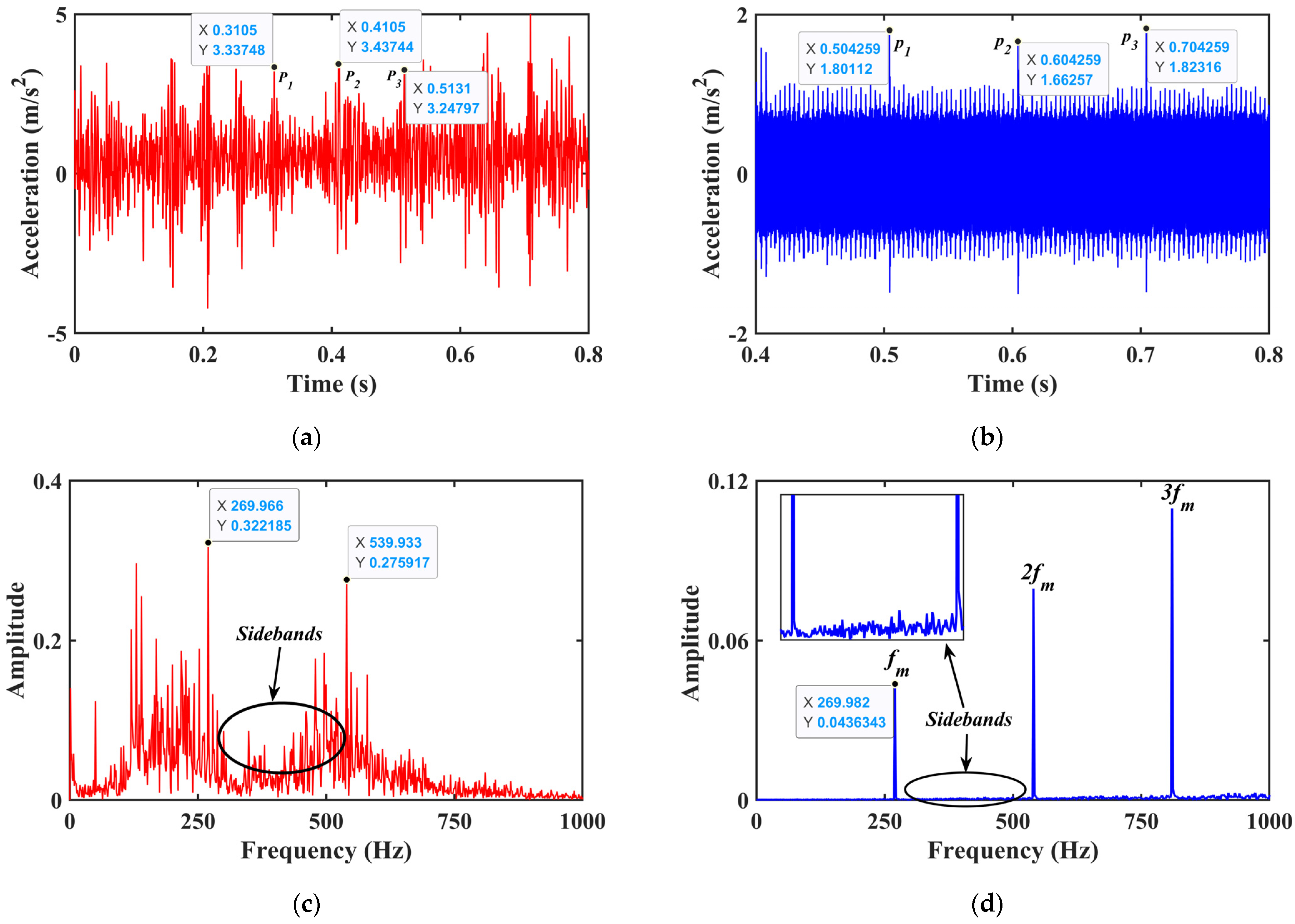
5. Experimental Validation
6. Conclusions
- (1)
- The system’s motion with ellipsoid tooth spalling fault exhibits rich bifurcation and chaotic characteristics under the influence of excitation frequency and gear backlash. The system presents diverse motion states, including single periodic motion, multi-periodic motion, quasi-periodic motion, and chaotic motion. There are three typical routes to chaos in the response, i.e., crisis to chaos, quasi-period to chaos, and period-doubling bifurcation to chaos.
- (2)
- The frequency spectrum of the gear system with localized spalling fault is mainly composed of the meshing frequency and its harmonic components. The fault frequency appears in the form of sidebands in the spectrum at low speed. The tooth spalling fault could lead to the periodic impulses in the time-domain waveform.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Dou, D.; Wang, J. Comparison on torsional mesh stiffness and contact ratio of involute internal gear and high contact ratio internal gear. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1423–1437. [Google Scholar] [CrossRef]
- Huang, K.; Xiong, Y.; Wang, T.; Chen, Q. Research on the dynamic response of high-contact-ratio spur gears influenced by surface roughness under EHL condition. Appl. Surf. Sci. 2017, 392, 8–18. [Google Scholar] [CrossRef]
- Huang, K.; Yi, Y.; Xiong, Y.; Cheng, Z.; Chen, H. Nonlinear dynamics analysis of high contact ratio gears system with multiple clearances. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 98. [Google Scholar] [CrossRef]
- Wang, J.; Howard, I. Finite element analysis of high contact ratio spur gears in mesh. J. Tribol. 2005, 127, 469–483. [Google Scholar] [CrossRef]
- Zhan, J.; Fard, M.; Jazar, R. A CAD-FEM-QSA integration technique for determining the time-varying meshing stiffness of gear pairs. Measurement 2017, 100, 139–149. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Zuo, M.J.; Qin, Y. Three new models for evaluation of standard involute spur gear mesh stiffness. Mech. Syst. Signal Process. 2018, 101, 424–434. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, H.; Huangfu, Y.; Chen, K.; Che, L.; Wen, B. A revised time-varying mesh stiffness model of spur gear pairs with tooth modifications. Mech. Mach. Theory 2018, 129, 261–278. [Google Scholar] [CrossRef]
- Chaari, F.; Baccar, W.; Abbes, M.S.; Haddar, M. Effect of spalling or tooth breakage on gear mesh stiffness and dynamic response of a one-stage spur gear transmission. Eur. J. Mech. A Solids 2008, 27, 691–705. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, Y.; Mechefske, C.K. Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng. Fail. Anal. 2014, 39, 92–107. [Google Scholar] [CrossRef]
- Han, L.; Qi, H. Influences of tooth spalling or local breakage on time-varying mesh stiffness of helical gears. Eng. Fail. Anal. 2017, 79, 75–88. [Google Scholar] [CrossRef]
- Luo, W.; Qiao, B.; Shen, Z.; Yang, Z.; Chen, X. Time-varying mesh stiffness calculation of a planetary gear set with the spalling defect under sliding friction. Meccanica 2020, 55, 245–260. [Google Scholar] [CrossRef]
- Meng, Z.; Shi, G.; Wang, F. Vibration response and fault characteristics analysis of gear based on time-varying mesh stiffness. Mech. Mach. Theory 2020, 148, 103786. [Google Scholar] [CrossRef]
- Ma, H.; Li, Z.; Feng, M.; Feng, R.; Wen, B. Time-varying mesh stiffness calculation of spur gears with spalling defect. Eng. Fail. Anal. 2016, 66, 166–176. [Google Scholar] [CrossRef]
- Saxena, A.; Parey, A.; Chouksey, M. Time varying mesh stiffness calculation of spur gear pair considering sliding friction and spalling defects. Eng. Fail. Anal. 2016, 70, 200–211. [Google Scholar] [CrossRef]
- Yoshida, A.; Ohue, Y.; Ishikawa, H. Diagnosis of tooth surface failure by wavelet transform of dynamic characteristics. Tribol. Int. 2000, 33, 273–279. [Google Scholar] [CrossRef]
- Jia, S.; Howard, I. Comparison of localised spalling and crack damage from dynamic modelling of spur gear vibrations. Mech. Syst. Signal Process. 2006, 20, 332–349. [Google Scholar] [CrossRef]
- Ma, R.; Chen, Y.; Cao, Q. Research on dynamics and fault mechanism of spur gear pair with spalling defect. J. Sound Vib. 2012, 331, 2097–2109. [Google Scholar] [CrossRef]
- Dadon, I.; Koren, N.; Klein, R.; Lipsett, M.G.; Bortman, J. Impact of gear tooth surface quality on detection of local faults. Eng. Fail. Anal. 2020, 108, 104291. [Google Scholar] [CrossRef]
- Rui, M.; Chen, Y. Research on the dynamic mechanism of the gear system with local crack and spalling failure. Eng. Fail. Anal. 2012, 26, 12–20. [Google Scholar]
- Yu, W.; Mechefske, C.K.; Timusk, M. A new dynamic model of a cylindrical gear pair with localized spalling defects. Nonlinear Dyn. 2017, 2018, 2077–2095. [Google Scholar] [CrossRef]
- Chen, K.; Ma, H.; Che, L.; Li, Z.; Wen, B. Comparison of meshing characteristics of helical gears with spalling fault using analytical and finite-element methods. Mech. Syst. Signal Process. 2019, 121, 279–298. [Google Scholar] [CrossRef]
- Huangfu, Y.; Chen, K.; Ma, H.; Li, X.; Han, H.; Zhao, Z. Meshing and dynamic characteristics analysis of spalled gear systems: A theoretical and experimental study. Mech. Syst. Signal Process. 2020, 139, 106640. [Google Scholar] [CrossRef]
- Luo, W.; Qiao, B.; Shen, Z.; Yang, Z.; Cao, H.; Chen, X. Investigation on the influence of spalling defects on the dynamic performance of planetary gear sets with sliding friction. Tribol. Int. 2021, 154, 106639. [Google Scholar] [CrossRef]
- Shi, L.; Wen, J.; Pan, B.; Xiang, Y.; Zhang, Q.; Lin, C. Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis. Appl. Sci. 2020, 10, 7058. [Google Scholar] [CrossRef]
- Ma, R.; Chen, Y. Bifurcation of multi-freedom gear system with spalling defect. Appl. Math. Mech. 2013, 34, 475–488. [Google Scholar] [CrossRef]
- Wu, J. Root Transition Curve and Root Stress; National Defense Industry Press: Arlington, VA, USA, 1989. [Google Scholar]
- Yang, L.; Baddour, N.; Ming, L. Dynamical modeling and experimental validation for tooth pitting and spalling in spur gears. Mech. Syst. Signal Process. 2018, 119, 155–181. [Google Scholar]
- Chen, Z.; Zhou, Z.; Zhai, W.; Wang, K. Improved analytical calculation model of spur gear mesh excitations with tooth profile deviations. Mech. Mach. Theory 2020, 149, 103838. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Tian, W.; Wu, Y.; Chen, Y. An improved nonlinear dynamic model of gear pair with tooth surface microscopic features. Nonlinear Dyn. 2019, 96, 1615–1634. [Google Scholar] [CrossRef]
- Chen, Q.; Zhou, J.; Khushnood, A.; Wu, Y.; Zhang, Y. Modelling and nonlinear dynamic behavior of a geared rotor-bearing system using tooth surface microscopic features based on fractal theory. AIP Adv. 2019, 9, 015201. [Google Scholar] [CrossRef] [Green Version]
- Xu, H. Development of a Generalized Mechanical Efficiency Prediction Methodology for Gear Pairs; The Ohio State University: Columbus, OH, USA, 2005. [Google Scholar]
- Yi, Y.; Huang, K.; Xiong, Y.; Sang, M. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. Mech. Syst. Signal Process. 2019, 132, 18–34. [Google Scholar] [CrossRef]
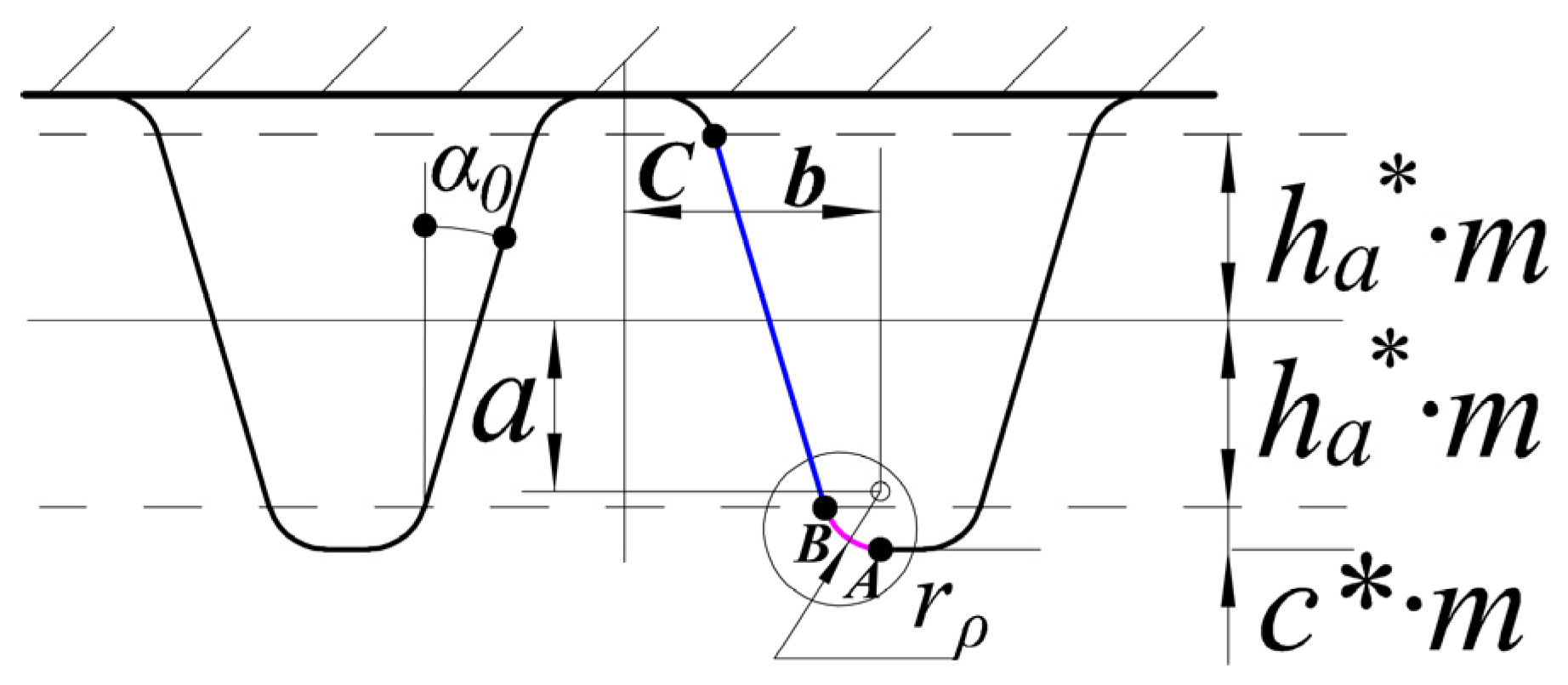
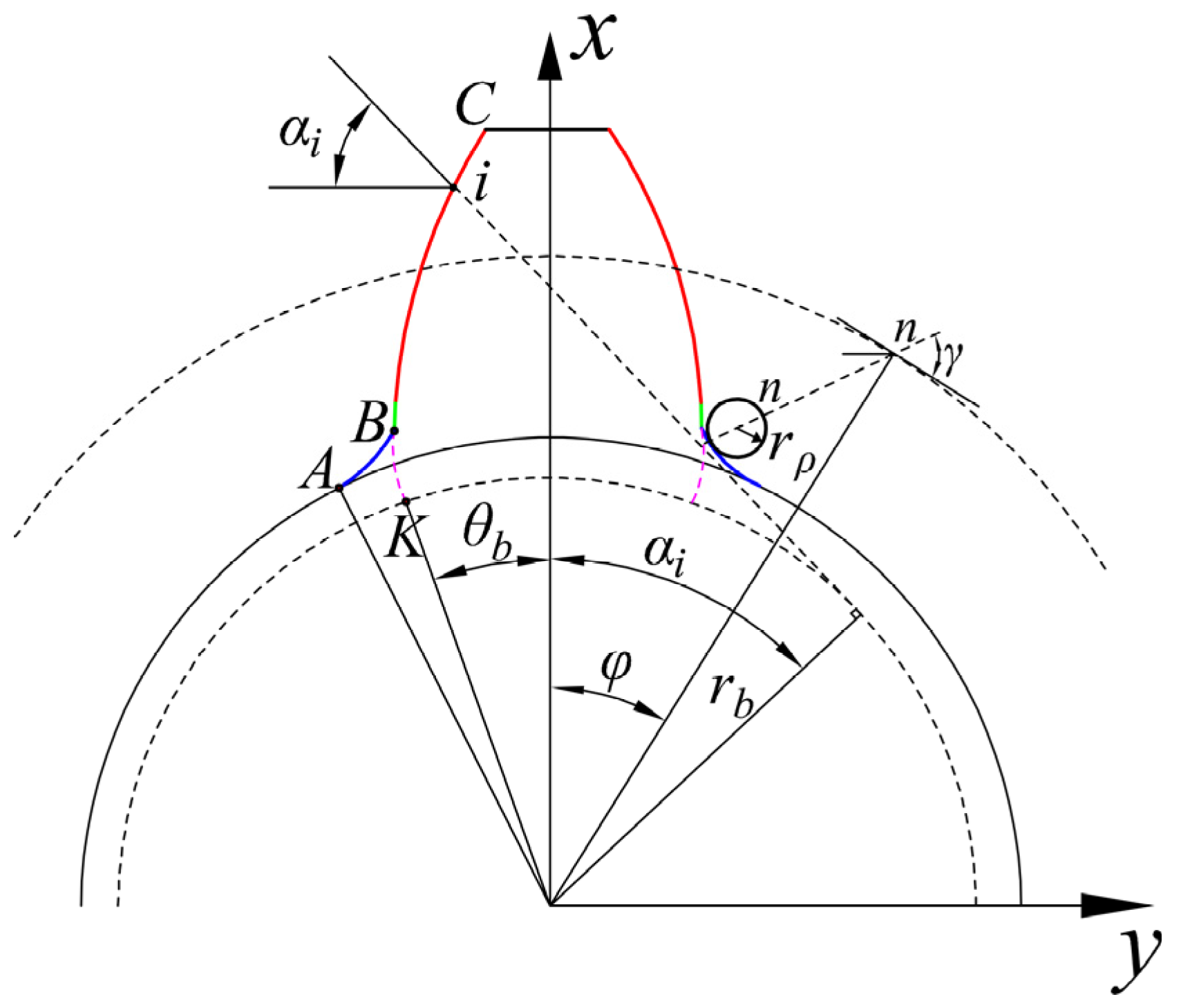
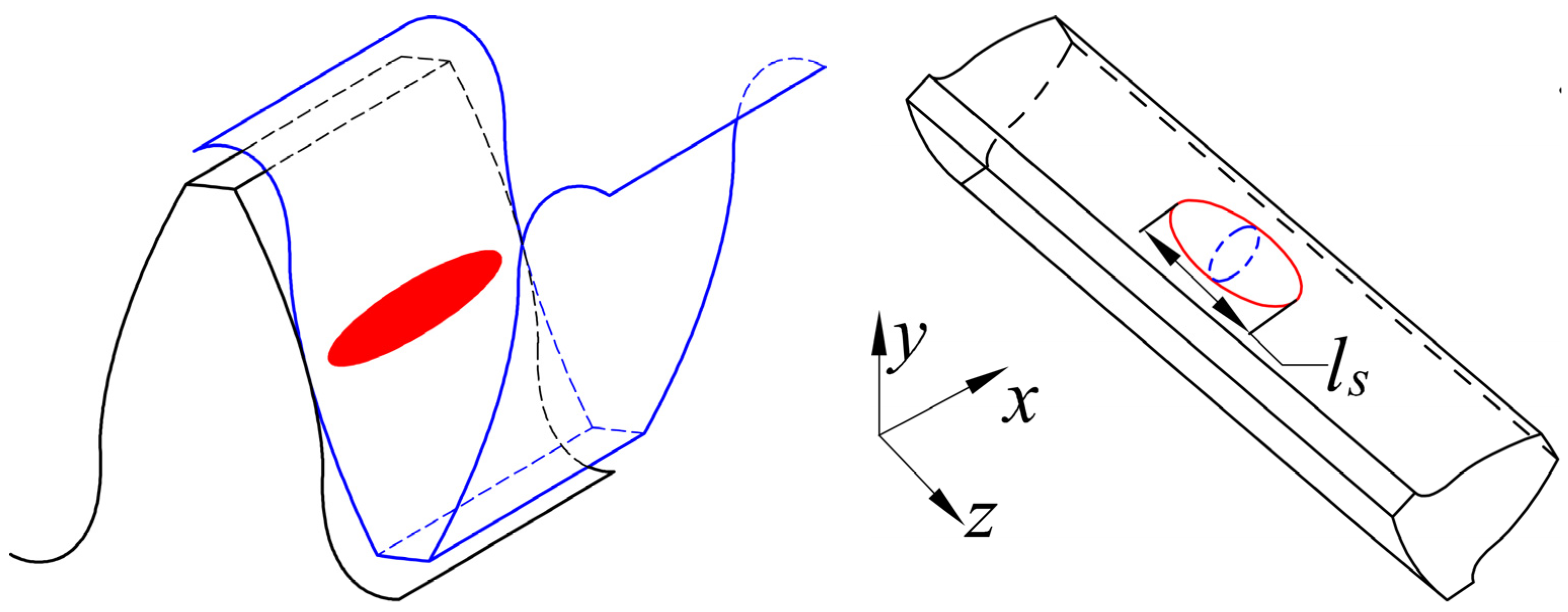
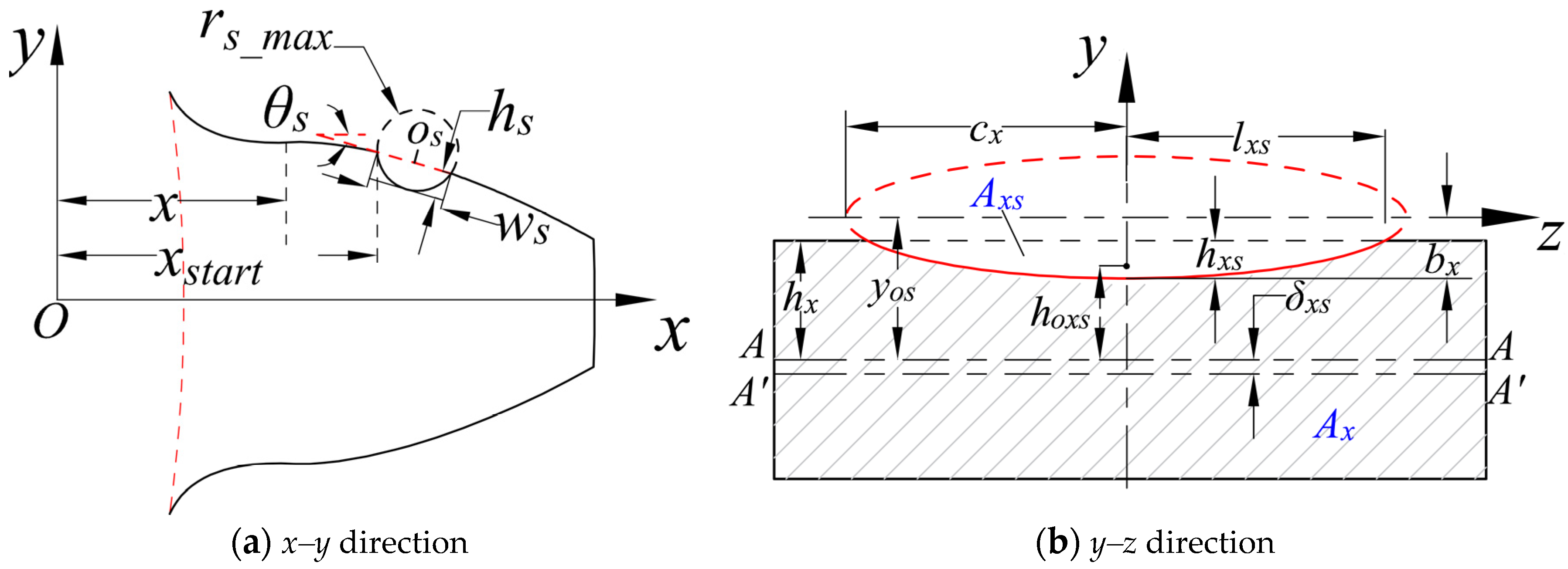
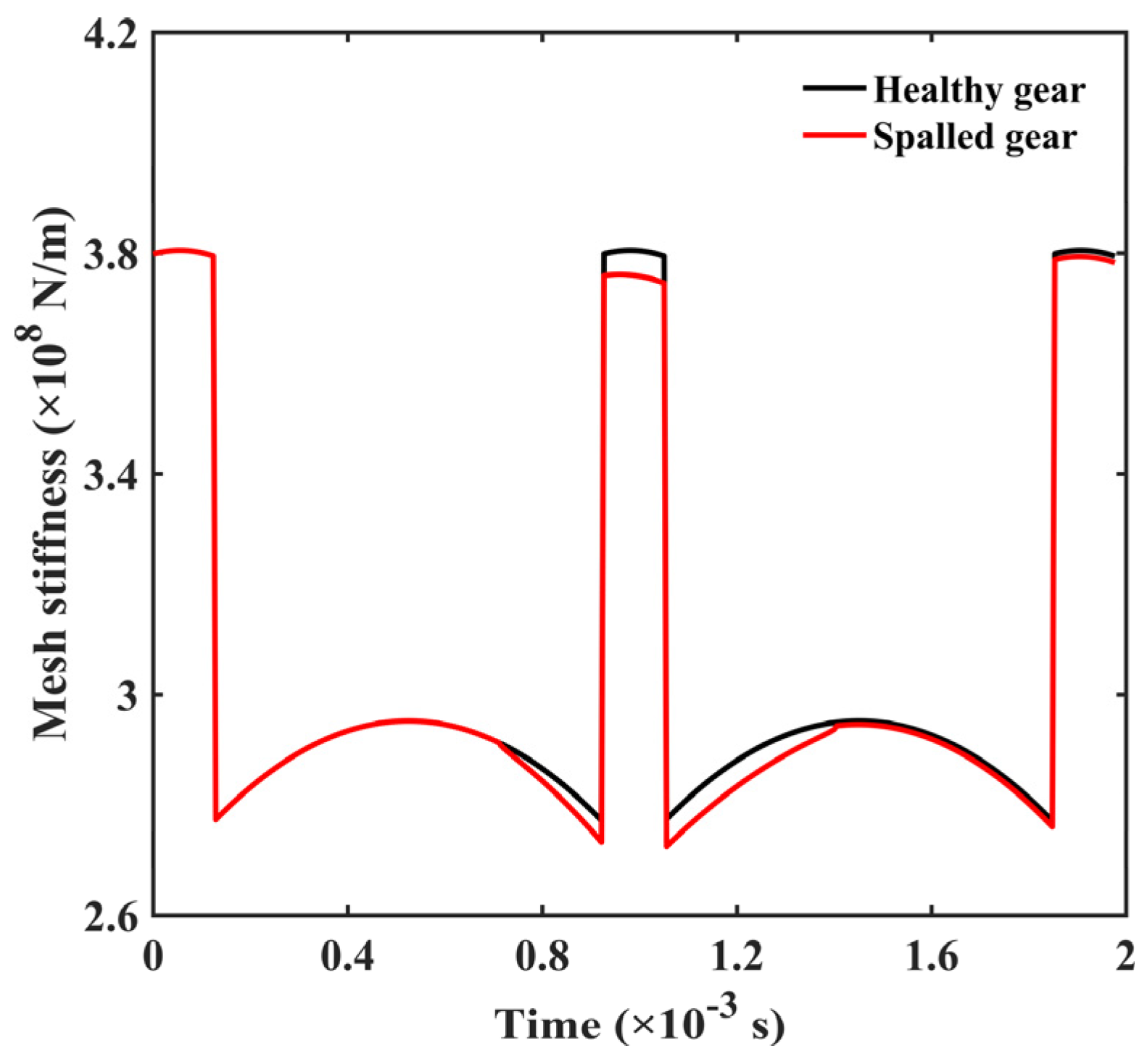


| Case | ws (mm) | ls (mm) | hs (mm) | θs (°) | xstart (mm) |
|---|---|---|---|---|---|
| Healthy gear | 0 | 0 | 0 | 0 | 0 |
| Spall gear | 4 | 16 | 2 | 18 | 66 |
| Parameters | Pinion/Gear | Parameters | Pinion/Gear |
|---|---|---|---|
| Tooth Number zp/zg | 27/31 | Designed contact ratio | 2.135 |
| Transverse modulus (mm) | 5 | Tooth width (mm) | 20 |
| Pressure angle (°) | 19 | Moments of inertia (kg·m2) Ip/Ig | 0.0051/0.0089 |
| Addendum coefficient | 1.32 | Mass (kg) mp/mg | 2.13/2.84 |
| Modification coefficient | 0 | Mesh damping ratio | 0.06 |
| Hub bore radius (mm) | 14 | Input power (kW) | 20 |
| Fault Frequency (fs) | Simulation Results | Experimental Results | Error |
|---|---|---|---|
| 10 Hz | 10 Hz | 0% | |
| 10 Hz | 9.75 Hz | 2.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Huang, K.; Xiong, Y.; Sang, M. Dynamic Analysis of a High-Contact-Ratio Spur Gear System with Localized Spalling and Experimental Validation. Machines 2022, 10, 154. https://doi.org/10.3390/machines10020154
Cheng Z, Huang K, Xiong Y, Sang M. Dynamic Analysis of a High-Contact-Ratio Spur Gear System with Localized Spalling and Experimental Validation. Machines. 2022; 10(2):154. https://doi.org/10.3390/machines10020154
Chicago/Turabian StyleCheng, Zhenbang, Kang Huang, Yangshou Xiong, and Meng Sang. 2022. "Dynamic Analysis of a High-Contact-Ratio Spur Gear System with Localized Spalling and Experimental Validation" Machines 10, no. 2: 154. https://doi.org/10.3390/machines10020154





