Truss Metamaterials: Multi-Physics Modeling for Band GapTuning
Abstract
:1. Introduction
2. Materials and Methods
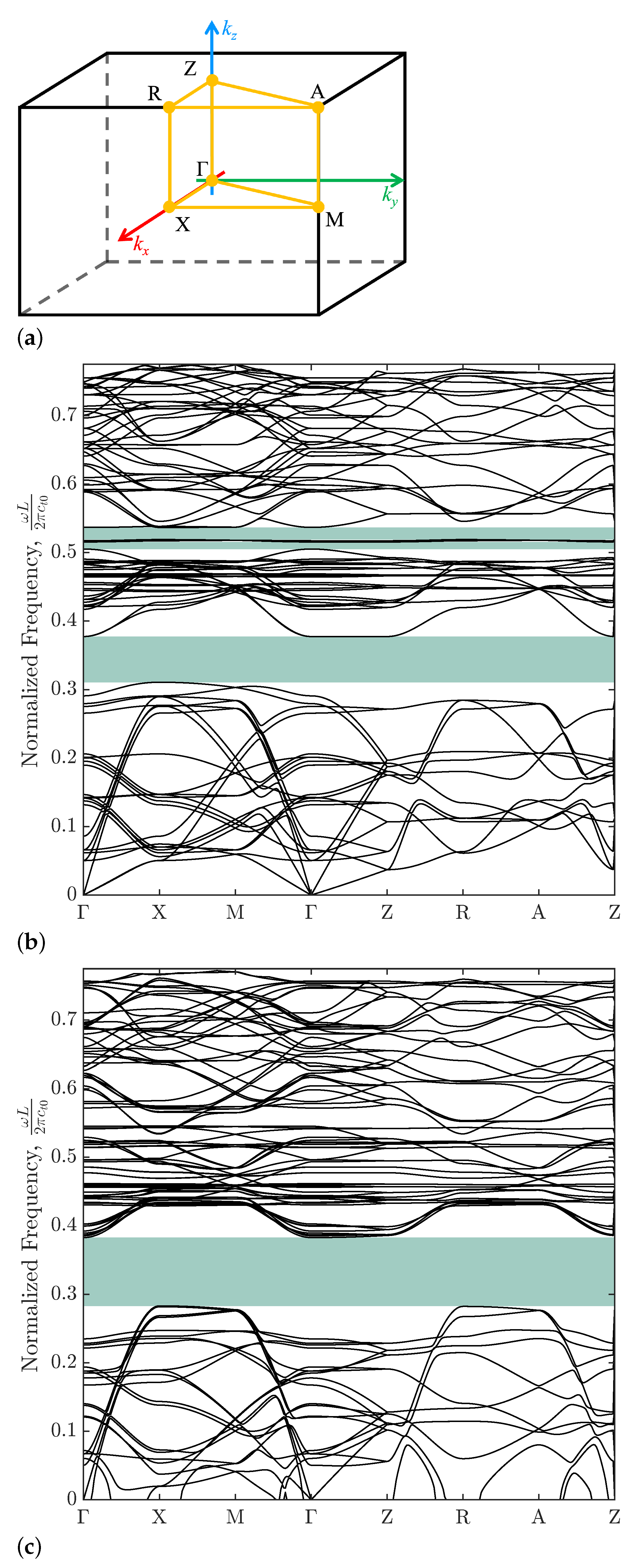
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Guo, H.; Wang, T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Lee, C.M.; Goverdovskiy, V.; Temnikov, A. Design of springs with “negative” stiffness to improve vehicle driver vibration isolation. J. Sound Vib. 2007, 302, 865–874. [Google Scholar] [CrossRef]
- Lee, C.M.; Goverdovskiy, V. A multi-stage high-speed railroad vibration isolation system with “negative” stiffness. J. Sound Vib. 2012, 331, 914–921. [Google Scholar] [CrossRef]
- Sarlis, A.; Pasala, D.T.; Constantinou, M.; Reinhorn, A.; Nagarajaiah, S.; Taylor, D. Negative Stiffness Device for Seismic Protection of Structures: Shake Table Testing of a Seismically Isolated Structure. J. Sound Vib. 2016, 142, 04016005. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, B.; Bai, Y.; Wang, L.; Rejab, M. Review of Phononic crystals and acoustic metamaterials. J. Sound Vib. 2020, 788, 012052. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Wang, Y.S.; Zhang, C. Effects of material parameters on elastic band gaps of two-dimensional solid phononic crystals. J. Appl. Phys. 2009, 106, 014903. [Google Scholar] [CrossRef]
- Elmadih, W.; Chronopoulos, D.; Zhu, J. Metamaterials for simultaneous acoustic and elastic bandgaps. Sci. Rep. 2021, 11, 14635. [Google Scholar] [CrossRef]
- Liu, M.; Xiang, J.; Zhong, Y. Band Structures Analysis Method of Two-Dimensional Phononic Crystals Using Wavelet-Based Elements. Crystals 2017, 7, 328. [Google Scholar] [CrossRef]
- Xiang, H.; Ma, X.; Xiang, J. Band Gaps and Transmission Characteristics Analysis on a Two-Dimensional Multiple-Scatter Phononic Crystal Structure. Materials 2020, 13, 2106. [Google Scholar] [CrossRef]
- Wu, L.; Zhai, Z.; Zhao, X.; Tian, X.; Li, D.; Wang, Q.; Jiang, H. Modular Design for Acoustic Metamaterials: Low-Frequency Noise Attenuation. Adv. Funct. Mater. 2022, 32, 2105712. [Google Scholar] [CrossRef]
- Du, Y.; Wu, W.; Chen, W.; Lin, Y.; Chi, Q. Control the structure to optimize the performance of sound absorption of acoustic metamaterial: A review. AIP Adv. 2021, 11, 060701. [Google Scholar] [CrossRef]
- Bruggi, M.; Corigliano, A. Optimal 2D auxetic micro-structures with band gap. Meccanica 2019, 54, 2001–2027. [Google Scholar] [CrossRef]
- Ye, H.; Shen, W.; Wang, W.; Tao, R. A systematic design of multifunctional lattice structures with energy absorption and phononic bandgap by topology and parameter optimization. Int. J. Smart Nano Mater. 2023, 14, 265–285. [Google Scholar] [CrossRef]
- Xiang, H.; Ma, X.; Xiang, J. Optimization for a Locally Resonant Phononic Crystal of Square Spiral with Circle Inside. IEEE Access 2019, 7, 145988–145995. [Google Scholar] [CrossRef]
- Yang, X.; Zhong, J.; Xiang, J. Broadband characteristics of high-performance energy-harvesting phononic crystals with point defect. Mod. Phys. Lett. B 2022, 36, 2250010. [Google Scholar] [CrossRef]
- Bertoldi, K.; Boyce, M. Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformations. Phys. Rev. B 2008, 78, 184107. [Google Scholar] [CrossRef]
- Bertoldi, K.; Wang, P.; Shim, J. Effects of geometric and material nonlinearities on tunable band gaps and low-frequency di-rectionality of phononic crystals. Phys. Rev. B 2013, 88, 014304. [Google Scholar]
- Bertoldi, K.; Boyce, M.; Deschanel, S.; Prange, S.; Mullin, T. Mechanics of deformation-triggered pattern transformations and superelastic behavior in periodic elastomeric structures. J. Mech. Phys. Solids 2008, 56, 2642–2668. [Google Scholar] [CrossRef]
- Ning, S.; Chu, D.; Jiang, H.; Yang, F.; Liu, Z.; Zhuang, Z. The role of material and geometric nonlinearities and damping effects in designing mechanically tunable acoustic metamaterials. Int. J. Mech. Sci. 2021, 197, 106299. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Ai, S.; Chen, H.; Pei, Y.; Zhou, X. Active acoustic metamaterials with tunable effective mass density by gradient magnetic fields. Appl. Phys. Lett. 2014, 105, 071913. [Google Scholar] [CrossRef]
- Bayat, A. Dynamic Response of Tunable Phononic Crystals and New Homogenization Approaches in Magnetoactive Composites. Ph.D. Thesis, University of Nevada, Reno, Nevada, 2015. [Google Scholar]
- Xia, B.; Chen, N.; Xie, L.; Qin, Y.; Yu, D. Temperature-controlled tunable acoustic metamaterial with active band gap and negative bulk modulus. Appl. Acoust. 2016, 112, 1–9. [Google Scholar] [CrossRef]
- Akl, W.; Baz, A. Active Acoustic Metamaterial with Simultaneously Programmable Density and Bulk Modulus. J. Vib. Acoust. 2013, 135, 031001. [Google Scholar] [CrossRef]
- Akl, W.; Baz, A. Multi-cell Active Acoustic Metamaterial with Programmable Bulk Modulus. J. Intell. Mater. Syst. Struct. 2010, 21, 541–556. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Bellis, M.D.; Misseroni, D. Design of tunable acoustic metamaterials with periodic piezoelectric microstructure. J. Intell. Mater. Syst. Struct. 2020, 40, 100977. [Google Scholar] [CrossRef]
- Cui, H.; Hensleigh, R.; Yao, D.; Maurya, D.; Kumar, P.; Kang, M.; Priya, S.; Zheng, X. Three-dimensional printing of piezoelectric materials with designed anisotropy and directional response. Nat. Mater. 2019, 18, 234–241. [Google Scholar] [CrossRef] [PubMed]
- Guo, S. A Coupled Multi-Physics Analysis Model for Integrating Transient ElectroMagnetics and Structural Dynamic Fields with Damage. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2017. [Google Scholar]
- COMSOL Multiphysics® v. 6.0. COMSOL AB: Stockholm, Sweden. Available online: www.comsol.com (accessed on 28 July 2023).
- Tiersten, H.F. Linear Piezoelectric Plate Vibrations, 1st ed.; Springer: New York, NY, USA, 1969; Volume 1. [Google Scholar]
- Corigliano, A.; Ardito, R.; Comi, C.; Frangi, A.; Ghisi, A.; Mariani, S. Mechanics of Microsystems, 1st ed.; Wiley: Chichester, UK, 2018; Volume 1. [Google Scholar]
- Calegaro, D.; Mariani, S. Active truss metamaterials: Modelling and tuning of band gaps. J. Mater. Sci. Chem. Eng. 2023, 11, 127–134. [Google Scholar] [CrossRef]
- Slesarenko, V.; Rudykh, S. Microscopic and macroscopic instabilities in hyperelastic fiber composites. J. Mech. Phys. Solids 2017, 99, 471–482. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calegaro, D.; Mariani, S. Truss Metamaterials: Multi-Physics Modeling for Band GapTuning. Machines 2023, 11, 913. https://doi.org/10.3390/machines11090913
Calegaro D, Mariani S. Truss Metamaterials: Multi-Physics Modeling for Band GapTuning. Machines. 2023; 11(9):913. https://doi.org/10.3390/machines11090913
Chicago/Turabian StyleCalegaro, Daniel, and Stefano Mariani. 2023. "Truss Metamaterials: Multi-Physics Modeling for Band GapTuning" Machines 11, no. 9: 913. https://doi.org/10.3390/machines11090913




