Cosmographic Constraints and Cosmic Fluids
Abstract
:1. Introduction
2. Cosmography: A Selection Criterion for Cosmological Models
3. Issues Related to Cosmography
4. Cosmography and the Equation of State of the Universe
5. Dark Energy Cosmological Models
- The ΛCDM model;
- DE models with a constant equation of state, derived from a scalar field coupling with curvature (ωCDM or quintessence);
- DE models with EoS parameterized in terms of the power of (e.g., the CPL parametrization);
- DE models interacting with CDM (e.g., the Chaplygin gas);
- DE from quantum effects (e.g., the Dvali–Gabadadze–Porrati (DGP) model and its phenomenological extension);
- -gravity models;
- -gravity models.
6. The ΛCDM Model
7. The Quintessence Model
8. The Chevalier–Polarsky–Linder Parameterization
9. The Chaplygin Gas
10. The Dvali–Gabadadze–Porrati Model
10.1. An Extension of DGP: The α Dark Energy Model
| Parameter | Fit 1 | Fit 2 | Fit 3 | Fit 4 |
|---|---|---|---|---|
11. Dark Energy from Extended Theories of Gravity
11.1. Cosmography of Gravity
11.2. Cosmography of Gravity
12. Experimental Procedures
12.1. The Observational Problem
12.2. Baryonic Acoustic Oscillations
12.2.1. Observations of Baryonic Acoustic Oscillations
12.3. The Supernova Ia Measurements
12.3.1. Supernova Ia Observations
12.4. The Cosmic Microwaves Background Measurement
12.4.1. Cosmic Microwaves Background Observations
12.5. Cosmographic Fits
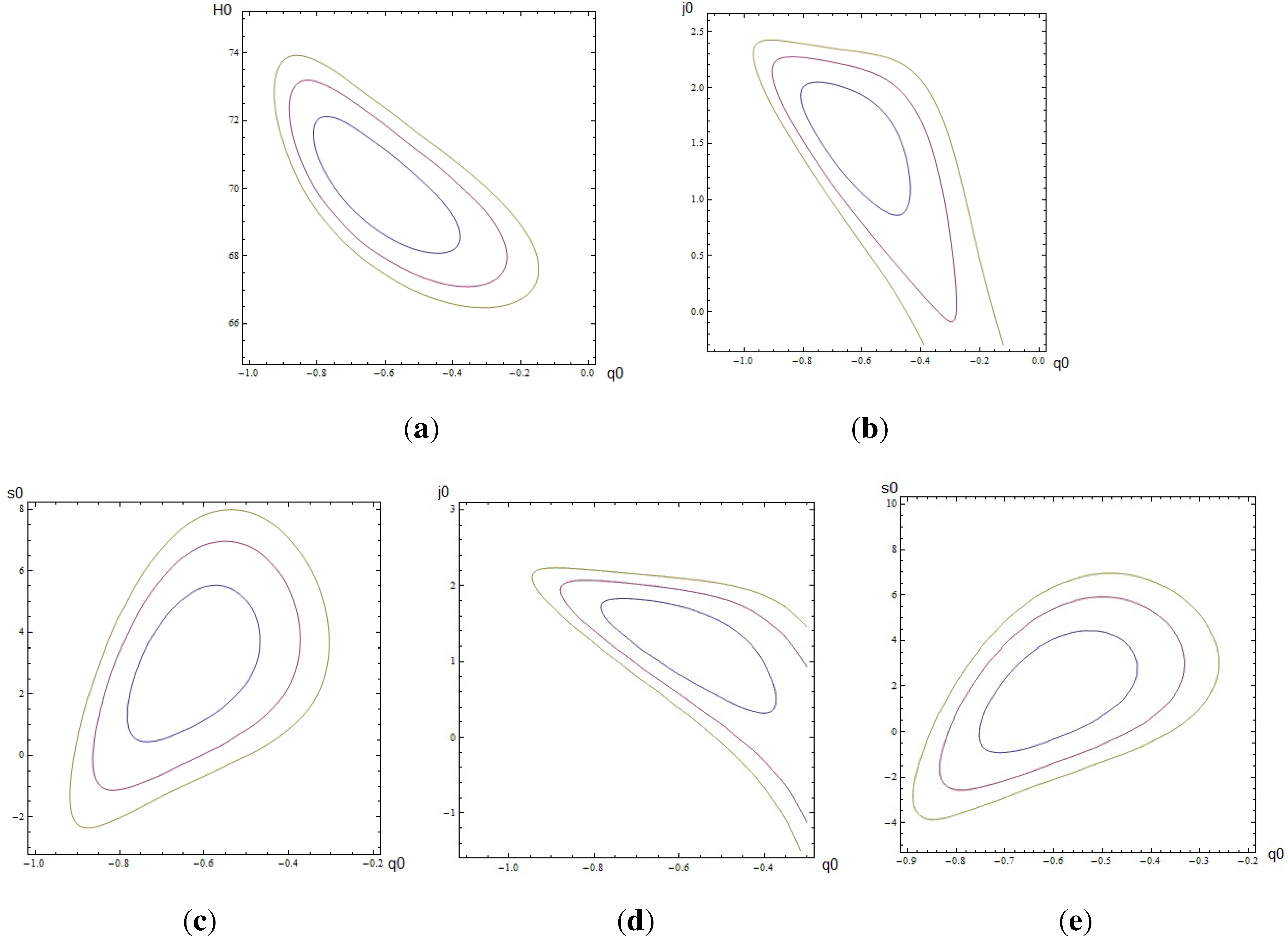
13. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Stairs, I.H. Testing general relativity with pulsar timing. Liv. Rev. Relativ. 2003, 6, 5. [Google Scholar] [CrossRef]
- Gair, J.R.; Vallisneri, M.; Larson, S.L.; Baker, J.G. Testing general relativity with low-frequency, space-based gravitational-wave detectors. Living Rev. Relativ. 2013, 16. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2006, 9, 1–100. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astronys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Knop, R.A.; Aldering, G.; Amanullah, R.; Astier, P.; Blanc, G.; Burns, M.S.; Conley, A.; Deustua, S.E.; Doi, M.; Ellis, R.; et al. New constraints on ΩM, ΩΛ, and w from an independent set of eleven high-redshift supernovae observed with HST. Astrophys. J. 2003, 598, 102–137. [Google Scholar] [CrossRef]
- Tonry, J.L.; Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Coil, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C.; et al. Cosmological results from high-z supernovae. Astrophys. J. 2003, 594, 1–24. [Google Scholar] [CrossRef]
- Barris, B.J.; Tonry, J.L.; Blondin, S.; Challis, P.; Chornock, R.; Clocchiatti, A.; Filippenko, A.V.; Garnavich, P.; Holland, S.T.; Jha, S.; et al. Twenty-three high-redshift supernovae from the Institute for Astronomy Deep Survey: Doubling the supernova sample at z > 0.7. Astrophys. J. 2004, 602, 571–594. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.-G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the Hubble space telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- De Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; De Gasperis, G.; Farese, P.C.; et al. A flat universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef] [PubMed]
- Stompor, R.; Abroe, M.; Ade, P.; Balbi, A.; Barbosa, D.; Bock, J.; Borrill, J.; Boscaleri, A.; De Bernardis, P.; Ferreira, P.G.; et al. Cosmological implications of the MAXIMA-1 high-resolution cosmic microwave background anisotropy measurement. Astrophys. J. 2001, 561, 7–10. [Google Scholar] [CrossRef]
- Dodelson, S.; Narayanan, V.K.; Tegmark, M.; Scranton, R.; Budavàri, T.; Connolly, A.; Csabai, I.; Eisenstein, D.; Frieman, J.A.; Gunn, J.E.; et al. The Three-dimensional power spectrum from angular clustering of galaxies in early sloan digital sky survey data. Astrophys. J. 2002, 572, 140–156. [Google Scholar] [CrossRef] [Green Version]
- Percival, W.J.; Sutherland, W.; Peacock, J.A.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; Collins, C.; et al. Parameter constraints for flat cosmologies from CMB and 2dFGRS power spectra. Mon. Not. R. Astron. Soc. 2002, 337, 1068–1080. [Google Scholar] [CrossRef]
- Szalay, A.S.; Jain, B.; Matsubara, T.; Scranton, R.; Vogeley, M.S.; Connolly, A.; Dodelson, S.; Eisenstein, D.; Frieman, J.A.; Gunn, J.E.; et al. Karhunen-Loève Estimation of the power spectrum parameters from the angular distribution of galaxies in early Sloan digital sky survey data. Astrophys. J. 2003, 591, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, E.; Maddox, S.; Cole, S.; Lahav, O.; Madgwick, D.S.; Norberg, P.; Peacock, J.A.; Baldry, I.K.; Baugh, C.M.; Bland-Hawthorn, J.; et al. The 2dF galaxy redshift survey: Correlation functions, peculiar velocities and the matter density of the universe. Mon. Not. R. Astrono. Soc. 2003, 346, 78–96. [Google Scholar] [CrossRef]
- McDonald, P.; Seljak, U.; Burles, S.; Schlegel, D.J.; Weinberg, D.H.; Shih, D.; Schaye, J.; Schneider, D.P.; Brinkmann, J.; Brunner, R.J.; et al. The Ly-α forest power spectrum from the Sloan digital sky survey. Astrophys. J. 2006, 163, 80–109. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Rev. Relativ. 2001, 3. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the euclid satellite. Living Rev. Relativ. 2013, 16. [Google Scholar] [CrossRef]
- Fujii, Y. Origin of the gravitational constant and particle masses in scale invariant scalar-tensor theory. Phys. Rev. D 1982, 26, 2580–2588. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 1988, 302, 668–696. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, J. Cosmological consequences of rolling homogeneus scalar field. Phys. Rev. D 1988, 37, 3406–3427. [Google Scholar] [CrossRef]
- Chiba, T.; Sugiyama, N.; Nakamura, T. Cosmology with x-matter. Mon. Not. R. Astrono. Soc. 1997, 289, 5–9. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Structure formation with a self-tuning scalar field. Phys. Rev. Lett. 1997, 79, 4740–4743. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Starobinsky, A.A. Reconstructing cosmological matter perturbations using standard candles and rulers. Astrophys. J. 2009, 704, 1086–1097. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686–4690. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Kunz, M. Degeneracy between the dark components resulting from the fact that gravity only measures the total energy-momentum tensor. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Vazquez, A.; Quevedo, H.; Sanchez, A. Thermodynamic systems as extremal hypersurfaces. J. Geom. Phys. 2010, 60, 1942–1949. [Google Scholar] [CrossRef]
- Bravetti, A.; Luongo, O. Dark energy from geometrothermodynamics. ArXiv E-Prints, 2013; arXiv:1306.6758. [Google Scholar] [CrossRef]
- Li, X.D.; Wang, S.; Huang, Q.G.; Zhang, X.; Li, M. Dark energy and fate of the Universe. Sci. China Phys. Mech. Astron. 2012, 55, 1330–1334. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The cosmological model. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Padmanabhan, T. Cosmological constant—The weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Farooq, O.; Ratra, B. Hubble parameter measurement constraints on the cosmological deceleration-acceleration transition redshift. Astrophys. J. Lett. 2013, 766, L7. [Google Scholar] [CrossRef]
- Farooq, O.; Crandall, S.; Ratra, B. Binned Hubble parameter measurements and the cosmological deceleration-acceleration transition. Phys. Lett. B 2013, 726, 72–82. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinski, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark energy: A brief review. Front. Phys. 2013, 8, 828–846. [Google Scholar] [CrossRef]
- Capozziello, S.; Luongo, O. Dark energy from entanglement entropy. Int. J. Theor. Phys. 2013, 52, 2698–2704. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.M.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Copeland, E.J. Constraining the quintessence equation of state with SnIa data and CMB peaks. Phys. Rev. D 2002, 65. [Google Scholar] [CrossRef]
- Sahni, V. Dark matter and dark energy. Lect. Notes Phys. 2004, 653, 141–179. [Google Scholar]
- Wang, Y.; Tegmark, M. New dark energy constraints from supernovae, microwave background, and Galaxy clustering. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Wang, Y; Garnavich, P.M. Measuring time dependence of dark energy density from type Ia supernova data. Astrophys. J. 2001, 552, 445–451. [Google Scholar]
- Linder, E.V. Mapping the cosmological expansion. Rep. Prog. Phys. 2008, 71. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating Universes with scaling dark matter. Int. J. Mod. Phys. D. 2001, 10, 213–224. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the Universe. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef]
- Horava, P. Quantum gravity at a Lifshitz point. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
- Horava, P. Spectral dimension of the Universe in quantum gravity at a Lifshitz point. Phys. Rev. Lett. 2009, 102. [Google Scholar] [CrossRef]
- Shafieloo, A.; Linder, E.V. Cosmographic degeneracy. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
- Rubano, C.; Scudellaro, P. Quintessence or phoenix? Gen. Relativ. Gravit. 2002, 34, 1931–1939. [Google Scholar] [CrossRef]
- Cattoen, C.; Visser, M. Cosmographic Hubble fits to the supernova data. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Rebolo, R.; Battye, R.A.; Carreira, P.; Cleary, K.; Davies, R.D.; Davis, R.J.; Dickinson, C.; Genova-Santos, R.; Grainge, K.; Gutiérrez, C.M.; et al. Cosmological parameter estimation using Very Small Array data out to l = 1500. Mon. Not. R. Astron. Soc. 2004, 353, 747–759. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological interpretation. Astrophys. J. 2011, 192. [Google Scholar] [CrossRef]
- Visser, M. General relativistic energy conditions: The Hubble expansion in the epoch of galaxy formation. Phys. Rev. D 1997, 56. [Google Scholar] [CrossRef]
- Luongo, O. Cosmography with the Hubble parameter. Mod. Phys. Lett. A 2011, 26, 1459–1466. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- Stephani, H. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambdrige, UK, 2003. [Google Scholar]
- Dayan, I.B.; Gasperini, M.; Marozzi, G.; Nugier, F.; Veneziano, G. Do stochastic inhomogeneities a dark-energy precision measurements? Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Capozziello, S.; Salzano, V. Cosmography and large scale structure by f(R) gravity: New results. Adv. Astron. 2009, 1. [Google Scholar] [CrossRef]
- Bianchi, E.; Rovelli, C. Why all these prejudices against a constant? ArXiv E-Prints, 2010; arXiv:1002.3966. [Google Scholar]
- Chaplygin, S. On gas jets. Sci. Mem. Moscow Univ. Math. Phys. 1904, 21, 1–14. [Google Scholar]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef] [PubMed]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507:1–043507:5. [Google Scholar] [CrossRef]
- Bilić, N.; Tupper, G.B.; Viollier, R.D. Unification of dark matter and dark energy: The inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
- Carturan, D.; Finelli, F. Cosmological effects of a class of fluid dark energy models. Phys. Rev. D 2003, 68, 103501:1–103501:5. [Google Scholar] [CrossRef]
- Amendola, L.; Finelli, F.; Burigana, C.; Carturan, D. WMAP and the generalized Chaplygin gas. J. Cosmol. Astropart. Phys. 2003, 7. [Google Scholar] [CrossRef]
- Sandvik, H.B.; Tegmark, M.; Zaldarriaga, M.; Waga, I. The end of unified dark matter? Phys. Rev. D 2004, 69. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely Kinetic k Essence as Unified Dark Matter. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef]
- Babichev, E. Global topological k-defects. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Calcagni, G.; Liddle, A.R. Tachyon dark energy models: Dynamics and constraints. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Li, H.; Guo, Z.-K.; Zhang, Y.-Z. Parametrization of k-ESSENCE and its Kinetic Term. Mod. Phys. Lett. A 2006, 21, 1683–1689. [Google Scholar] [CrossRef]
- Fang, W.; Lu, H.Q.; Huang, Z.G. Cosmologies with a general non-canonical scalar field. Class. Quantum Gravity 2007, 24, 3799–3811. [Google Scholar] [CrossRef]
- Bertacca, D.; Bartolo, N. The integrated SachsWolfe effect in unified dark matter scalar field cosmologies: An analytical approach. J. Cosmol. Astropart. Phys. 2007, 11. [Google Scholar] [CrossRef]
- De Putter, R.; Linder, E.V. Kinetic k-essence and quintessence. Astropart. Phys. 2007, 28, 263–272. [Google Scholar] [CrossRef]
- Linder, E.V.; Scherrer, R.J. Aetherizing Lambda: Barotropic fluids as dark energy. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Camera, S.; Bertacca, D.; Diaferio, A.; Bartolo, N.; Matarrese, S. Weak lensing signal in unified dark matter models. Mon. Not. R. Astron. Soc. 2009, 399, 1995–2003. [Google Scholar] [CrossRef]
- Bertacca, D.; Bartolo, N.; Matarrese, S. Unified dark matter scalar field models. Adv. Astron. 2010. [Google Scholar] [CrossRef]
- Camera, S.; Carbone, C.; Moscardini, L. Inclusive constraints on unified dark matter models from future large-scale surveys. J. Cosmol. Astropart. Phys. 2012, 03. [Google Scholar] [CrossRef]
- Maartens, R. Brane-world gravity. Living Rev. Relativ. 2004, 7. [Google Scholar] [CrossRef]
- Sch¨fer, B.M.; Koyama, K. Spherical collapse in modified gravity with the Birkhoff theorem. Mon. Not. R. Astron. Soc. 2008, 385, 411–422. [Google Scholar] [Green Version]
- Dvali, G.; Turner, M.S. Dark energy as a modification of the Friedmann Equation. ArXiv E-Prints, 2003; arXiv:astro-ph/0301510. [Google Scholar]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Capozziello, S.; Francaviglia, M. Extended theories of gravity and their cosmological and astrophysical applications. Gen. Relativ. Gravit. 2008, 40, 357–420. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 74, 115–146. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Faraoni, V. A bird’s eye view of f(R)-gravity. Open Astron. J. 2010, 3, 49–72. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From f(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Brans, C.H.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Capozziello, S.; De Ritis, R.; Rubano, C.; Scudellaro, P. Noether symmetries in cosmology. Nuovo Cimento 1996, 4, 1–114. [Google Scholar]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP Publishing: Bristol, UK, 1992. [Google Scholar]
- Capozziello, S.; De Laurentis, M.; Francaviglia, M.; Mercadante, S. From dark energy and dark matter to dark metric. Found. Phys. 2009, 39, 1161–1176. [Google Scholar] [CrossRef]
- Sciama, D.W. On the Origin of inertia. Mon. Not. R. Astron. Soc. 1953, 113, 34–42. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Vilkovisky, G. Effective action in quantum gravity. Class. Quantum Gravity 1992, 9, 894–903. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Capozziello, S.; Fang, L.Z. Curvature quintessence. Int. J. Mod. Phys. D 2002, 11, 483–491. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without Scalar Fields. In Recent Research Developments in Astronomy and Astrophysics 1; Research Signpost: Trivandrum, India, 2003. [Google Scholar]
- Capozziello, S.; Cardone, V.F.; Carloni, S.; Troisi, A. Curvature quintessence matched with observational data. Int. J. Mod. Phys. D 2003, 12, 1969–1982. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kawasaki, M. Can modified gravity explain accelerated cosmic expansion? Phys. Lett. B 2003, 573, 1–4. [Google Scholar] [CrossRef]
- Olmo, G.J. The gravity lagrangian according to solar system experiments. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Olmo, G.J. Post-Newtonian constraints on f(R) cosmologies in metric and Palatini formalism. Phys. Rev. D 2005, 72. [Google Scholar] [CrossRef]
- Erickcek, A.L.; Smith, T.L.; Kamionkowski, M. Solar system tests do rule out 1/R gravity. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Chiba, T.; Smith, T.L.; Erickcek, A.L. Solar System constraints to general f(R) gravity. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Navarro, I.; Van Acoleyen, K. f(R) actions, cosmic acceleration and local tests of gravity. J. Cosmol. Astropart. Phys. 2007, 2007. [Google Scholar] [CrossRef]
- Capozziello, S.; Tsujikawa, S. Solar system and equivalence principle constraints on f(R) gravity by the chameleon approach. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D. Cosmology of f(R) gravity in the metric variational approach. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Phantom crossing, equation-of-state singularities, and local gravity constraints in f(R) models. Phys. Lett. B 2008, 660, 125–132. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) cosmic acceleration that evade solar system tests. Phys. Rev. D 2007, 76. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. Lett. J. Exp. Theor. Phys. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A. Do consistent f(R) models mimic General Relativity plus Λ. Phys. Lett. B 2007, 654, 7–12. [Google Scholar] [CrossRef]
- Tsujikawa, S. Observational signatures of f(R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Deruelle, N.; Sasaki, M.; Sendouda, Y. “Detuned” f(R) gravity and dark energy. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Linder, E.V. Exponential gravity. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I. Testing f(R) theories using the first time derivative of the orbital period of the binary pulsars. Mon. Not. R. Astron. Soc. 2013, 431, 741–748. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Rosa, R.; Garufi, F.; Milano, L. Testing gravitational theories using Eccentric Eclipsing Detached Binaries. Mon. Not. R. Astron. Soc. 2012, 424, 2371–2379. [Google Scholar] [CrossRef]
- De Laurentis, M.; Capozziello, S. Quadrupolar gravitational radiation as a test-bed for f(R) gravity. Astropart. Phys. 2011, 35, 257–265. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Nojiri, S.; Odintsov, S.D. Classifying and avoiding singularities in the alternative gravity dark energy models. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Nojiri, S.; Odintsov, S.D. f(R) gravity constrained by PPN parameters and stochastic background of gravitational waves. Gen. Relativ. Gravit. 2009, 49, 2313–2344. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Cosmographic reconstruction of f(T) cosmology. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Updated constraints on f(R) gravity from cosmography. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Carroll, S.M.; Sawicki, I.; Silvestri, A.; Trodden, M. Modified-source gravity and cosmological structure formation. New J. Phys. 2006, 8. [Google Scholar] [CrossRef]
- Bean, R.; Bernat, D.; Pogosian, L.; Silvestri, A.; Trodden, M. Dynamics of linear perturbations in f(R) gravity. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Song, Y.S.; Hu, W.; Sawicki, I. Large scale structure of f(R) gravity. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Pogosian, L.; Silvestri, A. Pattern of growth in viable f(R) cosmologies. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f(R) gravity viewpoint. Annalen der Physik 2012, 524, 545–578. [Google Scholar] [CrossRef]
- De Martino, I.; De Laurentis, M.; Atrio-Barandela, F.; Capozziello, S. Constraining f(R) gravity with PLANCK data on galaxy cluster profiles. ArXiv E-Prints, 2013; arXiv:1310.0693. [Google Scholar] [CrossRef]
- Zhang, P. Testing gravity against the early time integrated Sachs-Wolfe effect. Phys. Rev. D 2006, 73. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Tatekawa, T. The effect of modified gravity on weak lensing. Phys. Lett. B 2008, 665, 325–331. [Google Scholar] [CrossRef]
- Schmidt, F. Stochastic background from inspiralling double neutron stars. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity; Springer: New York, NY, USA, 2013. [Google Scholar]
- Einstein, A. Theorie der Raume mit Riemannmetrik und Fernparallelismus. Preuss. Akad. Wiss. Phys. Math. Kl. 1930, 217. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s other gravity and the acceleration of the Universe. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Li, B.; Sotiriou, T.; Barrow, J.D. Large-scale structure in f(T) gravity. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Karami, K.; Abdolmaleki, A. f(T) modified teleparallel gravity models as an alternative for holographic and new agegraphic dark energy models. Res. Astron. Astrophys. 2013, 13, 757–771. [Google Scholar] [CrossRef]
- Tsyba, P.Y.; Kulnazarov, I.I.; Yerzhanov, K.K.; Myrzakulov, R. Int. J. Theor. Phys. 2011, 50, 1876–1886. [CrossRef]
- Bamba, K.; Geng, C.Q.; Lee, C.C.; Luo, L.W. Equation of state for dark energy in f(T) gravity. J. Cosm. Astropart. Phys. 2011, 1. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H.W. Observational constraints on f(T) theory. Phys. Lett. B 2010, 693, 415–420. [Google Scholar] [CrossRef]
- Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Cosmological perturbations in f(T) gravity. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, S.; Saridakis, E.N. f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmol. Astropart. Phys. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Setare, M.R.; Houndjo, M.J.S. Finite-time future singularities models in f(T) gravity and the effects of viscosity. Can. J. Phys. 2013, 91, 260–267. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Linder, E.V. First Principles of Cosmology; Addison-Wesley: London, UK, 1997. [Google Scholar]
- Tegmark, M. Measuring spacetime: From the big bang to black holes. Science 2002, 296, 1427–1433. [Google Scholar] [CrossRef] [PubMed]
- Durrer, R. What do we really know about dark energy? Philos. Trans. R. Soc. A 2011, 369, 5102–5114. [Google Scholar] [CrossRef] [PubMed]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Lazkoz, R.; Salzano, V.; Sendra, I. Tension between SNela and BAO: Current status and future forecasts. J. Cosmol. Astropart. Phys. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Peebles, P.J.E.; Yu, J.T. Primeval adiabatic perturbation in an expanding universe. Astrophys. J. 1970, 162, 815–839. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Seo, H.-J.; Sirko, E.; Spergel, D.N. Improving cosmological distance measurements by reconstruction of the baryonic acoustic peak. Astrophys. J. 2007, 664, 675–679. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N. Small scale cosmological perturbations: An analytic approach. Astrophys. J. 1996, 471, 542–570. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W. Baryonic features in the matter transfer function. Astrophys. J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- Meiksin, A.; White, M.; Peacock, J.A. Baryonic signatures in large scale structure. Mon. Not. R. Astron. Soc. 1999, 304, 851–864. [Google Scholar] [CrossRef]
- Seo, H.J.; Eisenstein, D.J. Baryonic acoustic oscillations in simulated galaxy redshift surveys. Astrophys. J. 2005, 633, 575–588. [Google Scholar] [CrossRef]
- Angulo, R.; Baugh, C.M.; Frenk, C.S.; Bower, R.G.; Jenkins, A.; Morris, S.L. Constraints on the dark energy equation of state from the imprint of baryons on the power spectrum of clusters. Mon. Not. R. Astron. Soc. 2005, 362, 25–29. [Google Scholar] [CrossRef] [Green Version]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.; Komatsu, E. Perturbation theory reloaded: Analytical calculation of non-linearity in baryonic oscillations in the real space matter power spectrum. Astrophys. J. 2006, 651, 619–626. [Google Scholar] [CrossRef]
- Huff, E.; Schulz, A.E.; White, M.; Schlegel, D.J.; Warren, M.S. Simulations of baryon oscillations. Astrophys. Phys. 2007, 26, 351–366. [Google Scholar] [CrossRef]
- Angulo, R.E.; Baugh, C.M.; Frenk, C.S.; Lacey, C.G. The detectability of baryonic acoustic oscillations in future galaxy surveys. Mon. Not. R. Astron. Soc. 2008, 383, 755–776. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87–255. [Google Scholar] [CrossRef]
- Percival, W.J.; Cole, S.; Eisenstein, D.J.; Nichol, R.C.; Peacock, J.A.; Pope, A.C.; Szalay, A.S. Measuring the baryon acoustic oscillation scale using the SDSS and 2dFGRS. Mon. Not. R. Astron. Soc. 2007, 381, 1053–1066. [Google Scholar] [CrossRef] [Green Version]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezić, Ž.; Knapp, G.R.; et al. Baryon acoustic oscillations in the sloan digital sky survey data release 7 galaxy sample. Mon. Not. R. Astron. Soc. 2010, 401, 2148–2168. [Google Scholar] [CrossRef] [Green Version]
- Shafieloo, A.; Clarkson, C. Model independent tests of the standard cosmological model. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Shafieloo, A.; Sahni, V.; Starobinsky, A.A. A new null diagnostic customized for reconstructing the properties of dark energy from baryon acoustic oscillations data. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- Phillips, M.M. The absolute magnitudes of Type IA supernovae. Astrophys. J. Lett. 1993, 413, 105–108. [Google Scholar] [CrossRef]
- Howell, D.A.; Sullivan, M.; Nugent, P.E.; Ellis, R.S.; Conley, A.J.; Le Borgne, D.; Carlberg, R.G.; Guy, J.; Balam, D.; Basa, S.; et al. The type Ia supernova SNLS-03D3bb from a super-Chandrasekhar-mass white dwarf star. Nature 2006, 443, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Filippenko, A.V. Optical spectra of supernovae. Annu. Rev. Astron. Astrophys. 1997, 35, 309–355. [Google Scholar] [CrossRef]
- Barbon, R.; Buondí, V.; Cappellaro, E.; Turatto, M. The Asiago Supernova Catalogue—10 years after. Astron. Astrophys. 1999, 139, 531–536. [Google Scholar] [CrossRef]
- Ho, L.C.; Van Dyk, S.D.; Pooley, G.G.; Sramek, R.A.; Weiler, K.W. Discovery of radio outbursts in the active nucleus of M81. Astron. J. 1999, 118, 843–852. [Google Scholar] [CrossRef]
- Kowalski, M.; Rubin, D.; Aldering, G.; Agostinho, R.J.; Amadon, A.; Amanullah, R.; Balland, C.; Barbary, K.; Blanc, G.; Challis, P.J.; et al. Improved cosmological constraints from new, old and combined supernova datasets. Astrophys. J. 2008, 686, 749–778. [Google Scholar] [CrossRef]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and light curves of six Type Ia supernovae at 0.511 < z < 1.12 and the union2 compilation. Astrophys. J. 2010, 716, 712–738. [Google Scholar]
- Guy, J.; Sullivan, M.; Conley, A.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. The Supernova Legacy Survey 3-year sample: Type Ia supernovae photometric distances and cosmological constraints. Astron. Astrophys. 2010, 523, 7:1–7:34. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. Supernova constraints and systematic uncertainties from the First 3 Years of the Supernova Legacy Survey. Astrophys. J. 2011, 192. [Google Scholar] [CrossRef]
- Sullivan, M.; Guy, J.; Conley, A.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. SNLS3: Constraints on dark energy combining the Supernova Legacy Survey three year data with other probes. Astrophys. J. 2011, 737. [Google Scholar] [CrossRef]
- Salzano, V.; Wang, Y.; Sendra, I.; Lazkoz, R. Linear dark energy equation of state revealed by supernovae? ArXiv E-Prints, 2012; arXiv:1211.1012. [Google Scholar] [CrossRef]
- Wilson, R.W.; Panzias, A.A. A measurement of excess antenna temperature at 4080 Mc/s. Astroph. J. 1965, 142, 419–421. [Google Scholar]
- Fixsen, D.J.; Cheng, E.S.; Gales, J.M.; Mather, J.C.; Shafer, R.A.; Wright, E.L. The cosmic microwave background spectrum from the full COBE/FIRAS data set. Astrophys. J. 1996, 473, 576–587. [Google Scholar] [CrossRef]
- Silk, J. Cosmic black-body radiation and galaxy formation. Astrophys. J. 1968, 151, 459:1–459:14. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a cosmological model and angular variations of the microwave background. Astrophys. J. 1967, 147, 73:1–73:18. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXIII. Isotropy and Statistics of the CMB. ArXiv E-Prints, 2013; arXiv:1303.5083. [Google Scholar]
- Francis, M. First Planck Results: The Universe Is still Weird and Interesting. Available online: http://arstechnica.com/science/2013/03/first-planck-results-the-universe-is-still-weird-and-interesting/ (accessed on 2 December 2013).
- Europe Space Agency Web Page. Planck Reveals An almost Perfect Universe. Available online: http://www.esa.int/Our_Activities/Space_Science/Planck/Planck_reveals_an_almost_perfect_Universe (accessed on 2 December 2013).
- Europe Space Agency. Planck Legacy Archive (PLA). Available online: http://www.sciops.esa.int/index.php?project=planck&page=Planck_Legacy_Archive (accessed on 2 December 2013).
- Vielva, P.; Martinez-Gonzalez, E.; Barreiro, R.B.; Sanz, L.J.; Cayon, L. Detection of non-Gaussianity in the WMAP 1-year data using spherical wavelets. Astrophys. J. 2004, 609, 22–34. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Bennett, C.L.; Hill, R.S.; Hinshaw, G.; Larson, D.; Smith, K.M.; Dunkley, J.; Gold, B.; Halpern, M.; Jarosik, N.; Kogut, A.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Are there cosmic microwave background anomalies? Astrophys. J. 2011, 192. [Google Scholar] [CrossRef]
- Bennett, C.L.; Larson, D.; Weiland, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observation. Astrophys. J. 2013, 208. [Google Scholar] [CrossRef]
- Melchiorri, A.; Griffiths, L.M. From anisotropy to omega. New Astron. Rev. 2001, 45, 321–328. [Google Scholar] [CrossRef]
- Riess, A.G. A redetermination of the Hubble constant with the Hubble Space Telescope from a differential distance ladder. Astrophys. J. 2009, 699, 539–563. [Google Scholar] [CrossRef]
- Gruber, C.; Luongo, O. Cosmographic analysis of the equation of state of the universe through Padé approximations. ArXiv E-Prints, 2013; arXiv:1309.3215. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. ArXiv E-Prints, 2013; arXiv:1303.5076. [Google Scholar]
- Neben, A.R.; Turner, M.S. Beyond H0 and q0: Cosmology is no longer just two numbers. Astrophys. J. 2013, 769, 133:1–133:8. [Google Scholar]
- Luongo, O. Dark energy from a positive jerk parameter. Mod. Phys. Lett. A 2013, 28. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Constraints from Cosmography in various parameterizations. ArXiv E-Prints, 2013; arXiv:1301.4044. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Capozziello, S.; De Laurentis, M.; Luongo, O.; Ruggeri, A.C. Cosmographic Constraints and Cosmic Fluids. Galaxies 2013, 1, 216-260. https://doi.org/10.3390/galaxies1030216
Capozziello S, De Laurentis M, Luongo O, Ruggeri AC. Cosmographic Constraints and Cosmic Fluids. Galaxies. 2013; 1(3):216-260. https://doi.org/10.3390/galaxies1030216
Chicago/Turabian StyleCapozziello, Salvatore, Mariafelicia De Laurentis, Orlando Luongo, and Alan Cosimo Ruggeri. 2013. "Cosmographic Constraints and Cosmic Fluids" Galaxies 1, no. 3: 216-260. https://doi.org/10.3390/galaxies1030216





