Towards Accurate Prediction of Unbalance Response, Oil Whirl and Oil Whip of Flexible Rotors Supported by Hydrodynamic Bearings
Abstract
:1. Introduction
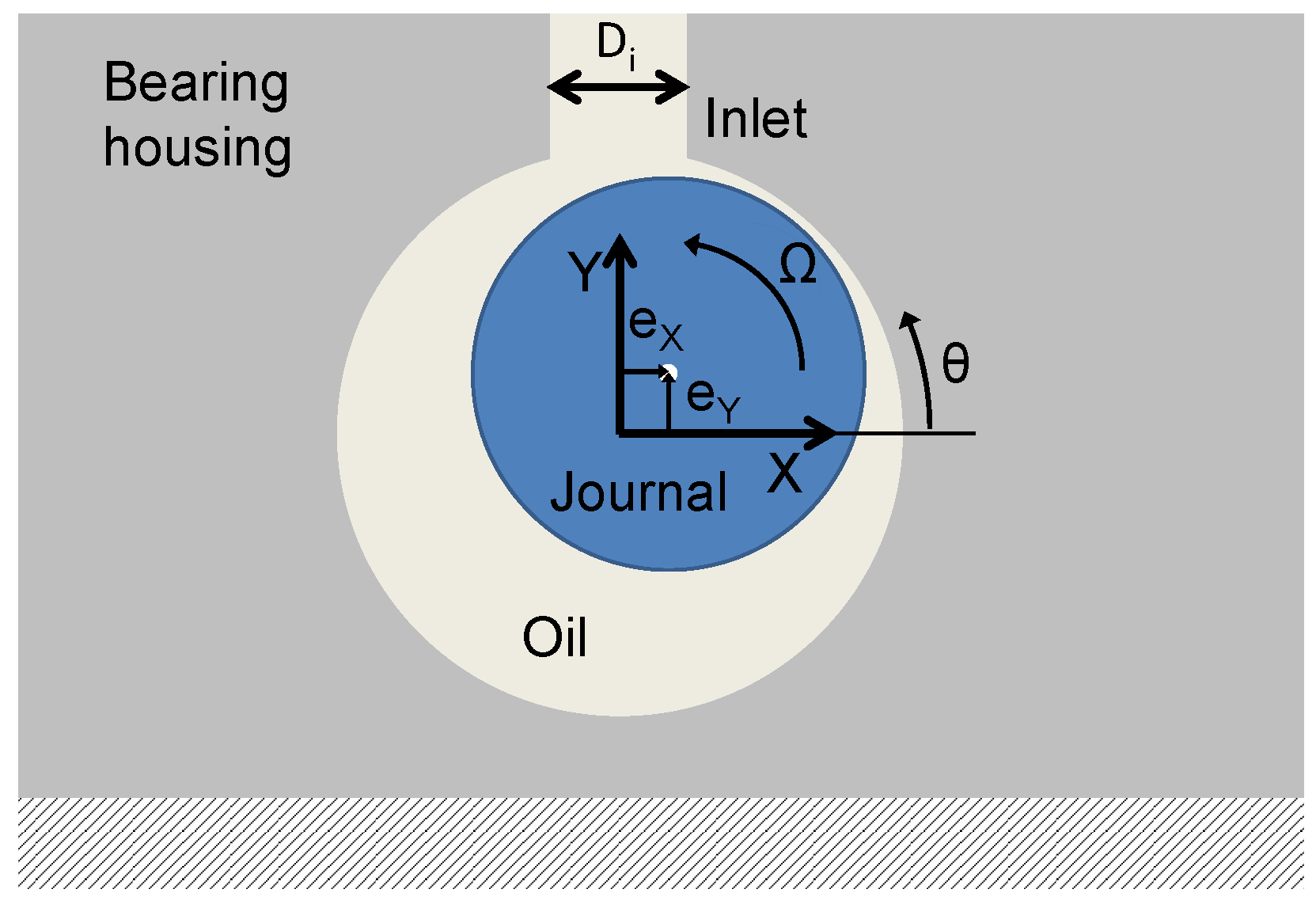
2. Bearing Models
2.1. Bearing Model 1: Isoviscous Short Bearings with Half-Sommerfeld Cavitation Conditions.
- the flow is dominated by the pressure gradients in the axial direction, and thus, the pressure gradient in circumferential direction can be ignored: .
- the fluid viscosity does not vary with time or location.
- the shaft is always aligned with the bearing bore, i.e., shaft tilting is not included in the fluid film thickness function.
- the pressure distribution is dominated by the hydrodynamic pressure buildup; therefore, the hydrostatic pressure contribution of the supply is neglected.
2.2. Bearing Model 2: Finite Length Journal Bearing with Gümbel Cavitation Conditions Including a Lumped Thermal Model
2.3. Bearing Model 3: Finite Length Journal Bearing Including a Mass-Conservative Cavitation Algorithm, Non-Newtonian Fluid Description, Shaft Tilting Kinematics and a Distributed Thermal Model
2.4. Summary of Bearing Models
3. Rotor-Bearing System A: A High Speed Laval Rotor on Plain Journal Bearings
3.1. Rotor and Bearing Layout
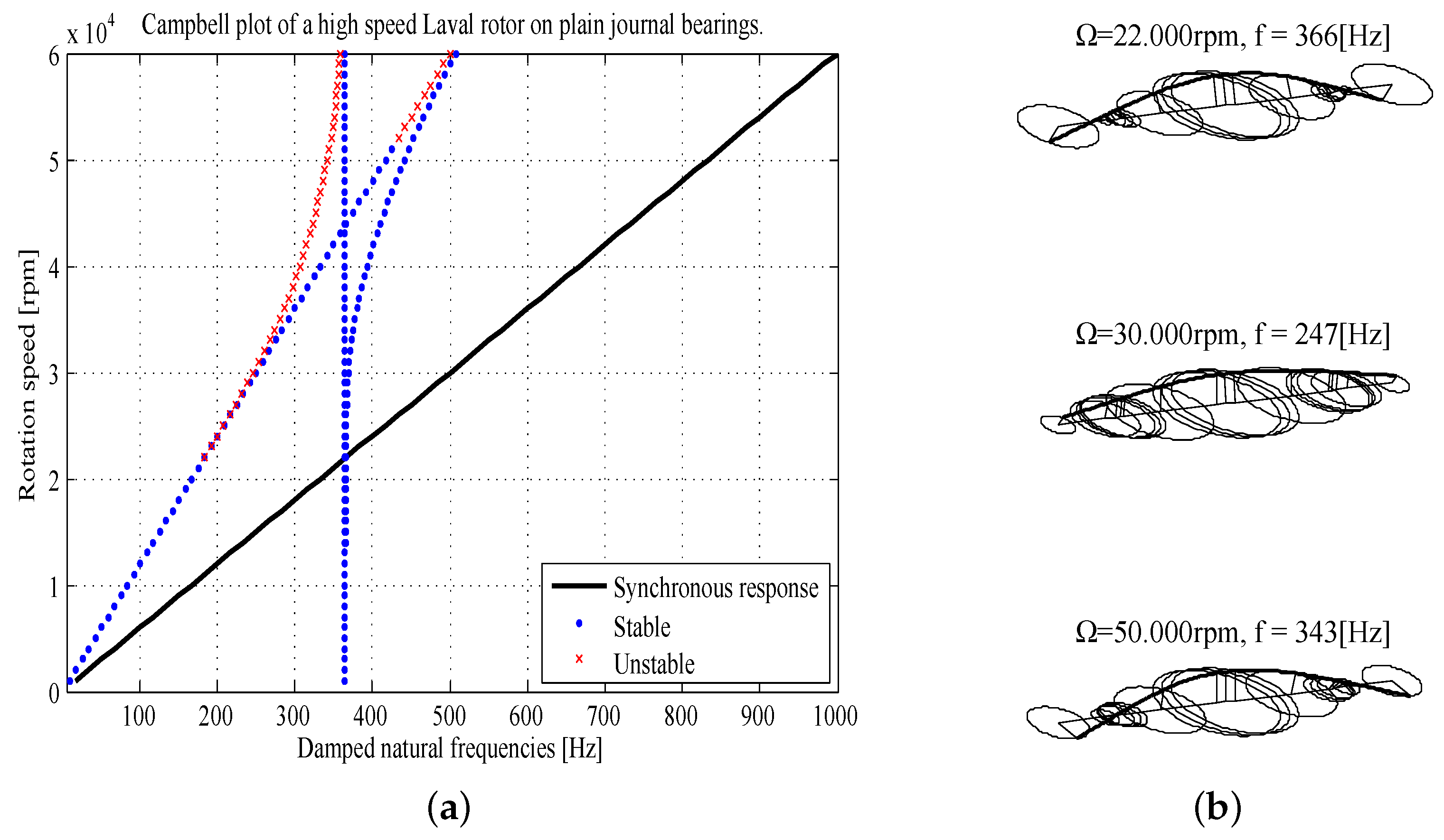
3.2. Rotor Model and Linear Rotodynamic Response
- traversal of a critical speed caused by the first shaft bending mode at Hz.
- above this critical speed, the first rigid body mode (a cylindrical mode, see Figure 6b) becomes linearly unstable at Hz.
- at rotation speeds above 40.000rpm, the whirl locks into the first shaft bending mode, resulting in a whip mode, which combines rigid body motion and bending motion.
3.3. Non-Linear Time-Transient Analysis
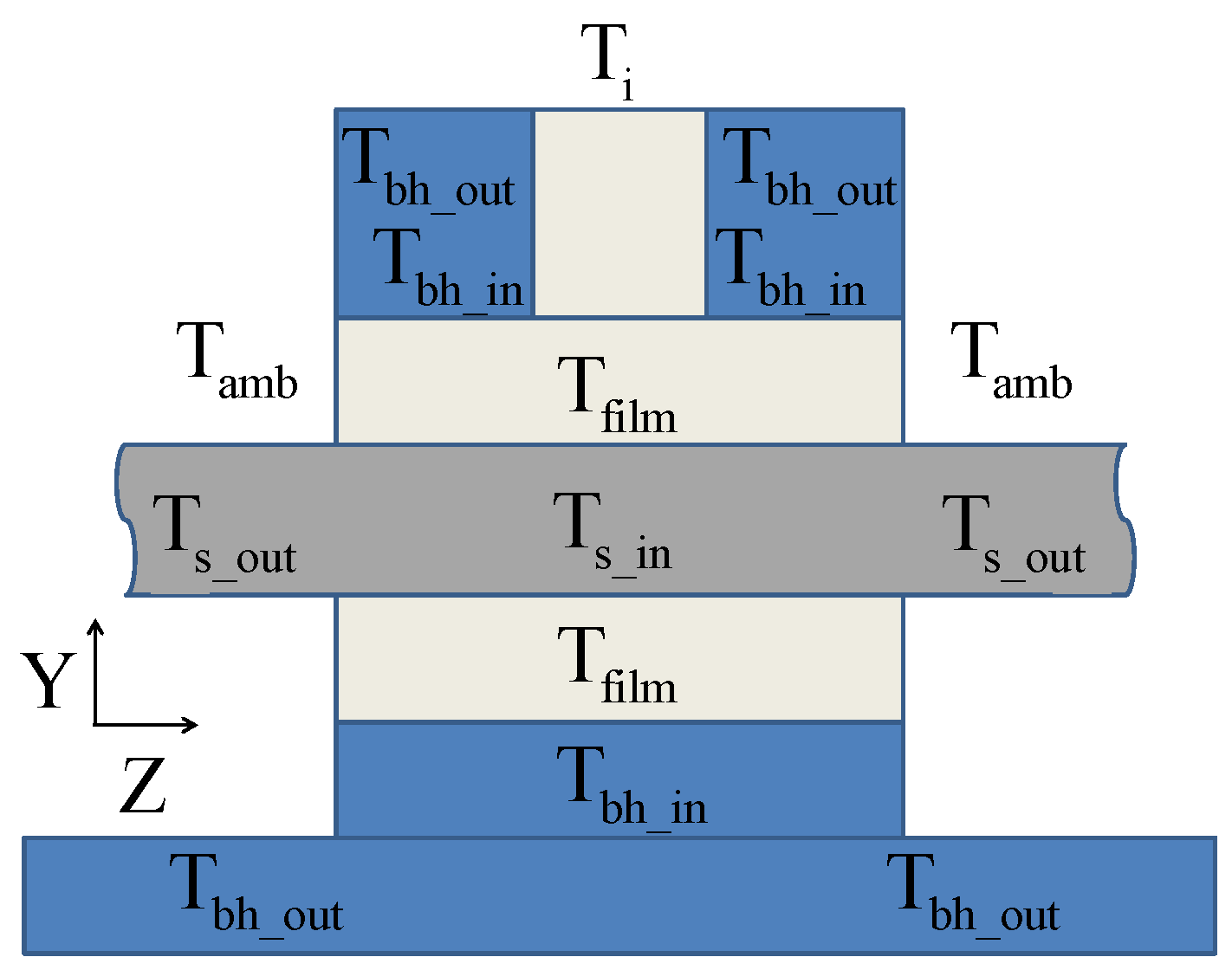
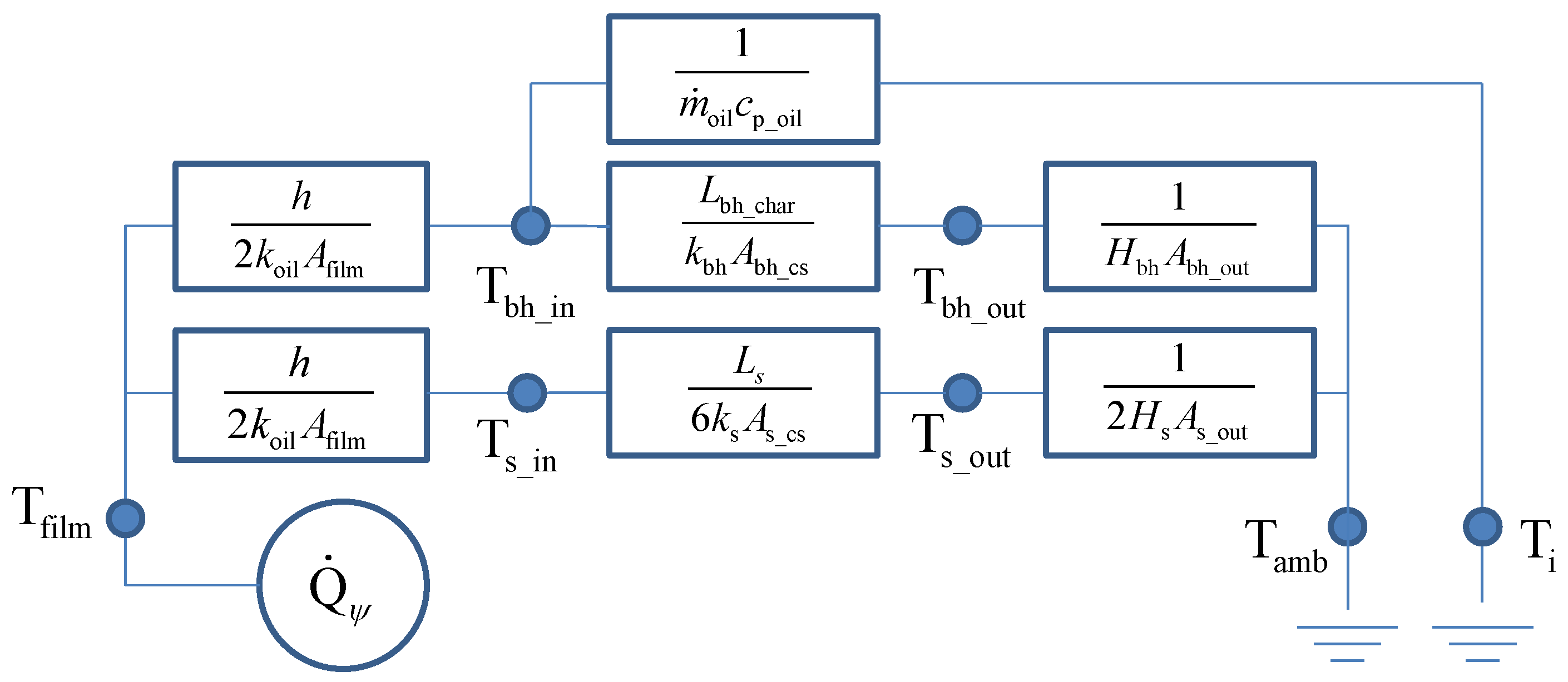
- the extension of the thermal model to include the heating of the shaft, the bearing housing and the oil in the inlet channel, as depicted in Figure 4. Especially the effect of heating the oil in the inlet channel inside the bearing housing just upstream the bearing was found to be having a major impact on the effective film temperature.
4. Rotor-Bearing System B: An Asymmetric Rotor with Multiple Disks on Plain Journal Bearings
4.1. Rotor and Bearing Layout
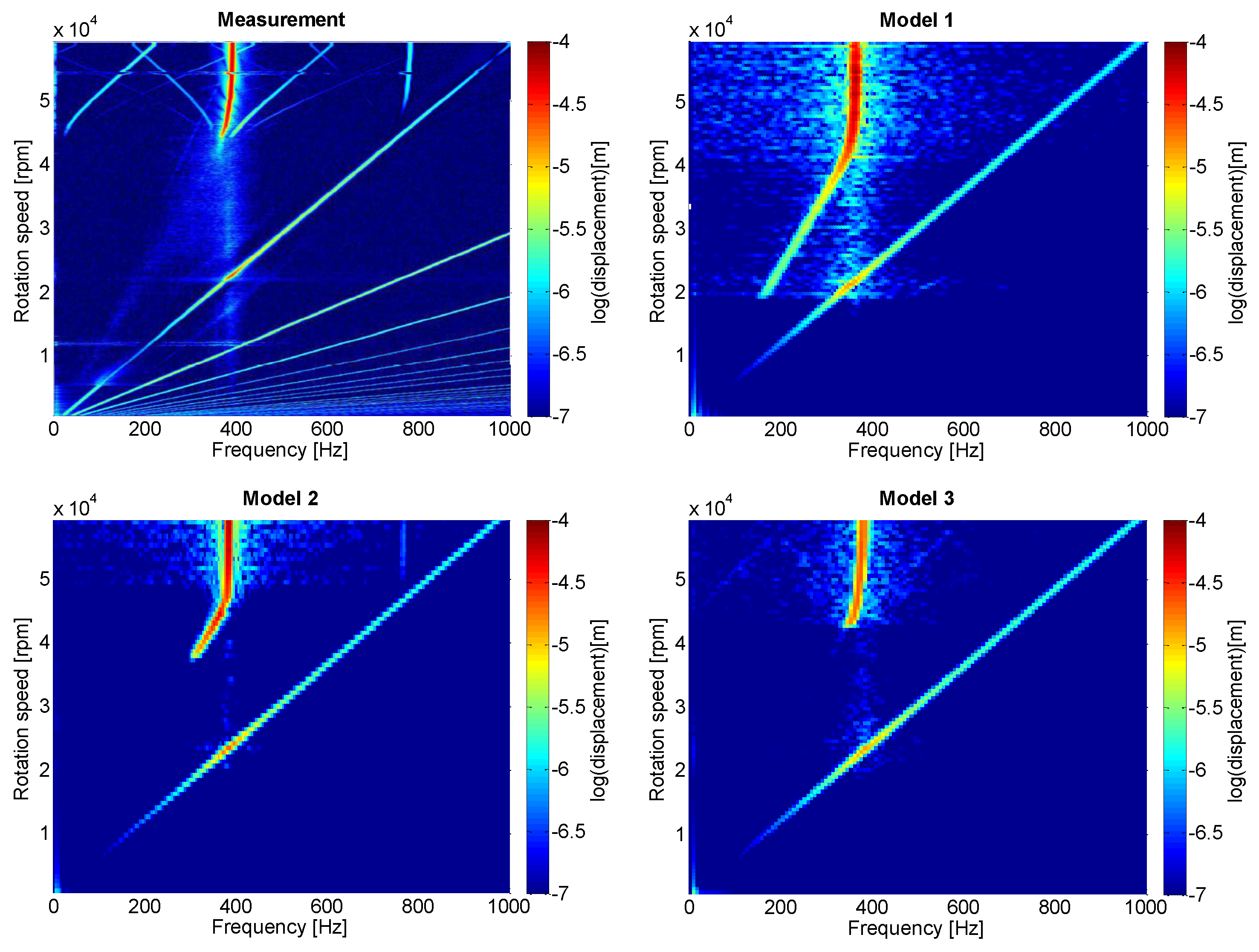
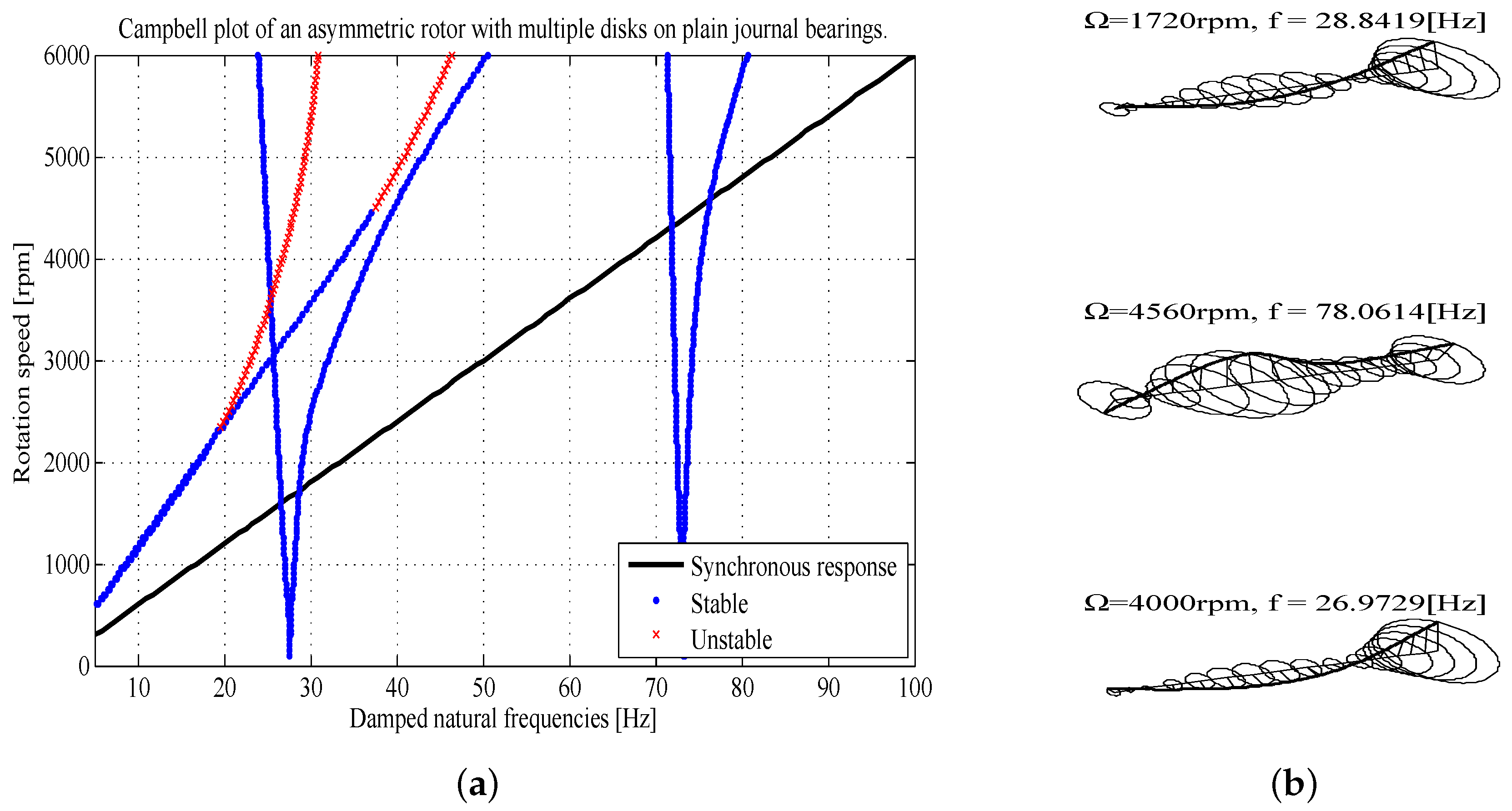
4.2. Linear Analysis: Campbell Plot
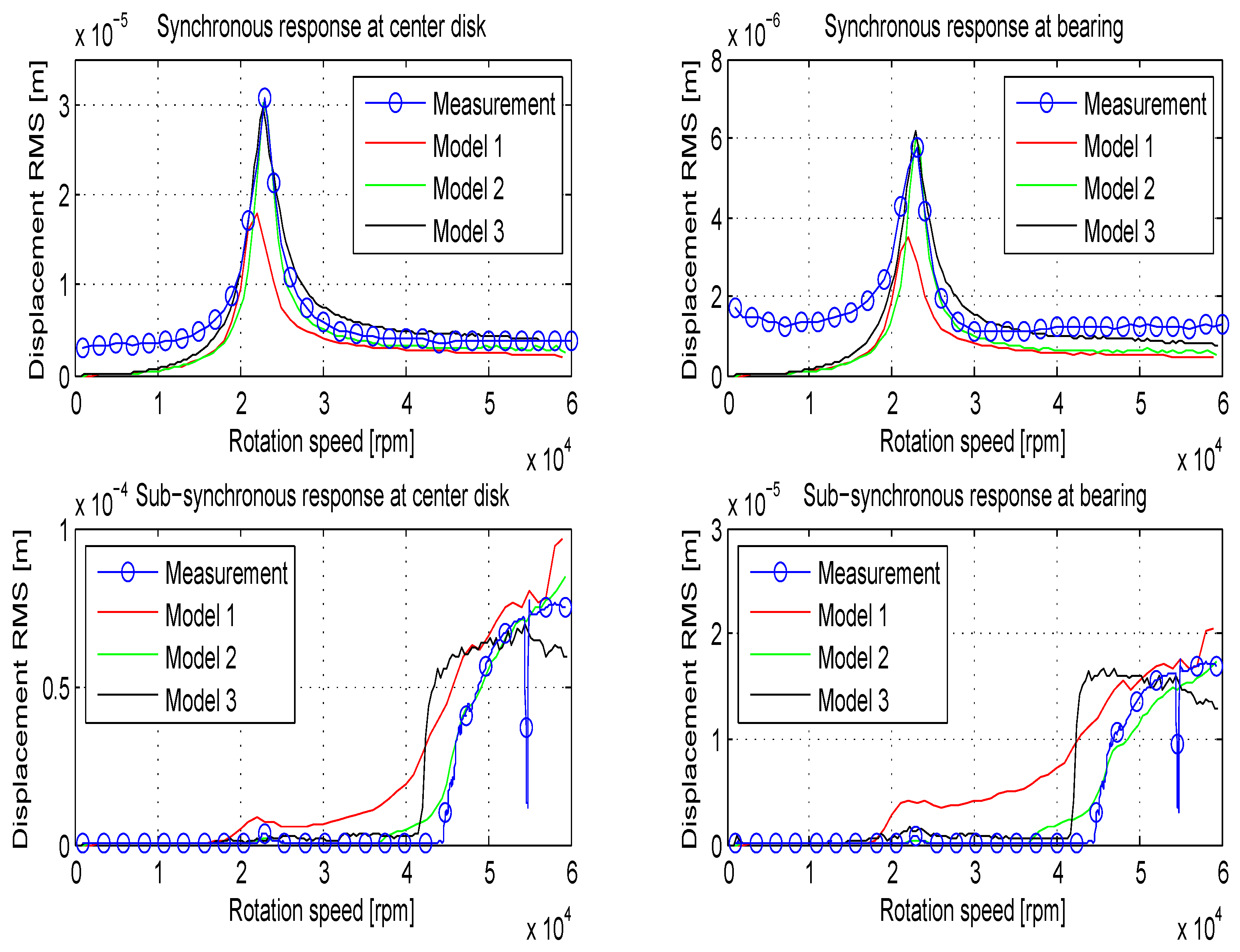
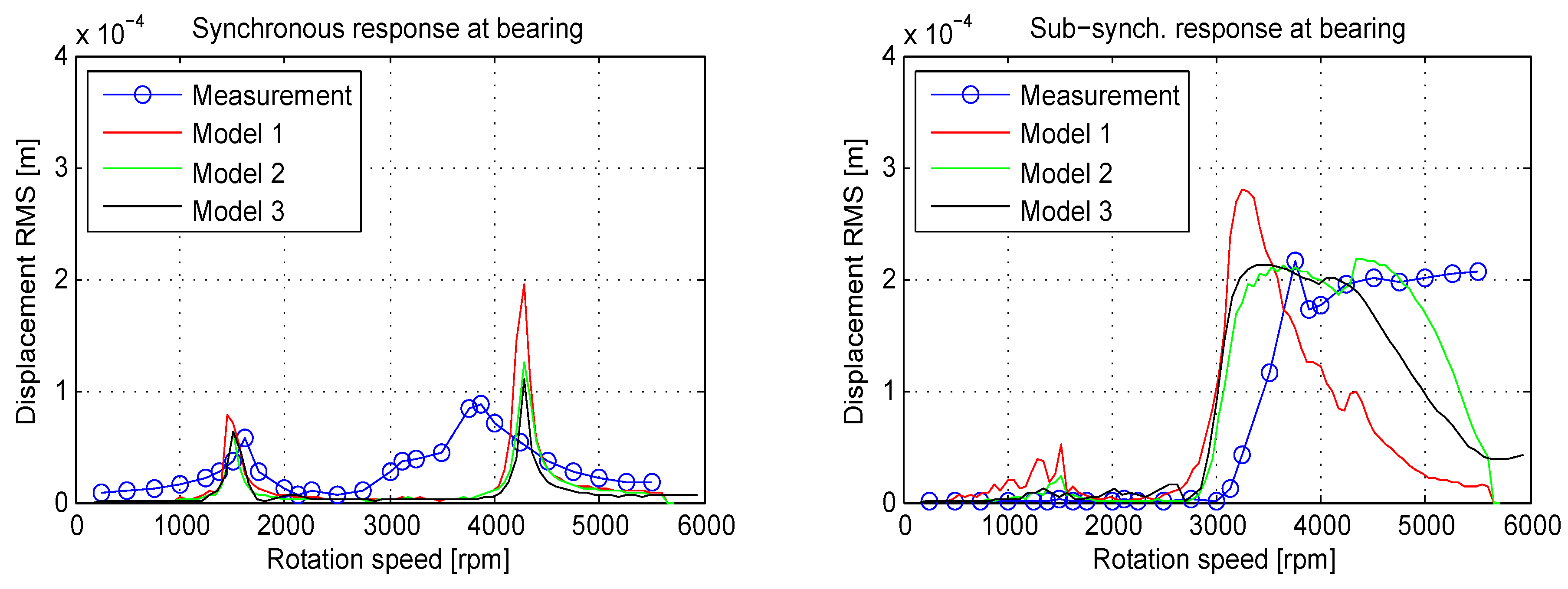
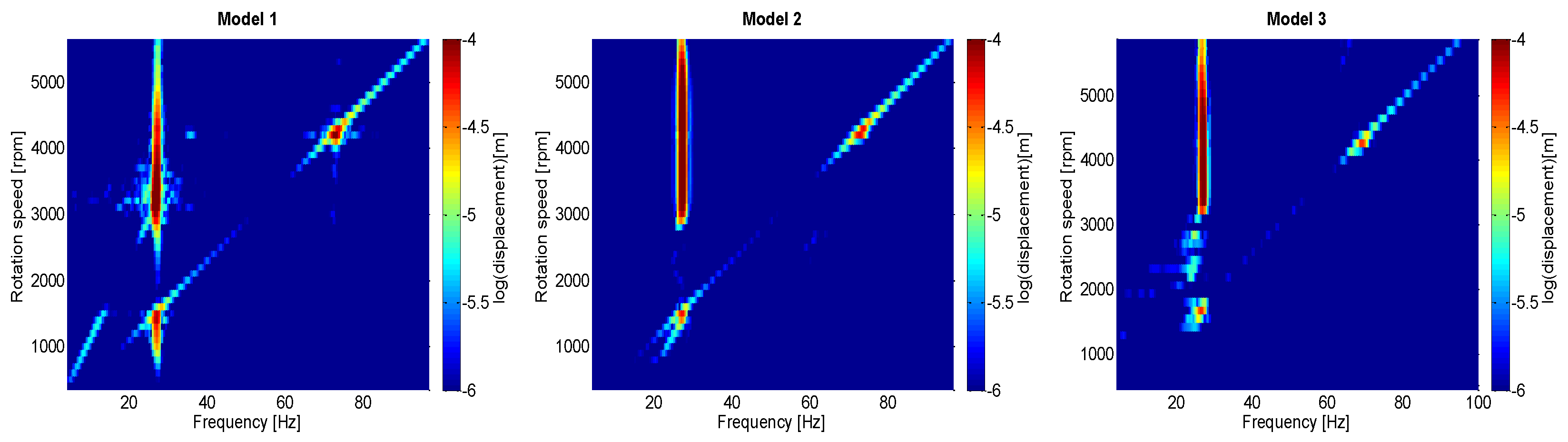
4.3. Non-Linear Time-Transient Analysis
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Numerical Values of Rotor-Bearing System A
| Symbol | Description | Value | Unit | Symbol | Description | Value | Unit |
|---|---|---|---|---|---|---|---|
| Cross-sectional area bearing housing | 3e | m | Thermal conductivity of oil | 0.145 | |||
| Outer surface area bearing housing | 6e | m | Thermal conductivity of shaft | 44 | |||
| Convection coefficient from bearing housing | 5 | Characteristic length of conductance in bearing housing | 1.14e | m | |||
| Thermal conductivity of air | 2.8e | Kinematic viscosity of air | 17e | ||||
| Thermal conductivity bearing housing | 201 | Specific heat of oil | 2.1e | ||||
| Prandtl number of air | 0.69 | − |
Appendix B. Numerical Values of Rotor-Bearing System B

| Symbol | Description | Value | Unit | Symbol | Description | Value | Unit |
|---|---|---|---|---|---|---|---|
| Cross-sectional area bearing housing | 6e | m | Thermal conductivity of oil | 0.145 | |||
| Outer surface area bearing housing | 5e | m | Thermal conductivity of shaft | 44 | |||
| Convection coefficient from bearing housing | 5 | Characteristic length of conductance in bearing housing | 2.9e | m | |||
| Thermal conductivity of air | 2.8e | Kinematic viscosity of air | 17e | ||||
| Thermal conductivity bearing housing | 44 | Specific heat of oil | 2.1e | ||||
| Prandtl number of air | 0.69 | − |
References
- Friswell, M.I.; Penny, J.E.T.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- San Andrés, L. Modern Lubrication Theory, Lecture Notes 5: Dynamics of Rigid Rotor-Fluid Film Bearings Systems. Available online: http://rotorlab.tamu.edu/me626/default.htm (accessed on 8 September 2016).
- Poritsky, H. Contribution to the Theory of Oil whip. Trans. ASME 1953, 75, 1153–1161. [Google Scholar]
- Stachowiak, G.; Batchelor, A.W. Engineering Tribology, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Genta, G. Dynamics of Rotating System; Springer Science & Business Media Inc.: New York, NY, USA, 2005. [Google Scholar]
- De Castro, H.F.; Cavalca, K.L.; Nordmann, R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. J. Sound Vib. 2008, 317, 273–293. [Google Scholar] [CrossRef]
- Jing, J.; Meng, G.; Sun, Y.; Xia, S. On the non-linear dynamic behavior of a rotor-bearing system. J. Sound Vib. 2004, 274, 1031–1044. [Google Scholar] [CrossRef]
- Schweizer, B. Total instability of turbocharger rotors—Physical explanation of the dynamic failure of rotors with full-floating ring bearings. J. Sound Vib. 2009, 328, 156–190. [Google Scholar] [CrossRef]
- Adiletta, G.; Guido, A.R.; Rossi, C. Nonlinear Dynamics of a Rigid Unbalanced Rotor in Journal Bearings. Part I: Theoretical Analysis. Nonlinear Dyn. 1997, 14, 57–87. [Google Scholar] [CrossRef]
- Adiletta, G.; Guido, A.R.; Rossi, C. Nonlinear Dynamics of a Rigid Unbalanced Rotor in Journal Bearings. Part II: Experimental Analysis. Nonlinear Dyn. 1997, 14, 57–87. [Google Scholar] [CrossRef]
- Chen, C.; Yau, H. Bifurcation in a Flexible Rotor Supported by Short Journal Bearings With Nonlinear Suspension. J. Vib. Control 2001, 7, 653–673. [Google Scholar] [CrossRef]
- Newkirk, B.L.; Taylor, H.D. Shaft whipping due to oil action in journal bearings. Gen. Electr. Rev. 1925, 28, 559–568. [Google Scholar]
- Pinkus, O. The Reynolds Centennial: A Brief History of the Theory of Hydrodynamic Lubrication. J. Tribol. 1987, 109, 2–15. [Google Scholar] [CrossRef]
- Lund, J.W.; Sternlicht, B. Rotor-Bearing Dynamics with Emphasis on Attenuation. J. Basic Eng. 1962, 84, 491–498. [Google Scholar] [CrossRef]
- Szeri, A.Z. Some Extensions of the Lubrication Theory of Osborne. J. Tribol. 1987, 109, 21–36. [Google Scholar] [CrossRef]
- Eling, R.; Wierik, M.; van Ostayen, R.A.J. Multiphysical modeling comprehensiveness to model a high speed Laval rotor on journal bearings. In Proceedings of the 14th EDF—Pprime Workshop: Influence of Design and Materials on Journal and Thrust Bearing Performance, Poitiers, France, 8–9 October 2015; pp. 1–14.
- Ding, Q.; Leung, A.Y.T. Numerical and Experimental Investigations on Flexible Multi-bearing Rotor Dynamics. J. Vib. Acoust. 2005, 127, 408–415. [Google Scholar] [CrossRef]
- Frene, J.; Nicolas, D.; Degueurce, B.; Berthe, D.; Godet, M. Hydrodynamic Lubrication: Bearings and Thrust Bearings, 33rd ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Comsol, A.B. COMSOL Multiphysics; Version: 5.2; COMSOL Inc.: Burlington, MA, USA, 2015. [Google Scholar]
- Nitzschke, S.; Woschke, E.; Daniel, C.; Strackeljan, J. Einfluss der masseerhaltenden Kavitation auf gleitgelagerte Rotoren unter instationärer Belastung. SIRM 2013, 2013, 1–11. [Google Scholar]
- Mahner, M.; Lehn, A.; Schweizer, B. Thermogas- and thermohydrodynamic simulation of thrust and slider bearings: Convergence and efficiency of different reduction approaches. Tribol. Int. 2016, 93, 539–554. [Google Scholar] [CrossRef]
- San Andres, L.; Kerth, J. Thermal effects on the performance of floating ring bearings for turbochargers. J. Eng. Tribol. 2004, 218, 437–450. [Google Scholar] [CrossRef]
- Mills, A. Basic Heat and Mass Transfer, 2nd ed.; Pearson Education: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Alakhramsing, S.; van Ostayen, R.; Eling, R. Thermo-Hydrodynamic Analysis of a Plain Journal Bearing on the Basis of a New Mass Conserving Cavitation Algorithm. Lubricants 2015, 3, 256–280. [Google Scholar] [CrossRef]
- Knauder, C.; Allmaier, H.; Sander, D.E.; Salhofer, S.; Reich, F.M.; Sams, T. Analysis of the Journal Bearing Friction Losses in a Heavy-Duty Diesel Engine. Lubricants 2015, 3, 142–154. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. Non-linearities in misaligned journal bearings. Tribol. Int. 1994, 27, 243–257. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- El-Shafei, A.; Tawfick, S.H.; Raafat, M.S.; Aziz, G.M. Some Experiments on Oil Whirl and Oil Whip. J. Eng. Gas Turbines Power 2007, 129, 144–153. [Google Scholar] [CrossRef]

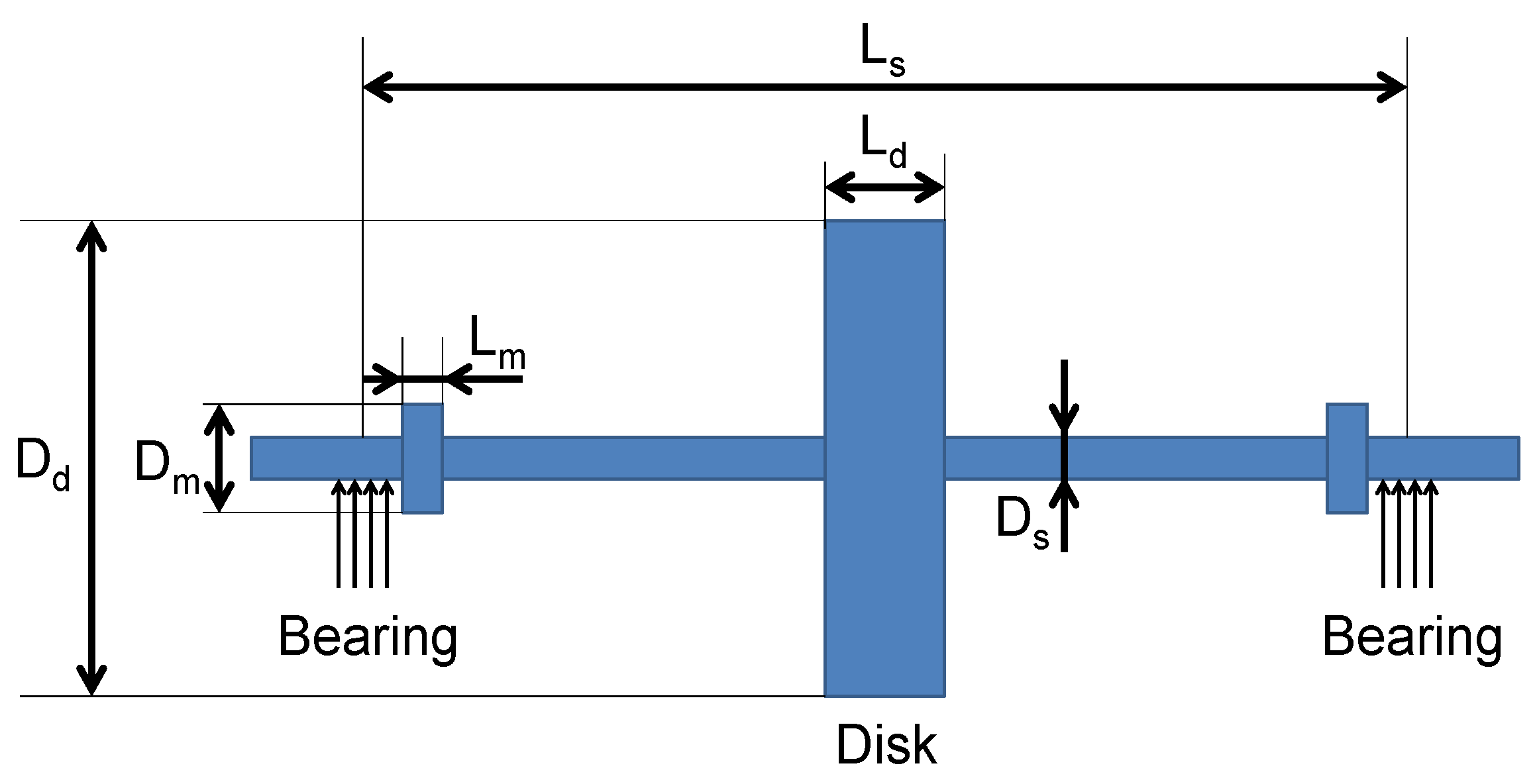
| Rotor Parameters | Bearing Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Symbol | Description | Value | Unit | Symbol | Description | Value | Unit |
| Bearing span | 0.12 | m | C | Bearing clearance | 11e | m | |
| Shaft diameter | 6e | m | Bearing length | 3.6e | m | ||
| Central disk length | 9e | m | Oil inlet diameter | 2e | m | ||
| Central disk diameter | 35e | m | a | Viscosity-temperature parameter | 4.4e | Pa·s | |
| Measurement disk length | 4e | m | b | Viscosity-temperature parameter | 633 | C | |
| Measurement disk diameter | 12e | m | c | Viscosity-temperature parameter | 88.6 | C | |
| Modulus of elasticity of shaft | 215 | GPa | m | Viscosity-shear rate parameter | 0.8 | - | |
| Density of shaft material | 7850 | r | Viscosity-shear rate parameter | 0.5 | - | ||
| Unbalance at center disk | 250 | mg·mm | K | Viscosity-shear rate parameter | 7.2e | s | |
| ρ | Oil density | 855 | |||||
| Rotor Parameters | Bearing Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Symbol | Description | Value | Unit | Symbol | Description | Value | Unit |
| Length of shaft section | 0.12 | m | C | Bearing clearance | 17.5e | m | |
| Length of shaft section | 0.40 | m | Bearing length | 15e | m | ||
| Length of shaft section | 0.143 | m | Oil inlet diameter | 3e | m | ||
| Length of shaft section | 0.05 | m | a | Viscosity-temperature parameter | 1.08e | Pa·s | |
| Disk length | 15e | m | b | Viscosity-temperature parameter | 324.3 | °C | |
| Shaft diameter | 25.4e | m | c | Viscosity-temperature parameter | 52.51 | °C | |
| Disk diameter | 170e | m | m | Viscosity-shear rate parameter | 0.8 | - | |
| Modulus of elasticity of shaft | 210 | GPa | r | Viscosity-shear rate parameter | 0.5 | - | |
| Density of shaft material | 7800 | K | Viscosity-shear rate parameter | 7.2e | s | ||
| Unbalance on central disk | 189 | g·mm | ρ | Oil density | 879 | ||
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| Pressure distribution | 1D | 2D | 2D |
| Fluid supply hole | neglected | inlet | inlet |
| Thermal distribution | Isoviscous | Lumped thermal | Distributed thermal |
| Fluid type | Newtonian | Newtonian | Non-Newtonian |
| Cavitation model | Half-Sommerfeld | Gümbel | Alakhramsing |
| Shaft alignment (tilting) | Fully aligned | Fully aligned | Misalignment included |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eling, R.; Te Wierik, M.; Van Ostayen, R.; Rixen, D. Towards Accurate Prediction of Unbalance Response, Oil Whirl and Oil Whip of Flexible Rotors Supported by Hydrodynamic Bearings. Lubricants 2016, 4, 33. https://doi.org/10.3390/lubricants4030033
Eling R, Te Wierik M, Van Ostayen R, Rixen D. Towards Accurate Prediction of Unbalance Response, Oil Whirl and Oil Whip of Flexible Rotors Supported by Hydrodynamic Bearings. Lubricants. 2016; 4(3):33. https://doi.org/10.3390/lubricants4030033
Chicago/Turabian StyleEling, Rob, Mathys Te Wierik, Ron Van Ostayen, and Daniel Rixen. 2016. "Towards Accurate Prediction of Unbalance Response, Oil Whirl and Oil Whip of Flexible Rotors Supported by Hydrodynamic Bearings" Lubricants 4, no. 3: 33. https://doi.org/10.3390/lubricants4030033
APA StyleEling, R., Te Wierik, M., Van Ostayen, R., & Rixen, D. (2016). Towards Accurate Prediction of Unbalance Response, Oil Whirl and Oil Whip of Flexible Rotors Supported by Hydrodynamic Bearings. Lubricants, 4(3), 33. https://doi.org/10.3390/lubricants4030033