Combined Analytical and Experimental Evaluation of Frictional Performance of Lubricated Untextured and Partially Textured Sliders
Abstract
:1. Introduction
2. Experimental Setup and Procedure
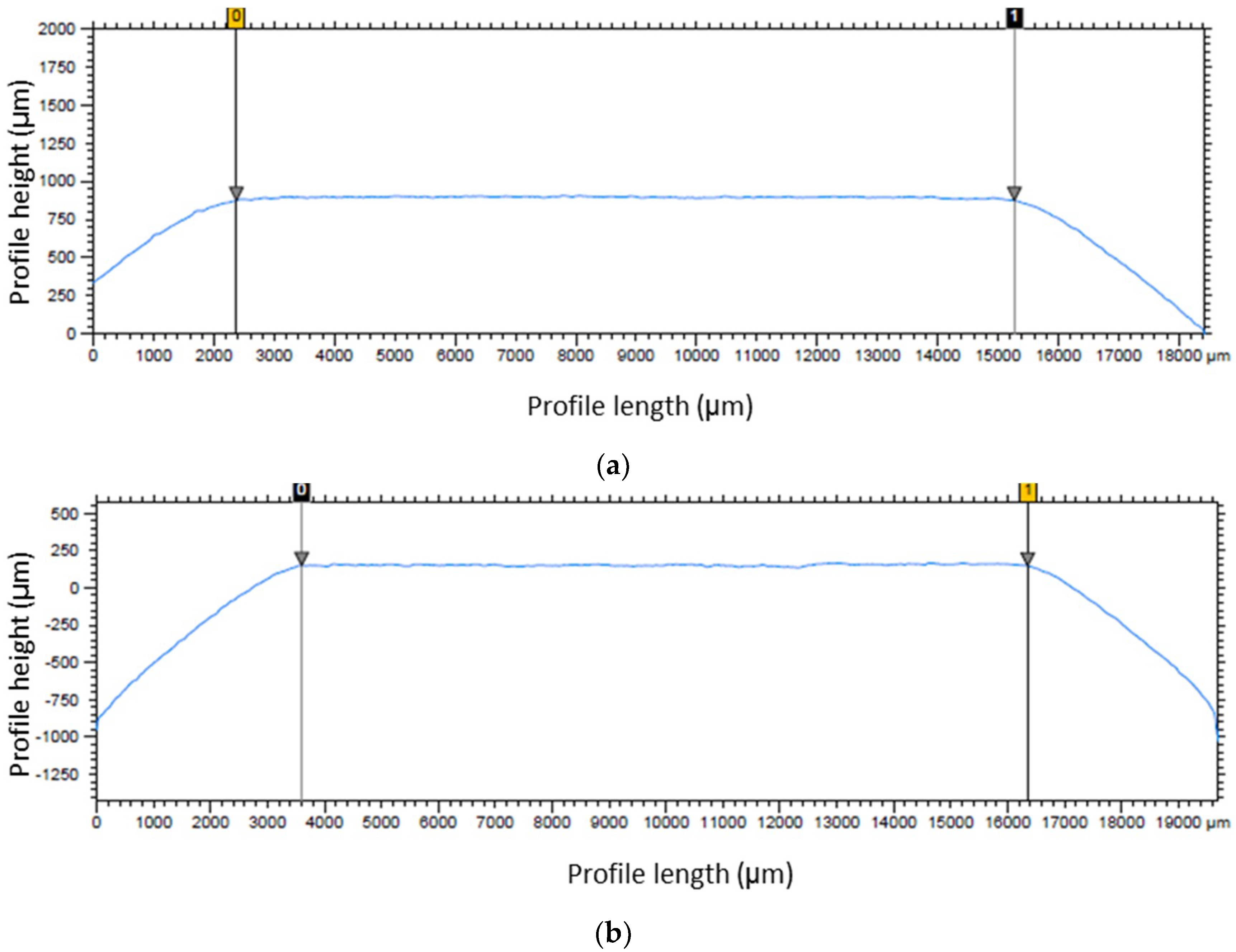
2.1. Preparation of Samples
2.2. Test Procedure
3. Analytical Model
3.1. Untextured Slider
3.2. Textured Slider
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| lateral width of the contact | |
| integration constants | |
| applied contact load | |
| friction | |
| dimensionless friction | |
| Hersey number | |
| contact gap/film thickness | |
| dimensionless contact gap | |
| minimum lubricant film thickness | |
| gap at the cavitation inception point | |
| dimensionless gap at cavitation inception point | |
| maximum height/depth of texture feature | |
| height at the inlet meniscus | |
| axial length of contact | |
| edge-to-edge distance between successive textures | |
| length of untextured leading portion of contact | |
| axial length of texture feature at the base | |
| number of texture features in the direction of entrainment | |
| hydrodynamic pressure | |
| dimensionless pressure | |
| local height of slider profile at different locations along the entraining direction | |
| dimensionless local height of slider profile segments | |
| local height of slider at inlet | |
| sliding speed | |
| load carrying capacity per unit lateral width | |
| dimensionless load carrying capacity per unit lateral width | |
| axial coordinate along the direction of entraining motion | |
| dimensionless distance | |
| locations where the slider profile changes | |
| dimensionless coordinate points | |
| cavitation inception point/lubricant film rupture boundary | |
| dimensionless cavitation inception point | |
| vertical coordinate perpendicular to the entrainment direction | |
| Greek Symbols | |
| ratio of texture base length to the edge-to-edge distance between he textures | |
| dynamic viscosity | |
| textured portion | |
| ratio of half-length of flat part of slider to the whole length | |
| coefficient of friction | |
| slider chamfer or texture height ratio | |
| scaled coefficient of friction | |
| Subscripts | |
| maximum | |
| minimum | |
| optimum | |
| Abbreviations | |
| AC | Alternating Current |
| ASTM | American Society for Testing and Materials |
| CFD | Computational Fluid Dynamics |
| DC | Direct Current |
| DIN | Deutsches Institut für Normung |
| EHL | Elastohydrodynamic lubrication |
| LST | Laser surface texturing |
| RMS | Root Mean Square |
| RPM | Revolutions per Minute |
References
- Etsion, I.; Burstein, L. A model for mechanical seals with regular microsurface structure. Tribol. Trans. 1996, 39, 677–683. [Google Scholar] [CrossRef]
- Etsion, I.; Kligerman, Y.; Halperin, G. Analytical and experimental investigation of laser-textured mechanical seal faces. Tribol. Trans. 1999, 42, 511–516. [Google Scholar] [CrossRef]
- Burstein, L.; Ingman, D. Pore ensemble statistics in application to lubrication under reciprocating motion. Tribol. Trans. 2000, 43, 205–212. [Google Scholar] [CrossRef]
- Ronen, A.; Etsion, I.; Kligerman, Y. Friction-reducing surface-texturing in reciprocating automotive components. Tribol. Trans. 2001, 44, 359–366. [Google Scholar] [CrossRef]
- Rahmani, R.; Shirvani, A.; Shirvani, H. Optimised textured surfaces with application in piston ring/cylinder liner contact. In Tribology and Dynamics of Engine and Powertrain; Woodhead Publishing Ltd.: Cambridge, UK, 2010; pp. 470–517. [Google Scholar] [Green Version]
- Pettersson, U.; Jacobson, S. Influence of surface texture on boundary lubricated sliding contacts. Tribol. Int. 2003, 36, 857–864. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. The effect of square-shaped pockets position in sliding line contacts under mixed regime of lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018. [Google Scholar] [CrossRef]
- Krupka, I.; Hartl, M. Effect of surface texturing on very thin film EHD lubricated contacts. Tribol. Trans. 2008, 52, 21–28. [Google Scholar] [CrossRef]
- Morris, N.; Leighton, M.; De la Cruz, M.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Combined numerical and experimental investigation of the micro-hydrodynamics of chevron-based textured patterns influencing conjunctional friction of sliding contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 316–335. [Google Scholar] [CrossRef] [Green Version]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Howell-Smith, S. A numerical model to study the role of surface textures at top dead center reversal in the piston ring to cylinder liner contact. J. Tribol. 2016, 138, 021703. [Google Scholar] [CrossRef] [Green Version]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Effects of honed cylinder liner surface texture on tribological properties of piston ring-liner assembly in short time tests. Tribol. Int. 2017, 113, 137–148. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Fillon, M.; Maspeyrot, P. Effect of textured area on the performances of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 211–219. [Google Scholar] [CrossRef]
- Morris, N.J.; Rahnejat, H.; Rahmani, R. Tribology of partial pad journal bearings with textured surfaces. In Proceedings of the 3rd European Conference on Tribology (ECOTRIB), Vienna, Austria, 7–9 June 2011. [Google Scholar]
- Morris, N.J.; Shahmohamadi, H.; Rahmani, R.; Rahnejat, H.; Garner, C.P. Combined experimental and multiphase computational fluid dynamics analysis of surface textured journal bearings in mixed regime of lubrication. Lubr. Sci. 2018, 30, 161–173. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Bao, Q.; Li, K.; Khonsari, M.M.; Zhao, H. An investigation into the transient behavior of journal bearing with surface texture based on fluid-structure interaction approach. Tribol. Int. 2018, 118, 246–255. [Google Scholar] [CrossRef]
- Etsion, I. Improving tribological performance of mechanical components by laser surface texturing. Tribol. Lett. 2004, 17, 733–737. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. A laser surface textured parallel thrust bearing. Tribol. Trans. 2003, 46, 397–403. [Google Scholar] [CrossRef]
- Kligerman, Y.; Etsion, I.; Shinkarenko, A. Improving tribological performance of piston rings by partial surface texturing. J. Tribol. 2005, 127, 632–638. [Google Scholar] [CrossRef]
- Ryk, G.; Etsion, I. Testing piston rings with partial laser surface texturing for friction reduction. Wear 2006, 261, 792–796. [Google Scholar] [CrossRef]
- Rahmani, R. An Investigation into Analysis and Optimisation of Textured Slider Bearings with Application in Piston Ring/Cylinder Liner Contact. Ph.D. Thesis, Anglia Ruskin University, Cambridge, UK, 2008. [Google Scholar]
- Rahmani, R.; Rahnejat, H. Enhanced performance of optimised partially textured load bearing surfaces. Tribol. Int. 2018, 117, 272–282. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- ASTM G115-10:2013, Standard Guide for Measuring and Reporting Friction Coefficients; ASTM International: West Conshohocken, PA, USA, 2013.
- ASTM G99-05, Standard Test Method for Wear Testing with a Pin-On-Disk Apparatus; ASTM International: West Conshohocken, PA, USA, 2016.
- Humphrey, E.; Gkinis, T.; Morris, N.; Leighton, M.; Rahmani, R.; Rahnejat, H. Clutch Lining Frictional Characteristics under Thermal Tribodynamic Conditions. In Proceedings of the 3rd Biennial International Conference on Powertrain Modelling and Control Testing, Mapping and Calibration (PMC 2016), Loughborough, UK, 7–9 September 2016. [Google Scholar]
- Gkinis, T.; Rahmani, R.; Rahnejat, H. Effect of Clutch Lining Frictional Characteristics on Take-up Judder. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2017, 231, 493–503. [Google Scholar] [CrossRef]
- Dolatabadi, N.; Rahmani, R.; Theodossiades, S.; Rahnejat, H.; Blundell, G.; Bernard, G. Tribodynamics of Clutch System for Engine-Downsizing in Heavy Duty Off-Highway Vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018. [Google Scholar] [CrossRef]
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Rahmani, R.; Mirzaee, I.; Shirvani, A.; Shirvani, H. An analytical approach for analysis and optimisation of slider bearings with infinite width parallel textures. Tribol. Int. 2010, 43, 1551–1565. [Google Scholar] [CrossRef] [Green Version]
- Tipei, N. Boundary conditions of a viscous flow between surfaces with rolling and sliding motion. J. Lubr. Technol. 1968, 90, 254–261. [Google Scholar] [CrossRef]
- Shahmohamadi, H.; Mohammadpour, M.; Rahmani, R.; Rahnejat, H.; Garner, C.P.; Howell-Smith, S. On the boundary conditions in multi-phase flow through the piston ring-cylinder liner conjunction. Tribol. Int. 2015, 90, 164–174. [Google Scholar] [CrossRef] [Green Version]
- Gohar, R. Elastohydrodynamics; Imperial College Press: London, UK, 2001. [Google Scholar]







| Property | Symbol | Plain Slider | Textured Slider | Disc | Unit |
|---|---|---|---|---|---|
| Material | _ | En36C | En36C | En36C | _ |
| Modulus of elasticity | 205 | 205 | 205 | ||
| Poisson ratio | 0.30 | 0.30 | 0.30 | _ | |
| RMS roughness | 0.33 | 0.35 | 0.74 | ||
| Arithmetic mean roughness | 0.26 | 0.27 | 0.57 | ||
| Skewness | 0.21 | −0.06 | −0.21 | _ | |
| Kurtosis | 5.45 | 4.44 | 3.54 | _ | |
| Total maximum height | 6.78 | 5.11 | 7.55 | ||
| Dimensions | _ | 20 × 12 | 20 × 12 | 105 | mm |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Textured portion | 0.595 | _ | |
| Texture’s length ratio | 0.75 | _ | |
| No. of textures in axial direction | 10 | _ | |
| Texture maximum depth | 28.2 | μm | |
| Leading edge length ratio | 0.405 | _ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teo, W.J.; Dolatabadi, N.; Rahmani, R.; Morris, N.; Rahnejat, H. Combined Analytical and Experimental Evaluation of Frictional Performance of Lubricated Untextured and Partially Textured Sliders. Lubricants 2018, 6, 88. https://doi.org/10.3390/lubricants6040088
Teo WJ, Dolatabadi N, Rahmani R, Morris N, Rahnejat H. Combined Analytical and Experimental Evaluation of Frictional Performance of Lubricated Untextured and Partially Textured Sliders. Lubricants. 2018; 6(4):88. https://doi.org/10.3390/lubricants6040088
Chicago/Turabian StyleTeo, Wei J., Nader Dolatabadi, Ramin Rahmani, Nick Morris, and Homer Rahnejat. 2018. "Combined Analytical and Experimental Evaluation of Frictional Performance of Lubricated Untextured and Partially Textured Sliders" Lubricants 6, no. 4: 88. https://doi.org/10.3390/lubricants6040088
APA StyleTeo, W. J., Dolatabadi, N., Rahmani, R., Morris, N., & Rahnejat, H. (2018). Combined Analytical and Experimental Evaluation of Frictional Performance of Lubricated Untextured and Partially Textured Sliders. Lubricants, 6(4), 88. https://doi.org/10.3390/lubricants6040088







