Estimating Density and Temperature Dependence of Juvenile Vital Rates Using a Hidden Markov Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Species and Field Methods
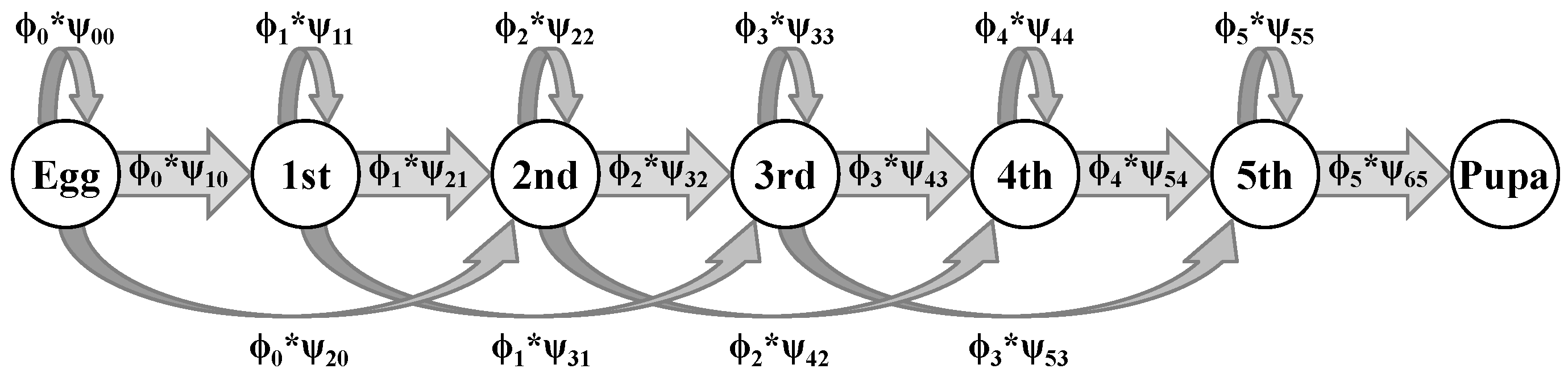
2.2. Model Description
2.3. Vital Rates and Covariates
2.4. Model Likelihood
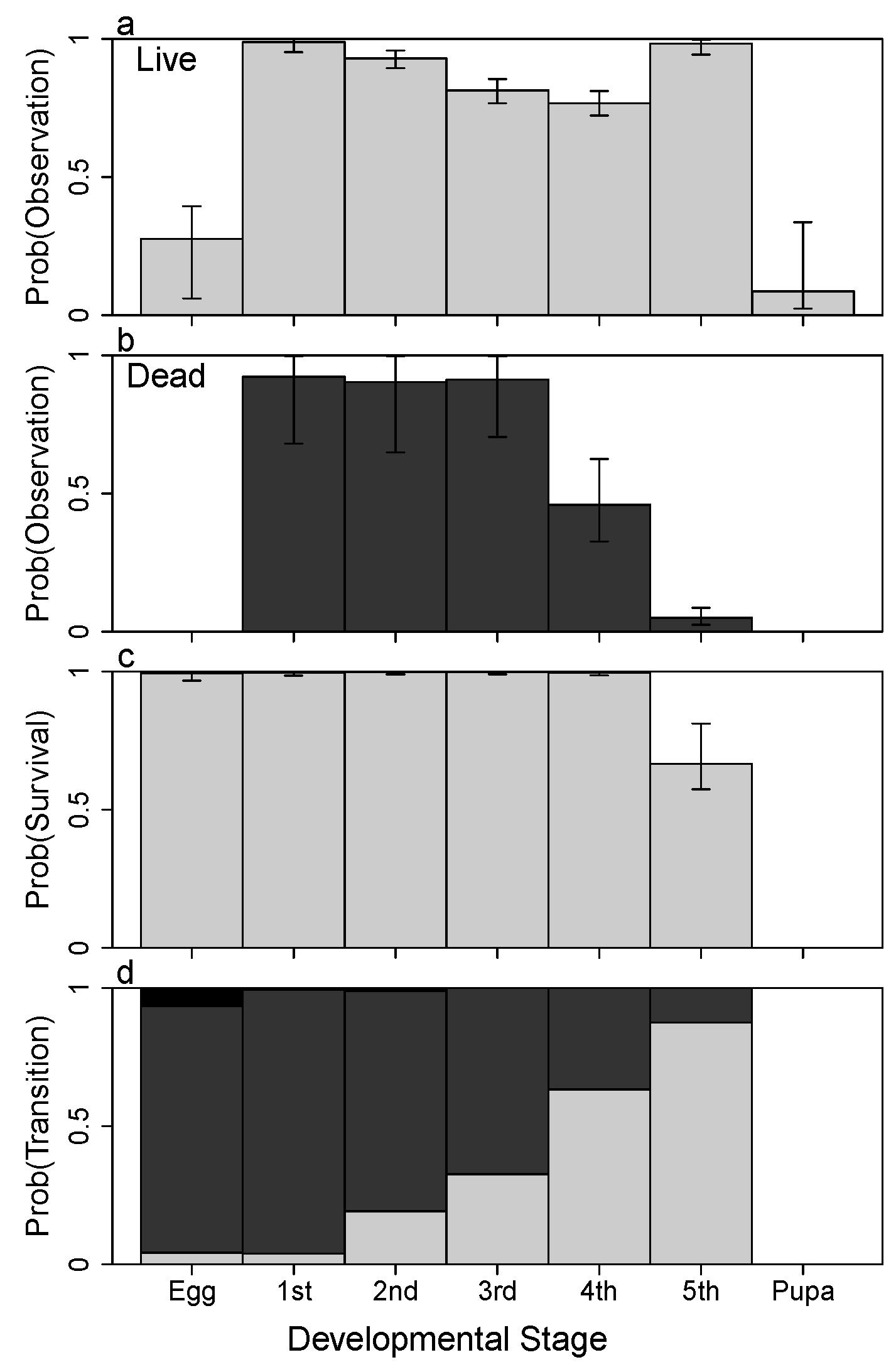
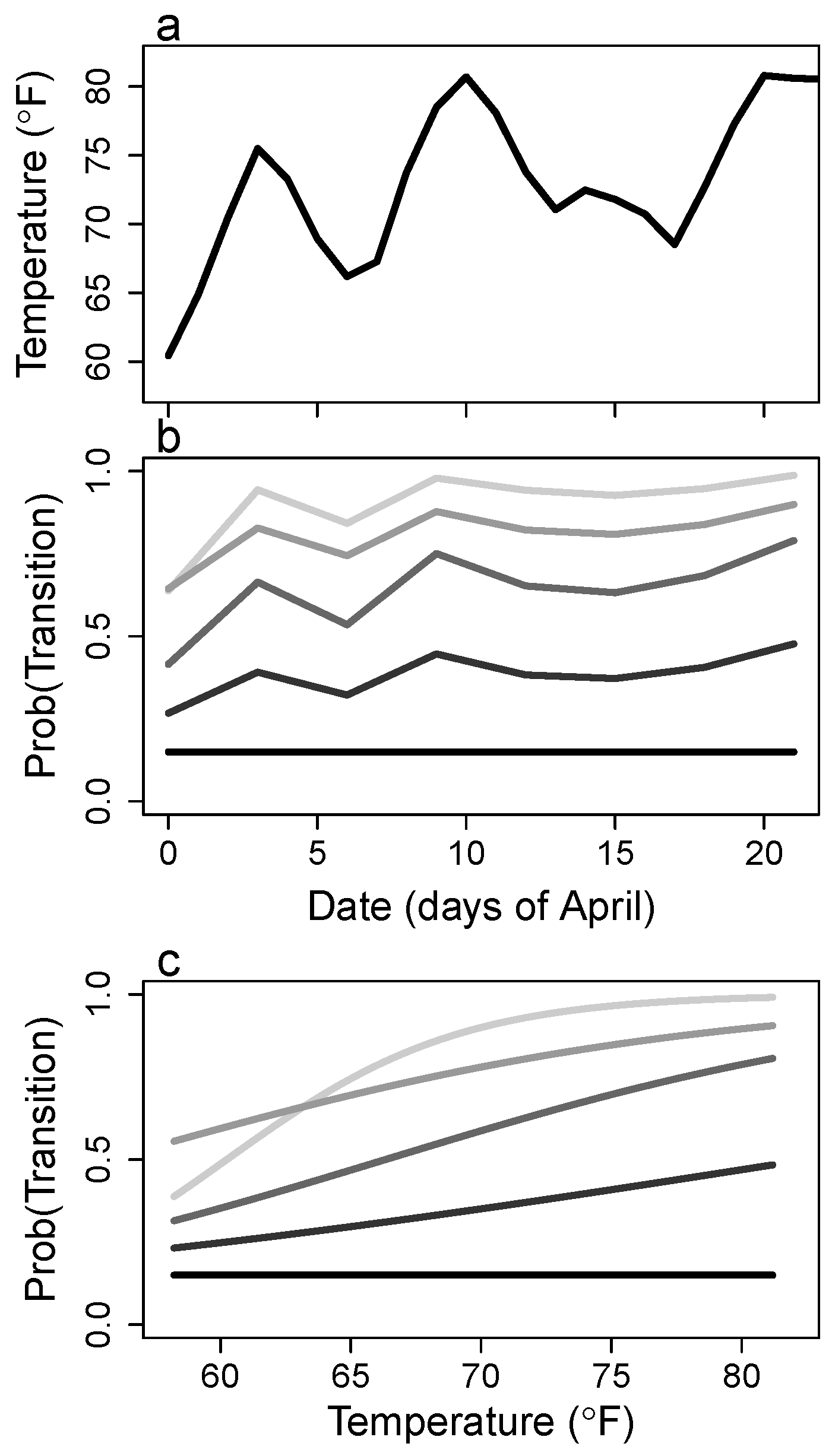
3. Results
4. Discussion
4.1. Detection
4.2. Survival
4.3. Growth
5. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
Abbreviations
| MR | Mark-recapture |
| MSMR | Multi-state mark-recapture |
| SSM | State space model |
| HMM | Hidden Markov model |
| MCMC | Markov chain Monte Carlo |
| AIC | Akaike’s information criteria |
| DIC | Deviance information criteria |
| psrf | Potential scale reduction factor |
| BFL | Brackenridge Field Laboratory |
Appendix A. Study Species and Field Methods
Appendix B. Description of the Demographic and Observation Matrices
Appendix C. Logit Transforms of Survival and Growth Rates
Appendix D. Per Capita Predation Rate
References
- Reich, K.J.; Bjorndal, K.A.; Bolten, A.B. The ‘lost years’ of green turtles: Using stable isotopes to study cryptic lifestages. Biol. Lett. 2007, 3, 712–714. [Google Scholar] [CrossRef] [PubMed]
- Paterson, J.E.; Steinberg, B.D.; Litzgus, J.D. Revealing a cryptic life-history stage: Differences in habitat selection and survivorship between hatchlings of two turtle species at risk (Glyptemys insculpta and Emydoidea blandingii). Wildl. Res. 2012, 39, 408–418. [Google Scholar] [CrossRef]
- Lamy, T.; Gimenez, O.; Pointier, J.-P.; Jarne, P.; David, P. Metapopulation dynamics of species with cryptic life stages. Am. Nat. 2013, 181, 479–491. [Google Scholar] [CrossRef] [PubMed]
- Radchuk, V.; Turlure, C.; Schtickzelle, N. Each life stage matters: The importance of assessing the response to climate change over the complete life cycle in butterflies. J. Anim. Ecol. 2013, 82, 275–285. [Google Scholar] [CrossRef] [PubMed]
- Merow, C.; Latimer, A.M.; Wilson, A.M.; McMahon, S.M.; Rebelo, A.G.; Silander, J.A. On using integral projection models to generate demographically driven predictions of species’ distributions: Development and validation using sparse data. Ecography 2014, 37, 1167–1183. [Google Scholar] [CrossRef]
- Logan, J.A.; Bentz, B.J. Model analysis of mountain pine beetle (Coleoptera: Scolytidae) seasonality. Environ. Entomol. 1999, 28, 924–934. [Google Scholar] [CrossRef]
- Molnár, P.K.; Derocher, A.E.; Thiemann, G.W.; Lewis, M.A. Predicting survival, reproduction and abundance of polar bears under climate change. Biol. Conserv. 2010, 143, 1612–1622. [Google Scholar] [CrossRef]
- IUCN. The IUCN Red List of Threatened Species. 2013. Available online: http://wwwiucnredlistorg/about/summary-statistics (accessed on 15 June 2016).
- Cormack, R. Estimates of survival from the sighting of marked animals. Biometrika 1964, 51, 429–438. [Google Scholar] [CrossRef]
- Jolly, G. Explicit estimates from capture-recapture data with both death and immigration-stochastic model. Biometrika 1965, 52, 225–247. [Google Scholar] [CrossRef] [PubMed]
- Seber, G.A.F. A note on the multiple-recapture census. Biometrika 1965, 52, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Lebreton, J.-D.; Burnham, K.P.; Clobert, J.; Anderson, D.R. Modeling survival and testing biological hypotheses using marked animals: A unified approach with case studies. Ecol. Monogr. 1992, 62, 67–118. [Google Scholar] [CrossRef]
- Nichols, J.D.; Sauer, J.R.; Pollock, K.H.; Hestbeck, J.B. Estimating transition probabilities for stage-based population projection matrices using capture recapture data. Ecology 1992, 73, 306–312. [Google Scholar] [CrossRef]
- Caswell, H. Matrix Population Models: Construction, Analysis, and Interpretation; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Morris, W.; Doak, D. Quantitative Conservation Biology: Theory and Practice of Population Viability Analysis; Sinauer Associates: Sunderland, MA, USA, 2002. [Google Scholar]
- Fujiwara, M.; Caswell, H. Estimating population projection matrices from multi-stage mark-recapture data. Ecology 2002, 83, 3257–3265. [Google Scholar]
- Caswell, H.; Fujiwara, M. Beyond survival estimation: Mark-recapture, matrix population models, and population dynamics. Anim. Biodivers. Conserv. 2004, 27, 471–488. [Google Scholar]
- Buckland, S.; Newman, K.; Thomas, L.; Koesters, N. State-space models for the dynamics of wild animal populations. Ecol. Model. 2004, 171, 157–175. [Google Scholar] [CrossRef]
- Thomas, L.; Buckland, S.T.; Newman, K.B.; Harwood, J. A unified framework for modelling wildlife population dynamics. Aust. N. Z. J. Stat. 2005, 47, 19–34. [Google Scholar] [CrossRef]
- Gimenez, O.; Lebreton, J.-D.; Gaillard, J.-M.; Choquet, R.; Pradel, R. Estimating demographic parameters using hidden process dynamic models. Theor. Popul. Biol. 2012, 82, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Patterson, T.A.; Basson, M.; Bravington, M.V.; Gunn, J.S. Classifying movement behaviour in relation to environmental conditions using hidden Markov models. J. Anim. Ecol. 2009, 78, 1113–1123. [Google Scholar] [CrossRef] [PubMed]
- Pradel, R. Multievent: An extension of multistate capture–recapture models to uncertain states. Biometrics 2005, 61, 442–447. [Google Scholar] [CrossRef] [PubMed]
- Langrock, R.; King, R. Maximum likelihood estimation of mark-recapture-recovery models in the presence of continuous covariates. Ann. Appl. Stat. 2013, 7, 1709–1732. [Google Scholar] [CrossRef]
- Johnson, D.S.; Laake, J.L.; Melin, S.R.; DeLong, R.L. Multivariate state hidden Markov models for mark-recapture data. Stat. Sci. 2016, 31, 233–244. [Google Scholar] [CrossRef]
- Schultz, C.B.; Crone, E.E. Burning prairie to restore butterfly habitat: A modeling approach to management tradeoffs for the Fender’s blue. Restor. Ecol. 1998, 6, 244–252. [Google Scholar] [CrossRef]
- Saastamoinen, M.; Ikonen, S.; Wong, S.C.; Lehtonen, R.; Hanski, I. Plastic larval development in a butterfly has complex environmental and genetic causes and consequences for population dynamics. J. Anim. Ecol. 2013, 82, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Caldas, A. Population ecology of Anaea ryphea (Nymphalidae): Immatures at Campinas, Brazil. J. Lepidopt. Soc. 1995, 49, 234–245. [Google Scholar]
- Nakajima, M.; Boggs, C.L.; Bailey, S.; Reithel, J.; Paape, T. Fitness costs of butterfly oviposition on a lethal non-native plant in a mixed native and non-native plant community. Oecologia 2013, 172, 823–832. [Google Scholar] [CrossRef] [PubMed]
- Young, A.M.; Moffett, M.W. Studies on the population biology of the tropical butterfly Mechanitis isthmia in Costa. Am. Midl. Nat. 1979, 101, 309–319. [Google Scholar] [CrossRef]
- Harrison, P.J.; Hanski, I.; Ovaskainen, O. Bayesian state-space modeling of metapopulation dynamics in the Glanville fritillary butterfly. Ecol. Monogr. 2011, 81, 581–598. [Google Scholar] [CrossRef]
- McElderry, R.M.; Salvato, M.H.; Horvitz, C.C. Population viability models for an endangered endemic subtropical butterfly: Effects of density and fire on population dynamics and risk of extinction. Biodivers. Conserv. 2015, 24, 1589–1608. [Google Scholar] [CrossRef]
- Knape, J.; de Valpine, P. Effects of weather and climate on the dynamics of animal population time series. Proc. R. Soc. Lond. B Biol. Sci. 2011, 278, 985–992. [Google Scholar] [CrossRef] [PubMed]
- Boggs, C.L.; Inouye, D.W. A single climate driver has direct and indirect effects on insect population dynamics. Ecol. Lett. 2012, 15, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Salvato, M.H.; Salvato, H.L. Notes on the status and ecology of Anaea troglodyta floridalis (Nympalidae) in Everglades National Park. J. Lepidopt. Soc. 2010, 64, 91–97. [Google Scholar] [CrossRef]
- Salvato, M.H.; Salvato, H.L. Parasitism of the Florida Leafwing and Bartram’s Hairstreak Butterlfy Immature Stages; Comprehensive Annual Report to Everglades National Park; Homestead, FL, USA, 2012; Unpublished report. [Google Scholar]
- Coll, C.; Horvitz, C.C.; McElderry, R. Stage-structured periodic population model for the Florida leafwing. Int. J. Complex Syst. Sci. 2012, 2, 1–5. [Google Scholar]
- Scott, J.A. The Butterflies of North America: A Natural History and Field Guide; Stanford University Press: Stanford, CA, USA, 1992. [Google Scholar]
- Gilbert, L.E.; University of Texas, Austin, TX, USA. Personal communication, 2010.
- Weseloh, R.M. Dispersal, survival, and population abundance of gypsy moth, Lymantria dispar (Lepidoptera: Lymantriidae), larvae determined by releases and mark-recapture studies. Ann. Entomol. Soc. Am. 1985, 78, 728–735. [Google Scholar] [CrossRef]
- Servanty, S.; Converse, S.J.; Bailey, L.L. Demography of a reintroduced population: Moving toward management models for an endangered species, the whooping crane. Ecol. Appl. 2014, 24, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Wagner, T.L.; Wu, H.-I.; Sharpe, P.J.; Schoolfield, R.M.; Coulson, R.N. Modeling insect development rates: A literature review and application of a biophysical model. Ann. Entomol. Soc. Am. 1984, 77, 208–220. [Google Scholar] [CrossRef]
- NOAA NWS. Weather Observations for the Past Three Days. Austin Camp Mabry. Austin, TX, USA, 28 March–1 May 2011. Available online: http://w1.weather.gov/data/obhistory/KATT.html (accessed every three days between March and May 2011).
- R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing; Version 3.1.0 (10 April 2014) edn.; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Plummer, M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing, Technische Universität Wien, Vienna, Austria, 20–22 March 2003. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Gosky, R.M.; Ghosh, S.K. A comparative study of Bayesian model selection criteria for capture-recapture models for closed populations. J. Mod. Appl. Stat. Methods 2009, 8, 68–80. [Google Scholar]
- McElderry, R.M.; University of Miami, Coral Gables, FL, USA. Personal observation, 2011.
- Patterson, T.A.; Thomas, L.; Wilcox, C.; Ovaskainen, O.; Matthiopoulos, J. State-space models of individual animal movement. Trends Ecol. Evol. 2008, 23, 87–94. [Google Scholar] [CrossRef] [PubMed]
- McElderry, R.M.; Duquesnel, J.A.; Maschinski, J. Gauging reintroduction success with a hidden Markov model and analysis of transient dynamics. 2017; Submit. [Google Scholar]
- Conn, P.B.; Cooch, E.G. Multistate capture–recapture analysis under imperfect state observation: An application to disease models. J. Appl. Ecol. 2009, 46, 486–492. [Google Scholar] [CrossRef]
- Schaub, M.; Abadi, F. Integrated population models: A novel analysis framework for deeper insights into population dynamics. J. Ornithol. 2011, 152, 227–237. [Google Scholar] [CrossRef]
- Nowicki, P.; Bonelli, S.; Barbero, F.; Balletto, E. Relative importance of density-dependent regulation and environmental stochasticity for butterfly population dynamics. Oecologia 2009, 161, 227–239. [Google Scholar] [CrossRef] [PubMed]
- Gimenez, O.; Rossi, V.; Choquet, R.; Dehais, C.; Doris, B.; Varella, H.; Vila, J.-P.; Pradel, R. State-space modelling of data on marked individuals. Ecol. Model. 2007, 206, 431–438. [Google Scholar] [CrossRef]
- McElderry, R.M.; University of Miami, Coral Gables, FL, USA. Unpublished data. 2013.
- Burnham, K.P. A theory for combined analysis of ring recovery and recapture data. In Marked Individuals in the Study of Bird Population; Lebreton, J., North, P., Eds.; Birkhauser Vet-lag: Basel, Switzerland, 1993; pp. 199–213. [Google Scholar]
- Schnute, J.T. A general framework for developing sequential fisheries models. Can. J. Fish. Aquat. Sci. 1994, 51, 1676–1688. [Google Scholar] [CrossRef]
- Lowman, M.D. Seasonal variation in insect abundance among three Australian rain forests, with particular reference to phytophagous types. Aust. J. Ecol. 1982, 7, 353–361. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Reiter, B.E. Changes in North American spring International. J. Climatol. 2000, 20, 929–932. [Google Scholar] [CrossRef]
- Dempster, J. The natural control of populations of butterflies and moths. Biol. Rev. 1983, 58, 461–481. [Google Scholar] [CrossRef]
- Clark, B.R.; Faeth, S.H. The consequences of larval aggregation in the butterfly Chlosyne lacinia. Ecol. Entomol. 1997, 22, 408–415. [Google Scholar] [CrossRef]
- Roughgarden, J. Primer of Ecological Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Salvato, M.; Salvato, H.; Sadle, J. Tent building by larval Anaea troglodyta floridalis (Nymphalidae). News Lepidopt. Soc. 2015, 57. [Google Scholar]
- Amarasekare, P.; Savage, V. A framework for elucidating the temperature dependence of fitness. Am. Nat. 2011, 179, 178–191. [Google Scholar] [CrossRef] [PubMed]
- Gillooly, J.F.; Charnov, E.L.; West, G.B.; Savage, V.M.; Brown, J.H. Effects of size and temperature on developmental time. Nature 2002, 417, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Chown, S.L.; Nicolson, S. Insect Physiological Ecology: Mechanisms and Patterns; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Birt, A.; Feldman, R.M.; Cairns, D.M.; Coulson, R.N.; Tchakerian, M.; Xi, W.; Guldin, J.M. Stage-structured matrix models for organisms with non-geometric development times. Ecology 2009, 90, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Caldas, A. Biology of Anaea ryphea (Nymphalidae) in Campinas, Brazil. J. Lepidopt. Soc. 1994, 48, 248–257. [Google Scholar]
- Muyshondt, A. Notes on the life cycle and natural history of butterflies of El Salvador. III. Anaea (Consul) fabius (Nymphalidae). J. Lepidopt. Soc. 1974, 28, 81–99. [Google Scholar]
- Muyshondt, A. Notes on the life cycle and natural history of butterflies of El Salvador. IV. Anaea (Memphis) eurypyle confusa (Nymphalidae). J. Lepidopt. Soc. 1974, 28, 306–314. [Google Scholar]
- Ramos, S.J. Notes on the life cycle and biology of Anaea troglodyte borinquenalis (Lepidoptera: Apaturidae). Caribb. J. Sci. 1984, 20, 19–24. [Google Scholar]
- DeVries, P.J. The Butterflies of Costa Rica and Their Natural History; Princeton University Press: Princeton, NJ, USA, 1987; Volume I. [Google Scholar]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McElderry, R.M. Estimating Density and Temperature Dependence of Juvenile Vital Rates Using a Hidden Markov Model. Insects 2017, 8, 51. https://doi.org/10.3390/insects8020051
McElderry RM. Estimating Density and Temperature Dependence of Juvenile Vital Rates Using a Hidden Markov Model. Insects. 2017; 8(2):51. https://doi.org/10.3390/insects8020051
Chicago/Turabian StyleMcElderry, Robert M. 2017. "Estimating Density and Temperature Dependence of Juvenile Vital Rates Using a Hidden Markov Model" Insects 8, no. 2: 51. https://doi.org/10.3390/insects8020051




