Fatigue Reliability Assessment of an Automobile Coil Spring under Random Strain Loads Using Probabilistic Technique
Abstract
:1. Introduction
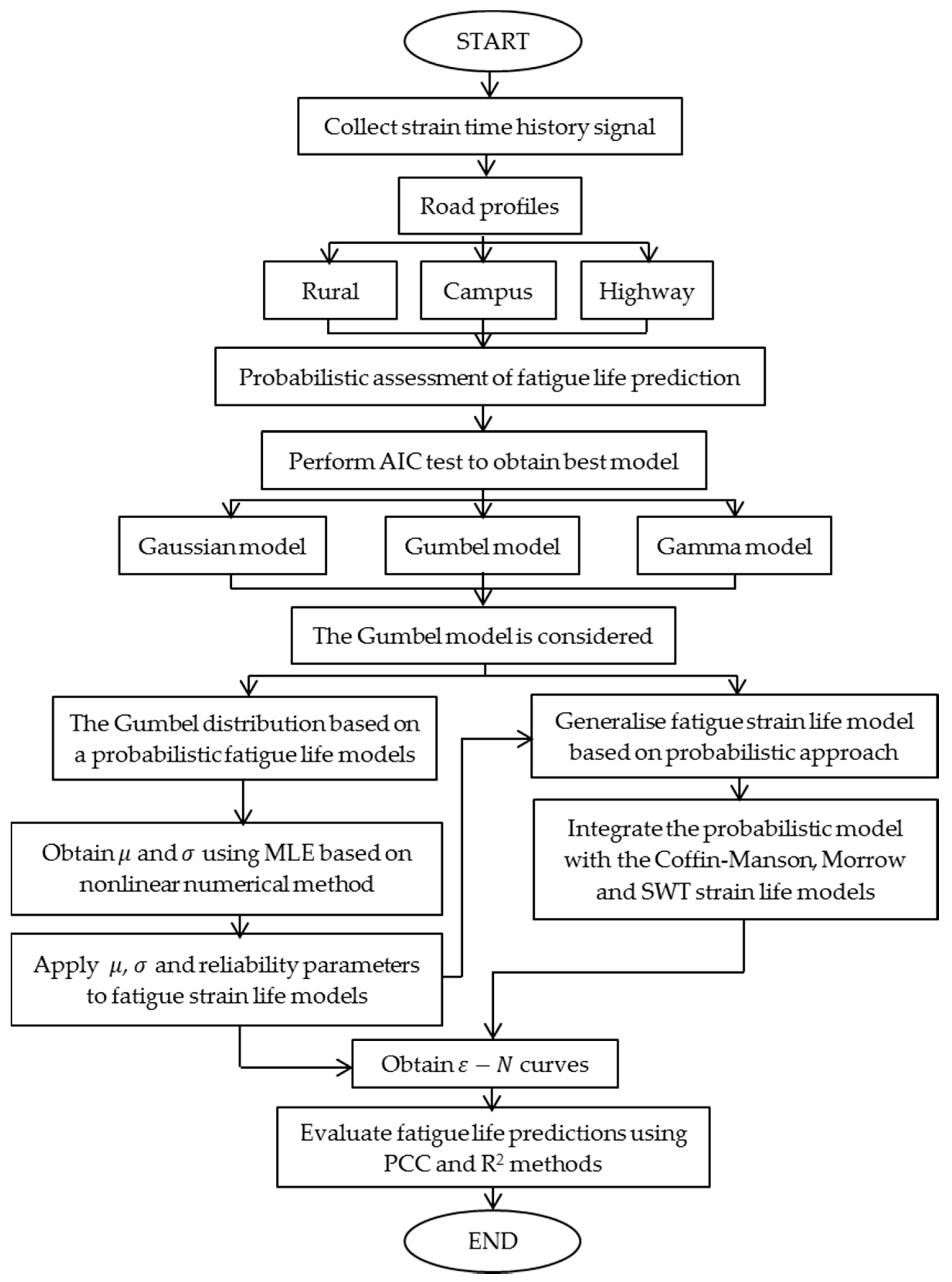
2. Methodology
2.1. Gumbel Distribution Based on Probabilistic Assessment of Fatigue Life Model
2.2. MLE Method to Estimate the Gumbel Model Parameters
2.3. Proposed Mathematical Model based on Probabilistic for Strain Fatigue Life Models
3. Results and Discussion
3.1. Measured Strain Time History Signals
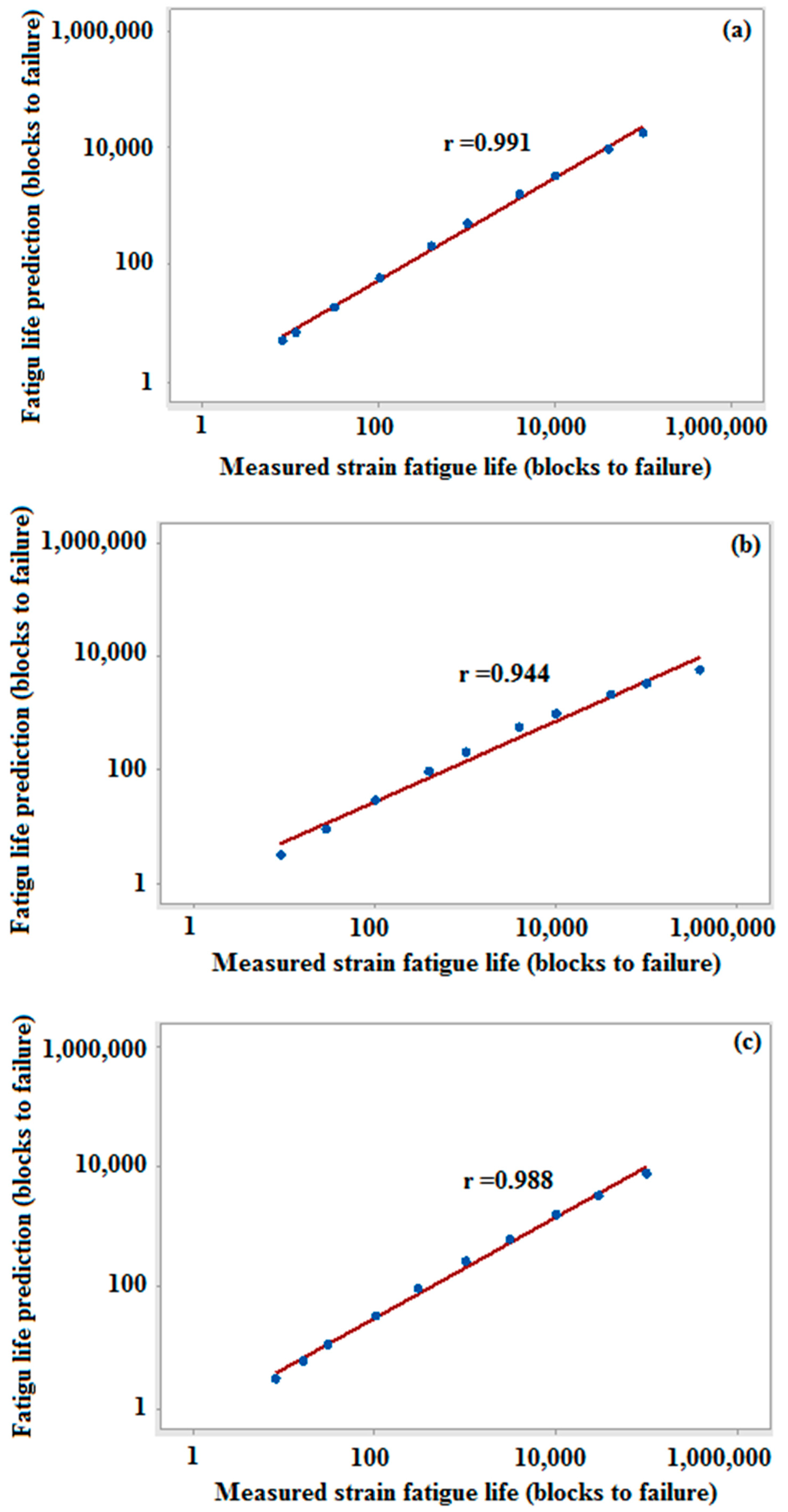
3.2. Approximate Best Model Compared with Other Models
3.3. Strain Fatigue Prediction based on Rural, Campus, and Highway Road Excitatuions
3.4. Proposed Probabilistic Method Based on the Gumbel Model
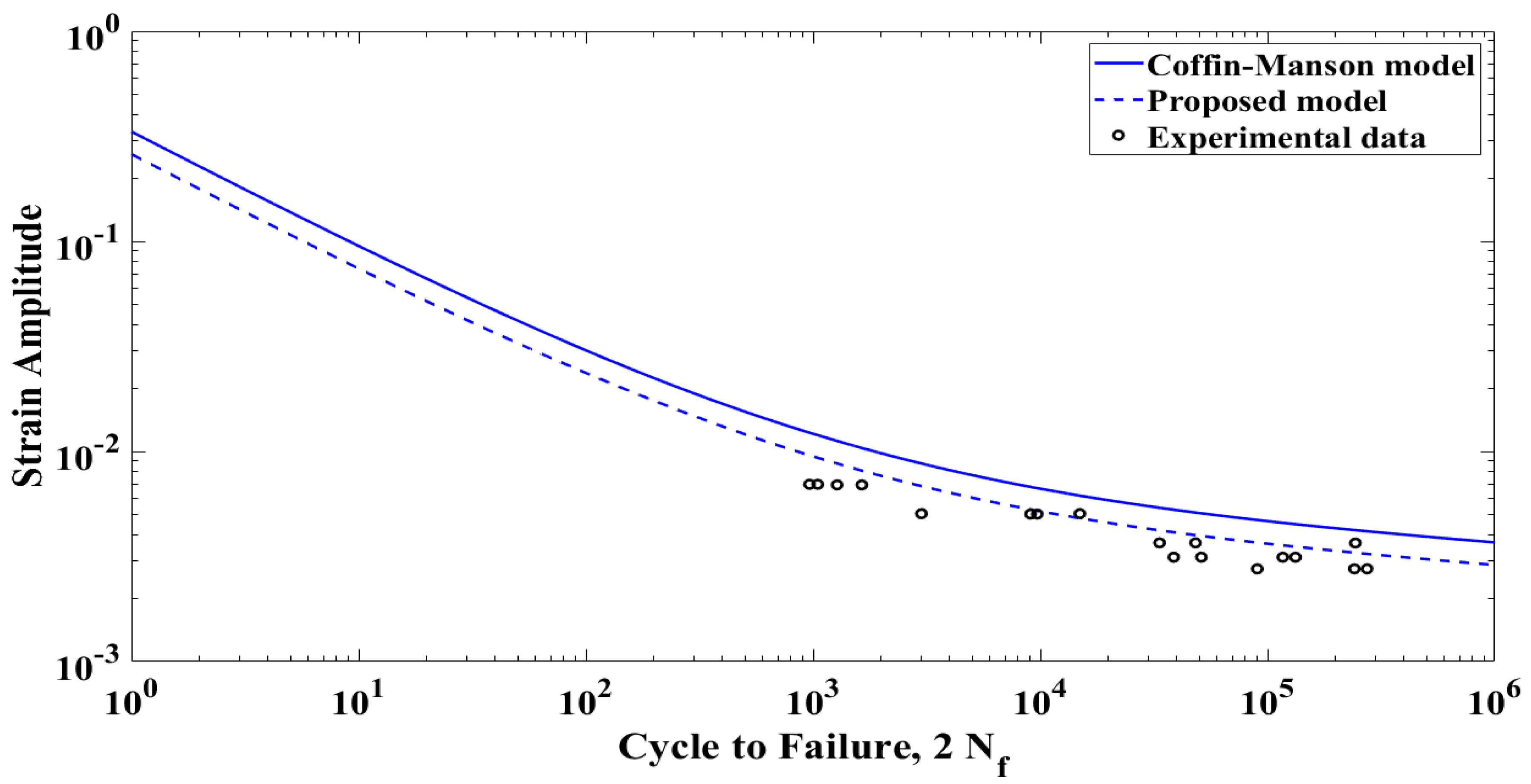
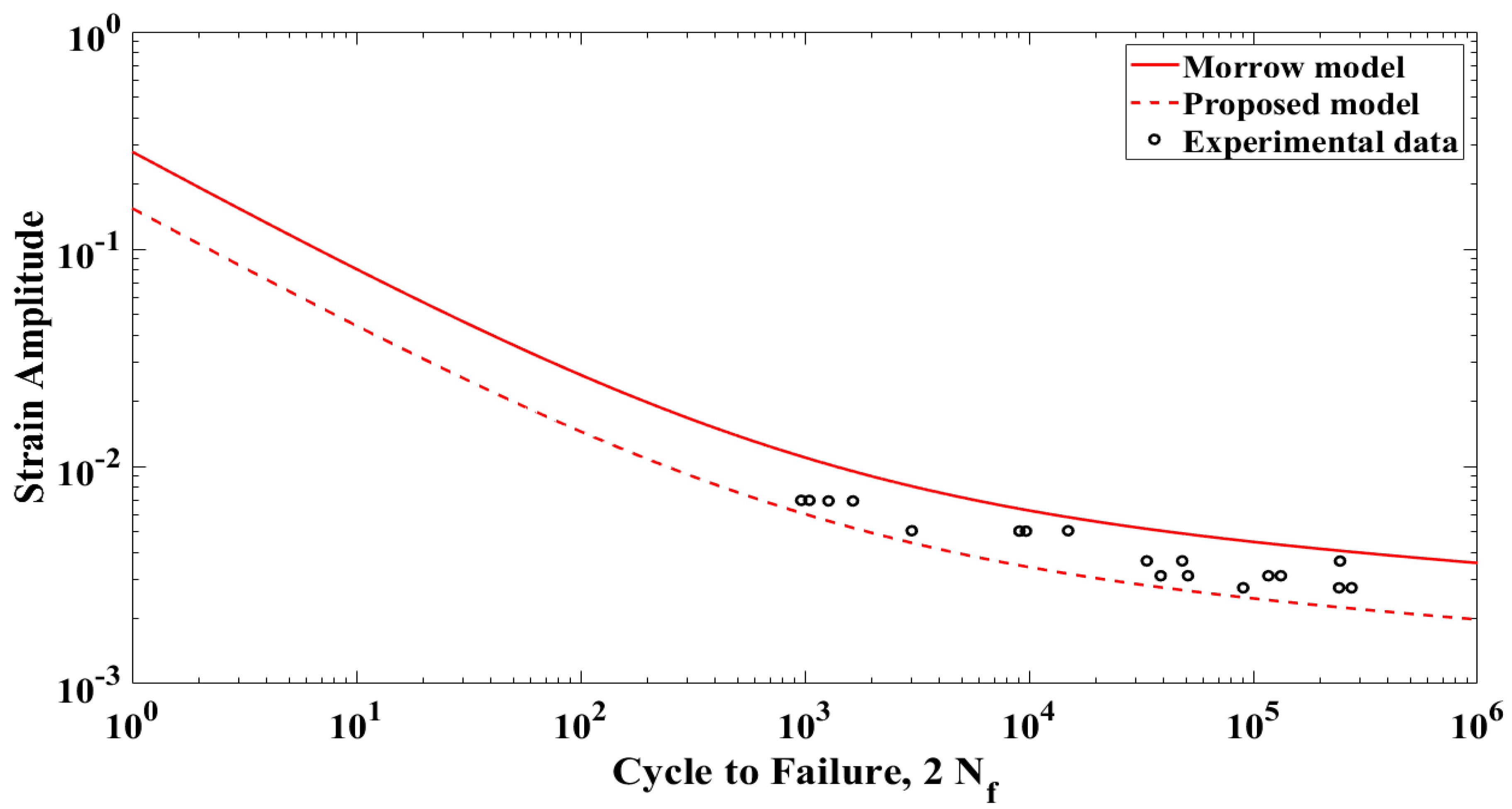
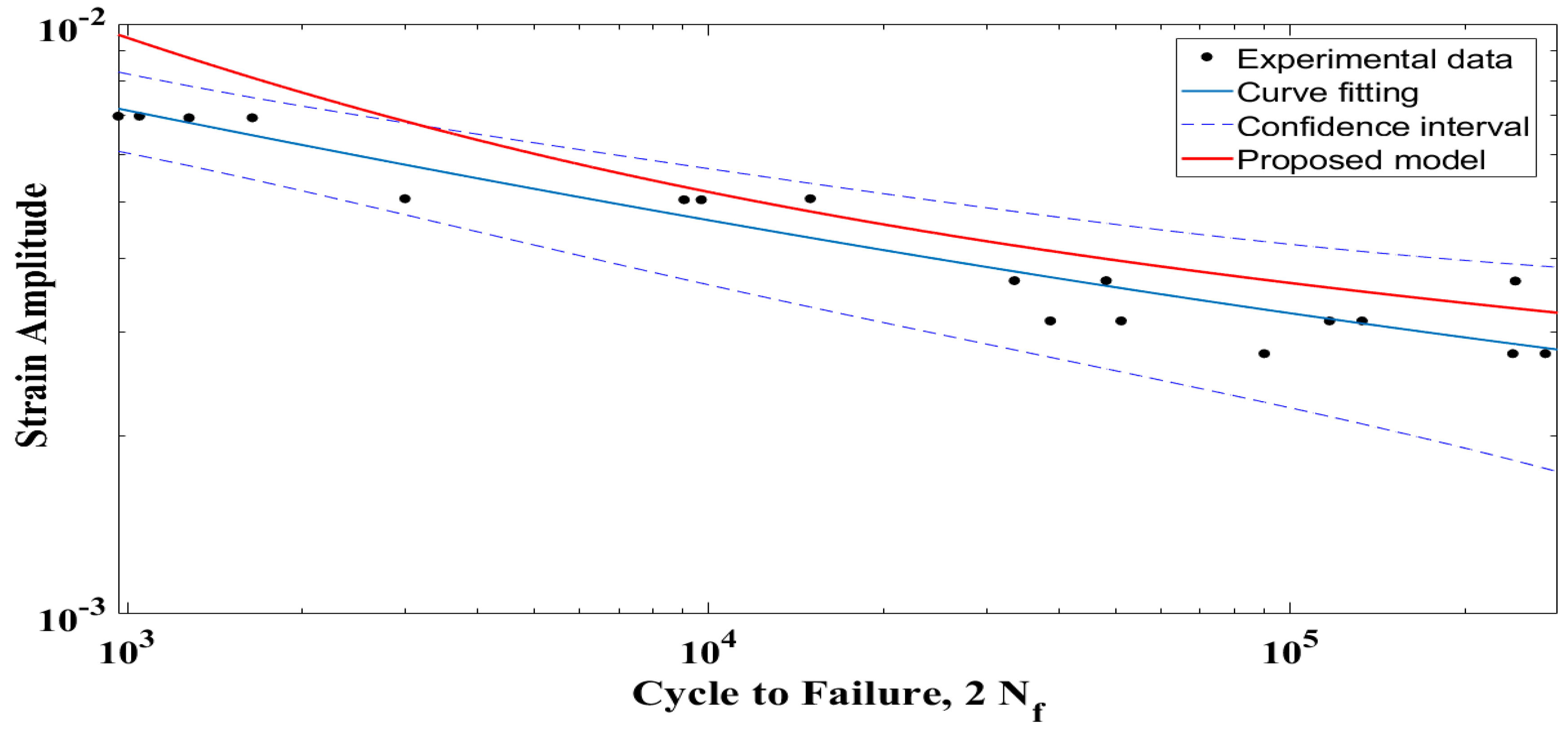
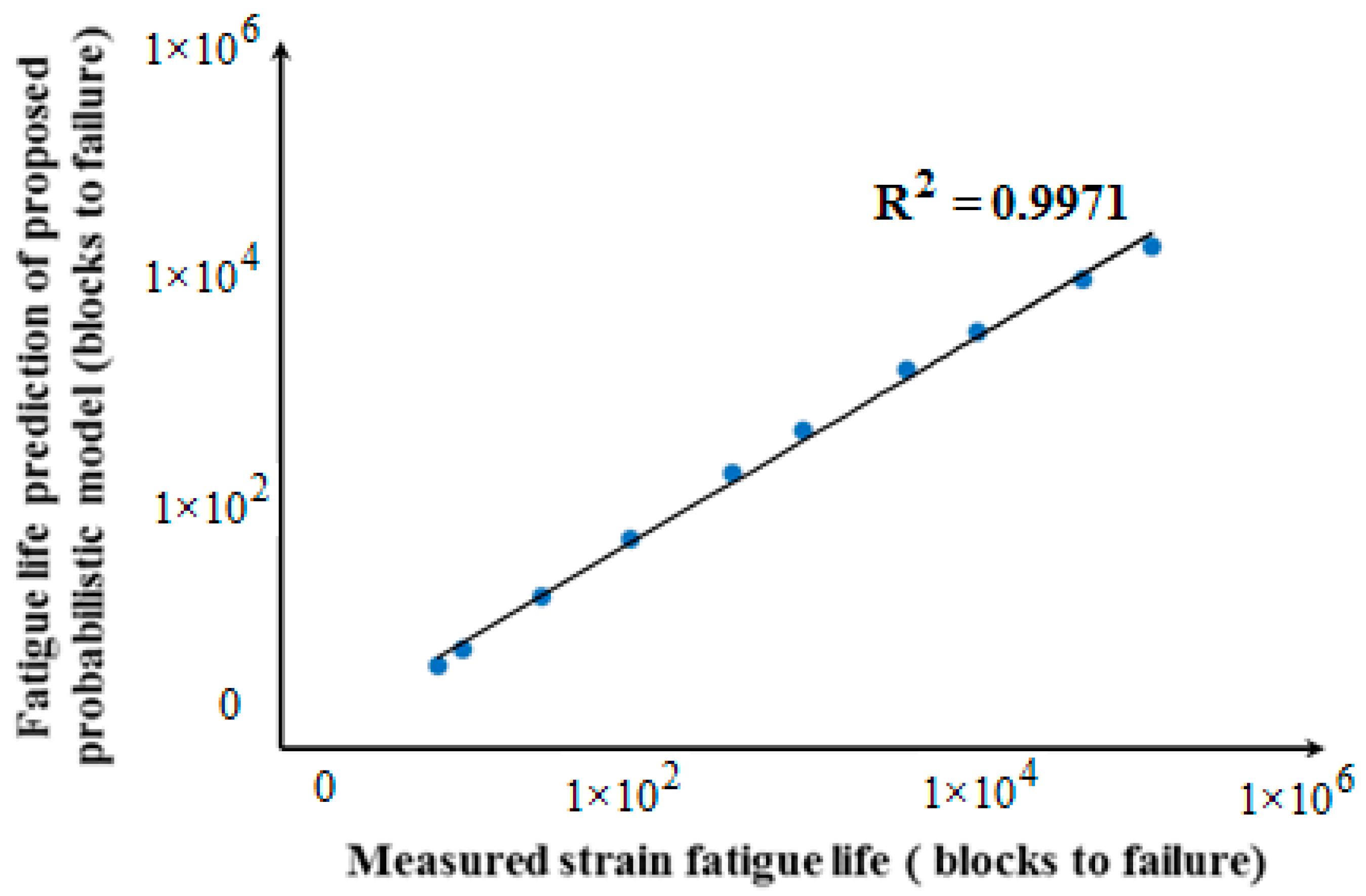
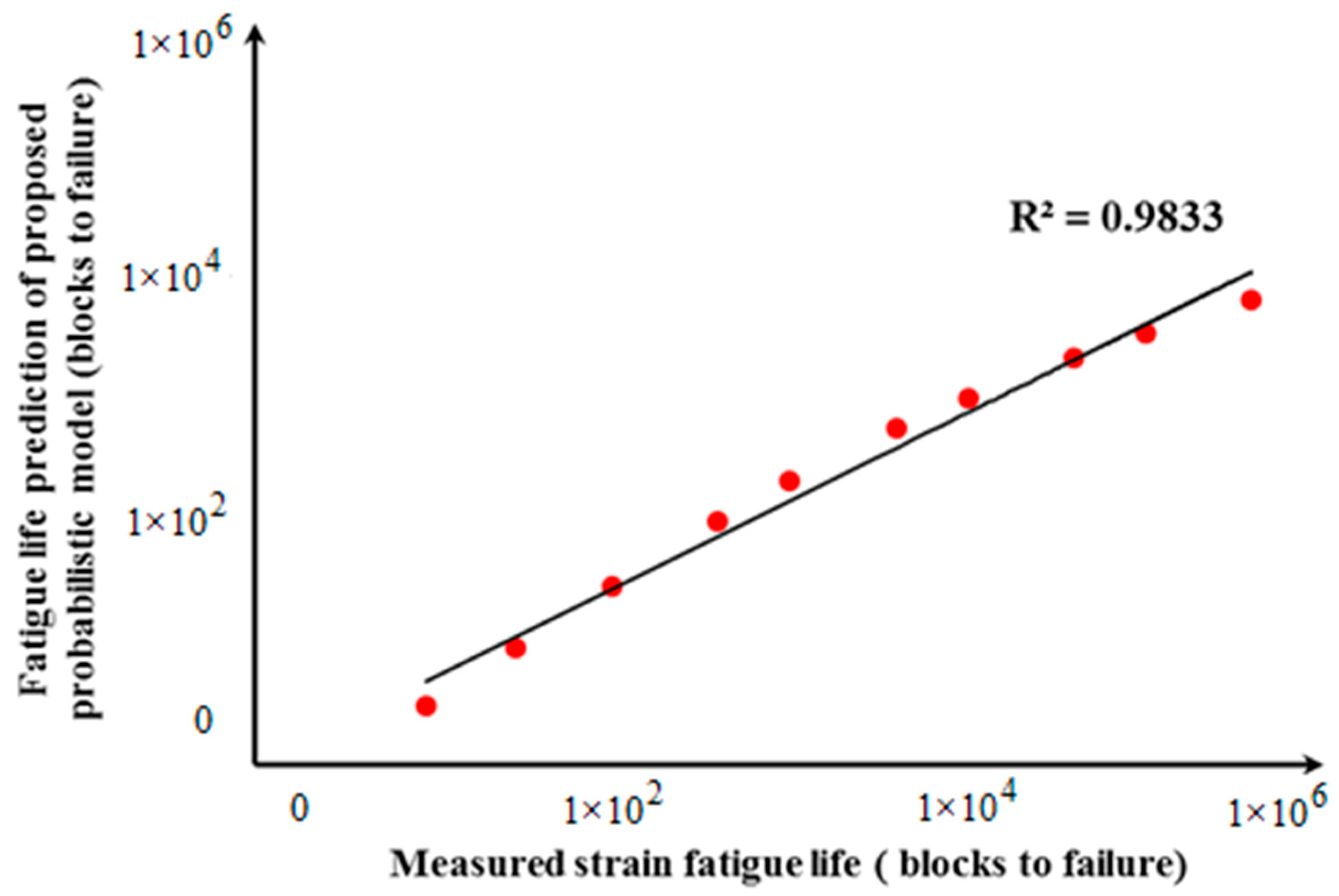
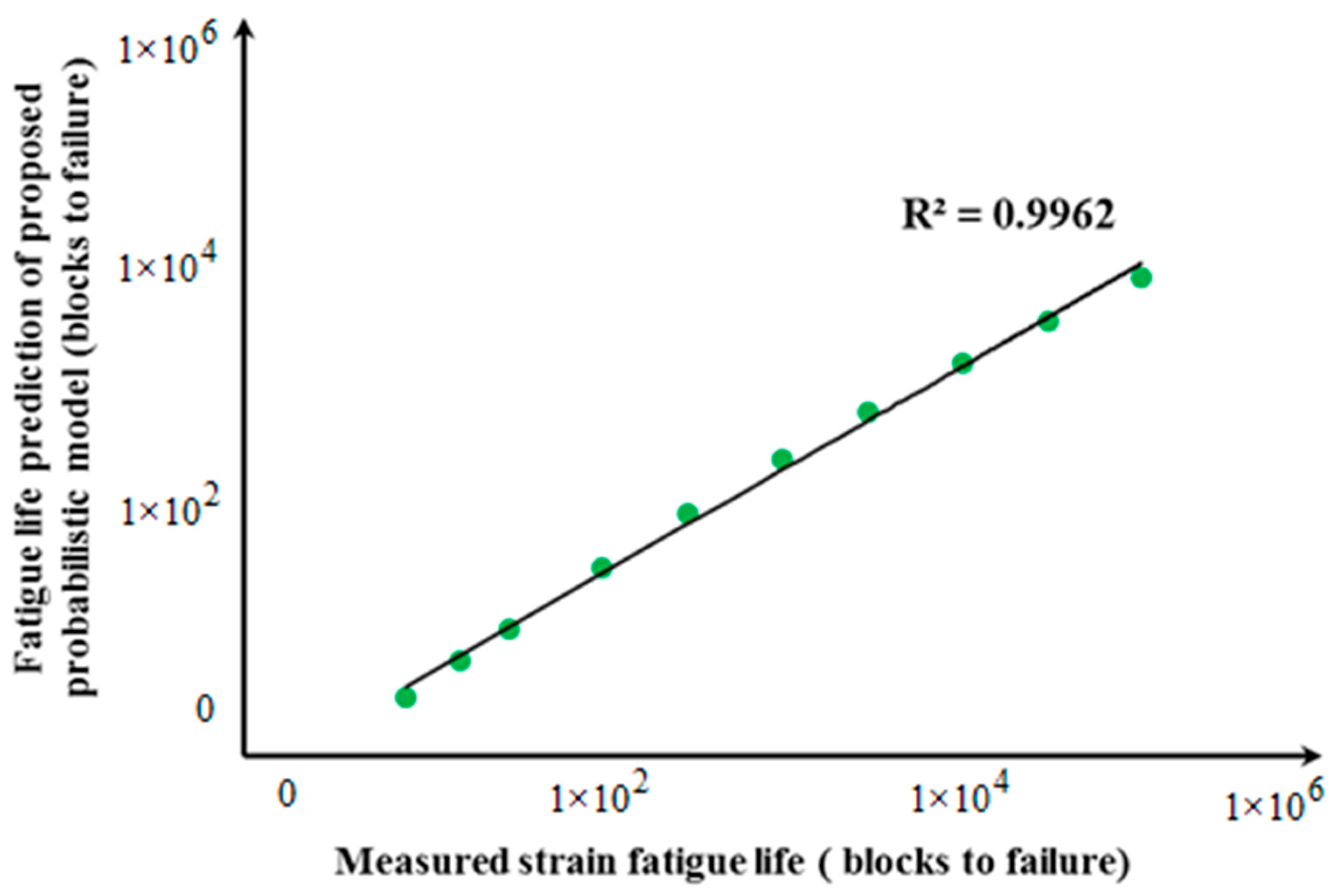
3.5. Validation of Fatigue Life Prediction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Altamura, A.; Straub, D. Reliability assessment of high cycle fatigue under variable amplitude loading: Review and solutions. Eng. Fract. Mech. 2014, 121, 40–66. [Google Scholar] [CrossRef]
- Singh, S.; Abdullah, S. Durability analysis using Markov chain modeling under random loading for automobile crankshaft. Int. J. Struct. Integr. 2019. [Google Scholar] [CrossRef]
- Lu, Y.; Zheng, H.; Zeng, J.; Chen, T.; Wu, P. Fatigue life reliability evaluation in a high-speed train bogie frame using accelerated life and numerical test. Reliab. Eng. Syst. Saf. 2019, 188, 221–232. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liu, Q.; Peng, W.; Zhang, X.-C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142, 502–517. [Google Scholar] [CrossRef]
- Chen, B.; Zhao, Y.; Yang, B. Scale-induced effects on fatigue properties of a cast steel for bogie frames of China railway rolling wagons. Int. J. Fatigue 2012, 35, 45–55. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, Q.; Zhou, J.; Yu, Z. Fatigue reliability assessment of turbine discs under multi-source uncertainties. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1291–1305. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liu, Q.; Lei, Q.; Wang, Q. Probabilistic fatigue life prediction and reliability assessment of a high pressure turbine disc considering load variations. Int. J. Damage Mech. 2018, 27, 1569–1588. [Google Scholar] [CrossRef]
- Azrulhisham, E.; Asri, Y.; Dzuraidah, A.; Nik Abdullah, N.; Shahrum, A.; Che Hassan, C. Evaluation of fatigue life reliability of steering knuckle using pearson parametric distribution model. Int. J. Qual. Stat. Reliab. 2011, 2010. [Google Scholar] [CrossRef]
- Kang, D.-H.; Jang, C.; Park, Y.-S.; Han, S.-Y.; Kim, J.H. Fatigue reliability assessment of steel member using probabilistic stress-life method. Adv. Mech. Eng. 2012, 4, 649215. [Google Scholar] [CrossRef]
- Grujicic, M.; Arakere, G.; Bell, W.; Marvi, H.; Yalavarthy, H.; Pandurangan, B.; Haque, I.; Fadel, G. Reliability-based design optimization for durability of ground vehicle suspension system components. J. Mater. Eng. Perform. 2010, 19, 301–313. [Google Scholar] [CrossRef]
- Song, C.Y.; Lee, J. Reliability-based design optimization of knuckle component using conservative method of moving least squares meta-models. Probabilistic Eng. Mech. 2011, 26, 364–379. [Google Scholar] [CrossRef]
- Mohammad, M.; Abdullah, S.; Jamaludin, N.; Innayatullah, O. Predicting the fatigue life of the SAE 1045 steel using an empirical Weibull-based model associated to acoustic emission parameters. Mater. Des. 2014, 54, 1039–1048. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Wang, X.; Wang, Y. Numerical method for estimating fatigue crack initiation size using elastic–plastic fracture mechanics method. Appl. Math. Model. 2019, 73, 365–377. [Google Scholar] [CrossRef]
- Palmieri, M.; Česnik, M.; Slavič, J.; Cianetti, F.; Boltežar, M. Non-Gaussianity and non-stationarity in vibration fatigue. Int. J. Fatigue 2017, 97, 9–19. [Google Scholar] [CrossRef]
- Niesłony, A.; Böhm, M.; Łagoda, T.; Cianetti, F. The use of spectral method for fatigue life assessment for non-gaussian random loads. Acta Mechanica et Automatica 2016, 10, 100–103. [Google Scholar] [CrossRef] [Green Version]
- Cianetti, F.; Palmieri, M.; Braccesi, C.; Morettini, G. Correction formula approach to evaluate fatigue damage induced by non-Gaussian stress state. Procedia Struct. Integr. 2018, 8, 390–398. [Google Scholar] [CrossRef]
- Capponi, L.; Česnik, M.; Slavič, J.; Cianetti, F.; Boltežar, M. Non-stationarity index in vibration fatigue: Theoretical and experimental research. Int. J. Fatigue 2017, 104, 221–230. [Google Scholar] [CrossRef]
- Česnik, M.; Slavič, J.; Capponi, L.; Palmieri, M.; Cianetti, F.; Boltežar, M. The relevance of non-stationarities and non-Gaussianities in vibration fatigue. MATEC Web Conf. 2018, 165, 10011. [Google Scholar] [CrossRef]
- Anderson, K.; Daniewicz, S. Statistical analysis of the influence of defects on fatigue life using a Gumbel distribution. Int. J. Fatigue 2018, 112, 78–83. [Google Scholar] [CrossRef]
- Shakhatreh, M.K.; Lemonte, A.J.; Moreno-Arenas, G. The log-normal modified Weibull distribution and its reliability implications. Reliab. Eng. Syst. Saf. 2019, 188, 6–22. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Hao, Y.-Z.; Liao, D. Probabilistic modeling and simulation of multiple surface crack propagation and coalescence. Appl. Math. Model. 2019, 78, 383–398. [Google Scholar] [CrossRef]
- Park, Y.-S. Fatigue Reliability Analysis of Steel Welded Member Using Probabilistic Stress-Life Method. Int. J. Steel Struct. 2019, 19, 71–81. [Google Scholar] [CrossRef]
- ASTM E112-96. Standard Test Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Karthik, J.; Chaitanya, K.; Sasanka, C.T. Fatigue life prediction of a parabolic spring under non-constant amplitude proportional loading using finite element method. Int. J. Adv. Sci. Technol. 2012, 46, 143–156. [Google Scholar]
- Yang, B.; Ma, B.; Xiao, S.; Zhao, Y. A probabilistic model for describing short fatigue crack growth behavior of LZ50 steel. Strength Mater. 2016, 48, 90–97. [Google Scholar] [CrossRef]
- Correia, J.; Huffman, P.; De Jesus, A.; Cicero, S.; Fernández-Canteli, A.; Berto, F.; Glinka, G. Unified two-stage fatigue methodology based on a probabilistic damage model applied to structural details. Theor. Appl. Fract. Mech. 2017, 92, 252–265. [Google Scholar] [CrossRef]
- Raposo, P.; Correia, J.; De Jesus, A.; Calçada, R.; Lesiuk, G.; Hebdon, M.; Fernández Canteli, A.C. Probabilistic fatigue SN curves derivation for notched components. Frattura ed Integrita Strutturale 2017, 42, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Sanches, R.F.; de Jesus, A.M.; Correia, J.A.; Da Silva, A.; Fernandes, A. A probabilistic fatigue approach for riveted joints using Monte Carlo simulation. J. Constr. Steel Res. 2015, 110, 149–162. [Google Scholar] [CrossRef] [Green Version]
- Correia, J.; Apetre, N.; Arcari, A.; De Jesus, A.; Muñiz-Calvente, M.; Calçada, R.; Berto, F.; Fernández-Canteli, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Fernández-Canteli, A.; Castillo, E.; Pinto, H.; López-Aenlle, M. Estimating the S–N field from strain–lifetime curves. Strain 2011, 47, e93–e97. [Google Scholar] [CrossRef]
- De Jesus, A.M.; Ripoll, M.L.R.; Fernández-Canteli, A.; Castillo, E.; Pereira, H.F. Probabilistic fatigue assessment of a notched detail taking into account mean stress effects. J. Press. Vessel Technol. 2012, 134, 021203. [Google Scholar] [CrossRef]
- Pinto, H.; De Jesus, A.M.; Fernández-Canteli, A.; Castillo, E.; Pereira, H.F. Analysis of constant and variable amplitude strain-life data using a novel probabilistic Weibull regression model. J. Press. Vessel Technol. 2010, 132, 061401. [Google Scholar] [CrossRef]
- Ao, D.; Hu, Z.; Mahadevan, S. Design of validation experiments for life prediction models. Reliab. Eng. Syst. Saf. 2017, 165, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Kernane, T.; Raizah, Z.A. Estimation of the Parameters of Extreme Value Distributions from Truncated Data Via the EM Algorithm. 2014. Available online: https://www.researchgate.net/publication/45226281_Estimation_of_the_Parameters_of_Extreme_Value_Distributions_from_Truncated_Data_Via_the_EM_Algorithm (accessed on 2 December 2014).
- Feng, H.; Wang, Y.; Jiang, X. A Maximum Likelihood method for estimating probabilistic strain amplitude–fatigue life curves. Acta Mech. Solida Sin. 2018, 31, 80–93. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Huang, H.-Z.; Peng, W.; Wang, H.-K.; Mahadevan, S. Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Mohamed Haris, S. Evaluation of Energy-Based Model Generated Strain Signals for Carbon Steel Spring Fatigue Life Assessment. Metals 2019, 9, 213. [Google Scholar] [CrossRef] [Green Version]
- Banks, H.T.; Joyner, M.L. AIC under the framework of least squares estimation. Appl. Math. Lett. 2017, 74, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Shields, M.D. On the quantification and efficient propagation of imprecise probabilities resulting from small datasets. Mech. Syst. Signal. Process. 2018, 98, 465–483. [Google Scholar] [CrossRef]
- Ahmed, E.A. Estimation of some lifetime parameters of generalized Gompertz distribution under progressively type-II censored data. Appl. Math. Model. 2015, 39, 5567–5578. [Google Scholar] [CrossRef]
- Magalhaes, R.R.; Fontes, C.H.; Vieira de Melo, S.A. Stress analysis using BEM as support for fatigue life prediction in the automotive industry. Int. J. Veh. Syst. Model. Test. 2013, 8, 88–103. [Google Scholar] [CrossRef]
- Kamaya, M.; Kawakubo, M. Mean stress effect on fatigue strength of stainless steel. Int. J. Fatigue 2015, 74, 20–29. [Google Scholar] [CrossRef]
- Wang, G.; He, Z.; Xue, L.; Cui, Q.; Lv, S.; Zhou, P. Bootstrap analysis of designed experiments for reliability improvement with a non-constant scale parameter. Reliab. Eng. Syst. Saf. 2017, 160, 114–121. [Google Scholar] [CrossRef]
- Gonçalves, V.R.M.; Podgornik, B.; Leskovšek, V.; Totten, G.E.; Canale, L.d.C.F. Influence of Deep Cryogenic Treatment on the Mechanical Properties of Spring Steels. J. Mater. Eng. Perform. 2019, 28, 769–775. [Google Scholar] [CrossRef]
- Ince, A. A mean stress correction model for tensile and compressive mean stress fatigue loadings. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 939–948. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A modification of Morrow and Smith–Watson–Topper mean stress correction models. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 854–867. [Google Scholar] [CrossRef]
- Singh, S.; Abdullah, S. Effects of Mean Stress on the Durability Assessment for an Automobile Crankshaft using Markov Chain Modelling Technique. J. Mech. Eng. 2018, 7, 19–28. [Google Scholar]
- Kong, Y.; Abdullah, S.; Schramm, D.; Omar, M.; Haris, S. Vibration fatigue analysis of carbon steel coil spring under various road excitations. Metals 2018, 8, 617. [Google Scholar] [CrossRef] [Green Version]













| Properties | Values |
|---|---|
| Yield strength (MPa) | 1070 |
| Ultimate tensile strength (MPa) | 1550 |
| Material modulus of elasticity (GPa) | 207 |
| Fatigue strength coefficient (MPa) | 2063 |
| Fatigue strength exponent | −0.08 |
| Fatigue ductility exponent | −1.05 |
| Fatigue ductility coefficient | 9.56 |
| Method | |||
|---|---|---|---|
| Gumbel | Gamma | Gaussian | |
| Akaike information criterion | |||
| Log–likelihood | |||
| Strain Life Model | Road Surface | Fatigue Life (Block Cycle) | Fatigue Damage (1/cycle) |
|---|---|---|---|
| Coffin–Manson | Rural | ||
| Campus | |||
| Highway | |||
| Morrow | Rural | ||
| Campus | |||
| Highway | |||
| Smith–Watson–Topper | Rural | ||
| Campus | |||
| Highway |
| Fatigue Life Model | Unbiased Scale | Unbiased Location | |
|---|---|---|---|
| Coffin–Manson | 39,526 | 259,524 | 0.0165 |
| Morrow | 58,299 | 124,304 | 0.0436 |
| Smith–Watson–Topper | 37,505 | 72,104 | 0.0444 |
| Road Surface | |||
|---|---|---|---|
| Rural | 189 | −116 | 39 |
| Campus | 87 | −118 | −0.47 |
| Highway | 114 | −72 | 22 |
| Fatigue Life Model | Measured Strain Fatigue Life Curve | Proposed Probabilistic Fatigue Life Curve | |||
|---|---|---|---|---|---|
| RMSE | |||||
| Coffin–Manson | 0.3329 | 0.0037 | 0.2599 | 0.0029 | 0.00114 |
| Morrow | 0.2808 | 0.0036 | 0.1542 | 0.002 | 0.00107 |
| Smith–Watson–Topper | 1.4128 | 0.0059 | 0.7845 | 0.0033 | 0.00509 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manouchehrynia, R.; Abdullah, S.; Singh Karam Singh, S. Fatigue Reliability Assessment of an Automobile Coil Spring under Random Strain Loads Using Probabilistic Technique. Metals 2020, 10, 12. https://doi.org/10.3390/met10010012
Manouchehrynia R, Abdullah S, Singh Karam Singh S. Fatigue Reliability Assessment of an Automobile Coil Spring under Random Strain Loads Using Probabilistic Technique. Metals. 2020; 10(1):12. https://doi.org/10.3390/met10010012
Chicago/Turabian StyleManouchehrynia, Reza, Shahrum Abdullah, and Salvinder Singh Karam Singh. 2020. "Fatigue Reliability Assessment of an Automobile Coil Spring under Random Strain Loads Using Probabilistic Technique" Metals 10, no. 1: 12. https://doi.org/10.3390/met10010012





