Next Article in Journal
Low Cycle Fatigue Behaviour of DP Steels: Micromechanical Modelling vs. Validation
Next Article in Special Issue
Transition of the Interface between Iron and Carbide Precipitate From Coherent to Semi-Coherent
Previous Article in Journal
Effect of Fe-Content on the Mechanical Properties of Recycled Al Alloys during Hot Compression
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 7
Issue 7
10.3390/met7070264
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Role of κ-Carbides as Hydrogen Traps in High-Mn Steels

by
Tobias A. Timmerscheidt
1,
Poulumi Dey
2,
Dimitri Bogdanovski
1,
Jörg Von Appen
1,
Tilmann Hickel
2,
Jörg Neugebauer
2 and
Richard Dronskowski
1,3,*
1
Institute of Inorganic Chemistry, Chair of Solid-State and Quantum Chemistry, RWTH Aachen University, 52056 Aachen, Germany
2
Max-Planck-Institute for Iron Research GmbH, 40237 Düsseldorf, Germany
3
Jülich-Aachen Research Alliance (JARA-HPC), RWTH Aachen University, 52056 Aachen, Germany
*
Author to whom correspondence should be addressed.
Metals 2017, 7(7), 264; https://doi.org/10.3390/met7070264
Submission received: 13 June 2017 / Revised: 30 June 2017 / Accepted: 3 July 2017 / Published: 11 July 2017
(This article belongs to the Special Issue First-Principles Approaches to Metals, Alloys, and Metallic Compounds)
Browse Figures
Versions Notes

Abstract

:
Since the addition of Al to high-Mn steels is known to reduce their sensitivity to hydrogen-induced delayed fracture, we investigate possible trapping effects connected to the presence of Al in the grain interior employing density-functional theory (DFT). The role of Al-based precipitates is also investigated to understand the relevance of short-range ordering effects. So-called E21-Fe3AlC κ-carbides are frequently observed in Fe-Mn-Al-C alloys. Since H tends to occupy the same positions as C in these precipitates, the interaction and competition between both interstitials is also investigated via DFT-based simulations. While the individual H–H/C–H chemical interactions are generally repulsive, the tendency of interstitials to increase the lattice parameter can yield a net increase of the trapping capability. An increased Mn content is shown to enhance H trapping due to attractive short-range interactions. Favorable short-range ordering is expected to occur at the interface between an Fe matrix and the E21-Fe3AlC κ-carbides, which is identified as a particularly attractive trapping site for H. At the same time, accumulation of H at sites of this type is observed to yield decohesion of this interface, thereby promoting fracture formation. The interplay of these effects, evident in the trapping energies at various locations and dependent on the H concentration, can be expressed mathematically, resulting in a term that describes the hydrogen embrittlement.

1. Introduction

Fe-Mn-Al-C quaternary alloys form an important class of modern advanced high-strength steels (AHSS). Synthetic variations of the Mn, Al, and C contents accompanied by sophisticated steel-processing techniques have led to the availability of different phases and microstructures such as ferrite (body-centered cubic, bcc), martensite (body-centered tetragonal, bct), austenite (face-centered cubic, fcc), or a mixture of those as observed in dual-phase (ferrite/martensite), duplex (ferrite/austenite), or triplex (ferrite/austenite/carbide) steels. In particular, so-called high-Mn steels, comprising a broad spectrum of Fe-based alloys with Mn contents in the range of 20–30 wt % and Al and C contents in the ranges of 0–10 wt % and 0–2 wt %, respectively, have attracted attention [1]. These steels exhibit particular deformation mechanisms, such as transformation-induced plasticity (TRIP), twinning-induced plasticity (TWIP), or microband-induced plasticity (MBIP) [2], thereby yielding extraordinarily high strength and ductility. Steels containing considerable amounts of Al in addition to Mn have raised recent interest due to the precipitation of ordered carbides, both from ferritic and austenitic matrices [1]. These κ-carbides have the stoichiometry Fe3AlC and crystallize in the perovskite structure type (also commonly labeled as E21 or L1’2) as visualized in Figure 1. Such phases have been shown to have an additional strengthening effect on these steels [3,4,5].
A critical aspect with respect to the application of high-Mn steels is their large susceptibility to hydrogen-induced delayed fracture (HIDF) [6]. Hydrogen, which is in contact with steels during the production and/or the application process, may dissolve into the material, followed by migration and preferred enrichment in critical regions, such as grain boundaries or dislocations. As a consequence, local embrittlement occurs, which can finally lead to crack formation and propagation, resulting in eventual failure of the material. It has been empirically observed that the presence of small amounts of Al lowers the tendency for hydrogen embrittlement [7]. Complete prevention, however, cannot be ensured. While an alleviation of local stress due to a change in stacking fault energy (SFE) with Al inclusion has been proposed as one possible factor [8], this behavior may also be attributed to the presence of homogeneously distributed nano-sized κ-carbides or short-range ordering of similar atomic configurations which can serve as H traps, often at a precipitate/matrix interface.
For instance, experimental studies using atom probe tomography have demonstrated segregation of hydrogen at an interface of TiC with a ferritic matrix [9]. This was later confirmed by first-principles calculations [10], which further demonstrated that H accumulation can weaken the interface, resulting in hydrogen-enhanced decohesion and subsequent fracture formation.
In the case of κ-carbides it is interesting to note that, in real materials where they are formed as precipitates, their composition (Fe,Mn)3+yAl1−yCx may significantly deviate from the ideal stoichiometry (Fe,Mn)3AlC of phase-pure κ-carbides such as the (nearly ideal) ternary Mn-rich carbide studied in a previous work [11]. For κ precipitates, the Al content depends on its concentration in the bulk phase, which leads to different values reported in the literature. For example, Andryushchenko et al. [12] quoted a range of −0.2 < y < 0.2, whereas Seol et al. [13] measured much lower Al contents with y ≈ 0.6. In recent works [14,15], the Al depletion in κ-carbide is correlated with the reduced C content in these precipitates. The latter varies a lot and is typically between 0.4 < x < 0.72 [13,16]. We explained the C off-stoichiometry as a compromise between the gain in chemical energy during partitioning and the elastic strains emerging in coherent microstructures. This off-stoichiometry is relevant for the interaction with H, because the vacant C positions are favorable trapping sites.
Traps are sometimes designated beneficial or benign [17] because they may capture diffusive hydrogen and delay its further migration to malign traps causing HIDF. By definition, the trapping energy Etrap is the capability of a microstructure feature to bind hydrogen better than the bulk matrix. The usual experimental approach to determine Etrap is thermal desorption spectroscopy (TDS) after galvanostatic or potentiostatic charging of the specimen with hydrogen. The relatively large scattering in the Etrap values collected from different experiments can be attributed to several causes. One particular problem is the absence of a definite reference. Measured trapping energies are often quoted relative to solution enthalpies of hydrogen in the respective bulk matrix. Since these depend on the crystal structure and the composition, a common reference state would ensure a better comparability of trapping energies from different studies.
Within theoretical studies, trapping energies have been calculated for various materials. In the case of Fe, the relevance of substitutional transition-metal atoms [18], vacancies [19], grain boundaries [20] and some precipitate phases [10] have been discussed. To the best of our knowledge, however, the hydrogen trapping by κ-phases has not been explicitly addressed theoretically. There are two experimental publications which assume an irreversible hydrogen trapping at the interface between κ-carbides and the Fe matrix [21,22], and another contribution attributing rather large activation energies of 76 and 80 kJ/mol for hydrogen desorption in the κ-carbides [23]. The mechanistic details, however, are not yet understood.
In the present work, the capability of κ-carbides to bind hydrogen is investigated using ab initio electronic-structure techniques within the framework of density-functional theory. We will analyze the role of C vacancies, as well as that of the interface between κ-carbide and Fe matrix in trapping H. In order to reveal the chemical nature of this trapping, the C–H and H–H interactions in the L12-Fe3Al phase are assessed. Further, the influence of manganese substitution on the trapping capability is calculated. Finally, the suitability of the κ-carbide/austenitic Fe matrix interface as a hydrogen trap is investigated, followed by the study of enhanced decohesion caused by the presence of hydrogen at the interface.

2. Computational Methods

All quantum-mechanical structure optimizations and total-energy calculations were performed with the Vienna ab initio Simulation Package (VASP, version 5.4.1, Computational Materials Physics, University of Vienna, Vienna, Austria, 2015) [24,25,26,27], a software package employing density-functional theory (DFT) and utilizing plane waves together with PAW/pseudopotentials, thereby especially suited for simulations of periodic systems. The crystal orbitals were expanded in plane waves by means of the projector-augmented wave method (PAW) [28,29] with a kinetic energy cutoff of 500 eV. Contributions from exchange and correlation interactions were approximated utilizing the generalized-gradient approximation (GGA) functional in the parametrization by Perdew, Burke, and Ernzerhof [30]. Brillouin zone integration was performed by the scheme of Monkhorst and Pack [31] using k-point grids of n × n × n with n = 12, 8, 4, and 4 for the four-atom (stoichiometric compounds), 32-atom (2 × 2 × 2 fcc supercell), 108-atom (3 × 3 × 3 fcc supercell), and 128-atom (4 × 4 × 4 bcc supercell) metal lattices, respectively. The interface (between κ-carbide and fcc-matrix) calculations were performed for a 92-atom (2 × 2 × 5 supercell) and 108-atom (2 × 2 × 6 supercell) system, where the total number of atoms varies with the thickness of the κ-carbide. The corresponding k-point grids employed were 8 × 8 × 5 and 8 × 8 × 3, respectively. Partial band occupancies were considered using the smearing scheme of Methfessel and Paxton [32] with the σ value set to 0.2 eV. The magnetic properties of the bulk κ-phases were taken into account by performing spin-polarized computations assuming a ferromagnetic model; nonetheless, this was restricted to ordered collinear magnetism. Non-collinearities are known to reduce the ground state energy in Fe-Mn alloys only slightly and will have little relevance at finite temperatures [33]. All other calculations, including interface models, were performed for the non-magnetic case, unless otherwise indicated.
For ideal κ-structures, the formation energies were calculated using:
ΔEel = Eel(Fe3AlX) − [Eel(fcc-Al) + 3 Eel(fcc-Fe) + Eel(X)]
where Eel(X) is the ground-state energy of graphite (X = C) or half the energy of an H2 molecule (X = H). We note that ΔEel is a theoretical energy, often provided in the ab initio community and used here solely for comparisons with earlier contributions in other studies. In order to evaluate precipitation behavior, not pure reference materials but the chemical potentials of the components as determined by the matrix materials are relevant. For both educts, the fcc structure was used as a reference, being the stable phase of Al and high-Mn steels, and forming a coherent interface with the perovskite-type κ-carbide.
The trapping energies were determined by the solution enthalpy (corresponding to the local chemical potential) of a hydrogen atom on the site in question as compared to an H atom in a γ-Fe (fcc) matrix, which is thus the reference state:
Etrap = [Eel(κ − Al8Fe24CxH) − Eel(κ − Al8Fe24Cx)] − [Eel(fcc-Fe108H) − Eel(fcc-Fe108)]
For determining the H solubility at a given site, (zero-point) vibrations can be important [34]. Our study, however, is primarily concerned with trapping energies of hydrogen, i.e., the difference in the solution enthalpy of hydrogen for different sites and regions of steel materials comprising ferritic and austenitic metal matrices, carbide precipitates, as well as the carbide/matrix interface. While the (zero-point) vibrational energies of hydrogen in a gas phase of H2 molecules and of interstitial hydrogen in a metal matrix differ substantially, the difference is negligible when various interstitial sites are compared with each other. Thus, for the remainder of our study, the total energy of all calculated structures is approximated as their DFT energy.
The choice of the reference state in Equation (2) does not alter the conclusions if different positions and configurations within the same trapping phase are compared, which is the primary scope of this work. Furthermore, the potential of a phase to trap diffusive hydrogen with respect to other metal matrices than γ-Fe (fcc) can be obtained by adding the trapping energy for such a matrix with respect to γ-Fe. Determining the trapping energy of solid solutions such as Al-containing ferrite or Mn-containing austenite can, however, be exhaustive since a very large number of possible hydrogen positions would have to be considered due to the statistically random, i.e., disordered, nature of these alloys.
Similarly to Equation (2), the hydrogen solution enthalpy in the interface was computed using the following expression:
Etrap(int) = [Eel(H @ κ-Al12Fe28C12/fcc-Fe56) − Eel(κ-Al12Fe28C12/fcc-Fe56)] − [Eel(fcc-Fe108H) − Eel (fcc-Fe108)]
where the first two electronic energies on the right-hand side of the expression correspond to the fully-relaxed energies of the supercell comprised of κ-carbide and fcc-Fe with and without hydrogen, respectively.

3. Results and Discussion

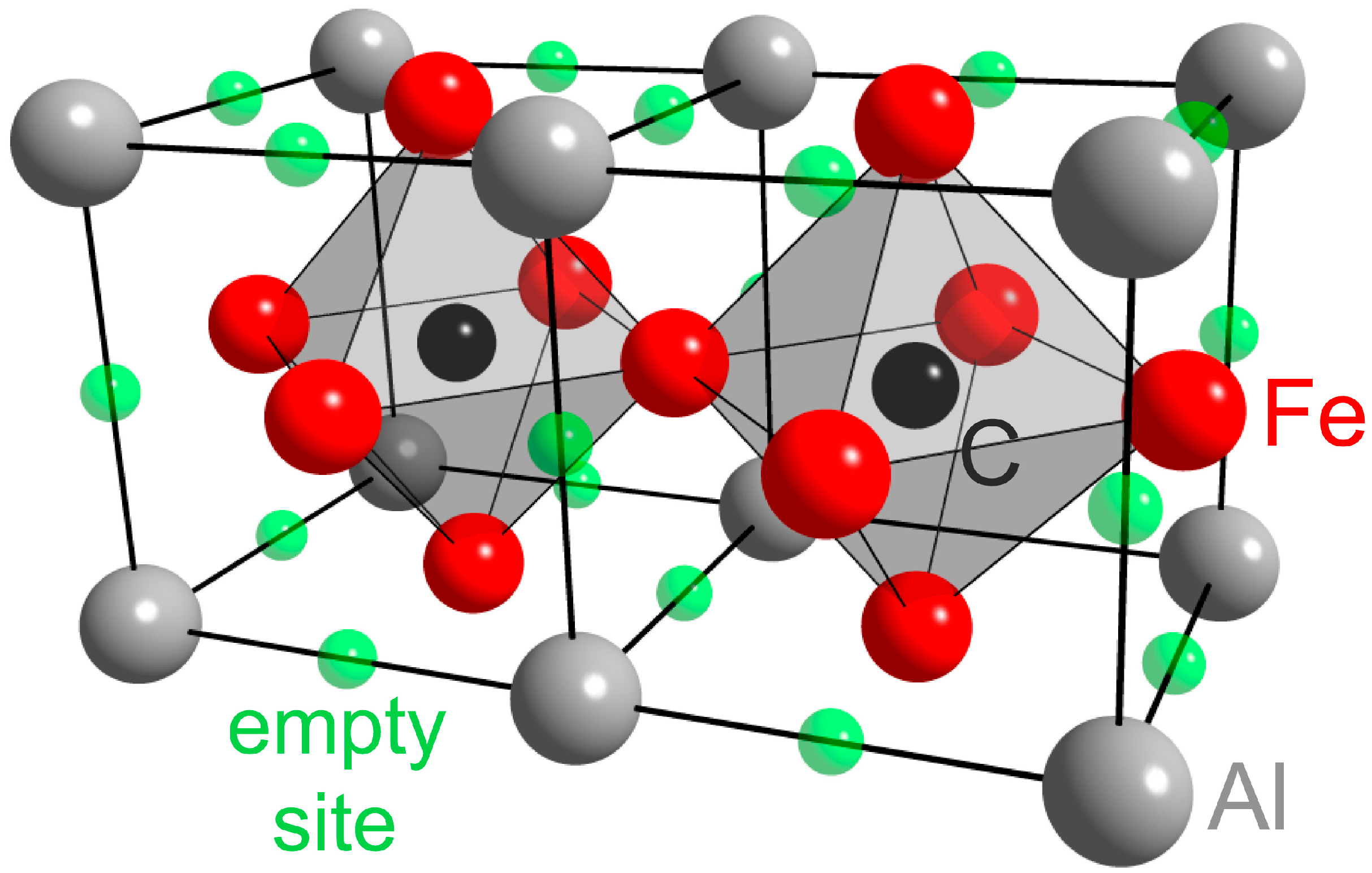
3.1. Stoichiometric Phases of L12 and E21 Symmetry

The formation of κ-carbide requires the simultaneous partitioning of substitutional Al and interstitial C from the solid solution. Here, we focus on the competing C and H interstitials and consider their energetics in Fe3Al. Although we cannot confirm a previous first-principles result that the L12 structure is the ground state of Fe3Al [35], but obtain D03 instead (Table 1), we will use L12 as a matrix phase in the upcoming considerations. This is because the small energy difference of approx. 1 kJ/mol is compensated by the stabilization effect due to C insertion, yielding the perovskite E21-Fe3AlC, commonly known as κ-carbide (Figure 1). Our calculations of the lattice parameter, total energy, and the local magnetic moments as given in Table 1 agree well with other calculations [35,36,37]. In particular, we confirmed earlier findings [15] that the formation of this phase out of pure elements is exothermic.
When investigating the relevance of these κ-carbides as a trap for H, we first consider the ideal phase with the composition Fe3AlC. The calculations confirm the finding for pure fcc-Fe [38] that the empty octahedral sites (green spheres in Figure 1) are more favorable for H (Etrap = 0.13 eV) than the tetrahedral ones (Etrap = 0.75 eV). Nonetheless, the absolute value is endothermic, i.e., H would not enter this phase. The reason for this repulsion can be the local atomic configuration with two Al atoms in nearest-neighbor positions (first coordination sphere, CS) and/or the presence of C in the adjacent octahedral sublattices.
In order to confirm the impact of the metallic atoms, we have investigated the Al–H interaction in an fcc-Fe matrix (Figure 2). Considering H as the central atom, the interaction turns out to be repulsive if Al is located in the first CS, but an energetic optimum exists if Al and H are second-nearest neighbors, Al being in the second CS. While the first configuration matches the H position in the empty octahedral sublattice sites of κ-carbide, the second corresponds to an H atom replacing a C atom on the central interstitial site (green and black spheres in Figure 1, respectively). Thus, the central interstitial site is energetically preferred for H incorporation while the non-central octahedral sites are generally assumed to be empty and, thus, not considered in the numbering of CS.
The attractive interaction between a single Al and a single H atom in the second CS lets one expect that the central (body-centered) interstitial sites in an L12-Fe3Al matrix could be completely occupied by H. This would result in an E21-Fe3AlH phase (κ-hydride), which has not been observed experimentally and has also been identified as chemically unstable in a theoretical contribution [35]. In contrast to said contribution, we obtain that the formation of this phase out of the pure elements according to Equation (1) is exothermic (−85 kJ/mol). In such a hypothetical E21-Fe3AlH phase, the effects of H on the κ-phase formation are qualitatively similar to those of C, but quantitatively much smaller: the lattice parameter increases by 0.8% from 3.65 to 3.68 Å (2.7% increase for C), and the local magnetic moments of the Fe atoms lower by 9% from 2.3 to 2.1 µB (57% for C).
We note, however, that C also prefers a local coordination with Al atoms in the second CS, as shown in previous studies [39,40]. There is, therefore, a competition between the interstitial elements C and H for the formation of the κ-phase. At T = 0 K, the formation energy of the κ-carbide Fe3AlC is slightly larger (−90 kJ/mol) than the one of κ-hydride (−85 kJ/mol). More important is the fact, however, that H already becomes too mobile to remain in the steel matrix before those temperatures are reached at which Al can form locally-ordered structures (approx. 600 °C for typical annealing times). We can, therefore, expect that the E21 phase is primarily formed as κ-carbide.

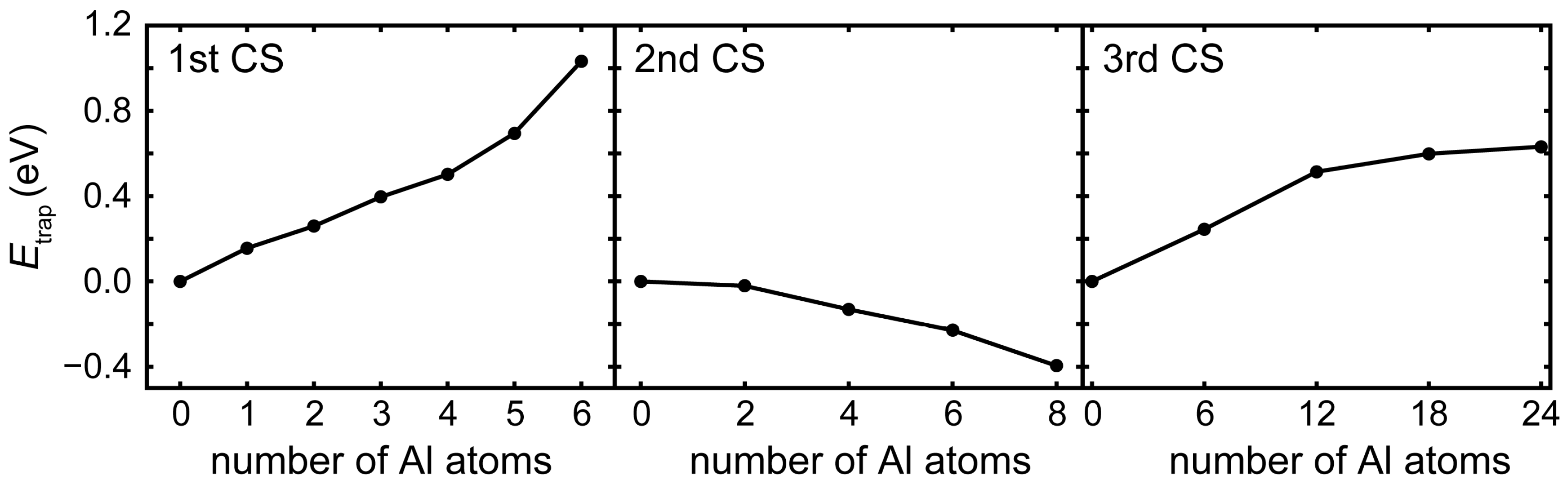
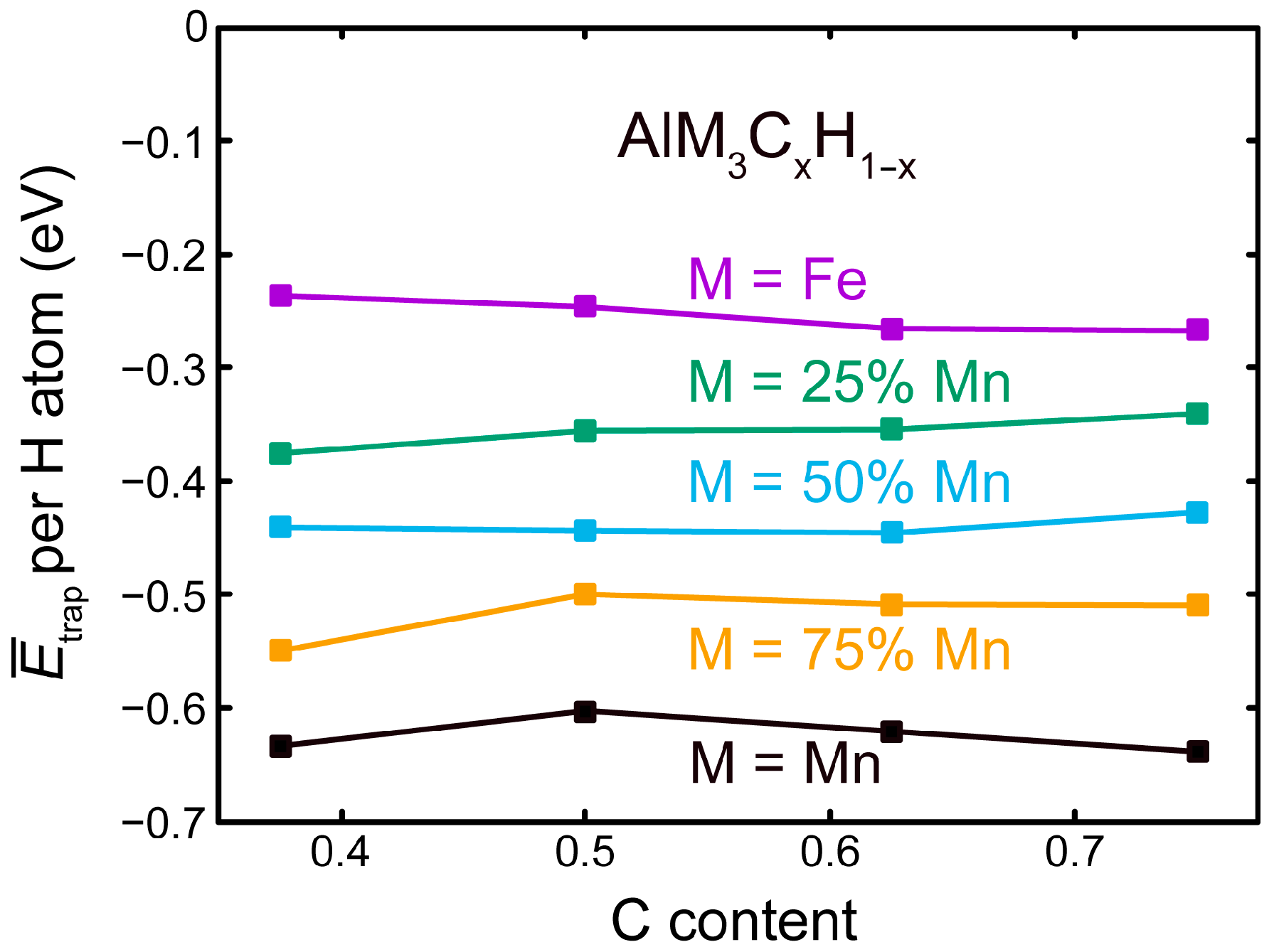
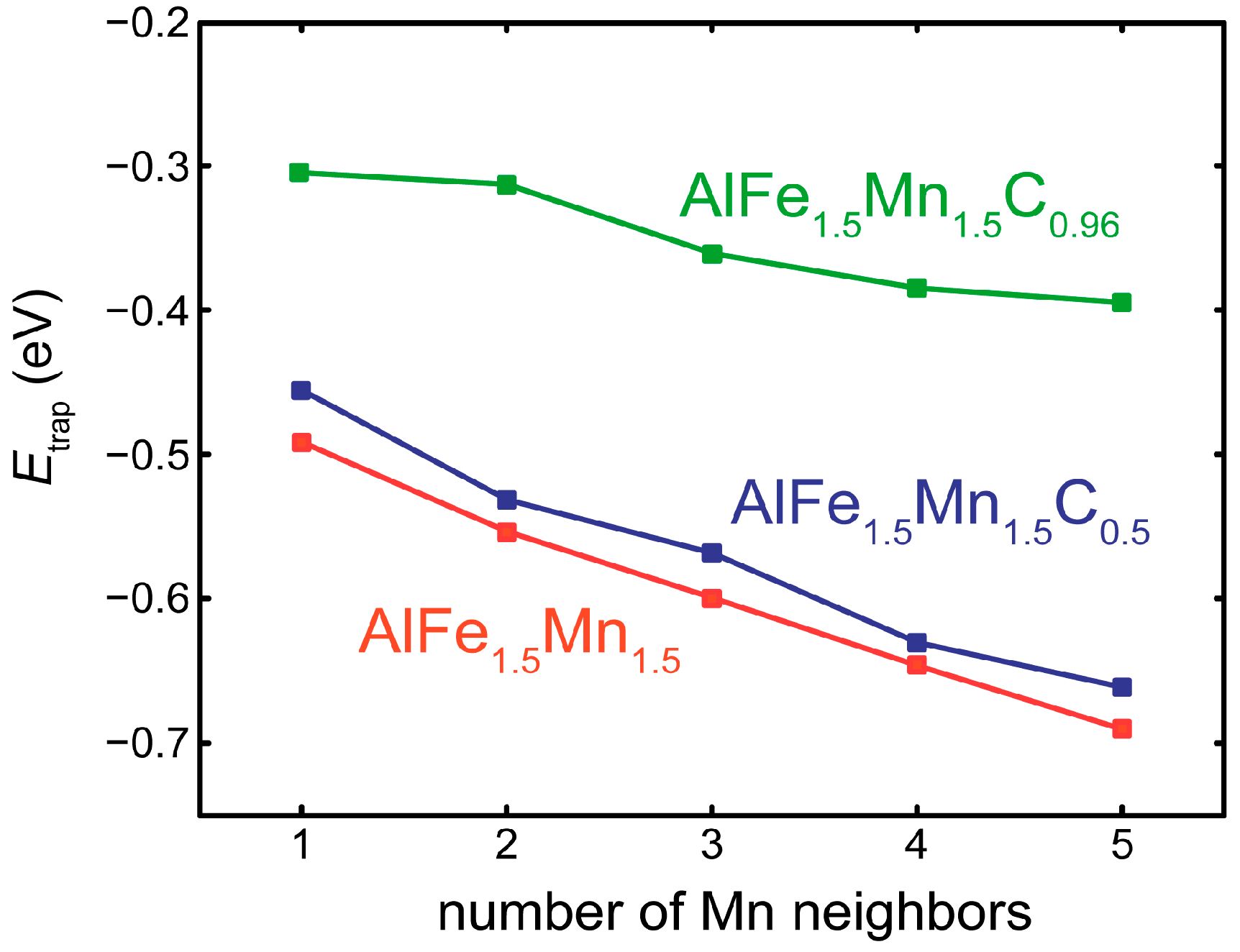
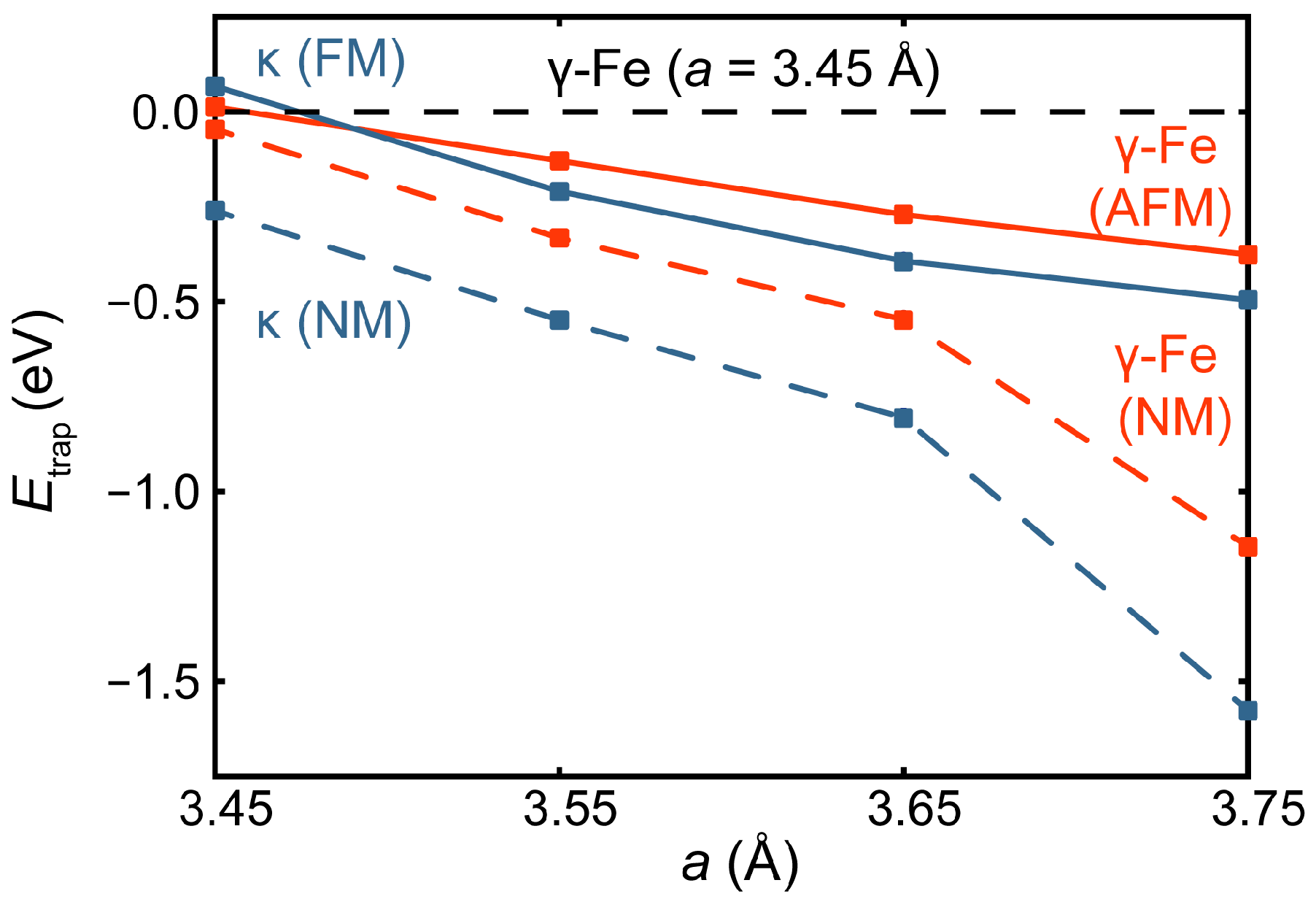
3.2. Competition of H and C in the L12 and E21 Structure

Despite the preference of κ-carbide formation, the typically observed C depletion in this phase yields various vacancies on its sublattice, i.e., potential sites for H that are in a favorable configuration with respect to Al. To further elaborate on this, the average trapping energy per H atom in a fully filled κ-matrix was calculated as a function of the C concentration. Carbon concentrations of 37.5–75 at % were taken into account in accordance with the typically experimentally observed C contents of Fe-rich κ-carbide precipitates. The distribution of C atoms among the different positions (central interstitial sites, referred to as κ positions) was random, while the remaining κ positions were occupied by H atoms. The calculations were performed employing 3 × 3 × 3 supercells with full structural optimization with respect to shape and volume. The results show, surprisingly, that the average trapping energy per H atom is largely independent of the C concentration (Figure 3, purple, uppermost curve).
The calculations in Figure 3 have also been performed for different Mn contents, the reason being that κ-carbides growing from Mn-rich austenitic matrices contain high amounts of manganese as a substituent for iron. For this purpose, the aforementioned calculations were repeated for a 3 × 3 × 3 E21-(Fe,Mn)3Al(C,H) supercell with randomly-distributed Mn atoms. Upon introducing manganese, no change can be observed with regard to the average trapping energy being independent of the carbon content (Figure 3).
The trapping capability, however, increases (i.e., the trapping energy is lowered) with increasing Mn content. This is consistent with previous findings that the short-range Mn–H interaction in austenitic alloys is attractive [38]. To study said interaction in κ-carbides, a 3 × 3 × 3 L12-Fe1.5Mn1.5Al supercell was used, where the Mn and Fe atoms were distributed randomly. The H atom was placed on κ positions with different numbers of Mn atoms (positions with 1–5 Mn atoms are present in the given supercell) in the surrounding octahedron. Our results show an almost linear dependence of the trapping energy on this number (Figure 4), confirming that previous findings apply to Al-containing systems as well. However, the results do not fully capture the changes of trapping energies with increased Mn content as seen in Figure 3. An important reason is that the data points in Figure 4 (for a fixed C content) all correspond to the same volume, while each Mn concentration in Figure 3 has its own equilibrium volume.
To understand this effect, the trapping energy was calculated as a function of the lattice parameter (Figure 5). The calculation was performed for the L12 configuration of Fe3Al, which has an equilibrium lattice parameter of a(L12) = 3.65 Å as well as pure fcc-Fe with a(γ-Fe) = 3.45 Å. The matrices consisted of 32-atom 2 × 2 × 2 supercells. In the L12-Fe3Al matrix a single H atom was again placed on an octahedral sublattice site normally occupied by C in the κ-phase. The calculations were performed for two different magnetic states. In all cases, the trapping capability increases with the volume. For the nonmagnetic state the H atom clearly favors the L12-matrix over pure fcc-Fe at all lattice parameters and, thus, volumes. If magnetism is considered, the ferromagnetic L12 matrix is, again, favored, apart from the special case when its volume is identical to the equilibrium volume of pure fcc-Fe (3.45 Å). Comparing both phases at the same lattice parameter, however, is only relevant in the case of a perfectly coherent interface between the matrix and the precipitate phase. Otherwise, the larger lattice parameter of the L12 phase will always yield a lower Etrap.
Additionally, the influence of carbon atoms on the Mn–H interaction was investigated (Figure 4). For this purpose, the supercell offering 27 κ positions was filled with 0, 14, or 26 C atoms (corresponding to a C sublattice concentration of 0, 50, or 96%), avoiding nearest-neighbor C–H configurations in the case of 14 C atoms. We observe that the E(xMn) linearity is independent from the C content although the attractive interaction between Mn and H seems to be reduced in the 96% C case. More importantly, however, one observes a small shift in the trapping energy if half the cell’s κ positions are filled with carbon, but a significantly larger shift if the entirety of these positions is filled, the latter being attributable to the interaction between direct C–H neighbors. One may, therefore, expect that the interaction of H with C affects the trapping energy, and this raises the question why such an effect is not observed in Figure 3.
In the next step we, therefore, investigated the interaction of H with other C and H atoms (Figure 6). For this purpose, we chose 3 × 3 × 3 L12-Fe3Al supercells. The trapping energy of a hydrogen atom was first calculated as a function of the number of neighboring C atoms in the third CS (being the nearest neighboring κ positions if other octahedral sites are unoccupied, labeled NN), keeping the shape and volume of the supercells fixed (Figure 6a). Similar to Figure 4, we observe a repulsive effect which results in an almost linear increase of Etrap. Furthermore, the trapping energy depends on the configuration of the neighboring C atoms. This observation, however, is partially due to the choice of the supercell: two C atoms in the trans isomer case are located in neighboring unit cells of the 3 × 3 × 3 supercell (energy difference to the cis isomer is 0.06 eV), while this is not the case in a 144-atom 4 × 3 × 3 L12-Fe3Al supercell (respective energy difference is 0.04 eV).
We further note that the C–H interaction for H on a κ position and C in the non-central interstitial site coplanar to Al is attractive (not shown). Concerning H–H interactions, we observe a similar, almost linear dependence of Etrap on the number of neighboring H atoms in the third CS (Figure 6b). This trend is (up to four third CS H atoms) almost identical to the C–H case and has a significantly lower dependence on the atomic configuration (rendering a distinction between the various configurations unnecessary). The similarity of C–C and C–H interactions explains the constant behavior in Figure 3, since the number of third CS H and C atoms is always six in this figure.
The impact of neighboring C atoms was compared to that of C atoms in other shells. In Figure 6c the situation is exemplified for C atoms in next-nearest-neighbor (NNN) positions (corners of a 3 × 3 × 3 L12-Fe3Al supercell). Despite a rather long distance of √3 × 3.69 Å = 6.4 Å, a repulsive effect is still observed (red diamonds). The slope of the C dependence, however, is smaller than for the third CS neighbors by a factor of ≈2. It is further observed that the dependence on the number of NNN carbon neighbors is strongly suppressed if the NN κ positions are occupied either by C or by H. These trends can be understood as resulting from local relaxations. They indicate, once again, that the nearest κ positions are most relevant for the value of the H solubility. The trends for distant H–H interactions are, as in the case of the third CS interactions, qualitatively identical to the C–H case, as seen in Figure 6d.

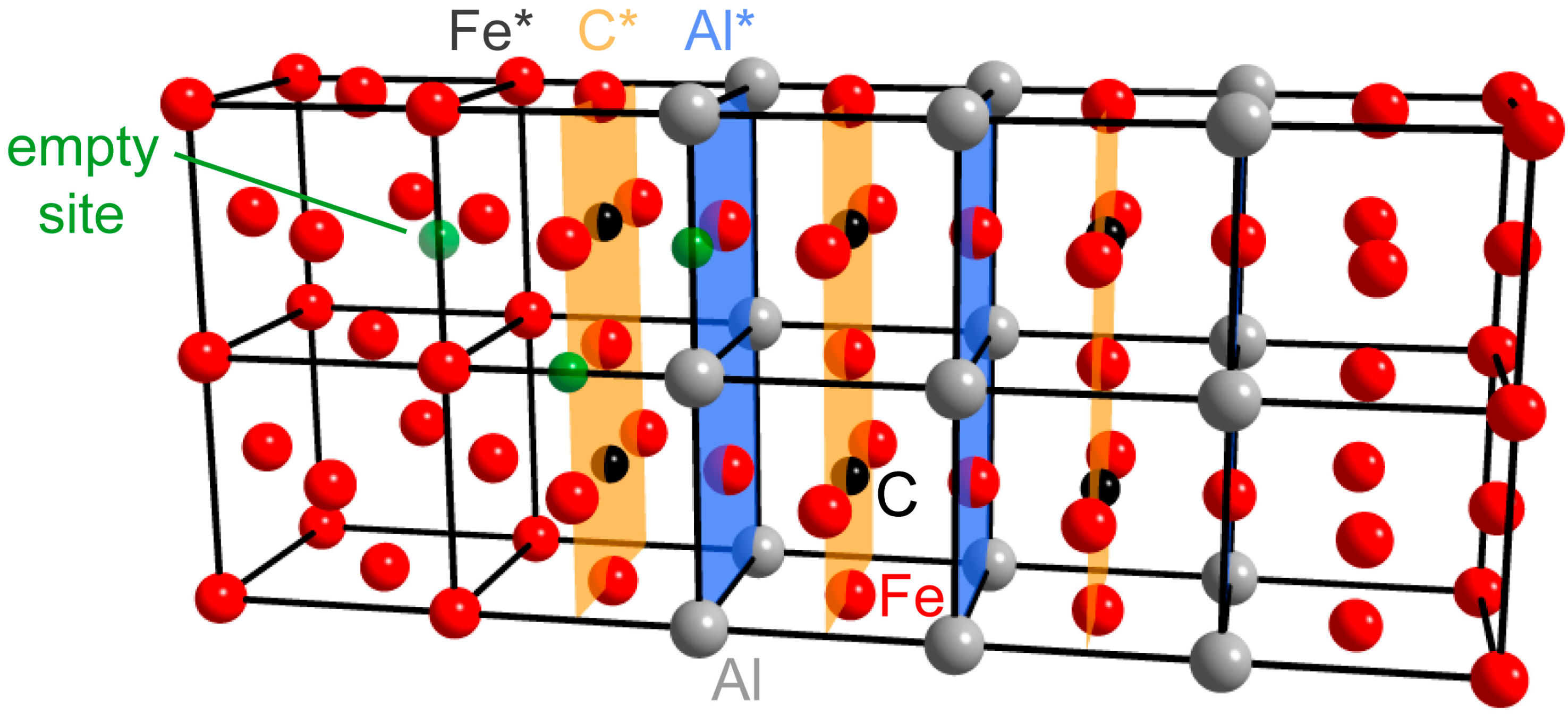
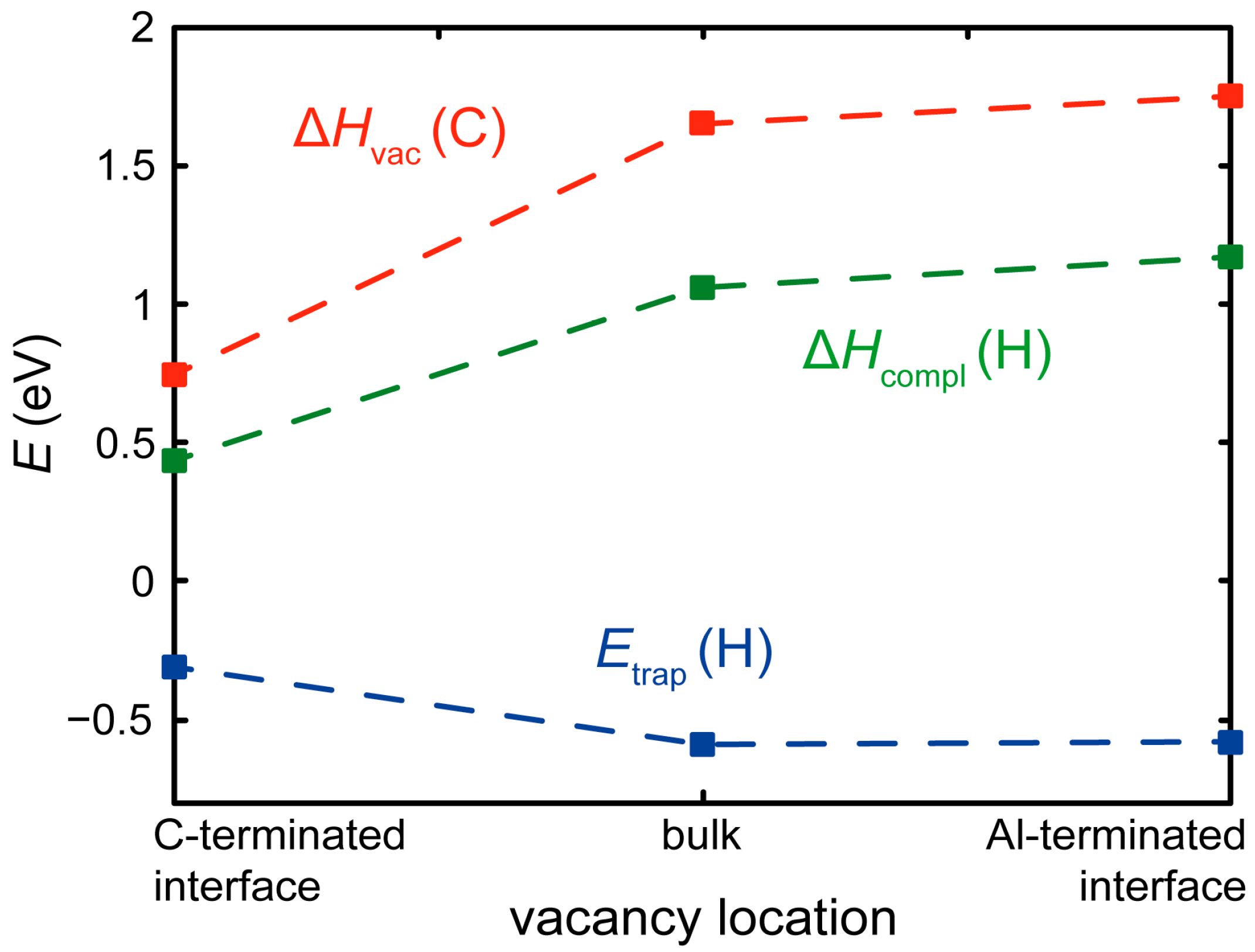
3.3. H at Interfaces between κ-Carbide and the fcc-Fe Matrix

The insights obtained for the Al–H and C–H interactions are used to understand chemical trends for incorporating hydrogen in the (100) interface between κ-carbide and the fcc-Fe matrix. In this case, however, we limit ourselves to a single H atom. Various scenarios for said incorporation are possible. We first note that stoichiometric κ-carbide has two kinds of (100) layers, one containing Al atoms in one of the fcc sublattices, the other containing C atoms in the central interstitial κ positions. The considered layers for the representation of the κ-carbide in Figure 7 are indicated by a stacking sequence, e.g., C*–Al*–C*–Al*–C*–Al*. The termination layer, which can contain C or Al, is considered as the interface plane.
The results for three different supercells, as given in Table 2, can be interpreted as follows: on the one hand, H tries to avoid positions with Al as closest neighbor in the first CS (compare with Figure 2), so incorporation into an Al-containing layer is unfavorable. On the other hand, a configuration with C in a second CS position (in contrast to the NN site shown in Figure 6a) yields an improved trapping behavior. The non-central octahedral sites in the C layer in a Fe–C–Al scenario (green sphere in orange-colored C* layer, Figure 7) are, therefore, most attractive for H, because they allow for four second CS neighbor C atoms, but only one first CS neighbor Al atom. Only slightly less favorable are the octahedral sites in Fe layers adjacent to a C-terminated κ-carbide (green sphere in Fe* layer, Figure 7), because in this case two second CS C atoms are available, but no first CS Al atoms are present. These configurations already yield a trapping at the interface.
Competing with the H incorporation discussed so far, the replacement of a C atom by an H atom should also be considered for the interface. To understand how efficiently C vacancies act as hydrogen traps near the interface, we also compare the vacancy formation energy at different positions (Figure 8). This energy amounts to 1.65 eV for a vacancy in the bulk of the κ-carbide phase, is almost the same (1.75 eV) for C atoms next to Al-terminated interfaces, but is significantly lower (approx. 0.75 eV) for C atoms at C-terminated interfaces. This is not surprising, since these C atoms have a lower number of Al neighbors in the second CS.
The differences in H trapping energies for the three different vacancy positions are less pronounced. For C vacancies in the bulk of the κ-carbide, H has a favorable configuration with respect to the Al atoms, but an unfavorable configuration with respect to the other C atoms. The resulting trapping energy is −0.59 eV. (Note that this data refers to non-magnetic calculations, so that the absolute values cannot be compared directly with Figure 4.) The situation is almost unchanged (−0.58 eV) for the C positions next to Al-terminated interfaces. If H is incorporated into C vacancies in a C-terminated interface, then both the number of Al neighbors in the second CS and the number of C atoms in NN positions are reduced from 8 to 4 and from 6 to 5, respectively. Since the change in the number of Al neighbors is more significant, the trapping energy for H in these sites is reduced (−0.31 eV).
It should be noted, however, that C vacancies which are more likely to form near the interface are more accessible, at least kinetically, to H atoms trapped near the interface than vacancies formed in the interior of the precipitate phase. Another possible scenario can be the formation of percolating networks of C vacancies which act as energetically favored pathways for hydrogen to diffuse from the interface to the bulk of the carbide, as observed for TiC [10]. We can further define the hydrogen–vacancy complex formation energy as the sum of the C vacancy formation energy and the H trapping energy within this vacancy. The comparison for C vacancies at different positions (near the interface) shows that this energy is lowest for vacancies at C-terminated interfaces and, hence, such a scenario is, energetically, the most favorable.

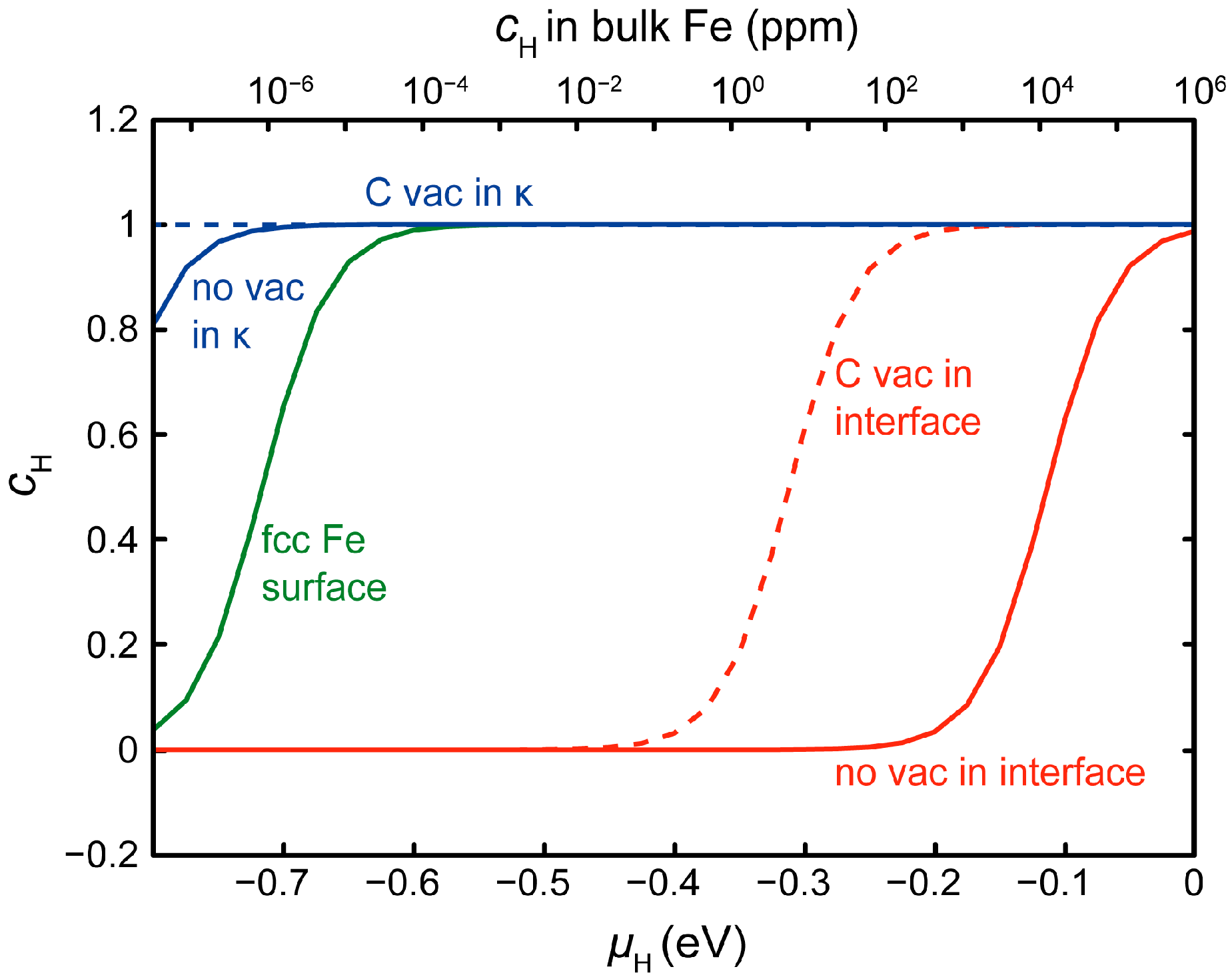
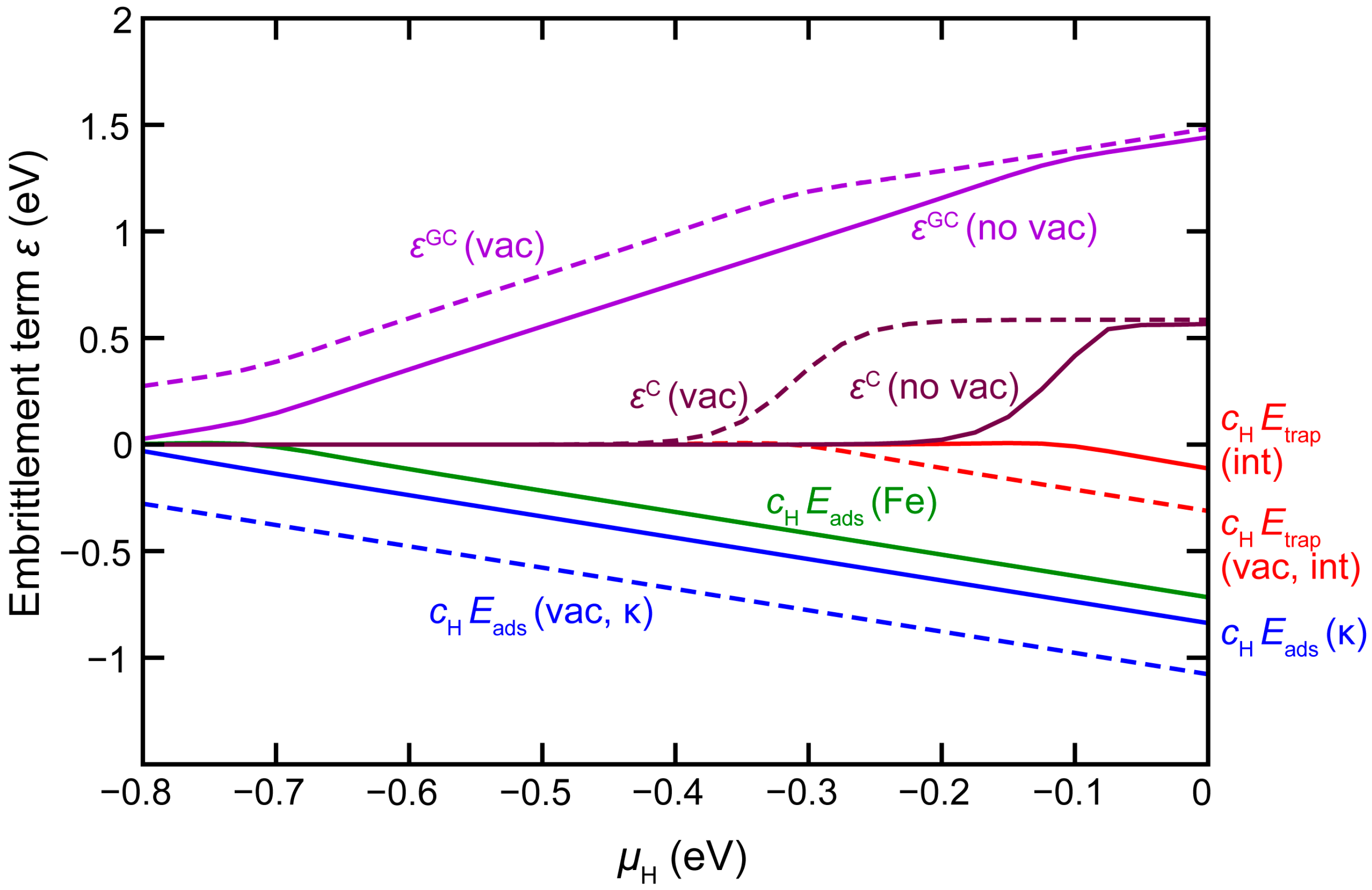
3.4. H Enhanced Decohesion of Interfaces

It is a decisive follow-up question whether the trapped H in the interface causes decohesion along the interface, which might serve as a mechanism of hydrogen embrittlement. To understand this, we need to answer the question whether the presence of H in the interface enables or suppresses the separation of the interface into respective free surfaces. To do so, the adsorption energy of H at the interface was compared to the energy of H at the free surfaces of the carbide and the austenitic Fe matrix after possible crack formation. The corresponding energy of separation is given by the expression:
Esep = [Eel(int) − Eel(κ-surf) – Eel(Fe-surf)]
+ [cH(int) Etrap(int) − cH(κ) Eads(κ-surf) − cH(Fe) Eads(Fe-surf)]
where Eel(int) is the total energy of the supercell containing the interface of κ-carbide and fcc-Fe without H. Eel(κ-surf) and Eel(Fe-surf) are the total energies of supercells containing κ-carbide and fcc-Fe, respectively, with a surface adjacent to a vacuum layer. cH is the concentration of H at the planar defects, which depends on its chemical potential μH. Etrap(int) and Eads(X-surf) are the corresponding trapping and adsorption energies of hydrogen at the interface or the surface (X = κ or Fe) given by:
Etrap(int) = Eel(H@int) – Eel(int) − μH and
Eads(X-surf) = Eel(H@X-surf) – Eel(X-surf) − μH
The tendency of trapped H to cause decohesion at the interface is indicated by the “embrittlement term” as given by the second term in Equation (4), namely:
ε = cH(int)Etrap(int) − cH(κ)Eads(κ-surf) − cH(Fe)Eads(Fe-surf).
A positive value of ε implies that it is energetically favorable to have hydrogen on free surfaces rather than at the interface, which provides a driving force for the formation of free surfaces. On the other hand, a negative value indicates that H prefers to stay at the interface, thereby stabilizing it.
The equilibrium concentration of hydrogen at the interface is given by its trapping energy, i.e., cH(int) = 1/(exp(βEtrap(int)) + 1) with β = 1/(kBT), and depends via Equation (5) on the chemical potential μH (Figure 9). We compare an interface without C vacancies (solid line) with an interface that contains a single C vacancy (dashed line). In the first case, a maximum concentration of 1 H atom per 2 × 2 interface area is considered (corresponding to cH = 1), to avoid strong H–H interactions. In the second case, only the filling of the single vacancy per 2 × 2 interface area with H is considered. Due to the lower trapping energy, the occupation of the vacancy sets in at much lower chemical potentials than for the perfect interface. The concentration of H at the free surfaces depends on the kinetics of the separation process. If it is very fast, then the particle conservation cH(κ) + cH(Fe) = cH(int) can be assumed, corresponding to the canonical limit. If the diffusibility of H is faster than the separation, then an equilibrium H concentration cH(X) = 1/(exp(βEads(X-surf)) + 1) can also be used for the surfaces, corresponding to the grand-canonical limit. Our result points in this limit towards a strong driving force for H to segregate to a free κ-carbide surface with respect to a position at the interface (Figure 9).
Based on these concentrations, the embrittlement term was determined for both limits according to Equation (6) and plotted in Figure 10. Looking first at the results for the perfect interface in the grand-canonical (GC) limit, we observe large positive values for all considered chemical potentials of H. This is because the free surfaces of κ-carbide and fcc-Fe are substantially more favorable for H than the interface. A similar effect has been observed for several other precipitate phases [41]. We note, however, that this is a purely thermodynamic argument. It ignores the fact that the H concentration at the perfect interface is negligibly small for μH < −0.3 eV and that kinetics would not provide H significantly fast in order to stabilize the forming free surfaces. Therefore, we have plotted the canonical (C) limit in addition, for which the embrittlement term is almost vanishing for these chemical potentials. The processes in reality will occur between these two limits.
In order to come closer to reality, it is also important to consider the existence of C vacancies in the interface. Due to the substantial trapping effect of these defects, these sites will be quickly filled with H for chemical potentials µH > −0.5 eV. This affects the first term of Equation (6), indicated by the red dashed line in Figure 10. At the same time, the H incorporation at the forming κ-carbide surface, which contains this vacancy as well, also becomes even more favorable (blue dashed line in Figure 10). Depending on the H kinetics, i.e., the grand-canonical vs. the canonical limit, the combined embrittlement term ε increases further (purple and maroon dashed lines in Figure 10). Since in particular the canonical line shifts substantially upwards, we can conclude that the presence of these lattice imperfections is decisive for a destabilization of the interface if H comes into play.

4. Conclusions

The potential of κ-carbides to trap diffusive hydrogen was studied using density-functional theory. The hydrogen analog of the κ-carbide, the κ-hydride, was shown to be a theoretically stable compound. Its formation, however, is kinetically disadvantageous when compared to the carbide.
Substituting Mn for Fe was clearly shown to be preferable to the trapping energy, since the chemical potential of hydrogen decreases linearly with the number of manganese atoms in the octahedron surrounding the hydrogen atom. This effect is independent of the overall carbon concentration although directly neighboring carbon atoms seem to reduce the Mn–H attraction. As a result, the trapping capability of κ-carbides is proportional to the manganese content of the carbide.
The interaction of hydrogen with different metal matrices, including the L12-Fe3Al matrix, was investigated, and it was observed that the κ-matrix is a favorable environment for H as a result of both its chemical environment, owing to attractive Al–H interactions in κ-like arrangements, and the increased lattice parameter. The interaction between carbon and hydrogen as well as between different hydrogen atoms within the κ-matrix was examined. Both the C–H and the H–H interaction proved to be repulsive, with the H–H interaction showing a stronger repulsion in the short range while C–H repulsion is stronger in the long range. Additionally, directly neighboring C and H atoms suppress the long-range interaction.
For κ-carbides with a carbon content of about 35–75% with respect to the stoichiometric compound, the repulsion between the interstitials is compensated by the increase in trapping capability due to an increase of the lattice parameter. The average trapping energy of a fully filled κ-carbide is, thus, independent from the carbon loading of the carbide.
We conclude that the trapping efficiency of diffusive hydrogen by κ-carbides depends on its C, as well as its Mn, content. While the C content determines the number of vacant κ positions and thereby the capacity of the phase to trap hydrogen, the manganese content determines the overall trapping efficiency, i.e., the average gain in energy if an H atom is removed from the matrix and stored in the carbide precipitate. Efficient strategies to control diffusive H in steel materials should thus consider lowering the carbon contents of κ-carbide precipitates while raising their manganese contents.
Finally, we demonstrate that hydrogen located in the interface between carbides and the matrix material has a high solubility only in the presence of vacancies near the interface, thereby making the carbide/austenite interface an efficient trapping center for hydrogen. Our DFT calculations further suggest a possible hydrogen-induced separation of the interface into free surfaces of κ-carbide and fcc-Fe, thereby leading to embrittlement caused by a hydrogen-enhanced decohesion mechanism. Said embrittlement can be expressed via a quantitative model to assess the dependence of the interface decohesion upon hydrogen concentration.

Acknowledgments

This work is part of the Collaborative Research Center 761 “Steel ab initio” funded by the Deutsche Forschungsgemeinschaft (German Research Foundation, DFG). We gratefully acknowledge their financial support. Furthermore, we gratefully thank Salzgitter Mannesmann Forschung GmbH (SZMF) for their cooperation and funding of the project. We would also like to thank the JARA-HPC supercomputing center (ITC) of RWTH Aachen University for providing computational resources within grant JARA0057.

Author Contributions

Tobias A. Timmerscheidt, Dimitri Bogdanovski, and Jörg von Appen conceived and performed all simulations concerned with C–H/H–H interactions and the influence of Mn in bulk κ-carbide; Poulumi Dey and Tilmann Hickel conceived and performed all simulations focusing on the interface and conceptualized the embrittlement term; Tobias A. Timmerscheidt, Poulumi Dey, Dimitri Bogdanovski, and Jörg von Appen performed the data analysis and wrote the initial draft of the manuscript. Jörg Neugebauer and Richard Dronskowski initiated and supervised the project. All authors contributed equally to the interpretation of the data and the writing of the final version of the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gutierrez-Urrutia, I.; Raabe, D. Influence of Al content and precipitation state on the mechanical behavior of austenitic high-Mn low-density steels. Scr. Mater. 2013, 68, 343–347. [Google Scholar] [CrossRef]
  2. Park, K.-T.; Kim, G.; Kim, S.K.; Lee, S.W.; Hwang, S.W.; Lee, C.S. On the transitions of deformation modes of fully austenitic steels at room temperature. Met. Mater. Int. 2010, 16, 1–6. [Google Scholar] [CrossRef]
  3. Gutierrez-Urrutia, I.; Raabe, D. High strength and ductile low density austenitic FeMnAlC steels: Simplex and alloys strengthened by nanoscale ordered carbides. Mater. Sci. Technol. 2014, 30, 1099–1104. [Google Scholar] [CrossRef]
  4. Zambrano, O.A.; Valdés, J.; Aguilar, Y.; Coronado, J.J.; Rodríguez, S.A.; Logé, R.E. Hot deformation of a Fe-Mn-Al-C steel susceptible of κ-carbide precipitation. Mater. Sci. Eng. A 2017, 689, 269–285. [Google Scholar] [CrossRef]
  5. Haase, C.; Zehnder, C.; Ingendahl, T.; Bikar, A.; Tang, F.; Hallstedt, B.; Hu, W.; Bleck, W.; Molodov, D.A. On the deformation behavior of κ-carbide-free and κ-carbide-containing high-Mn light-weight steel. Acta Mater. 2017, 122, 332–343. [Google Scholar] [CrossRef]
  6. Hirth, J.P. Effects of hydrogen on the properties of iron and steel. MTA 1980, 11, 861–890. [Google Scholar] [CrossRef]
  7. Hojo, T.; Sugimoto, K.-I.; Mukai, Y.; Ikeda, S. Effects of Aluminum on Delayed Fracture Properties of Ultra High Strength Low Alloy TRIP-aided Steels. ISIJ Int. 2008, 48, 824–829. [Google Scholar] [CrossRef]
  8. Song, S.W.; Kwon, Y.J.; Lee, T.; Lee, C.S. Effect of Al addition on low-cycle fatigue properties of hydrogen-charged high-Mn TWIP steels. Mater. Sci. Eng. A 2016, 677, 421–430. [Google Scholar] [CrossRef]
  9. Takahashi, J.; Kawakami, K.; Kobayashi, Y.; Tarui, T. The first direct observation of hydrogen trapping sites in TiC precipitation-hardening steel through atom probe tomography. Scr. Mater. 2010, 63, 261–264. [Google Scholar] [CrossRef]
  10. Di Stefano, D.; Nazarov, R.; Hickel, T.; Neugebauer, J.; Mrovec, M.; Elsässer, C. First-principles investigation of hydrogen interaction with TiC precipitates in α-Fe. Phys. Rev. B 2016, 93, 184108. [Google Scholar] [CrossRef]
  11. Dierkes, H.; van Leusen, J.; Bogdanovski, D.; Dronskowski, R. Synthesis, Crystal Structure, Magnetic Properties, and Stability of the Manganese-Rich “Mn3AlC” κ Phase. Inorg. Chem. 2017, 56, 1045–1048. [Google Scholar] [CrossRef] [PubMed]
  12. Andryushchenko, V.A.; Gavrilyuk, V.G.; Nadutov, V.M. Atomic and magnetic ordering in k-phase of Fe-Al-C alloys. Phys. Met. Metallogr. 1985, 60, 50–55. [Google Scholar]
  13. Seol, J.-B.; Raabe, D.; Choi, P.; Park, H.S.; Kwak, J.H.; Park, C.G. Direct evidence for the formation of ordered carbides in a ferrite based low-density Fe–Mn–Al–C alloy studied by transmission electron microscopy and atom probe tomography. Scr. Mater. 2013, 68, 348–353. [Google Scholar] [CrossRef]
  14. Yao, M.J.; Dey, P.; Seol, J -B.; Choi, P.; Herbig, M.; Marceau, R.K.W.; Hickel, T.; Neugebauer, J.; Raabe, D. Combined atom probe tomography and density functional theory investigation of the Al off-stoichiometry of kappa-carbides in an austenitic Fe-Mn-Al-C low density steel. Acta Mater. 2016, 106, 229–238. [Google Scholar]
  15. Dey, P.; Nazarov, R.; Dutta, B.; Yao, M.; Herbig, M.; Friák, M.; Hickel, T.; Raabe, D.; Neugebauer, J. Ab initio explanation of disorder and off-stoichiometry in Fe-Mn-Al-C κ carbides. Phys. Rev. B 2017, 95, 104108. [Google Scholar] [CrossRef]
  16. Palm, M.; Inden, G. Experimental determination of phase equilibria in the Fe-Al-C system. Intermetallics 1995, 3, 443–454. [Google Scholar]
  17. Desai, S.K.; Neeraj, T.; Gordon, P.A. Atomistic mechanism of hydrogen trapping in bcc Fe–Y solid solution: A first principles study. Acta Mater. 2010, 58, 5363–5369. [Google Scholar] [CrossRef]
  18. Psiachos, D.; Hammerschmidt, T.; Drautz, R. Ab initio study of the interaction of H with substitutional solute atoms in α-Fe: Trends across the transition-metal series. Comput. Mater. Sci. 2012, 65, 235–238. [Google Scholar] [CrossRef]
  19. Nazarov, R.; Hickel, T.; Neugebauer, J. Ab initio study of H-vacancy interactions in fcc metals: Implications for the formation of superabundant vacancies. Phys. Rev. B 2014, 89, 144108. [Google Scholar] [CrossRef]
  20. Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
  21. Baligidad, R.G.; Prakash, U.; Radhakrishna, A.; Ramakrishna Rao, V. Effect of carbides on embrittlement of Fe3Al based intermetallic alloys. Scr. Mater. 1997, 36, 667–671. [Google Scholar] [CrossRef]
  22. Sen, M.; Balasubramaniam, R. Hydrogen trapping at carbide-matrix interfaces in Fe3AlC intermetallics. Scr. Mater. 2001, 44, 619–623. [Google Scholar] [CrossRef]
  23. Koyama, M.; Springer, H.; Merzlikin, S.V.; Tsuzaki, K.; Akiyama, E.; Raabe, D. Hydrogen embrittlement associated with strain localization in a precipitation-hardened Fe–Mn–Al–C light weight austenitic steel. Int. J. Hydrogen Energy 2014, 39, 4634–4646. [Google Scholar] [CrossRef]
  24. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
  25. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  26. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  27. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11185. [Google Scholar] [CrossRef]
  28. Blöchl, P.E. Projector-augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  29. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1774. [Google Scholar] [CrossRef]
  30. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  31. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  32. Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
  33. Ekholm, M.; Abrikosov, I.A. Structural and magnetic ground-state properties of γ-FeMn alloys from ab initio calculations. Phys. Rev. B 2011, 84, 104423. [Google Scholar] [CrossRef]
  34. Lee, K.; Yuan, M.; Wilcox, J. Understanding Deviations in Hydrogen Solubility Predictions in Transition Metals through First-Principles Calculations. J. Phys. Chem. C 2015, 119, 19642–19653. [Google Scholar] [CrossRef]
  35. Kellou, A.; Raulot, J.M.; Grosdidier, T. Structural and thermal properties of Fe3Al, Fe3AlC and hypothetical Fe3AlX (X = H, B, N, O) compounds: Ab initio and quasi-harmonic Debye modelling. Intermetallics 2010, 18, 1293–1296. [Google Scholar] [CrossRef]
  36. Connétable, D.; Maugis, P. First principle calculations of the k-Fe3AlC perovskite and iron/aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
  37. Noh, J.Y.; Kim, H. Ab initio calculations on the effect of Mn substitution in the κ-carbide Fe3AlC. J. Korean Phys. Soc. 2013, 62, 481–485. [Google Scholar] [CrossRef]
  38. von Appen, J.; Dronskowski, R.; Chakrabarty, A.; Hickel, T.; Spatschek, R.; Neugebauer, J. Impact of Mn on the solution enthalpy of hydrogen in austenitic Fe-Mn alloys: A first-principles study. J. Comp. Chem. 2014, 35, 2239–2244. [Google Scholar] [CrossRef] [PubMed]
  39. Song, W.; Zhang, W.; von Appen, J.; Dronskowski, R.; Bleck, W. κ-phase Formation in Fe–Mn–Al–C Austenitic Steels. Steel Res. Int. 2015, 86, 1161–1169. [Google Scholar] [CrossRef]
  40. Timmerscheidt, T.A.; Dronskowski, R. An Ab Initio Study of Carbon-Induced Ordering in Austenitic Fe-Mn-Al-C Alloys. Steel Res. Int. 2017, 88, 1600292. [Google Scholar] [CrossRef]
  41. Milella, P.P. Fatigue and Corrosion in Metals, 1st ed.; Springer: Milan, Italy, 2013. [Google Scholar]
Metals 07 00264 g001 550
Figure 1. Crystal structure of Fe3AlC, a κ-carbide crystallizing in the E21 type, shown as a 2 × 1 × 1 supercell. Grey, red, and black spheres denote Al, Fe, and C atoms, respectively. Green translucent spheres indicate the unoccupied octahedral sublattice sites.
Figure 1. Crystal structure of Fe3AlC, a κ-carbide crystallizing in the E21 type, shown as a 2 × 1 × 1 supercell. Grey, red, and black spheres denote Al, Fe, and C atoms, respectively. Green translucent spheres indicate the unoccupied octahedral sublattice sites.
Metals 07 00264 g001
Metals 07 00264 g002 550
Figure 2. Hydrogen trapping energy Etrap as a function of the local atomic environment with respect to the amount of Al atoms in the first, second, or third coordination sphere (CS) around a single interstitial H atom in a 3 × 3 × 3 supercell of fcc-Fe. Al atoms occupy Fe sites in the host matrix. The energies are defined according to Equation (2).
Figure 2. Hydrogen trapping energy Etrap as a function of the local atomic environment with respect to the amount of Al atoms in the first, second, or third coordination sphere (CS) around a single interstitial H atom in a 3 × 3 × 3 supercell of fcc-Fe. Al atoms occupy Fe sites in the host matrix. The energies are defined according to Equation (2).
Metals 07 00264 g002
Metals 07 00264 g003 550
Figure 3. Average trapping energy Ētrap per H atom as a function of the C content for a 3 × 3 × 3 E21-(Fe,Mn)3Al(C,H) supercell with all κ positions filled and considering different Mn contents.
Figure 3. Average trapping energy Ētrap per H atom as a function of the C content for a 3 × 3 × 3 E21-(Fe,Mn)3Al(C,H) supercell with all κ positions filled and considering different Mn contents.
Metals 07 00264 g003
Metals 07 00264 g004 550
Figure 4. Trapping energy Etrap of a single H atom as a function of the number of Mn atoms in its first CS for a 3 × 3 × 3 L12-Fe1.5Mn1.5Al supercell with C sublattice concentrations of 0% (red), 50% (blue), and 96% (green).
Figure 4. Trapping energy Etrap of a single H atom as a function of the number of Mn atoms in its first CS for a 3 × 3 × 3 L12-Fe1.5Mn1.5Al supercell with C sublattice concentrations of 0% (red), 50% (blue), and 96% (green).
Metals 07 00264 g004
Metals 07 00264 g005 550
Figure 5. Trapping energy Etrap of a single H atom as a function of cell volume (via the lattice parameter a) for fcc-Fe (red) and the L12-Fe3Al matrix (blue) considering different magnetic states, with the dashed/solid lines signifying the nonmagnetic/magnetic cases.
Figure 5. Trapping energy Etrap of a single H atom as a function of cell volume (via the lattice parameter a) for fcc-Fe (red) and the L12-Fe3Al matrix (blue) considering different magnetic states, with the dashed/solid lines signifying the nonmagnetic/magnetic cases.
Metals 07 00264 g005
Metals 07 00264 g006 550
Figure 6. Trapping energies Etrap for a single H atom in the central κ position as a function of the number of C or H atoms in various κ positions in a 3 × 3 × 3 L12-Fe3Al supercell. (a) C atoms are present as nearest neighbors for H in the third CS (nearest κ neighbors, NN), under consideration of structural isomers. The lattice parameter is a = 3.69 Å. Squares signify arrangements without structural isomers with zero, one, five, or six neighbors; open/closed diamonds signify the two isomers for two neighbors (cis and trans); open/closed circles signify the two arrangements for three neighbors (mer and fac). (b) As before but for H atoms in the third CS. Energetic differences between structural isomers are negligible in this case. The lattice parameter is a = 3.65 Å. (c) C atoms are next-nearest neighbors (NNN) located at the cell corners (dC–C = 6.4 Å), with no atoms (red diamonds), six H atoms (blue diamonds) or six C atoms (green diamonds) located simultaneously in the third CS (NN) κ positions, respectively. Lattice parameter as in (a). (d) As in (c), but considering H atoms as NNN neighbors. Lattice parameter as in (b). The difference in a explains the slight energetic difference in the case of zero NN/NNN neighbors.
Figure 6. Trapping energies Etrap for a single H atom in the central κ position as a function of the number of C or H atoms in various κ positions in a 3 × 3 × 3 L12-Fe3Al supercell. (a) C atoms are present as nearest neighbors for H in the third CS (nearest κ neighbors, NN), under consideration of structural isomers. The lattice parameter is a = 3.69 Å. Squares signify arrangements without structural isomers with zero, one, five, or six neighbors; open/closed diamonds signify the two isomers for two neighbors (cis and trans); open/closed circles signify the two arrangements for three neighbors (mer and fac). (b) As before but for H atoms in the third CS. Energetic differences between structural isomers are negligible in this case. The lattice parameter is a = 3.65 Å. (c) C atoms are next-nearest neighbors (NNN) located at the cell corners (dC–C = 6.4 Å), with no atoms (red diamonds), six H atoms (blue diamonds) or six C atoms (green diamonds) located simultaneously in the third CS (NN) κ positions, respectively. Lattice parameter as in (a). (d) As in (c), but considering H atoms as NNN neighbors. Lattice parameter as in (b). The difference in a explains the slight energetic difference in the case of zero NN/NNN neighbors.
Metals 07 00264 g006
Metals 07 00264 g007 550
Figure 7. The 5 × 2 × 1 supercell composed of κ-carbide and fcc-Fe (assuming coherent interfaces) for a given thickness of the κ-phase. Orange planes, labeled C*, signify (100) layers containing C and Fe atoms, while blue planes, labeled Al*, contain Fe and Al. Layers containing Fe only are unmarked and labeled Fe*. The translucent green spheres represent empty octahedral sites which (in addition to C vacancies) may incorporate H atoms.
Figure 7. The 5 × 2 × 1 supercell composed of κ-carbide and fcc-Fe (assuming coherent interfaces) for a given thickness of the κ-phase. Orange planes, labeled C*, signify (100) layers containing C and Fe atoms, while blue planes, labeled Al*, contain Fe and Al. Layers containing Fe only are unmarked and labeled Fe*. The translucent green spheres represent empty octahedral sites which (in addition to C vacancies) may incorporate H atoms.
Metals 07 00264 g007
Metals 07 00264 g008 550
Figure 8. C vacancy formation energy (shown in red), H trapping energy within the vacancy (shown in blue) and their combination, i.e., the H–vacancy complex formation energy, (shown in green) for three different positions of vacancies. Note that trapping of H by vacancies near C-terminated interfaces is energetically the most favorable.
Figure 8. C vacancy formation energy (shown in red), H trapping energy within the vacancy (shown in blue) and their combination, i.e., the H–vacancy complex formation energy, (shown in green) for three different positions of vacancies. Note that trapping of H by vacancies near C-terminated interfaces is energetically the most favorable.
Metals 07 00264 g008
Metals 07 00264 g009 550
Figure 9. Equilibrium concentration of H at the C-terminated interface, free κ-carbide (C-terminated) and fcc-Fe surfaces as a function of the chemical potential of hydrogen. A perfect κ-carbide (solid lines) is compared with a κ-carbide that contains a C vacancy (dashed lines).
Figure 9. Equilibrium concentration of H at the C-terminated interface, free κ-carbide (C-terminated) and fcc-Fe surfaces as a function of the chemical potential of hydrogen. A perfect κ-carbide (solid lines) is compared with a κ-carbide that contains a C vacancy (dashed lines).
Metals 07 00264 g009
Metals 07 00264 g010 550
Figure 10. Embrittlement term ε and the different energy contributions in Equation (6) as a function of μH. A perfect κ-carbide (solid lines) is compared with a κ-carbide that contains a C vacancy (dashed lines). Furthermore, the grand-canonical (GC) and the canonical (C) limit are compared (see text for details).
Figure 10. Embrittlement term ε and the different energy contributions in Equation (6) as a function of μH. A perfect κ-carbide (solid lines) is compared with a κ-carbide that contains a C vacancy (dashed lines). Furthermore, the grand-canonical (GC) and the canonical (C) limit are compared (see text for details).
Metals 07 00264 g010
Table
Table 1. Lattice parameter a, magnetic saturation moments μtheo and formation energies ΔEel at T = 0 K of various compounds related to the κ-phase.
Table 1. Lattice parameter a, magnetic saturation moments μtheo and formation energies ΔEel at T = 0 K of various compounds related to the κ-phase.
CompoundStructurea0 (Å)μtheo
(μB/Fe atom)		ΔEel
(kJ/mol)
Fe3AlBiF3, D035.742.0−78
Fe3AlCu3Au, L123.652.3−77
Fe3AlCperovskite, E213.751.0−90
Fe3AlHperovskite, E213.682.1−85
Table
Table 2. Hydrogen trapping energies Etrap for octahedral sites at the interface layer between κ-carbide and fcc-Fe, or one of the adjacent layers. Three kinds of stacking sequences in a 2 × 2 × 5 supercell (SC) are provided, where layers used for H incorporation are highlighted in bold face.
Table 2. Hydrogen trapping energies Etrap for octahedral sites at the interface layer between κ-carbide and fcc-Fe, or one of the adjacent layers. Three kinds of stacking sequences in a 2 × 2 × 5 supercell (SC) are provided, where layers used for H incorporation are highlighted in bold face.
Stacking Sequence of Layers in SCEtrap (H) Adjacent Fe Layer (eV)Etrap (H) Interface Layer (eV)Etrap (H) Adjacent κ Layer (eV)
Fe*–C*–Al*–C*–Fe*–Fe*–Fe*–Fe*–Fe*–Fe*−0.20−0.18 (C)0.04 (Al)
Fe*–Al*–C*–Al*–C*–Fe*–Fe*–Fe*–Fe*–Fe*0.010.003 (Al)−0.05 (C)
Fe*–C*–Al*–C*–Al*–C*–Al*–Fe*–Fe*–Fe*−0.20−0.24 (C)0.04 (Al)

Share and Cite

MDPI and ACS Style

Timmerscheidt, T.A.; Dey, P.; Bogdanovski, D.; Von Appen, J.; Hickel, T.; Neugebauer, J.; Dronskowski, R. The Role of κ-Carbides as Hydrogen Traps in High-Mn Steels. Metals 2017, 7, 264. https://doi.org/10.3390/met7070264

AMA Style

Timmerscheidt TA, Dey P, Bogdanovski D, Von Appen J, Hickel T, Neugebauer J, Dronskowski R. The Role of κ-Carbides as Hydrogen Traps in High-Mn Steels. Metals. 2017; 7(7):264. https://doi.org/10.3390/met7070264

Chicago/Turabian Style

Timmerscheidt, Tobias A., Poulumi Dey, Dimitri Bogdanovski, Jörg Von Appen, Tilmann Hickel, Jörg Neugebauer, and Richard Dronskowski. 2017. "The Role of κ-Carbides as Hydrogen Traps in High-Mn Steels" Metals 7, no. 7: 264. https://doi.org/10.3390/met7070264

APA Style

Timmerscheidt, T. A., Dey, P., Bogdanovski, D., Von Appen, J., Hickel, T., Neugebauer, J., & Dronskowski, R. (2017). The Role of κ-Carbides as Hydrogen Traps in High-Mn Steels. Metals, 7(7), 264. https://doi.org/10.3390/met7070264

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop