Numerical Simulation of the Depth-Sensing Indentation Test with Knoop Indenter
Abstract
:1. Introduction
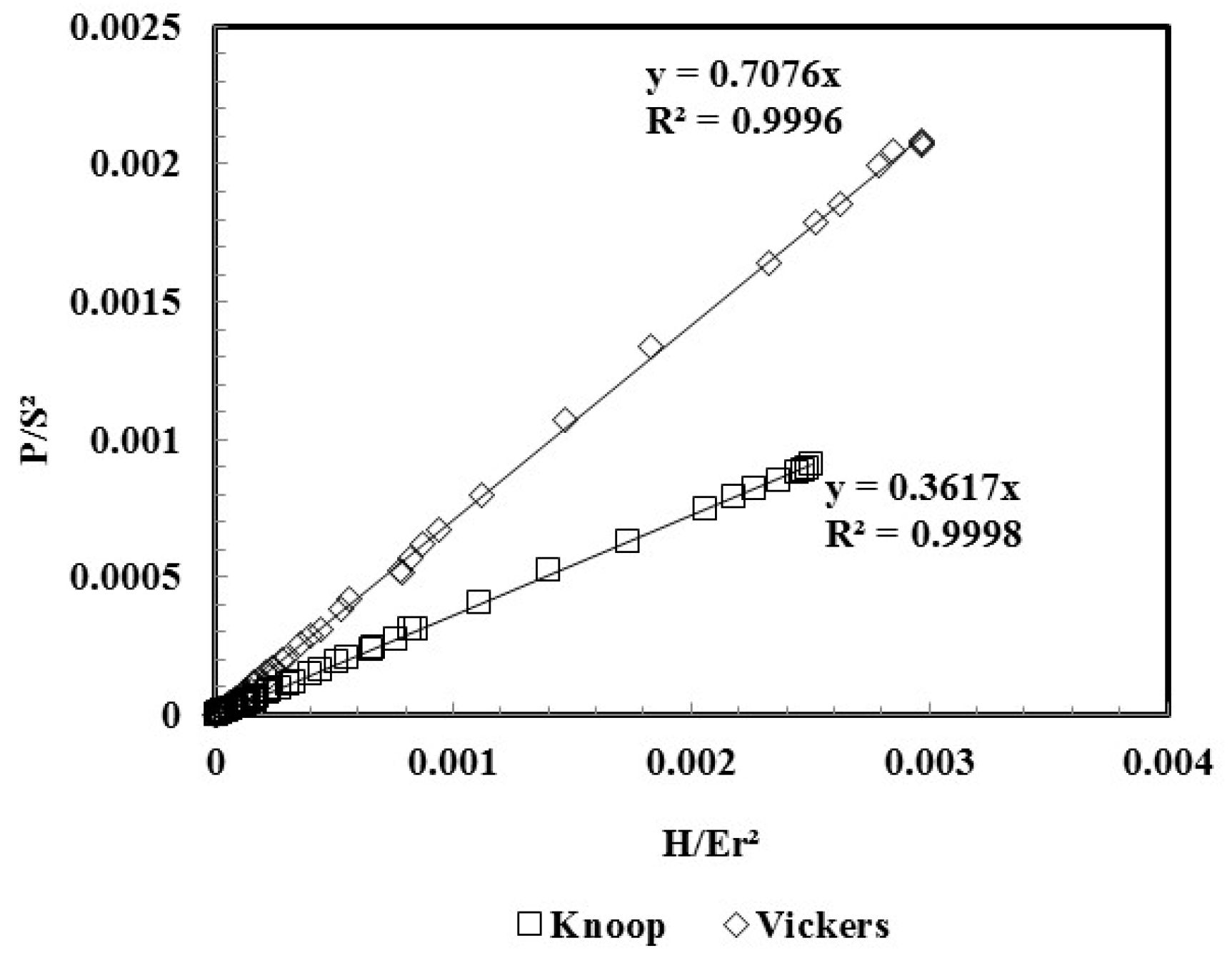
2. Theoretical Aspects
3. Numerical Simulation and Materials
3.1. Indenters
3.2. Finite Element Mesh
3.3. Materials
4. Results
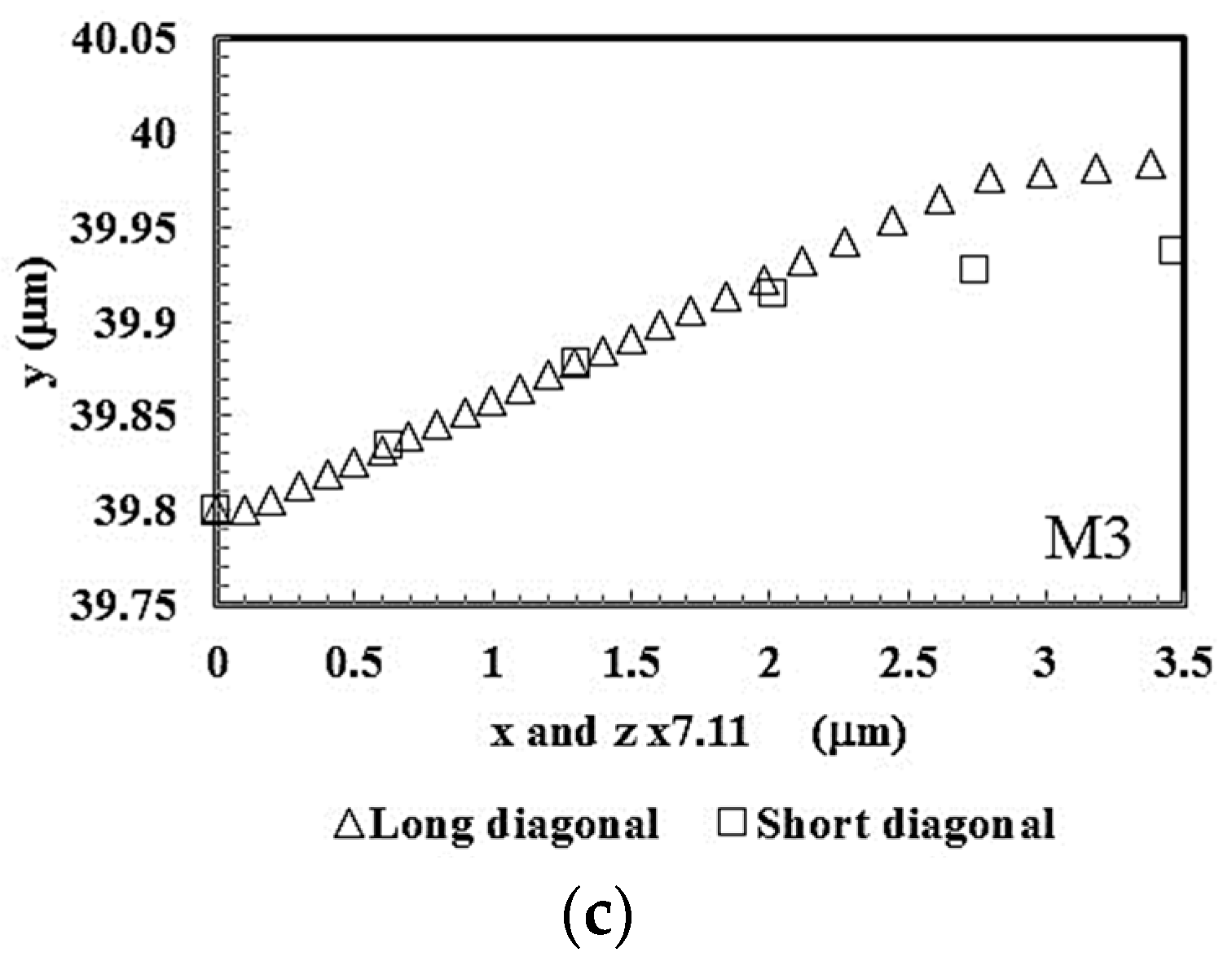
4.1. Indentation Geometry and Equivalent Plastic Strain Distributions
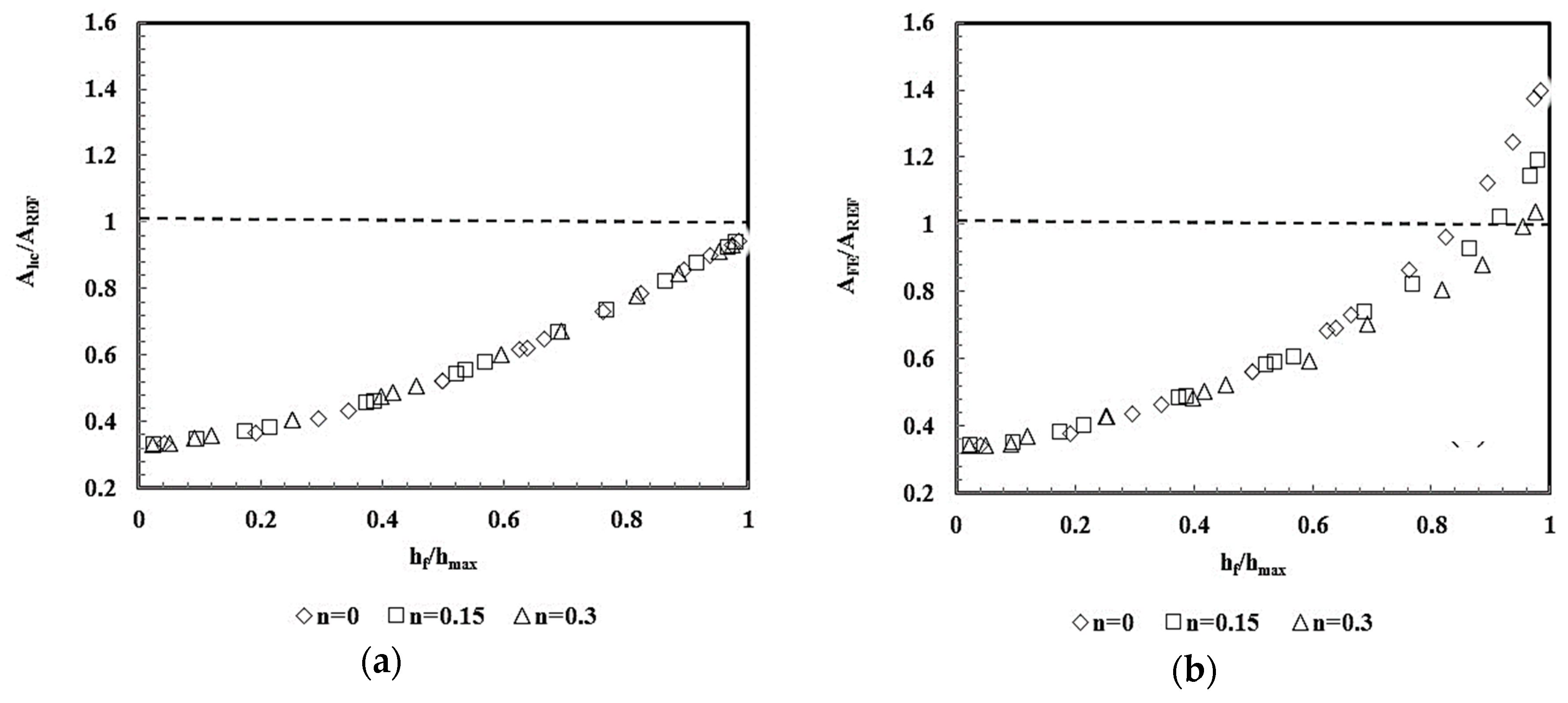
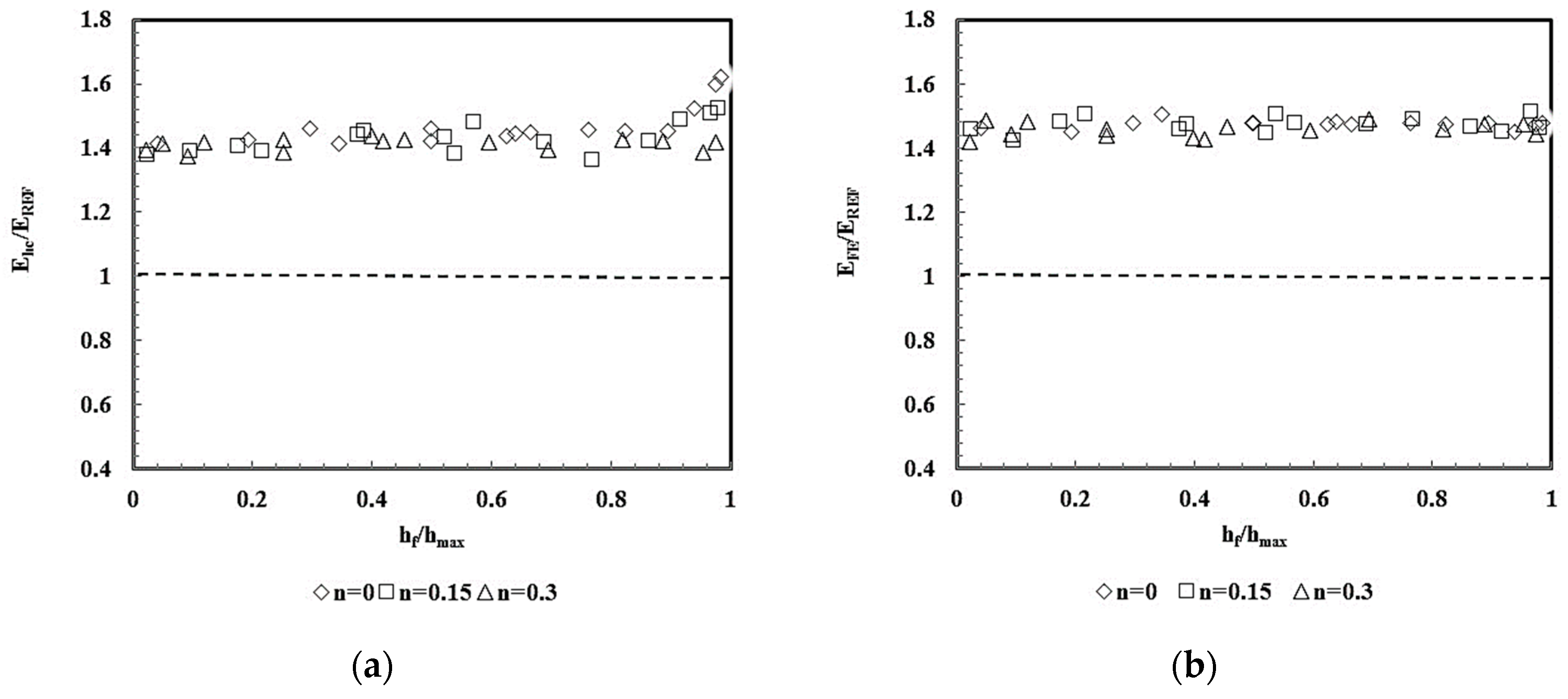
4.2. Indentation Contact Area and Young’s Modulus
4.3. Flat Indenter
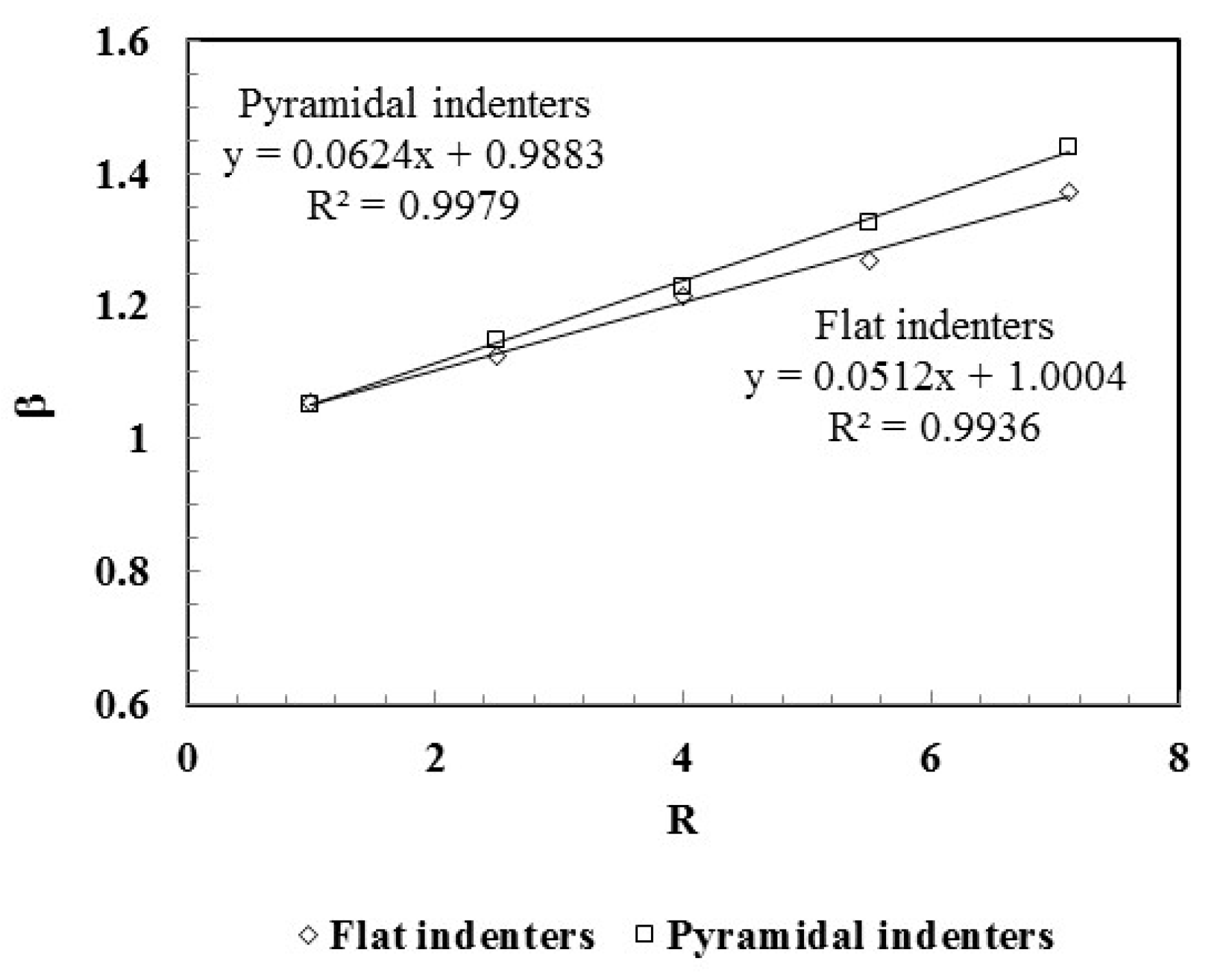
4.4. Correlation with Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fernandes, J.V.; Trindade, A.C.; Menezes, L.F.; Cavaleiro, A. Influence of substrate hardness on the response of W-C-Co-coated samples to depth-sensing indentation. J. Mater. Res. 2000, 15, 1766–1772. [Google Scholar] [CrossRef]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modelling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Chollacoop, N.; Dao, M.; Suresh, S. Depth-sensing instrumented indentation with dual sharp indenters. Acta Mater. 2003, 51, 3713–3729. [Google Scholar] [CrossRef]
- Antunes, J.M.; Menezes, L.F.; Fernandes, J.V.; Chaparro, B.M. A New Approach for Reverse Analyses in Depth-sensing Indentation Using Numerical Simulation. Acta Mater. 2007, 55, 69–81. [Google Scholar] [CrossRef]
- Knoop, F.; Peters, C.G.; Emerson, W.B. A sensitive pyramidal-diamond toll for indentation measurements. J. Res. Natl. Bur. Stand. 1939, 23, 39–61. [Google Scholar] [CrossRef]
- Hasan, M.F.; Wang, J.; Berndt, C.J. Determination of the mechanical properties of plasma-sprayed hydroxyapatite coatings using the Knoop indentation technique. J. Therm. Spray Technol. 2015, 24, 865–877. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, Z.; Tang, B.; Rogachev, A.V. Catalytic effect of Al and AlN interlayer on the growth and properties of containing carbon films. Appl. Surf. Sci. 2015, 326, 174–180. [Google Scholar] [CrossRef]
- Sinavarat, P.; Anunmana, C.; Muanjit, T. Simplified method for determining fracture toughness of two dental ceramics. Dent. Mater. J. 2016, 35, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Vu, V.Q.; Beygelzimer, Y.; Kulagin, R.; Toth, L.S. Mechanical modelling of the plastic flow machining process. Materials 2018, 11, 1218. [Google Scholar] [CrossRef] [PubMed]
- Kulagin, R.; Beygelzimer, Y.; Ivanisenko, Y.; Mazilkin, A.; Hahn, H. Instabilities of interfaces between dissimilar metals induced by pressure torsion. Mater. Lett. 2018, 222, 172–175. [Google Scholar] [CrossRef]
- Borc, J. Study of Knoop microhardness anisotropy on the (001), (100) and (010) faces of gadolinium calcium oxyborate single crystals. Mater. Chem. Phys. 2014, 148, 680–685. [Google Scholar] [CrossRef]
- Rabinovich, V.L.; Sarin, V.K. Three-dimensional modelling of indentation fracture in brittle materials. Mater. Sci. Eng. A 1996, 206, 208–214. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E. Elastic and viscoelastic indentation of flat surfaces by pyramid indentors. J. Mech. Phys. Solids 2006, 54, 1305–1332. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Zisis, T. Analysis of Knoop indentation. Int. J. Solids Struct. 2011, 48, 175–190. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Zisis, T. Analysis of Knoop indentation of cohesive frictional materials. Mech. Mater. 2013, 57, 53–74. [Google Scholar] [CrossRef]
- Riester, L.; Blau, P.J.; Lara-Curzio, E.; Breder, K. Nanoindentation with a Knoop indenter. Thin Solid Films 2000, 377–378, 635–639. [Google Scholar] [CrossRef]
- Riester, L.; Bell, T.J.; Fischer-Cripps, A.C. Analysis of depth-sensing indentation tests with a Knoop indenter. J. Mater. Res. 2001, 16, 1660–1667. [Google Scholar] [CrossRef] [Green Version]
- Ghorbal, G.B.; Tricoteaux, A.; Thuault, A.; Louis, G. Comparison of conventional Knoop and Vickers hardness of ceramic materials. J. Eur. Ceram. Soc. 2017, 37, 2531–2535. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. Technol. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Doerner, M.F.; Nix, W.D. A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1986, 1, 601–609. [Google Scholar] [CrossRef]
- Antunes, J.M.; Menezes, L.F.; Fernandes, J.V. Three-Dimensional Numerical Simulation of Vickers indentation Tests. Int. J. Solids Struct. 2006, 43, 784–806. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Joslin, D.L.; Oliver, W.C. New method for analysing data from continuous depth-sensing microindentation tests. J. Mater. Res. 1990, 5, 123–126. [Google Scholar] [CrossRef]
- Antunes, J.M.; Menezes, L.F.; Fernandes, J.V. Influence of the Vickers Tip Imperfection on the Sensing Indentation Tests. Int. J. Solids Struct. 2007, 44, 2732–2747. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Fernandes, J.V.; Antunes, J.M.; Oliveira, M.C. Comparison between Berkovich, Vickers and conical indentation tests: A three-dimensional numerical simulation study. Int. J. Solids Struct. 2009, 46, 1095–1104. [Google Scholar] [CrossRef] [Green Version]
- Menezes, L.F.; Teodosiu, C. Three-dimensional numerical simulation of the deep-drawing process using solid finite elements. J. Mater. Process. Technol. 2000, 97, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Algorithms and Strategies for Treatment of Large Deformation Frictional Contact in the Numerical Simulation of Deep Drawing Process. Arch. Comput. Meth. Eng. 2008, 15, 113–162. [Google Scholar] [CrossRef] [Green Version]
- Antunes, J.M.; Cavaleiro, A.; Menezes, L.F.; Simões, M.I.; Fernandes, J.V. Ultra-microhardness testing procedure with Vickers indenter. Surf. Coat. Technol. 2002, 149, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Bolshakov, A.; Pharr, G.M. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques. Int. J. Solids Struct. 1998, 13, 1049–1058. [Google Scholar] [CrossRef]
- Marshall, D.B.; Noma, T.; Evans, A.G. A simple method for determining elastic-modulus-to-hardness ratios using Knoop indentation measurements. J. Am. Ceram. Soc. 1982, 65, 175–176. [Google Scholar] [CrossRef]
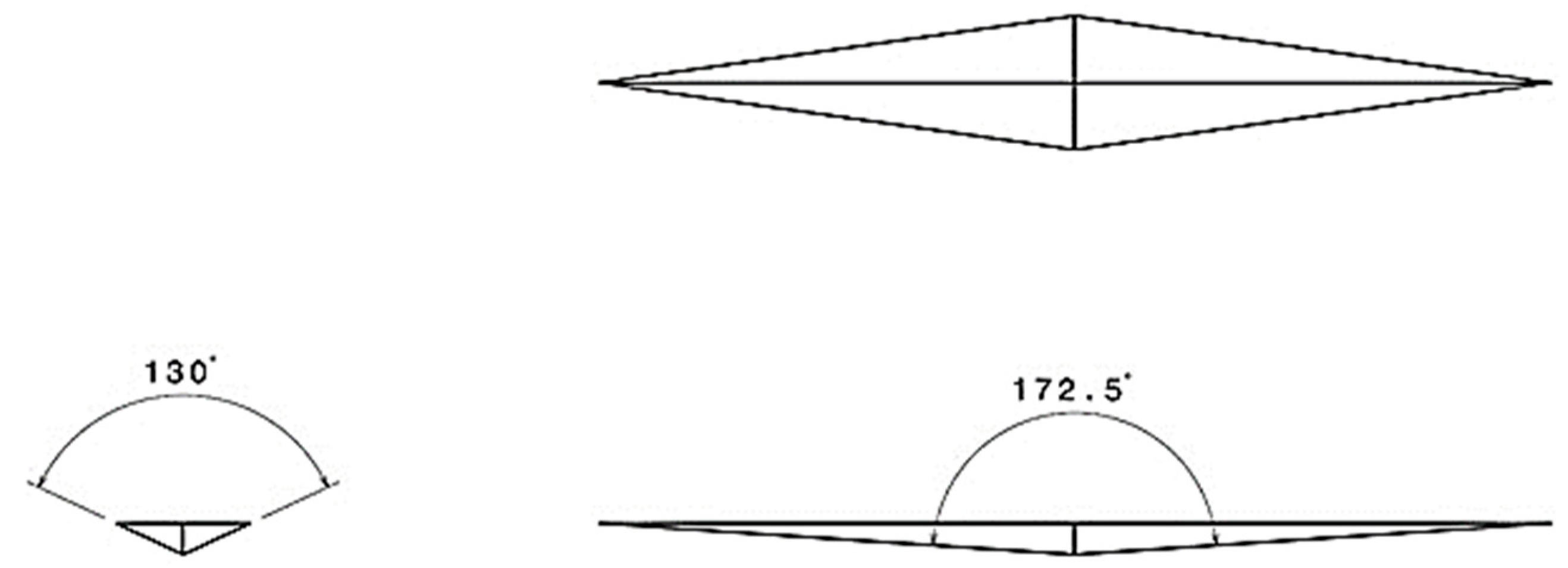

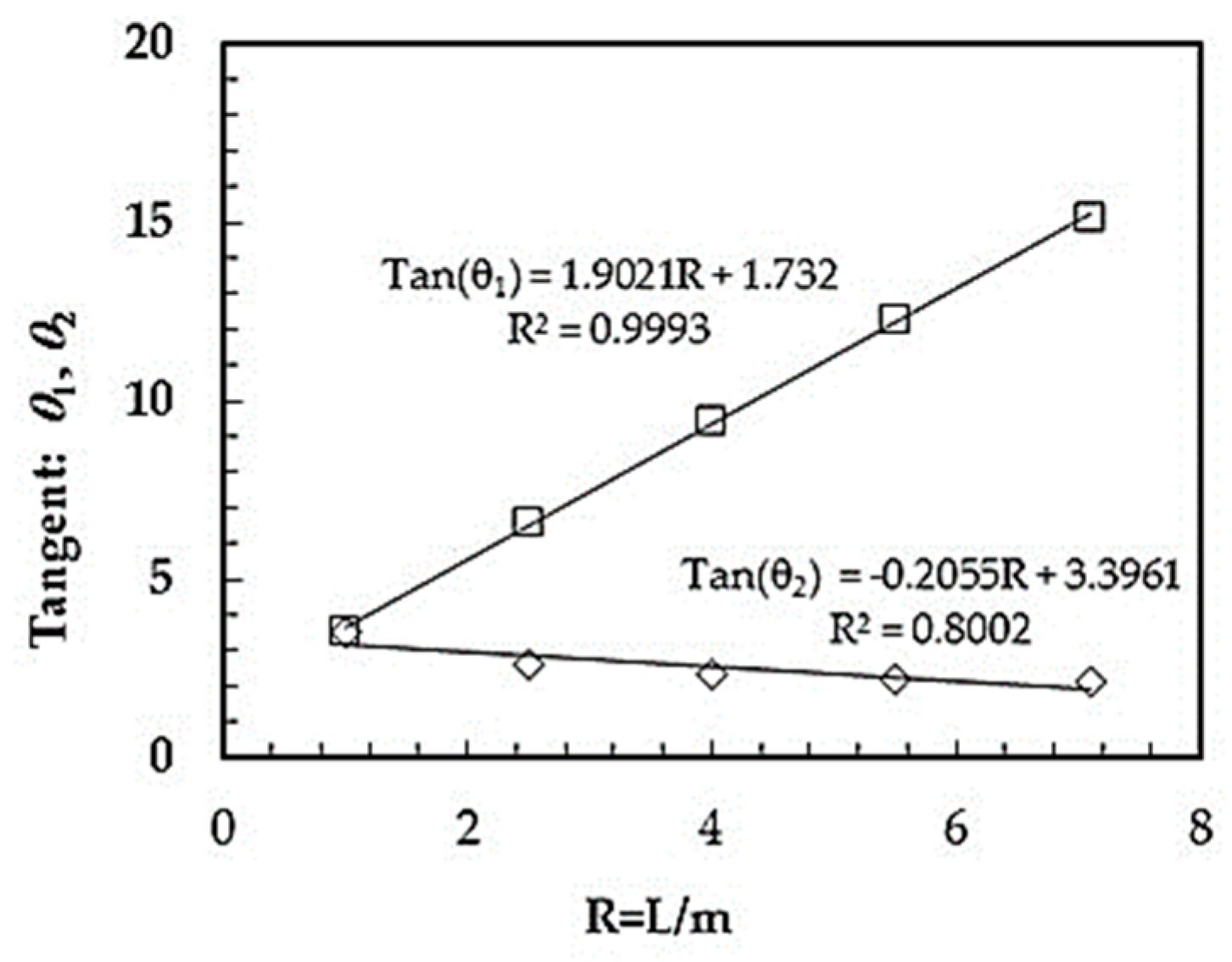

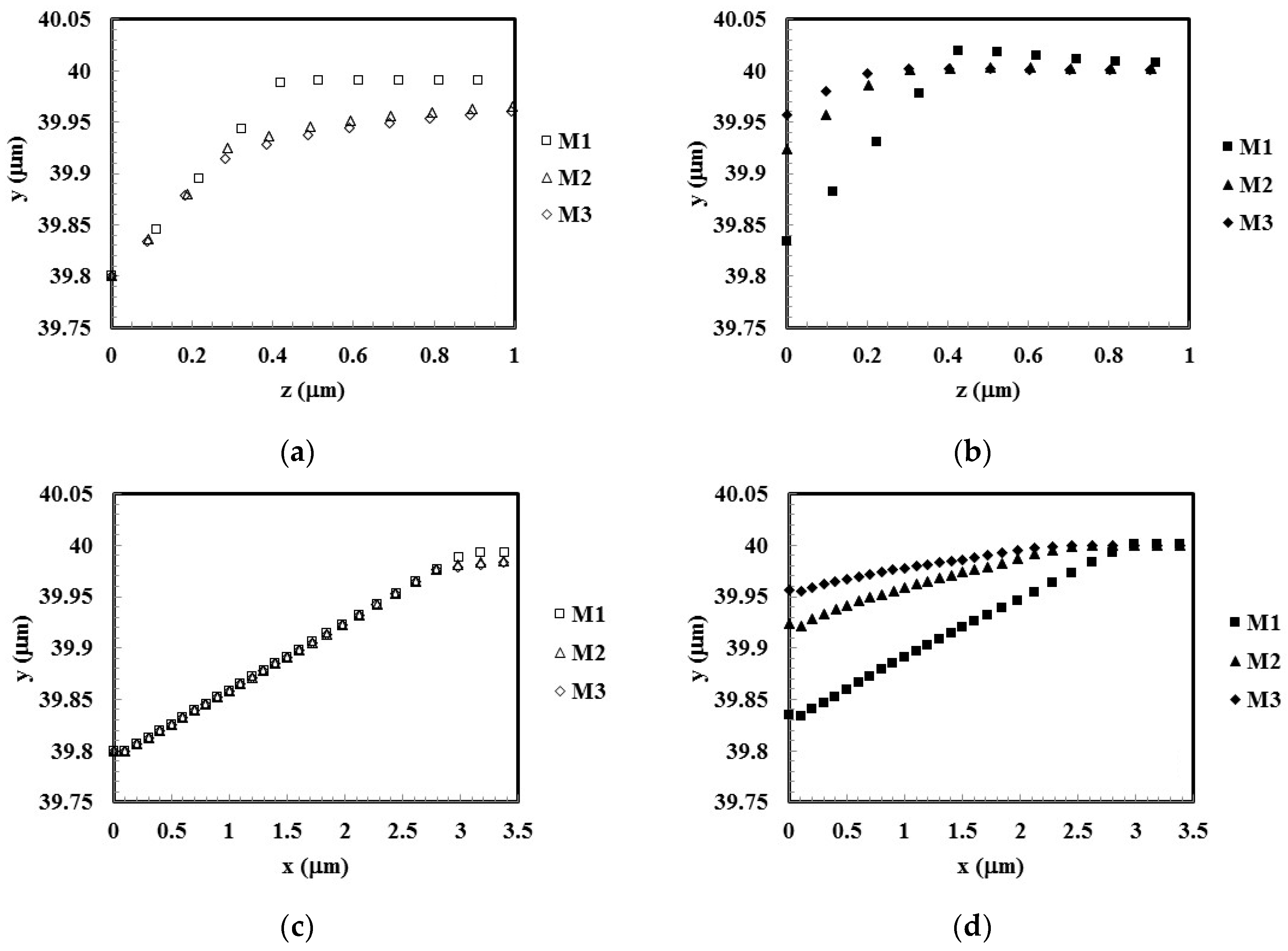
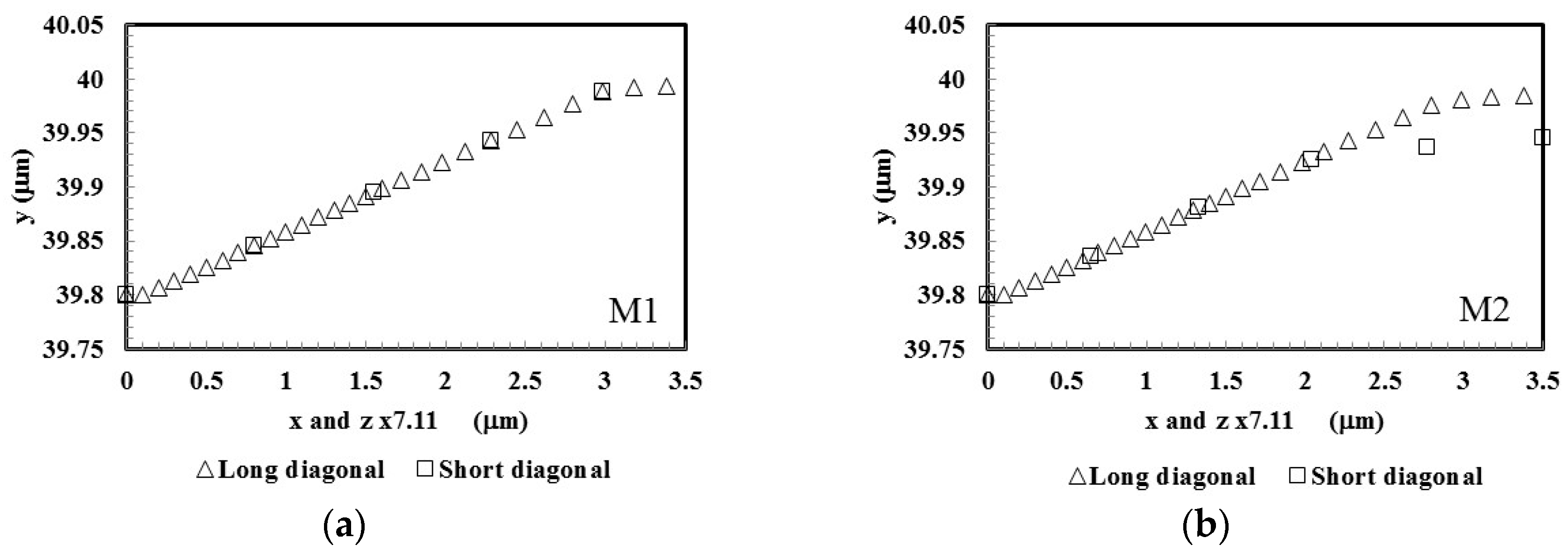


| R = L/m | θ1 | θ2 | Area Function |
|---|---|---|---|
| 1 (Vickers) | 74.0546 | 74.0546 | |
| 2.5 | 69.1723 | 81.3478 | |
| 4 | 67.0462 | 83.9559 | |
| 5.5 | 65.8369 | 85.3366 | |
| 7.11 (Knoop) | 64.8379 | 86.2199 |
| Materials | Studied Cases | n | (GPa) | E (GPa) |
|---|---|---|---|---|
| Without strain hardening | 5 | ≈0 | 0.2, 2, 6, 10 and 20 | 70 |
| 5 | 200 | |||
| 5 | 400 | |||
| With strain hardening | 5 | 0.15 | 70 | |
| 5 | 200 | |||
| 5 | 400 | |||
| 5 | 0.30 | 70 | ||
| 5 | 200 | |||
| 5 | 400 |
| Material | (GPa) | n | E (GPa) | ν | |
|---|---|---|---|---|---|
| M1 | 0.2 | 0.01 | 200 | 0.3 | 0.97 |
| M2 | 6 | 0.3 | 0.40 | ||
| M3 | 20 | 400 | 0.25 |
| R = L/m | E (GPa) | Average Values of | ||||
|---|---|---|---|---|---|---|
| 30 | 200 | 400 | 600 | 800 | ||
| 1.00 | 1.055 | 1.054 | 1.053 | 1.054 | 1.054 | 1.054 |
| 2.50 | 1.125 | 1.123 | 1.124 | 1.125 | 1.124 | 1.124 |
| 4.00 | 1.215 | 1.214 | 1.214 | 1.214 | 1.215 | 1.214 |
| 5.50 | 1.269 | 1.266 | 1.267 | 1.267 | 1.266 | 1.267 |
| 7.11 | 1.374 | 1.372 | 1.371 | 1.371 | 1.372 | 1.372 |
| Materials | (GPa) [19] | (GPa) [19] | Error (%) | (GPa) [19] | Error (%) | [19] | (GPa) | Error (%) |
|---|---|---|---|---|---|---|---|---|
| Si3N4 | 317 ± 4 | 316.5 ± 4.24 | −0.16 | 300 ± 20.0 | −5.36 | 2.548 ± 0.029 | 302.8 ± 4.40 | −4.48 |
| Ceramic-glass | 82 ± 2 | 85.0 ± 0.36 | 3.66 | 85 ± 4.0 | 3.66 | 7.930 ± 0.031 | 82.1 ± 0.35 | 0.15 |
| Alumina | 385 ± 6 | 386.0 ± 7.75 | 0.26 | 380 ± 18.5 | −1.30 | 2.233 ± 0.032 | 359.4 ± 6.90 | −6.64 |
| -TCP | 130 ± 2 | 129.0 ± 0.85 | −0.77 | 142 ± 14.0 | 9.23 | 5.568 ± 0.032 | 120.7 ± 0.70 | −7.12 |
| Fused silica | 68 ± 1 | 65.0 ± 0.30 | −3.00 | 70 ± 4.0 | 2.94 | 9.221 ± 0.034 | 69.9 ± 0.25 | 2.80 |
| Average of the absolute value of the error | 1.57 | 4.50 | 4.27 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simões, M.I.; Antunes, J.M.; Fernandes, J.V.; Sakharova, N.A. Numerical Simulation of the Depth-Sensing Indentation Test with Knoop Indenter. Metals 2018, 8, 885. https://doi.org/10.3390/met8110885
Simões MI, Antunes JM, Fernandes JV, Sakharova NA. Numerical Simulation of the Depth-Sensing Indentation Test with Knoop Indenter. Metals. 2018; 8(11):885. https://doi.org/10.3390/met8110885
Chicago/Turabian StyleSimões, Maria I., Jorge M. Antunes, José V. Fernandes, and Nataliya A. Sakharova. 2018. "Numerical Simulation of the Depth-Sensing Indentation Test with Knoop Indenter" Metals 8, no. 11: 885. https://doi.org/10.3390/met8110885





