Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
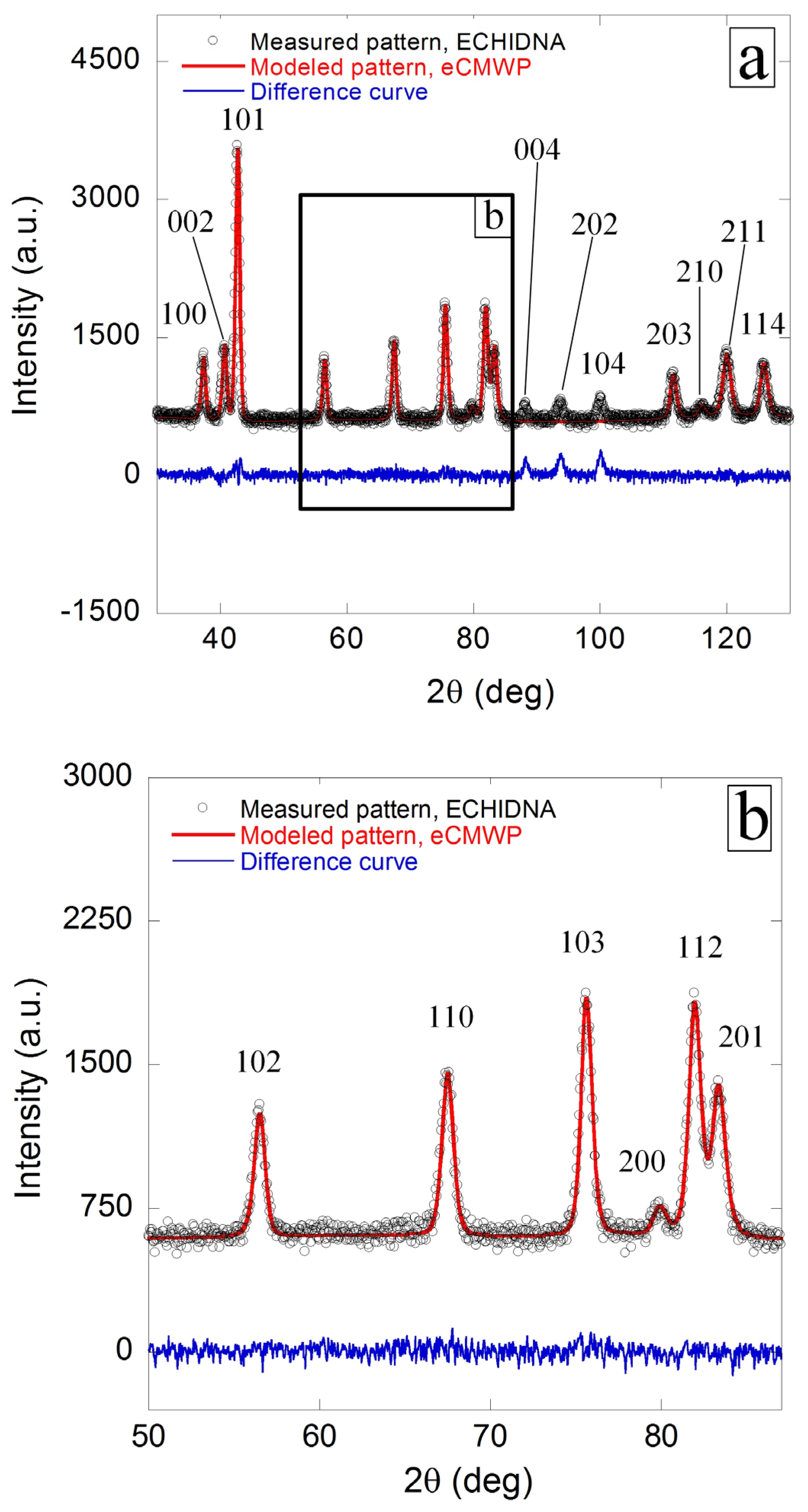
2.2. Neutron Diffraction Set Parameters and Extended Convolution Multiple Whole Profile (eCMWP) Analysis
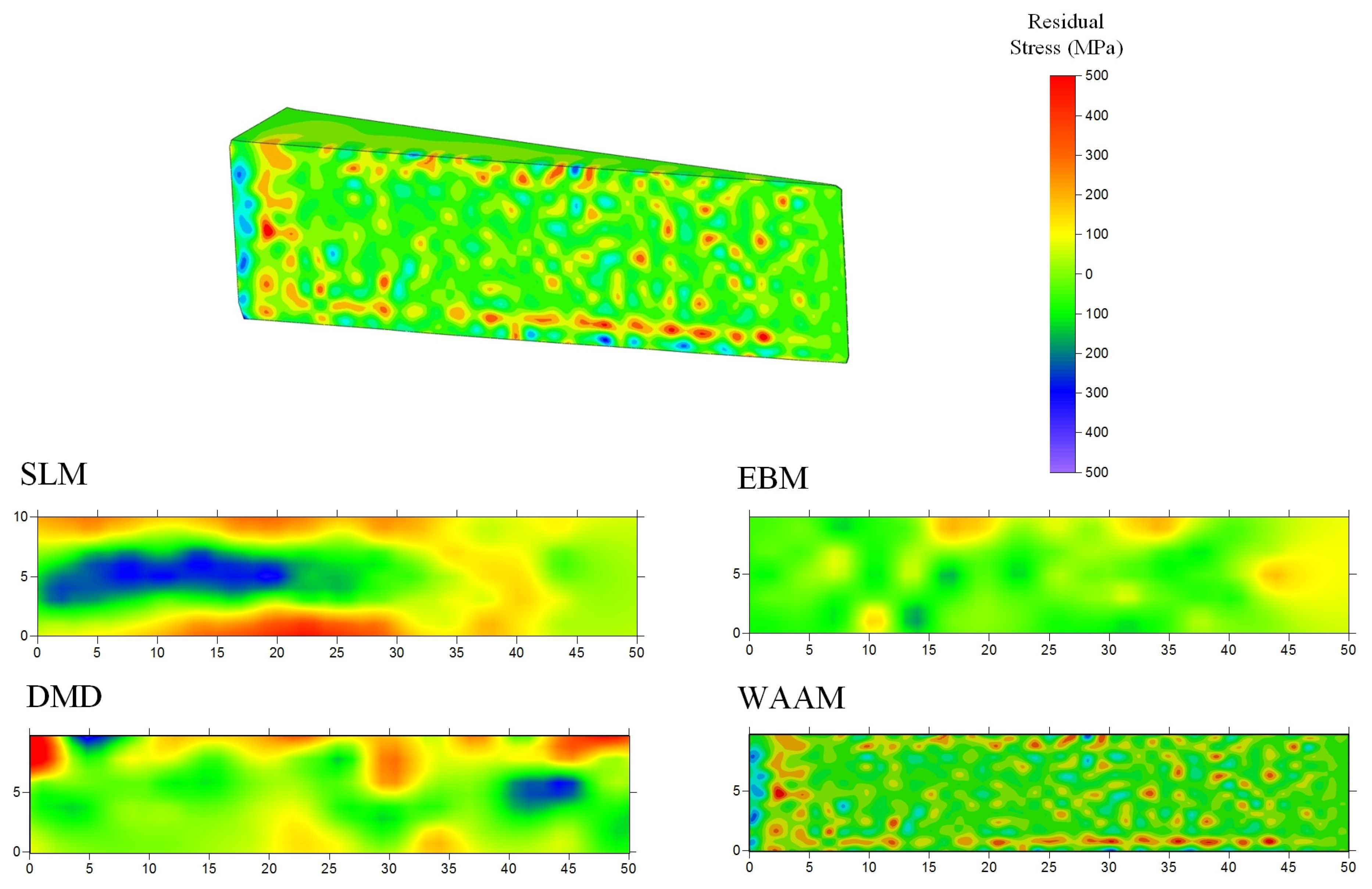
2.3. Residual Stress Analysis
2.4. Microstructural Analysis
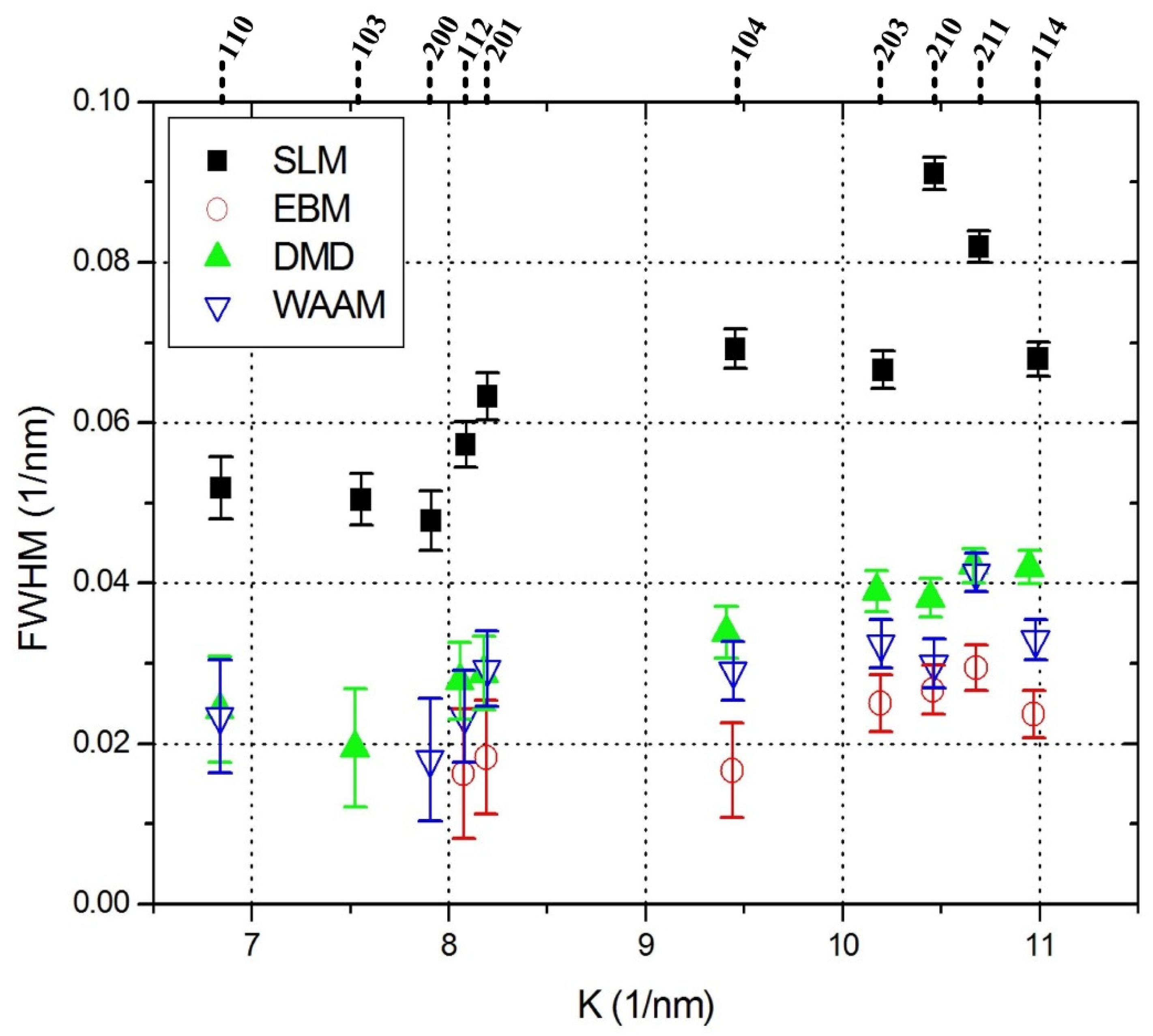
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| 3D | Three Dimensional |
| AM | Additive Manufacturing |
| BCC | Body Centered-Cubic |
| EBM | Electron Beam Melting |
| eCMWP | extended Convolution Multiple Whole Profile |
| DLPA | Diffraction Line Profile Analysis |
| DMD | Direct Metal Deposition |
| FWHM | Full Width at Half Maximum |
| HCP | Hexagonal Close-Packed |
| Convolution of diffraction peaks at 2θ diffraction angle | |
| Dislocation cell/sub-grain size distribution at [hkl] crystal plane | |
| Contribution of the dislocations at [hkl] crystal plane | |
| Contribution of the planar defects at [hkl] crystal plane | |
| Instrumental peak broadening and shape at [hkl] crystal plane | |
| Background of the diffraction pattern | |
| K | Reciprocal of the lattice spacing |
| SLM | Selective Laser Melting |
| TEM | Transmission Electron Microscope |
| WAAM | Wire Arc Additive Manufacturing |
| WH | Williamson-Hall |
| <X>A | Area weighted average sub-grain size |
| ρTotal | Total dislocation density |
References
- Kruth, J.P.; Leu, M.C.; Nakagawa, T. Progress in additive manufacturing and rapid prototyping. CIRP Ann. Manuf. Technol. 1998, 47, 525–540. [Google Scholar] [CrossRef]
- Attar, H.; Ehtemam-Haghighi, S.; Kent, D.; Dargusch, M.S. Recent developments and opportunities in additive manufacturing of titanium-based matrix composites: A review. Int. J. Mach. Tools Manuf. 2018, 133, 85–102. [Google Scholar] [CrossRef]
- Rashid, R.; Masood, S.H.; Ruan, D.; Palanisamy, S.; Rahman Rashid, R.A.; Elambasseril, J.; Brandt, M. Effect of energy per layer on the anisotropy of selective laser melted AlSi12 aluminium alloy. Addit. Manuf. 2018, 22, 426–439. [Google Scholar] [CrossRef]
- Ponnusamy, P.; Masood, S.H.; Palanisamy, S.; Rahman Rashid, R.A.; Ruan, D. Characterization of 17-4PH alloy processed by selective laser melting. Mater. Today 2017, 4, 8498–8506. [Google Scholar] [CrossRef]
- Agius, D.; Kourousis, K.; Wallbrink, C. A Review of the As-Built SLM Ti-6Al-4V Mechanical Properties towards Achieving Fatigue Resistant Designs. Metals 2018, 8, 75. [Google Scholar] [CrossRef]
- Hoye, N.; Cuiuri, D.; Rahman Rashid, R.A.; Palanisamy, S. Machining of GTAW additively manufactured Ti-6Al-4V structures. Int. J. Adv. Manuf. Technol. 2018, 99, 313–326. [Google Scholar] [CrossRef]
- Sames, W.J.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 315–360. [Google Scholar] [CrossRef]
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Ribárik, G.; Ungár, T. Characterization of the microstructure in random and textured polycrystals and single crystals by diffraction line profile analysis. Mater. Sci. Eng. A 2010, 528, 112–121. [Google Scholar] [CrossRef]
- Máthis, K.; Nyilas, K.; Axt, A.; Dragomir-Cernatescu, I.; Ungár, T.; Lukáč, P. The evolution of non-basal dislocations as a function of deformation temperature in pure magnesium determined by X-ray diffraction. Acta Mater. 2004, 52, 2889–2894. [Google Scholar] [CrossRef]
- Glavicic, M.G.; Salem, A.A.; Semiatin, S.L. X-ray line-broadening analysis of deformation mechanisms during rolling of commercial-purity titanium. Acta Mater. 2004, 52, 647–655. [Google Scholar] [CrossRef]
- Glavicic, M.G.; Semiatin, S.L. X-ray line-broadening investigation of deformation during hot rolling of Ti–6Al–4V with a colony-alpha microstructure. Acta Mater. 2006, 54, 5337–5347. [Google Scholar] [CrossRef]
- Brown, D.W.; Adams, D.P.; Balogh, L.; Carpenter, J.S.; Clausen, B.; King, G.; Reedlunn, B.; Palmer, T.A.; Maguire, M.C.; Vogel, S.C. In Situ Neutron Diffraction Study of the Influence of Microstructure on the Mechanical Response of Additively Manufactured 304L Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2017, 48, 6055–6069. [Google Scholar] [CrossRef]
- Pokharel, R.; Balogh, L.; Brown, D.W.; Clausen, B.; Gray, G.T., III; Livescu, V.; Vogel, S.C.; Takajo, S. Signatures of the unique microstructure of additively manufactured steel observed via diffraction. Scr. Mater. 2018, 155, 16–20. [Google Scholar] [CrossRef]
- Rahman Rashid, R.A.; Palanisamy, S.; Attar, H.; Bermingham, M.; Dargusch, M.S. Metallurgical features of direct laser-deposited Ti6Al4V with trace boron. J. Manuf. Process. 2018, 35, 651–656. [Google Scholar] [CrossRef]
- Ahmed, T.; Rack, H.J. Phase transformations during cooling in α+β titanium alloys. Mater. Sci. Eng. A 1998, 243, 206–211. [Google Scholar] [CrossRef]
- Carroll, B.E.; Palmer, T.A.; Beese, A.M. Anisotropic tensile behavior of Ti–6Al–4V components fabricated with directed energy deposition additive manufacturing. Acta Mater. 2015, 87, 309–320. [Google Scholar] [CrossRef]
- Ribarik, G.; Ungar, T.; Gubicza, J. MWP-fit: a program for multiple whole-profile fitting of diffraction peak profiles by ab initio theoretical functions. J. Appl. Crystallogr. 2001, 34, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Ungár, T.; Tichy, G.; Gubicza, J.; Hellmig, R. Correlation between subgrains and coherently scattering domains. Powder Diffr. 2005, 20, 366–375. [Google Scholar] [CrossRef] [Green Version]
- Ungár, T.; Tichy, G. The Effect of Dislocation Contrast on X-Ray Line Profiles in Untextured Polycrystals. Phys. Status Solidi 1999, 171, 425–434. [Google Scholar] [CrossRef]
- Borbély, A.; Ungár, T. X-ray line profiles analysis of plastically deformed metals. C. R. Phys. 2012, 13, 293–306. [Google Scholar] [CrossRef]
- Balogh, L.; Ribárik, G.; Ungár, T. Stacking faults and twin boundaries in fcc crystals determined by x-ray diffraction profile analysis. J. Appl. Phys. 2006, 100, 023512. [Google Scholar] [CrossRef]
- Balogh, L.; Tichy, G.; Ungár, T. Twinning on pyramidal planes in hexagonal close packed crystals determined along with other defects by X-ray line profile analysis. J. Appl. Crystallogr. 2009, 42, 580–591. [Google Scholar] [CrossRef]
- Stokes, A.R. A numerical Fourier-analysis method for the correction of widths and shapes of lines on X-ray powder photographs. Proc. Phys. Soc. 1948, 61, 382. [Google Scholar] [CrossRef]
- Ungár, T.; Balogh, L.; Ribárik, G. Defect-Related Physical-Profile-Based X-Ray and Neutron Line Profile Analysis. Metall. Mater. Trans. A 2010, 41, 1202–1209. [Google Scholar] [CrossRef]
- Ungár, T. Dislocation model of strain anisotropy. Powder Diffr. 2008, 23, 125–132. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Chapter 6 - Recovery After Deformation. In Recrystallization and Related Annealing Phenomena, 2nd ed.; Humphreys, F.J., Hatherly, M., Eds.; Elsevier: Oxford, UK, 2004; pp. 169–213. [Google Scholar]
- Dąbrowski, R. The Kinetics of Phase Transformations During Continuous Cooling of the Ti6Al4V Alloy from the Single-Phase β Range. Arch. Metall. Mater. 2011, 56, 703. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.Y.; Fang, X.Y.; Guo, Y.B. Residual Stress in Metal Additive Manufacturing. Proc. CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Vasinonta, A.; Beuth, J.L.; Griffith, M. Process Maps for Predicting Residual Stress and Melt Pool Size in the Laser-Based Fabrication of Thin-Walled Structures. J. Manuf. Sci. Eng. 2006, 129, 101–109. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Developments in martensitic and bainitic steels: Role of the shape deformation. Mater. Sci. Eng. A 2004, 378, 34–39. [Google Scholar] [CrossRef]
- Christien, F.; Telling, M.T.F.; Knight, K.S. Neutron diffraction in situ monitoring of the dislocation density during martensitic transformation in a stainless steel. Scr. Mater. 2013, 68, 506–509. [Google Scholar] [CrossRef]
- Mishurova, T.; Cabeza, S.; Artzt, K.; Haubrich, J.; Klaus, M.; Genzel, C.; Requena, G.; Bruno, G. An Assessment of Subsurface Residual Stress Analysis in SLM Ti-6Al-4V. Materials 2017, 10, 348. [Google Scholar] [CrossRef] [PubMed]
- Yadroitsev, I.; Yadroitsava, I. Evaluation of residual stress in stainless steel 316L and Ti6Al4V samples produced by selective laser melting. Virtual Phys. Prototyp. 2015, 10, 67–76. [Google Scholar] [CrossRef]
- Cottam, R.; Thorogood, K.; Lui, Q.; Wong, Y.C.; Brandt, M. The Effect of Laser Cladding Deposition Rate on Residual Stress Formation in Ti-6Al-4V Clad Layers. Key Eng. Mater. 2012, 520, 309–313. [Google Scholar] [CrossRef]
- Szost, B.A.; Terzi, S.; Martina, F.; Boisselier, D.; Prytuliak, A.; Pirling, T.; Hofmann, M.; Jarvis, D.J. A comparative study of additive manufacturing techniques: Residual stress and microstructural analysis of CLAD and WAAM printed Ti–6Al–4V components. Mater. Des. 2016, 89, 559–567. [Google Scholar] [CrossRef]
- Ali, H.; Ma, L.; Ghadbeigi, H.; Mumtaz, K. In-situ residual stress reduction, martensitic decomposition and mechanical properties enhancement through high temperature powder bed pre-heating of Selective Laser Melted Ti6Al4V. Mater. Sci. Eng. A 2017, 695, 211–220. [Google Scholar] [CrossRef]



| AM Process | <X>A (nm) | ρTOTAL (m−2) | <a> % | <c+a> % | <c> % |
|---|---|---|---|---|---|
| SLM | 100 ± 15 | (24 ± 3) × 1014 | 85 ± 10 | 10 ± 10 | 5 ± 10 |
| EBM | >500 | (1.4 ± 0.5) × 1014 | 70 ± 15 | 30 ± 15 | 0 ± 15 |
| DMD | 120 ± 20 | (4.1 ± 0.5) × 1014 | 60 ± 15 | 30 ± 15 | 10 ± 15 |
| WAAM | >500 | (4.1 ± 0.5) × 1014 | 80 ± 10 | 20 ± 10 | 0 ± 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cottam, R.; Palanisamy, S.; Avdeev, M.; Jarvis, T.; Henry, C.; Cuiuri, D.; Balogh, L.; Abdul Rahman Rashid, R. Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes. Metals 2019, 9, 60. https://doi.org/10.3390/met9010060
Cottam R, Palanisamy S, Avdeev M, Jarvis T, Henry C, Cuiuri D, Balogh L, Abdul Rahman Rashid R. Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes. Metals. 2019; 9(1):60. https://doi.org/10.3390/met9010060
Chicago/Turabian StyleCottam, Ryan, Suresh Palanisamy, Maxim Avdeev, Tom Jarvis, Chad Henry, Dominic Cuiuri, Levente Balogh, and Rizwan Abdul Rahman Rashid. 2019. "Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes" Metals 9, no. 1: 60. https://doi.org/10.3390/met9010060
APA StyleCottam, R., Palanisamy, S., Avdeev, M., Jarvis, T., Henry, C., Cuiuri, D., Balogh, L., & Abdul Rahman Rashid, R. (2019). Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes. Metals, 9(1), 60. https://doi.org/10.3390/met9010060






