Experiments and Modeling of Fatigue Behavior of Friction Stir Welded Aluminum Lithium Alloy
Abstract
1. Introduction
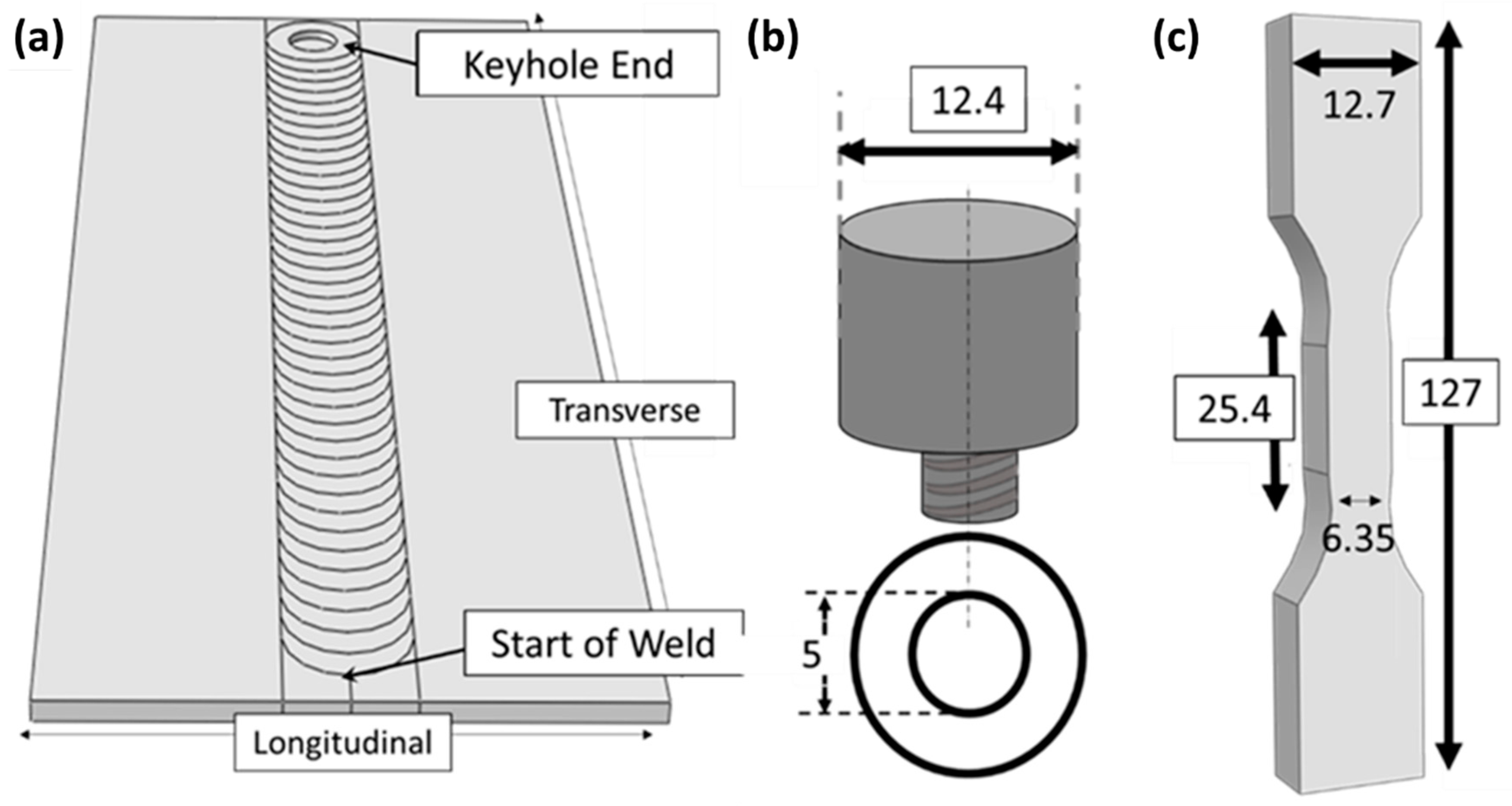
2. Materials and Methods
2.1. Multistage Fatigue Model
2.1.1. Incubation
2.1.2. Small Crack Growth
2.1.3. Long Crack Growth
3. Results
3.1. Microstructure
3.1.1. Grain Structure
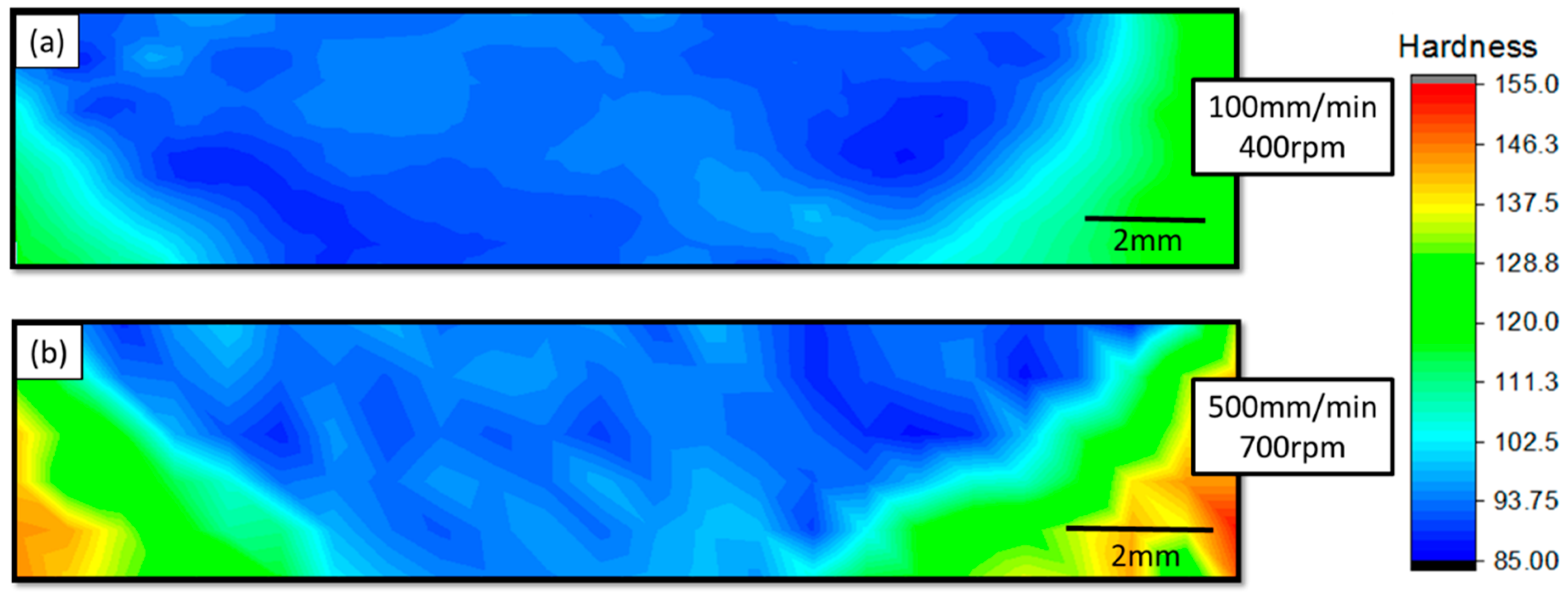
3.1.2. Microhardness
3.1.3. Secondary Phase Characterization
3.2. Monotonic Stress–Strain Behavior
3.3. Low-Cycle Fatigue Parameters
3.4. Fracture Analysis
3.5. MSF Model Correlation
4. Conclusions
- AA2099 was successfully friction stir welded free of large voids or welding defects. In both of the welds, four characteristic regions could be identified: the stir zone (SZ), the thermo-mechanical affected zone (TMAZ), the heat-affected zone (HAZ), and base metal (BM).
- The SZ in Weld II was considerably smaller than that of Weld I, yet the grain size in the SZ of Weld I was smaller than that of Weld II. These size effects were correlated to the heat inputs.
- Although Welds I and II displayed similar cross-section hardness profiles, the hardness values in the SZ of weld I were slightly lower than those of Weld II. Weld I was produced at a lower transverse speed, which increased the heat input in the material and further enabled the dissolution of strengthening precipitates resulting in these lower values.
- The heat input of the FSW process enabled the dissolution of the strengthening precipitate δ’ and the dissolution or coarsening of fine T1 precipitates. Welds I and II had lower amounts of T1 particles than that in the BM. Although the sizes of the T1 precipitates in Weld II increased in relation to the BM, they were noticeably smaller than those of Weld I.
- For strain amplitudes below 0.3%, the elastic strain amplitude was significant in the cyclic deformation. In contrast, at strains amplitudes above 0.1%, the plastic strain amplitude was the dominant factor.
- Overall, the base material demonstrated higher fatigue resistance in both high-cycle and low-cycle fatigue than the FSW specimens.
- For low-cycle fatigue, the two welded parameters displayed similar fatigue results.
- The high-cycle fatigue of Weld II (700 rpm and 500 mm/min) showed fatigue lives 1.5–2 times greater than that of Weld I (400 rpm and 100 mm/min).
- Fracture specimens displayed crack deflection, delamination failure features commonly observed in Al–Li alloys. Fatigue cracks initiated at particles located near the surface of the samples.
- The MSF model was successfully modified to account for competing effects of grain size and hardness variations within an FSW.
Author Contributions
Funding
Conflicts of Interest
References
- Bois-Brochu, A.; Blais, C.; Tchitembo Goma, F.A.; Larouche, D. Modelling of anisotropy for Al-Li 2099 T83 extrusions and effect of precipitate density. Mater. Sci. Eng. A 2016, 673, 581–586. [Google Scholar] [CrossRef]
- Sidhar, H.; Mishra, R.S. Aging kinetics of friction stir welded Al-Cu-Li-Mg-Ag and Al-Cu-Li-Mg alloys. Mater. Des. 2016, 110, 60–71. [Google Scholar] [CrossRef]
- Jordon, J.B.; Rao, H.M.; Yuan, W.; Badarinarayan, H.; Ghaffari, B. Effect of process parameters on microstructure and mechanical behaviors of friction stir linear welded aluminum to magnesium. Mater. Sci. Eng. A 2015, 651, 27–36. [Google Scholar]
- Chiumenti, M.; Cervera, M.; Agelet de Saracibar, C.; Dialami, N. Numerical modeling of friction stir welding processes. Comput. Methods Appl. Mech. Eng. 2013, 254, 353–369. [Google Scholar] [CrossRef]
- Mishra, R.S.; Ma, Z.Y. Friction stir welding and processing. Mater. Sci. Eng. R Rep. 2005, 50, 1–78. [Google Scholar] [CrossRef]
- Michael, J. Troughton Friction Stir Welding. Weld. J. 2009, 8, 131–134. [Google Scholar]
- Gibson, B.T.; Lammlein, D.H.; Prater, T.J.; Longhurst, W.R.; Cox, C.D.; Ballun, M.C.; Dharmaraj, K.J.; Cook, G.E.; Strauss, A.M. Friction stir welding: Process, automation, and control. J. Manuf. Process. 2014, 16, 56–73. [Google Scholar] [CrossRef]
- Su, J.Q.; Nelson, T.W.; Mishra, R.; Mahoney, M. Microstructural investigation of friction stir welded 7050-T651 aluminium. Acta Mater. 2003, 51, 713–729. [Google Scholar] [CrossRef]
- Da Silva, A.A.M.; Arruti, E.; Janeiro, G.; Aldanondo, E.; Alvarez, P.; Echeverria, A. Material Flow and Mechanical Behaviour of Dissimilar AA2024-T3 and AA7075-T6 Aluminium Alloys Friction Stir Welds. Mater. Des. 2011, 32, 2021–2027. [Google Scholar] [CrossRef]
- John, R.; Jata, K.V.; Sadananda, K. Residual stress effects on near-threshold fatigue crack growth in friction stir welds in aerospace alloys. Int. J. Fatigue 2003, 25, 939–948. [Google Scholar] [CrossRef]
- Fratini, L.; Pasta, S.; Reynolds, A.P. Fatigue crack growth in 2024-T351 friction stir welded joints: Longitudinal residual stress and microstructural effects. Int. J. Fatigue 2009, 31, 495–500. [Google Scholar] [CrossRef]
- Cavaliere, P.; De Santis, A.; Panella, F.; Squillace, A. Effect of welding parameters on mechanical and microstructural properties of dissimilar AA6082-AA2024 joints produced by friction stir welding. Mater. Des. 2009, 30, 609–616. [Google Scholar] [CrossRef]
- Ciliberto, S.; Astarita, A.; Squillace, A. FSW of T joints in overlap configuration: Process optimization in joining dissimilar aluminium alloys for the aeronautic application. Surf. Interface Anal. 2013, 45, 1631–1637. [Google Scholar] [CrossRef]
- Sepe, R.; Armentani, E.; Di Lascio, P.; Citarella, R. Crack Growth Behavior of Welded Stiffened Panel. Procedia Eng. 2015, 109, 473–483. [Google Scholar] [CrossRef]
- Ghaffari, B.; Khosrovaneh, A.K.; Su, X.; Jordon, J.B.; Rao, H.M.; Lee, Y.L.; Yuan, W. Fatigue Behavior of Friction Stir Linear Welded Dissimilar Aluminum-to-Magnesium Alloys. In Friction Stir Welding and Processing VIII; Springer: New York City, NY, USA, 2016; Volume 82, pp. 145–152. [Google Scholar]
- Solanki, K.N.; Jordon, J.B.; Whittington, W.; Rao, H.; Hubbard, C.R. Structure–property relationships and residual stress quantification of a friction stir spot welded magnesium alloy. Scr. Mater. 2012, 66, 797–800. [Google Scholar] [CrossRef]
- WANG, S.; HUANG, Y.; ZHAO, L. Effects of different aging treatments on microstructures and mechanical properties of Al-Cu-Li alloy joints welded by electron beam welding. Chin. J. Aeronaut. 2018, 31, 363–369. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Li, L.; Huang, T.; Liu, Z.; Xiao, R. Microstructure and mechanical properties of laser beam-welded AA2060 Al-Li alloy. J. Mater. Process. Technol. 2016, 237, 301–308. [Google Scholar]
- Fu, B.; Qin, G.; Meng, X.; Ji, Y.; Zou, Y.; Lei, Z. Microstructure and mechanical properties of newly developed aluminum-lithium alloy 2A97 welded by fiber laser. Mater. Sci. Eng. A 2014, 617, 1–11. [Google Scholar] [CrossRef]
- Ma, Y.E.; Xia, Z.C.; Jiang, R.R.; Li, W.Y. Effect of welding parameters on mechanical and fatigue properties of friction stir welded 2198 T8 aluminum lithium alloy joints. Eng. Fract. Mech. 2013, 114, 1–11. [Google Scholar] [CrossRef]
- Lee, H.S.; Yoon, J.H.; Yoo, J.T.; No, K. Friction stir welding process of aluminum-lithium alloy 2195. Procedia Eng. 2016, 149, 62–66. [Google Scholar] [CrossRef]
- Tao, Y.; Ni, D.R.; Xiao, B.L.; Ma, Z.Y.; Wu, W.; Zhang, R.X.; Zeng, Y.S. Origin of unusual fracture in stirred zone for friction stir welded 2198-T8 Al-Li alloy joints. Mater. Sci. Eng. A 2017, 693, 1–13. [Google Scholar] [CrossRef]
- Sili, A.; Calogero, V.; Costanza, G.; Tata, M.E.; Missori, S. A Weldability Study of Al–Cu–Li 2198 Alloy. Metallurgist 2014, 57, 1134–1141. [Google Scholar]
- Cai, B.; Zheng, Z.Q.; He, D.Q.; Li, S.C.; Li, H.P. Friction stir weld of 2060 Al-Cu-Li alloy: Microstructure and mechanical properties. J. Alloys Compd. 2015, 649, 19–27. [Google Scholar] [CrossRef]
- Mao, Y.; Ke, L.; Liu, F.; Huang, C.; Chen, Y.; Liu, Q. Effect of welding parameters on microstructure and mechanical properties of friction stir welded joints of 2060 aluminum lithium alloy. Int. J. Adv. Manuf. Technol. 2015, 81, 1419–1431. [Google Scholar] [CrossRef]
- Giles, T.L.; Oh-Ishi, K.; Zhilyaev, A.P.; Swaminathan, S.; Mahoney, M.W.; McNelley, T.R. The effect of friction stir processing on the microstructure and mechanical properties of an aluminum lithium alloy. Metall. Mater. Trans. A 2009, 40, 104–115. [Google Scholar] [CrossRef]
- Gao, C.; Zhu, Z.; Han, J.; Li, H. Correlation of microstructure and mechanical properties in friction stir welded 2198-T8 Al-Li alloy. Mater. Sci. Eng. A 2015, 639, 489–499. [Google Scholar] [CrossRef]
- Bitondo, C.; Prisco, U.; Squilace, A.; Buonadonna, P.; Dionoro, G. Friction-stir welding of AA 2198 butt joints: mechanical characterization of the process and of the welds through DOE analysis. Int. J. Adv. Manuf. Technol. 2011, 53, 505–516. [Google Scholar] [CrossRef]
- Moreira, P.M.G.P.; de Jesus, A.M.P.; de Figueiredo, M.A.V.; Windisch, M.; Sinnema, G.; de Castro, P.M.S.T. Fatigue and fracture behaviour of friction stir welded aluminium–lithium 2195. Theor. Appl. Fract. Mech. 2012, 60, 1–9. [Google Scholar] [CrossRef]
- Akhtar, N.; Jin, H.J.; Jia, F.; Wu, S.J. Fatigue crack growth rates in friction stir welding joints of Al-Li 2060-T8X Alloy. In Proceedings of the 2015 12th International Bhurban Conference on Applied Sciences and Technology, IBCAST 2015, Islamabad, Pakistan, 13–17 January 2015; pp. 6–13. [Google Scholar]
- McDowell, D.L. Simulation-based strategies for microstructure-sensitive fatigue modeling. Mater. Sci. Eng. A 2007, 468–470, 4–14. [Google Scholar] [CrossRef]
- Xue, Y.; McDowell, D.L.; Horstemeyer, M.F.; Dale, M.H.; Jordon, J.B. Microstructure-based multistage fatigue modeling of aluminum alloy 7075-T651. Eng. Fract. Mech. 2007, 74, 2810–2823. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Baird, J.C.; Jordon, J.B.; Gibson, J.B.; Luo, A.A.; Kadiri, H. El Effect of twinning, slip, and inclusions on the fatigue anisotropy of extrusion-textured AZ61 magnesium alloy. Mater. Sci. Eng. A 2011, 528, 6860–6871. [Google Scholar]
- Rettberg, L.H.; Jordon, J.B.; Horstemeyer, M.F.; Jones, J.W. Low-Cycle Fatigue Behavior of Die-Cast Mg Alloys AZ91 and AM60. Metall. Mater. Trans. A 2012, 43, 2260–2274. [Google Scholar] [CrossRef]
- Allison, P.G.; Hammi, Y.; Jordon, J.B.; Horstemeyer, M.F. Modelling and experimental study of fatigue of powder metal steel (FC-0205). Powder Metall. 2013, 56, 388–396. [Google Scholar] [CrossRef]
- Jordon, J.B.; Horstemeyer, M.F.; Yang, N.; Major, J.F.; Gall, K.A.; Fan, J.; McDowell, D.L. Microstructural Inclusion Influence on Fatigue of a Cast A356 Aluminum Alloy. Metall. Mater. Trans. A 2009, 41, 356–363. [Google Scholar] [CrossRef]
- Rodriguez, R.I.; Jordon, J.B.; Allison, P.G.; Rushing, T.; Garcia, L. Low-cycle fatigue of dissimilar friction stir welded aluminum alloys. Mater. Sci. Eng. A 2016, 654, 236–248. [Google Scholar] [CrossRef]
- McCullough, R.R.; Jordon, J.B.; Brammer, A.T.; Manigandan, K.; Srivatsan, T.S.; Allison, P.G.; Rushing, T.W. A Fatigue Model for Discontinuous Particulate-Reinforced Aluminum Alloy Composite: Influence of Microstructure. J. Mater. Eng. Perform. 2013, 23, 65–76. [Google Scholar] [CrossRef]
- Jordon, J.B.; McCullough, R.R.; Garcia, L.; Rushing, T.; Allison, P.G. Fatigue crack nucleation and small crack growth in an extruded 6061 aluminum alloy. Int. J. Fatigue 2018, 119, 52–61. [Google Scholar]
- Rodriguez, R.I.; Jordon, J.B.; Allison, P.G.; Rushing, T.W.; Garcia, L. Corrosion effects on fatigue behavior of dissimilar friction stir welding of high-strength aluminum alloys. Mater. Sci. Eng. A 2019, 742, 255–268. [Google Scholar] [CrossRef]
- Armel, F.; Goma, T.; Larouche, D.; Bois-brochu, A.; Blais, C.; Boselli, J. Effect of extrusion aspect ratio and test temperatures on fatigue crack growth behavior of a 2099-T83 Al – Li alloy. Int. J. Fatigue 2014, 59, 244–253. [Google Scholar]
- Ma, Y.; Zhou, X.; Thompson, G.E.; Hashimoto, T.; Thomson, P.; Fowles, M. Distribution of intermetallics in an AA 2099-T8 aluminium alloy extrusion. Mater. Chem. Phys. 2011, 126, 46–53. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, Z. Microstructural evolution of 2099 Al Li alloy during friction stir welding process. Mater. Charact. 2017, 123, 307–314. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, Z.; Li, S.; Kong, X.; Han, Y. Microstructures and properties of 2099 Al-Li alloy. Mater. Charact. 2013, 84, 88–99. [Google Scholar] [CrossRef]
- McDowell, D.L.; Gall, K.; Horstemeyer, M.F.; Fan, J. Microstructure-based fatigue modeling of cast A356-T6 alloy. Eng. Fract. Mech. 2003, 70, 49–80. [Google Scholar] [CrossRef]
- Chen, D.L.; Chaturvedi, M.C. Near-threshold fatigue crack growth behavior of 2195 aluminum-lithium-alloy-prediction of crack propagation direction and influence of stress ratio. Metall. Mater. Trans. A 2000, 31, 1531–1541. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.B.; Wang, Z.G.; Zhang, Y.; Hu, Q.Z. Fatigue and fracture behavior of an aluminum-lithium alloy 8090-T6 at ambient and cryogenic temperature. Metall. Trans. A 2007, 22, 723–729. [Google Scholar]
- Wu, X.J.; Wallace, W.; Raizenne, M.D.; Koul, A.K. The orientation dependence of fatigue-crack growth in 8090 Al-Li plate. Metall. Mater. Trans. A 1994, 25, 575–588. [Google Scholar] [CrossRef]
- Zhong, J.; Zhong, S.; Zheng, Z.Q.; Zhang, H.F.; Luo, X.F. Fatigue crack initiation and early propagation behavior of 2A97 Al-Li alloy. Trans. Nonferrous Met. Soc. China (English Ed.) 2014, 24, 303–309. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, J.Z.; Huang, X.; Zhang, J.Z.; Yue, G.Q. Fatigue crack growth and delamination behaviours of advanced Al-Li alloy laminate under single tensile overload. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 47–56. [Google Scholar] [CrossRef]
- Kalyanam, S.; Beaudoin, A.J.; Dodds, R.H.; Barlat, F. Delamination cracking in advanced aluminum—lithium alloys—Experimental and computational studies. Eng. Fract. Mech. 2009, 76, 2174–2191. [Google Scholar] [CrossRef]










| Chemical Composition Limits of Wrought AA2099 (Weight %) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Elements | Cu | Li | Zn | Mg | Mn | Zr | Ti | Fe | Si | Al |
| Min | 2.40 | 1.60 | 0.40 | 0.10 | 0.10 | 0.05 | - | - | - | Remainder |
| Max | 3.00 | 2.00 | 1.00 | 0.50 | 0.50 | 0.12 | 0.10 | 0.07 | 0.05 | Remainder |
| Low Cycle Fatigue Parameters | Al–Li Alloy 2099 (BM) | Weld I (400 rpm 100 mm/min) | Weld II (700 rpm 500 mm/min) |
|---|---|---|---|
| Cyclic strain-hardening exponent n′ | 0.0601 | 0.123 | 0.147 |
| Cyclic strength coefficient K′, MPa | 664 | 666.4 | 798.5 |
| Fatigue strength coefficient , MPa | 1009 | 515 | 559 |
| Fatigue strength exponent b | −0.126 | −0.084 | −0.089 |
| Fatigue ductility coefficient | 0.648 | 0.1231 | 0.0884 |
| Fatigue ductility exponent c | −0.899 | −0.684 | −0.604 |
| Coefficients | AA 2099 Base Metal | Weld I: 400 rpm and 100 mm/min | Weld II: 700 rpm and 500 mm/min |
|---|---|---|---|
| Ultimate Strength (MPa) | 558 | 342 | 390 |
| Yield Strength (MPa) | 510 | 245 | 284 |
| Grain Size (µm) | 1000 | 20 | 35 |
| Hardness (HV) | 155 | 83 | 98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cisko, A.R.; Jordon, J.B.; Avery, D.Z.; Liu, T.; Brewer, L.N.; Allison, P.G.; Carino, R.L.; Hammi, Y.; Rushing, T.W.; Garcia, L. Experiments and Modeling of Fatigue Behavior of Friction Stir Welded Aluminum Lithium Alloy. Metals 2019, 9, 293. https://doi.org/10.3390/met9030293
Cisko AR, Jordon JB, Avery DZ, Liu T, Brewer LN, Allison PG, Carino RL, Hammi Y, Rushing TW, Garcia L. Experiments and Modeling of Fatigue Behavior of Friction Stir Welded Aluminum Lithium Alloy. Metals. 2019; 9(3):293. https://doi.org/10.3390/met9030293
Chicago/Turabian StyleCisko, Abby R., James B. Jordon, Dustin Z. Avery, Tian Liu, Luke N. Brewer, Paul G. Allison, Ricolindo L. Carino, Youssef Hammi, Timothy W. Rushing, and Lyan Garcia. 2019. "Experiments and Modeling of Fatigue Behavior of Friction Stir Welded Aluminum Lithium Alloy" Metals 9, no. 3: 293. https://doi.org/10.3390/met9030293
APA StyleCisko, A. R., Jordon, J. B., Avery, D. Z., Liu, T., Brewer, L. N., Allison, P. G., Carino, R. L., Hammi, Y., Rushing, T. W., & Garcia, L. (2019). Experiments and Modeling of Fatigue Behavior of Friction Stir Welded Aluminum Lithium Alloy. Metals, 9(3), 293. https://doi.org/10.3390/met9030293







