Avrami Kinetic-Based Constitutive Relationship for Armco-Type Pure Iron in Hot Deformation
Abstract
:1. Introduction
2. Materials and Experimental Details
3. Analysis Methods
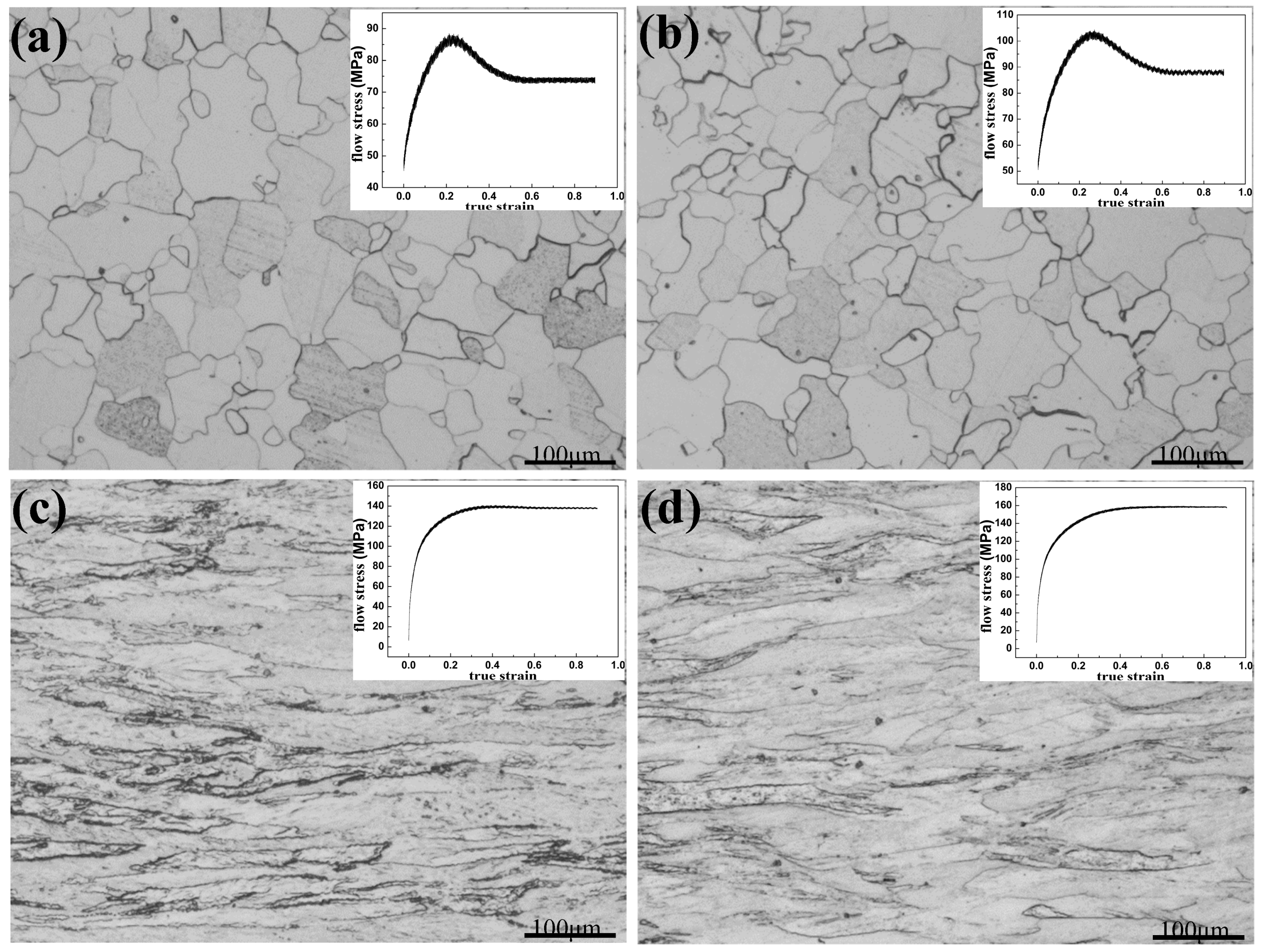
4. Flow Behavior and Microstructure Evolvement
5. Constitutive Relationship in Hot Deformation
5.1. Constitutive Relationship of Part I
5.1.1. Constitutive Models Only Relating to DRV Process
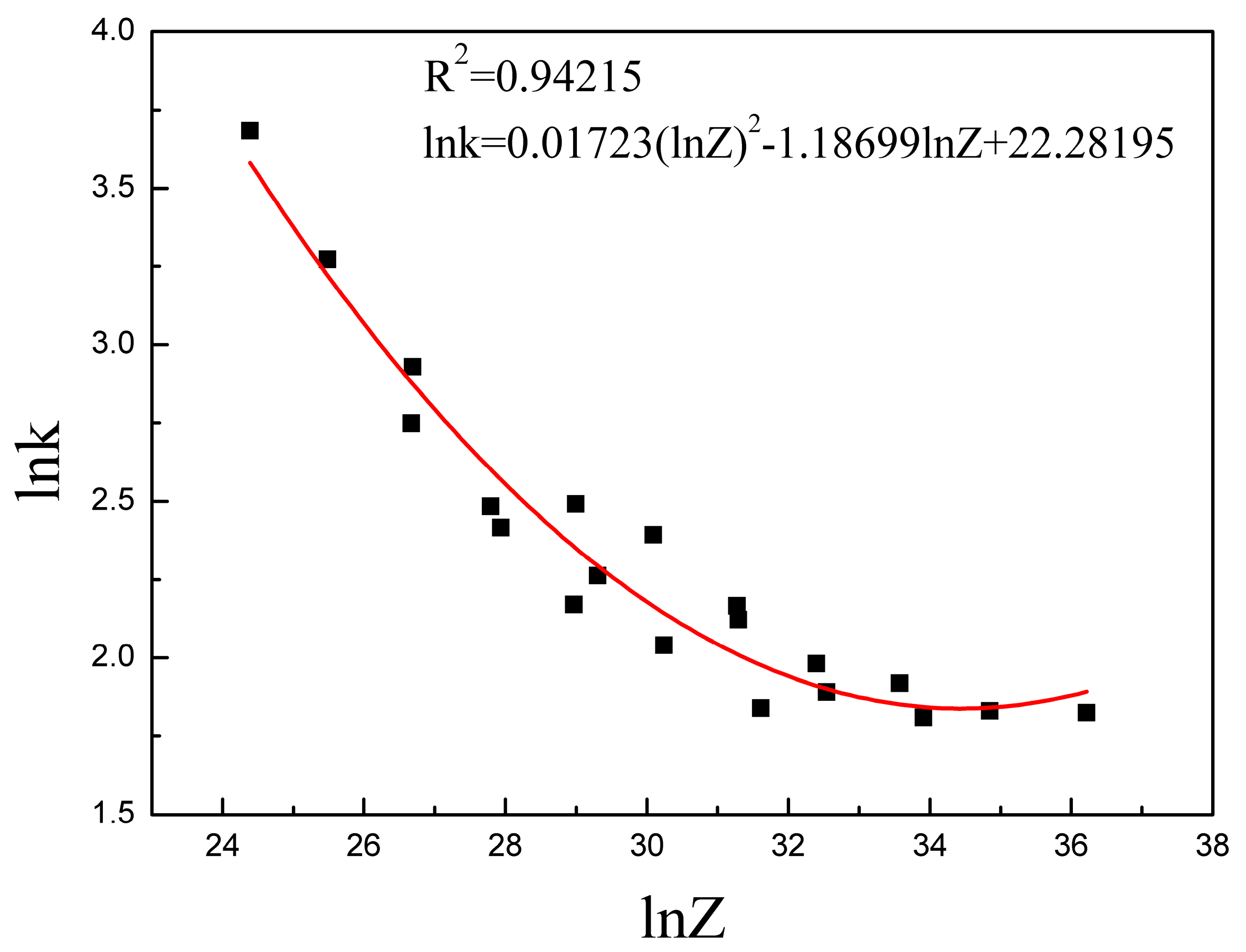
5.1.2. Determination of Constant
5.2. Constitutive Relationship of Part II
5.2.1. Avrami Kinetic Equation for DRX
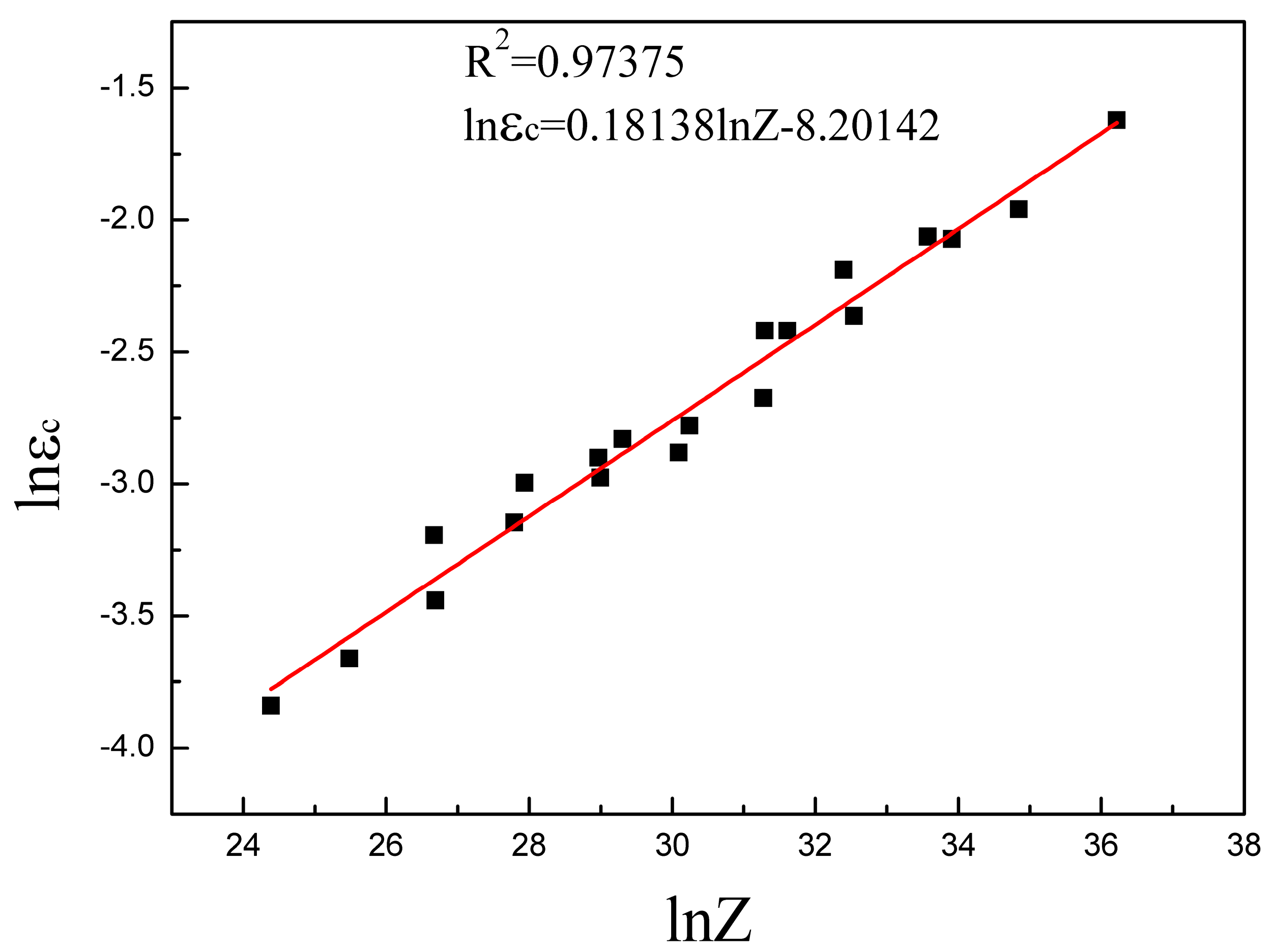
5.2.2. Determination of Critical Strain
5.2.3. Description of Fractional Softening
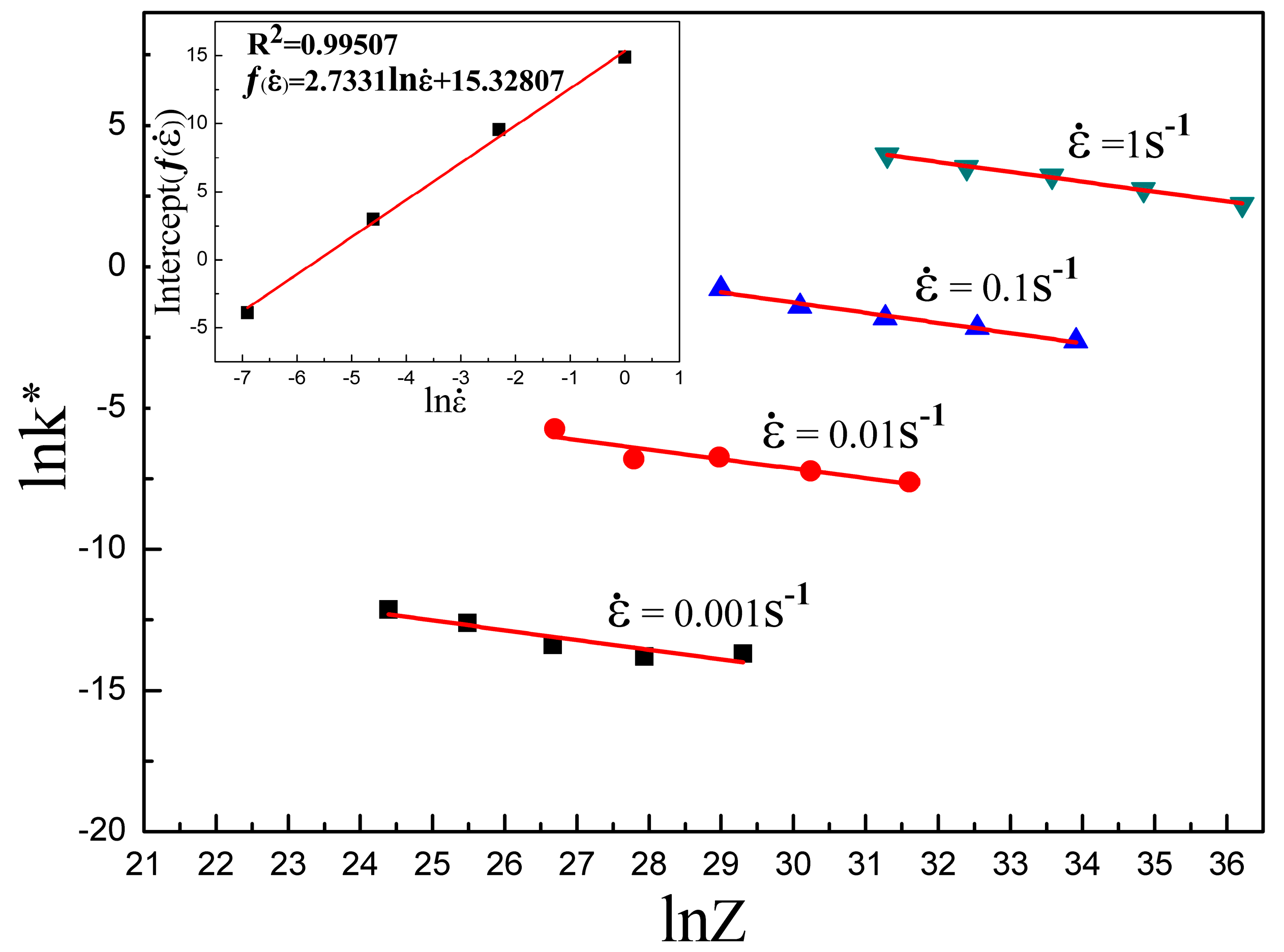
5.2.4. Determination of Avrami Constant and Time Exponent
5.2.5. Constitutive Models Relating to the DRX and DRV Processes
5.3. Constitutive Relationship of Part III
5.3.1. Constitutive Model of Part III
5.3.2. Determination of Constants , and
5.4. Integrated Constitutive Relationship for Hole Part
5.4.1. Determination of Yield Stress and Saturation Stress
5.4.2. Avrami Kinetic-Based Constitutive Model of Whole Part
6. Conclusions
- (1)
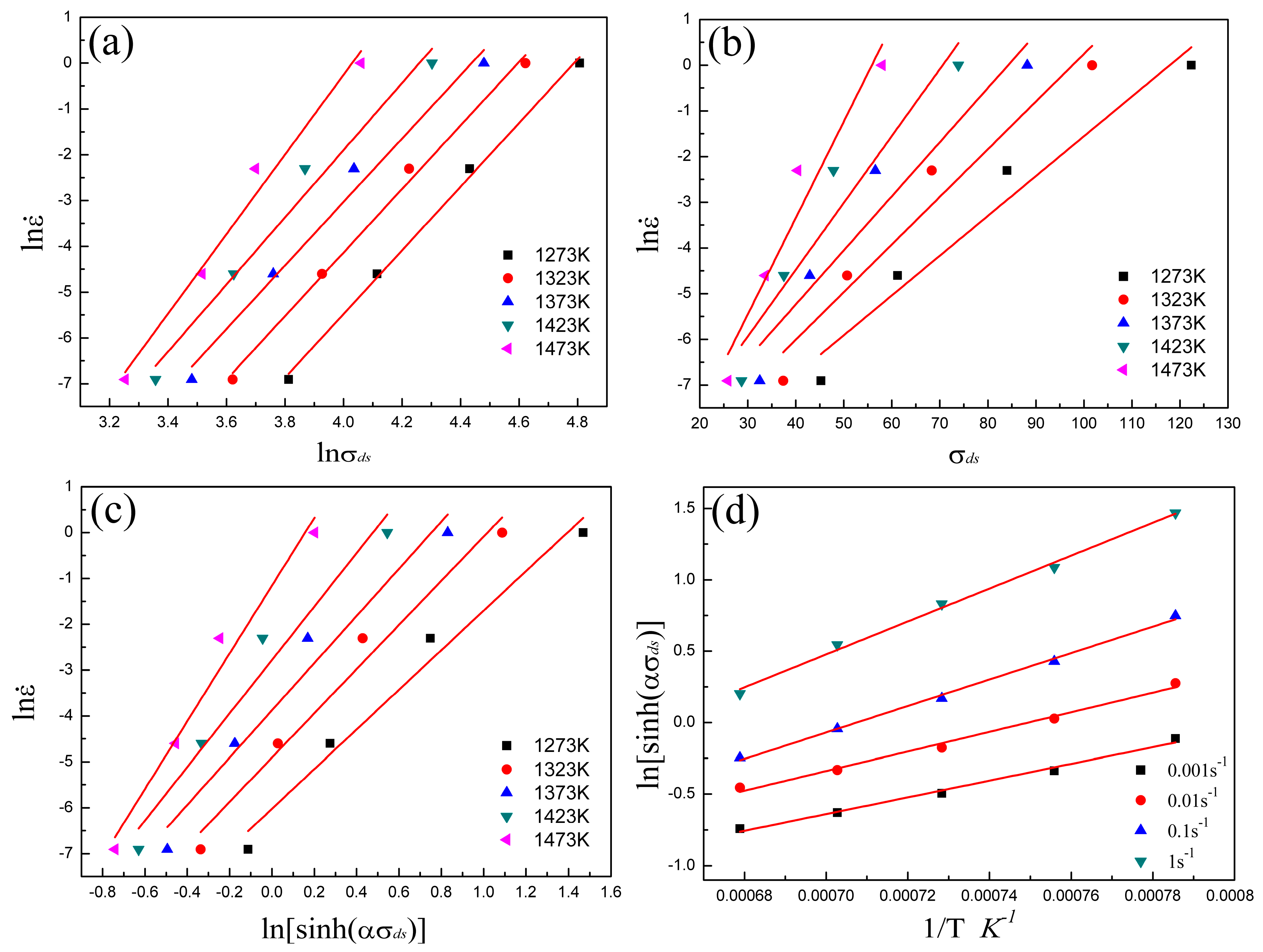
- Based on the KM model, the strain-hardening process relating only to DRV can be described by the equation: . is determined by the part of the true stress-strain curve before the initiation of DRX. As for Armco-type pure iron, and show combined effects on , and in the form of the Z parameter with expressions as: , and , respectively.
- (2)
- Considering the strain-hardening process, the model used to describe the fractional softening for alloys under DRX is modified as: . The volume fraction of DRX increases as long as the temperature increases and the strain rate decreases. The critical points for the onset of DRX are determined as the inflection point in the vs. curve. As for Armco-type pure iron, the relation between and the Z parameter is expressed as: .
- (3)
- The Avrami kinetic equation is used to describe the kinetic of DRX with the modified expression as: , where and . As for Armco-type pure iron, including an individual effect, the strain rate also presents a combined effect with on in the form of the Z parameter, and the relation is expressed as: . is only the function of with the expression: .
- (4)
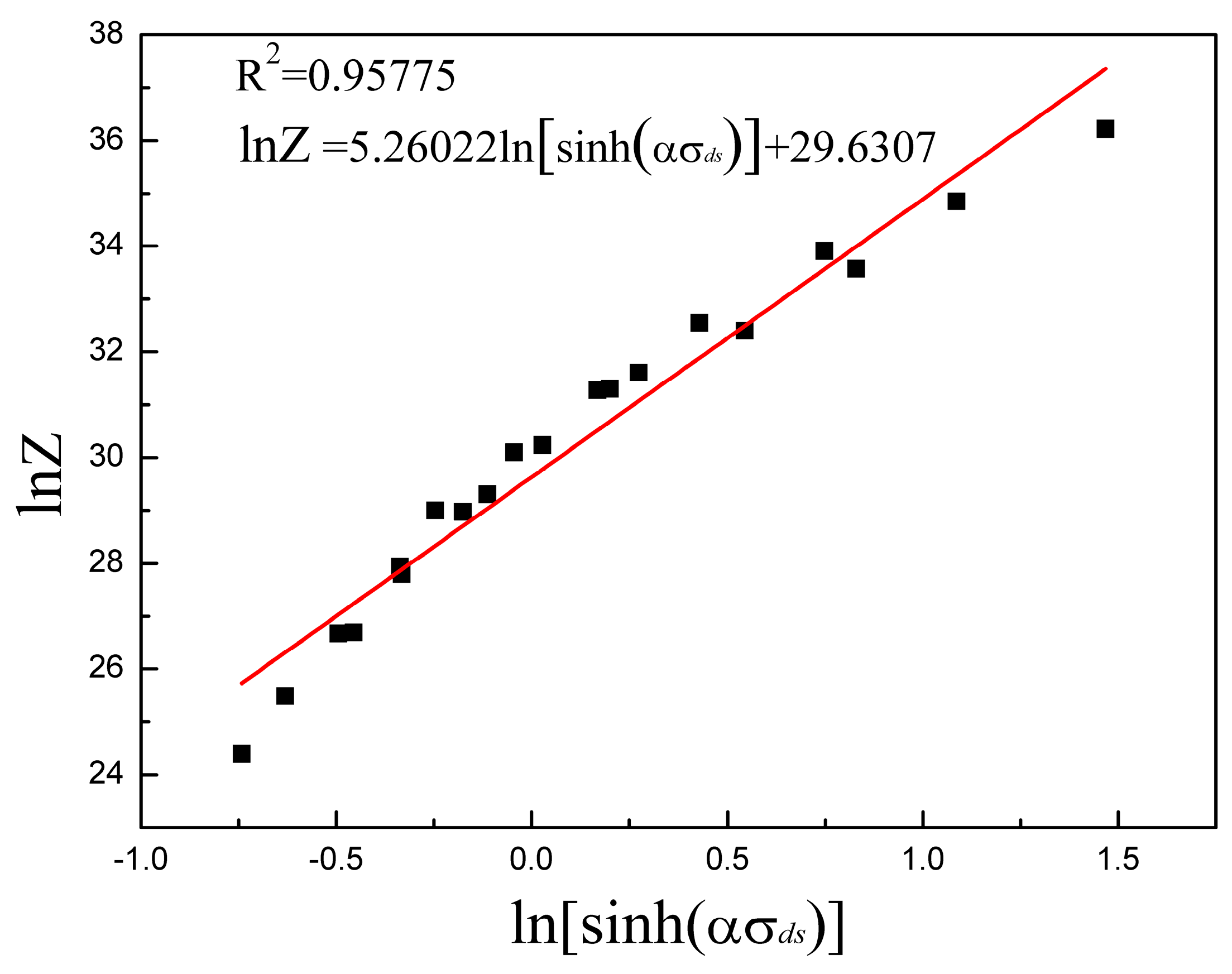
- Arrhenius-type equations are suitable for describing the flow behavior of the steady state. Regressing from the equations, the DRX activation energy for Armco-type pure iron is 383094 J mol−1, and the expressions for the parameter and are determined as Equations (35) and (36), respectively.
- (5)
- Based on strain hardening, fractional softening models and the modified Avrami kinetic equation, the constitutive model for alloys considering the effects of DRV and DRX is constructed as Equation (39). The constitutive model can be well used to describe the flow behavior of Armco-type pure iron. The DRV and DRX characters are clearly presented in these curves determined by this model.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| strain rate (s−1) | |
| temperature (K) | |
| activation energy (J mol−1) | |
| universal gas constant (8.31 J mol−1K−1) | |
| Zener–Hollomon parameter | |
| strain | |
| yield strain | |
| strain at maximum softening rate | |
| , | critical strain and critical stress (MPa) |
| , | peak strain and peak stress (MPa) |
| , | flow stress (MPa) and steady value of it |
| , | recovery stress (MPa) and saturation value of it |
| average dislocation density corresponding to whole deforming process | |
| dislocation density corresponding to only DRV process | |
| dislocation density at yield point | |
| dislocation density at the steady state of flow stress | |
| dislocation density at the saturation state of recovery stress | |
| shear modulus | |
| burgers vector | |
| recrystallized volume fraction | |
| Avrami constant | |
| time (s) | |
| characteristic time | |
| time exponent | |
| grain size | |
| , , , , , , , , , , , , | constants |
References
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- He, Z.B.; Wang, Z.B.; Lin, Y.L.; Fan, X.B. Hot Deformation behavior of a 2024 aluminum alloy sheet and its modeling by Fields-Backofen model considering strain rate evolution. Metals 2019, 9, 243. [Google Scholar] [CrossRef]
- Salinas, A.; Celentano, D.; Carvajal, L.; Artigas, A.; Monsalve, A. Microstructure-Based Constitutive Modelling of Low-Alloy Multiphase TRIP Steels. Metals 2019, 9, 250. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Ulacia, I.; Salisbury, C.P.; Hurtado, I.; Worswick, M.J. Tensile characterization and constitutive modeling of AZ31B magnesium alloy sheet over wide range of strain rates and temperatures. J. Mater. Process. Technol. 2011, 211, 830–839. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Lanc, Y.J.; Wynne, B.P.; Davis, B.; Rainforth, W.M. Constitutive equations of flow stress of magnesium AZ31 under dynamically recrystallizing conditions. J. Mater.Process. Technol. 2014, 214, 1408–1417. [Google Scholar] [CrossRef]
- Gambirasio, L.; Rizzi, E. On the calibration strategies of the Johnson–Cook strength model: Discussion and applications to experimental data. Mater. Sci. Eng. A 2014, 610, 370–413. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef] [Green Version]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Choudhary, B.K.; Christopher, J. Comparative tensile flow and work-hardening behavior of 9 Pct chromium ferritic-martensitic steels in the framework of the Estrin-Mecking internal-variable approach. Metall. Mater. Trans. A 2016, 47, 2642–2655. [Google Scholar] [CrossRef]
- Haghdadi, N.; Martin, D.; Hodgson, P. Physically-based constitutive modeling of hot deformation behavior in a LDX 2101 duplex stainless steel. Mater. Des. 2016, 106, 420–427. [Google Scholar] [CrossRef]
- Chalimba, S.A.; Mostert, R.; Stumpf, W.; Siyasiya, C.; Banks, K. Modeling of work hardening during hot rolling of vanadium and niobium microalloyed steels in the low temperature austenite region. J. Mater. Eng. Perform. 2017, 26, 5217–5227. [Google Scholar] [CrossRef]
- Sellars, C.M.; Tegart, W.M. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Li, J.D.; Liu, J.S. Strain Compensation Constitutive Model and Parameter Optimization for Nb-Contained 316LN. Metals 2019, 9, 212. [Google Scholar] [CrossRef]
- Tabei, A.; Abed, F.H.; Voyiadjis, G.Z.; Garmestani, H. Constitutive modeling of Ti-6Al-4V at a wide range of temperatures and strain rates. Eur. J. Mech.-A/Solids 2017, 63, 128–135. [Google Scholar] [CrossRef]
- Zhang, C.S.; Ding, J.; Dong, Y.Y.; Zhao, G.Q.; Gao, A.J.; Wang, L.J. Identification of friction coefficients and strain-compensated Arrhenius-type constitutive model by a two-stage inverse analysis technique. Int. J. Mech. Sci. 2015, 98, 195–204. [Google Scholar] [CrossRef]
- Kugler, G.; Turk, R. Modeling the dynamic recrystallization under multi-stage hot deformation. Acta Mater. 2004, 52, 4659–4668. [Google Scholar] [CrossRef]
- Martin, E.; Jonas, J.J. Evolution of microstructure and microtexture during the hot deformation of Mg–3% Al. Acta Mater. 2010, 58, 4253–4266. [Google Scholar] [CrossRef]
- Tian, B.; Lind, C.; Schafler, E.; Paris, O. Evolution of microstructures during dynamic recrystallization and dynamic recovery in hot deformed Nimonic 80a. Mater. Sci. Eng. A 2004, 367, 198–204. [Google Scholar] [CrossRef]
- Beladi, H.; Cizek, P.; Hodgson, P.D. On the characteristics of substructure development through dynamic recrystallization. Acta Mater. 2010, 58, 3531–3541. [Google Scholar] [CrossRef]
- Graetz, K.; Miessen, C.; Gottstein, G. Analysis of steady-state dynamic recrystallization. Acta Mater. 2014, 67, 58–66. [Google Scholar] [CrossRef]
- Haghdadi, N.; Cizek, P.; Beladi, H.; Hodgson, P.D. The austenite microstructure evolution in a duplex stainless steel subjected to hot deformation. Philos. Mag. 2017, 97, 1209–1237. [Google Scholar] [CrossRef]
- Babu, K.A.; Mandal, S.; Athreya, C.N.; Shakthipriya, B.; Sarma, V.S. Hot deformation characteristics and processing map of a phosphorous modified super austenitic stainless steel. Mater. Des. 2017, 115, 262–275. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I. General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, E. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Kim, S.I.; Yoo, Y.C. Dynamic recrystallization behavior of AISI 304 stainless steel. Mater. Sci. Eng. A 2001, 311, 108–113. [Google Scholar] [CrossRef]
- Quan, G.Z.; Wu, D.S.; Luo, G.C.; Xia, Y.F.; Zhou, J.; Liu, Q.; Gao, L. Dynamic recrystallization kinetics in α phase of as-cast Ti–6Al–2Zr–1Mo–1V alloy during compression at different temperatures and strain rates. Mater. Sci. Eng. A 2014, 589, 23–33. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Serajzadeh, S.; Taheri, A.K. An investigation on the effect of carbon and silicon on flow behavior of steel. Mater. Des. 2002, 23, 271–276. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, Y.C.; Li, J.P.; He, F.; Xia, F.; Liang, M.X. Plastic deformation and dynamic recrystallization behaviors of Mg–5Gd–4Y–0.5Zn–0.5Zr alloy. Mater. Sci. Eng. A 2008, 485, 487–491. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Lin, Y.C.; Xia, Y.C.; Chen, X.M.; Chen, M.S. Constitutive descriptions for hot compressed 2124-T851 aluminum alloy over a wide range of temperature and strain rate. Comput. Mater. Sci. 2010, 50, 227–233. [Google Scholar] [CrossRef]










| C | Si | Mn | P | S |
|---|---|---|---|---|
| 0.0019 | 0.0294 | 0.1298 | 0.0056 | 0.0038 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Fan, Q.; Zhang, X.; Zhou, Z.; Xia, Z.; Qian, Z. Avrami Kinetic-Based Constitutive Relationship for Armco-Type Pure Iron in Hot Deformation. Metals 2019, 9, 365. https://doi.org/10.3390/met9030365
Zhang Y, Fan Q, Zhang X, Zhou Z, Xia Z, Qian Z. Avrami Kinetic-Based Constitutive Relationship for Armco-Type Pure Iron in Hot Deformation. Metals. 2019; 9(3):365. https://doi.org/10.3390/met9030365
Chicago/Turabian StyleZhang, Yan, Qichao Fan, Xiaofeng Zhang, Zhaohui Zhou, Zhihui Xia, and Zhiqiang Qian. 2019. "Avrami Kinetic-Based Constitutive Relationship for Armco-Type Pure Iron in Hot Deformation" Metals 9, no. 3: 365. https://doi.org/10.3390/met9030365




