Study on the Influence and Optimization Design of Viscous Damper Parameters on the Damping Efficiency of Frame Shear Wall Structure
Abstract
:1. Introduction
2. Methodology
2.1. Optimization Method for Damper Parameters Based on Response Surface Method
2.1.1. Establishment of Response Surface Model
2.1.2. Solution of Extremum for Multivariate Function
- Assume the bi-variate function is . Calculate the first-order partial derivatives and set them equal to zero to find the stationary point p0, as shown in Equation (6).
- Calculate the second-order partial derivatives of p0 and obtain the coefficients A, B, and C, as shown in Equation (7).
- Determine the extremum situation obtained, as shown in Equation (8).
2.2. Engineering Case on the Optimization of Damper Parameters in Frame Shear wall Structure
2.2.1. Engineering Overview
- Determine the target additional damping ratio added to the structure by the viscous dampers. In this study, a value of 3.0% is considered.
- The formula for calculating the additional damping ratio through the energy method is used to deduce the total damping coefficient and the selected damping exponent required for the structure under the target additional damping ratio. The detailed procedure of this derivation can be referred to in reference [41].
- Divide the total damping coefficient by the damping coefficient of a single damper to obtain the number of dampers. The damping coefficient and exponent of a single damper are generally selected based on engineering experience. In this study, the damping coefficient is taken as C = 60 kN/(mm/s)0.25, and the damping exponent α is 0.25.
- Determine the number and placement of dampers in each floor. The dampers are typically arranged in a simplified manner with uniform distribution in height, and the placement is the same so as not to affect the functionality of the building. Therefore, in this study, the number and placement of viscous dampers are the same for the 1st to 5th floors. Four sets of dampers are arranged in the X and Y directions on each floor, resulting in a total of 40 sets of dampers. The arrangement diagram of dampers is shown in Figure 1a.
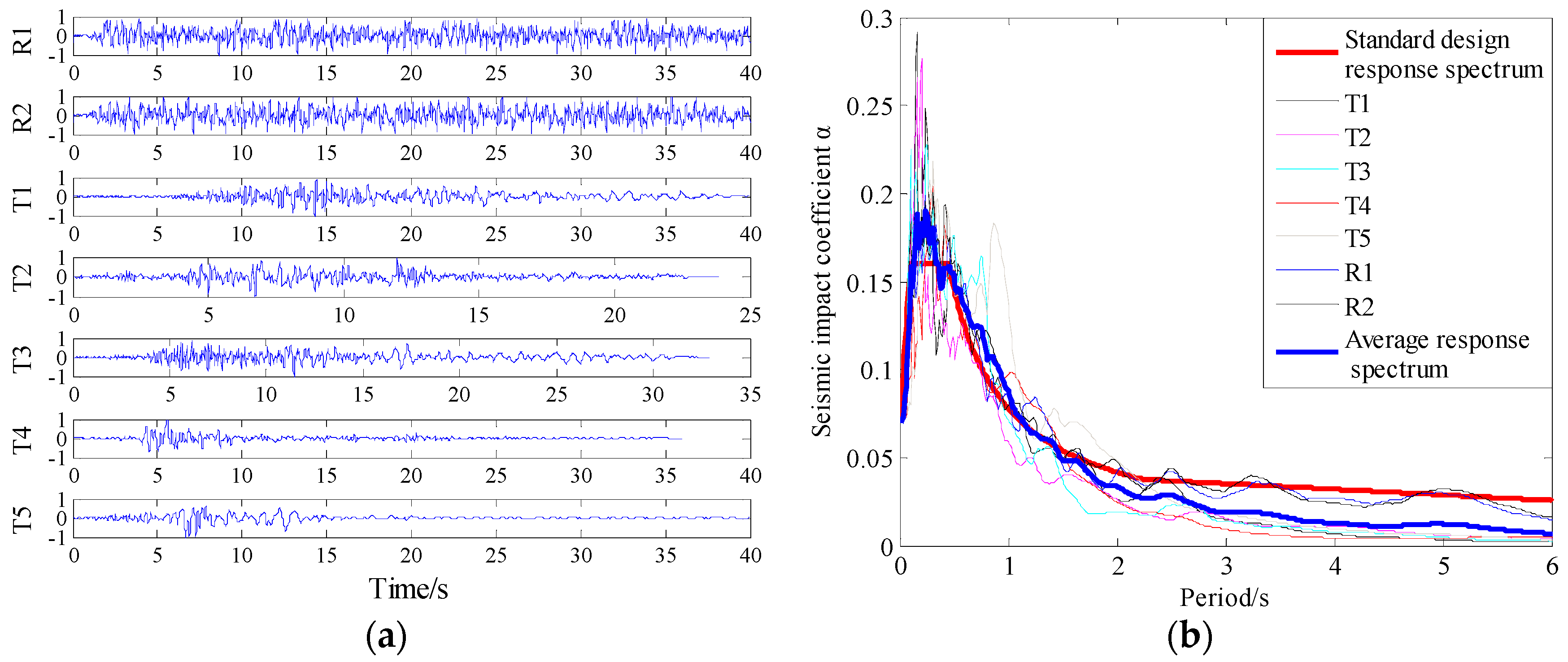
2.2.2. Finite Element Model Establishment and Earthquake Waves Selection
3. Results and Discussion
3.1. Sensitivity Analysis of the Impact of Damping Parameters
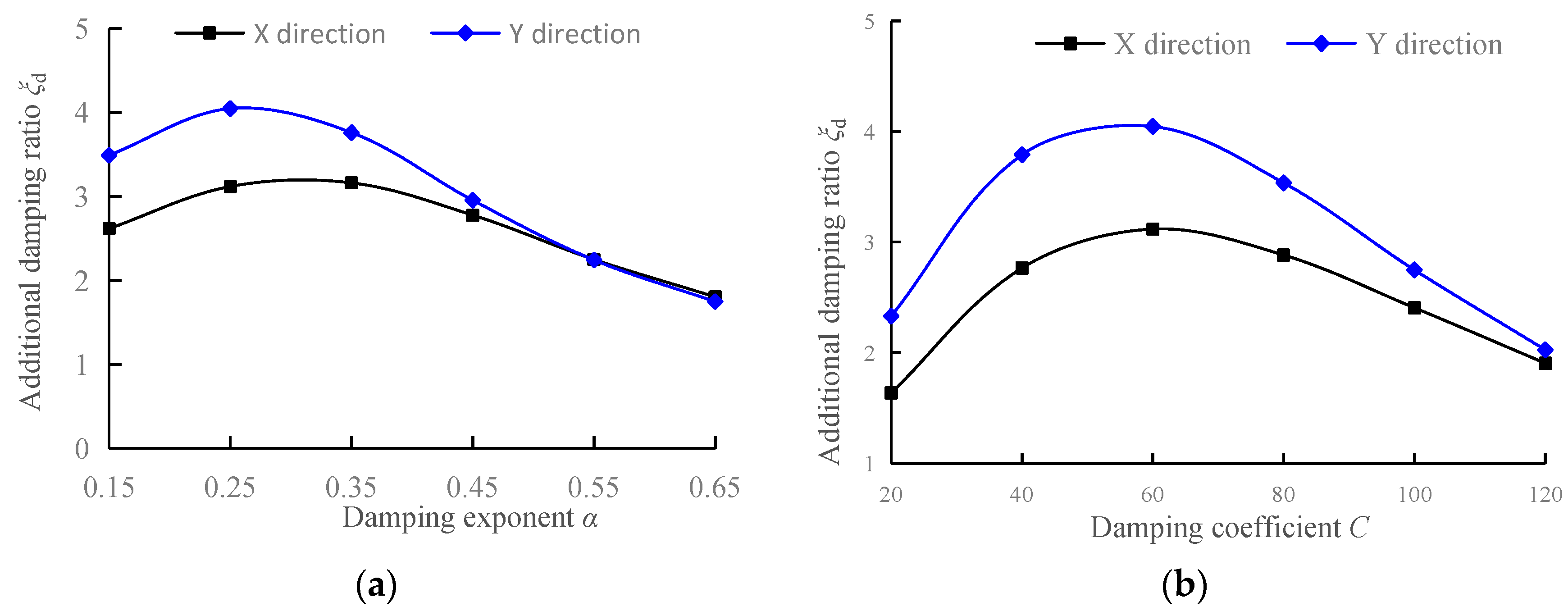
3.1.1. The Additional Damping Ratio
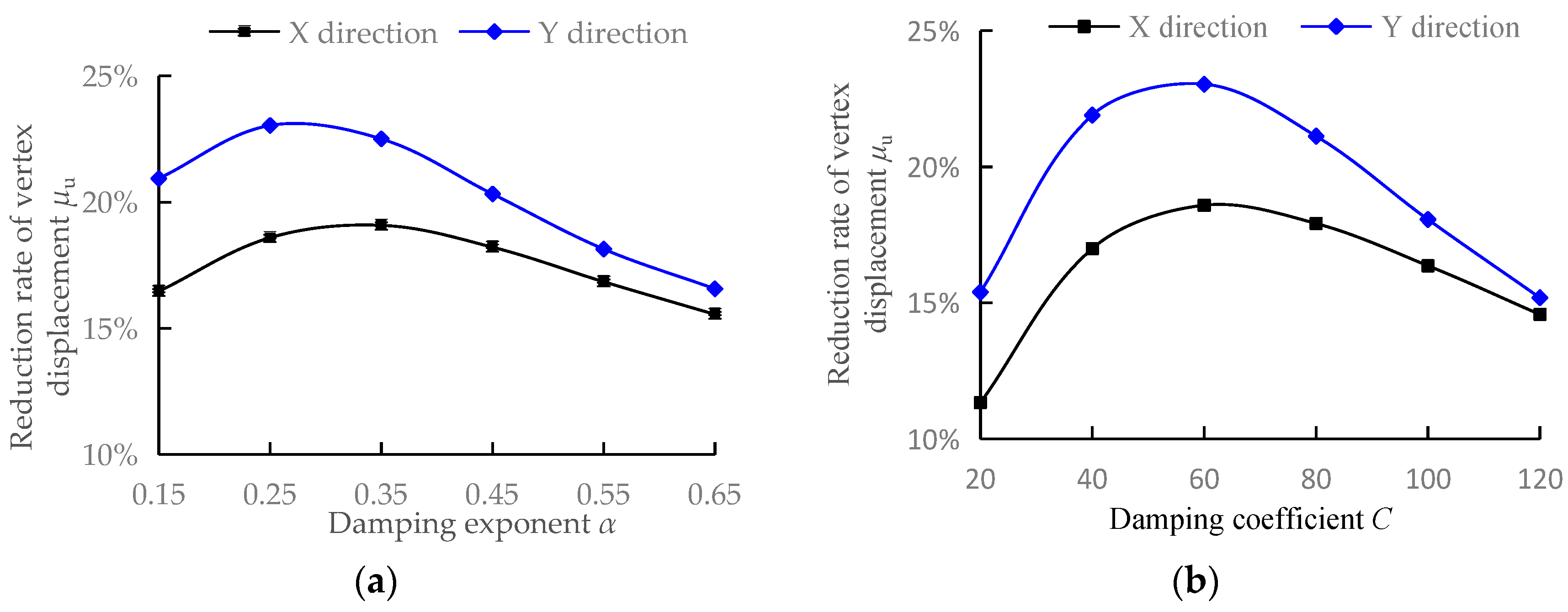
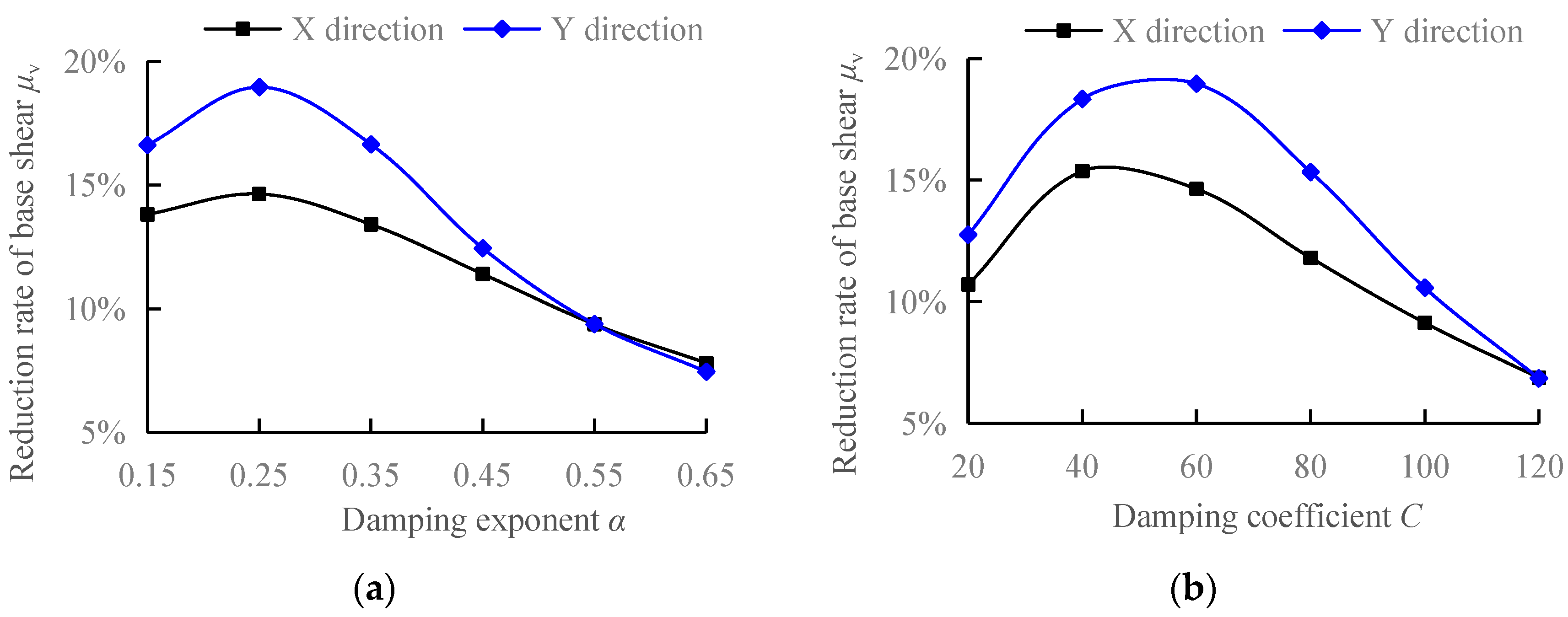
3.1.2. The Reduction Rate of Vertex Displacement
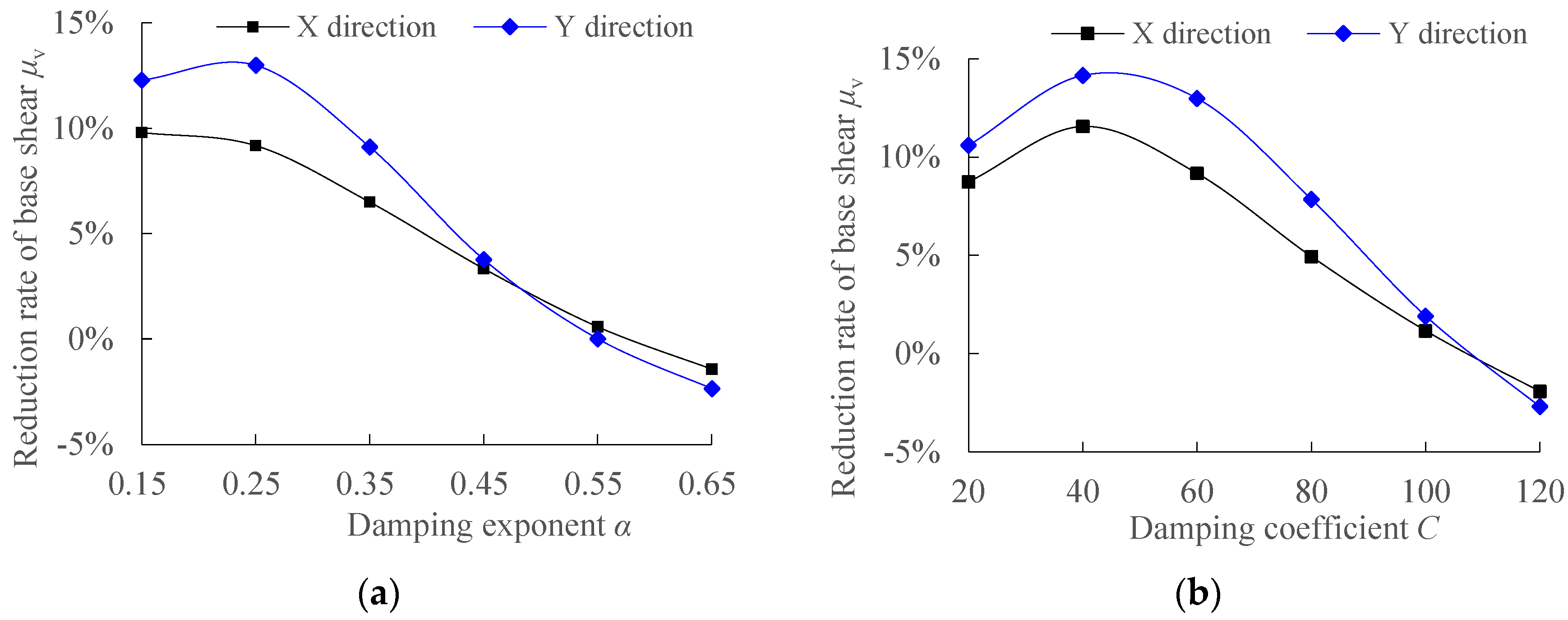
3.1.3. The Reduction Rate of Base Shear
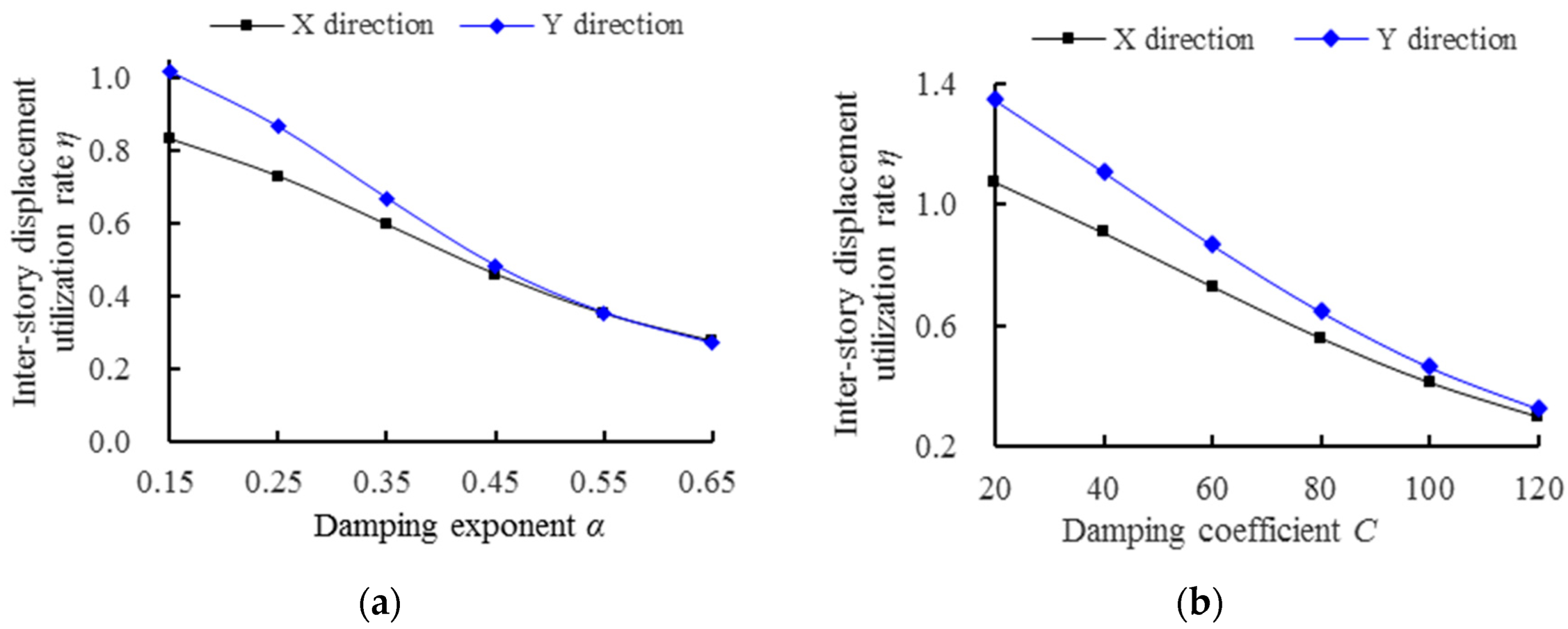
3.1.4. The Inter-Story Displacement Utilization Rate
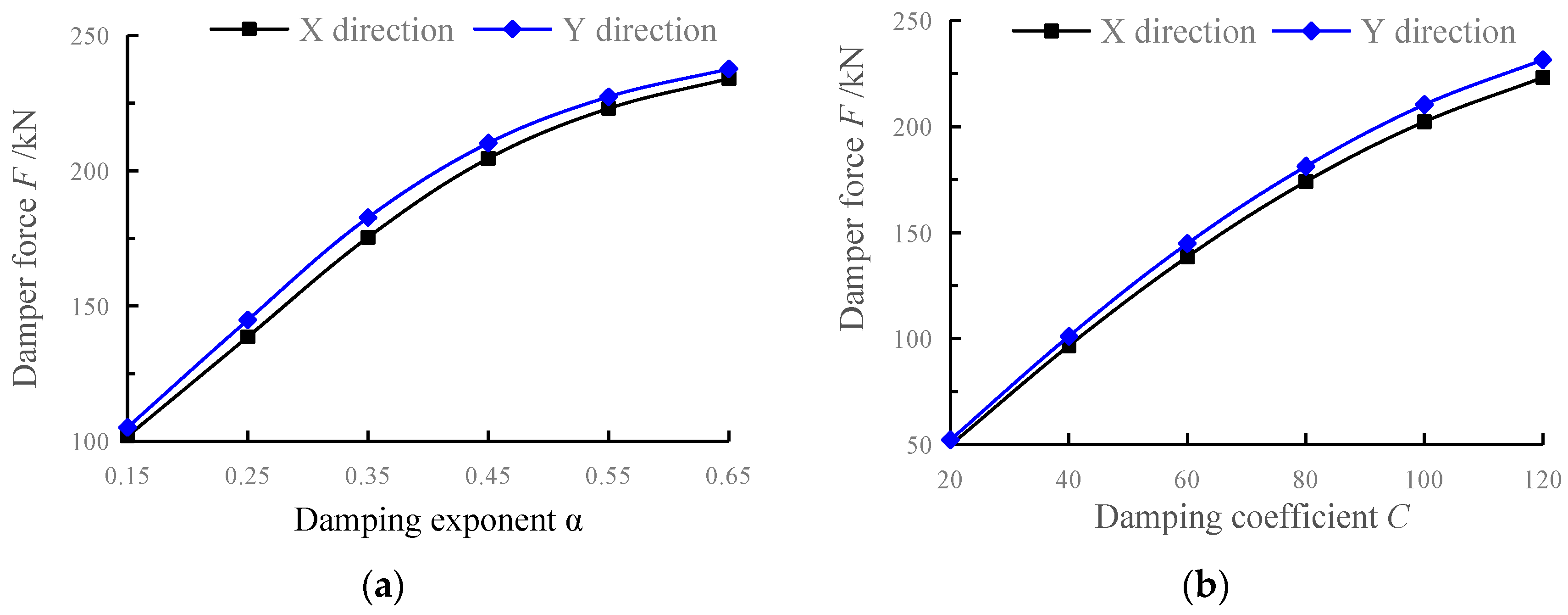
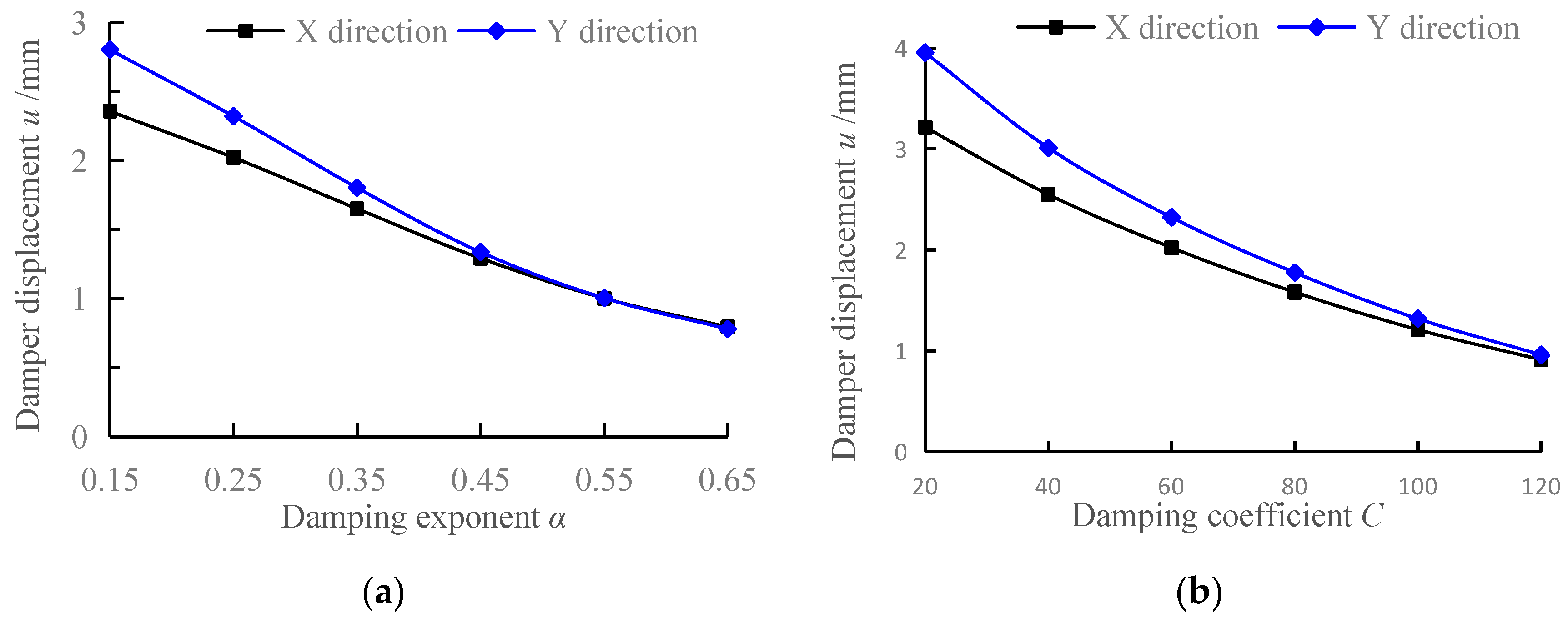
3.1.5. Damping Force and Displacement
3.2. Optimization of Parameters for Viscous Dampers and Flowchart for Damping Design
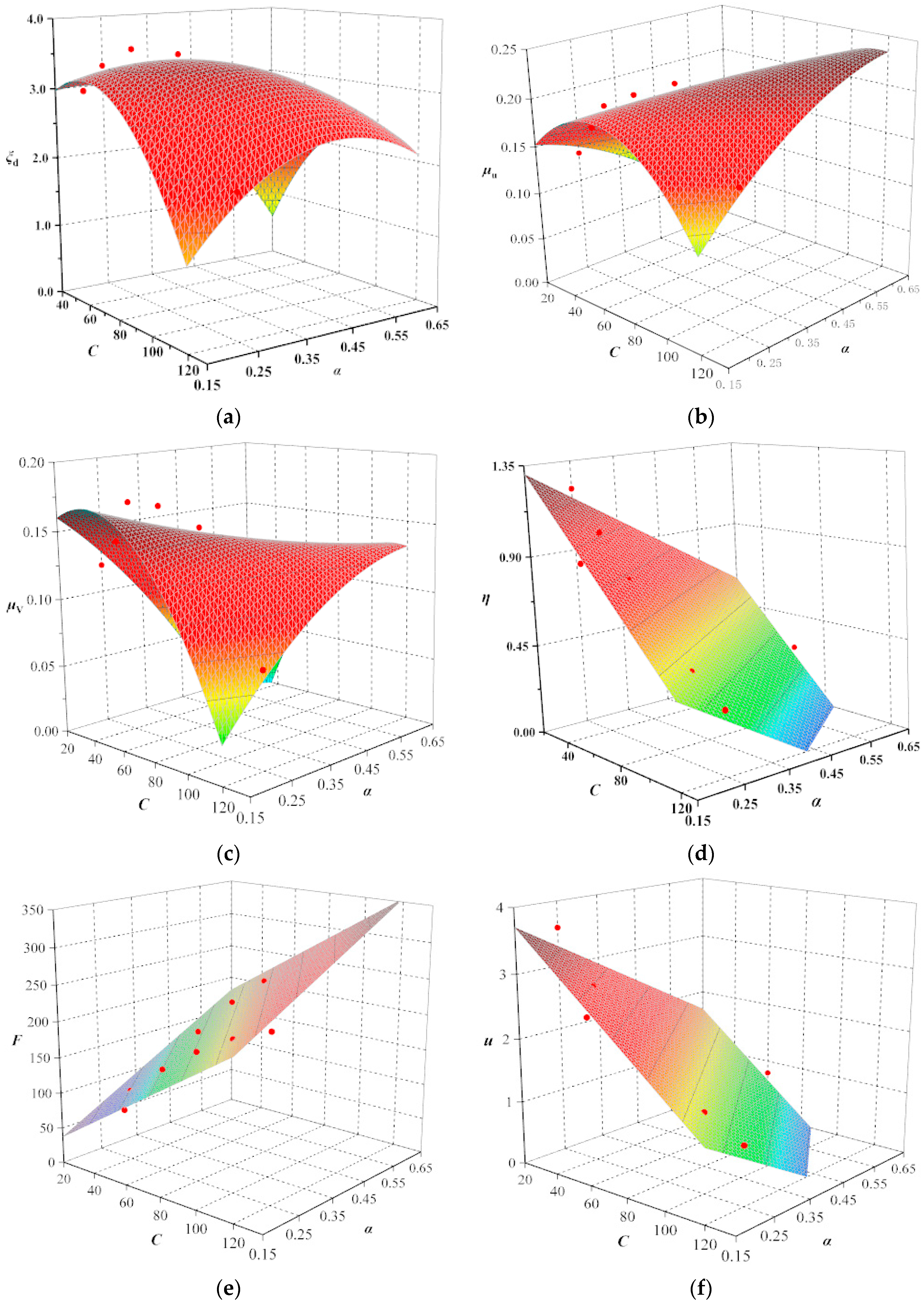
3.2.1. Response Surface Model
3.2.2. Objective Function
3.2.3. Analysis of Optimized Results
3.2.4. The Damping Design Flowchart
4. Conclusions
- (1)
- The parameters within the range of damping coefficient 20~120 kN/(mm/s)α and damping exponent 0.15~0.65 are combined, and the traditional sensitivity analysis method is used to calculate various damping efficiency indicators. When the damping coefficient and damping exponent are approximately (60, 0.25), the additional damping ratio, reduction rate of vertex displacement, and reduction rate of base shear achieve relatively large values of 4.05%, 23%, and 19%, respectively. As the damping coefficient and damping exponent increase, the inter-story displacement utilization rate decreases from significantly greater than 1.0 to far less than 1.0, and the displacement of the damper decreases while the damping force increases. The study shows that the influence of different combinations of viscous damper parameters on the response of damping efficiency indicators is complex, and it is difficult for the traditional sensitivity analysis method to comprehensively consider the combined effects of different damping efficiency indicators to obtain the optimal parameters.
- (2)
- By explicitly formulating the relationship between viscous damper parameters and various damping efficiency indicators of the structural system using response surface methodology, and combining the F-test and coefficient of determination R2 to evaluate the fitting effect of the response surface function, high fitting accuracy and good predictability are achieved, making our model suitable as an optimization model.
- (3)
- The influence of support component stiffness on the damping efficiency indicators of the structure is significant. After the variation of damper parameters, it is advisable to match the corresponding support component stiffness according to the specifications in order to obtain the true results of various damping efficiency indicators under optimal parameters. After matching the stiffness of the supporting members, the additional damping ratios in the case increased from 2.91% and 3.38% to 4.50% and 5.70%, respectively, representing an approximately 55% increase. Other damping efficiency indicators also showed significant improvement. This pattern is applicable to other frame shear wall structures with additional viscous dampers.
- (4)
- A simple and easy-to-use “damping design flowchart considering the impact of damper parameters on the damping efficiency” is proposed. By following the idea and method presented in this flowchart, designers can complete the damping design of other frame shear wall structures with additional viscous dampers. This flowchart can provide important guidance and reference for future designers in conducting damping design for frame shear wall structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- GB 50011-2016; Chinese Standard, Code for Seismic Design of Buildings. Chinese Architecture and Building Press: Beijing, China, 2016.
- JGJ 297-2013; Chinese Standard, Technical Specification for Seismic Energy Dissipation of Buildings. Chinese Architecture and Building Press: Beijing, China, 2013.
- Titirla, M.D. A state-of-the-art review of passive energy dissipation systems in steel braces. Buildings 2023, 13, 851. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Application of smart dampers for preventing of seismic pounding in isolated structures subjected to near-fault earthquakes. J. Earthq. Eng. 2020, 26, 4069–4084. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Seismic Collapse Probability and Life Cycle Cost Assessment of Isolated Structures Subjected to Pounding with Smart Hybrid Isolation Systems Using a Modified Fuzzy Based Controller. Structures 2022, 44, 30–41. [Google Scholar] [CrossRef]
- Zoccolini, L.; Bruschi, E.; Cattaneo, S.; Quaglini, V. Current trends in fluid viscous dampers with semi-active and adaptive behavior. Appl. Sci. 2023, 13, 10358. [Google Scholar] [CrossRef]
- Lin, W.H.; Chopra, A.K. Earthquake response of elastic SDF systems with nonlinear fluid viscous dampers. Earthq. Eng. Struct. D 2002, 31, 1623–1642. [Google Scholar] [CrossRef]
- Gherbi, A.; Belgasmia, M. A simplified design strategy of nonlinear fluid viscous dampers for MDOF structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 857–864. [Google Scholar] [CrossRef]
- Dargush, G.F.; Sant, R.S. Evolutionary aseismic design and retrofit of structures with passive energy dissipation. Earthq. Eng. Struct. D 2005, 34, 1601–1626. [Google Scholar] [CrossRef]
- Rayegani, A.; Soureshjani, O.K.; Alaee, S.A.M.; Mualla, I.H.; Nemati, F. Seismic performance of buildings equipped with four-joint rotational friction dampers in mainshock-aftershock sequences. J. Struct. Eng. 2024, 150, 12980. [Google Scholar] [CrossRef]
- Ding, J.; Wang, S.; Wu, H. Seismic performance analysis of viscous damping outrigger in super high-rise buildings. Struct. Des. Tall Spec. Build. 2018, 27, e1486. [Google Scholar] [CrossRef]
- Chen, P.; Wu, X. Investigations on the dynamic response of adjacent buildings connected by viscous dampers. Buildings 2022, 12, 1480. [Google Scholar] [CrossRef]
- De Souza Pippi, A.; Avila, S.M.; Doz, G. A review on the use of the inerter device in the structural coupling technique for adjacent building vibration control. Structures 2022, 42, 480–501. [Google Scholar] [CrossRef]
- Tubaldi, E. Dynamic behavior of adjacent buildings connected by linear viscous/viscoelastic dampers. Struct. Control Health Monit. 2015, 22, 1086–1102. [Google Scholar] [CrossRef]
- Palermo, M.; Silvestri, S. Damping reduction factors for adjacent buildings connected by viscous-viscous dampers. Soil. Dyn. Earthq. Eng. 2020, 138, 106323. [Google Scholar] [CrossRef]
- Kazemi, F.; Miari, M.; Jankowski, R. Investigating the effects of structural pounding on the seismic performance of adjacent RC and steel MRFs. Bull. Earthq. Eng. 2021, 19, 317–343. [Google Scholar] [CrossRef]
- Zhai, C.; Jiang, S.; Li, S.; Xie, L. Dimensional analysis of earthquake-induced pounding between adjacent inelastic MDOF buildings. Earthq. Eng. Eng. Vib. 2015, 14, 295–313. [Google Scholar] [CrossRef]
- Xu, W.; Du, D.; Wang, S.; Li, W. A new method to calculate additional damping ratio considering the effect of excitation frequency. Adv. Civ. Eng. 2020, 2020, 3172982. [Google Scholar] [CrossRef]
- Diotallevi, P.P.; Landi, L.; Dellavalle, A. A methodology for the direct assessment of the damping ratio of structures equipped with nonlinear viscous dampers. J. Earthq. Eng. 2012, 16, 350–373. [Google Scholar] [CrossRef]
- Hwang, J.S.; Huang, Y.N.; Yi, S.L.; Song, Y.H. Design formulations for supplemental viscous dampers to building structures. J. Struct. Eng. 2008, 134, 22–31. [Google Scholar] [CrossRef]
- Rama, R.K.; Ansu, M.; Iyer, N.R. A methodology of design for seismic performance enhancement of buildings using viscous fluid dampers. Struct. Control Health Monit. 2014, 21, 342–355. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J.; Xi, W. Effectiveness evaluation and optimal design of nonlinear viscous dampers for inelastic structures under pulse-type ground motions. Earthq. Eng. Struct. D 2018, 47, 2802–2820. [Google Scholar] [CrossRef]
- Occhiuzzi, A. Additional viscous dampers for civil structures: Analysis of design methods based on effective evaluation of modal damping ratios. Eng. Struct. 2009, 31, 1093–1101. [Google Scholar] [CrossRef]
- Singh, M.P.; Moreschi, L.M. Optimal seismic response control with dampers. Earthq. Eng. Struct. D 2001, 30, 553–572. [Google Scholar] [CrossRef]
- Aguirre, J.J.; Almazan, J.L.; Paul, C.J. Optimal control of linear and nonlinear asymmetric structures by means of passive energy dampers. Earthq. Eng. Struct. D 2013, 42, 377–395. [Google Scholar] [CrossRef]
- Lopez, G.D. A simple method for the design of optimal damper configurations in MDOF structures. Earthq. Spectra 2001, 17, 387–398. [Google Scholar]
- Takewaki, I. Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct. D 1997, 26, 1113–1124. [Google Scholar] [CrossRef]
- Takewaki, I. Optimal damper placement for critical excitation. Probabilist. Eng. Mech. 2000, 15, 317–325. [Google Scholar] [CrossRef]
- Lin, T.K.; Hwang, J.S.; Chen, K.H. Optimal distribution of damping coefficients for viscous dampers in buildings. Int. J. Struct. Stab. Dyn. 2017, 17, 1750054. [Google Scholar] [CrossRef]
- Pollini, N.; Lavan, O.; Amir, O. Minimum-cost optimization of nonlinear fluid viscous dampers and their supporting members for seismic retrofitting. Earthq. Eng. Struct. D 2017, 46, 1941–1961. [Google Scholar] [CrossRef]
- Parcianello, E.; Chisari, C.; Amadio, C. Optimal design of nonlinear viscous dampers for frame structures. Soil. Dyn. Earthq. Eng. 2017, 100, 257–260. [Google Scholar] [CrossRef]
- Domenico, D.D.; Hajirasouliha, I. Multi-level performance-based design optimisation of steel frames with nonlinear viscous dampers. Bull. Earthq. Eng. 2021, 19, 5015–5049. [Google Scholar] [CrossRef]
- Lavan, O.; Amir, O. Simultaneous topology and sizing optimization of viscous dampers in seismic retrofitting of 3D irregular frame structures. Earthq. Eng. Struct. D 2014, 43, 1325–1342. [Google Scholar] [CrossRef]
- Tubaldi, E.; Kougioumtzoglou, I.A. Nonstationary stochastic response of structural systems equipped with nonlinear viscous dampers under seismic excitation. Earthq. Eng. Struct. D 2015, 44, 121–138. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.; Du, D.; Wang, S. Stochastic optimization of dissipation structures based on lyapunov differential equations and the full stress design method. Buildings 2023, 13, 665. [Google Scholar] [CrossRef]
- Su, C.; Li, B.; Chen, T.; Dai, X. Stochastic optimal design of nonlinear viscous dampers for large-scale structures subjected to non-stationary seismic excitations based on dimension-reduced explicit method. Eng. Struct. 2018, 175, 217–230. [Google Scholar] [CrossRef]
- Tubaldi, E.; Ragni, L.; Dall’Asta, A. Probabilistic seismic response assessment of linear systems equipped with nonlinear viscous dampers. Earthq. Eng. Struct. D 2015, 44, 101–120. [Google Scholar] [CrossRef]
- Rodolfo, J.T.G.; Yeudy, F.V.A.; Ramon, G.D. Probabilistic estimation of the dynamic response of high-rise buildings via transfer functions. Eng. Struct. 2024, 302, 117299. [Google Scholar]
- Worden, K.; Cross, E.J. On switching response surface models, with applications to the structural health monitoring of bridges. Mech. Syst. Signal Process. 2018, 98, 139–156. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Bridge model updating using response surface method and genetic algorithm. J. Bridge Eng. 2010, 15, 553–564. [Google Scholar] [CrossRef]
- Lan, X.; Pan, W.; Zhang, L.; Yu, W.; Wu, K. Application and research of viscous fluid damper in frame structure. Sichuan Build. Sci. 2022, 48, 10–17. (In Chinese) [Google Scholar] [CrossRef]
- Aydin, E.; Boduroglu, M.H.; Guney, D. Optimal damper distribution for seismic rehabilitation of planar building structures. Eng. Struct. 2007, 29, 176–185. [Google Scholar] [CrossRef]


| The First Set of Parameters | The Second Set of Parameters | ||||
|---|---|---|---|---|---|
| Serial Number | Damping Coefficient C | Damping Exponent α | Serial Number | Damping Coefficient C | Damping Exponent α |
| 1 | 60 | 0.15 | 1 | 20 | 0.25 |
| 2 | 60 | 0.25 | 2 | 40 | 0.25 |
| 3 | 60 | 0.35 | 3 | 60 | 0.25 |
| 4 | 60 | 0.45 | 4 | 80 | 0.25 |
| 5 | 60 | 0.55 | 5 | 100 | 0.25 |
| 6 | 60 | 0.65 | 6 | 120 | 0.25 |
| Indicators | Response Surface Types | p | R2 |
|---|---|---|---|
| Additional damping ratio ξd | Poly2D | <0.0001 | 0.917 |
| Reduction rate of vertex displacement μu | Poly2D | <0.0001 | 0.900 |
| Reduction rate of base shear μV | Poly2D | <0.0001 | 0.901 |
| Inter-story displacement utilization rate η | Plane | <0.0001 | 0.988 |
| Damper force F/kN | Plane | <0.0001 | 0.970 |
| Damper displacement u/mm | Plane | <0.0001 | 0.973 |
| Indicators | X Direction | Y Direction |
|---|---|---|
| Additional damping ratio ξd | 2.91% | 3.38% |
| Reduction rate of vertex displacement μu | 18% | 21% |
| Reduction rate of base shear μV | 12% | 14% |
| Inter-story displacement utilization rate η | 0.53 | 0.59 |
| Damper force F/kN | 186 | 194 |
| Damper displacement u/mm | 1.48 | 1.61 |
| Indicators | X Direction | Y Direction |
|---|---|---|
| Additional damping ratio ξd | 4.50% | 5.70% |
| Reduction rate of vertex displacement μu | 25% | 30% |
| Reduction rate of base shear μV | 19% | 24% |
| Inter-story displacement utilization rate η | 0.70 | 0.81 |
| Damper force F/kN | 199 | 209 |
| Damper displacement u/mm | 1.79 | 1.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, X.; Wei, G.; Zhang, X. Study on the Influence and Optimization Design of Viscous Damper Parameters on the Damping Efficiency of Frame Shear Wall Structure. Buildings 2024, 14, 497. https://doi.org/10.3390/buildings14020497
Lan X, Wei G, Zhang X. Study on the Influence and Optimization Design of Viscous Damper Parameters on the Damping Efficiency of Frame Shear Wall Structure. Buildings. 2024; 14(2):497. https://doi.org/10.3390/buildings14020497
Chicago/Turabian StyleLan, Xiang, Guanglan Wei, and Xingxian Zhang. 2024. "Study on the Influence and Optimization Design of Viscous Damper Parameters on the Damping Efficiency of Frame Shear Wall Structure" Buildings 14, no. 2: 497. https://doi.org/10.3390/buildings14020497






