Interval Estimations of Building Heating Energy Consumption using the Degree-Day Method and Fuzzy Numbers
Abstract
:1. Introduction
2. Implementing Fuzzy Numbers in the Degree-Day Method
2.1. The Degree-Day Method for the Estimation of Heating Energy Consumption
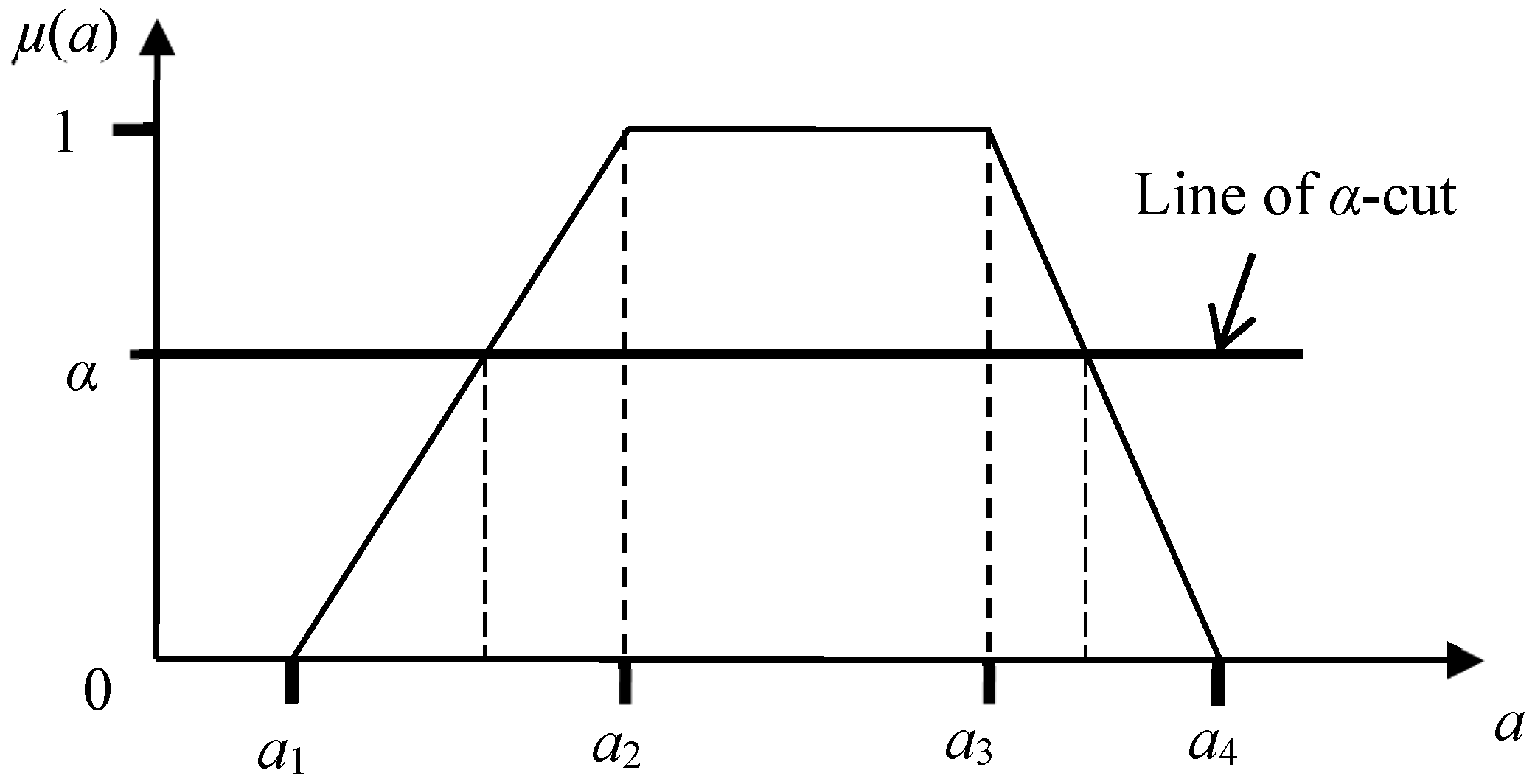
2.2. Fuzzy Numbers and Their Arithmetic
2.3. Application of Fuzzy Numbers to the Degree-Day Method
3. Building Application and Verification
3.1. Application of the Degree-Day Method
- Operating hours
- Restaurant: 11:00 a.m. to 1:00 a.m. (Tuesday to Sunday)
- Office: 8:00 a.m. to 5:00 a.m. (Monday to Friday)
- Indoor conditions (occupied)
- Restaurant and office (summer): 21 °C (or 70 °F)
- Restaurant and office (winter): 20 °C (or 68 °F)
- Indoor conditions (unoccupied)
- Restaurant and office (summer): 28 °C (or 82 °F)
- Restaurant and office (winter): 18 °C (or 64 °F)
3.2. Application of the Fuzzy Degree-Day Method and Verification
4. Closing Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Al-Homoud, M.S. Computer-aided building energy analysis techniques. Build. Environ. 2001, 36, 421–433. [Google Scholar] [CrossRef]
- Moreci, E.; Ciulla, G.; Lo Brano, V. Annual heating energy requirements of office buildings in a European climate. Sustain. Cities Soc. 2016, 20, 81–95. [Google Scholar] [CrossRef]
- Kohler, M.; Blond, N.; Clappier, A. A city scale degree-day method to assess building space heating energy demands in Strasbourg Eurometropolis (France). Appl. Energy 2016, 184, 40–54. [Google Scholar] [CrossRef]
- Sarak, H.; Satman, A. The degree-day method to estimate the residential heating natural gas consumption in Turkey: A case study. Energy 2003, 28, 929–939. [Google Scholar] [CrossRef]
- Valor, E.; Meneu, V.; Caselles, V. Daily air temperature and electricity load in Spain. J. Appl. Meteorol. 2001, 40, 1413–1421. [Google Scholar] [CrossRef]
- Moral-Carcedo, J.; Vicéns-Otero, J. Modelling the non-linear response of Spanish electricity demand to temperature variations. Energy Econ. 2005, 27, 477–494. [Google Scholar] [CrossRef]
- Azevedo, J.A.; Chapman, L.; Muller, C.L. Critique and suggested modifications of the degree days methodology to enable long-term electricity consumption assessments: A case study in Birmingham, UK: Critique and suggested modifications of the degree days methodology. Meteorol. Appl. 2015, 22, 789–796. [Google Scholar] [CrossRef]
- Amato, A.D.; Ruth, M.; Kirshen, P.; Horwitz, J. Regional energy demand responses to climate change: Methodology and application to the commonwealth of Massachusetts. Clim. Chang. 2005, 71, 175–201. [Google Scholar] [CrossRef]
- Guan, L. Preparation of future weather data to study the impact of climate change on buildings. Build. Environ. 2009, 44, 793–800. [Google Scholar] [CrossRef]
- Cox, R.A.; Drews, M.; Rode, C.; Nielsen, S.B. Simple future weather files for estimating heating and cooling demand. Build. Environ. 2015, 83, 104–114. [Google Scholar] [CrossRef] [Green Version]
- Coydon, F.; Herkel, S.; Kuber, T.; Pfafferott, J.; Himmelsbach, S. Energy performance of façade integrated decentralised ventilation systems. Energy Build. 2015, 107, 172–180. [Google Scholar] [CrossRef]
- Bolattürk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- Kurekci, N.A. Determination of optimum insulation thickness for building walls by using heating and cooling degree-day values of all Turkey’s provincial centers. Energy Build. 2016, 118, 197–213. [Google Scholar] [CrossRef]
- Verbai, Z.; Lakatos, Á.; Kalmár, F. Prediction of energy demand for heating of residential buildings using variable degree day. Energy 2014, 76, 780–787. [Google Scholar] [CrossRef]
- Mitchell, J.W.; Braun, J.E. Principles of Heating, Ventilation, and Air Conditioning in Buildings; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2013 ASHRAE Handbook, Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2013. [Google Scholar]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]
- Guyonnet, D.; Bourgine, B.; Dubois, D.; Fargier, H.; Come, B.; Chilès, J.-P. Hybrid approach for addressing uncertainty in risk assessments. J. Environ. Eng. 2003, 129, 68–78. [Google Scholar] [CrossRef]
- Baudrit, C.; Dubois, D.; Guyonnet, D. Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment. IEEE Trans. Fuzzy Syst. 2006, 14, 593–608. [Google Scholar] [CrossRef]
- Thom, H. Seasonal degree-day statistics for the United States. Mon. Weather Rev. 1952, 80, 143–147. [Google Scholar] [CrossRef]
- Lam, J.C.; Hui, S.C.M.; Chan, A.L.S. A statistical approach to the development of a typical meteorological year for Hong Kong. Archit. Sci. Rev. 1996, 39, 201–209. [Google Scholar] [CrossRef]
- Janjai, S.; Deeyai, P. Comparison of methods for generating typical meteorological year using meteorological data from a tropical environment. Appl. Energy 2009, 86, 528–537. [Google Scholar] [CrossRef]
- Pusat, S.; Ekmekçi, İ.; Akkoyunlu, M.T. Generation of typical meteorological year for different climates of Turkey. Renew. Energy 2015, 75, 144–151. [Google Scholar] [CrossRef]
- Kneifel, J.D.; O’Rear, E.G. An Assessment of Typical Weather Year Data Impacts vs. Multi-Year Weather Data on Net-Zero Energy Building Simulations; Report No. NIST SP 1204; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016.
- Dubois, D.; Prade, H. Fuzzy sets and probability: Misunderstandings, bridges and gaps. In Proceedings of the Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993; pp. 1059–1068. [Google Scholar]
- Giachetti, R.E.; Young, R.E. A parametric representation of fuzzy numbers and their arithmetic operators. Fuzzy Sets Syst. 1997, 91, 185–202. [Google Scholar] [CrossRef]
- Schjær-Jacobsen, H. Comparison of probabilistic and possibilistic approaches to modelling of economic uncertainty. In Proceedings of the 8th Workshop on Uncertainty Processing 2009, Liblice, Czech Republic, 19–23 September 2009; pp. 213–225. [Google Scholar]
- Michalik, G.; Khan, M.E.; Bonwick, W.J.; Mielczarski, W. Structural modelling of energy demand in the residential sector: 2. The use of linguistic variables to include uncertainty of customers’ behaviour. Energy 1997, 22, 949–958. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Grisostomi, M.; Ippoliti, G.; Longhi, S. Fuzzy logic home energy consumption modeling for residential photovoltaic plant sizing in the new Italian scenario. Energy 2014, 74, 359–367. [Google Scholar] [CrossRef]
- Kolokotsa, D. Artificial intelligence in buildings: A review of the application of fuzzy logic. Adv. Build. Energy Res. 2007, 1, 29–54. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic and approximate reasoning. Synthese 1975, 30, 407–428. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Lee, K.H. First Course on Fuzzy Theory and Applications; Springer: Berlin, Germany, 2006. [Google Scholar]
- Singer, D. A fuzzy set approach to fault tree and reliability analysis. Fuzzy Sets Syst. 1990, 34, 145–155. [Google Scholar] [CrossRef]
- Cheng, C.H.; Mon, D.L. Fuzzy system reliability analysis by interval of confidence. Fuzzy Sets Syst. 1993, 56, 29–35. [Google Scholar] [CrossRef]
- Moens, D.; Hanss, M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Anal. Des. 2011, 47, 4–16. [Google Scholar] [CrossRef]
- Erdogan, Y.S.; Bakir, P.G. Inverse propagation of uncertainties in finite element model updating through use of fuzzy arithmetic. Eng. Appl. Artif. Intell. 2013, 26, 357–367. [Google Scholar]
- Wang, C.; Qiu, Z.; Xu, M. Collocation methods for fuzzy uncertainty propagation in heat conduction problem. Int. J. Heat Mass Transfer. 2017, 107, 631–639. [Google Scholar] [CrossRef]
- Maskey, S.; Guinot, V.; Price, R.K. Treatment of precipitation uncertainty in rainfall-runoff modelling: A fuzzy set approach. Adv. Water Resour. 2004, 27, 889–898. [Google Scholar] [CrossRef]
- Scherm, H. Simulating uncertainty in climate–pest models with fuzzy numbers. Environ. Pollut. 2000, 108, 373–379. [Google Scholar] [CrossRef]
- Wu, D.; Gao, W.; Wang, C.; Tangaramvong, S.; Tin-Loi, F. Robust fuzzy structural safety assessment using mathematical programming approach. Fuzzy Sets Syst. 2016, 293, 30–49. [Google Scholar] [CrossRef]
- Dubois, D. An application of fuzzy arithmetic to the optimization of industrial machining processes. Math. Modell. 1987, 9, 461–475. [Google Scholar] [CrossRef]
- Wang, L.; Mathew, P.; Pang, X. Uncertainties in energy consumption introduced by building operations and weather for a medium-size office building. Energy Build. 2012, 53, 152–158. [Google Scholar] [CrossRef]
- Day, A.R.; Knight, I.; Dunn, G.; Gaddas, R. Improved methods for evaluating base temperature for use in building energy performance lines. Build. Serv. Eng. Res. Technol. 2003, 24, 221–228. [Google Scholar] [CrossRef]
- Layberry, R.L. Degree days for building energy management—Presentation of a new data set. Build. Serv. Eng. Res. Technol. 2008, 29, 273–282. [Google Scholar] [CrossRef]
- Layberry, R.L. Analysis of errors in degree days for building energy analysis using Meteorological Office weather station data. Build. Serv. Eng. Res. Technol. 2009, 30, 79–86. [Google Scholar] [CrossRef]
- Day, A.R. An improved use of cooling degree-days for analysing chiller energy consumption in buildings. Build. Serv. Eng. Res. Technol. 2005, 26, 115–127. [Google Scholar] [CrossRef]
- De Rosa, M.; Bianco, V.; Scarpa, F.; Tagliafico, L.A. Heating and cooling building energy demand evaluation; a simplified model and a modified degree days approach. Appl. Energy 2014, 128, 217–229. [Google Scholar] [CrossRef]
- Shin, M.; Do, S.L. Prediction of cooling energy use in buildings using an enthalpy-based cooling degree days method in a hot and humid climate. Energy Build. 2016, 110, 57–70. [Google Scholar] [CrossRef]
- Day, A.R.; Karayiannis, T.G. Identification of the uncertainties in degree-day-based energy estimates. Build. Serv. Eng. Res. Technol. 1999, 20, 165–172. [Google Scholar] [CrossRef]
- Ning, M.; Zaheeruddin, M. Fuzzy set-based uncertainty analysis of HVAC&R systems: A simulation study. Build. Serv. Eng. Res. Technol. 2009, 30, 241–262. [Google Scholar]
- Government of Canada. Historical Climate Data. Available online: www.climate.weather.gc.ca (accessed on 15 April 2015).
| Fuzzy number addition | |
| Fuzzy number subtraction | |
| Fuzzy number multiplication | |
| Fuzzy number division |
| Month | Record Low | Average Low | Daily Mean | Average High | Record High |
|---|---|---|---|---|---|
| Jan. | −44.4 °C | −13.2 °C | −7.1 °C | −0.9 °C | 17.6 °C |
| Feb. | −45.0 °C | −11.4 °C | −5.4 °C | 0.7 °C | 22.6 °C |
| Mar. | −37.2 °C | −7.5 °C | −1.6 °C | 4.4 °C | 25.4 °C |
| Apr. | −30.0 °C | −2.0 °C | 4.6 °C | 11.2 °C | 29.4 °C |
| May | −16.7 °C | 3.1 °C | 9.7 °C | 16.3 °C | 32.4 °C |
| Jun. | −3.3 °C | 7.5 °C | 13.7 °C | 19.8 °C | 35.0 °C |
| Jul. | −0.6 °C | 9.8 °C | 16.5 °C | 23.2 °C | 36.1 °C |
| Aug. | −3.2 °C | 8.8 °C | 15.8 °C | 22.8 °C | 35.6 °C |
| Sep. | −13.3 °C | 4.1 °C | 11.0 °C | 17.8 °C | 33.3 °C |
| Oct. | −25.7 °C | −1.4 °C | 5.2 °C | 11.7 °C | 29.4 °C |
| Nov. | −35 °C | −8.2 °C | −2.4 °C | 3.4 °C | 22.8 °C |
| Dec. | −42.8 °C | −12.8 °C | −6.8 °C | −0.8 °C | 19.5 °C |
| The U Factor (∑UAo) | 1400.8 W/°C |
| The ventilation factor (NV) | 4689.5 W/°C |
| Total heat loss coefficient (Ktot) | 2963.9 W/°C |
| Heat loss coefficient of the 1st floor (Ktot_1) | 2246.1 W/°C |
| Heat loss coefficient of the 2nd floor (Ktot_2) | 717.8 W/°C |
| Average balance point temperature of 1st floor (Tbal_1) | 13.4 °C |
| Average balance point temperature of 2nd floor (Tbal_2) | 1.5 °C |
| Furnace efficiency (ηfr) | 0.95 |
| Energy consumption estimated by the degree-day method | 236 × 103 kWh |
| Energy consumption estimated by eQuest® | 234 × 103 kWh |
| α Level | α-Cut Interval | % Number of Years Included in the α-Cut Interval |
|---|---|---|
| α = 0.3 | [Ei,low, Ei,up] = [153, 322] (×103) kWh | 100% |
| α = 0.5 | [Ei,low, Ei,up] = [171, 294] (×103) kWh | 98% (1 year excluded) |
| α = 0.7 | [Ei,low, Ei,up] = [189, 266] (×103) kWh | 85% (8 years excluded) |
| Year | Energy Consumption (103 kWh) | Year | Energy Consumption (103 kWh) | Year | Energy Consumption (103 kWh) | Year | Energy Consumption (103 kWh) |
|---|---|---|---|---|---|---|---|
| 1960 | 242 | 1973 | 245 | 1986 | 202 | 1999 | 204 |
| 1961 | 234 | 1974 | 230 | 1987 | 172 | 2000 | 245 |
| 1962 | 228 | 1975 | 259 | 1988 | 202 | 2001 | 218 |
| 1963 | 226 | 1976 | 203 | 1989 | 235 | 2002 | 246 |
| 1964 | 250 | 1977 | 228 | 1990 | 227 | 2003 | 239 |
| 1965 | 274 | 1978 | 265 | 1991 | 213 | 2004 | 215 |
| 1966 | 271 | 1979 | 255 | 1992 | 211 | 2005 | 210 |
| 1967 | 259 | 1980 | 240 | 1993 | 222 | 2006 | 212 |
| 1968 | 253 | 1981 | 188 | 1994 | 234 | 2007 | 219 |
| 1969 | 275 | 1982 | 274 | 1995 | 250 | 2008 | 229 |
| 1970 | 265 | 1983 | 231 | 1996 | 298 | 2009 | 245 |
| 1971 | 261 | 1984 | 232 | 1997 | 231 | 2010 | 224 |
| 1972 | 278 | 1985 | 238 | 1998 | 233 | 2011 | 232 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Li, S. Interval Estimations of Building Heating Energy Consumption using the Degree-Day Method and Fuzzy Numbers. Buildings 2018, 8, 21. https://doi.org/10.3390/buildings8020021
Cheng X, Li S. Interval Estimations of Building Heating Energy Consumption using the Degree-Day Method and Fuzzy Numbers. Buildings. 2018; 8(2):21. https://doi.org/10.3390/buildings8020021
Chicago/Turabian StyleCheng, Xin, and Simon Li. 2018. "Interval Estimations of Building Heating Energy Consumption using the Degree-Day Method and Fuzzy Numbers" Buildings 8, no. 2: 21. https://doi.org/10.3390/buildings8020021





