On the Optimization of a Multimodal Electromagnetic Vibration Energy Harvester Using Mode Localization and Nonlinear Dynamics
Abstract
:1. Introduction
2. Mechanical Model
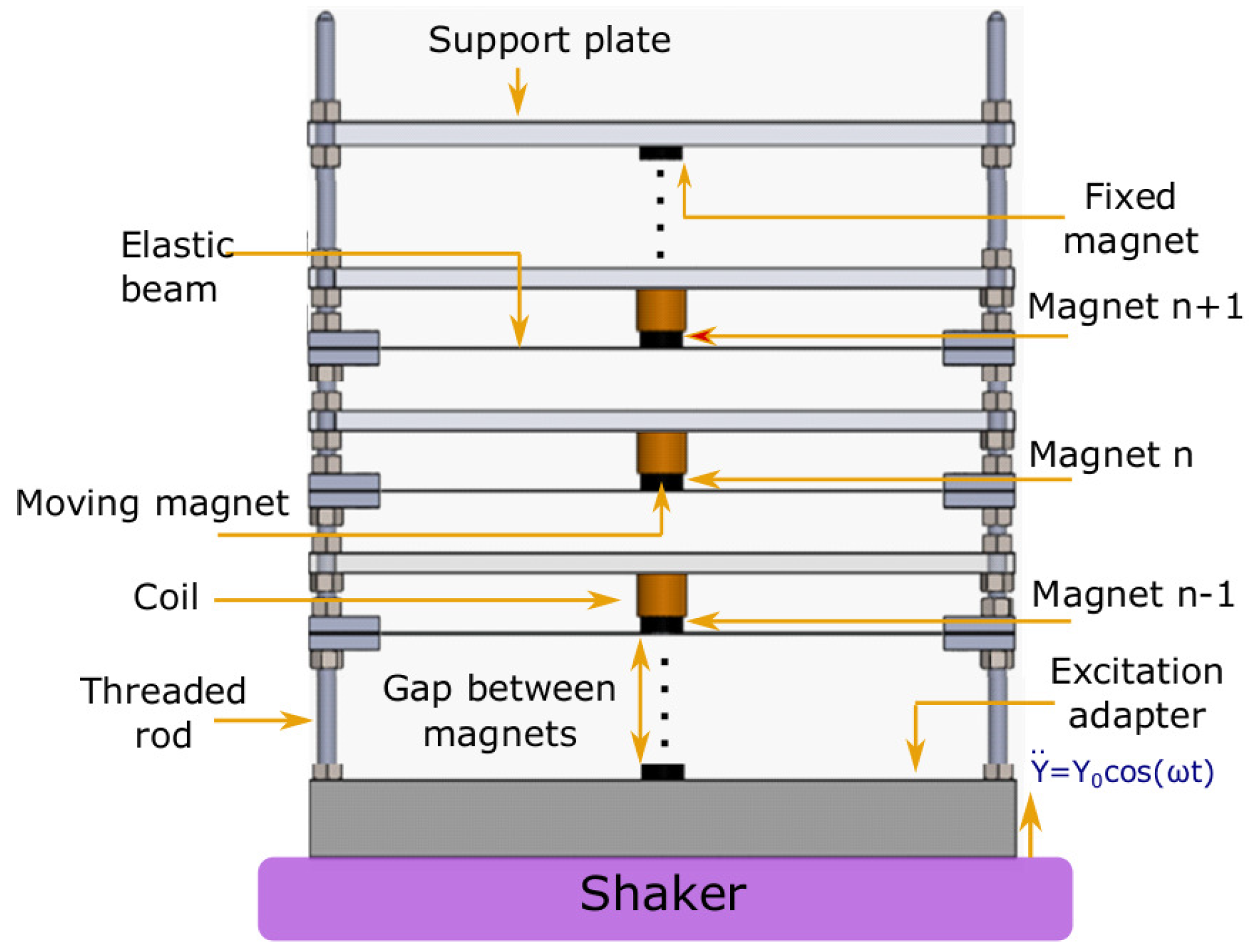
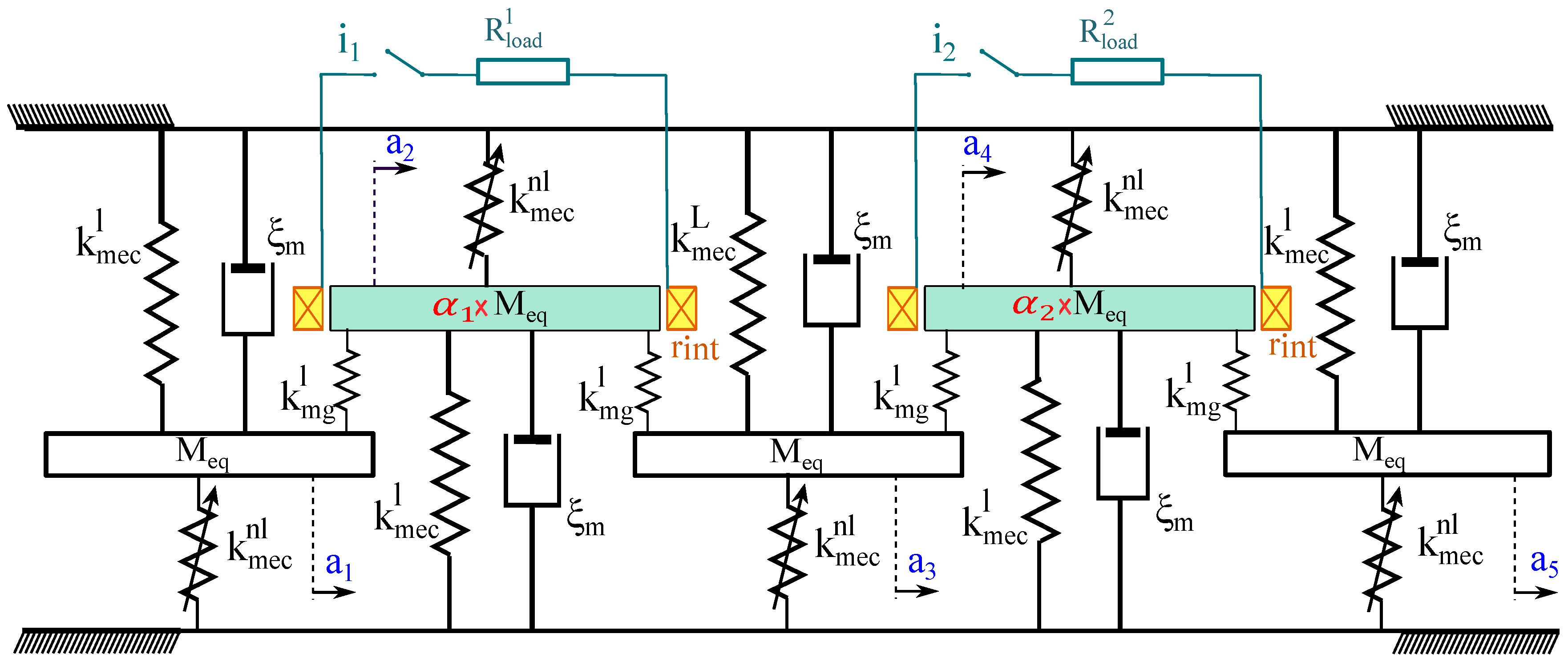
2.1. Proposed Design
2.2. Equation of Motion
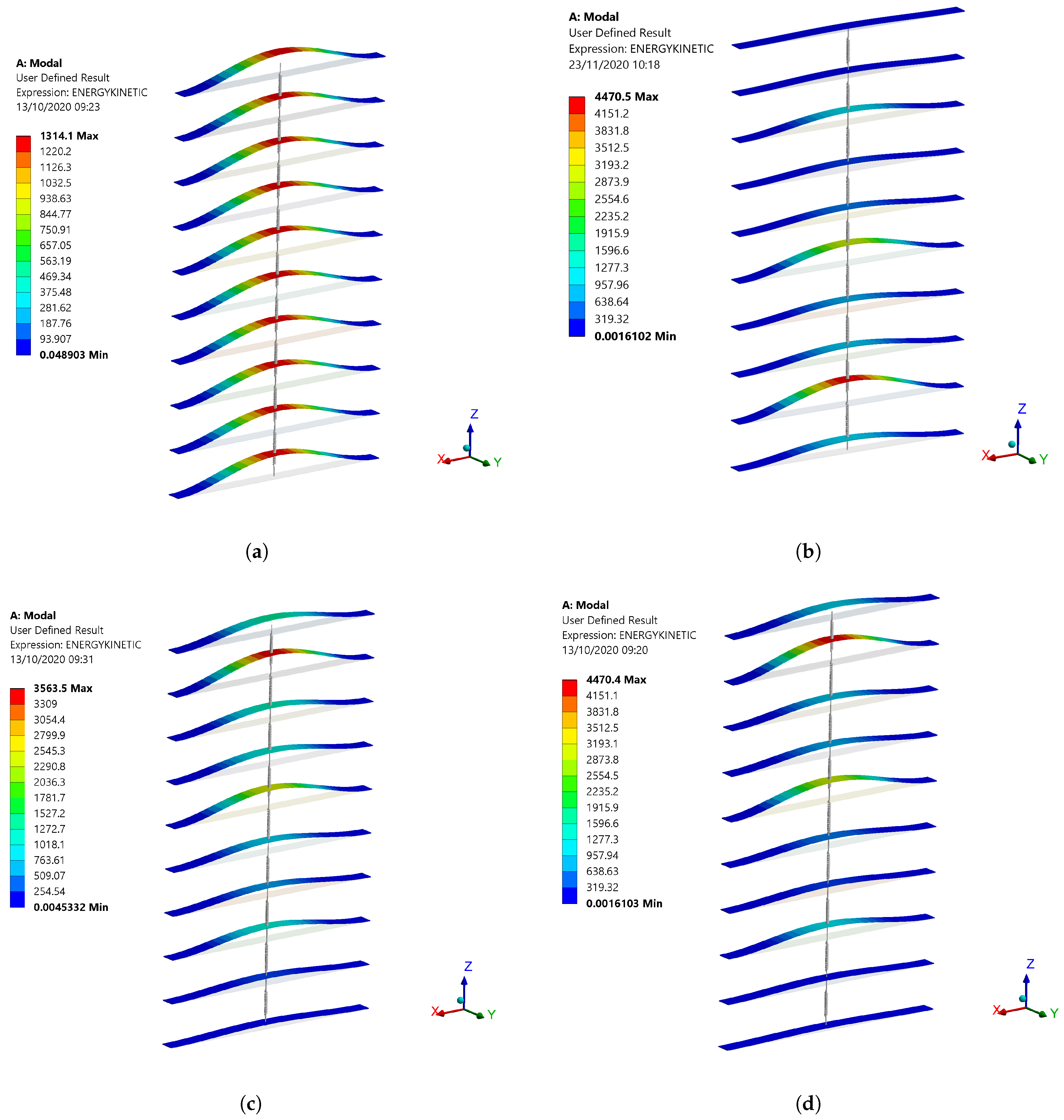
2.3. Modal Localization Phenomenon
3. Multiobjective Optimization of the Validated Two-Coupled-Beams Harvester
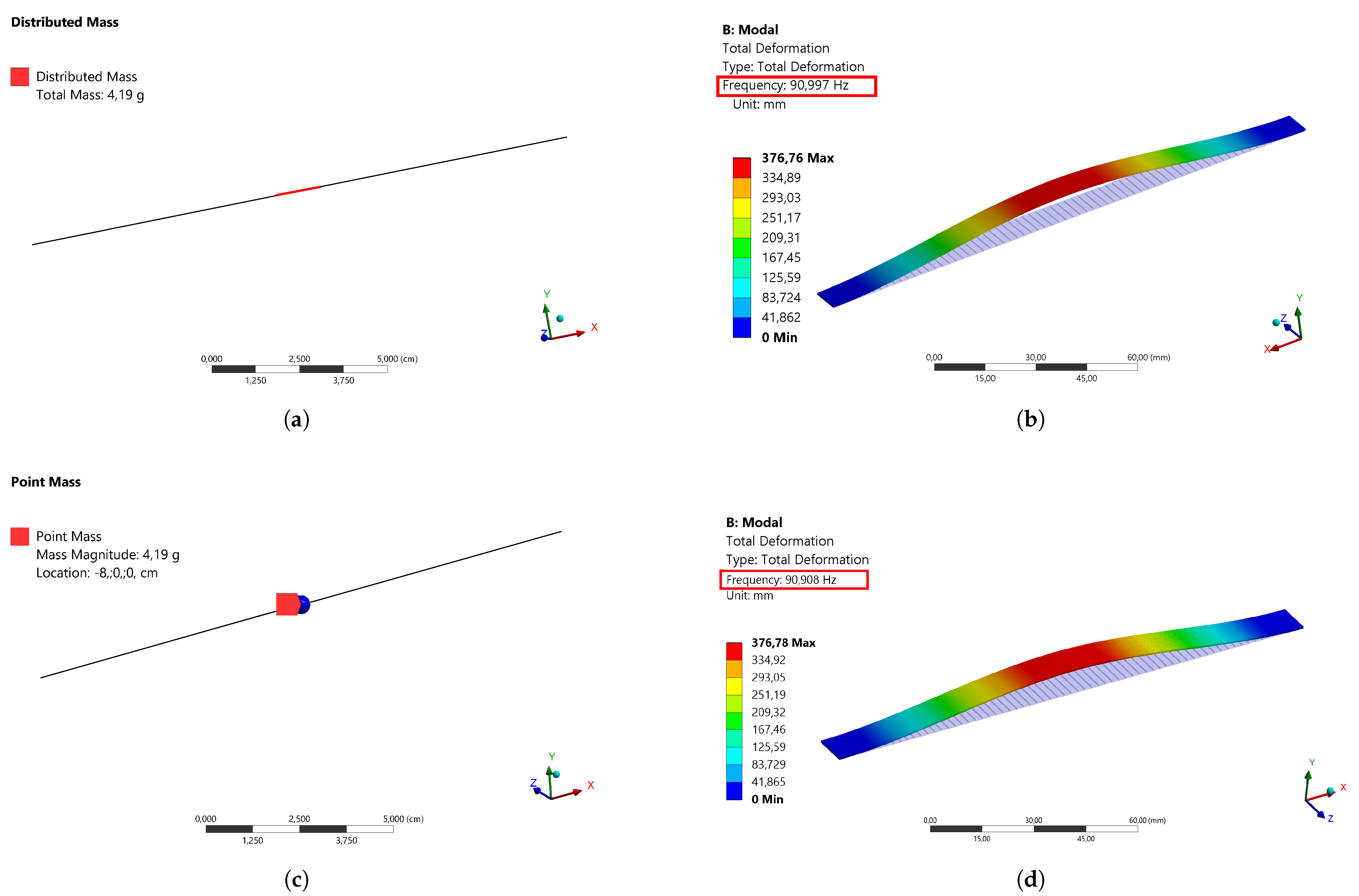
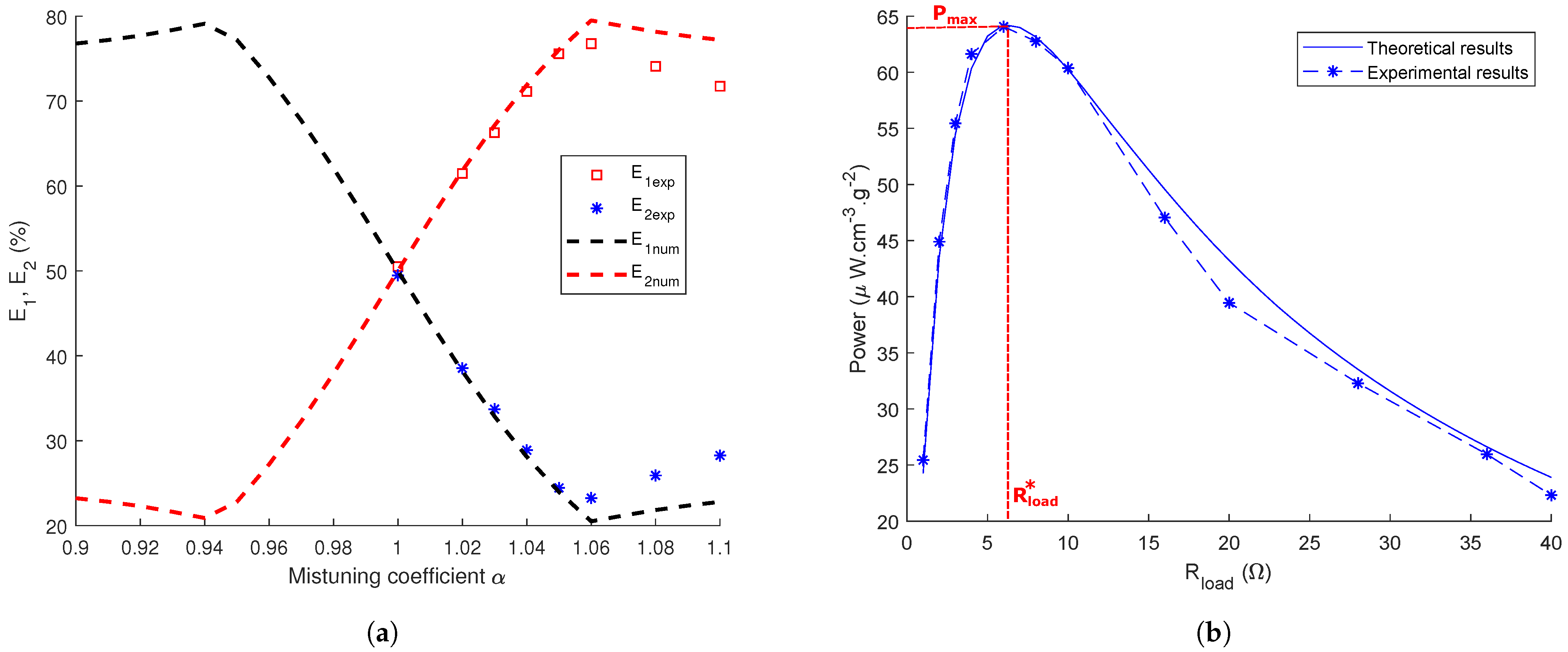
3.1. Numerical-Experimental Confrontation
3.2. Optimization of the Validated Model
4. Optimization of a Multiple-Degree-of-Freedom: Five-Coupled-Beams
4.1. Optimal Position of the Introduced Mistuning
4.2. Multiobjective Optimization of the Five-Coupled-Beams Harvester
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Dynamic Equations of Motion of the Continuous Structure
Appendix A.1. About the Hypothesis of the Localized Point Mass Magnet
Appendix A.2. Equation of Motion
Appendix B. Reduced Model by Galerkin Modal Decomposition
References
- An, P.Q.; Scully, T.; Breen, M.; Murphy, M.D. Determination of optimal battery utilization to minimize operating costs for a grid-connected building with renewable energy sources. Energy Convers. Manag. 2018, 174, 157–174. [Google Scholar]
- Suzhi, B.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar]
- Saha, C.R.; O’Donnell, T.; Wang, N.; McCloskey, P. Electromagnetic generator for harvesting energy from human motion. Sens. Actuators A Phys. 2008, 147, 248–253. [Google Scholar] [CrossRef]
- Kazmierski, T.J.; Beeby, S. Energy Harvesting Systems; Springer: New York, NY, USA, 2014. [Google Scholar]
- Shashank, P.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; Volume 21. [Google Scholar]
- Vasan, P.; Kirubaveni, S.; Sreeja, B.S.; Radha, S. Vibration energy harvesting for low power devices. In Proceedings of the Online International Conference on Green Engineering and Technologies (IC-GET), Coimbatore, India, 19 November 2016; pp. 1–4. [Google Scholar]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Lu, C.; Tsui, C.; Ki, W. Vibration Energy Scavenging System With Maximum Power Tracking for Micropower Applications. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2011, 19, 2109–2119. [Google Scholar] [CrossRef]
- Shim, M.; Kim, J.; Jeong, J.; Park, S.; Kim, C. Self-Powered 30 μW to 10 mW Piezoelectric Energy Harvesting System with 9.09 ms/V Maximum Power Point Tracking Time. IEEE J. Solid State Circuits 2015, 50, 2367–2379. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Zhang, A.; Peng, Z.; Luo, D. Electrostatic energy harvesting device with dual resonant structure for wideband random vibration sources at low frequency. Rev. Sci. Instrum. 2016, 87, 125001. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Chiba, D.; Narita, F. Magnetostrictive clad steel plates for high-performance vibration energy harvesting. Appl. Phys. Lett. 2018, 112, 073902. [Google Scholar] [CrossRef]
- Wang, D.W.; Mo, J.L.; Wang, X.F. Experimental and numerical investigations of the piezoelectric energy harvesting via friction-induced vibration. Energy Convers. Manag. 2018, 171, 1134–1149. [Google Scholar] [CrossRef]
- Shashank, P.; Song, H.-C.; Zhou, Y. A review on piezoelectric energy harvesting: Materials, methods, and circuits. Energy Harvest. Syst. 2017, 4, 3–39. [Google Scholar]
- Beeby, S.P.; Torah, R.N.; Tudor, M.J.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.R. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257. [Google Scholar] [CrossRef]
- Toyabur, R.M.; Salauddin, M.; Cho, H.; Park, J.Y. A multimodal hybrid energy harvester based on piezoelectric-electromagnetic mechanisms for low-frequency ambient vibrations. Energy Convers. Manag. 2018, 168, 454–466. [Google Scholar] [CrossRef]
- Wang, J.; Liao, W.-H. Attaining the high-energy orbit of nonlinear energy harvesters by load perturbation. Energy Convers. Manag. 2019, 192, 30–36. [Google Scholar] [CrossRef]
- Cammarano, A. The bandwidth of optimized nonlinear vibration-based energy harvesters. Smart Mater. Struct. 2014, 23, 055019. [Google Scholar] [CrossRef]
- Tang, X.; Lei, Z. Enhanced vibration energy harvesting using dual-mass systems. J. Sound Vib. 2011, 330, 5199–5209. [Google Scholar] [CrossRef]
- Soobum, L.; Youn, B.D. A new piezoelectric energy harvesting design concept: Multimodal energy harvesting skin. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 629–645. [Google Scholar]
- Yonas, T.; Zhang, S.; Priya, S. Multimodal energy harvesting system: Piezoelectric and electromagnetic. J. Intell. Mater. Syst. Struct. 2009, 20, 625–632. [Google Scholar]
- Roundy, S. Improving power output for vibration-based energy scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Ibrahim, S.; Balkan, T.; Kulah, H. An electromagnetic micro power generator for wideband environmental vibrations. Sens. Actuators A Phys. 2008, 145, 405–413. [Google Scholar]
- Bin, Y.; Lee1, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar]
- Malaji, P.V.; Ali, S.F. Energy harvesting from near periodic structures. In Vibration Engineering and Technology of Machinery; Springer: Cham, Switzerland, 2015; pp. 411–420. [Google Scholar]
- Zakaria, Z.; Kacem, N.; Bouhaddi, N. On the energy localization in weakly coupled oscillators for electromagnetic vibration energy harvesting. Smart Mater. Struct. 2019, 28, 07LT02. [Google Scholar]
- Anderson, P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958, 109, 1492. [Google Scholar] [CrossRef]
- Hodges, C.H. Confinement of vibration by structural irregularity. J. Sound Vib. 1982, 82, 411–424. [Google Scholar] [CrossRef]
- Hodges, C.H.; Woodhouse, J. Vibration isolation from irregularity in a nearly periodic structure: Theory and measurements. J. Acoust. Soc. Am. 1983, 74, 894–905. [Google Scholar] [CrossRef]
- Takashi, I.; Harata, Y. Localization phenomena in pendulum arrays subjected to vertical excitation. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Zhou, X.; Gao, S.; Liu, H. Effects of introducing nonlinear components for a random excited hybrid energy harvester. Smart Mater. Struct. 2016, 26, 015008. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Baglio, S. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sens. Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef] [Green Version]
- Jessy, B.; Roundy, S.; Wright, P. Alternative geometries for increasing power density in vibration energy scavenging for wireless sensor networks. In Proceedings of the 3rd International Energy Conversion Engineering Conference, San Francisco, CA, USA, 15–18 August 2005; p. 5617. [Google Scholar]
- Amri, M.; Basset, P. Novel nonlinear spring design for wideband vibration energy harvesters. In Proceedings of the PowerMEMS 2011, Seoul, Korea, 15–18 November 2011; pp. 189–193. [Google Scholar]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kacem, N.; Bouhaddi, N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Smart Mater. Struct. 2014, 23, 075024. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef] [Green Version]
- Cyril, D.; Kacem, N.; Bouhaddi, N. Design of a nonlinear energy harvester based on high static low dynamic stiffness for low frequency random vibrations. Sens. Actuators A Phys. 2018, 283, 54–64. [Google Scholar]
- Gammaitoni, L.; Neri, I.; Vocca, H. Nonlinear oscillators for vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 164102. [Google Scholar] [CrossRef] [Green Version]
- Kacem, N.; Hentz, S.; Pinto, D.; Reig, B.; Nguyen, V. Nonlinear dynamics of nanomechanical beam resonators: Improving the performance of NEMS-based sensors. Nanotechnology 2009, 20, 275501. [Google Scholar] [CrossRef] [PubMed]
- Aouali, K. Exploiting Nonlinear Dynamics and Energy Localization to Enhance the Performances of an Electromagnetic Vibration Energy Harvester. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019; p. 59285. [Google Scholar]
- Aouali, K.; Kacem, N.; Bouhaddi, N.; Mrabet, E.; Haddar, M. Efficient broadband vibration energy harvesting based on tuned non-linearity and energy localization. Smart Mater. Struct. 2020, 29, 10LT01. [Google Scholar] [CrossRef]
- Muhammad, F.F.; Thein, C.K.; Yurchenko, D. Important considerations in optimising the structural aspect of a SDOF electromagnetic vibration energy harvester. J. Sound Vib. 2020, 482, 115470. [Google Scholar]
- Dirk, S.; Manoli, Y. Electromagnetic Vibration Energy Harvesting Devices: Architectures, Design, Modeling and Optimization; Springer Science and Business Media: Berlin, Germany, 2012; Volume 35. [Google Scholar]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation. Smart Mater. Struct. 2016, 25, 025018. [Google Scholar] [CrossRef]
- Seyedfakhreddin, N.; Zhang, L. Design and optimization of a low-resonant-frequency piezoelectric MEMS energy harvester based on artificial intelligence. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 13. [Google Scholar]
- Abdullah, K.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Muriel, B. Dual methods for discrete structural optimization problems. Int. J. Numer. Methods Eng. 2000, 48, 1761–1784. [Google Scholar]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, K.; Khir, M.H.M.; Dennis, J.O.; Baharudin, Z. A wideband, frequency up-converting bounded vibration energy harvester for a low frequency environment. Smart Mater. Struct. 2013, 22, 025018. [Google Scholar] [CrossRef]
- Galchev, T.; Kim, H.; Najafi, K. A parametric frequency increased power generator for scavenging low frequency ambient vibrations. Procedia Chem. 2009, 1, 1439–1442. [Google Scholar] [CrossRef] [Green Version]
- Renaud, M.; Fiorini, P.; van Schaijk, R.; van Hoof, C. Harvesting energy from the motion of human limbs: The design and analysis of an impact-based piezoelectric generator. Smart Mater. Struct. 2009, 18, 035001. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C. Non-resonant electromagnetic wideband energy harvesting mechanism for low frequency vibrations. Microsyst. Technol. 2010, 16, 961–966. [Google Scholar] [CrossRef]
- Sardini, E.; Serpelloni, M. An efficient electromagnetic power harvesting device for low-frequency applications. Sens. Actuators A 2011, 172, 475–482. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; Harris, N. Vibration energy harvesting using the Halbach array. Smart Mater. Struct. 2012, 21, 11. [Google Scholar] [CrossRef]
- Berdy, D.F.; Srisungsitthisunti, P.; Xu, X.; Rhoads, J.; Jung, B.; Peroulis, D. Compact low frequency meandered piezoelectric energy harvester. Power MEMS 2009, 59, 71–74. [Google Scholar]
- Kulkarni, S.; Koukharenko, E.; Torah, R.; Tudor, J.; Beeby, S.; Odonnell, T. Design, fabrication and test of integrated micro-scale vibration-based electromagnetic generator. Sens. Actuators A Phys. 2008, 145–146, 336–342. [Google Scholar] [CrossRef] [Green Version]
- Aymen, J.; Kacem, N.; Bouhaddi, N. Stabilization of solitons in coupled nonlinear pendulums with simultaneous external and parametric excitations. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 1–11. [Google Scholar]

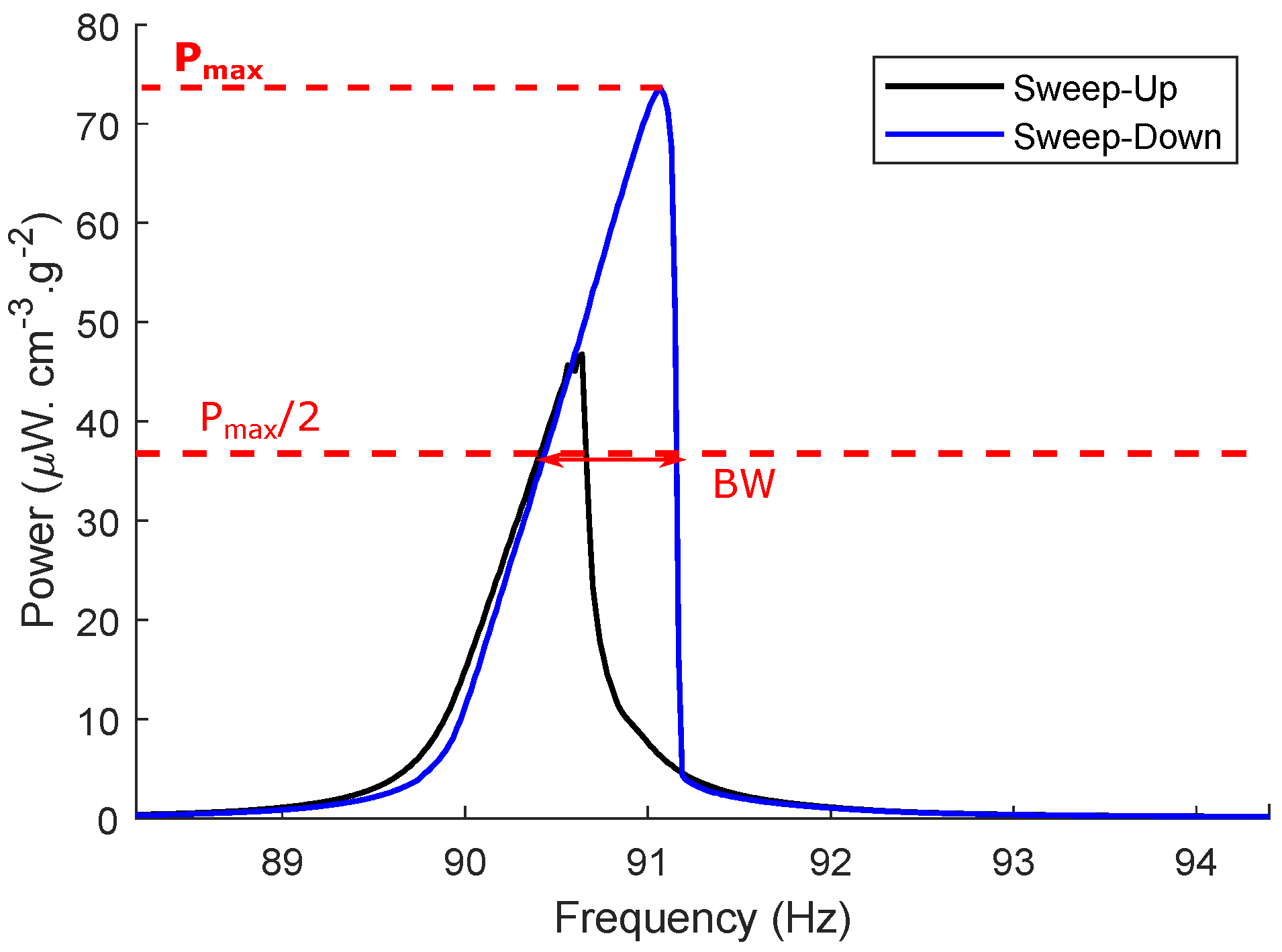
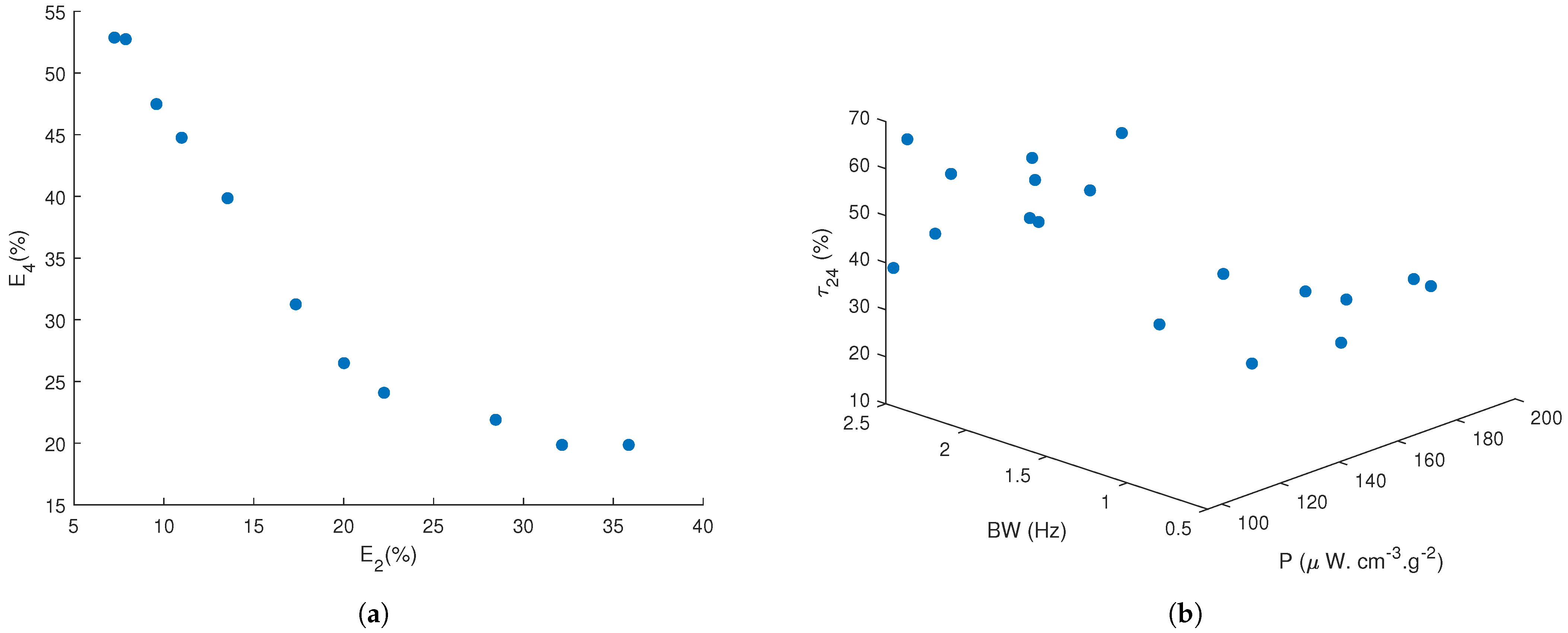



| 120.8924 | 120.8996 | 120.9109 | 120.9253 | 120.9418 | 120.9590 | 120.9756 | 120.9900 | 121.0013 | 121.0084 |
| Objective Function |
|---|
| Maximize: (P, BW) = f (, , ) |
| Constraints |
| 1 ≤ ≤ |
| ≤ |
| < |
| Compromise Solution |
|---|
| (, ) = ( μW·cmg, Hz) |
| With |
| Objective Function |
|---|
| Maximize: P = f (, , , , ) |
| Constraints |
| 1 ≤ ≤ |
| ≤ |
| < ≤ 40 |
| Objective Function |
|---|
| Maximize: (P, BW, ) = f (, , , , ) |
| Constraints |
| 1 ≤ ≤ |
| ≤ |
| < ≤ 40 |
| Compromised Solution |
|---|
| (, ,) = ( μW·cm·g, 1.87 Hz, ) |
| With |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aouali, K.; Kacem, N.; Bouhaddi, N.; Haddar, M. On the Optimization of a Multimodal Electromagnetic Vibration Energy Harvester Using Mode Localization and Nonlinear Dynamics. Actuators 2021, 10, 25. https://doi.org/10.3390/act10020025
Aouali K, Kacem N, Bouhaddi N, Haddar M. On the Optimization of a Multimodal Electromagnetic Vibration Energy Harvester Using Mode Localization and Nonlinear Dynamics. Actuators. 2021; 10(2):25. https://doi.org/10.3390/act10020025
Chicago/Turabian StyleAouali, Kaouthar, Najib Kacem, Noureddine Bouhaddi, and Mohamed Haddar. 2021. "On the Optimization of a Multimodal Electromagnetic Vibration Energy Harvester Using Mode Localization and Nonlinear Dynamics" Actuators 10, no. 2: 25. https://doi.org/10.3390/act10020025






