Reliability Evaluation for Cable-Spring Folding Wing Considering Synchronization of Deployable Mechanism
Abstract
:1. Introduction
2. Dynamic Theory of Deployable Mechanism
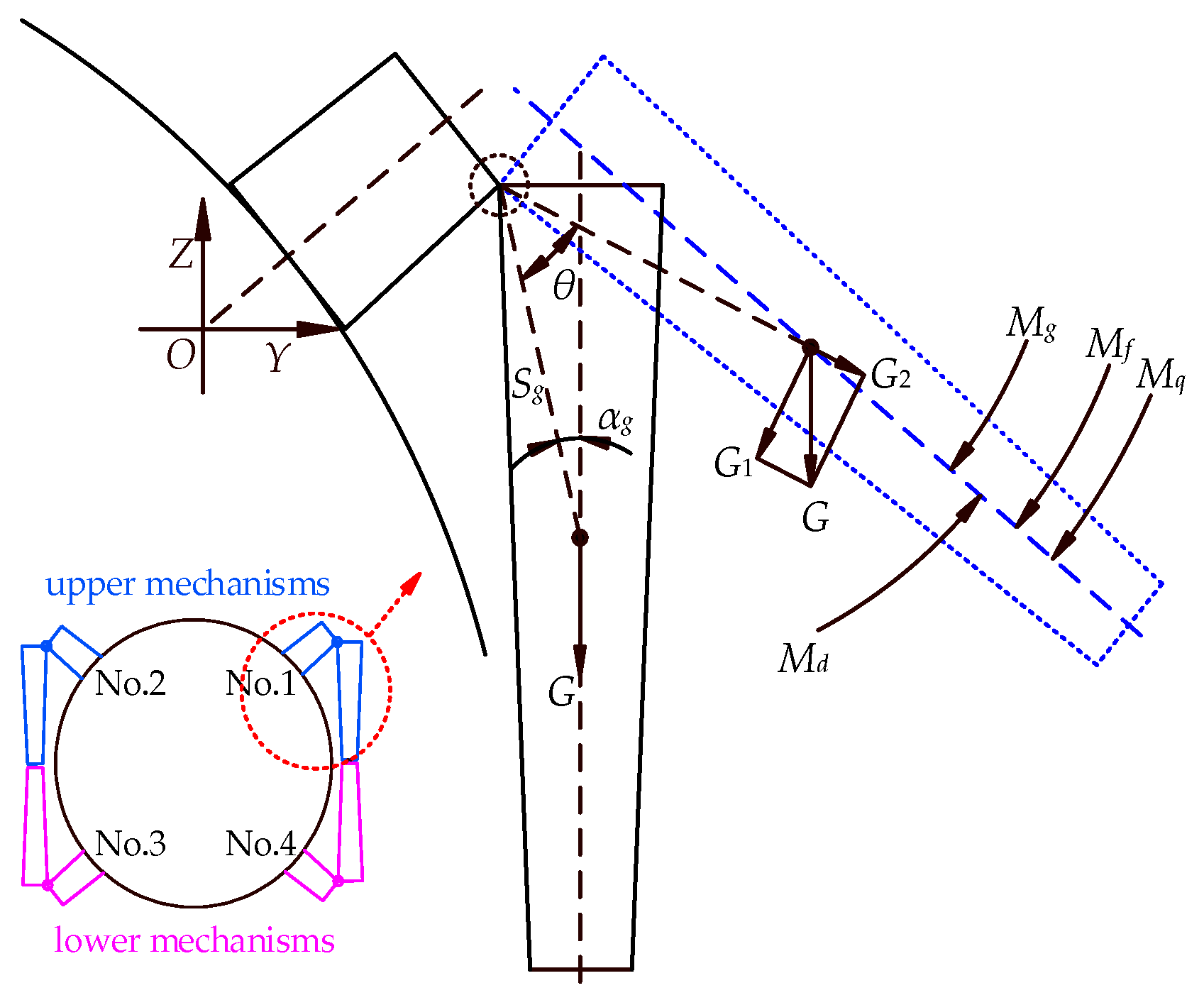
2.1. Working Principle
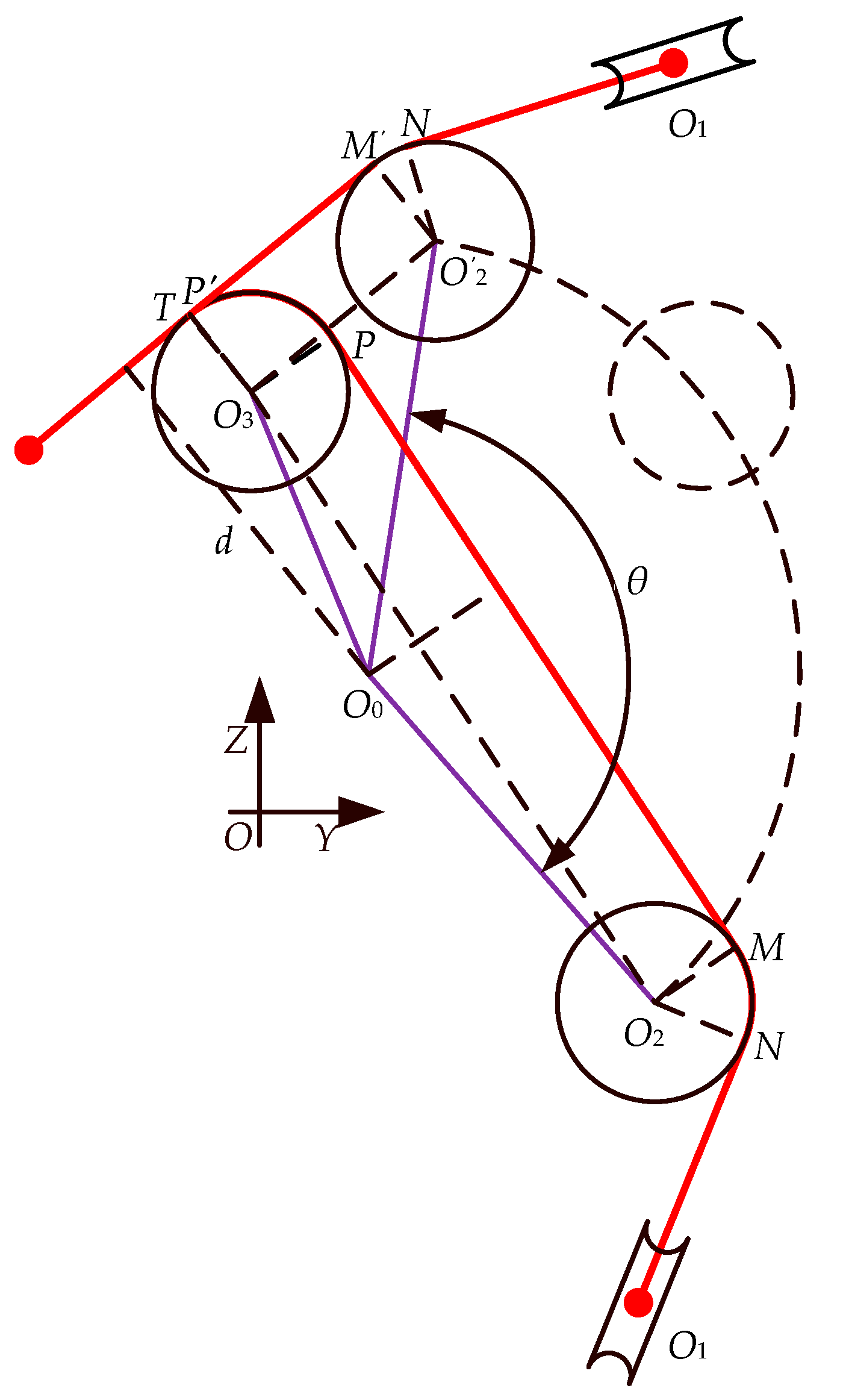
2.2. Theoretical Modeling
2.3. Solution of Theoretical Model
3. Dynamic Simulation
3.1. Simulation Model
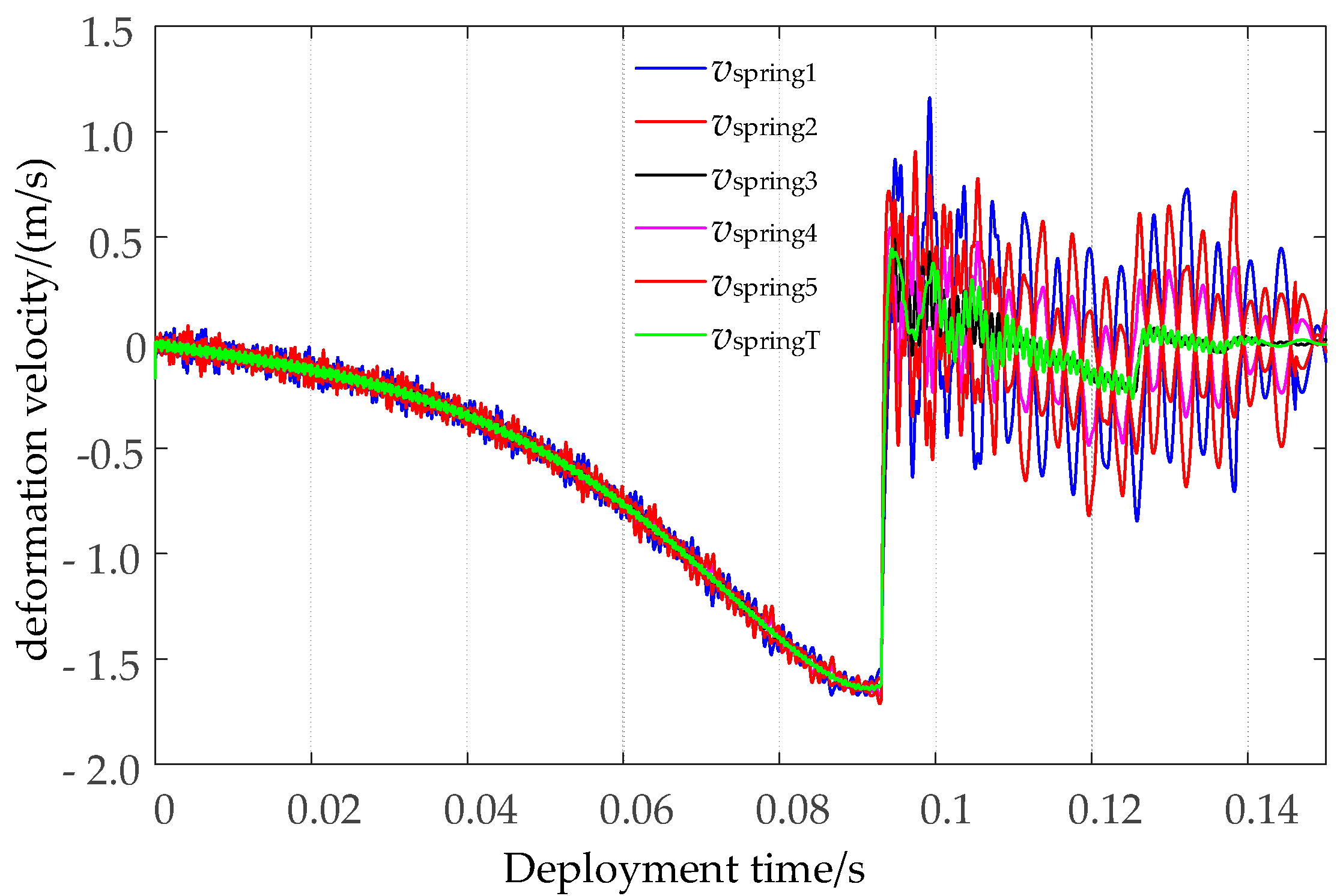
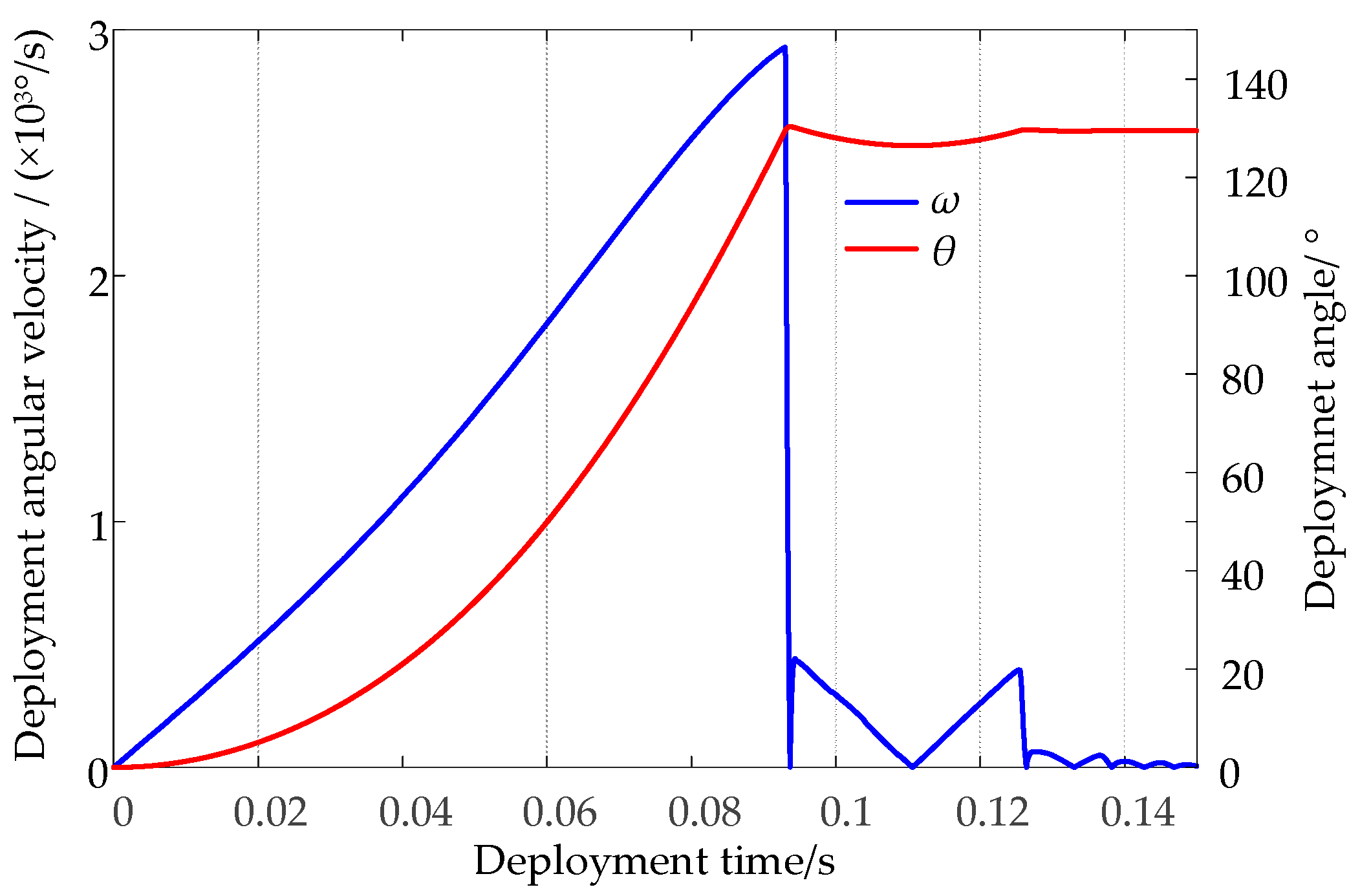
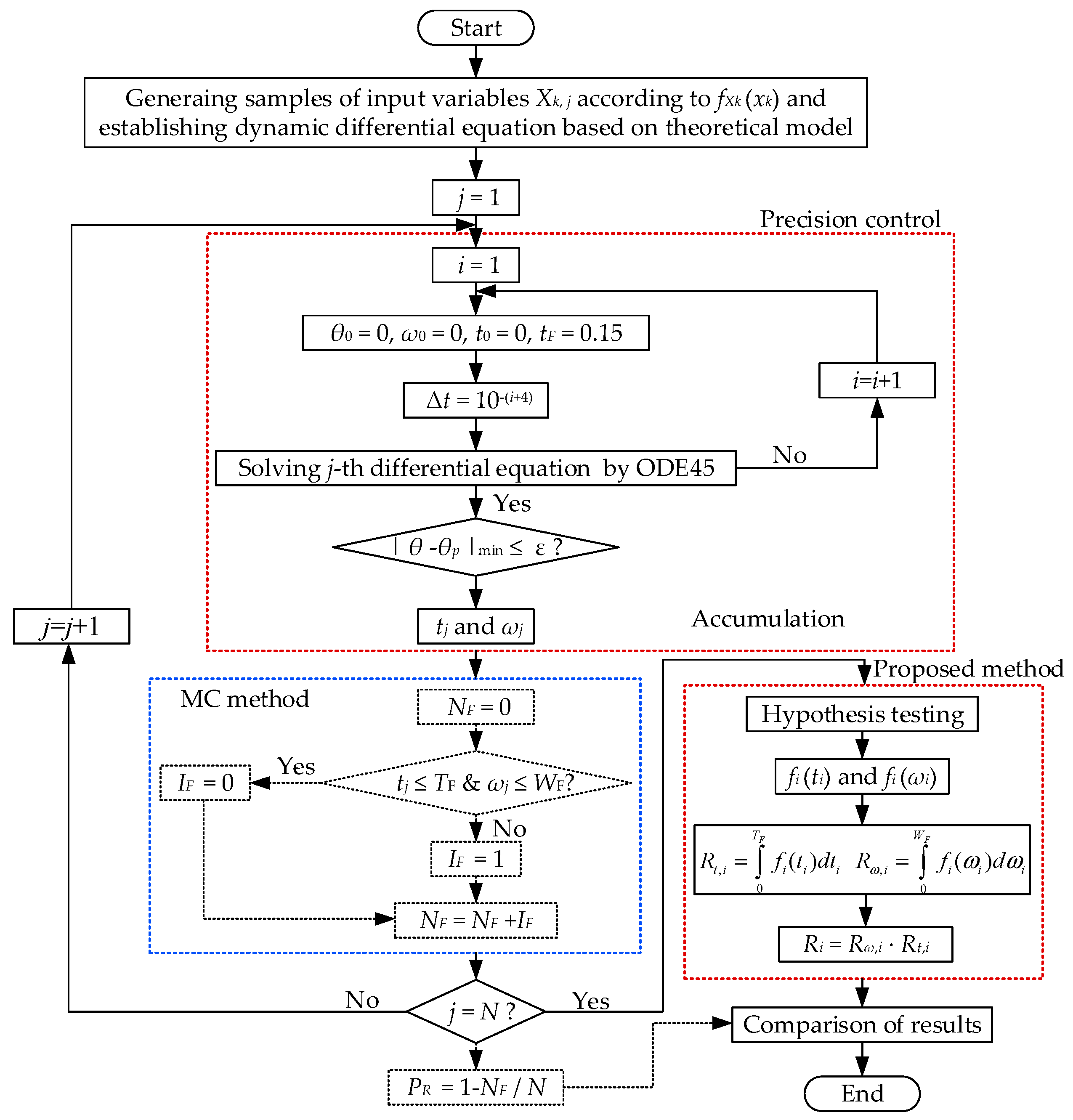
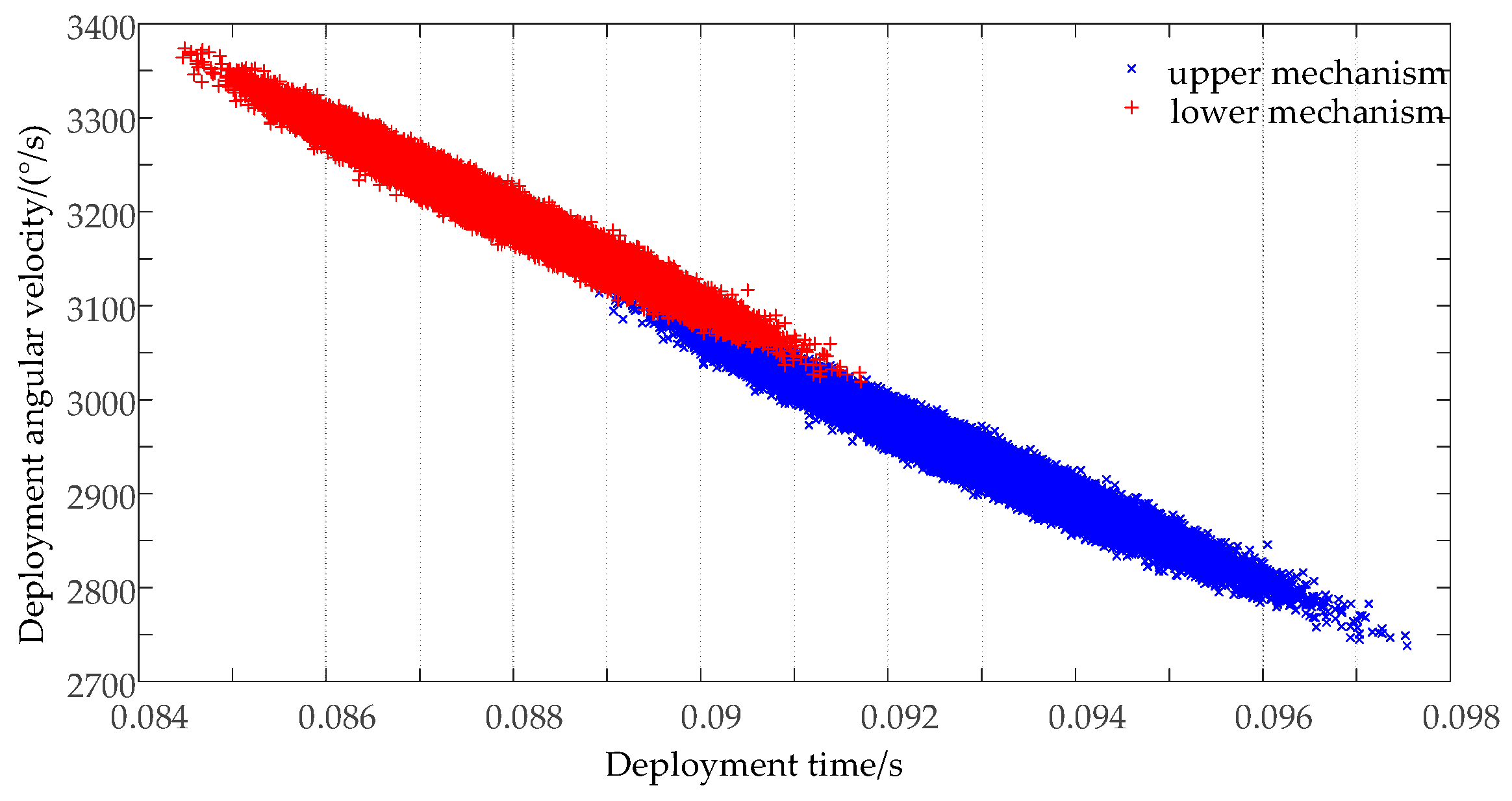
3.2. Solution of Dynamic Simulation Model
3.3. Comparison of Results
4. Reliability Evaluation
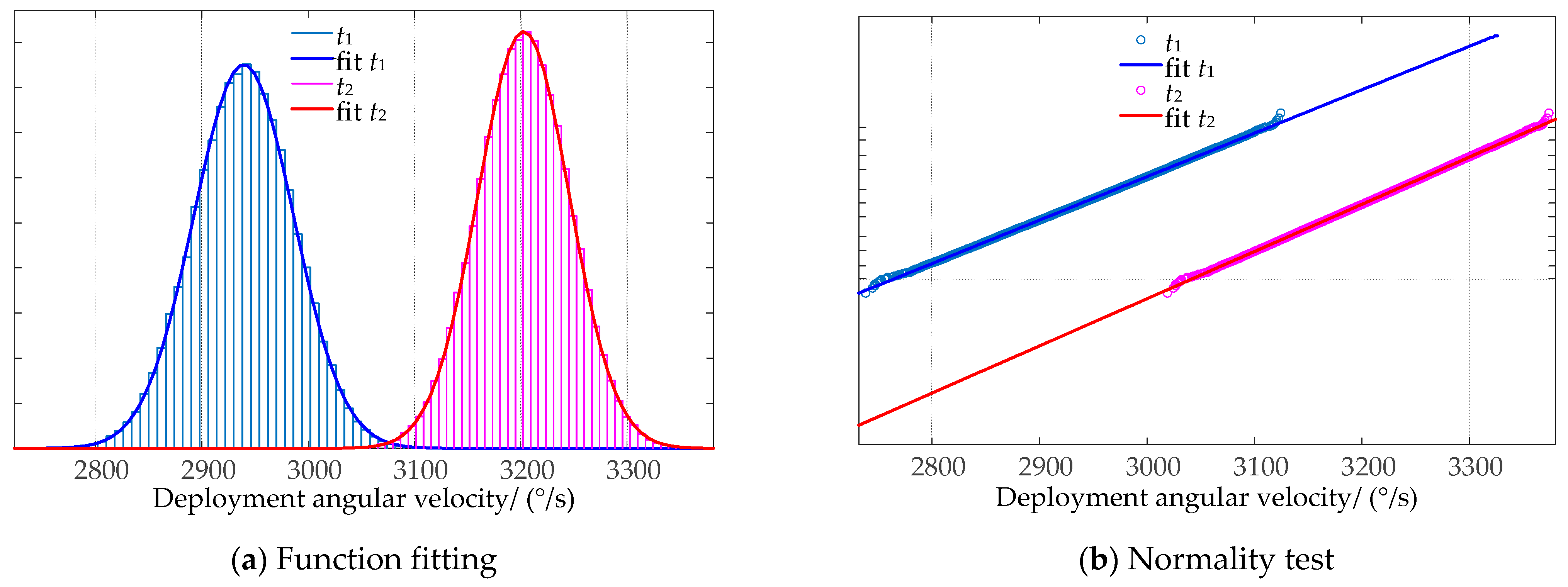
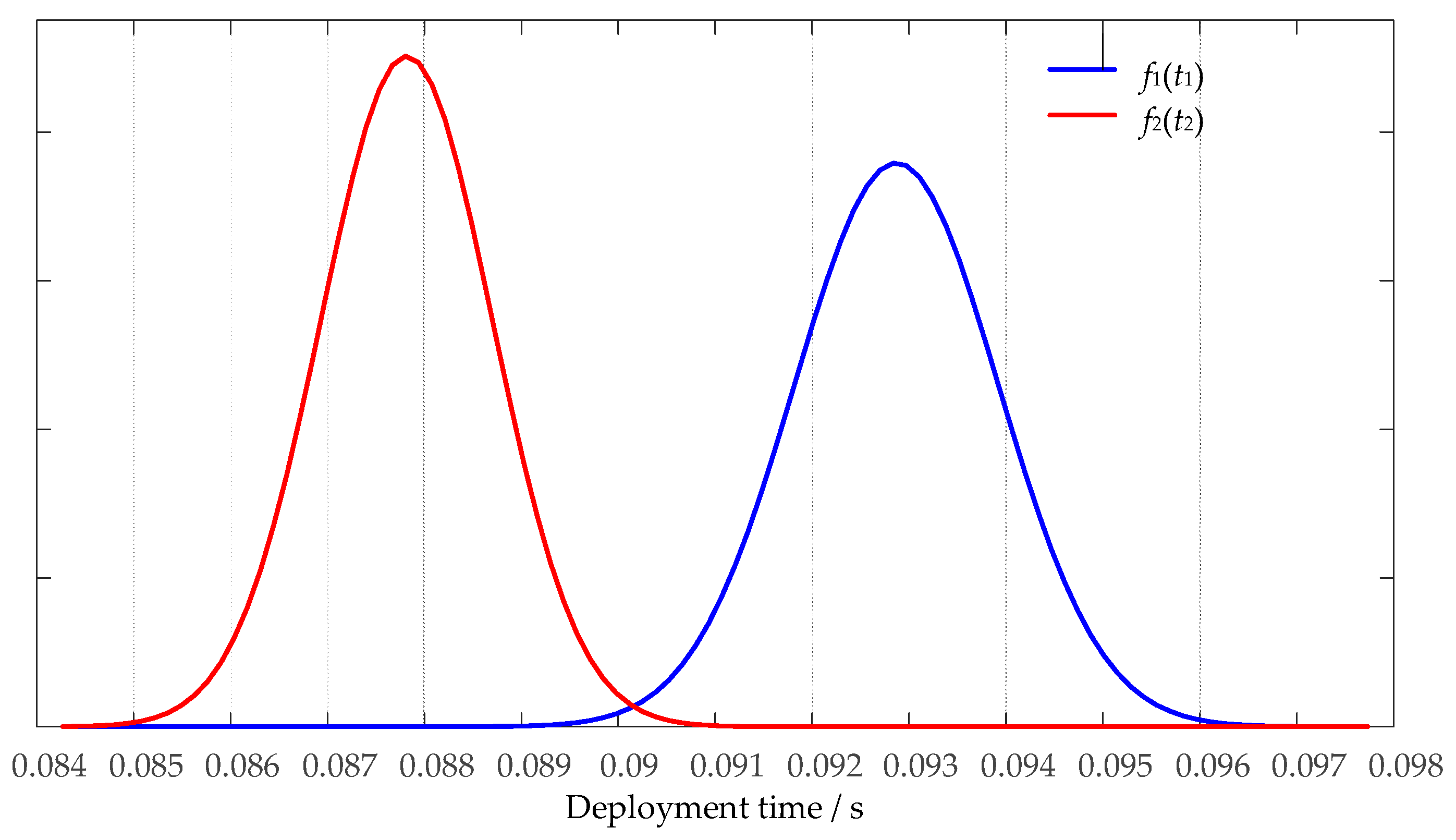
4.1. Reliability of Deployable Mechanism
4.2. Reliability of Folding Wing
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, X.; Ge, J.; Duan, D.; Ni, J. Modern Structure Design of Missiles; National Defense Industry Press: Beijin, China, 2007; pp. 184–235. [Google Scholar]
- Gao, Y.; Hu, M.; Zhao, D.; Gao, X.; Lin, J. Dynamics and reliability analysis of the deployment process of spring folding wing. In Proceedings of the 2020 Inernational Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 8–11 October 2020. [Google Scholar] [CrossRef]
- Yu, J.; Wen, Z.; Mei, Y. Design of Tactical Missile; Beihang University Press: Beijing, China, 2010; pp. 120–157. [Google Scholar]
- Xilun, D.; Anwei, Q.; Kun, X.U. Design and analysis of a scissor-bending deployable and foldable mechanism. J. Mech. Eng. 2020, 56. [Google Scholar] [CrossRef]
- Henry, J.; Schwartz, D.R.; Soukup, M.A.; Altman, A. Design, construction, and testing of a folding-wing, tube-launched micro air vehicle. In Proceedings of the 42rd AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Xu, H.; Huang, Q.; Han, J.; Yun, H.; Xie, X.P. Calculation of hinge moments for a folding wing aircraft based on high-order panel method. Math. Probl. Eng. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Otsuka, K.; Wang, Y.; Makihara, K. Deployable wing model considering structural flexibility and aerodynamic unsteadiness for deployment system design. J. Sound Vib. 2017, 408, 105–122. [Google Scholar] [CrossRef]
- Dowell, E.H.; Tang, D.; Attar, P.J. Nonlinear aeroelastic study for folding wing structure. AIAA J. 2010, 48, 2187–2195. [Google Scholar]
- Tang, D.; Dowell, E.H. Theoretical and experimental aeroelastic study for folding wing structures. J. Aircr. 2008, 45, 1136–1147. [Google Scholar] [CrossRef]
- Wang, B.; Xie, L.; Fan, F.; Ma, H.; Zhao, B.; Li, H. Reliability analysis of folding wing deployable mechanism considering common cause failure. J. Mech. Eng. 2020, 56, 161–171. [Google Scholar] [CrossRef]
- Kroyer, R. Wing mechanism analysis. Comput. Struct. 1999, 72, 253–265. [Google Scholar] [CrossRef]
- Wang, I.; Dowell, E. A structural dynamics model of a multi-segmented folding wing: Theory and experiment. J. Aircr. 2013, 48, 2149–2160. [Google Scholar] [CrossRef]
- Wang, I.; Iv, S.C.G.; Dowell, E. Aeroelastic analysis of a folding wing: Comparison of simple and higher fidelity models for a wide range of fold angles. In Proceedings of the AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, & Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar]
- Coffin, P.; Marzocca, P.; Jha, R.; Ahmadi, G. Deployment dynamics of a small carbon fiber tape-spring UAV wing. In Proceedings of the ASME 2011 International Mechanical Engineering Congress & Exposition, Denver, CO, USA, 11–17 November 2011; pp. 1–6. [Google Scholar]
- Harris, J.; Slegers, N. Performance of a fire-and-forget anti-tank missile with a damaged wing. Math. Comput. Model. 2009, 50, 292–305. [Google Scholar] [CrossRef] [Green Version]
- Liao, M.; Renaud, G. Fatigue analysis for CF-18 component:wing fold shear-tie lug. Procedia Eng. 2010, 2, 1673–1682. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, M.; Chen, W.; Tian, F.; Zhang, H.; Zhou, X. Expand performance and simulation verification of line-styled folding-wing. China Mech. Eng. 2015, 26, 1801–1805. [Google Scholar]
- Pang, H.; Yu, T.; Wang, N. Synchronization reliability evaluation method for mechanisms with different time distribution. Math. Probl. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Qiao, S.; L.iu, R.; Guo, H.; Ding, S.; Li, B.; Deng, Z. Motion control of 3-DOF under-actuated cable-truss robotic hand. J. Mech. Eng. 2020, 56, 78–88. [Google Scholar] [CrossRef]
- Lu, Z.; Song, S.; Li, H. Reliability and Reliability Sensitivity Analysis of Structures and Mechanisms; Science Press: Beijing, China, 2009; pp. 210–280. [Google Scholar]
- Wu, Y.; Mohanty, S. Variable screening and ranking using sampling-based sensitivity measures. Reliab. Eng. Syst. Saf. 2006, 91, 634–647. [Google Scholar] [CrossRef]
- Guo, W.; Cui, W.; Shi, Y.; Liu, J.; Song, B. Function failure and failure boundary analysis for an aircraft lock mechanism. Eng. Fail. Anal. 2016, 70, 428–442. [Google Scholar] [CrossRef]
- Lv, Z.; Song, S.; Li, L.; Wang, Y. The Basis of Structural or Mechanism Reliability Design; Northwestern Polytechnical University Press: Xi’an, China, 2019; pp. 65–66. [Google Scholar]





| Parameter | O1 | O2 | O3 |
|---|---|---|---|
| With/mm | 7.0 | 7.0 | 6.6 |
| Depth/mm | 3 | 1.8 | 1.8 |
| Radius/mm | 2.0 | 2.0 | 2.0 |
| Angle/° | 20.0 | 20.0 | 20.0 |
| Location | O1 | O2 | O3 |
| Diameter/mm | 25.6 | 16.0 | 16.0 |
| Mis-alignment X/° | 66.6715 | 0.0 | 0.0 |
| Mis-alignment Y/° | 7800 | 7800 | 7800 |
| Joint Type | Fixed | Revolute | Revolute |
| Connection Part | Outer wing | Outer wing | Inner wing |
| Variables | Factors | Distribution Type | Mean | Standard Deviation | Bias | Range |
|---|---|---|---|---|---|---|
| x1 | y2 | Normal distribution | 6.50 | 0.01 | (−0.03, 0.03) | (6.47, 6.53) |
| x2 | z2 | −249.50 | 0.01 | (−0.03, 0.03) | (−249.53, −249.47) | |
| x3 | y3 | −26.67 | 0.01 | (−0.03, 0.03) | (−26.7, −26.64) | |
| x4 | z3 | −200.16 | 0.01 | (−0.03, 0.03) | (−200.19, −200.13) | |
| x5 | R | 8 | 0.0167 | (−0.05, 0.05) | (7.95, 8.05) | |
| x6 | f0 | 520 | 10 | (−30, 30) | (490, 550) | |
| x7 | ks | 5.6 | 0.1 | (−0.3, 0.3) | (5.3, 5.9) | |
| x8 | fv | 0.1 | 0.0067 | (−0.02, 0.02) | (0.08, 0.12) | |
| x9 | fr | 4 | 0.0167 | (−0.05, 0.05) | (3.95, 4.05) |
| Specified Condition | Reliability Ri | Error % | ||
|---|---|---|---|---|
| TF | WF | Proposed Method | MC Method | |
| 0.0935 | 2975 | 0.56338 | 0.50484 | 10.391 |
| 0.0935 | 3000 | 0.65453 | 0.63205 | 3.434 |
| 0.094 | 3000 | 0.77471 | 0.76106 | 1.761 |
| 0.094 | 3025 | 0.82970 | 0.82605 | 0.440 |
| 0.0945 | 3025 | 0.90765 | 0.90505 | 0.286 |
| 0.0945 | 3050 | 0.93087 | 0.92898 | 0.203 |
| 0.095 | 3050 | 0.96966 | 0.96842 | 0.127 |
| 0.095 | 3075 | 0.97673 | 0.97519 | 0.158 |
| 0.0955 | 3075 | 0.99191 | 0.99101 | 0.091 |
| 0.096 | 3100 | 0.99823 | 0.99766 | 0.057 |
| 0.0965 | 3125 | 0.99968 | 0.99949 | 0.019 |
| 0.097 | 3150 | 0.99996 | 0.99985 | 0.011 |
| 0.0935 | 2975 | 0.56338 | 0.50484 | 10.391 |
| Deployment Performance | Synchronization | Methodology | Error % | |||
|---|---|---|---|---|---|---|
| TF/ms | ΔT/ms | Rt,1 | Rt,2 | Rt,3 | Rt,4 | |
| 95 | 5.5 | 0.97685 | 0.99440 | 0.97685 | 0.97138 | 0.56 |
| 95 | 5.4 | 0.97685 | 0.98077 | 0.97623 | 0.95807 | 1.86 |
| 94 | 5.5 | 0.85841 | 0.99440 | 0.85841 | 0.85360 | 0.56 |
| 94 | 5.2 | 0.85841 | 0.80969 | 0.81198 | 0.69505 | 14.40 |
| 94 | 5.0 | 0.85841 | 0.38450 | 0.38446 | 0.33006 | 14.15 |
| 93 | 5.1 | 0.55622 | 0.61034 | 0.55622 | 0.33948 | 38.97 |
| 92 | 5.0 | 0.20687 | 0.38450 | 0.20687 | 0.07954 | 61.55 |
| 92 | 4.9 | 0.20687 | 0.18065 | 0.18033 | 0.03737 | 79.28 |
| 95 | 5.5 | 0.97685 | 0.99440 | 0.97685 | 0.97138 | 0.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Hu, M.; Zhou, X.; Zhang, M. Reliability Evaluation for Cable-Spring Folding Wing Considering Synchronization of Deployable Mechanism. Actuators 2021, 10, 99. https://doi.org/10.3390/act10050099
Gao Y, Hu M, Zhou X, Zhang M. Reliability Evaluation for Cable-Spring Folding Wing Considering Synchronization of Deployable Mechanism. Actuators. 2021; 10(5):99. https://doi.org/10.3390/act10050099
Chicago/Turabian StyleGao, Yun, Ming Hu, Xiaohong Zhou, and Mingzhong Zhang. 2021. "Reliability Evaluation for Cable-Spring Folding Wing Considering Synchronization of Deployable Mechanism" Actuators 10, no. 5: 99. https://doi.org/10.3390/act10050099






