Adaptive Terminal Sliding Mode Control of Picking Manipulator Based on Uncertainty Estimation
Abstract
:1. Introduction
2. Preliminaries
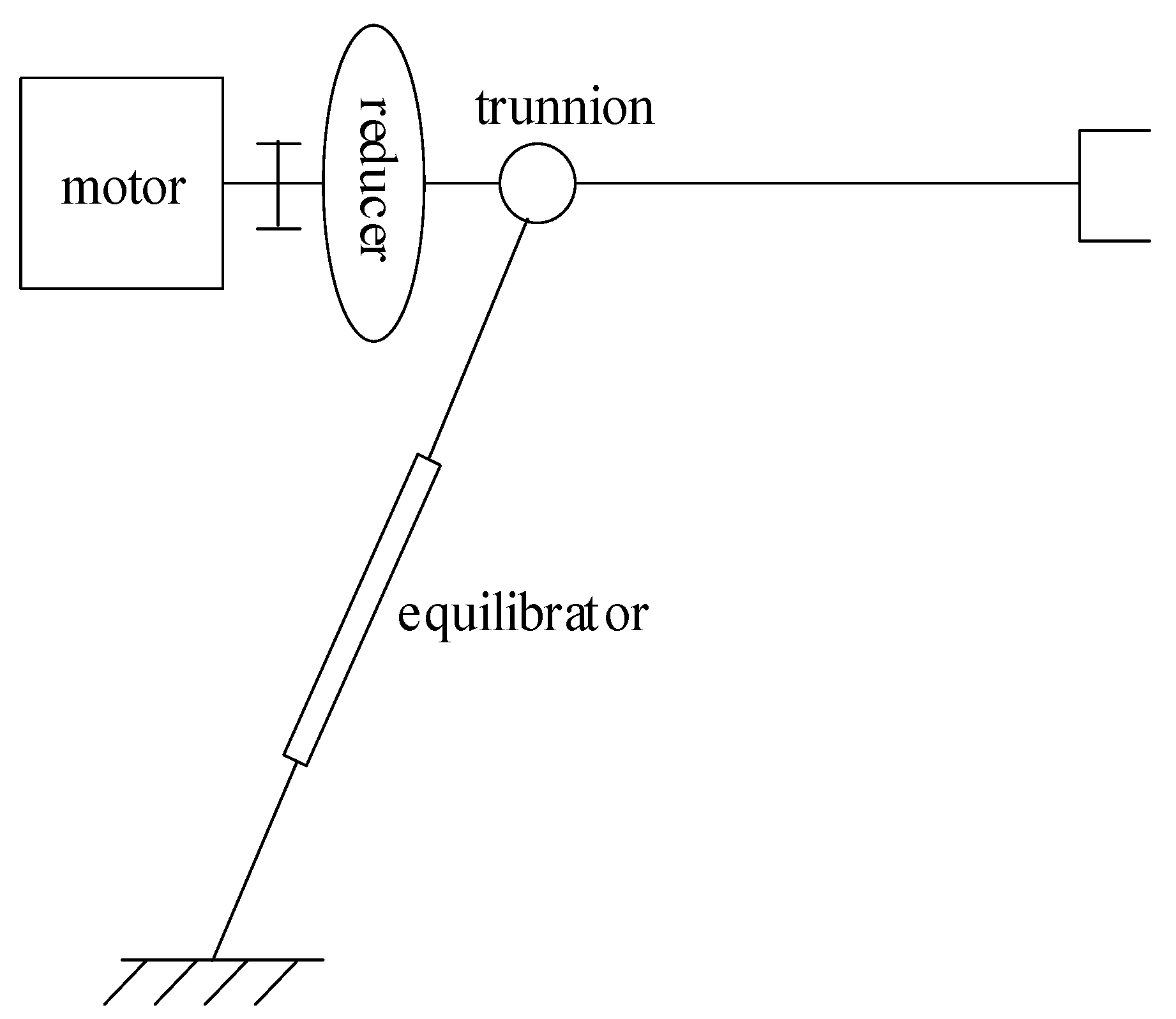
2.1. Dynamic Model of Picking Manipulator
2.2. Problem Description
3. Controller Design of the Picking Manipulator
3.1. ANFTSM Controller
3.2. Stability Analysis
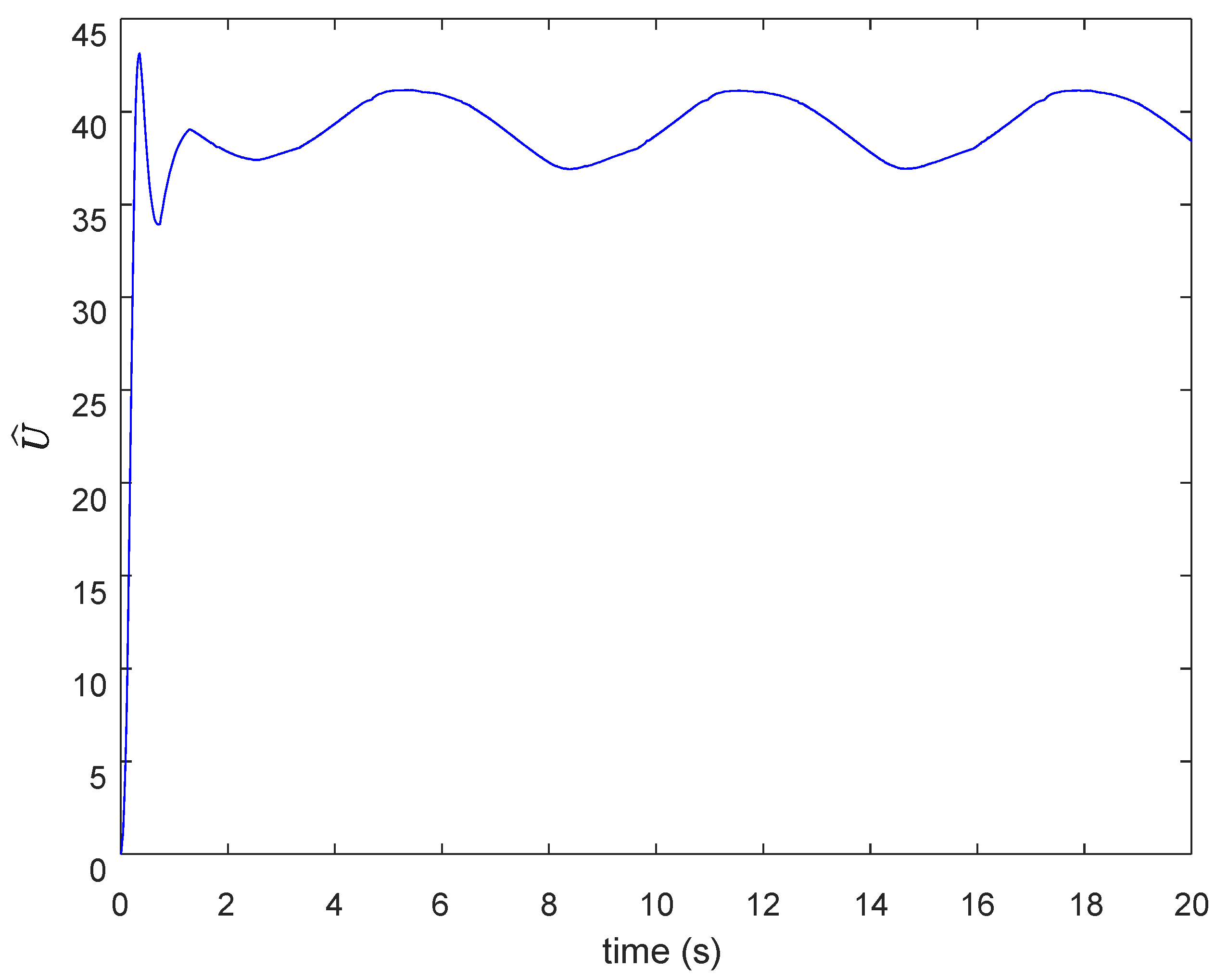
3.3. Friction Parameter Identification
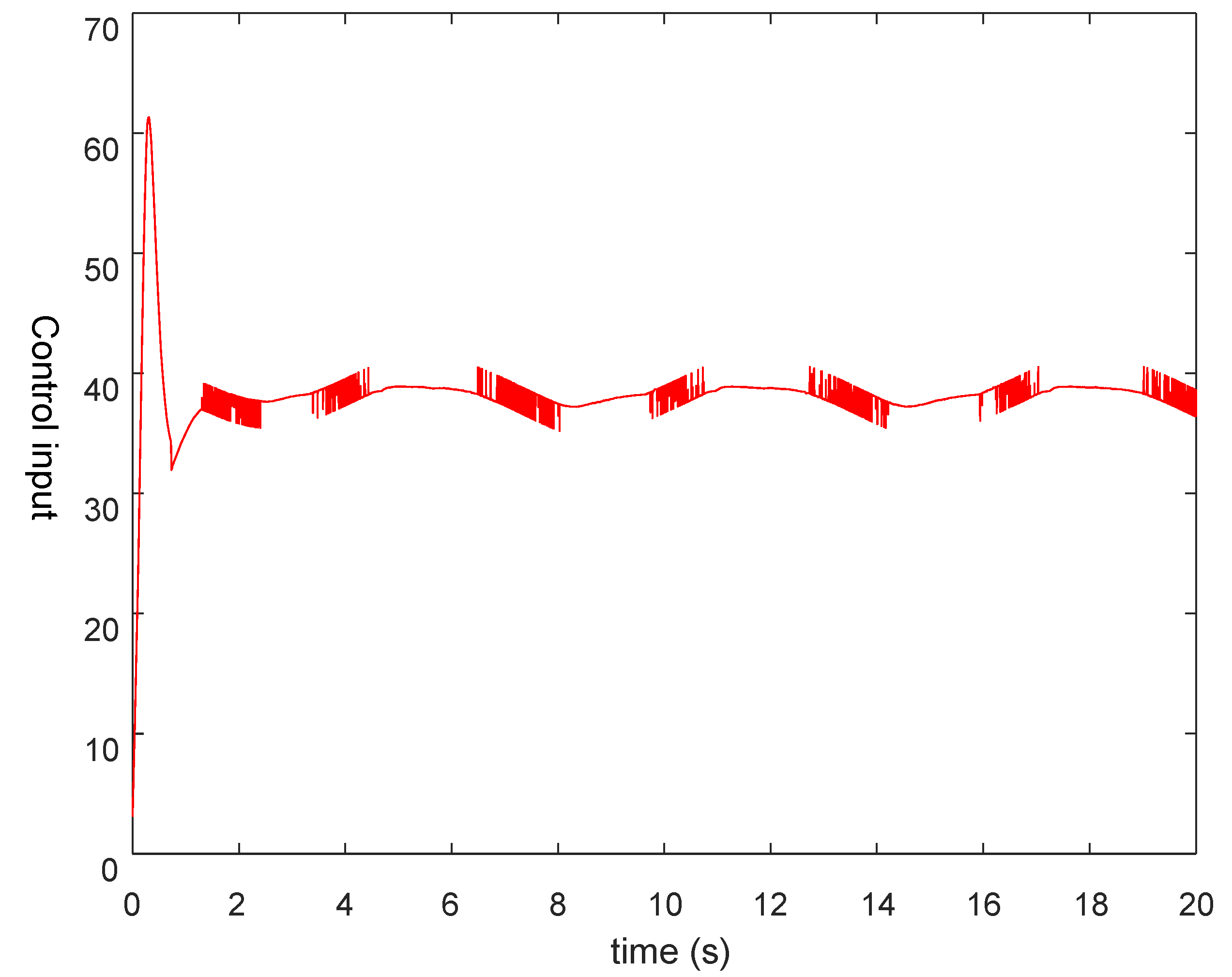
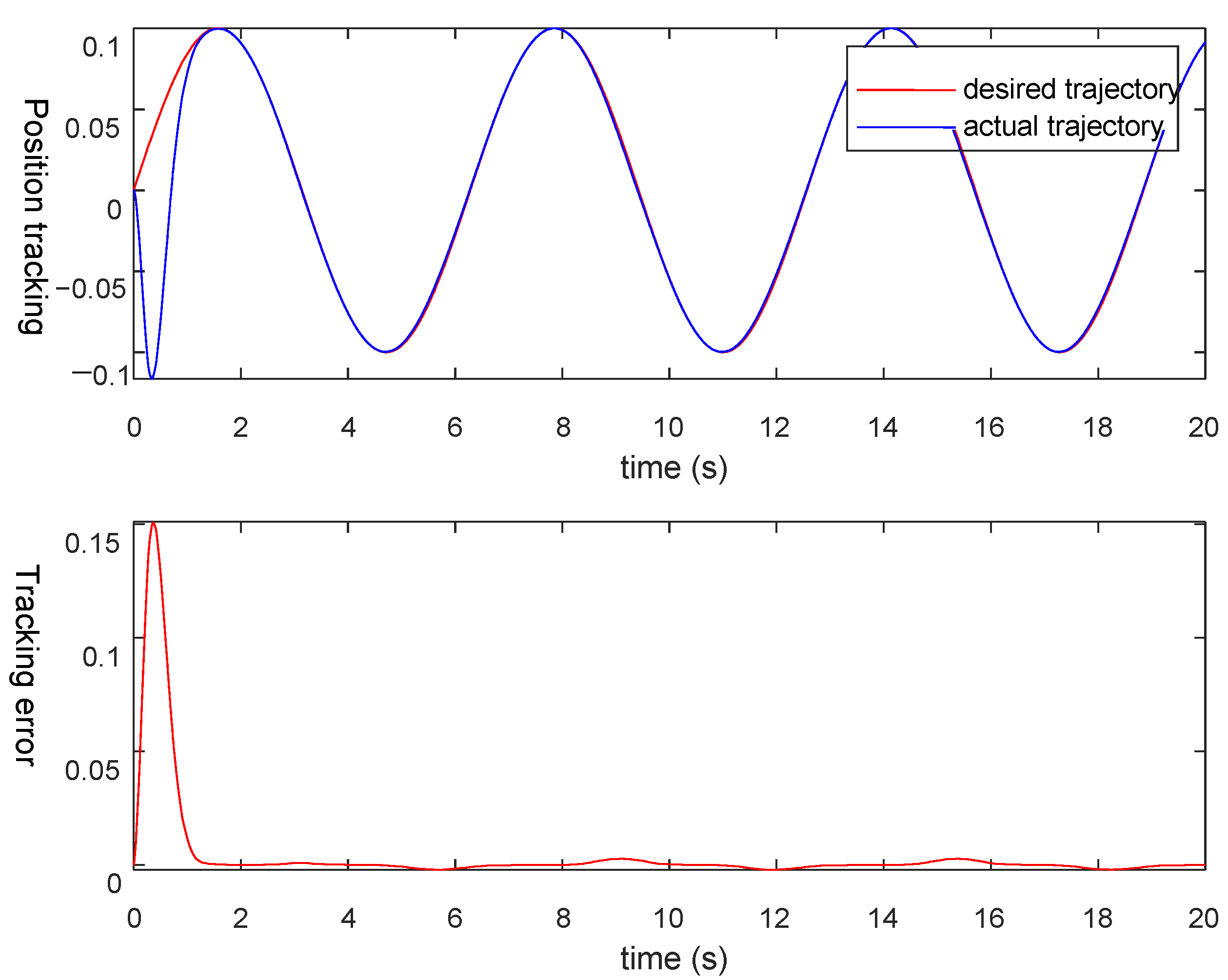
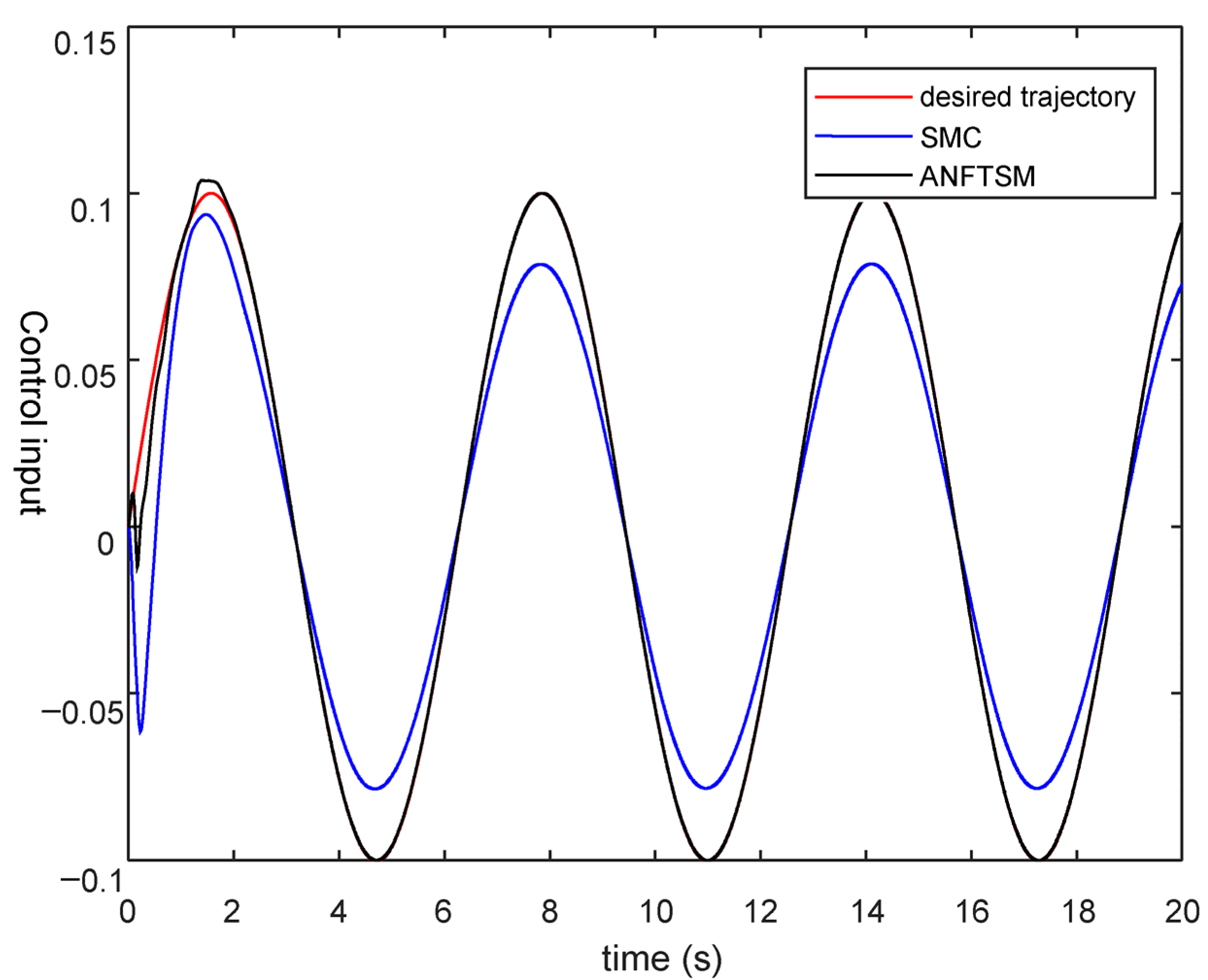
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Cheng, Z.; Zhang, F. Design of the Divided No-till Wheat Planter Orchard Picking Manipulator Research. J. Agric. Mech. Res. 2020, 14, 158–163. [Google Scholar]
- Yu, X.; Fan, Z.; Wang, X.; Wan, H.; Wang, P.; Zeng, X.; Jia, F. A lab-customized autonomous humanoid apple harvesting robot. Comput. Electr. Eng. 2021, 96, 107459. [Google Scholar] [CrossRef]
- Fang, Z.; Liang, X.F. Intelligent obstacle avoidance path planning method for picking manipulator combined with artificial potential field method. Ind. Robot 2022, 49, 835–850. [Google Scholar] [CrossRef]
- Schuetz, C.; Baur, J.; Pfaff, J.; Buschmann, T.; Ulbrich, H. Evaluation of a direct optimization method for trajectory planning of a 9-DOF redundant fruit-picking manipulator. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2660–2666. [Google Scholar]
- Liu, Y.C.; Yan, W.; Zhang, T.; Yu, C.X.; Tu, H.Y. Trajectory Tracking for a Dual-Arm Free-Floating Space Robot with a Class of General Nonsingular Predefined-Time Terminal Sliding Mode. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3273–3286. [Google Scholar] [CrossRef]
- Khurram, A.; Adeel, M.; Jamshed, I. Terminal Sliding Mode Control of an Anthropomorphic Manipulator with Friction Based Observer. In Proceedings of the 2021 International Conference on Robotics and Automation in Industry, Xi’an, China, 30 May –5 June 2021; pp. 143–150. [Google Scholar]
- Xu, H.; Li, M.; Lu, C.L. Nonlinear sliding mode control of manipulator based on iterative learning algorithm. J. Electr. Syst. 2021, 17, 421–437. [Google Scholar]
- Su, L.Q.; Guo, X.; Ji, Y. Tracking control of cable-driven manipulator with adaptive fractional-order nonsingular fast terminal sliding mode control. JVC/J. Vib. Control 2021, 27, 2482–2493. [Google Scholar] [CrossRef]
- Lu, Z.P.; Li, Y.; Fan, X.; Li, Y.C. Decentralized Fault Tolerant Control for Modular Robot Manipulators via Integral Terminal Sliding Mode and Disturbance Observer. Int. J. Control Autom. Syst. 2022, 20, 3274–3284. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R. Adaptive fuzzy global coupled nonsingular fast terminal sliding mode control of n-rigid-link elastic-joint robot manipulators in presence of uncertainties. Mech. Syst. Signal Process. 2022, 163, 108165. [Google Scholar] [CrossRef]
- Song, T.Z.; Fang, L.; Wang, H.Z. Model-free finite-time terminal sliding mode control with a novel adaptive sliding mode observer of uncertain robot systems. Asian J. Control 2022, 24, 1437–1451. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef]
- Zhang, S.J.; Cao, Y. Cooperative Localization Approach for Multi-Robot Systems Based on State Estimation Error Compensation. Sensors 2019, 19, 3842–3852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Li, B.; Yan, F. Practical adaptive fractional-order nonsingular terminal sliding mode control for a cable-driven manipulator. Int. J. Robust Nonlinear Control 2019, 29, 1396–1417. [Google Scholar] [CrossRef]
- Hao, S.; Hu, L.Y.; Liu, P. Second-order adaptive integral terminal sliding mode approach to tracking control of robotic manipulators. IET Control Theory Appl. 2021, 15, 2145–2157. [Google Scholar] [CrossRef]
- Van, M.; Mavrovouniotis, M.; Ge, S.Z. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1448–1458. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.Y.; Sun, G.H.; Xue, C. Nonsingular terminal sliding mode control for free-floating space manipulator with disturbance. Acta Astronaut. 2021, 181, 396–404. [Google Scholar] [CrossRef]
- Zhang, S.; Cao, Y. Consensus in networked multi-robot systems via local state feedback robust control. Int. J. Adv. Robot. Syst. 2019, 16, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.M.; Han, F.L.; Feng, Y. Hybrid continuous nonsingular terminal sliding mode control of uncertain flexible manipulators. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Dallas, TX, USA, 29 October–1 November 2014; pp. 190–196. [Google Scholar]
- Fang, H.R.; Wu, Y.; Xu, T.; Wan, F.X. Adaptive neural sliding mode control of uncertain robotic manipulators with predefined time convergence. Int. J. Robust Nonlinear Control 2022, 32, 223–238. [Google Scholar] [CrossRef]
- Mourad, K.; Magdi, S.M. Robust-QSR γ-dissipative sliding mode control for uncertain discrete-time descriptor systems with time-varying delay. IMA J. Math. Control Inf. 2018, 35, 735–756. [Google Scholar]
- Charfeddine, S.; Boudjemline, A.; Ben Aoun, S.; Jerbi, H.; Kchaou, M.; Alshammari, O.; Elleuch, Z.; Abbassi, R. Design of a fuzzy optimization control structure for nonlinear systems: A disturbance-rejection method. Appl. Sci. 2021, 11, 2612. [Google Scholar] [CrossRef]
- Abbassi, A.; Ben Mehrez, R.; Bensalem, Y.; Abbassi, R.; Kchaou, M.; Jemli, M.; Abualigah, L.; Altalhi, M. Improved Arithmetic Optimization Algorithm for Parameters Extraction of Photovoltaic Solar Cell Single-Diode Model. Arab. J. Sci. Eng. 2022, 47, 10435–10451. [Google Scholar] [CrossRef]
- Yang, G.C.; Yao, J.Y.; Dong, Z.L. Neuroadaptive learning algorithm for constrained nonlinear systems with disturbance rejection. Int. J. Robust Nonlinear Control 2022, 32, 6127–6147. [Google Scholar] [CrossRef]
- Yang, G.C.; Yao, J.Y.; Dong, Z.L. Multilayer neuroadaptive force control of electro-hydraulic load simulators with uncertainty rejection. Appl. Soft Comput. 2022, 130, 109672. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, B.; Liu, W. A compound scheme on parameters identification and adaptive compensation of nolinear friction disturbance for the aerial intertially stabilized platform. ISA Trans. 2017, 67, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Si, Y.J.; Song, S.M. Adaptive reaching law based three-dimensional finite-time guidance law against maneuvering targets with input saturation. Aerosp. Sci. Technol. 2017, 70, 198–210. [Google Scholar] [CrossRef]
- Sun, H.Q.; Zhang, S.J.; Quan, Q.L. Trajectory Tracking Robust Control Method Based on Finite-Time Convergence of Manipulator with Nonsingular Fast Terminal Sliding Mode Surface. J. Control Sci. Eng. 2022, 2022, 2271804. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| 0.35/MPa | |
| S | 6.8 × 10−5/m2 |
| V0 | 7.654 × 10−5/m3 |
| n | 1.2 |
| i1 | 630 |
| 0 |
| Parameters | Identification Results |
|---|---|
| 7.2401/Nm | |
| 6.0127/Nm | |
| 0.3102/Nm | |
| 6.2149/Nm | |
| 0.3660 rad/s | |
| 1.2681 rad/s | |
| 0.9460 Nms/rad | |
| 1.7982 Nms/rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Zhang, S. Adaptive Terminal Sliding Mode Control of Picking Manipulator Based on Uncertainty Estimation. Actuators 2022, 11, 347. https://doi.org/10.3390/act11120347
Wu C, Zhang S. Adaptive Terminal Sliding Mode Control of Picking Manipulator Based on Uncertainty Estimation. Actuators. 2022; 11(12):347. https://doi.org/10.3390/act11120347
Chicago/Turabian StyleWu, Caizhang, and Shijie Zhang. 2022. "Adaptive Terminal Sliding Mode Control of Picking Manipulator Based on Uncertainty Estimation" Actuators 11, no. 12: 347. https://doi.org/10.3390/act11120347





