Modeling and Clamping Force Tracking Control of an Integrated Electric Parking Brake System Using Sliding-Mode-Based Observer
Abstract
:1. Introduction
2. System Modeling
2.1. Vehicle Model
2.2. Tire Model
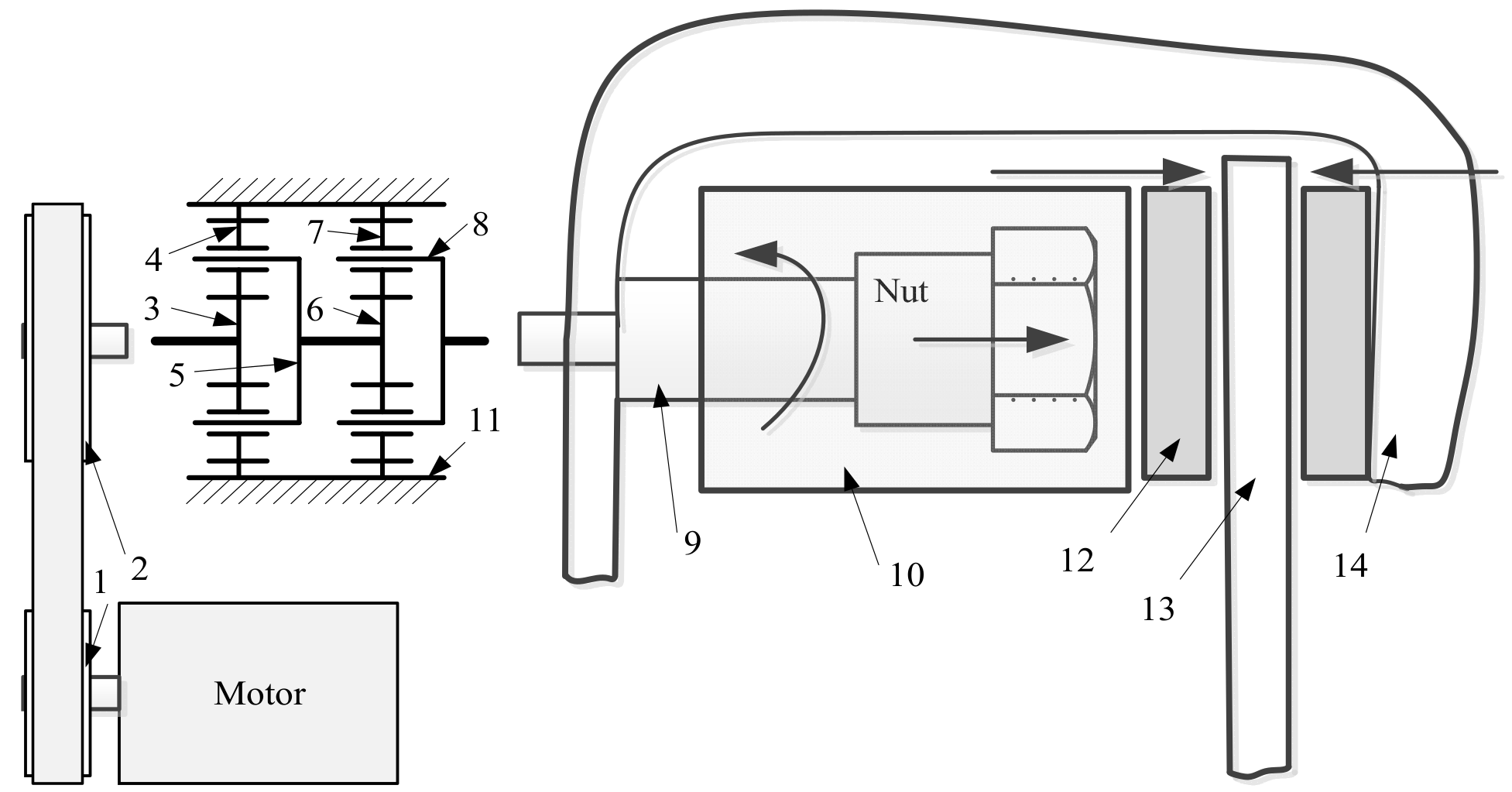
2.3. Structure and DC Motor Model of the iEPB
2.4. Screw-Nut and Caliper Mechanism Model
2.5. Control-Oriented Transmission Mechanism Model
2.6. Brake Model
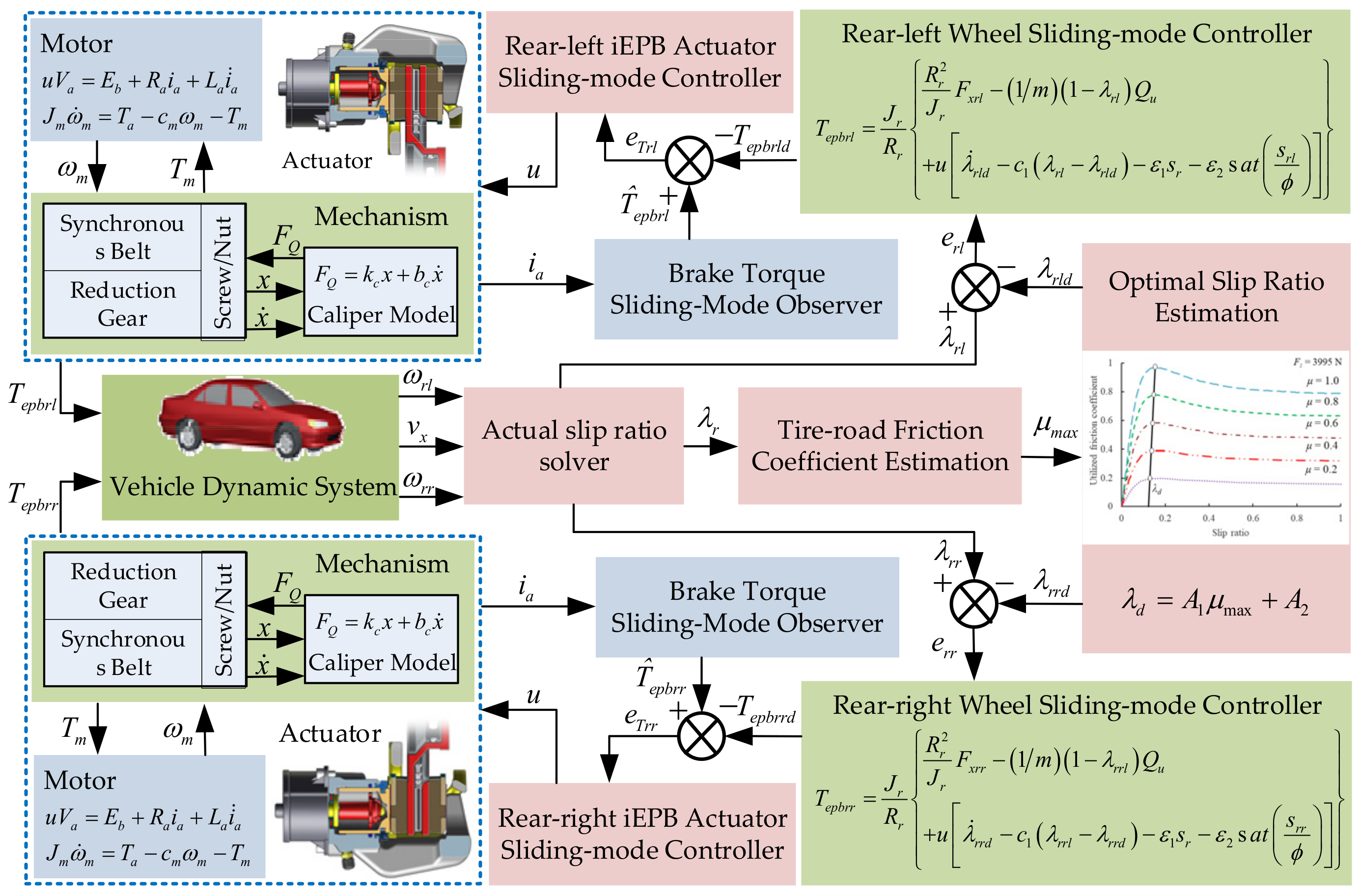
3. Sliding-Mode-Based Load Torque Observer
4. Hierarchical Semi-ABS Controller Design
4.1. Upper Controller
4.2. Lower Controller
5. Experimental Test and Analysis
5.1. HIL Test Bench Design
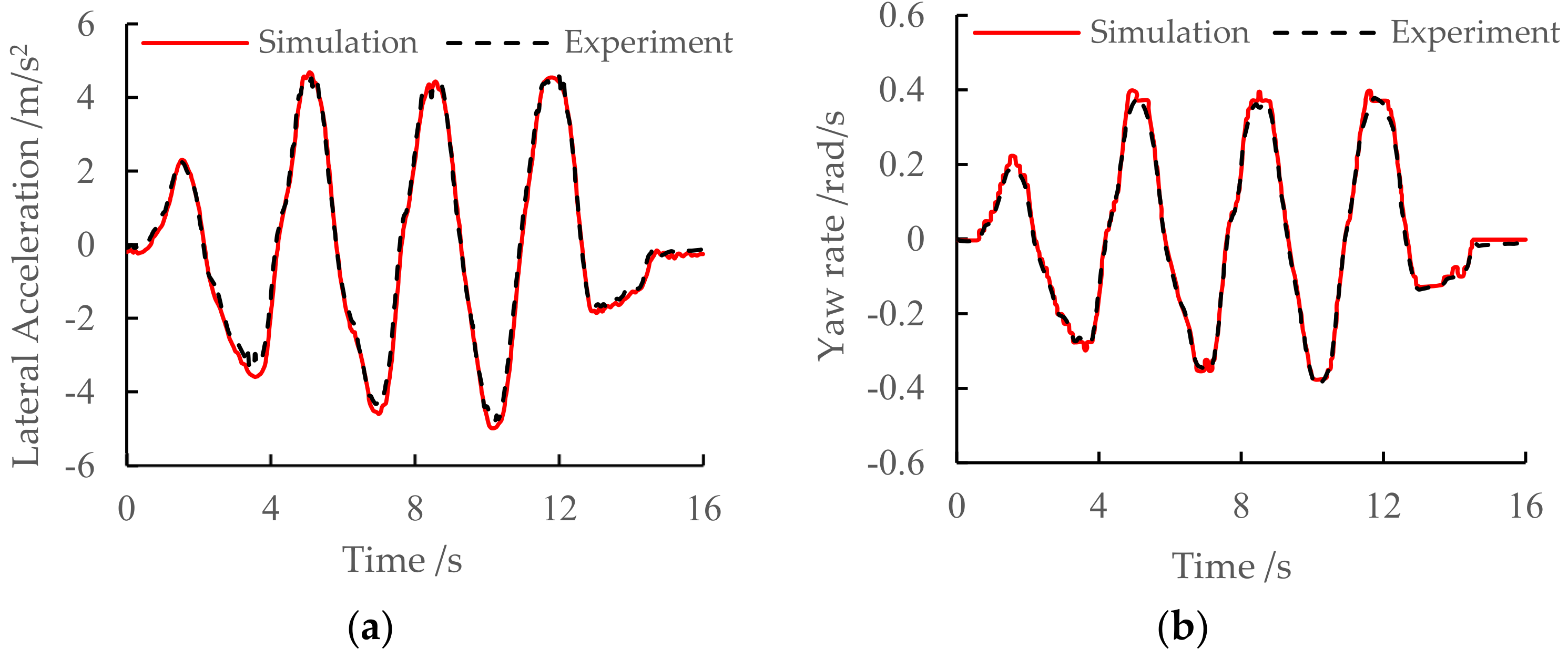
5.2. Vehicle Model Validation and Modification
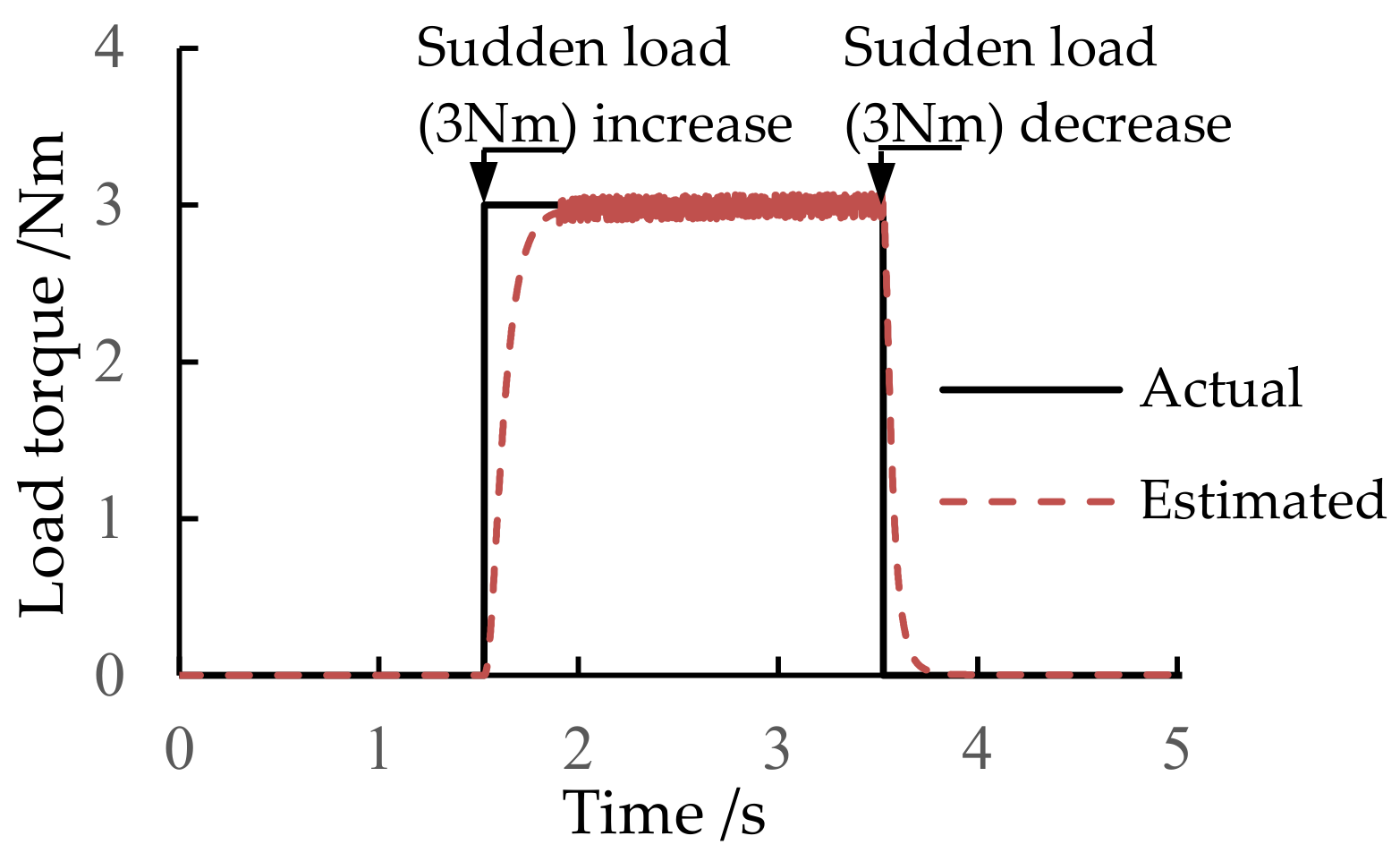
5.3. Experimental Validation of the Load Torque Observer
5.4. Experiment Results and Analysis of the Proposed Controller
5.4.1. Straight-line Braking on High-μ Homogeneous Surface
5.4.2. Straight-Line Braking on Low-μ Homogeneous Surface
5.4.3. Straight-Line Braking on μ-Jump Surface
5.4.4. Straight-Line Braking on μ-Split Surface
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Guo, X.X.; Zhang, W.; Chen, Z.F. A study of an electric parking brake system for emergency braking. Int. J. Veh. Des. 2015, 67, 315–346. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, W.; Zhao, X.; Meng, A.H.; Fahad, M. Force-tracking control of a novel electric parking brake actuator based on a load-sensing, continuously variable transmission. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1569–1582. [Google Scholar] [CrossRef]
- He, Z.J.; Shi, Q.; Wei, Y.J.; Gao, B.Z.; Zhu, B.; He, L. A model predictive control approach with slip ratio estimation for electric motor anti-lock braking of battery electric vehicle. IEEE Trans. Ind. Electron. 2022, 69, 9225–9234. [Google Scholar] [CrossRef]
- Jung, S.; Kim, T.; Yoo, W. Advanced slip ratio for ensuring numerical stability of low-speed driving simulation Part I: Longitudinal slip ratio. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2903–2911. [Google Scholar] [CrossRef]
- Jia, F.J.; Liu, Z.Y.; Zhou, H.J.; Chen, W. A novel design of traction control based on a piecewise-linear parameter-varying technique for electric vehicles with in-wheel motors. IEEE Trans. Veh. Technol. 2018, 67, 9324–9336. [Google Scholar] [CrossRef]
- Li, W.F.; Du, H.P.; Li, W.H. Four-wheel electric braking system configuration with new braking torque distribution strategy for improving energy recovery efficiency. IEEE Trans. Intell. Transp. Syst. 2020, 21, 87–103. [Google Scholar] [CrossRef]
- Milad, J.; Ehsan, H.; Amir, K.; Shih-ken, C.; Bakhtiar, L. A combined-slip predictive control of vehicle stability with experimental verification. Veh. Syst. Dyn. 2018, 56, 319–340. [Google Scholar]
- Li, Z.H.; Wang, P.; Liu, H.H.; Hu, Y.F.; Chen, H. Coordinated longitudinal and lateral vehicle stability control based on the combined-slip tire model in the MPC framework. Mech. Syst. Signal Process 2021, 161, 107947. [Google Scholar] [CrossRef]
- Liu, Y.H.; Li, T.; Yang, Y.Y.; Wu, J. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm. Mech. Syst. Signal Process 2017, 88, 25–35. [Google Scholar] [CrossRef]
- Hu, J.Q.; Subhash, R.; Zhang, Y.M. Real-time estimation of tire-road friction coefficient based on lateral vehicle dynamics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2444–2457. [Google Scholar] [CrossRef]
- Feng, Y.C.; Chen, H.; Zhao, H.Y.; Zhou, H. Road tire friction coefficient estimation for four wheel drive electric vehicle based on moving optimal estimation strategy. Mech. Syst. Signal Process 2020, 139, 106416. [Google Scholar] [CrossRef]
- Ramdane, T.; Driss, B.; Zheng, G.; Frédéric, K.; Rachid, E.G. Rotor speed, load torque and parameters estimations of a permanent magnet synchronous motor using extended observer forms. IET Control Theory Appl. 2017, 11, 1485–1492. [Google Scholar]
- Kchaou, M.; Jerbi, H. Reliable H∞ and passive fuzzy observer-based sliding mode control for nonlinear descriptor systems subject to actuator failure. Int. J. Fuzzy Syst. 2022, 24, 105–120. [Google Scholar] [CrossRef]
- Kchaou, M.; Regaieg, M.A.; Al-Haijaji, A. Quantized asynchronous extended dissipative observer-based sliding mode control for Markovian jump TS fuzzy systems. J. Franklin Inst. 2022, 359, 9636–9665. [Google Scholar] [CrossRef]
- Kchaou, M.; Jerbi, H.; Abassi, R.; VijiPriya, J.; Hmidi, F.; Kouzou, A. Passivity-based asynchronous fault-tolerant control for nonlinear discrete-time singular Markovian jump systems: A sliding-mode approach. Eur. J. Control 2021, 60, 95–113. [Google Scholar] [CrossRef]
- Lian, C.Q.; Xiao, F.; Gao, S.; Liu, J.L. Load torque and moment of inertia identification for permanent magnet synchronous motor drives based on sliding mode observer. IEEE Trans. Power Electron. 2019, 34, 5675–5683. [Google Scholar] [CrossRef]
- Zhang, X.G.; Cheng, Y.; Zhao, Z.H.; He, Y.K. Robust model predictive direct speed control for SPMSM drives based on full parameter disturbances and load observer. IEEE Trans. Power Electron. 2020, 35, 8361–8373. [Google Scholar] [CrossRef]
- Lu, W.Q.; Zhang, Z.Y.; Wang, D.; Lu, K.Y.; Wu, D.; Ji, K.H.; Guo, L. A new load torque identification sliding mode observer for permanent magnet synchronous machine drive system. IEEE Trans. Power Electron. 2019, 34, 7852–7862. [Google Scholar] [CrossRef]
- Craig, E.B.; Sean, B. Modeling and friction estimation for automotive steering torque at very low speeds. Veh. Syst. Dyn. 2021, 59, 458–484. [Google Scholar]
- Bart, F.; Frank, N.; Wim, D. Broadband load torque estimation in mechatronic powertrains using nonlinear Kalman filtering. IEEE Trans. Ind. Electron. 2018, 65, 2378–2387. [Google Scholar]
- Jia, Z.W.; Zhang, Q.H.; Wang, D. A sensorless control algorithm for the circular winding brushless DC motor based on phased voltages and DC current detection. IEEE Trans. Ind. Electron. 2021, 68, 9174–9184. [Google Scholar] [CrossRef]
- Lee, Y.O.; Son, Y.S.; Chung, C.C. Clamping force control for an electric parking brake system: Switched system approach. IEEE Trans. Veh. Technol. 2013, 62, 2937–2948. [Google Scholar] [CrossRef]
- Lee, Y.O.; Jang, M.; Lee, W.; Lee, C.W.; Chung, C.C.; Son, Y.S. Novel clamping force control for electric parking brake systems. Mechatronics 2021, 21, 1156–1162. [Google Scholar] [CrossRef]
- Giseo, P.; Seibum, B.C. Clamping force control based on dynamic model estimation for electromechanical brakes. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 2000–2013. [Google Scholar]
- Li, Y.J.; Shim, T.; Shin, D.H.; Lee, S.H.; Jin, S.H. Control system design for electromechanical brake system using novel clamping force model and estimator. IEEE Trans. Veh. Technol. 2021, 70, 8653–8668. [Google Scholar] [CrossRef]
- Ding, N.G.; Saied, T. An adaptive integrated algorithm for active front steering and direct yaw moment based on direct Lyapunov method. Veh. Syst. Dyn. 2010, 48, 1193–1213. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tyre and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Ding, N.G. Method and Application of Parameter Estimation for Automotive Active Control; Beihang University Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Tustin, A. The effects of backlash and of speed-dependent friction on the stability of closed-cycle control system. J. Inst. Electr. Eng. 1947, 94, 143–151. [Google Scholar] [CrossRef]
- Li, X.L.; Xue, Z.W.; Yan, X.Y.; Zhang, L.X.; Ma, W.Z.; Hua, W. Low-Complexity Multivector-Based Model Predictive Torque Control for PMSM With Voltage Preselection. IEEE Trans. Power Electron. 2021, 36, 11726–11738. [Google Scholar] [CrossRef]
- Ji, X.W.; He, X.K.; Lv, C.; Liu, Y.H.; Wu, J. A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation. Veh. Syst. Dyn. 2018, 56, 923–946. [Google Scholar] [CrossRef]
- Yong, J.W.; Gao, F.; Ding, N.G.; He, Y.P. Design and validation of an electro-hydraulic brake system using hardware-in-the-loop real-time simulation. Int. J. Automot. Technol. 2017, 18, 603–612. [Google Scholar] [CrossRef]








| Symbols | Value | Symbols | Value |
|---|---|---|---|
| ap1 | −3.12 | bp1 | 148.26 |
| ap2 | 2.35 | bp2 | 60.05 |
| an1 | −3.74 | bn1 | −137.72 |
| an2 | 2.97 | bn2 | −55.79 |
| vpm (mm/s) | 6.8 | vnm (mm/s) | −6.76 |
| vpmax (mm/s) | 50 | vnmax (mm/s) | −50 |
| Parameters | Value |
|---|---|
| Vehicle mass (m) | 1855 kg |
| Tire radius (Rf, Rr) | 316 mm |
| Rotational inertia of the front/rear tire (Jf, Jr) | 1.5 kg•m2 |
| Height of the center of gravity (hg) | 530 mm |
| Distance between the front and rear axles (tw) | 2490 mm |
| Front axle to the center of gravity (a) | 1100 mm |
| Rear axle to the center of gravity (b) | 1390 mm |
| Brake disc friction coefficient (ub) | 0.35 |
| Effective brake disc radius (rp) | 105 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, J.; Li, L.; Wang, D.; Liu, Y. Modeling and Clamping Force Tracking Control of an Integrated Electric Parking Brake System Using Sliding-Mode-Based Observer. Actuators 2024, 13, 39. https://doi.org/10.3390/act13010039
Yong J, Li L, Wang D, Liu Y. Modeling and Clamping Force Tracking Control of an Integrated Electric Parking Brake System Using Sliding-Mode-Based Observer. Actuators. 2024; 13(1):39. https://doi.org/10.3390/act13010039
Chicago/Turabian StyleYong, Jiawang, Liang Li, Dongliang Wang, and Yahui Liu. 2024. "Modeling and Clamping Force Tracking Control of an Integrated Electric Parking Brake System Using Sliding-Mode-Based Observer" Actuators 13, no. 1: 39. https://doi.org/10.3390/act13010039





