Interval Type-2 Fuzzy-Model-Based Sampled-Data Control of an AUV Depth System with Input Saturation

Abstract

This paper proposes a sampled-data fuzzy controller design technique for an autonomous underwater vehicle (AUV) depth system represented by an interval type-2 (IT-2) fuzzy model, considering input saturation. In the Takagi–Sugeno (T–S) fuzzy model of an AUV depth system, surge velocity is chosen as a premise variable. To address the associated uncertainty with this variable, we employ the IT-2 fuzzy modeling technique. Also, the controller proposed in this paper utilizes time-varying gains, ensuring superior exponential stability compared with traditional fixed gain approaches. Furthermore, a membership function-dependent (MFD) $H_{\infty }$ criterion is employed to enhance robustness for each subsystem individually. Taking into account the mentioned aspects, the controller design condition is derived in the form of linear matrix inequalities (LMIs). Finally, the effectiveness of the proposed method is validated through simulation examples.

1. Introduction

In recent decades, the exploration of the ocean environment has been significantly enhanced through the utilization of autonomous underwater vehicles (AUVs). With ongoing advancements in AUV research, their movements have progressively become more precise, playing a crucial role in underwater exploration. To undertake various missions, AUVs require versatile capabilities, including mapping, localization, and navigation [1,2,3,4,5]. In [1], a simultaneous localization and mapping technique for AUVs was studied by employing a set membership approach. Furthermore, ref. [3] introduced a navigation strategy for AUVs based on the unscented Kalman filter. While the implementation of precise control techniques is necessary for these tasks, the design problem for AUV controllers remains challenging due to their intricate and highly nonlinear dynamics.

Researchers have shown significant interest in Takagi–Sugeno (T–S) fuzzy model-based control due to its advantages in analyzing and synthesizing nonlinear control systems [6,7,8,9]. The T–S fuzzy model represents a nonlinear system through multiple IF-THEN rules, each with a consequence part being a linear subsystem. This characteristic allows the application of conventional linear control theories to nonlinear systems. Due to these advantages, there has been some research on the T–S fuzzy model-based AUV control. In [10], researchers designed an adaptive fuzzy tracking controller using the direct adaptive fuzzy control method to alleviate the effects of actuator saturation. Additionally, in [11], the robust control problem of a perturbed T–S fuzzy-model-based lift–feedback–fin system was addressed. Previous studies, however, suffer from parameter uncertainties. In conventional studies, there exists a disparity between the actual behavior of the AUV and its T-S fuzzy model due to the assumption of unknown system parameters as constant. By extending the previous type-1 T–S fuzzy model, the interval type-2 (IT-2) fuzzy model was recently proposed. This model is constructed with upper and lower membership functions, capturing uncertainty in the system. Consequently, the IT-2 fuzzy model has been predominantly applied to systems with uncertainties [12,13,14,15,16]. Therefore, it becomes necessary to control the AUV system using an IT-2 fuzzy-model-based control approach to address uncertainties in the system dynamics effectively.

Recent advancements in computer engineering have led to the widespread implementation of control systems using digital hardware, resulting in the coexistence of continuous- and discrete-time signals within a single control system. Conventional control theories are not suitable for such systems. Therefore, researchers have studied sampled-data control theory, designed for continuous-time control systems controlled by digital hardware. Stability analysis in sampled-data control systems commonly relies on Lyapunov–Krasovskii functionals (LKFs) [17,18,19,20,21]. To mention a few notable studies, ref. [22] introduced a novel LKF with a partitioned sampling interval tailored for large sampling periods, and ref. [23] explored the memory sampled-data control method to address delayed signals between the sampler and controller. Also, in [24], the synchronization control for delayed neural networks was studied using the novel augmented Lyapunov functional, which consists of a mixed-delay-based augmented part and a time-squared two-sided looped part. In [25], a matrix-injection-based method was developed to deal with the negativity condition of the forward difference in the Lyapunov functional. However, not only are there few studies of the sampled-data control of the AUV depth system, but they also use outdated control methods.

AUVs, operating in unpredictable conditions like ocean currents and water pressure, require controllers capable of tolerating disturbances. The widely adopted $H_{\infty }$ control attenuates disturbance affecting T–S fuzzy model-based control systems [26,27,28,29]. Thus, there has been active research on $H_{\infty }$ control; for instance, in [30], $H_{\infty }$ performance criteria were applied to handle exogenous inputs, and ref. [31] derived static output feedback design conditions for uncertain T–S fuzzy systems under $H_{\infty }$ performance using switched control methods. Previous research used a fixed $H_{\infty }$ performance index, leading to conservativeness issues. Recently, the membership function-dependent (MFD) $H_{\infty }$ control, employing a distinct $H_{\infty }$ performance index for each rule of the T–S fuzzy model, has been explored as a less conservative alternative to the fixed $H_{\infty }$ approaches [32,33].

For practical applications, actuators have specified limits in force, torque, and voltage, and excessive force can potentially damage the system or degrade control performance, leading to instability. Therefore, it is crucial to consider appropriate input saturation and constraints. In this context, ref. [34] proposed less conservative sufficient conditions for nonlinear active suspension systems by addressing actuator saturation. Additionally, ref. [35] investigated active fault-tolerant control for discrete-time T-S fuzzy systems in the presence of input constraints, applying it to a three-DoF helicopter. However, to the best of the authors’ knowledge, there is a lack of studies on AUV control design considering actuator saturation.

Motivated by the aforementioned analysis, we proposed an IT-2 fuzzy sampled-data controller for a AUV depth system, accounting for uncertain parameters and actuator saturation. The main contributions of this paper are summarized as follows:

• A novel IT-2 fuzzy sampled-data controller for AUV depth systems was introduced, addressing challenges related to input saturation and uncertainty in surge velocity due to physical limitations.
• The employed controller incorporated time-varying gains, ensuring superior exponential stability in AUV depth control.
• The designed controller improved overall system robustness by applying the MFD $H_{\infty }$ criterion, ensuring robustness for each subsystem.
• The proposed controller design was expressed in the form of LMIs, providing a systematic and practical framework for designing an AUV depth control system.

Notation: For a positive integer a, ${\mathcal{I}}_a$ defines an integer set $\{1,2,\dots ,a\}$. In the symmetric position of a square matrix, ∗ denotes the transposed element. For any matrix X, Sym$\left\{X\right\}$ represents $X+X^T$. $\mathrm{diag}\{\cdots \}$ and $\mathrm{col}\{\cdots \}$ indicate a diagonal matrix and a column vector, respectively. For a square matrix X, ${\lambda }_{min}$ denotes the minimum eigenvalue of X. For a symmetric matrix X, $X\succ 0$ (resp. $X\prec 0$) means that X is positive (resp. negative) definite.

2. Problem Formulation

In this paper, we design the depth controller for the AUV described by the IT-2 fuzzy model by considering the input saturation. The IF–THEN rules for the IT-2 fuzzy model are given as follows:

$$\begin{array}{cc}\hfill & \mathrm{Rule}i:\mathrm{IF}{\nu }_1\left(t\right)\mathrm{is}{\mathcal{M}}_{i1}\mathrm{and}\cdots \mathrm{and}{\nu }_p\left(t\right)\mathrm{is}{\mathcal{M}}_{ip},\hfill \\ \hfill & \mathrm{THEN}\left\{\begin{array}{c}\dot{x}\left(t\right)=A_{i}x\left(t\right)+B_i{\overline{\delta }}_s\left(t\right)+D_i\omega \left(t\right)\hfill \\ y\left(t\right)=C_{i}x\left(t\right),\hfill \end{array}\right.\hfill \end{array}$$

where ${\nu }_j\left(t\right)$ and ${\mathcal{M}}_{ij}$ with $(i,j)\in {\mathcal{I}}_r\times {\mathcal{I}}_p$ are the jth premise variable and its IT-2 fuzzy sets in the ith rule; $x\left(t\right)\in {\mathbb{R}}^n$, ${\overline{\delta }}_s\left(t\right)\in {\mathbb{R}}^m$, $\omega \left(t\right)\in {\mathcal{L}}_2^d$, and $y\left(t\right)\in {\mathbb{R}}^c$ are the state, saturated input, disturbance, and output vectors, respectively. In the AUV control system, $m=1$, so we can say that the control input is a scalar variable. Considering the uncertainties in premise variables, the firing strength of the ith rule is described as follows:

$$\begin{array}{cc}\hfill w_i\left(\nu \left(t\right)\right)& \in \left[\prod _{j=1}^p{\mathcal{M}}_{ij}^L\left({\nu }_j\left(t\right)\right),\prod _{j=1}^p{\mathcal{M}}_{ij}^U\left({\nu }_j\left(t\right)\right)\right]=\left[w_i^L\left(\nu \left(t\right)\right),w_i^U\left(\nu \left(t\right)\right)\right],\hfill \end{array}$$

where ${\mathcal{M}}_{ij}^L\left(\nu \left(t\right)\right)\in [0,1]$ and ${\mathcal{M}}_{ij}^U\left(\nu \left(t\right)\right)\in [0,1]$ represent the lower and upper grade of membership; $w_i^L\left(\nu \left(t\right)\right)$ and $w_i^U\left(\nu \left(t\right)\right)$ are the lower and upper firing strength functions satisfying $0\le w_i^L\left(\nu \left(t\right)\right)\le w_i^U\left(\nu \left(t\right)\right)\le 1$. Applying the standard inference process to the above IF–THEN rules, we have

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& \sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)\{A_{i}x\left(t\right)+B_i{\overline{\delta }}_s\left(t\right)+D_i\omega \left(t\right)\},\hfill \\ \hfill y\left(t\right)=& \sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)C_{i}x\left(t\right),\hfill \end{array}$$

(1)

where $w_i\left(\nu \left(t\right)\right)=\phi \left(t\right)w_i^L\left(\nu \left(t\right)\right)+\left(1-\phi \left(t\right)\right)w_i^U\left(\nu \left(t\right)\right)$ and ${\sum }_{i=1}^r{w}_i\left(\nu \left(t\right)\right)=1$; $\phi \left(t\right)\in [0,1]$ is an unknown time-varying function representing the uncertainty of the premise variables.

The bounded control input ${\overline{\delta }}_s\left(t\right)$ is determined by $\mathrm{sat}\left({\delta }_s\left(t\right)\right)$, where

$$\begin{array}{c}\hfill \mathrm{sat}\left({\delta }_s\left(t\right)\right)=\left\{\begin{array}{cc}-{\delta }_{lim},\hfill & \mathrm{if}{\delta }_s\left(t\right)<-{\delta }_{lim}\hfill \\ {\delta }_s\left(t\right),\hfill & \mathrm{if}-{\delta }_{lim}\le {\delta }_s\left(t\right)\le {\delta }_{lim}\hfill \\ {\delta }_{lim},\hfill & \mathrm{if}{\delta }_{lim}<{\delta }_s\left(t\right)\hfill \end{array}\right.\end{array}$$

(2)

where ${\delta }_s\left(t\right)$ is a nonbounded control input computed by the proposed controller, and ${\delta }_{lim}$ is a control input limitation determined by the physical specifications.

Next, based on the time-varying gain control concept, we propose the IT-2 fuzzy sampled-data controller with exponential time-varying gain matrices. Its IF–THEN rules are constructed as below:

$$\begin{array}{cc}\hfill & \mathrm{Rule}i:\mathrm{IF}{\nu }_1\left(t_k\right)\mathrm{is}{\mathcal{M}}_{i1}\mathrm{and}\cdots \mathrm{and}{\nu }_p\left(t_k\right)\mathrm{is}{\mathcal{M}}_{ip},\hfill \\ \hfill & \mathrm{THEN}{\delta }_s\left(t\right)=e^{-\eta (t-t_k)}{K}_{i}x\left(t_k\right),\hfill \end{array}$$

for $t_k\le t\le t_{k+1}$, where $K_i\in {\mathbb{R}}^{m\times n}$ is the sampled-data control gain; $\eta \in {\mathbb{R}}_{>0}$ is a given constant scalar describing the rate of change in the control gain matrices; $t_k$ with $k\in {\mathbb{Z}}_{\ge 0}$ as the sampling time. Also, we define the sampling period as $h_k:=t_{k+1}-t_k\le h$ with a known $h\in {\mathbb{R}}_{>0}$. Using the same inference method as in (1), we can derive the above IF–THEN rules of the proposed controller as follows:

$$\begin{array}{c}\hfill {\delta }_s\left(t\right)=\sum _{i=1}^r{m}_i\left(\nu \left(t_k\right)\right)e^{-\eta (t-t_k)}{K}_{i}x\left(t_k\right),\end{array}$$

(3)

where

$$\begin{array}{c}\hfill m_i\left(\nu \left(t_k\right)\right)=\frac{w_i^L\left(\nu \left(t_k\right)\right)+w_i^U\left(\nu \left(t_k\right)\right)}{{\sum }_{j=1}^p\left\{w_j^L\left(\nu \left(t_k\right)\right)+w_j^U\left(\nu \left(t_k\right)\right)\right\}}.\end{array}$$

Remark 1.

Implementing the proposed controller faces two main challenges. First, solving the LMI conditions in Theorem 1 is required for the controller design. Numerical software aids in solving this condition and takes a few seconds. However, once the physical parameters of the AUV are determined, this process needs to be performed only once and is not considered a significant challenge.

Second, the controller is represented by (3), which needs to be computed at each sampling instant. Since the controller equation is similar to a typical T-S fuzzy-model-based controller, there are no particular difficulties in implementation. However, the controller in (3) contains exponentially decaying terms, which must be implemented using analog hardware. These exponentially decaying terms can be implemented by a cheap RC filter. Apart from this, there are no significantly complex or challenging issues compared with existing approaches.

Now, by using the notations $x_{\eta }\left(t\right)=e^{\eta t}x\left(t\right)$ and $y_{\eta }\left(t\right)=e^{\eta t}y\left(t\right)$, the closed-loop IT-2 fuzzy model (1) is written as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_{\eta }\left(t\right)& =\eta e^{\eta t}x+\left(t\right)+e^{\eta t}\dot{x}\left(t\right)\hfill \\ \hfill & =\eta e^{\eta t}x\left(t\right)+e^{\eta t}\sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)\left\{A_{i}x\left(t\right)+B_i{\overline{\delta }}_s\left(t\right)+D_i\omega \left(t\right)\right\}\hfill \\ \hfill & =\sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)\left\{A_{\eta i}{x}_{\eta }\left(t\right)+e^{\eta t}{\overline{\delta }}_s\left(t\right)+D_i{\omega }_{\eta }\left(t\right)\right\}\hfill \\ \hfill y_{\eta }\left(t\right)& =\sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)C_i{x}_{\eta }\left(t\right),\hfill \end{array}$$

(4)

where ${A_{\eta }}_i=A_i+\eta I$ and ${\omega }_{\eta }\left(t\right)=e^{\eta t}\omega \left(t\right)$.

This paper aims to design the IT-2 fuzzy sampled-data controller for a AUV depth control system under the input saturation consideration. This is realized by solving the following design problem:

Problem 1.

Find the control gain matrix $K_j$ for the depth control system of the AUV (4) such that the following criteria are guaranteed for given scalars $\eta >0$, $\alpha \in (-\eta ,0]$, $\gamma >0$, $\sigma \in [0,1]$, and h:

(1) 

When ${\omega }_{\eta }\left(t\right)=0$, the equilibrium of (4) is exponentially stable with decay rate of $\eta +\alpha$.

(2) 

Under the zero initial condition, the following MFD $H_{\infty }$ criterion is satisfied

$$\begin{array}{c}\hfill {\int }_0^{t_f}{e}^{2\alpha t}{y}_{\eta }^T\left(t\right)y_{\eta }\left(t\right)dt\le {\overline{\gamma }}^2{\int }_0^{t_f}{e}^{2\alpha t}{\omega }_{\eta }^T\left(t\right){\omega }_{\eta }\left(t\right)dt,\end{array}$$

(5)

where $\overline{\gamma }=\gamma \sqrt{\sigma w_1\left(\nu \left(t\right)\right)+{\sum }_{i=2}^r{w}_i\left(\nu \left(t\right)\right)}$; $t_f>0$ is given terminate time of control.

Before closing this section, we provide some lemmas that help derive the proposed controller design condition given in the next section.

Lemma 1

([36]). For positive scalar $\varrho >0$, we have the following inequality:

$$\begin{array}{c}\hfill X^{T}Y+Y^{T}X\le \varrho X^{T}X+{\varrho }^{-1}{Y}^{T}Y,\end{array}$$

where X and Y are the appropriate dimensional matrices.

Lemma 2

([37]). As long as the following holds with a given scalar $\vartheta \in (0,1)$: $|{\delta }_s\left(t\right)|\le \frac{{\delta }_{lim}}{\vartheta }$, the following is always satisfied:

$$\begin{array}{c}\hfill ∥{\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)∥\le \frac{1-\vartheta }{2}\parallel {\delta }_s\left(t\right)\parallel \end{array}$$

and hence

$$\begin{array}{c}\hfill {\left[{\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right]}^T\left[{\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right]\le {\left(\frac{1-\vartheta }{2}\right)}^T{\delta }_s^T\left(t\right){\delta }_s\left(t\right).\end{array}$$

(6)

Lemma 3

([38]). Consider the scalars ${\rho }_i$ satisfying $\left|w_i\left(\nu \left(t\right)\right)-m_j\left(\nu \left(t_k\right)\right)\right|\le {\rho }_i$ for $t\in [t_k,t_{k+1})$. The inequalities ${\sum }_{i=1}^r{\sum }_{j=1}^r{w}_i\left(\nu \left(t\right)\right)m_j\left(\nu \left(t_k\right)\right){\Theta }_{ij}\prec 0$ hold if there exist symmetric matrices $H_{ij}\succ 0$ and $L_{ij}\succ 0$ and full rank matrices $S_{ij}=S_{ij}^T$ and $S_{i(j+r)}=S_{(j+r)i}^T$, $(i,j)\in {\mathcal{I}}_r\times {\mathcal{I}}_r$ such that the following LMIs hold:

$$\begin{array}{cc}\hfill X_{ij}+X_{ji}-S_{ij}-S_{ji}& \ge 0,\hfill \\ \hfill -{\Theta }_{ij}-2X_{ij}-\sum _{k=1}^r{\rho }_k(X_{ik}^{+}+X_{ki}^{+})-S_{i(j+r)}-S_{(j+r)i}& \ge 0,\hfill \\ \hfill \left[\begin{array}{cc}{Z}_{11}& Z_{12}\\ \ast & Z_{11}\end{array}\right]& \succ 0,\hfill \end{array}$$

where $X_{ij}=H_{ij}-L_{ij}$, $X_{ij}^{+}=H_{ij}+L_{ij}$, $Z_{11}=\left[\begin{array}{ccc}{S}_{11}& \cdots & S_{1r}\\ ⋮& \ddots & ⋮\\ S_{r1}& \cdots & S_{rr}\end{array}\right]$, $Z_{12}=\left[\begin{array}{ccc}{S}_{1(r+1)}& \cdots & S_{1\left(2r\right)}\\ ⋮& \ddots & ⋮\\ S_{r(r+1)}& \cdots & S_{r\left(2r\right)}\end{array}\right]$.

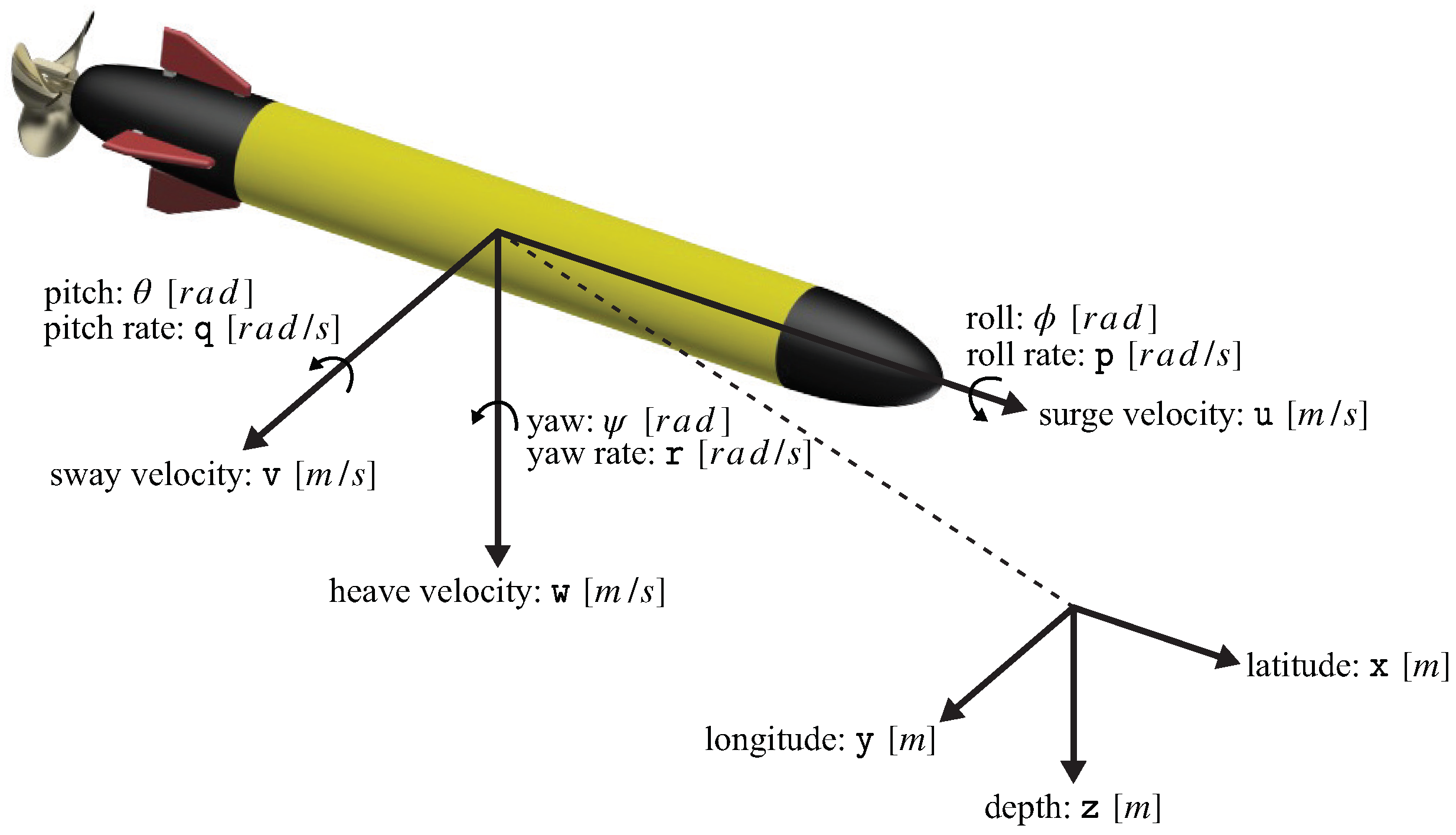
3. IT-2 Fuzzy Modeling of the AUV Depth System

In this section, we derive the IT-2 fuzzy model for the AUV depth system depicted in Figure 1. Its nonlinear dynamic equation is given as follows [39]:

$$\begin{array}{cc}\hfill \dot{q}\left(t\right)& =\frac{M_q}{I_y-M_{\dot{q}}}q\left(t\right)+\frac{M_{\theta }}{I_y-M_{\dot{q}}}\theta \left(t\right)+\frac{M_{\delta }}{I_y-M_{\dot{q}}}{\delta }_s\left(t\right),\hfill \\ \hfill \dot{\theta }\left(t\right)& =cos\left(\theta \left(t\right)\right)q\left(t\right),\hfill \\ \hfill \dot{z}\left(t\right)& =-u\left(t\right)sin\left(\theta \left(t\right)\right),\hfill \end{array}$$

(7)

where $q\left(t\right)$, $\theta \left(t\right)$, $z\left(t\right)$, and ${\delta }_s\left(t\right)$ are the pitch rate, pitch angle, depth, and stern plane angle, respectively; an unknown parameter $u\left(t\right)$ is the surge velocity; $I_y$ is the moment of inertia along Y axis; $M_{\dot{q}}$, $M_q$, $M_{\theta }$, and $M_{\delta }$ represent the added mass, combined term, hydrostatic, and fin lift, respectively. The actual values of all parameters are summarized in

Table 1. The parameters of the AUV.

Parameter	Value	Parameter	Value
$I_y$	$3.45\left[{\mathrm{kgm}}^2\right]$	$M_{\dot{q}}$	$-4.88\left[{\mathrm{kgm}}^2\right]$
$M_q$	$-6.87\left[{\mathrm{kgm}}^2/\mathrm{s}\right]$	$M_{\delta }$	$-34.6\left[{\mathrm{kgm}}^2/{\mathrm{s}}^2\right]$
$M_{\theta }$	$-5.77\left[{\mathrm{kgm}}^2/{\mathrm{s}}^2\right]$

.

This paper aims to regulate the depth $z\left(t\right)$ to the desired depth $z_d$. To this end, we define the depth regulation error $z_e\left(t\right)$ as $z_e\left(t\right)=z\left(t\right)-z_d$. Then, the dynamics of the depth system (7) can be reformulated as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{c}\dot{q}\left(t\right)\\ \dot{\theta }\left(t\right)\\ {\dot{z}}_e\left(t\right)\end{array}\right]=\left[\begin{array}{ccc}\frac{M_q}{I_y-M_{\dot{q}}}& \frac{M_{\theta }}{I_y-M_{\dot{q}}}& 0\\ cos\left(\theta \left(t\right)\right)& 0& 0\\ 0& -u\left(t\right)\sin \mathrm{c}\left(\theta \left(t\right)\right)& 0\end{array}\right]\left[\begin{array}{c}q\left(t\right)\\ \theta \left(t\right)\\ z_e\left(t\right)\end{array}\right]+\left[\begin{array}{c}\frac{M_{\delta }}{I_y-M_{\dot{q}}}\\ 0\\ 0\end{array}\right]{\delta }_s\left(t\right).\end{array}$$

We adopted a decentralized control system structure, where the surge velocity and the depth are independently regulated. Accordingly, the surge velocity, denoted as $u\left(t\right)$, is considered an uncertain parameter in the depth control system. Thus, we assumed that the surge velocity is an uncertain parameter varying within the range of $[u_m,u_M]$, where $u_m$ and $u_M$ are arbitrarily selectable scalars.

Remark 2.

In prior research on fuzzy model-based control for AUV depth systems such as [39,40], the dynamic behavior was approximately linearized, or the surge velocity was treated as a constant value. In the depth control system, the actual surge velocity cannot be accurately accessed due to perturbations caused by various factors, including ocean currents. Thus, its perturbation should be captured when designing the controller. In this study, we mitigated the uncertainty in surge velocity by employing upper and lower membership functions.

Letting the premise variable be $\{{\nu }_1\left(t\right),{\nu }_2\left(t\right)\}=\left\{cos\left(\theta \left(t\right)\right),u\left(t\right)\sin \mathrm{c}\left(\theta \left(t\right)\right)\right\}$, parameters for the surge velocity be $u_m=8$, $u_M=12$, and the operating regions be ${\nu }_1\left(t\right)\in [a_1,a_2]$ and ${\nu }_2\left(t\right)\in [b_1,b_2]$, we obtain the following IF-THEN rules with $i\in {\mathcal{I}}_4$

$$\begin{array}{cc}\hfill & \mathrm{Rule}i:\mathrm{IF}{\nu }_1\left(t\right)\mathrm{is}{\mathcal{M}}_{i1}\mathrm{and}{\nu }_2\left(t\right)\mathrm{is}{\mathcal{M}}_{i2},\hfill \\ \hfill & \mathrm{THEN}\left\{\begin{array}{c}\dot{x}\left(t\right)=A_{i}x\left(t\right)+B_i{\overline{\delta }}_s\left(t\right)+D_i\omega \left(t\right)\hfill \\ y\left(t\right)=C_{i}x\left(t\right),\hfill \end{array}\right.\hfill \end{array}$$

where $a_1=cos\left(\frac{50\pi }{180}\right)$, $a_2=1$, $b_1=10\sin \mathrm{c}\left(\frac{50\pi }{180}\right)$, $b_2=10$, ${\delta }_{lim}=\frac{\pi }{4}$. Then, we can infer the following IT-2 fuzzy model:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& \sum _{i=1}^4{w}_i\left(\nu \left(t\right)\right)\left\{A_{i}x\left(t\right)+B_i{\overline{\delta }}_s\left(t\right)+D_i\omega \left(t\right)\right\},\hfill \\ \hfill y\left(t\right)=& \sum _{i=1}^4{C}_{i}x\left(t\right),\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill A_i& =\left[\begin{array}{ccc}\frac{M_q}{I_y-M_{\dot{q}}}& \frac{M_{\theta }}{I_y-M_{\dot{q}}}& 0\\ {\mathcal{A}}_i& 0& 0\\ 0& -{\mathcal{B}}_i& 0\end{array}\right],B_i=\left[\begin{array}{c}\frac{M_{\delta }}{I_y-M_{\dot{q}}}\\ 0\\ 0\end{array}\right],C_i=\left[\begin{array}{ccc}0& 0& 1\end{array}\right],D_i=\left[\begin{array}{c}0.1\\ 0.1\\ 0.1\end{array}\right],\hfill \end{array}$$

${\mathcal{A}}_i$ and ${\mathcal{B}}_i$ are the ith elements of $\{a_2,a_2,a_1,a_1\}$ and $\{b_2,b_1,b_2,b_1\}$, respectively. The lower and upper grades of membership are determined as follows:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{11}^L\left({\nu }_1\left(t\right)\right)=& {\mathcal{M}}_{11}^U\left({\nu }_1\left(t\right)\right)={\mathcal{M}}_{21}^L\left({\nu }_1\left(t\right)\right)={\mathcal{M}}_{21}^U\left({\nu }_1\left(t\right)\right)=\frac{{\nu }_1\left(t\right)-a_1}{a_2-a_1},\hfill \\ \hfill {\mathcal{M}}_{31}^L\left({\nu }_1\left(t\right)\right)=& {\mathcal{M}}_{31}^U\left({\nu }_1\left(t\right)\right)={\mathcal{M}}_{41}^L\left({\nu }_1\left(t\right)\right)={\mathcal{M}}_{41}^U\left({\nu }_1\left(t\right)\right)=1-{\mathcal{M}}_{11}^L\left({\nu }_1\left(t\right)\right),\hfill \\ \hfill {\mathcal{M}}_{12}^L\left({\nu }_2\left(t\right)\right)=& {\mathcal{M}}_{32}^L\left({\nu }_2\left(t\right)\right)=\frac{{\nu }_2\left(t\right)-u_M\sin \mathrm{c}\left(\frac{50\pi }{180}\right)}{b_2-b_1},\hfill \\ \hfill {\mathcal{M}}_{22}^L\left({\nu }_2\left(t\right)\right)=& {\mathcal{M}}_{42}^L\left({\nu }_2\left(t\right)\right)=1-{\mathcal{M}}_{12}^L\left({\nu }_2\left(t\right)\right),\hfill \\ \hfill {\mathcal{M}}_{12}^U\left({\nu }_2\left(t\right)\right)=& {\mathcal{M}}_{32}^U\left({\nu }_2\left(t\right)\right)=\frac{{\nu }_2\left(t\right)-u_m}{b_2-b_1},\hfill \\ \hfill {\mathcal{M}}_{22}^U\left({\nu }_2\left(t\right)\right)=& {\mathcal{M}}_{42}^U\left({\nu }_2\left(t\right)\right)=1-{\mathcal{M}}_{12}^U\left({\nu }_2\left(t\right)\right).\hfill \end{array}$$

Setting the unknown time-varying function $\phi \left(t\right)=\frac{cos\left(t\right)+1}{2}$, $w_i\left(\nu \left(t\right)\right)$ are obtained

$$\begin{array}{c}\hfill w_1\left(\nu \left(t\right)\right)=\phi \left(t\right){\mathcal{M}}_{11}^L\left({\nu }_1\left(t\right)\right)\times {\mathcal{M}}_{12}^L\left({\nu }_1\left(t\right)\right)+\left(1-\phi \left(t\right)\right){\mathcal{M}}_{11}^U\left({\nu }_1\left(t\right)\right)\times {\mathcal{M}}_{12}^U\left({\nu }_1\left(t\right)\right),\\ \hfill w_2\left(\nu \left(t\right)\right)=\phi \left(t\right){\mathcal{M}}_{21}^L\left({\nu }_1\left(t\right)\right)\times {\mathcal{M}}_{22}^L\left({\nu }_1\left(t\right)\right)+\left(1-\phi \left(t\right)\right){\mathcal{M}}_{21}^U\left({\nu }_1\left(t\right)\right)\times {\mathcal{M}}_{22}^U\left({\nu }_1\left(t\right)\right),\\ \hfill w_3\left(\nu \left(t\right)\right)=\phi \left(t\right){\mathcal{M}}_{31}^L\left({\nu }_2\left(t\right)\right)\times {\mathcal{M}}_{32}^L\left({\nu }_2\left(t\right)\right)+\left(1-\phi \left(t\right)\right){\mathcal{M}}_{31}^U\left({\nu }_2\left(t\right)\right)\times {\mathcal{M}}_{32}^U\left({\nu }_2\left(t\right)\right),\\ \hfill w_4\left(\nu \left(t\right)\right)=\phi \left(t\right){\mathcal{M}}_{41}^L\left({\nu }_2\left(t\right)\right)\times {\mathcal{M}}_{42}^L\left({\nu }_2\left(t\right)\right)+\left(1-\phi \left(t\right)\right){\mathcal{M}}_{41}^U\left({\nu }_2\left(t\right)\right)\times {\mathcal{M}}_{42}^U\left({\nu }_2\left(t\right)\right).\end{array}$$

In the next section, we derive the stability and stabilization conditions for the AUV depth control system described by the IT-2 fuzzy model (8).

4. Controller Design

In this section, we derive the IT-2 fuzzy sampled-data controller design condition satisfying the design criteria given in Problem 1. First, we derive the following theorem that gives the matrix inequality condition determining whether the given control gain matrix satisfies the design criteria given in Problem 1:

Theorem 1.

For the given matrix $K_j\in {\mathbb{R}}^{m\times n}$ and scalars $\eta >0$, $\alpha \in (-\eta ,0]$, $\gamma >0$, $\varrho >0$, $\varsigma >0$, $\vartheta \in (0,1)$, $ϵ\in (0,1)$, and $\sigma \in (0,1)$, the design criteria given in Problem 1 are satisfied if there exist positive definite matrices $P\in {\mathbb{R}}^{n\times n}$, $U_1\in {\mathbb{R}}^{n\times n}$, $U_3\in {\mathbb{R}}^{n\times n}$, $W_1\in {\mathbb{R}}^{n\times n}$, $W_3\in {\mathbb{R}}^{n\times n}$, $N_1\in {\mathbb{R}}^{n\times n}$, $N_4\in {\mathbb{R}}^{n\times n}$, and $N_6\in {\mathbb{R}}^{n\times n}$; full-rank matrices $G_1\in {\mathbb{R}}^{n\times n}$, $G_2\in {\mathbb{R}}^{n\times n}$, $U_2\in {\mathbb{R}}^{n\times n}$, $W_2\in {\mathbb{R}}^{n\times n}$, $N_2\in {\mathbb{R}}^{n\times n}$, $N_3\in {\mathbb{R}}^{n\times n}$, and $N_5\in {\mathbb{R}}^{n\times n}$; and any matrices ${\mathcal{Y}}_1\in {\mathbb{R}}^{(6n+d)\times 2n}$ and ${\mathcal{Y}}_2\in {\mathbb{R}}^{(6n+d)\times 2n}$ such that the following matrix inequalities hold for all $h_k\in \{0,h\},(i,j)\in {\mathcal{I}}_r\times {\mathcal{I}}_r$:

$$\begin{array}{cc}\hfill {\mathcal{N}}_1=\left[\begin{array}{cc}{N}_1+W_1& N_2\\ \ast & N_4\end{array}\right]& \succ 0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathcal{N}}_2=\left[\begin{array}{cc}{N}_1+U_1& N_2\\ \ast & N_4\end{array}\right]& \succ 0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccccc}{\mathsf{\Gamma }}_{1ij}+h_k{\mathsf{\Gamma }}_2& e_1{C}_i^T& e_2{K}_j^T& h_kϵ\left(1-\frac{\alpha h}{2}\right){\mathcal{Y}}_1& h_k(1-ϵ)\left(1-\frac{\alpha h}{2}\right){\mathcal{Y}}_2\\ \ast & -I_{c\times c}& 0_{c\times m}& 0_{c\times 2n}& 0_{c\times 2n}\\ \ast & \ast & -\varrho {\left(\frac{1-\vartheta }{2}\right)}^{-2}{I}_{m\times m}& 0_{m\times 2n}& 0_{m\times 2n}\\ \ast & \ast & \ast & -h_kϵ\left(1-\frac{\alpha h}{2}\right){\mathcal{N}}_1& 0_{2n\times 2n}\\ \ast & \ast & \ast & \ast & -h_k(1-ϵ)\left(1-\frac{\alpha h}{2}\right){\mathcal{N}}_2\end{array}\right]& \prec 0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccccc}{\mathsf{\Gamma }}_{1ij}+h_k{\mathsf{\Gamma }}_3& e_1{C}_i^T& e_2{K}_j^T& -\frac{h_kϵ\alpha h}{2}{\mathcal{Y}}_1& -\frac{h_k(1-ϵ)\alpha h}{2}{\mathcal{Y}}_2\\ \ast & -I_{c\times c}& 0_{c\times m}& 0_{c\times 2n}& 0_{c\times 2n}\\ \ast & \ast & -\varrho {\left(\frac{1-\vartheta }{2}\right)}^{-2}{I}_{m\times m}& 0_{m\times 2n}& 0_{m\times 2n}\\ \ast & \ast & \ast & \frac{h_kϵ\alpha h}{2}{\mathcal{N}}_1& 0_{2n\times 2n}\\ \ast & \ast & \ast & \ast & \frac{h_k(1-ϵ)\alpha h}{2}{\mathcal{N}}_2\end{array}\right]& \prec 0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\left(\frac{{\delta }_{lim}}{\vartheta }\right)}^2& K_i\\ K_i^T& \frac{P}{\varsigma }\end{array}\right]& \ge 0,\hfill \end{array}$$

(13)

where

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{1ij}=& \mathrm{Sym}\{\alpha e_{1}P{e}_1^T+e_{1}P{e}_4^T-e_5{U}_2{e}_2^T-e_6{W}_2{e}_2^T-(e_5+e_6)N_3{e}_2^T-(e_1-e_2)N_5{e}_2^T\hfill \\ \hfill & +\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\mathcal{Y}}_1^T+\left[\begin{array}{cc}{e}_5& e_1-e_3\end{array}\right]{\mathcal{Y}}_2^T+\left(e_1{G}_1^T+e_4{G}_2^T\right){\mathsf{\Phi }}_{ij}\}\hfill \\ \hfill & +\varrho \left(e_1{G}_1^T+e_4{G}_2^T\right)B_i{B}_i^T{\left(e_1{G}_1^T+e_4{G}_2^T\right)}^T-e_7{{\rm Y}}_i{I}_{d\times d}{e}_7^T,\hfill \\ \hfill {\mathsf{\Gamma }}_2=& -e_2\{(1-ϵ)U_3+ϵW_3+N_6\}{e}_2^T,\hfill \\ \hfill {\mathsf{\Gamma }}_3=& \mathrm{Sym}\left\{2\alpha \right(e_5{U}_2{e}_2^T+e_6{W}_2{e}_2^T+(e_5+e_6)N_3{e}_2^T+(e_1-e_2)N_5{e}_2^T-\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\mathcal{Y}}_1^T\hfill \\ \hfill & -\left[\begin{array}{cc}{e}_5& e_1-e_3\end{array}\right]{\mathcal{Y}}_2^T\left)\right\}+\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]U{\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]}^T-ϵ\left[\begin{array}{cc}{e}_3& e_2\end{array}\right](U-W){\left[\begin{array}{cc}{e}_3& e_2\end{array}\right]}^T\hfill \\ \hfill & +\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]N{\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]}^T,\hfill \\ \hfill e_p=& {\left[\begin{array}{cccc}{0}_{n\times (p-1)n}& I_{n\times n}& 0_{n\times (6-p)n}& 0_{n\times d}\end{array}\right]}^T,p\in {\mathcal{I}}_6,e_7={\left[\begin{array}{cc}{0}_{d\times 6n}& I_{d\times d}\end{array}\right]}^T,\hfill \\ \hfill {\mathsf{\Phi }}_{ij}=& {A_{\eta }}_i{e}_1^T+B_i\left(\frac{1+\vartheta }{2}\right)K_j{e}_2^T-e_4^T+D_i{e}_7^T,\hfill \\ \hfill {\mathsf{{\rm Y}}}_1=& \sigma {\gamma }^2,{{\rm Y}}_s={\gamma }^2\mathrm{for}s\in \{2,3,\cdots ,r\},\hfill \\ \hfill U=& \left[\begin{array}{cc}{U}_1& U_2\\ \ast & U_3\end{array}\right],W=\left[\begin{array}{cc}{W}_1& W_2\\ \ast & W_3\end{array}\right],N=\left[\begin{array}{ccc}{N}_1& N_2& N_3\\ \ast & N_4& N_5\\ \ast & \ast & N_6\end{array}\right].\hfill \end{array}$$

Proof. 

Consider the following LKF:

$$\begin{array}{c}\hfill V\left(t\right)=\sum _{v=1}^3{V}_v\left(t\right)\mathrm{for}t\in [t_k,t_{k+1}),\end{array}$$

(14)

where

$$\begin{array}{cc}\hfill V_1\left(t\right)& =e^{2\alpha t}{x}_{\eta }^T\left(t\right)P{x}_{\eta }\left(t\right),\hfill \\ \hfill V_2\left(t\right)& =(t_{k+1}-t)e^{2\alpha t}\left\{{\int }_{\epsilon (t_k,t)}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds+{\int }_{t_k}^{\epsilon (t_k,t)}{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}W\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds\right\},\hfill \\ \hfill V_3\left(t\right)& =(t_{k+1}-t)e^{2\alpha t}{\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}N\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds,\hfill \end{array}$$

where $\epsilon (t_k,t)=t_k+ϵ(t-t_k)$ and $ϵ\in (0,1)$.

First, let us define

$$\begin{array}{c}\hfill \xi \left(t\right)=\mathrm{col}\left\{x_{\eta }\left(t\right),x_{\eta }\left(t_k\right),x_{\eta }\left(\epsilon (t_k,t)\right),{\dot{x}}_{\eta }\left(t\right),{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds,{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds,{\omega }_{\eta }\left(t\right)\right\}.\end{array}$$

Then, the time derivative of $V_1\left(t\right)$ is obtained as below:

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)=& 2\alpha e^{2\alpha t}{x}_{\eta }^T\left(t\right)P{x}_{\eta }\left(t\right)+2e^{2\alpha t}{x}_{\eta }^T\left(t\right)P{\dot{x}}_{\eta }\left(t\right)\hfill \\ \hfill =& 2e^{2\alpha t}\left(\alpha x_{\eta }^T\left(t\right)P{x}_{\eta }\left(t\right)+x_{\eta }^T\left(t\right)P{\dot{x}}_{\eta }\left(t\right)\right)\hfill \\ \hfill =& e^{2\alpha t}{\xi }^T\left(t\right)\left\{\mathrm{Sym}\left\{\alpha e_{1}P{e}_1^T+e_{1}P{e}_4^T\right\}\right\}\xi \left(t\right).\hfill \end{array}$$

(15)

Next, ${\dot{V}}_2\left(t\right)$ is derived as follows:

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)=& -e^{2\alpha t}\left\{{\int }_{\epsilon (t_k,t)}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds+{\int }_{t_k}^{\epsilon (t_k,t)}{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}W\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds\right\}\hfill \\ \hfill & +2\alpha (t_{k+1}-t)e^{2\alpha t}\left\{{\int }_{\epsilon (t_k,t)}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds+{\int }_{t_k}^{\epsilon (t_k,t)}{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}W\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds\right\}\hfill \\ \hfill & +(t_{k+1}-t)e^{2\alpha t}\{{\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]-ϵ{\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\hfill \\ \hfill & +ϵ{\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}W\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\}\hfill \\ \hfill =& e^{2\alpha t}[-{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right)U_1{x}_{\eta }\left(s\right)ds-2{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right)U_2{x}_{\eta }\left(t_k\right)ds\hfill \\ \hfill & -(1-ϵ)(t-t_k)x_{\eta }^T\left(t_k\right)U_3{x}_{\eta }\left(t_k\right)-{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right)W_1{x}_{\eta }\left(s\right)ds\hfill \\ \hfill & -2{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right)W_2{x}_{\eta }\left(t_k\right)ds-ϵ(t-t_k)x_{\eta }^T\left(t_k\right)W_3{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & +(t_{k+1}-t)\left\{2\alpha \right({\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right)U_1{x}_{\eta }\left(s\right)ds+2{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right)U_2{x}_{\eta }\left(t_k\right)ds\hfill \\ \hfill & +(1-ϵ)(t-t_k)x_{\eta }^T\left(t_k\right)U_3{x}_{\eta }\left(t_k\right)+{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right)W_1{x}_{\eta }\left(s\right)ds\hfill \\ \hfill & +2{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right)W_2{x}_{\eta }\left(t_k\right)ds+ϵ(t-t_k)x_{\eta }^T\left(t_k\right)W_3{x}_{\eta }\left(t_k\right))\hfill \\ \hfill & +{\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]-ϵ{\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^T(U-W)\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\left\}\right].\hfill \end{array}$$

The time derivative of $V_3\left(t\right)$ is given as follows:

$$\begin{array}{cc}\hfill {\dot{V}}_3\left(t\right)=& -e^{2\alpha t}{\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}N\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds+(t_{k+1}-t)2\alpha e^{2\alpha t}{\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}N\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]ds\hfill \\ \hfill & +(t_{k+1}-t)e^{2\alpha t}{\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}N\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\hfill \\ \hfill =& e^{2\alpha t}[-{\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T\left[\begin{array}{cc}{N}_1& N_2\\ \ast & N_4\end{array}\right]\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds\hfill \\ \hfill & -2{\left({\int }_{t_k}^t{x}_{\eta }\left(s\right)ds\right)}^T{N}_3{x}_{\eta }\left(t_k\right)-2{\left(x_{\eta }^T\left(t\right)-x_{\eta }\left(t_k\right)\right)}^T{N}_5{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & -(t-t_k)x_{\eta }^T\left(t_k\right)N_6{x}_{\eta }\left(t_k\right)+(t_{k+1}-t)\left\{2\alpha \right({\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T\left[\begin{array}{cc}{N}_1& N_2\\ \ast & N_4\end{array}\right]\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds\hfill \\ \hfill & +2{\left({\int }_{t_k}^t{x}_{\eta }\left(s\right)ds\right)}^T{N}_3{x}_{\eta }\left(t_k\right)+2{\left(x_{\eta }^T\left(t\right)-x_{\eta }\left(t_k\right)\right)}^T{N}_5{x}_{\eta }\left(t_k\right)+(t-t_k)x_{\eta }^T\left(t_k\right)N_6{x}_{\eta }\left(t_k\right))\hfill \\ \hfill & +\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]N\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\left\}\right].\hfill \end{array}$$

(16)

In (16), the integral interval of the following term can be divided as

$$\begin{array}{cc}\hfill & {\int }_{t_k}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T\left[\begin{array}{cc}{N}_1& N_2\\ \ast & N_4\end{array}\right]\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds\hfill \\ \hfill =& {\int }_{\epsilon (t_k,t)}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T\left[\begin{array}{cc}{N}_1& N_2\\ \ast & N_4\end{array}\right]\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds+{\int }_{t_k}^{\epsilon (t_k,t)}{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T\left[\begin{array}{cc}{N}_1& N_2\\ \ast & N_4\end{array}\right]\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds.\hfill \end{array}$$

In addition, since $2\alpha (t_{k+1}-t)(t-t_k)\le 0$ for $t\in [t_k,t)$, we can omit $2\alpha (t_{k+1}-t)(t-t_k)$ term from the above inequality. Thus, by combining ${\dot{V}}_2\left(t\right)$ and ${\dot{V}}_3\left(t\right)$, we have

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)+{\dot{V}}_3\left(t\right)\le & e^{2\alpha t}[-2{\left({\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds\right)}^T{U}_2{x}_{\eta }\left(t_k\right)-2{\left({\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds\right)}^T{W}_2{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & -{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right){\mathcal{N}}_1{x}_{\eta }\left(s\right)ds-{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right){\mathcal{N}}_2{x}_{\eta }\left(s\right)ds\hfill \\ \hfill & -2{\left({\int }_{t_k}^t{x}_{\eta }\left(s\right)ds\right)}^T{N}_3{x}_{\eta }\left(t_k\right)-2{\left(x_{\eta }\left(t\right)-x_{\eta }\left(t_k\right)\right)}^T{N}_5{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & -(t-t_k)\left\{x_{\eta }^T\left(t_k\right)\{(1-ϵ)U_3+ϵW_3+N_6\}{x}_{\eta }\left(t_k\right)\right\}\hfill \\ \hfill & +(t_{k+1}-t)\{4\alpha {\left({\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds\right)}^T{U}_2{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & +4\alpha {\left({\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds\right)}^T{W}_2{x}_{\eta }\left(t_k\right)+4\alpha {\left({\int }_{t_k}^t{x}_{\eta }\left(s\right)ds\right)}^T{N}_3{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & +4\alpha {\left(x_{\eta }\left(t\right)-x_{\eta }\left(t_k\right)\right)}^T{N}_5{x}_{\eta }\left(t_k\right)\hfill \\ \hfill & +2\alpha {\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right){\mathcal{N}}_1{x}_{\eta }\left(s\right)ds+2\alpha {\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right){\mathcal{N}}_2{x}_{\eta }\left(s\right)ds\hfill \\ \hfill & +2\alpha (t-t_k)\left\{x_{\eta }^T\left(t_k\right)\{(1-ϵ)U_3+ϵW_3+N_6\}{x}_{\eta }\left(t_k\right)\right\}\hfill \\ \hfill & +{\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^{T}U\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]-ϵ{\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]}^T(U-W)\left[\begin{array}{c}{x}_{\eta }\left(\epsilon (t_k,t)\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\hfill \\ \hfill & +\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]N\left[\begin{array}{c}{x}_{\eta }\left(t\right)\\ {\dot{x}}_{\eta }\left(t\right)\\ x_{\eta }\left(t_k\right)\end{array}\right]\left\}\right],\hfill \end{array}$$

(17)

where ${\mathcal{N}}_1=\left[\begin{array}{cc}{N}_1+W_1& N_2\\ \ast N_4\end{array}\right]$ and ${\mathcal{N}}_2=\left[\begin{array}{cc}{N}_1+U_1& N_2\\ \ast N_4\end{array}\right]$.

Meanwhile, letting ${\mathcal{N}}_1\succ 0$ and ${\mathcal{N}}_2\succ 0$, the following inequalities for full-rank matrices ${\mathcal{Y}}_1$ and ${\mathcal{Y}}_2$ can be derived by [22]

$$\begin{array}{cc}\hfill -{\int }_{t_k}^{\epsilon (t_k,t)}{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T{\mathcal{N}}_1\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds& \le 2{\left[\begin{array}{c}{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(\epsilon (t_k,t)\right)-x_{\eta }\left(t_k\right)\end{array}\right]}^T{\mathcal{Y}}_1^T\xi \left(t\right)\hfill \\ \hfill & +ϵ(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\xi \left(t\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill -{\int }_{\epsilon (t_k,t)}^t{\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]}^T{\mathcal{N}}_2\left[\begin{array}{c}{x}_{\eta }\left(s\right)\\ {\dot{x}}_{\eta }\left(s\right)\end{array}\right]ds& \le 2{\left[\begin{array}{c}{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(t\right)-x_{\eta }\left(\epsilon (t_k,t)\right)\end{array}\right]}^T{\mathcal{Y}}_2^T\xi \left(t\right)\hfill \\ \hfill & +(1-ϵ)(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\xi \left(t\right).\hfill \end{array}$$

(19)

From (18) and (19), the following terms exiting in (17) are ensured as

$$\begin{array}{cc}\hfill & -{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right){\mathcal{N}}_1{x}_{\eta }\left(s\right)ds-{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right){\mathcal{N}}_2{x}_{\eta }\left(s\right)ds\hfill \\ \hfill & +(t_{k+1}-t)\left\{2\alpha {\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }^T\left(s\right){\mathcal{N}}_1{x}_{\eta }\left(s\right)ds+2\alpha {\int }_{\epsilon (t_k,t)}^t{x}_{\eta }^T\left(s\right){\mathcal{N}}_2{x}_{\eta }\left(s\right)ds\right\}\hfill \\ \hfill \le & 2{\left[\begin{array}{c}{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(\epsilon (t_k,t)\right)-x_{\eta }\left(t_k\right)\end{array}\right]}^T{\mathcal{Y}}_1^T\xi \left(t\right)+ϵ(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\xi \left(t\right)\hfill \\ \hfill & +2{\left[\begin{array}{c}{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(t\right)-x_{\eta }\left(\epsilon (t_k,t)\right)\end{array}\right]}^T{\mathcal{Y}}_2^T\xi \left(t\right)+(1-ϵ)(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\xi \left(t\right)\hfill \\ \hfill & +(t_{k+1}-t)\{-4\alpha {\left[\begin{array}{c}{\int }_{t_k}^{\epsilon (t_k,t)}{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(\epsilon (t_k,t)\right)-x_{\eta }\left(t_k\right)\end{array}\right]}^T{\mathcal{Y}}_1^T\xi \left(t\right)-2\alpha ϵ(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\xi \left(t\right)\hfill \\ \hfill & -4\alpha {\left[\begin{array}{c}{\int }_{\epsilon (t_k,t)}^t{x}_{\eta }\left(s\right)ds\\ x_{\eta }\left(t\right)-x_{\eta }\left(\epsilon (t_k,t)\right)\end{array}\right]}^T{\mathcal{Y}}_2^T\xi \left(t\right)-2\alpha (1-ϵ)(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\xi \left(t\right)\}.\hfill \end{array}$$

(20)

Similarly, $-2\alpha (t_{k+1}-t)(t-t_k)$ has a maximum at $t=\frac{t_{k+1}+t_k}{2}$ by differentiating it, which is bounded as follows

$$\begin{array}{c}\hfill -2\alpha (t_{k+1}-t)(t-t_k)\le -2\alpha {\left(\frac{t_{k+1}-t_k}{2}\right)}^2\le -\frac{\alpha h}{2}\{(t_{k+1}-t)+(t-t_k)\}.\end{array}$$

Hence, in (20), we have

$$\begin{array}{cc}\hfill & (t_{k+1}-t)\left\{-2\alpha ϵ(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\xi \left(t\right)-2\alpha (1-ϵ)(t-t_k){\xi }^T\left(t\right){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\xi \left(t\right)\right\}\hfill \\ \hfill \le & -\frac{\alpha h}{2}\{(t_{k+1}-t)+(t-t_k)\}\left\{ϵ{\xi }^T\left(t\right){\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\xi \left(t\right)+(1-ϵ){\xi }^T\left(t\right){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\xi \left(t\right)\right\}.\hfill \end{array}$$

(21)

Lastly, from (17), (20), and (21), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)+{\dot{V}}_3\left(t\right)\le & e^{2\alpha t}{\xi }^T\left(t\right)\left[\mathrm{Sym}\right\{-e_5{U}_2{e}_2^T-e_6{W}_2{e}_2^T-(e_5+e_6)N_3{e}_2^T-(e_1-e_2)N_5{e}_2^T\hfill \\ \hfill & +\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\mathcal{Y}}_1^T+\left[\begin{array}{cc}{e}_5& e_1-e_3\end{array}\right]{\mathcal{Y}}_2^T\}\hfill \\ \hfill & +(t-t_k)\{-e_2\{(1-ϵ)U_3+ϵW_3+N_6\}{e}_2^T+\left(1-\frac{\alpha h}{2}\right)\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T\hfill \\ \hfill & +(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\left\}\right\}+(t_{k+1}-t)\left\{\mathrm{Sym}\right\{2\alpha (e_5{U}_2{e}_2^T+e_6{W}_2{e}_2^T\hfill \\ \hfill & +(e_5+e_6)N_3{e}_2^T+(e_1-e_2)N_5{e}_2^T-\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\mathcal{Y}}_1^T-\left[\begin{array}{cc}{e}_5& e_1-e_3\end{array}\right]{\mathcal{Y}}_2^T\left)\right\}\hfill \\ \hfill & -\frac{\alpha h}{2}\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}+\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]U{\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]}^T\hfill \\ \hfill & -ϵ\left[\begin{array}{cc}{e}_3& e_2\end{array}\right](U-W){\left[\begin{array}{cc}{e}_3& e_2\end{array}\right]}^T+\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]N{\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]}^T\left\}\right]\xi \left(t\right).\hfill \end{array}$$

(22)

To apply Lemma 2, we rewrite the system (4) as follows:

$$\begin{array}{c}\hfill {\dot{x}}_{\eta }\left(t\right)=\sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)\left\{{A_{\eta }}_i{x}_{\eta }\left(t\right)+e^{\eta t}{B}_i\frac{1+\vartheta }{2}{\delta }_s\left(t\right)+e^{\eta t}{B}_i\left({\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right)+D_i{\omega }_{\eta }\left(t\right)\right\}.\end{array}$$

(23)

Based on (23), we introduce the following null term:

$$\begin{array}{cc}\hfill 0=& 2e^{2\alpha t}\sum _{i=1}^r{w}_i\left(\nu \left(t\right)\right)\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)\hfill \\ \hfill & \times \left\{-{\dot{x}}_{\eta }\left(t\right)+{A_{\eta }}_i{x}_{\eta }\left(t\right)+e^{\eta t}{B}_i\frac{1+\vartheta }{2}{\delta }_s\left(t\right)+e^{\eta t}{B}_i\left({\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right)+D_i{\omega }_{\eta }\left(t\right)\right\}.\hfill \end{array}$$

(24)

The following term in (24) is obtained using Lemma 1

$$\begin{array}{cc}\hfill & 2\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)\times e^{\eta t}{B}_i\left({\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right)\hfill \\ \hfill \le & \varrho \left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)B_i{B}_i^T{\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)}^T\hfill \\ \hfill & +{\varrho }^{-1}{e}^{2\eta t}{\left({\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right)}^T\left({\overline{\delta }}_s\left(t\right)-\frac{1+\vartheta }{2}{\delta }_s\left(t\right)\right),\hfill \end{array}$$

(25)

where $\varrho$ is a given positive scalar. Then, applying Lemma 2, (25) can be rewritten as follows:

$$\begin{array}{cc}\hfill \left(25\right)\le & \varrho \left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)B_i{B}_i^T{\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)}^T\hfill \\ \hfill & +{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{\left(K_j{x}_{\eta }\left(t_k\right)\right)}^T\left(K_j{x}_{\eta }\left(t_k\right)\right).\hfill \end{array}$$

(26)

From (26), the following inequality is given:

$$\begin{array}{cc}\hfill \left(24\right)\le & e^{2\alpha t}\sum _{i=1}^r\sum _{j=1}^r{w}_i\left(\nu \left(t\right)\right)m_j\left(\nu \left(t_k\right)\right)\left[\right\{2\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)\hfill \\ \hfill & \times \left(-{\dot{x}}_{\eta }\left(t\right)+{A_{\eta }}_i{x}_{\eta }\left(t\right)+B_i\frac{1+\vartheta }{2}{K}_j{x}_{\eta }\left(t_k\right)\left(t\right)+D_i{\omega }_{\eta }\left(t\right)\right)\hfill \\ \hfill & +\varrho \left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)B_i{B}_i^T{\left(x_{\eta }^T\left(t\right)G_1^T+{\dot{x}}_{\eta }^T\left(t\right)G_2^T\right)}^T\hfill \\ \hfill & +{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{\left(K_j{x}_{\eta }\left(t_k\right)\right)}^T\left(K_j{x}_{\eta }\left(t_k\right)\right)\left\}\right]\hfill \\ \hfill =& e^{2\alpha t}\sum _{i=1}^r\sum _{j=1}^r{w}_i\left(\nu \left(t\right)\right)m_j\left(\nu \left(t_k\right)\right){\xi }^T\left(t\right)[\mathrm{Sym}\left\{\left(e_1{G}_1^T+e_4{G}_2^T\right){\mathsf{\Phi }}_{ij}\right\}\hfill \\ \hfill & +\varrho \left(e_1\left(t\right)G_1^T+e_4{G}_2^T\right)B_i{B}_i^T{\left(e_1{G}_1^T+e_4{G}_2^T\right)}^T+{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T]\xi \left(t\right),\hfill \end{array}$$

(27)

where $\varrho >0$ is positive scalar and ${\mathsf{\Phi }}_{ij}={A_{\eta }}_i{e}_1^T+B_i\left(\frac{1+\vartheta }{2}\right)K_j{e}_2^T-e_4^T+D_i{e}_7^T$.

By combining (15), (22), and (27) and considering the MFD $H_{\infty }$ criterion (5), we obtain the following inequality:

$$\begin{array}{c}\hfill \dot{V}\left(t\right)+e^{2\alpha t}\left\{y_{\eta }^T\left(t\right)y_{\eta }\left(t\right)-{\overline{\gamma }}^2{\omega }_{\eta }^T\left(t\right){\omega }_{\eta }\left(t\right)\right\}\le e^{2\alpha t}\sum _{i=1}^r\sum _{j=1}^r{w}_i\left(\nu \left(t\right)\right)m_j\left(\nu \left(t_k\right)\right){\xi }^T\left(t\right){\mathsf{\Gamma }}_{ij}\xi \left(t\right),\end{array}$$

(28)

where ${\mathsf{\Gamma }}_{ij}={\mathsf{\Gamma }}_{1ij}+e_1{C}_i^T{C}_i{e}_1^T+{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T+(t-t_k)\{{\mathsf{\Gamma }}_2+\left(1-\frac{\alpha h}{2}\right)\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T$

$+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\left\}\right\}+(t_{k+1}-t)\left\{{\mathsf{\Gamma }}_3-\frac{\alpha h}{2}\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}\right\}$.

In addition, for $h_k\in [0,h]$, the right hand side of (28) can be reformulated as follows:

$$\begin{array}{cc}\hfill \mathrm{R}.\mathrm{H}.\mathrm{S}\mathrm{of}\left(28\right)=& e^{2\alpha t}\sum _{i=1}^r\sum _{j=1}^r{w}_i\left(\nu \left(t\right)\right)m_j\left(\nu \left(t_k\right)\right){\xi }^T\left(t\right)\left[\frac{t-t_k}{h_k}\right\{{\mathsf{\Gamma }}_{1ij}+e_1{C}_i^T{C}_i{e}_1^T\hfill \\ \hfill & +{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T+h_k{\mathsf{\Gamma }}_2\hfill \\ \hfill & +h_k\left(1-\frac{\alpha h}{2}\right)\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}\}\hfill \\ \hfill & +\frac{t_{k+1}-t}{h_k}\{{\mathsf{\Gamma }}_{1ij}+e_1{C}_i^T{C}_i{e}_1^T+{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T\hfill \\ \hfill & +h_k{\mathsf{\Gamma }}_3-\frac{\alpha h{h}_k}{2}\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}\left\}\right]\xi \left(t\right).\hfill \end{array}$$

(29)

Therefore, we can say that $\dot{V}\left(t\right)\le 0$ if the following matrix inequalities hold:

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{1ij}+e_1{C}_i^T{C}_i{e}_1^T+{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T\hfill \\ \hfill +& h_k{\mathsf{\Gamma }}_2+h_k\left(1-\frac{\alpha h}{2}\right)\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}\prec 0,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_{1ij}+e_1{C}_i^T{C}_i{e}_1^T+{\varrho }^{-1}{\left(\frac{1-\vartheta }{2}\right)}^2{e}_2{K}_j^T{K}_j{e}_2^T\hfill \\ \hfill +& h_k{\mathsf{\Gamma }}_3-\frac{\alpha h{h}_k}{2}\left\{ϵ{\mathcal{Y}}_1{\mathcal{N}}_1^{-1}{\mathcal{Y}}_1^T+(1-ϵ){\mathcal{Y}}_2{\mathcal{N}}_2^{-1}{\mathcal{Y}}_2^T\right\}\prec 0.\hfill \end{array}$$

(31)

Finally, by applying the Schur complement to (30) and (31), we obtain (11) and (12). In other words, if there exists a solution to the matrix inequalities of (11) and (12), then the following inequality is guaranteed:

$$\begin{array}{c}\hfill \dot{V}\left(t\right)+e^{2\alpha t}\left(y_{\eta }^T\left(t\right)y_{\eta }\left(t\right)-{\overline{\gamma }}^2{\omega }_{\eta }^T\left(t\right){\omega }_{\eta }\left(t\right)\right)\le 0.\end{array}$$

(32)

Assuming that ${\omega }_{\eta }\left(t\right)=0$, we obtain

$$\begin{array}{c}\hfill 0\ge \dot{V}\left(t\right)+e^{2\alpha t}{y}_{\eta }^T\left(t\right)y_{\eta }\left(t\right)\ge \dot{V}\left(t\right),\end{array}$$

which indicates that $\dot{V}\left(t\right)\le V\left(0\right)$ for all t. Therefore, it is easy to prove that the following holds:

$$\begin{array}{c}\hfill {\lambda }_{min}\left(P\right)e^{2\alpha t}{\parallel x_{\eta }\left(t\right)\parallel }^2\le {\lambda }_{min}\left(P\right)e^{2(\eta +\alpha )t}{\parallel x\left(t\right)\parallel }^2\le V\left(t\right)\le V\left(0\right),\end{array}$$

from which we can say that the first design criterion of Problem 1 is satisfied.

In addition, integrating (32) with respect to t from $t=0$ to $t=t_f$ under zero initial condition, we have

$$\begin{array}{c}\hfill V\left(t\right)-V\left(0\right)+{\int }_0^t{e}^{2\alpha s}\left(y_{\eta }^T\left(s\right)y_{\eta }\left(s\right)-{\overline{\gamma }}^2{\omega }_{\eta }^T\left(s\right){\omega }_{\eta }\left(s\right)\right)ds\le 0.\end{array}$$

Since $V\left(t\right)\ge 0$ and $V\left(0\right)=0$, we can conclude that the MFD $H_{\infty }$ criterion is also satisfied.

On the other hand, from (3), $\left|{\delta }_s\left(t\right)\right|\le \frac{{\delta }_{lim}}{\vartheta }$ can represented as

$$\begin{array}{c}\hfill \left|\sum _{i=1}^r{m}_i\left(\nu \left(t_k\right)\right)e^{-\eta (t-t_k)}{K}_{i}x\left(t_k\right)\right|\le \frac{{\delta }_{lim}}{\vartheta }.\end{array}$$

(33)

It is evident that if $\left|K_i{x}_{\eta }\left(t_k\right)\right|\le \frac{{\delta }_{lim}}{\vartheta }$, then (33) holds. Let $\mathsf{\Omega }\left(K\right)=\{x_{\eta }\left(t_k\right)||x_{\eta }^T\left(t_k\right)K_i^T{K}_i{x}_{\eta }$$\left(t_k\right)|\le {\left(\frac{{\delta }_{lim}}{\vartheta }\right)}^2\}$, the equivalent condition for an ellipsoid $\mathsf{\Omega }(P,\varsigma )=\left\{x_{\eta }\left(t_k\right)|x_{\eta }^T\left(t_k\right)P{x}_{\eta }\left(t_k\right)\le \varsigma \right\}$ being a subset of $\mathsf{\Omega }\left(K\right)$, i.e., $\mathsf{\Omega }(P,\varsigma )\subset \mathsf{\Omega }\left(K\right)$, is [41]

$$\begin{array}{c}\hfill K_i{\left(\frac{P}{\varsigma }\right)}^{-1}{K}_i^T\le {\left(\frac{{\delta }_{lim}}{\vartheta }\right)}^2.\end{array}$$

(34)

By Schur complement, inequality (34) can be rewritten as (13). This completes the proof for this theorem. □

Remark 3.

Given the complicated dynamics of the AUV control system, its stability condition is excessively conservative. In response, we reformulated the previously introduced LKF [22,42] to be suitable for the proposed control system, effectively relaxing the conservatism.

Remark 4.

The stability condition proposed in Theorem 1 is formulated as bilinear matrix inequalities (BMIs). However, solving this condition efficiently presents challenges for contemporary numerical solvers. Additionally, the closed-loop control system involves two distinct membership functions due to uncertainties in the system’s membership function, resulting in the imperfect premise matching problem. In the subsequent theorem, we reformulate the conditions given in Theorem 1 into linear matrix inequalities (LMIs) and address the imperfect premise matching problem using the method proposed in [38].

Theorem 2.

For given scalars $\eta >0$, $\alpha \in (-\eta ,0]$, $\mu >0$, $\gamma >0$, $\varsigma >0$$\varrho >0$, $\vartheta \in (0,1)$, $ϵ\in (0,1)$ and $\sigma \in (0,1)$, the system (4) holds the criteria given in Problem 1 if there exist scalars ${\rho }_i^l$ guaranteeing $\left|w_i\left(\nu \left(t\right)\right)-m_j\left(\nu \left(t_k\right)\right)\right|\le {\rho }_i^l$; positive definite matrices $\overline{P}\in {\mathbb{R}}^{n\times n}$, ${\overline{U}}_1\in {\mathbb{R}}^{n\times n}$, ${\overline{U}}_3\in {\mathbb{R}}^{n\times n}$, ${\overline{W}}_1\in {\mathbb{R}}^{n\times n}$, ${\overline{W}}_3\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_1\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_4\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_6\in {\mathbb{R}}^{n\times n}$, $H_{ij}^l\in {\mathbb{R}}^{(10n+c+d+m)\times (10n+c+d+m)}$, and $L_{ij}^l\in {\mathbb{R}}^{(10n+c+d+m)\times (10n+c+d+m)}$; full-rank matrices $G\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_2\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_3\in {\mathbb{R}}^{n\times n}$, ${\overline{N}}_5\in {\mathbb{R}}^{n\times n}$, and $S_{ij}^l={\left(S_{ij}^l\right)}^T\in {\mathbb{R}}^{(10n+c+d+m)\times (10n+c+d+m)}$; $S_{i(j+r)}^l={\left(S_{(j+r)i}^l\right)}^T\in {\mathbb{R}}^{(10n+c+d+m)\times (10n+c+d+m)}$; and any matrices $T_j\in {\mathbb{R}}^{m\times n}$, ${\overline{\mathcal{Y}}}_1\in {\mathbb{R}}^{(6n+d)\times 2n}$, and ${\overline{\mathcal{Y}}}_2\in {\mathbb{R}}^{(6n+d)\times 2n}$ such that the following LMIs satisfy for $h_k\in [0,h]$, $(i,j,l)\in {\mathcal{I}}_r\times {\mathcal{I}}_r\times {\mathcal{I}}_2$:

$$\begin{array}{cc}\hfill {\overline{\mathcal{N}}}_1=\left[\begin{array}{cc}{\overline{N}}_1+{\overline{W}}_1& {\overline{N}}_2\\ \ast & {\overline{N}}_4\end{array}\right]& \succ 0,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\overline{\mathcal{N}}}_2=\left[\begin{array}{cc}{\overline{N}}_1+{\overline{U}}_1& {\overline{N}}_2\\ \ast & {\overline{N}}_4\end{array}\right]& \succ 0,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill X_{ij}^l+X_{ji}^l-S_{ij}^l-S_{ji}^l& \ge 0,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\Theta }_{ij}^l+2X_{ij}^l+\sum _{k=1}^r{\rho }_k^l(X_{ik}^{l+}+X_{ki}^{l+})+S_{i(j+r)}^l+S_{(j+r)i}^l& \le 0,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{Z}_{11}^l& Z_{12}^l\\ \ast & Z_{11}^l\end{array}\right]& \succ 0,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\left(\frac{{\delta }_{lim}}{\vartheta }\right)}^2& T_i\\ T_i^T& \frac{\overline{P}}{\varsigma }\end{array}\right]& \ge 0,\hfill \end{array}$$

(40)

where $X_{ij}^l=H_{ij}^l-L_{ij}^l$, $X_{ij}^{l+}=H_{ij}^l+L_{ij}^l$,

$$\begin{array}{cc}\hfill Z_{11}^l=& \left[\begin{array}{ccc}{S}_{11}^l& \cdots & S_{1r}^l\\ ⋮& \ddots & ⋮\\ S_{r1}^l& \cdots & S_{rr}^l\end{array}\right],Z_{12}^l=\left[\begin{array}{ccc}{S}_{1(r+1)}^l& \cdots & S_{1\left(2r\right)}^l\\ ⋮& \ddots & ⋮\\ S_{r(r+1)}^l& \cdots & S_{r\left(2r\right)}^l\end{array}\right],\hfill \\ \hfill {\Theta }_{ij}^1=& \left[\begin{array}{ccccc}{\overline{\mathsf{\Gamma }}}_{1ij}+h_k{\overline{\mathsf{\Gamma }}}_2& e_1{G}^T{C}_i^T& e_2{T}_j^T& h_kϵ\left(1-\frac{\alpha h}{2}\right){\overline{\mathcal{Y}}}_1& h_k(1-ϵ)\left(1-\frac{\alpha h}{2}\right){\overline{\mathcal{Y}}}_2\\ \ast & -I_{c\times c}& 0_{c\times m}& 0_{c\times 2n}& 0_{c\times 2n}\\ \ast & \ast & -\varrho {\left(\frac{1-\vartheta }{2}\right)}^{-2}{I}_{m\times m}& 0_{m\times 2n}& 0_{m\times 2n}\\ \ast & \ast & \ast & -h_kϵ\left(1-\frac{\alpha h}{2}\right){\overline{\mathcal{N}}}_1& 0_{2n\times 2n}\\ \ast & \ast & \ast & \ast & -h_k(1-ϵ)\left(1-\frac{\alpha h}{2}\right){\overline{\mathcal{N}}}_2\end{array}\right],\hfill \\ \hfill {\Theta }_{ij}^2=& \left[\begin{array}{ccccc}{\overline{\mathsf{\Gamma }}}_{1ij}+h_k{\overline{\mathsf{\Gamma }}}_3& e_1{G}^T{C}_i^T& e_2{T}_j^T& -\frac{h_kϵ\alpha h}{2}{\overline{\mathcal{Y}}}_1& -\frac{h_k(1-ϵ)\alpha h}{2}{\overline{\mathcal{Y}}}_2\\ \ast & -I_{c\times c}& 0_{c\times m}& 0_{c\times 2n}& 0_{c\times 2n}\\ \ast & \ast & -\varrho {\left(\frac{1-\vartheta }{2}\right)}^{-2}{I}_{m\times m}& 0_{m\times 2n}& 0_{m\times 2n}\\ \ast & \ast & \ast & \frac{h_kϵ\alpha h}{2}{\overline{\mathcal{N}}}_1& 0_{2n\times 2n}\\ \ast & \ast & \ast & \ast & \frac{h_k(1-ϵ)\alpha h}{2}{\overline{\mathcal{N}}}_2\end{array}\right],\hfill \\ \hfill {\overline{\mathsf{\Gamma }}}_{1ij}=& \mathrm{Sym}\{\alpha e_1\overline{P}{e}_1^T+e_1\overline{P}{e}_4^T-e_5{\overline{U}}_2{e}_2^T-e_6{\overline{W}}_2{e}_2^T-(e_5+e_6){\overline{N}}_3{e}_2^T-(e_1-e_2){\overline{N}}_5{e}_2^T\hfill \\ \hfill & +\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\overline{\mathcal{Y}}}_1^T+\left[\begin{array}{cc}{e}_5& e_1-e_2\end{array}\right]{\overline{\mathcal{Y}}}_2^T+(e_1+\mu e_4){\overline{\mathsf{\Phi }}}_{ij}\}+\varrho (e_1+\mu e_4)B_i{B}_i^T{(e_1+\mu e_4)}^T\hfill \\ \hfill & -e_7{{\rm Y}}_i{I}_{d\times d}{e}_7^T,\hfill \\ \hfill {\overline{\mathsf{\Gamma }}}_2=& -e_2\left\{(1-ϵ){\overline{U}}_3+ϵ{\overline{W}}_3+{\overline{N}}_6\right\}{e}_2^T,\hfill \\ \hfill {\overline{\mathsf{\Gamma }}}_3=& \mathrm{Sym}\left\{2\alpha \right(e_5{\overline{U}}_2{e}_2^T+e_6{\overline{W}}_2{e}_2^T+(e_5+e_6){\overline{N}}_3{e}_2^T+(e_1-e_2){\overline{N}}_5{e}_2^T-\left[\begin{array}{cc}{e}_6& e_3-e_2\end{array}\right]{\overline{\mathcal{Y}}}_1^T\hfill \\ \hfill & -\left[\begin{array}{cc}{e}_5& e_1-e_2\end{array}\right]{\overline{\mathcal{Y}}}_2^T\left)\right\}+\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]\overline{U}{\left[\begin{array}{cc}{e}_1& e_2\end{array}\right]}^T-ϵ\left[\begin{array}{cc}{e}_3& e_2\end{array}\right](\overline{U}-\overline{W}){\left[\begin{array}{cc}{e}_3& e_2\end{array}\right]}^T\hfill \\ \hfill & +\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]\overline{N}{\left[\begin{array}{ccc}{e}_1& e_4& e_2\end{array}\right]}^T,\hfill \\ \hfill {\overline{\mathsf{\Phi }}}_{ij}=& {A_{\eta }}_{i}G{e}_1^T+B_i{T}_j{e}_2^T-G{e}_4^T+D_i{e}_7^T,\hfill \\ \hfill \overline{U}=& \left[\begin{array}{cc}{\overline{U}}_1& {\overline{U}}_2\\ \ast & {\overline{U}}_3\end{array}\right],\overline{W}=\left[\begin{array}{cc}{\overline{W}}_1& {\overline{W}}_2\\ \ast & {\overline{W}}_3\end{array}\right],\overline{N}=\left[\begin{array}{ccc}{\overline{N}}_1& {\overline{N}}_2& {\overline{N}}_3\\ \ast & {\overline{N}}_4& {\overline{N}}_5\\ \ast & \ast & {\overline{N}}_6\end{array}\right].\hfill \end{array}$$

Then, the gain matrices are obtained by $K_j=T_j{G}^{-1}$.

Proof. 

Denote $G_1=G^{-1}$, $G_2=\mu G^{-1}$, $\overline{P}=G^{T}PG$, $\overline{R}=G^{T}RG$, $\overline{Q}=G^{T}QG$, $T_j=K_{j}G$, $\overline{U}=diag{\{G,G\}}^{T}Udiag\{G,G\}$, $\overline{W}=diag{\{G,G\}}^{T}Wdiag\{G,G\}$, $\overline{N}=diag{\{G,G,G\}}^{T}Ndiag\{G,G,G\}$, ${\overline{\mathcal{N}}}_1=diag{\{G,G\}}^T{\mathcal{N}}_{1}diag\{G,G\}$, ${\overline{\mathcal{N}}}_2=diag{\{G,G\}}^T{\mathcal{N}}_{2}diag\{G,G\}$, ${\overline{\mathcal{Y}}}_1=diag{\{G,G,G,G,G,G,I_{d\times d}\}}^T{\mathcal{Y}}_{1}diag\{G,G\}$, ${\overline{\mathcal{Y}}}_2=diag{\{G,G,G,G,G,G,I_{d\times d}\}}^T{\mathcal{Y}}_{2}diag\{G,G\}$. Pre- and postmultiplying (9) and (10) by $diag{\{G,G\}}^T$ and its transpose, respectively, (35) and (36) are obtained. In addition, pre- and postmultiplying (11) and (12) by $\mathrm{diag}\{G,G,G,G,G,G,I_{d\times d},I_{c\times c},I_{m\times m}{,G,G,G,G\}}^T$ and its transpose and utilizing Lemma 3 to solve the imperfect premise matching problem, respectively, we can obtain (37)–(39). Also, by pre- and postmultiplying (13) by $diag{\{I_{n\times n},G\}}^T$ and its transpose, (40) is given. This completes the proof for this theorem. □

Remark 5.

When compared with existing papers, this paper considered the following improvements:

1 

In the conventional studies of AUV depth systems, the surge velocity $u\left(t\right)$ was treated as a constant [39,43,44]. However, in real-world scenarios, $u\left(t\right)$ varies due to various reasons. To address this fluctuation, this paper proposes an interval type-2 fuzzy model for the AUV’s depth system, considering $u\left(t\right)$ as an uncertain premise variable. This approach allows the model to effectively represent the fluctuations in $u\left(t\right)$ using its membership function.

2 

Typically, research on AUV depth control assumes operation in the continuous-time domain. However, due to the cost-effectiveness of digital computers, AUV control systems are generally designed as sampled-data systems, where the plant and controller operate in different time domains. Although there are existing studies on sampled-data control for the AUV depth system, they rely on traditional sampled-data control techniques [45,46]. Motivated by this observation, this paper introduces a novel approach to control the AUV depth system by combining a recently developed sampled-data control method with an IT-2 fuzzy model for the AUV depth control system.

3 

Previous studies on AUV depth control systems have not extensively addressed real-world challenges like fault estimation, tolerance control, and control input saturation. Control input saturation, in particular, presents a significant limitation for AUV depth control systems. This is due to the physical constraints on the control input, which is typically related to the angle of a fin lift and is limited in its operational range. By addressing the input saturation problem, this paper proposes a more practical controller design strategy for AUV depth control systems than the previous studies.

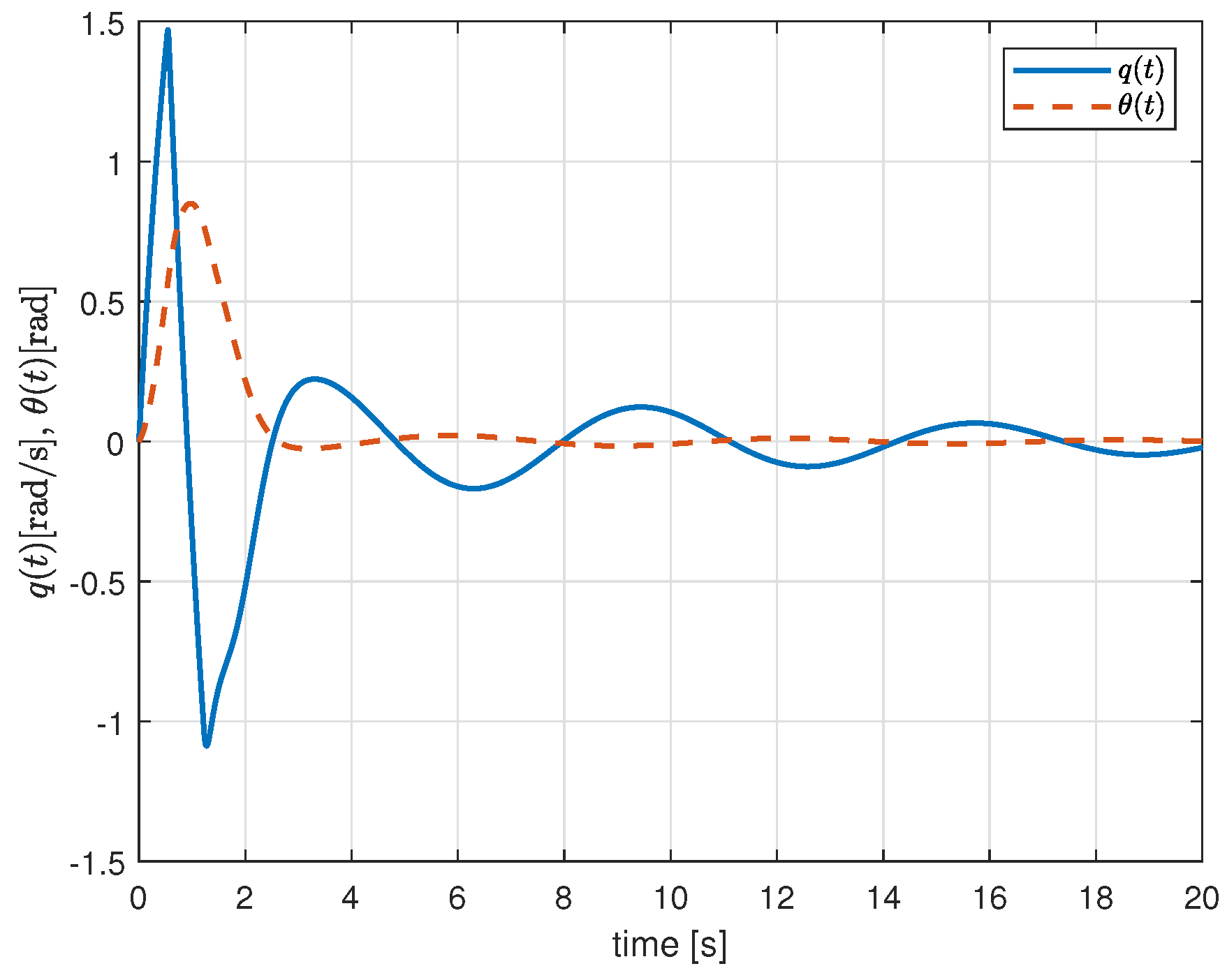
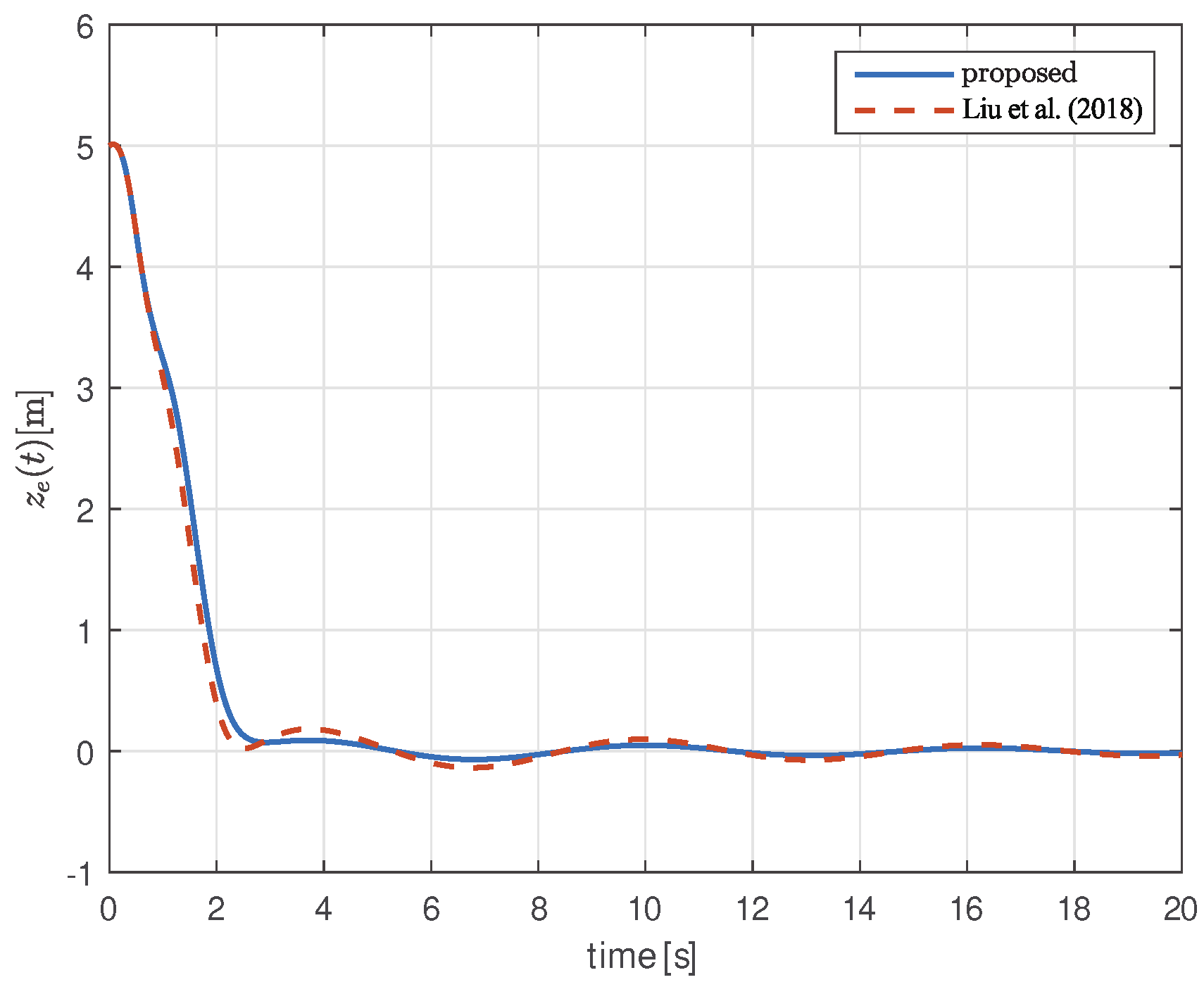
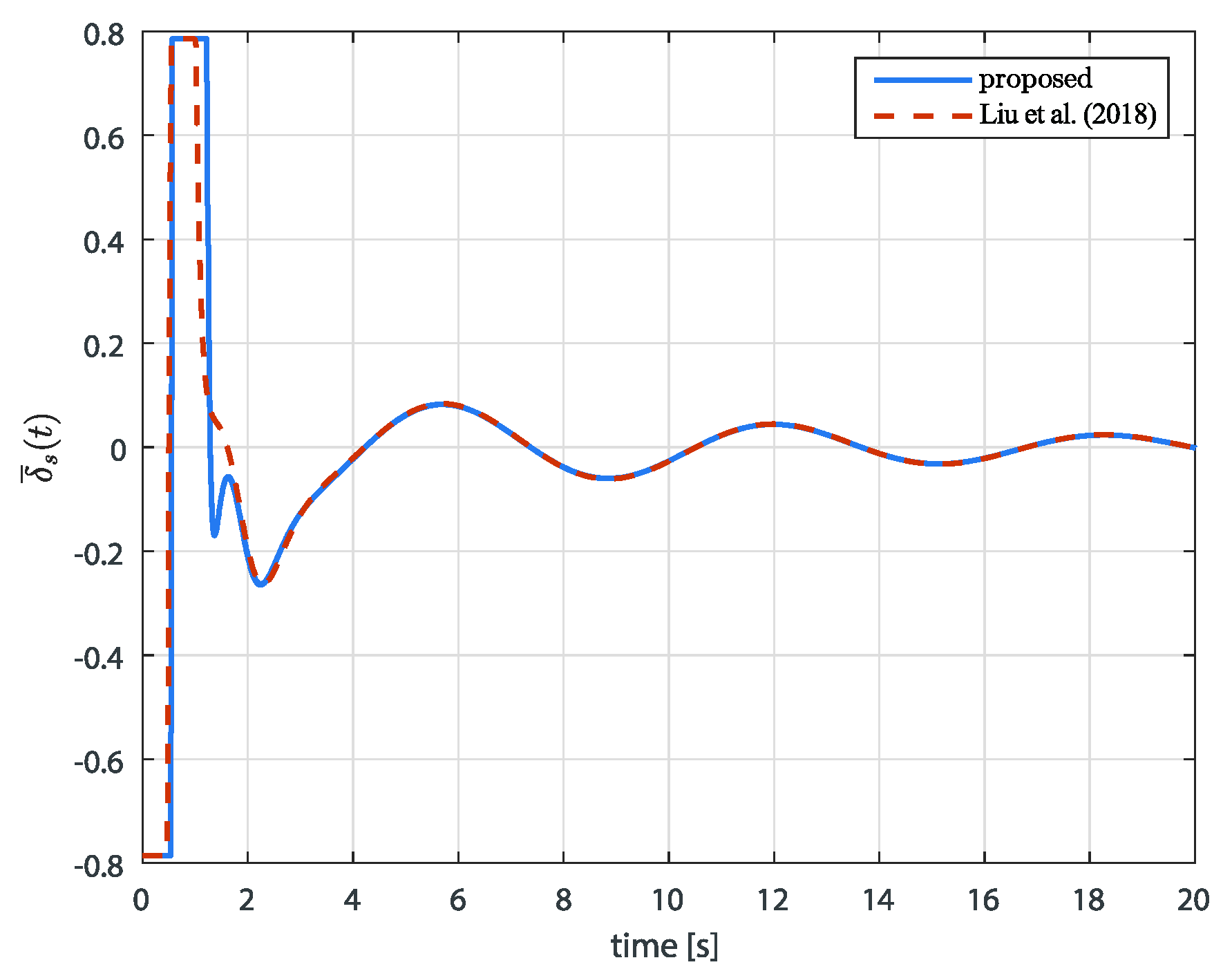
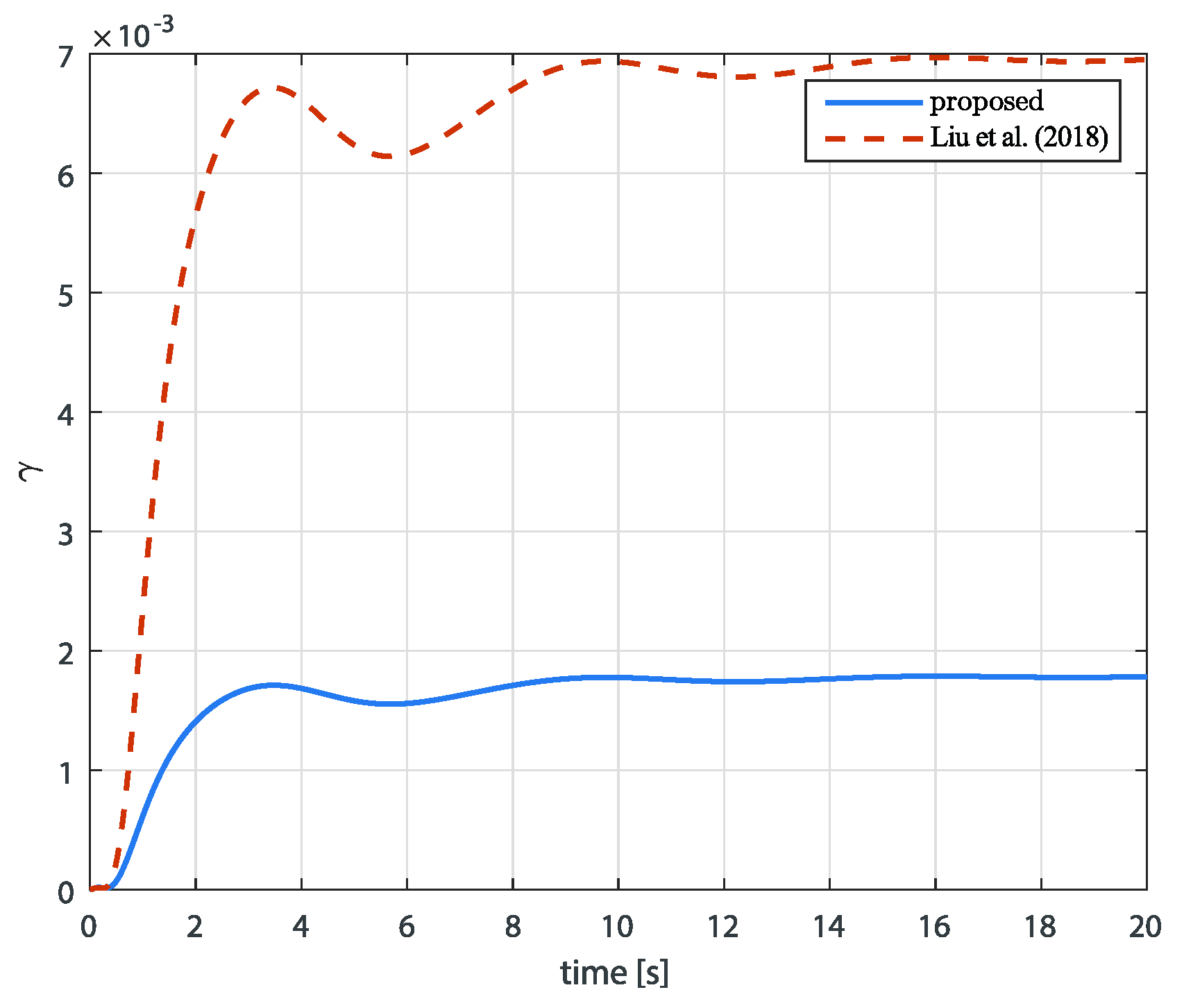
5. Simulation Validation

In this section, we illustrate the design process of an IT-2 fuzzy sampled-data controller for an AUV depth system, considering input saturation. Furthermore, we evaluate and analyze the performance of the designed controller through simulation examples.

The parameter values for solving the LMIs presented in Theorem 2 (35)–(40) are chosen as follows: decay rate $\eta =1$ and $\alpha =-0.8$, sampling period $h=0.01$, input saturation ${\delta }_{lim}=\frac{\pi }{4}$, bounds on the membership functions ${\rho }_i^l=0.5,(i,l)\in {\mathcal{I}}_r\times {\mathcal{I}}_2$, and remaining constants $\mu =10$, $\varsigma =0.5$, $\varrho =0.01$, $\vartheta =0.7$, $ϵ=0.5$, and $\sigma =0.5$. From the selection of the parameters, we can see that the maximum allowable sampling period is $0.01\mathrm{s}$, which means that the controller operates at $100\mathrm{Hz}$. From the solution, we obtain the following control gains:

$$\begin{array}{cc}\hfill K_1=& \left[\begin{array}{ccc}4.9529& 28.7597& -5.7042\end{array}\right],K_2=\left[\begin{array}{ccc}4.9529& 28.7598& -5.7043\end{array}\right],\hfill \\ \hfill K_3=& \left[\begin{array}{ccc}4.9529& 28.7598& -5.7043\end{array}\right],K_4=\left[\begin{array}{ccc}4.9529& 28.7596& -5.7042\end{array}\right].\hfill \end{array}$$

Now, we analyze the control performance of the designed control system. In the simulation, we demonstrate the regulation of the depth of the AUV to $-5\mathrm{m}$. For this purpose, we initialize the system with $x\left(0\right)=\mathrm{col}\left\{\mathrm{q}\right(0),$$\theta \left(0\right)$$,z_e\left(0\right)\}=\mathrm{col}\{0,0,5\}$, indicating that the pitch, pitch rate, and depth are all zero at the start of control. In addition, to validate the disturbance attenuation performance, we arbitrarily chose the disturbance as $\omega \left(t\right)=3e^{-0.1t}cos\left(t\right)$.

The results of the AUV depth control are illustrated in Figure 2, Figure 3, Figure 4 and Figure 5. In Figure 2, the time responses of $q\left(t\right)$ and $\theta \left(t\right)$ are presented. The AUV regulates its depth by adjusting its pitch angle. As depicted in Figure 2, from 0 s to 2 s, the AUV’s pitch angle rotates to adjust its depth. Once the depth is regulated, the pitch rate is perturbed to robustly maintain the depth even in the presence of disturbances.

In Figure 3, the time responses of the depth controlled by both the proposed method and the method from [47] are presented. The approach in [47] does not account for input saturation. However, since the AUV in this simulation has limitations on the fin-lift angle, both time responses are obtained equally considering input saturation. The control input trajectories are displayed in Figure 4. As shown in Figure 4, the control input is saturated, even though the controller designed by [47] does not compensate for it. Consequently, as observed in Figure 3, the proposed controller exhibits less perturbation in the AUV’s depth, attributed to the consideration of input saturation. Additionally, as $z_e\left(t\right)\to 0$, the depth of the AUV given by $z\left(t\right)=z_e\left(t\right)+z_d\left(t\right)$ converges to $-5\mathrm{m}$, which meets the objective of this simulation.

Next, the trajectory of the MFD $H_{\infty }$ performance index $\overline{\gamma }$ and fixed $H_{\infty }$ performance index are shown in Figure 5. The MFD $H_{\infty }$ performance index is obtained by

$$\begin{array}{c}\hfill \overline{\gamma }=\sqrt{\left(\sigma w_1\left(\nu \left(t\right)\right)+\sum _{i=2}^4{w}_i\left(\nu \left(t\right)\right)\right)\times 2.2132}.\end{array}$$

Therefore, we observe that it changes in $w_1\left(\nu \left(t\right)\right)$, and it varies within the ranges of $[1.0520,1.4877]$. As depicted in the figure, the proposed MFD $H_{\infty }$ index exhibits better disturbance attenuation performance compared with the fixed $H_{\infty }$ index when $w_1>0.6$.

Next, we show the comparison of the disturbance attenuation performance of the proposed method with [47]. As in the second objective in Problem 2, we set the initial condition as $x\left(0\right)=\mathrm{col}\left\{\mathrm{q}\right(0),$$\theta \left(0\right)$$,z_e\left(0\right)\}=\mathrm{col}\{0,0,0\}$, indicating that the pitch, pitch rate, and depth are all zero at the start of control. In the comparison, the disturbance was set as $\omega \left(t\right)=5e^{-0.1t}cos\left(0.5t\right)$, and the control gain is the same as in the previous setting. In Figure 6, the results of the $H_{\infty }$ norm ratio of $y\left(t\right)$ to $w\left(t\right)$ are depicted. The results demonstrate that the proposed method provides better disturbance attenuation performance than [47]. This is due to the MFD $H_{\infty }$ criterion considering the disturbance attenuation performance of each subsystem.

Summarizing the aforementioned analysis, the simulation results indicate that the proposed method outperforms the previous study in disturbance attenuation performance, even in the presence of the actuator limitation. Additionally, the MFD $H_{\infty }$ approach demonstrates superior disturbance attenuation performance compared with the fixed $H_{\infty }$-based method.

6. Conclusions

This paper presented a technique for designing a sampled-data fuzzy controller for an AUV depth system represented by an IT-2 fuzzy model, taking into account input saturation. The surge velocity was chosen as the premise variable to capture the perturbations in the surge velocity. As the premise variable is uncertain, the IT-2 fuzzy modeling technique was employed in this paper. The controller designed in this paper employed time-varying gains, ensuring superior exponential stability compared with conventional fixed gain approaches. Additionally, an MDF $H_{\infty }$ criterion was used to enhance robustness for each subsystem individually. Combining the proposed techniques, the controller design conditions were formulated as LMIs from the LKF. Finally, by simulation, we validated that the proposed method achieves better robustness compared with a previous study.

When we conducted a simulation using the method [38] to solve the imperfect premise problem, there was a problem that the dimension of LMIs was too large and the gain calculation took too long. Thus, in future work, we will study a simple and effective method to address the imperfect premise problem. Also, we will study a method of relaxing the conservativeness by constructing novel LKFs using a variety of methods, such as in [24,25].