A Generalized Unbiased Control Strategy for Radial Magnetic Bearings
Abstract
:1. Introduction
2. Generalized Unbiased Control Problem
3. Numerical Solutions to the Generalized Problem
4. Analytical Solutions
5. Load Capacity
6. Back Iron Thickness
7. Fault Tolerance
8. Other Practically Important Configurations
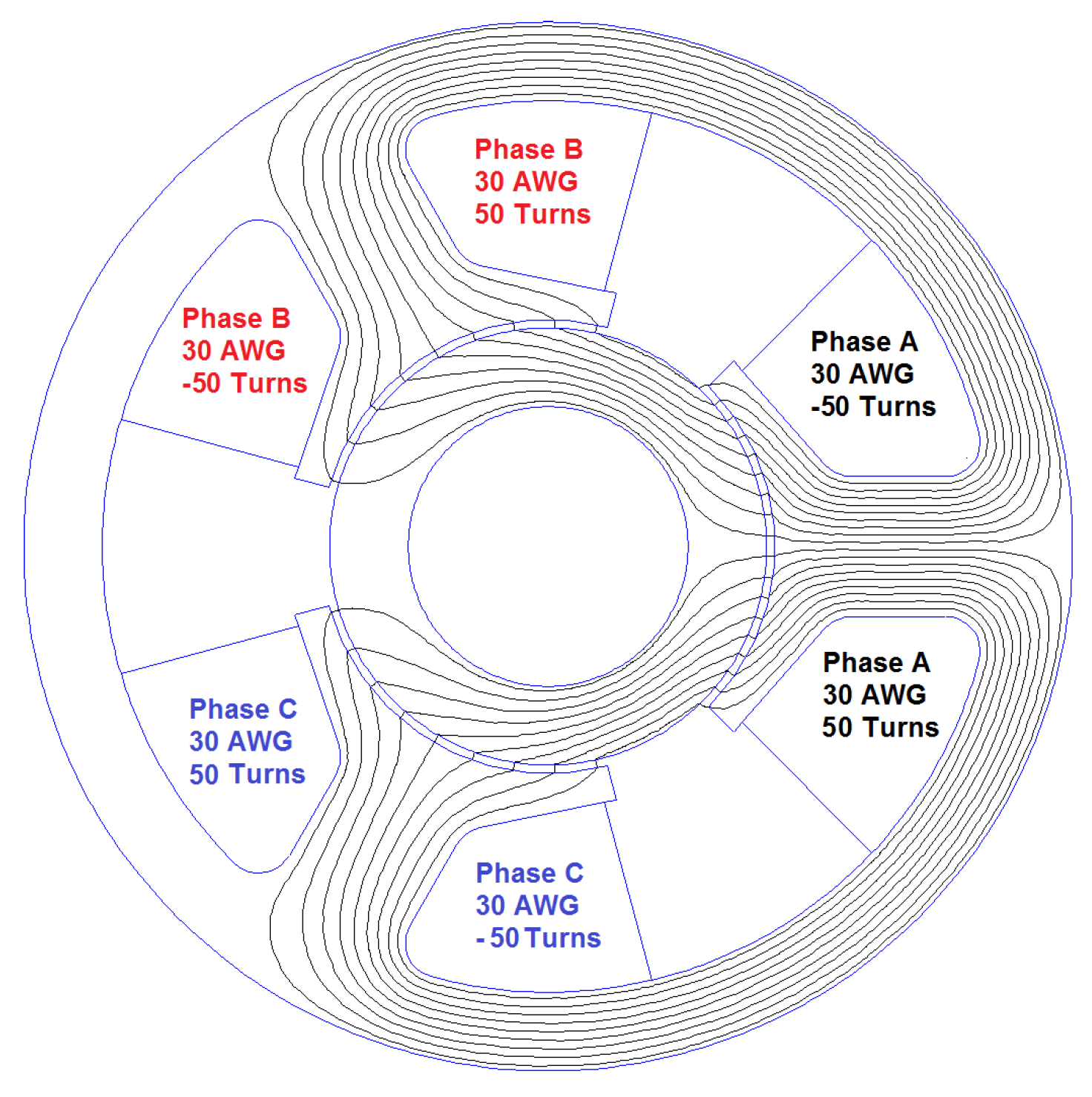
8.1. Nine Pole 3-Phase Bearing
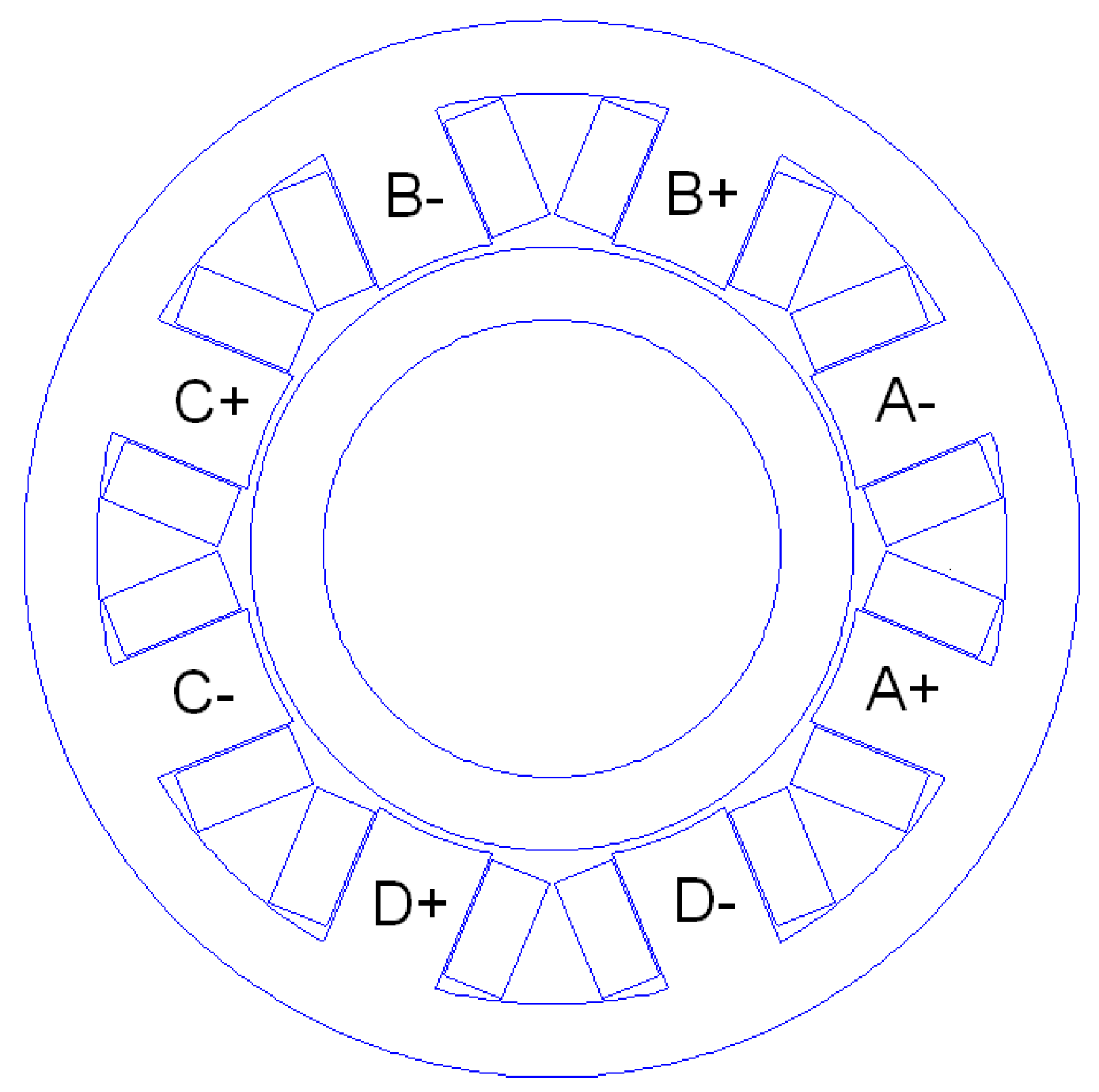
8.2. Eight-Pole Horseshoe Bearing
9. Position Variation
10. Conclusions
Conflicts of Interest
References
- Meeker, D.C.; Maslen, E.H. Analysis and control of a three pole radial magnetic bearing. In Proceedings of the Tenth International Symposium on Magnetic Bearings, Martigny, Switzerland, 21–23 August 2006.
- Vadillo, J.; Echeverria, J.M.; Elosegui, I.; Fontan, L. An approach to a three-pole active magnetic bearing system fed by a matrix converter. In Proceedings of the Eleventh International Symposium on Magnetic Bearings, Nara, Japan, 26–29 August 2008.
- Beizama, A.M.; Echeverria, J.M.; Martinez-Iturralde, M.; Egana, I.; Fontan, L. Comparison between pole-placement control and sliding mode control for three-pole radial magnetic bearings. In Proceedings of the International Symposium on Power Electronics, Electric Drives, Automation, and Motion (SPEEDAM 2008), Ischia, Italy, 11–13 June 2008.
- Matsuda, K.; Kijimoto, S. An approach to designing a magnetic-baring system for smaller rotating machines. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008.
- Maslen, E.H.; Meeker, D.C. Fault tolerance of magnetic bearings by generalized bias current linearization. IEEE Trans. Magn. 1995, 31, 2304–2314. [Google Scholar] [CrossRef]
- Popescu, M. Induction Motor Modelling for Vector Control Purposes; Helsinki University of Technology: Espoo, Finland, 2000. [Google Scholar]
- Na, U.J.; Palazzolo, A. Optimized realization of fault-tolerant heteropolar magnetic bearings. J. Vib. Acoust. 2000, 122, 209–221. [Google Scholar] [CrossRef]
- Boyd, S. Least-Norm Solutions of Underdetermined Equations. Available online: https://see.stanford.edu/materials/lsoeldsee263/08-min-norm.pdf (accessed on 6 November 2016).
- Maslen, E.H.; Sortore, C.K.; Gillies, G.T.; Williams, R.D.; Fedigan, S.J.; Aimone, R.J. Fault tolerant magnetic bearings. Trans. ASME 1999, 121, 504–508. [Google Scholar] [CrossRef]
- Jastrzebski, R.P.; Smirnov, A.; Mystkowski, A.; Pyrhönen, O. Cascaded position-flux controller for AMB system operating at zero bias. Energies 2014, 7, 3561–3575. [Google Scholar] [CrossRef]
- Mystkowski, A.; Pawluszewicz, E.; Dragašius, E. Robust nonlinear position-flux zero-bias control for uncertain AMB system. Int. J. Control 2015, 88, 619–1629. [Google Scholar] [CrossRef]


| Poles | Thickness Ratio | Load Capacity |
|---|---|---|
| 3 | 0.57735 | 0.375 |
| 5 | 0.525731 | 0.625 |
| 7 | 0.512858 | 0.875 |
| 9 | 0.507713 | 1.125 |
| 11 | 0.505142 | 1.375 |
| 13 | 0.503672 | 1.625 |
| 15 | 0.502754 | 1.825 |
| ∞ | 0.5 | n/8 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meeker, D. A Generalized Unbiased Control Strategy for Radial Magnetic Bearings. Actuators 2017, 6, 1. https://doi.org/10.3390/act6010001
Meeker D. A Generalized Unbiased Control Strategy for Radial Magnetic Bearings. Actuators. 2017; 6(1):1. https://doi.org/10.3390/act6010001
Chicago/Turabian StyleMeeker, David. 2017. "A Generalized Unbiased Control Strategy for Radial Magnetic Bearings" Actuators 6, no. 1: 1. https://doi.org/10.3390/act6010001
APA StyleMeeker, D. (2017). A Generalized Unbiased Control Strategy for Radial Magnetic Bearings. Actuators, 6(1), 1. https://doi.org/10.3390/act6010001






