Multicamera, Multimethod Measurements for Hydromorphologic Laboratory Experiments
Abstract
:1. Introduction
2. Laboratory Facility and Measurement Methods
2.1. Facility
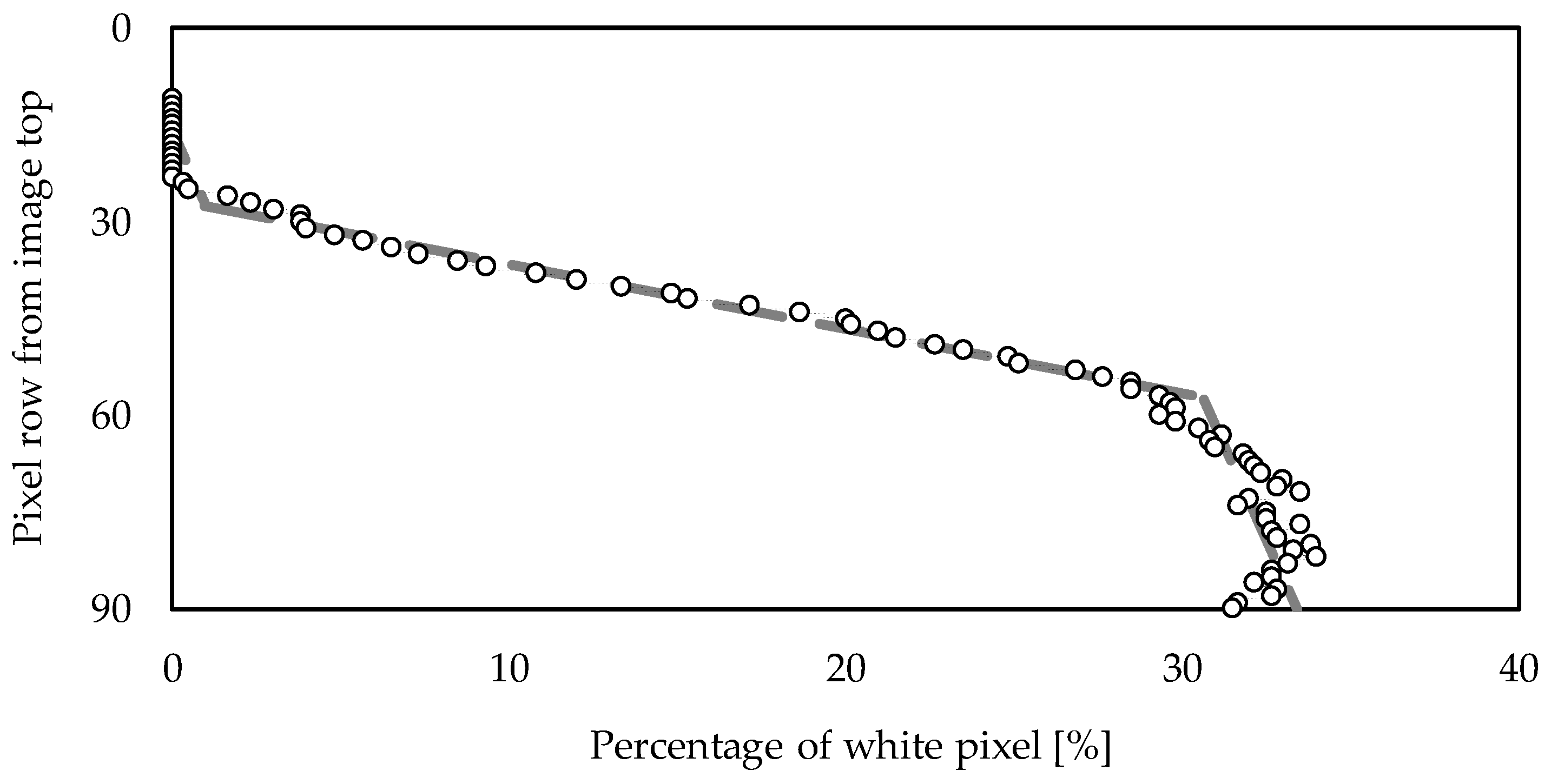
2.2. Measurement of the Profile of the Free Surface
2.2.1. Removal of Lens Distortion, Region Choice, and Image Calibration
2.2.2. Measurement of the Water Elevation in the Piezometer Pipes
2.3. Measurement of the Sediment Feeding Rate
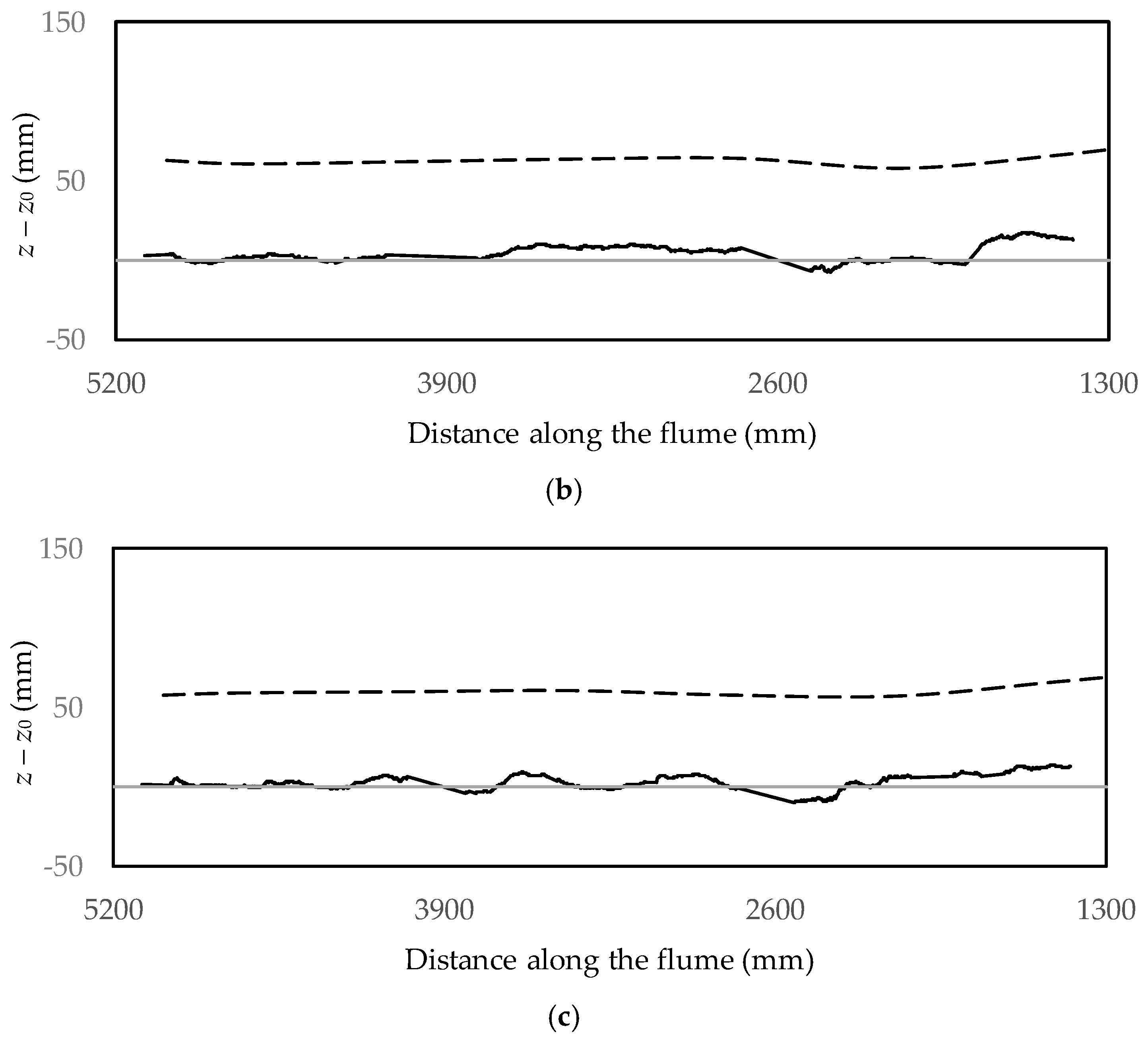
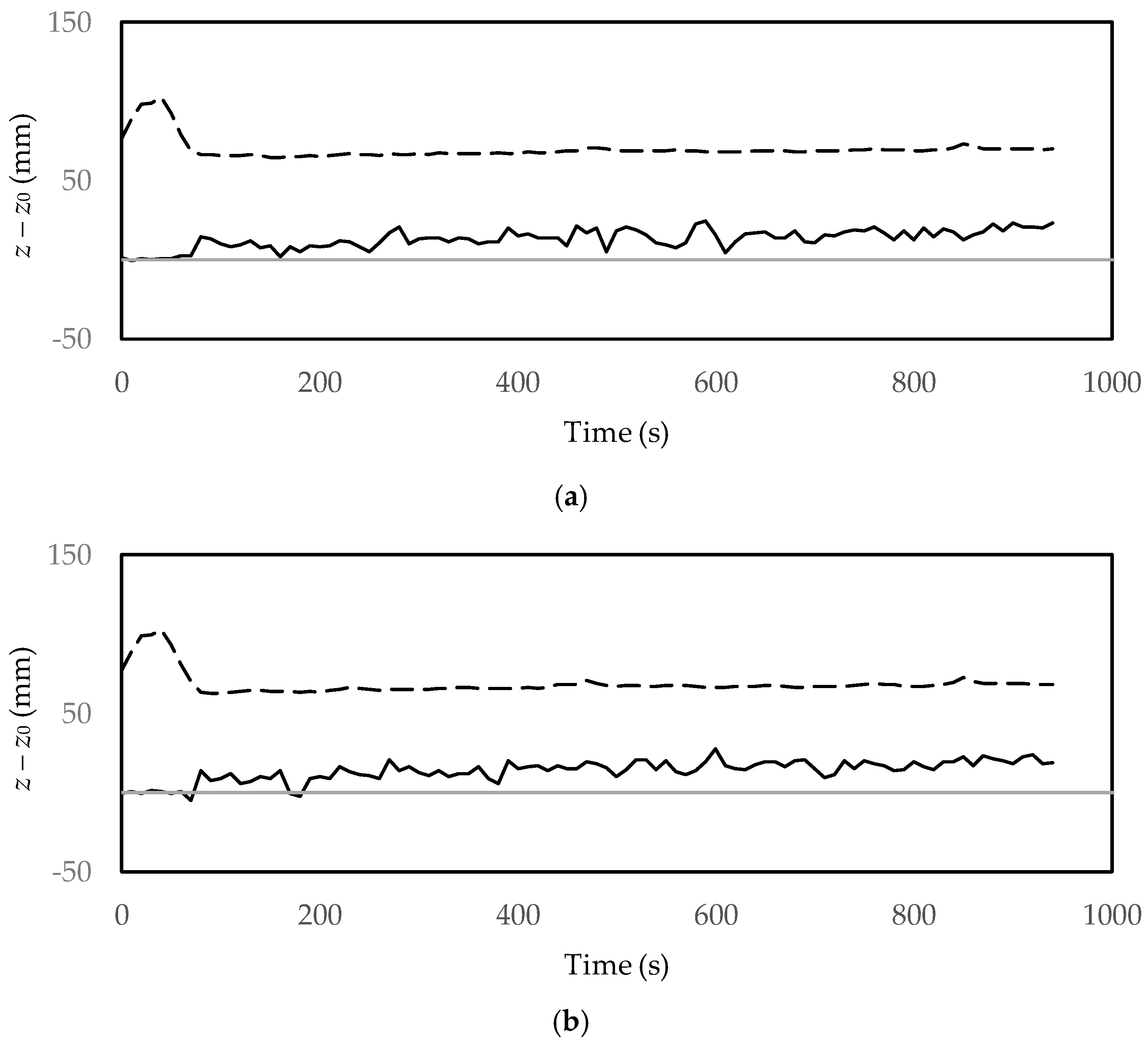
2.4. Measurement of the Bed Profile
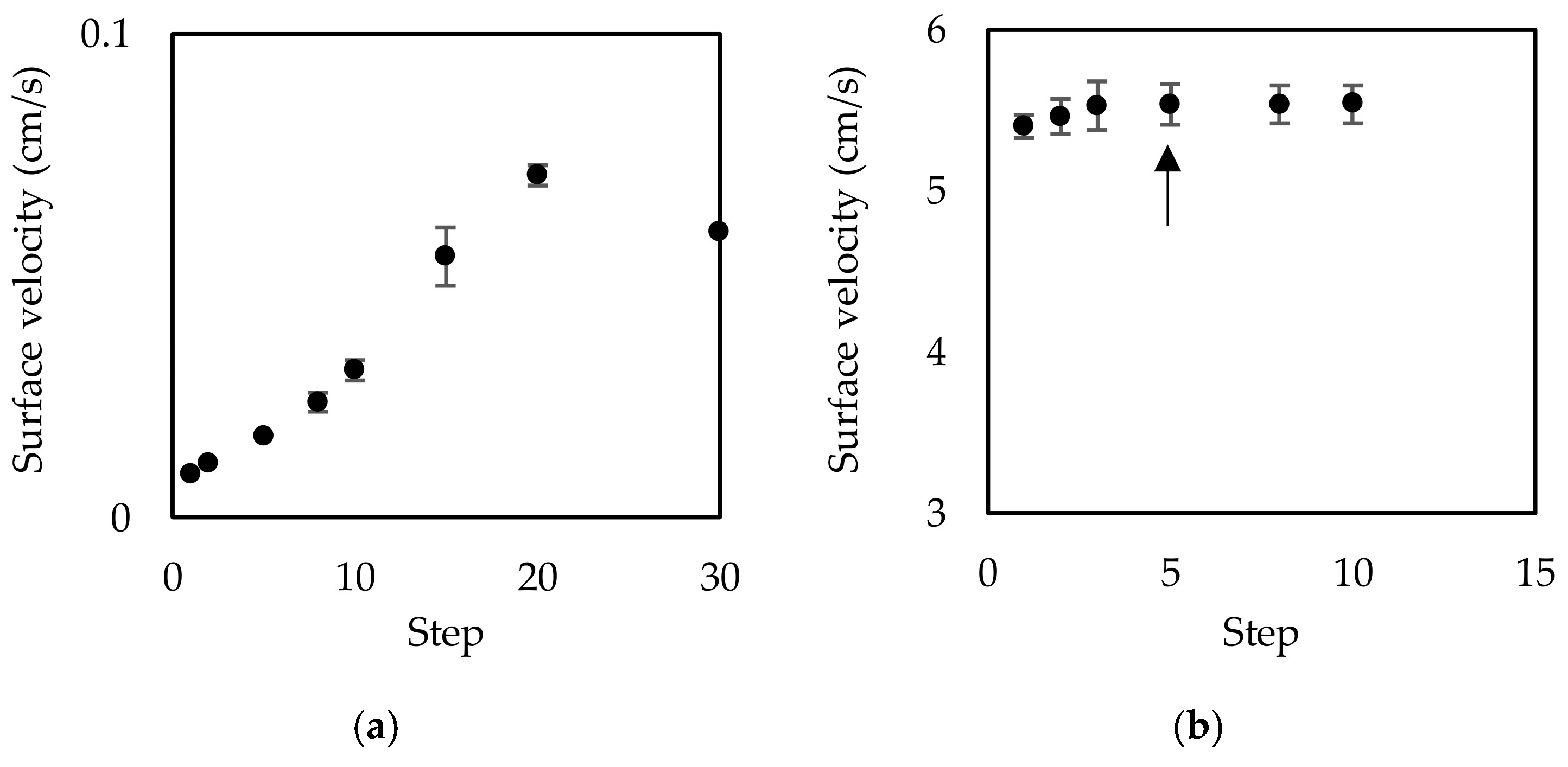
3. Application to an Experiment
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lenzi, M.A.; D’Agostino, V.; Billi, P. Bedload transport in the instrumented catchment of the Rio Cordon. Part I: Analysis of bedload records, conditions and threshold of bedload entrainment. Catena 1999, 36, 171–190. [Google Scholar] [CrossRef]
- Milzow, C.; Molnar, P.; McArdell, B.W.; Burlando, P. Spatial organization in the step-pool structure of a steep mountain stream (Vogelbach, Switzerland). Water Resour. Res. 2006, 42, W04418. [Google Scholar] [CrossRef]
- Turowski, J.M.; Yager, E.M.; Badoux, A.; Rickenmann, D.; Molnar, P. The impact of exceptional events on erosion, bedload transport and channel stability in a step-pool channel. Earth Surf. Proc. Land. 2009, 34, 1661–1673. [Google Scholar] [CrossRef]
- Cohen, H.; Laronne, J.B.; Reid, I. Simplicity and complexity of bed load response during flash floods in a gravel bed ephemeral river: A 10 year field study. Water Resour. Res. 2010, 46, W11542. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Bloomer, D.J.; Church, M. Evolution of an advancing gravel front: Observations from Vedder Canal, British Columbia. Earth Surf. Proc. Land. 2011, 36, 1172–1182. [Google Scholar] [CrossRef]
- Dell’Agnese, A.; Brardinoni, F.; Toro, M.; Mao, L.; Engel, M.; Comiti, F. Bedload transport in a formerly glaciated mountain catchment constrained by particle tracking. Earth Surf. Dyn. 2015, 3, 527–542. [Google Scholar] [CrossRef]
- Szilo, J.; Bialik, R.J. Grain size distribution of bedload transport in a glaciated catchment (Baranowski Glacier, King George Island, Western Antarctica). Water 2018, 10, 360. [Google Scholar] [CrossRef]
- Soni, J.P.; Garde, R.J.; Ranga Raju, K.G. Aggradation in streams due to overloading. ASCE J. Hydraul. Div. 1980, 106, 117–132. [Google Scholar]
- Soni, J.P. Laboratory study of aggradation in alluvial channels. J. Hydrol. 1981, 49, 87–106. [Google Scholar] [CrossRef]
- Yen, C.L.; Chang, S.Y.; Lee, H.Y. Aggradation-degradation process in alluvial channels. J. Hydraul. Eng. 1992, 118, 1651–1669. [Google Scholar] [CrossRef]
- Alves, E.; Cardoso, A. Experimental study on aggradation. Int. J. Sediment Res. 1999, 14, 1–15. [Google Scholar]
- Cui, Y.; Parker, G.; Lisle, T.E.; Gott, J.; Hansler-Ball, M.E.; Pizzuto, J.E.; Allmendinger, N.E.; Reed, J.M. Sediment pulses in mountain rivers: 1. Experiments. Water Resour. Res. 2003, 39, 1239. [Google Scholar] [CrossRef]
- Sklar, L.S.; Fadde, J.; Venditti, J.G.; Nelson, P.; Wydzga, M.A.; Cui, Y.; Dietrich, W.E. Translation and dispersion of sediment pulses in flume experiments simulating gravel augmentation below dams. Water Resour. Res. 2009, 45, W08439. [Google Scholar] [CrossRef]
- Wang, L.; Cuthbertson, A.; Pender, G.; Cao, Z. The response of bed-load sediment transport and bed evolution under unsteady hydrograph flows. In Proceedings of the River Flow 2014, Lausanne, Switzerland, 3–5 September 2014. [Google Scholar]
- Unigarro Villota, S. Laboratory Study of Channel Aggradation Due to Overloading. Master’s Thesis, Politecnico di Milano, Milan, Italy, December 2017. [Google Scholar]
- Cui, Y.; Parker, G.; Pizzuto, J.E.; Lisle, T.E. Sediment pulses in mountain rivers: 2. Comparison between experiments and numerical predictions. Water Resour. Res. 2003, 39, 1240. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Bdour, A.; Wicklein, E. One-dimensional hydrodynamic/sediment transport model applicable to mountain streams. J. Hydraul. Res. 2004, 42, 357–375. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P. Kinematic wave model for transient bed profiles in alluvial channels under nonequilibrium conditions. Water Resour. Res. 2007, 43, W12412. [Google Scholar] [CrossRef]
- Miglio, A.; Gaudio, R.; Calomino, F. Mobile-bed aggradation and degradation in a narrow flume: Laboratory experiments and numerical simulations. J. Hydro-Environ. Res. 2009, 3, 9–19. [Google Scholar] [CrossRef]
- Chiari, M.; Friedl, K.; Rickenmann, D. A one-dimensional bedload transport model for steep slopes. J. Hydraul. Res. 2010, 48, 152–160. [Google Scholar] [CrossRef]
- Neuhold, C.; Stanzel, P.; Nachtnebel, H.P. Incorporating river morphological changes to flood risk assessment: Uncertainties, methodology and application. Nat. Hazards Earth Syst. Sci. 2009, 9, 789–799. [Google Scholar] [CrossRef]
- Verhaar, P.M.; Biron, P.M.; Ferguson, R.I.; Hoey, T.B. Implications of climate change in the twenty-first century for simulated magnitude and frequency of bed-material transport in tributaries of the Saint-Lawrence River. Hydrol. Process. 2011, 25, 1558–1573. [Google Scholar] [CrossRef]
- Radice, A.; Rosatti, G.; Ballio, F.; Franzetti, S.; Mauri, M.; Spagnolatti, M.; Garegnani, G. Management of flood hazard via hydro-morphological river modelling. The case of the Mallero in Italian Alps. J. Flood Risk Manag. 2013, 6, 197–209. [Google Scholar] [CrossRef]
- Pender, D.; Patidar, S.; Hassan, K.; Haynes, H. Method for incorporating morphological sensitivity into flood inundation modeling. J. Hydraul. Eng. 2016, 142, 04016008. [Google Scholar] [CrossRef]
- Radice, A.; Longoni, L.; Papini, M.; Brambilla, D.; Ivanov, V.I. Generation of a design flood-event scenario for a mountain river with intense sediment transport. Water 2016, 8, 597. [Google Scholar] [CrossRef]
- Singh, A.; Fienberg, K.; Jerolmack, D.J.; Marr, J.; Foufoula-Georgiou, E. Experimental evidence for statistical scaling and intermittency in sediment transport rates. J. Geophys. Res. Earth Surf. 2009, 114, F01025. [Google Scholar] [CrossRef]
- Mendes, L.; Antico, F.; Sanches, P.; Alegria, F.; Aleixo, R.; Ferreira, R.M.L. A particle counting system for calculation of bedload fluxes. Meas. Sci. Technol. 2016, 27, 125305. [Google Scholar] [CrossRef]
- Frey, P.; Ducottet, C.; Jay, J. Fluctuations of bed load solid discharge and grain size distribution on steep slopes with image analysis. Exp. Fluids 2003, 35, 589–597. [Google Scholar] [CrossRef]
- Lajeunesse, E.; Malverti, L.; Charru, F. Bed load transport in turbulent flow at the grain scale: Experiments and modeling. J. Geophys. Res. Earth Surf. 2010, 115, F04001. [Google Scholar] [CrossRef]
- Heays, K.G.; Friedrich, H.; Melville, B.W.; Nokes, R. Quantifying the dynamic evolution of graded gravel beds using Particle Tracking Velocimetry. J. Hydraul. Eng. 2014, 140, 04014027. [Google Scholar] [CrossRef]
- Campagnol, J.; Radice, A.; Ballio, F.; Nikora, V. Particle motion and diffusion at weak bed load: Accounting for unsteadiness effects of entrainment and disentrainment. J. Hydraul. Res. 2015, 53, 633–648. [Google Scholar] [CrossRef]
- Fathel, S.; Furbish, D.; Schmeeckle, M. Parsing anomalous versus normal diffusive behavior of bedload sediment particles. Earth Surf. Proc. Land. 2016, 41, 1797–1803. [Google Scholar] [CrossRef]
- Heyman, J.; Bohorquez, P.; Ancey, C. Entrainment, motion and deposition of coarse particles transported by water over a sloping mobile bed. J. Geophys. Res. Earth Surf. 2016, 121, 1931–1952. [Google Scholar] [CrossRef]
- Spinewine, B.; Zech, Y. Small-scale laboratory dam-break waves on movable beds. J. Hydraul. Res. 2007, 45, 73–86. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Wang, L.; Zhang, Y. Measurement of sand creep on a flat sand bed using a high-speed digital camera. Sedimentology 2009, 56, 1705–1712. [Google Scholar] [CrossRef]
- Huang, M.Y.F.; Huang, A.Y.L.; Capart, H. Joint mapping of bed elevation and flow depth in microscale morphodynamics experiments. Exp. Fluids 2010, 49, 1121–1134. [Google Scholar] [CrossRef]
- Redolfi, M.; Guidorizzi, L.; Tubino, M.; Bertoldi, W. Capturing the spatiotemporal variability of bedload transport: A time-lapse imagery technique. Earth Surf. Proc. Land. 2017, 42, 1140–1147. [Google Scholar] [CrossRef]
- Radice, A.; Aleixo, R.; Hosseini Sadabadi, S.A.; Sarkar, S. On image grabbing and processing for measurement of geophysical flows. In Proceedings of the HydroSenSoft 2017, Madrid, Spain, 1–3 March 2017. [Google Scholar]
- Radice, A.; Sarkar, S.; Ballio, F. Image-based Lagrangian particle tracking in bed-load experiments. J. Vis. Exp. 2017, 125, e55874. [Google Scholar] [CrossRef] [PubMed]
- Radice, A.; Malavasi, S.; Ballio, F. Solid transport measurements through image processing. Exp. Fluids 2006, 41, 721–734. [Google Scholar] [CrossRef]
- Keshavarzy, A.; Ball, J.E. An application of image processing in the study of sediment motion. J. Hydr. Res. 1999, 37, 559–576. [Google Scholar] [CrossRef]
- Radice, A.; Ballio, F. Double-average characteristics of sediment motion in one-dimensional bed load. Acta Geophys. 2008, 56, 654–668. [Google Scholar] [CrossRef]
- Radice, A.; Porta, G.; Franzetti, S. Analysis of the time-averaged properties of sediment motion in a local scour process. Water Resour. Res. 2009, 45, W03401. [Google Scholar] [CrossRef]
- Radice, A.; Ballio, F.; Nikora, V. Statistics and characteristic scales for bed load in a channel flow with sidewall effects. Acta Geophys. 2010, 58, 1072–1093. [Google Scholar] [CrossRef]
- Radice, A.; Tran, C.K. Study of sediment motion in scour hole of a circular pier. J. Hydraul. Res. 2012, 50, 44–51. [Google Scholar] [CrossRef]
- Longoni, L.; Ivanov, V.; Brambilla, D.; Papini, M.; Brebbia, C.; Teanini, E.; Radice, A. Application of multiple surveying techniques at a to-be-gauged river section. In Proceedings of the HydroSenSoft 2017, Madrid, Spain, 1–3 March 2017. [Google Scholar]
- McEwan, I.K.; Sheen, T.M.; Cunningham, G.J.; Allen, A.R. Estimating the size composition of sediment surfaces through image analysis. Proc. Inst. Civ. Eng. Water Marit. Eng. 2000, 142, 189–195. [Google Scholar] [CrossRef]
- Parchkoohi, M.H.; Farajkhah, N.K.; Delshad, M.S. Automatic detection of karstic sinkholes in seismic 3D images using circular Hough transform. J. Geophys. Eng. 2015, 12, 764–769. [Google Scholar] [CrossRef]
- Radice, A.; Nikora, V.; Campagnol, J.; Ballio, F. Active interactions between turbulence and bed load: Conceptual picture and experimental evidence. Water Resour. Res. 2013, 49, 90–99. [Google Scholar] [CrossRef]
- Lisle, T.E.; Vui, Y.; Parker, G.; Pizzuto, J.E.; Dodd, A.M. The dominance of dispersion in the evolution of bed material waves in gravel-bed rivers. Earth Surf. Proc. Land. 2001, 26, 1409–1420. [Google Scholar] [CrossRef]















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radice, A.; Zanchi, B. Multicamera, Multimethod Measurements for Hydromorphologic Laboratory Experiments. Geosciences 2018, 8, 172. https://doi.org/10.3390/geosciences8050172
Radice A, Zanchi B. Multicamera, Multimethod Measurements for Hydromorphologic Laboratory Experiments. Geosciences. 2018; 8(5):172. https://doi.org/10.3390/geosciences8050172
Chicago/Turabian StyleRadice, Alessio, and Barbara Zanchi. 2018. "Multicamera, Multimethod Measurements for Hydromorphologic Laboratory Experiments" Geosciences 8, no. 5: 172. https://doi.org/10.3390/geosciences8050172
APA StyleRadice, A., & Zanchi, B. (2018). Multicamera, Multimethod Measurements for Hydromorphologic Laboratory Experiments. Geosciences, 8(5), 172. https://doi.org/10.3390/geosciences8050172





