1. Introduction
Since the launch of the Gravity Recovery and Climate Experiment (GRACE) mission, several research works, e.g., [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13] have investigated the performance of next generation satellite gravity missions. Inline (GRACE-like), alternative (advanced) formations (e.g., Pendulum, Cartwheel, LISA), as well as double-pair mission scenarios (two pairs of inline formation) have been studied.
Furthermore, the European Space Agency (ESA) projects “Assessment of a Next Generation Mission for Monitoring the Variations of Earth’s Gravity” [
14] and “Assessment of Satellite Constellations for Monitoring the Variations in Earth’s Gravity Field” [
15] investigated the science requirements, performance criteria and design of future satellite gravity missions. These two ESA studies briefly discussed two advanced formations and Bender configurations. However, because of the complexity of the technical implementation of alternative formations such as Pendulum, Cartwheel and LISA, their employment as a future gravity mission is currently not of interest to the community [
11], although the future technical improvements may bring them back to the consideration.
Some of the aforementioned studies also suggested a range of parameter choices for double-pair satellite missions for full repeat period and sub-Nyquist solutions.
Most of the aforementioned works chose individual constellation scenarios by rough assessments of the sampling behavior of the missions. However, the studies by [
5,
6,
8,
15] investigated some performance criteria for their optimal double-pair mission scenario search strategies.
In gravity satellite missions, two sampling descriptions exist, which dictate the quality of the gravity recovery change in space and time domains. First, a Heisenberg-like uncertainty theorem in satellite geodesy addresses the trade-off between spatial and temporal resolution by
i.e., the product of spatial resolution
and the time resolution
is constant and equal to
with
as the revolution time [
8,
16,
17]. Second, the Colombo-Nyquist rule (CNR) requires
where
is the number of satellite revolutions within a repeat period in nodal days (α). The formulation means that the number of satellite revolutions in a repeat period should be equal to or larger than twice the maximum spherical harmonic degree (
) or order (
) to be detected [
18,
19]. Indeed, this rule limits the spatial resolution of the gravity recovery. However, the works by [
20,
21] argue that the spatial resolution can be improved, not by twice the maximum degree or order
or
, but by a smaller degree or order values. In particular, the work by [
21] discusses that those values can even reach
or
themselves, depending on the parity of the satellite repeat orbit. However, the description by [
21] is not fully applicable, and requires further investigations. In fact, this study states that a recoverable gravity solution in a full repeat period can be achieved by the new modified rule when
is odd for the near-polar orbits. Later, [
8] took the benefit of the proposed modified Colombo-Nyquist rule (MCNR) to achieve sub-Nyquist gravity recovery, although it should be mentioned that the term “sub-Nyquist” in that work is not defined according to sampling distribution and groundtrack pattern evolution, but by fixed values defined by mission revolutions per nodal days. Therefore, in that context, one can consider Nyquist as the upper limit in sampling theorem.
The short-time intervals solutions, called sub-Nyquist solutions, in consequence, may benefit from higher temporal resolution, and thus, less temporal aliasing, compared to the longer span solutions, e.g., defined by CNR. An important benefit of having those solutions is that they can also be employed as de-aliasing products when time-variable gravity solutions of longer time intervals are targeted [
22].
Besides the two aforementioned rules, the spatio-temporal groundtrack pattern distribution of a satellite mission scenario can significantly affect the quality of the gravity recovery. Therefore, studying the gap evolution of the satellite mission groundtrack is of a great interest as well. Some studies like [
8,
12,
13,
14] investigate the impact of sampling evolution on the gravity recovery quality. For example, [
8,
14] look into different categories of orbits where drifting, slow skipping and fast skipping orbits, and their impacts on the quality of gravity solutions for single-pair satellite missions are discussed. Moreover, the work by [
12] studies the refinement of Colombo-Nyquist and modified Colombo-Nyquist rules for different latitudes rather than at the equator, where the former studies have focused. The paper by [
13], on the other hand, looks into the groundtrack pattern evolution of double pair missions where the influence of relative difference of the right ascension of ascending nodes between the two pairs (
∆Ω) is investigated. In fact, the paper discusses three reasons for the quality variations of the gravity solutions: (i) the sampling pattern of each satellite pair of a double pair mission with different repeat periods evolves differently in the time domain. (Hence, one should expect that within a specific time-interval gravity solution, e.g., 10-day solution, the groundtrack pattern also changes). (ii) the time-variation of
∆Ω can be responsible for the pattern change which, in turn, influences the quality of the gravity recovery. (That is because the two orbits with different inclination angles have different drifting rates of
∆Ω), and (iii) the gravity signals on the Earth are themselves time-variable and cause quality variations of the solutions within the time.
Besides studying the aforementioned concepts which were briefly discussed, several research works examine the sub-cycle concept. For example, the works by [
8,
14,
15] discuss the meaning of sub-cycle in terms of homogeneity of gap evolution for single pair mission scenarios. The works investigate the impact of the groundtrack pattern and sub-cycle concept on the global gravity recovery up to a fixed spherical harmonic coefficient degree where a big difference between the quality of gravity solutions of drifting and skipping orbits are observed. However, the study by [
8] shows that the sub-cycle has no significant meaning in terms of global recovery for a fixed spherical harmonic degree to be solved.
Obviously, it makes more sense if the impact of groundtrack pattern and its time evolution, as well as the sub-cycle concept, are investigated for maximum spherical harmonic degrees by Colombo-Nyquist rule (CNR) and modified Colombo-Nyquist rule (MCNR). In this way, for Low Earth Orbit (LEO) missions, adding a day to the time span of the recovery means adding approximately 8 and 16 degrees and orders to the maximum spherical harmonic coefficient to be solved, respectively, for CNR and MCNR, but as long as the number of nodal days is still smaller than or equal to the full repeat period. Moreover, it might be of interest to observe the impact of even and odd orbit parities () on gravity solutions which are shorter than the full repeat cycle of the mission orbit scenario. The impact of groundtrack pattern on the regional gravity field (i.e., gravity retrieval for a specific region out of the global recovery) where the pattern is denser or when the sub-cycle happens is also worthy of further study. This paper, therefore, addresses the aforementioned research issues. We try to provide a few examples for different scenarios, and discuss potential future work in this research field.
In order to have a clearer overall view of this paper, it is important to mention that the GRACE Follow-on (GFO) mission has already been realized; therefore, the result of this research does not directly address the performance of GFO in the course of its orbit. However, our study tries to address the general impact of the sampling pattern on gravity recovery, which is also of great importance for understanding the quality variations by GFO products in its future life, as it is expected that by different sampling (ground-track pattern change) within GFO at different time-interval solutions, its recovery quality is also going to vary significantly.
Another important point to be mentioned is that, similar to the GRACE mission in the recent years, the science community expects to have short-interval gravity recovery (shorter than month) for GFO as well, particularly since GFO is benefiting from more advanced instrumentation, and hence, fewer measurement errors. That makes the weekly and shorter than weekly solutions more interesting which can be allowed by CNR and partially MCNR, and is the focus of this paper. For this purpose and to investigate the sampling impact on the recovery quality, a few examples are chosen for our study’s scope. Here, we test some scenarios with different “right ascension of ascending node” (RAAN) values over a hydrological basin in central Africa. Indeed, in both theory and reality, RAAN changes with time, and unless implementing mission control by humans during the satellite lifetime (which is rare, and mainly for altitude and repeat-orbit correction), the satellite path is not continuously corrected in order to bring RAAN to its initial value. Therefore, the selected RAAN values and the choice of central Africa in this research work should be seen as examples to study the recovery quality variations in different sampling scenarios. In fact, in this study, we do not address orbit optimization in specifics (which is the function of many other parameters), but instead, we try to address the importance of sampling pattern on the quality of gravity recovery through few examples. The choice of central Africa in the paper refers to its location close to the equator, which means a bigger area on the Earth, and so less dense sampling in the spatial domain when compared with sampling the higher latitudes. This choice can therefore address the sampling impact in a clearer way. Furthermore, the particular choice of the RAAN values refers to different sampling behavior, i.e., to the case where sub-cycle happens and to the cases where it does not happen in that area (and at that specific time).
4. Discussion
This work aimed to look more closely into the sampling patterns impact on the gravity recovery quality for global and regional studies, as the Colombo-Nyquist and modified Colombo-Nyquist rules apply. We tried to focus on the pure sampling impact in this paper, so no post-processing was considered. In reality, smoothing global or local filter (as one of the filter choices) is implemented. However, higher quality raw solutions (for example, due to denser sampling, and hence less spatial aliasing) can result in using more relaxed filters (e.g., a Gaussian smoothing with smaller radius). That would be then very beneficial in terms of signal-to-noise ratio, although the subject is outside the scope of this paper.
In particular, for the regional study, the groundtrack patterns impact of different satellite constellation scenarios have been investigated for a hydrological basin in central Africa. The quality of the gravity products have been assessed by different metrics such as spatial covariance representation. We also tried to investigate the potential meaning of the sub-cycle concept in terms of global and local impacts by different repeat-orbit scenarios with even and odd parities. Furthermore, different recovery scenarios in terms of the original and modified Colombo-Nyquist rules have been discussed.
The main points of our results can be summarized as follows:
In general, for 12 selected mission scenarios of
Table 1:
For the case Lmax = 32, with the increase of the time-pan of the solutions, the recovery error decreases. This is because of more sampling in space, and hence, less spatial aliasing, although the temporal aliasing gradually increases (but not significantly). The same argument applies for the case Lmax = 64 as well. For Lmax = CNR and MCNR, it is generally different. That means that for most of the scenarios, the longer the recovery time-span, the bigger the error. But here, it is important to notice that different scenarios have different performances. For some scenarios of the case Lmax = CNR, the error increase is significant. The cause of such an increase should be associated with the spatial aliasing which is more predominant for some mission scenarios, most likely because of the geometry of their orbits and therefore their time evolution of their groundtracks. A similar statement also applies for the case MCNR, even though more fluctuations are seen in the recovery error of few scenarios.
In terms of global recovery and for the selected inline formation scenarios of
Table 2:
Considering the inline formation missions, for Lmax = 32, the recovery by Ω = 132° after the 5th day is better than Ω = 116°. The recovery by Ω = 0° is the worst. Odd parity usually performs a bit better than the even parity. The 6th day as sub-cycle period is not significantly important in the global point of view. However, the concept might be more noticeable for Lmax = 64. For this case, the performance of the odd parity is better than the even parity. That is also the case for Lmax = CNR. In this case, different impact of odd and even parities on the gravity solutions larger than 7-day are significant. Moreover, the impact of Ω can be seen (Ω = 132° usually performs better than Ω = 116°, and Ω = 0° is the worst). In terms of global recovery, the 6th day as sub-cycle period also has a significant influence. After the 6th day, the error increases with the increase of the recovery time-interval. This effect is mainly assumed to be associated with the impact of temporal aliasing, since the spatial aliasing is tried to be largely avoided, according to CNR (although the spatial aliasing still exits by the impact of orbit geometry).
For the MCNR recovery, the odd parity performs better than the even parity above 6-day solutions. Surprisingly, Ω = 0° performs almost equal or even better (for longer time recovery) than the other two cases. Spatial aliasing is thought to be the biggest source of the error which increases as time span of the solutions increases (although temporal aliasing also contributes, as it is valid for all the other cases).
6-day (as sub-cycle period) does not show noticeable meaning. Very likely, the domination of spatial aliasing and the distribution of the geophysical signals with different strength over the globe hinder the emergence of any meaningful pattern.
Considering the Pendulum formation of the
Table 2 scenarios, and in the terms of global recovery, for the
Lmax = 32,
Ω = 132° performs better than
Ω = 116°. The recovery by
Ω = 0° is the worst and getting even worse over longer periods. One can not see significant difference by the performance of the odd and even parities. The 6th day as sub-cycle period is not significantly important in this case. For
Lmax = 64, the recovery by
Ω = 132° is better than
Ω = 116°. After day 5, recovery by
Ω = 0° is the worst and getting even worse at the longer periods. No significant difference is seen by the performance of the odd and even parities, although the even parity performs only a bit better than the odd parity after day 5. In terms of global recovery, the 6th day as sub-cycle period shows no important feature, although it may depict a very small impact on the recovery by
Ω = 0° and
Ω = 116°.
Unlike the case of CNR by inline formation, reduction of errors for Ω =116° and Ω = 132° by the longer period of the solutions are seen (possibly by less spatial aliasing). However, that is not the case for Ω = 0°. Therefore, one potential question to be addressed in future works might be the way that combination of isotropy (by Pendulum formation) and sampling plays role. The Ω = 132° case performs better than Ω = 116° which outperforms Ω = 0°. The even parity illustrates a slightly better performance than the odd parity. In terms of global recovery, the 6th day (as sub-cycle period) should not be considered significantly important.
For the MCNR case, the error increases for all cases after the 6-day solution. Therefore, it is not clear whether day 6 has meaning in terms of being sub-cycle or not. It is noticeable to see the better performance of the odd parity than the even parity at longer periods of solutions. The case Ω = 132° mostly performs better than the two other cases.
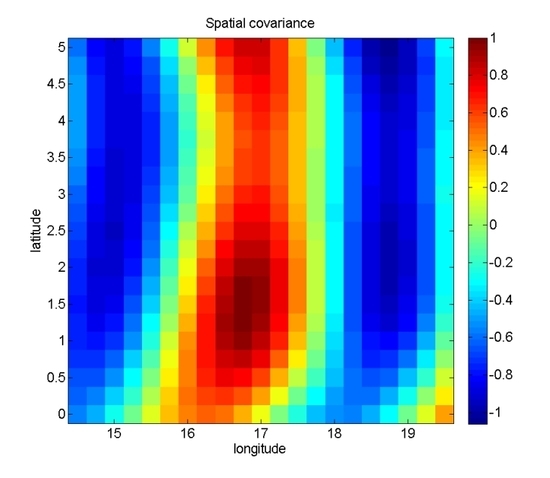
This paper also illustrates covariance matrices for 6-day solutions of the scenario (a) inline and Pendulum formations for Ω = 116°, where Lmax = 32, Lmax = 64, Lmax = CNR and Lmax = MCNR. The illustrations show that for the inline formation when the maximum spherical harmonic coefficient degree and order are above the CNR rule for 6-day (i.e., Lmax = 64 and Lmax = MCNR), the error level gets significant (assumed to be associated with spatial aliasing). However, for the Pendulum formation, those error patterns are not as noticeable as the inline formation (very likely associated to the more isotropic sampling by Pendulum formation).
Interpreting the results above, it should be emphasized that with our starting date choice for recovery simulation (1 January 1996), Ω = 0° corresponds to the groundtrack starting point at Pacific Ocean, east of South America, while Ω = 116° and Ω = 132° respectively stand for starting points at West-Africa and East-Africa. The results of this paper show that the best global performance (the smallest error) usually happens at Ω = 132°. This outcome might be expected since, among the three different values of Ω, the satellite mission track passes over significant hydrological signals when Ω = 132° (i.e., over East-Africa and the corresponding regions in the same longitudes). In terms of regional investigation, the results are usually optimal for the Ω = 116° case. In fact, this outcome is also expected, since that is the area where sub-cycle happens for the region targeted in this study (West-Africa). Nevertheless, for both global and regional study, the above statements are not always valid. When the maximum spherical degree and order of the solution goes beyond the Colombo-Nyquist rule (CNR), exceptions can be observed. A possible explanation for those exceptions could be the large spatial aliasing and the leakage from the surroundings which very likely deteriorates the impact of the sub-cycle. Obviously, more detailed studies should be directed in this way.
The results of our study also emphasize the impact of the mission formation on the error, where the Pendulum formation usually outperforms the inline (GRACE-like) formation, as expected through its more isotropic sampling behavior.
The spatial covariance illustrations of this research work for the GRACE-like formation depict the symmetry of the spatial covariance around the selected points for the cases Lmax = 32, 64, and CNR, although in the case of Lmax = 64, the spatial covariance graph center is shifted a bit, although for the Ω = 116° (where sub-cycle happens) the shift is less noticeable than for Ω = 0°. For the Pendulum formation, the graphs of Lmax = 32 and CNR feature symmetric patterns, but the graph centers are shifted towards left where it is more predominant for Lmax = 32. That is not the case for maximum spherical harmonic coefficient 64. It is interesting to say that for the MCNR recovery, the scenario (a) significantly outperforms the scenario (b) in terms of the symmetry.
Regarding the orbit parity impact on the gravity recovery, one should notice that the parity state (odd or even) is usually meaningful for the full repeat cycle. However, the evolution of the groundtrack pattern before the full cycle might be sophisticated and differ in each case; hence it is more reasonable to see the impact by its association to the groundtrack pattern distribution at a specific time span. That means, for the recovery time-spans shorter than the full-repeat cycle, instead of talking about the parity impact on the gravity recovery, it makes more sense to study the groundtrack pattern at that specific time interval and look for its potential association with the recovery quality. This issue will be addressed in our future works in more detail.