Simulation of Three Constitutive Behaviors Based on Nonlinear Ultrasound
Abstract
:1. Introduction
2. Classical Nonlinear Elasticity
2.1. Nonlinear Wave Equation
2.2. General Constitutive Relationship
2.3. Nonlinear Classic: 1st Perturbation ()
2.4. Nonlinear Classic: 2nd Perturbation ()
2.5. Nonlinear Hysteretic ()
3. Numerical Simulation
3.1. Verifying the Model
3.2. Wave Propagation Model
4. Simulation Result and Discussion
4.1. Verification Simulation
4.1.1. Nonlinear Classic: 1st Perturbation ()
4.1.2. Nonlinear Classic: 2nd Perturbation ()
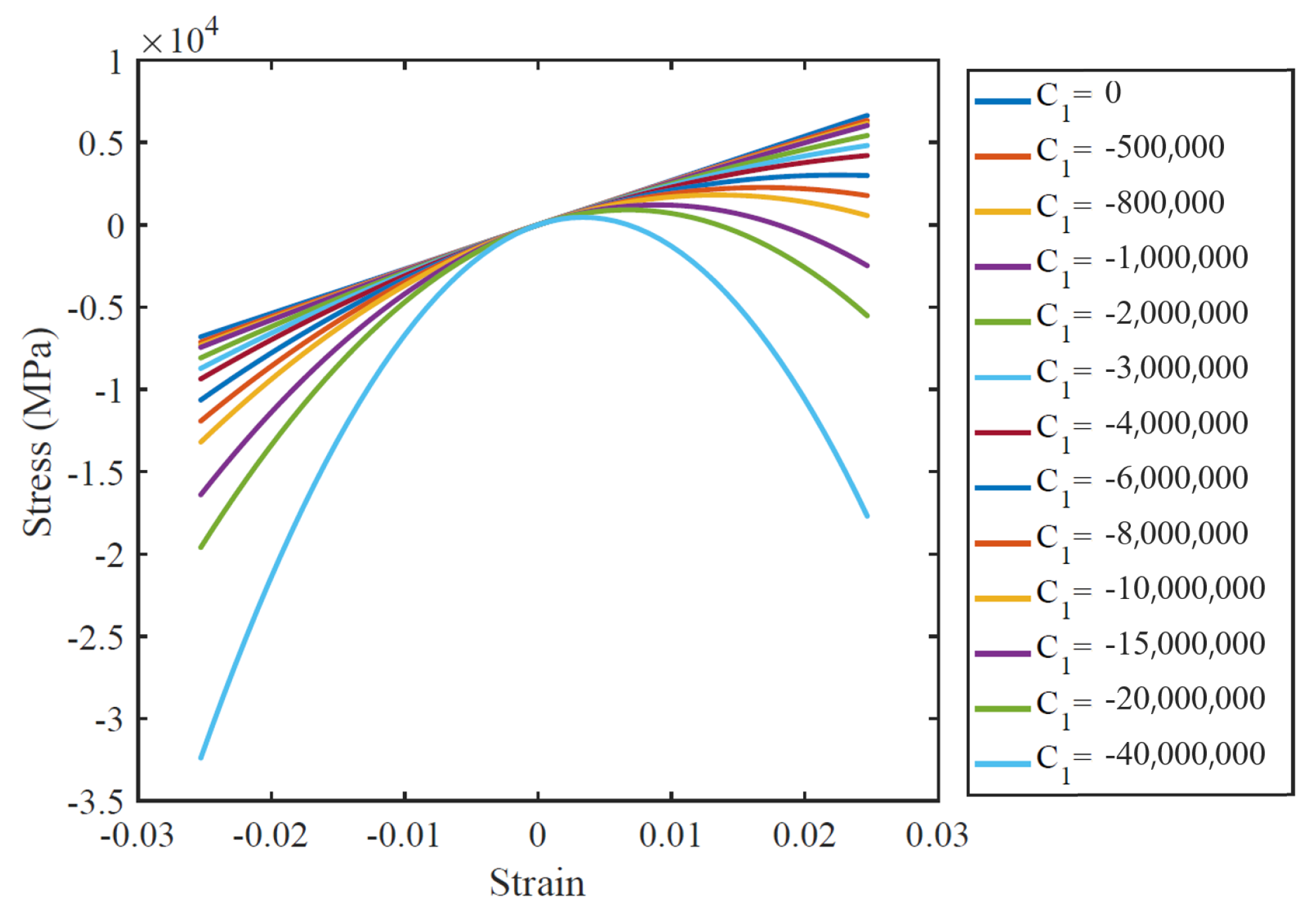
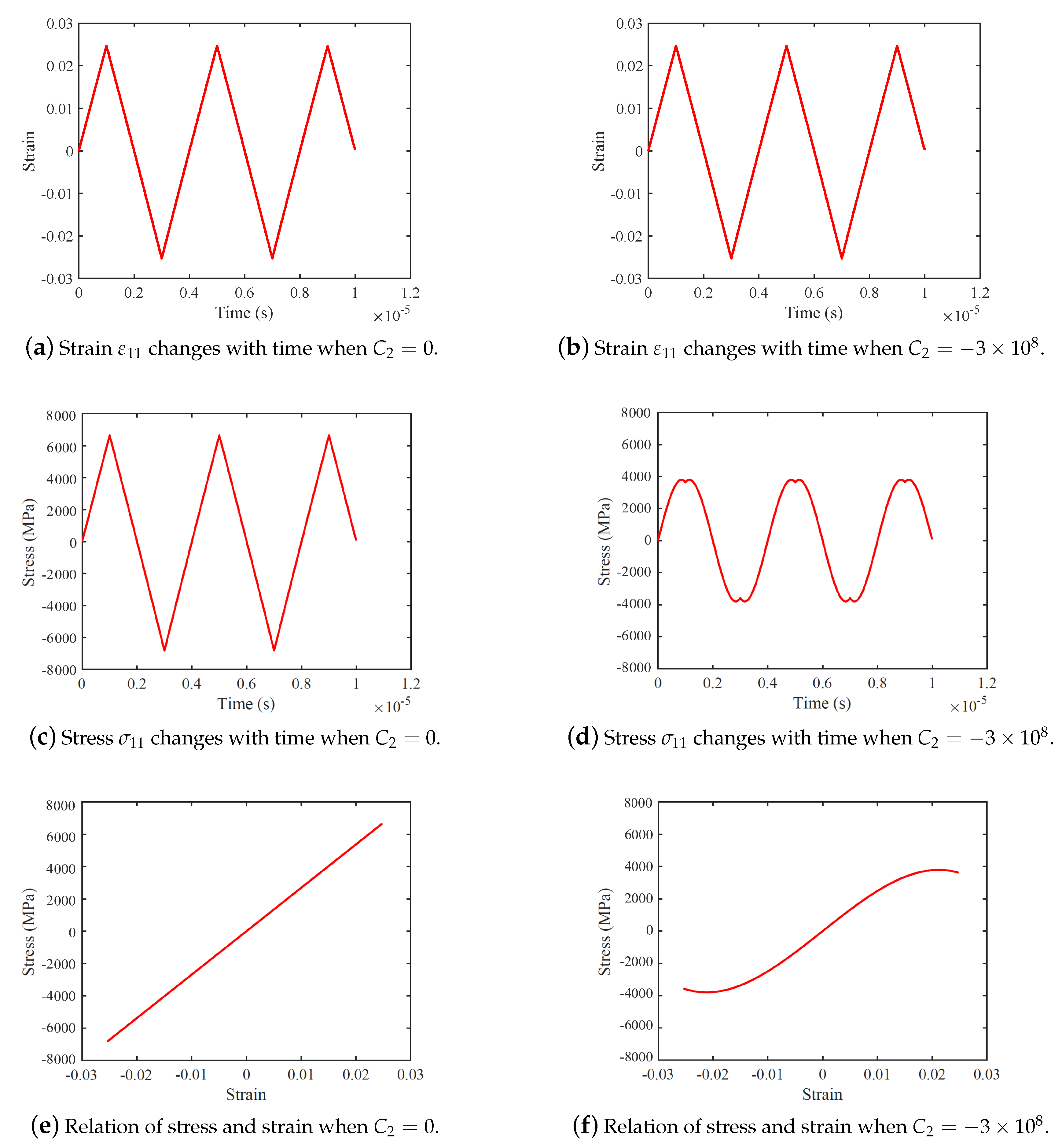
4.1.3. Nonlinear Hysteresis ()
4.2. Wave Propagation Simulation
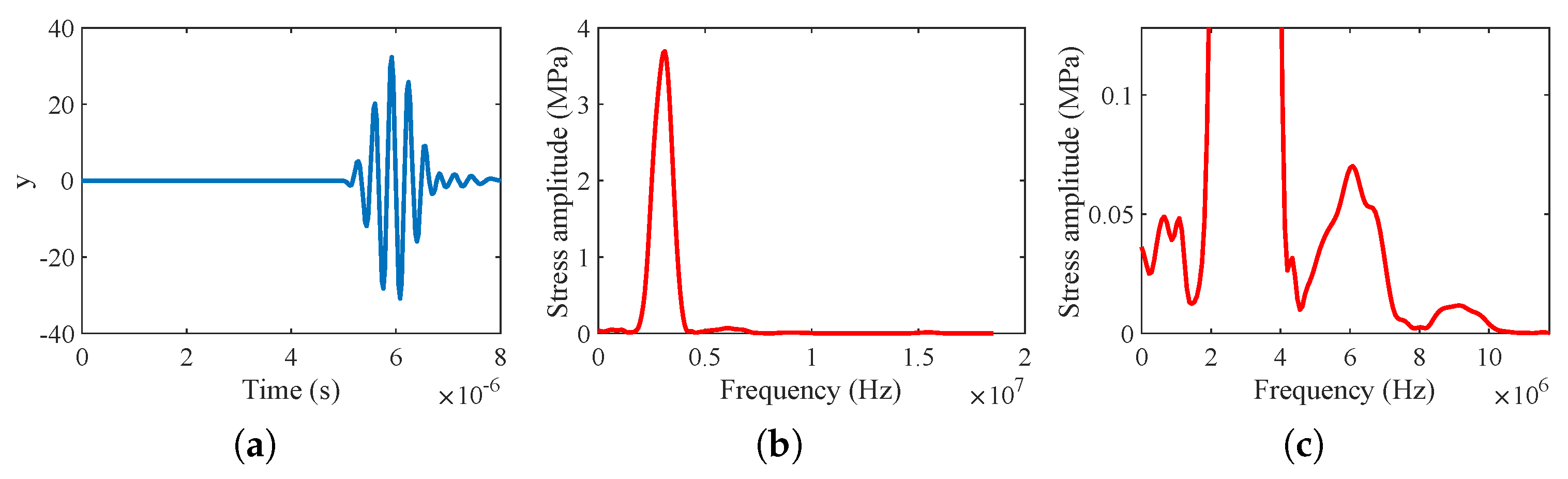
4.2.1. Nonlinear Classic: 1st Perturbation ()
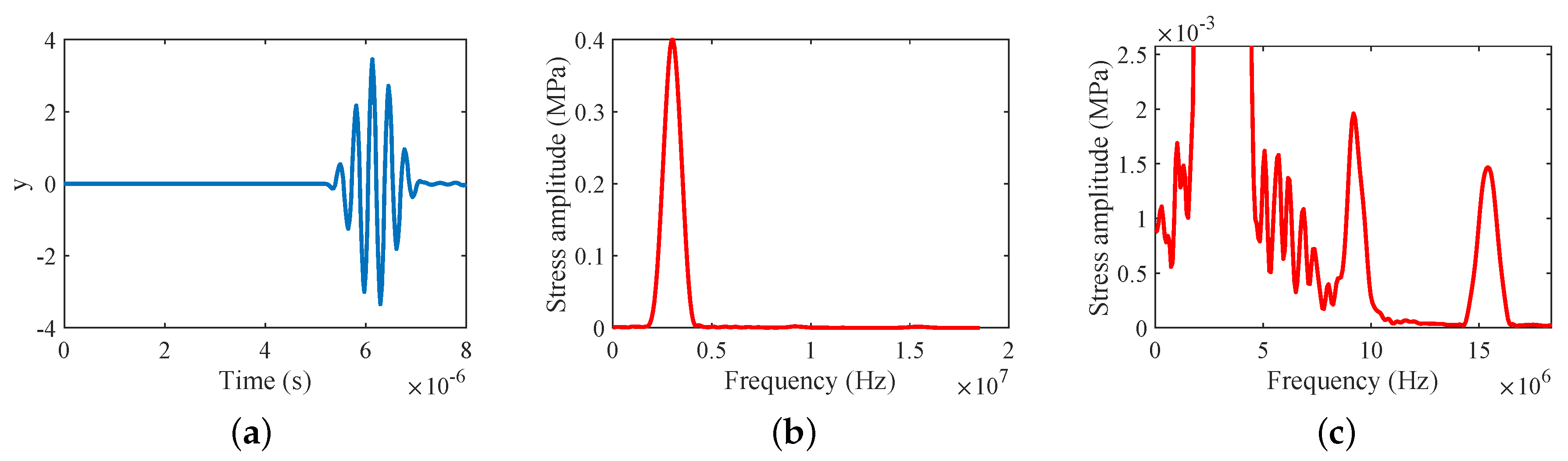
4.2.2. Nonlinear Classic: 2nd Perturbation ()
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Marcantonio, V.; Monarca, D.; Colantoni, A.; Cecchini, M. Ultrasonic waves for materials evaluation in fatigue, thermal and corrosion damage: A review. Mech. Syst. Signal Process. 2019, 120, 32–42. [Google Scholar] [CrossRef]
- Blanloeuil, P.; Rose, L.; Veidt, M.; Wang, C.H. Time reversal invariance for a nonlinear scatterer exhibiting contact acoustic nonlinearity. J. Sound Vib. 2019, 417, 413–431. [Google Scholar] [CrossRef]
- Aleshin, V.; Delrue, S.; Trifonov, A.; Matar, O.B.; Abeele, K.V.D. Two dimensional modeling of elastic wave propagation in solids containing cracks with rough surfaces and friction—Part I: Theoretical background. Ultrasonics 2017, 82, 11–17. [Google Scholar] [CrossRef]
- Kim, J.; Park, S.J.; Yim, H. Nonlinear Resonance Vibration Assessment to Evaluate the Freezing and Thawing Resistance of Concrete. Materials 2019, 12, 325. [Google Scholar] [CrossRef] [Green Version]
- Meyendorf, N.G.; Rösner, H.; Kramb, V.; Sathish, S. Thermo-acoustic fatigue characterization. Ultrasonics 2002, 40, 427–434. [Google Scholar] [CrossRef]
- Cantrell, J.H. Substructural organization, dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 757–780. [Google Scholar] [CrossRef]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Herrmann, J.; Kim, J.Y.; Jacobs, L.J.; Qu, J.; Littles, J.W.; Savage, M.F. Assessment of material damage in a nickel-base superalloy using nonlinear Rayleigh surface waves. J. Appl. Phys. 2006, 99, 124913. [Google Scholar] [CrossRef]
- Kim, J.Y. Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves. J. Acoust. Soc. Am. 2006, 120, 1266–1273. [Google Scholar] [CrossRef]
- Raghavan, A. Guided-wave structural health monitoring. Diss. Abstr. Int. 2007, 975, 91–114. [Google Scholar] [CrossRef]
- Solodov, I.Y.; Krohn, N.; Busse, G. CAN: An example of nonclassical acoustic nonlinearity in solids. Ultrasonics 2002, 40, 621–625. [Google Scholar] [CrossRef]
- Zarembo, I.K.; Krasil’Nikov, V.A. Nonlinear Phenomena in the Propagation of Elastic Waves in Solids. Sov. Phys. Uspekhi 1970, 102, 778. [Google Scholar] [CrossRef] [Green Version]
- Jhang, K.Y.; Kim, K.C. Evaluation of material degradation using nonlinear acoustic effect. Ultrasonics 1999, 37, 39–44. [Google Scholar] [CrossRef]
- Zheng, Y.; Maev, R.G.; Solodov, I.Y. Nonlinear acoustic applications for material characterization: A review. Can. J. Phys. 1999, 77, 927–967. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.; Martowicz, A.; Uhl, T.; Silberschmidt, V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.; Wang, Q.; Cheng, L.; Qing, X. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: Theory, simulation, and experimental validation. Ultrasonics 2014, 54, 770–778. [Google Scholar] [CrossRef]
- Ruiz, A.; Ortiz, N.; Medina, A.; Kim, J.Y.; Jacobs, L. Application of ultrasonic methods for early detection of thermal damage in 2205 duplex stainless steel. NDT E Int. 2013, 54, 19–26. [Google Scholar] [CrossRef]
- Fierro, G.M.; Ciampa, F.; Ginzburg, D.; Onder, E.; Meo, M. Nonlinear ultrasound modelling and validation of fatigue damage. J. Sound Vib. 2015, 343, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Feilong, L.; Youxuan, Z.; Yongmei, X.; Ning, H.; Peng, C.; Mingxi, D. Generation Mechanism of Nonlinear Rayleigh Surface Waves for Randomly Distributed Surface Micro-Cracks. Materials 2019, 11, 644. [Google Scholar] [CrossRef] [Green Version]
- Wan, X.; Zhang, Q.; Xu, G.; Tse, P. Numerical Simulation of Nonlinear Lamb Waves Used in a Thin Plate for Detecting Buried Micro-Cracks. Sensors 2014, 14, 8528–8546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melchora, J.; Parnell, W.; Bochud, N.; Peralta, L.; Rusa, G. Damage prediction via nonlinear ultrasound: A micro-mechanical approach. Ultrasonics 2019, 93, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Šofer, M.; Ferfecki, P.; Fusek, M.; Šofer, P.; Gnatowska, R.; Malujda, I.; Dudziak, M.; Krawiec, P.; Talaśka, K.; Wilczyński, D.A. The numerical analysis of the interaction between the low-order Lamb wave modes and surface breaking cracks. MATEC Web Conf. 2019, 254. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Shui, G.; Wang, Y.; Qu, J. Advances in nodestructive test and evaluation of material degradation using nonlinear ultrasound. Adv. Mech. 2005, 35, 54–70. [Google Scholar]
- Jiao, J.; Lv, H.; He, C.; Wu, B. Fatigue crack evaluation using the non-collinear wave mixing technique. Smart Mater. Struct. 2017, 26, 65–71. [Google Scholar] [CrossRef]
- Landau, L.D.; Pitaevskii, L.P.; Kosevich, A.M.; Lifshitz, E.M. Theory of Elasticity; Elsevier Ltd.: Oxford, UK, 1986. [Google Scholar]
- Van Den Abeele, K.A.; Johnson, P.A.; Sutin, A. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage, Part I: Nonlinear Wave Modulation Spectroscopy (NWMS). Res. Nondestruct. Eval. 2000, 12, 31–42. [Google Scholar] [CrossRef]
- Van Den Abeele, K.; Breazeale, M.A. Theoretical model to describe dispersive nonlinear properties of lead zirconate–titanate ceramics. J. Acoust. Soc. Am. 1996, 99, 1430–1437. [Google Scholar] [CrossRef]
- Jingpin, J.; Xiangji, M.; Cunfu, H.; Bin, W. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT E Int. 2016, 85, 63–71. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento della Soc. Ital. Fis. 2001, 24, 1–46. [Google Scholar]














| Free energy | F |
| Lamé coefficients | , |
| Strain tensor | |
| Displacement component | |
| Cartesian coordinate | |
| Quadratic nonlinear perturbation coefficient | |
| Cubic nonlinear perturbation coefficient | |
| Hysteresis | |
| Simplified first perturbation coefficient | |
| Simplified second perturbation coefficient | |
| Simplified nonlinear hysteretic coefficient | |
| Young’s modulus | E |
| Kronecker symbol | |
| Strain rate |
| Material Type | Mass Density | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|
| Steel | 7800 kg/m | Pa | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Z.; Wang, S.; Wang, F.; Huang, S.; Zhao, W.; Wang, Z. Simulation of Three Constitutive Behaviors Based on Nonlinear Ultrasound. Appl. Sci. 2020, 10, 1982. https://doi.org/10.3390/app10061982
Zhan Z, Wang S, Wang F, Huang S, Zhao W, Wang Z. Simulation of Three Constitutive Behaviors Based on Nonlinear Ultrasound. Applied Sciences. 2020; 10(6):1982. https://doi.org/10.3390/app10061982
Chicago/Turabian StyleZhan, Zaifu, Shen Wang, Fuping Wang, Songling Huang, Wei Zhao, and Zhe Wang. 2020. "Simulation of Three Constitutive Behaviors Based on Nonlinear Ultrasound" Applied Sciences 10, no. 6: 1982. https://doi.org/10.3390/app10061982





