Gaussian Process Model-Based Performance Uncertainty Quantification of a Typical Turboshaft Engine
Abstract
:1. Introduction
2. Modeling of the Turboshaft Engine Performance
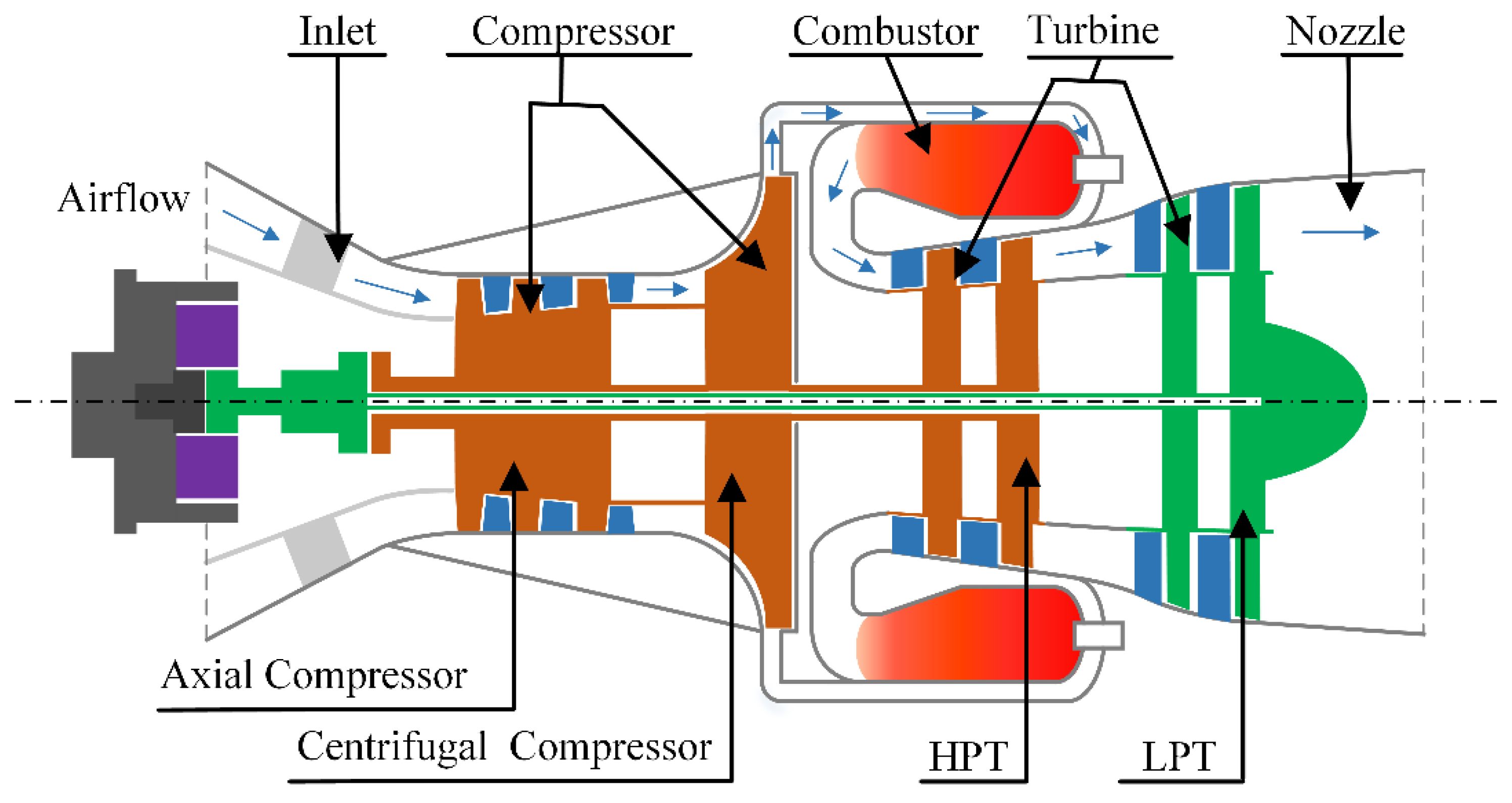
2.1. The Configuration and Operating Principle of the Turboshaft Engine
2.2. Turboshaft Engine Performance Simulation Model
- (1)
- Flow continuity in the interrelated components;
- (2)
- Power balance for the components in a rotor;
- (3)
- Rotational speed equality for the components in a rotor;
- (4)
- Pressure balance at the flow mixed sections.
- (1)
- The power balance equation for compressor and HPT is:where denotes the power provided by the HPT, denotes the power required by the compressor, and is the mechanical efficiency of the HPR.
- (2)
- The flow continuity equation for compressor and HPT is:where denotes the mass flow in the compressor, and denotes the mass flow in the HPT.
- (3)
- The flow continuity equation for HPT and LPT is:where denotes the mass flow in the LPT.
- (4)
- The pressure balance equation at the outlet of nozzle is:where denotes the static pressure at the outlet of the nozzle, and denotes the ambient pressure.
3. Methodologies
3.1. Gasussian Process Model
3.2. Gaussian Process Model-Based Latin Hypercube Sampling
- (1)
- Stratify the vertical axis on the plot of of into nonoverlapping intervals with the same length: , where ;
- (2)
- Map the boundary values on the vertical axis to the values of defined on the horizontal axis using the inverse CDF ;
- (3)
- Stratify the random variable using the mapped values and obtain intervals: ;
- (4)
- Select a random value from each interval of and generate a matrix where the ith column contains random values of ;
- (5)
- Order the values in every column of the matrix randomly and complete the LHS.
3.3. Variance-Based Sensitivity Analysis
4. Results and Discussion
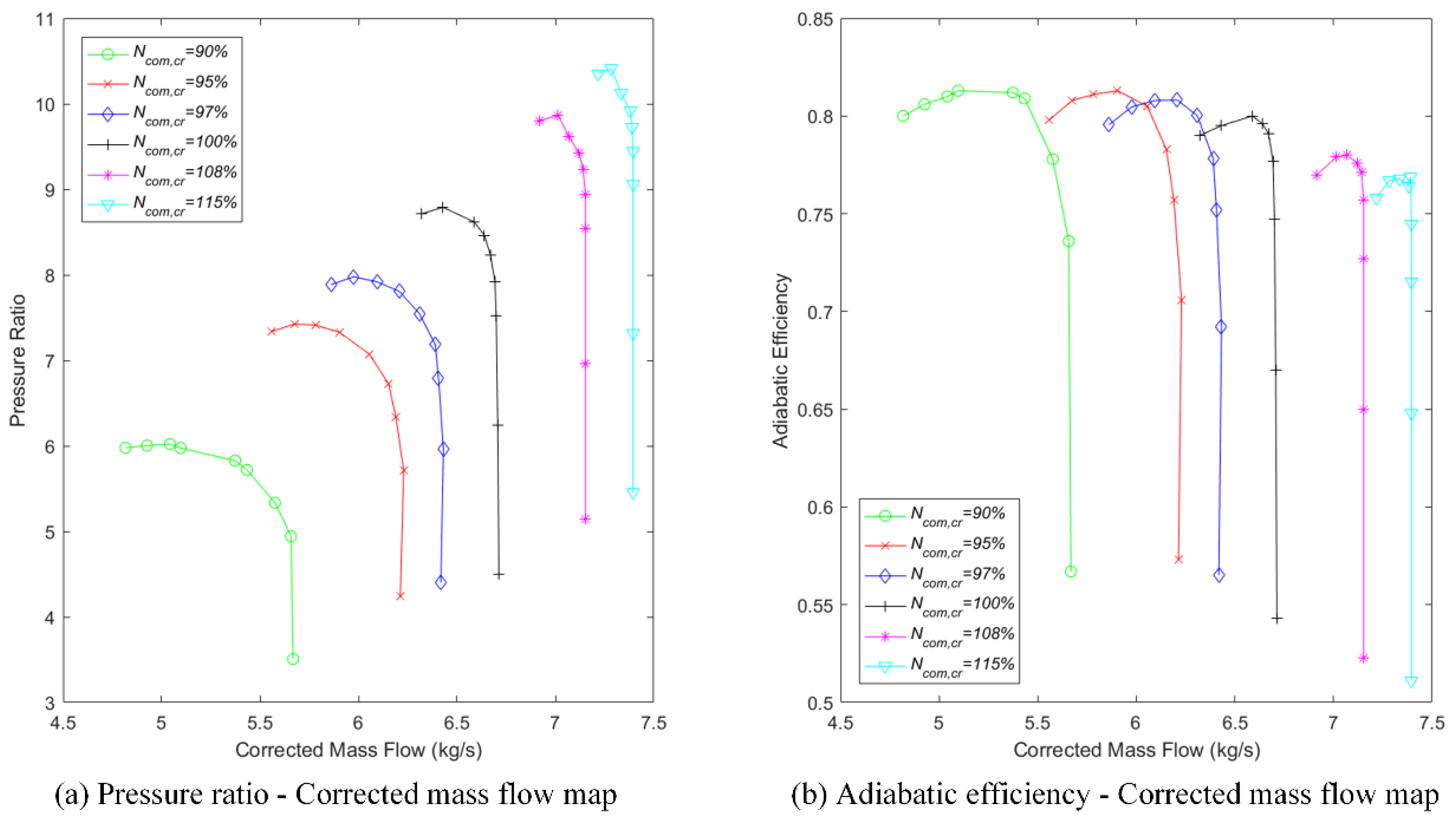
4.1. Engine Performance Baseline and Uncertain Parameters
4.2. Gaussian Process Modeling for the Turboshaft Engine Performance
4.3. Uncertainty Quantification of the Turboshaft Engine Performance
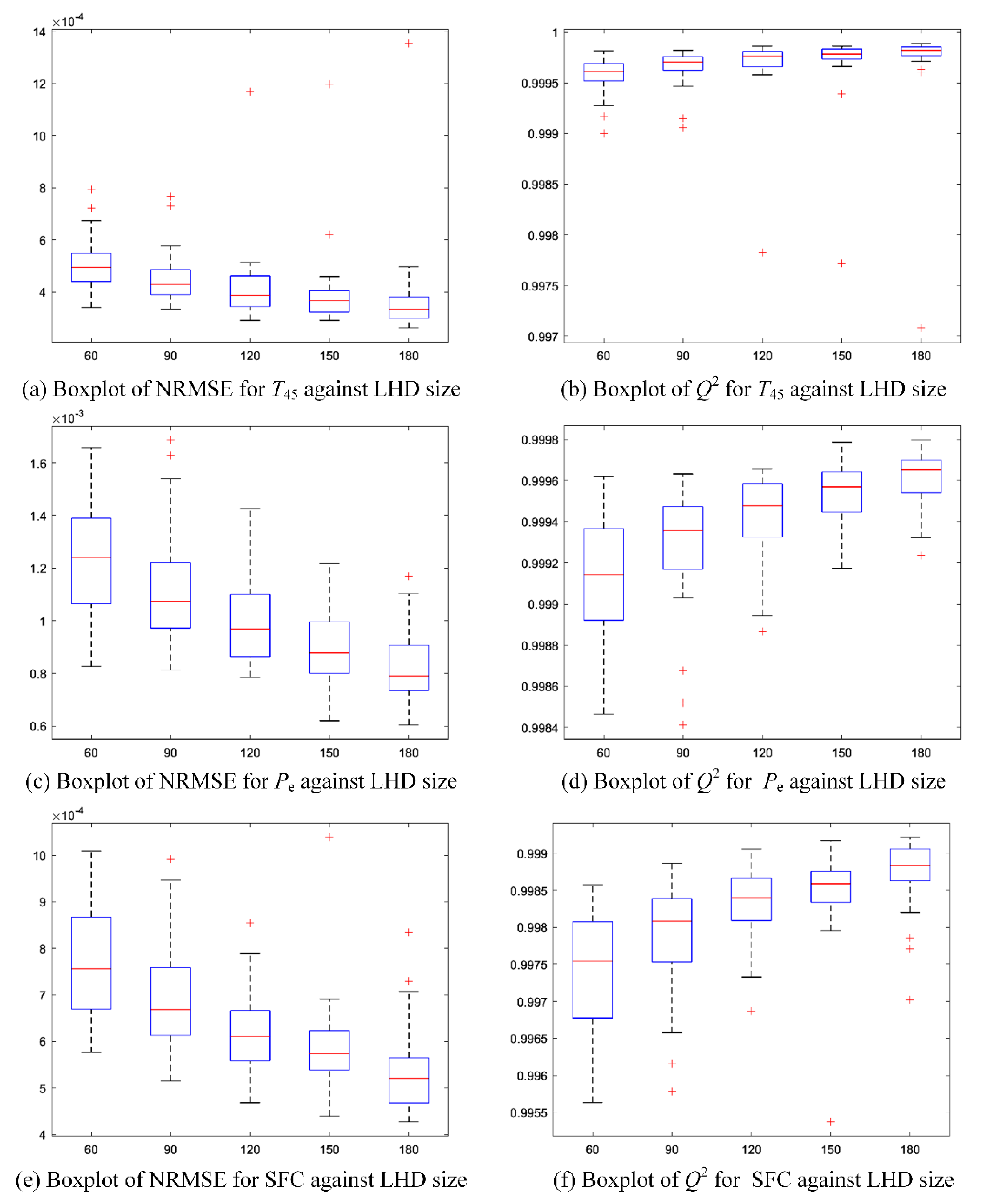
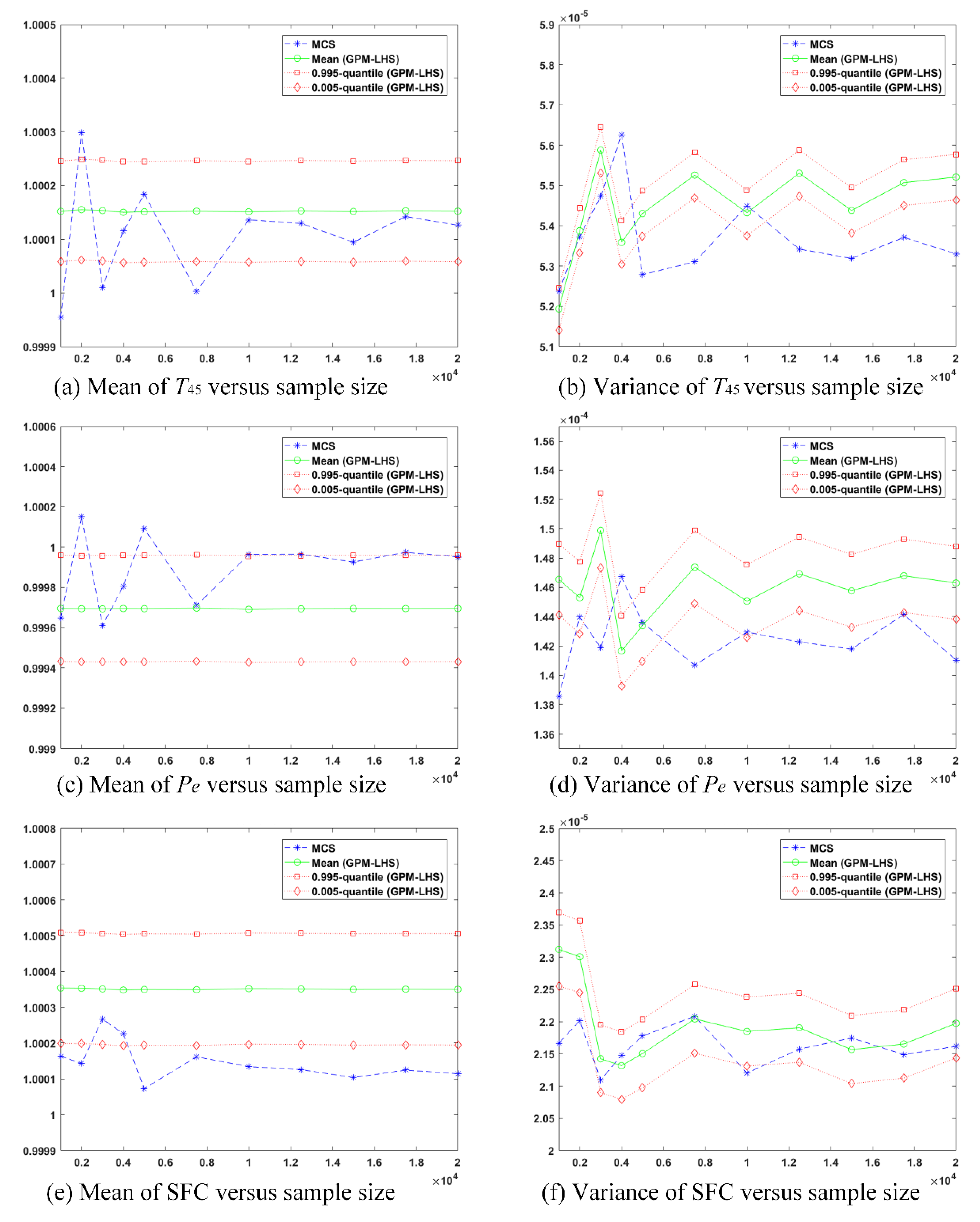
4.3.1. Comparison of the GPM-Based LHS with the Simulation-Based MCS
4.3.2. Comparison of Effects of the Independent and Correlated Uncertain Parameters
4.3.3. Uncertainty Analysis of the Turboshaft Engine Performance
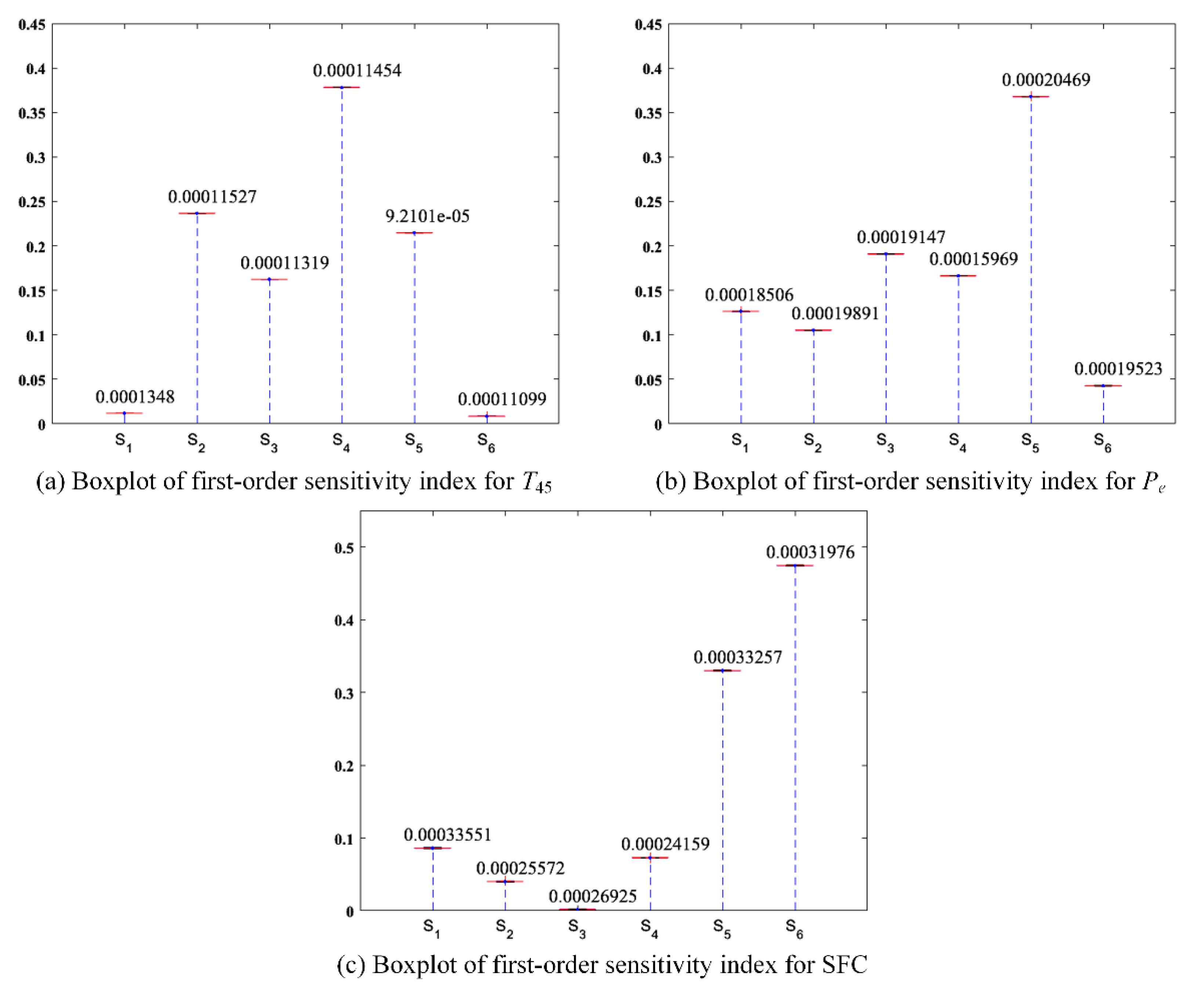
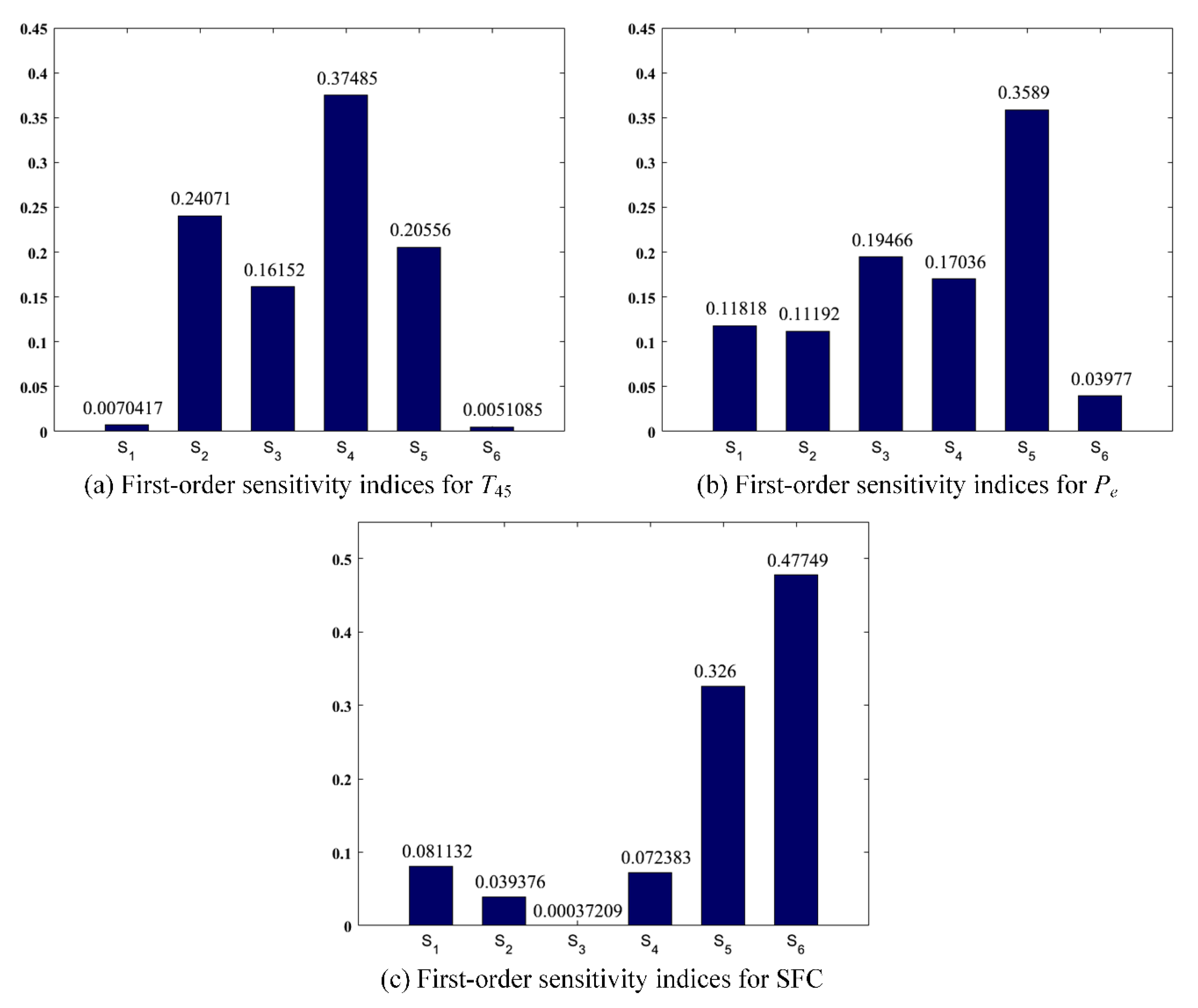
4.4. Sensitivity Analysis of the Turboshaft Engine Performance
5. Conclusions
- (1)
- A strong correlation (with a correlation efficiency of 60%) between the flow capacity and adiabatic efficiency of compressor only has a small influence on the standard deviation of the turboshaft engine performance. Specifically, the standard deviation of decreases by around 6.6–8.7% as the standard deviation of uncertain parameters varies from 0.002 to 0.004. Likewise, a reduction of 2.3–4.2% is observed for , but an increase of 3.0–3.7% for SFC.With an assumption of independent parameters, the maximum , minimum , and maximum SFC deviate 1.3%, 2.2%, and 0.84% from their nominal design values in the unfavorable direction when the standard deviations of uncertain parameters are equal to 0.002. The deviations almost double as the standard deviations increase to 0.004.
- (2)
- The first-order sensitivity indices of six uncertain parameters almost account for 100% of the total variabilities of the three PMs, more specifically, 99.48% of the total variability in , 99.38% of the total variability in , and 99.68% of the total variability in SFC. Only a very small proportion of total variability is attributed to the sum of high-order sensitivity indices.
- (3)
- The important parameters for are , , , and . All the uncertain parameters other than are the important parameters for . Only and are the important parameters for SFC. In particular, is important to all the three PMs of the turboshaft engine.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurzke, J.; Halliwell, I. Propulsion and Power; Springer: Cham, Switzerland, 2018; pp. 5–42. [Google Scholar] [CrossRef]
- Giampaolo, T. Gas Turbine Handbook: Principles and Practice, 5th ed.; The Fairmont Press: Lilburn, GA, USA, 2014; pp. 45–77. [Google Scholar]
- Garzon, V.E.; Darmofal, D.L. Impact of Geometric Variability on Axial Compressor Performance. J. Turbomach. 2003, 125, 1199–1213. [Google Scholar] [CrossRef] [Green Version]
- Lange, A.; Voigt, M.; Vogeler, K.; Johann, E. Principal component analysis on 3D scanned compressor blades for probabilistic CFD simulation. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Spieler, S.; Staudacher, S.; Fiola, R.; Sahm, P.; Weißschuh, M. Probabilistic engine performance scatter and deterioration modeling. J. Eng. Gas. Turbines Power 2008, 130, 150–158. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Tang, H.L.; Chen, M. Linear substitute model-based uncertainty analysis of complicated non-linear energy system performance (case study of an adaptive cycle engine). Appl. Energy 2019, 249, 87–108. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, K.; Tang, H.L. A Probabilistic Design Methodology for a Turboshaft Engine Overall Performance Analysis. Adv. Mech. Eng. 2014, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Cao, D.; Bai, G. A Study on Aeroengine Conceptual Design Considering Multi-Mission Performance Reliability. Appl. Sci. 2020, 10, 46–68. [Google Scholar] [CrossRef]
- Tai, J.C.M.; Mines, J.M.; Inclan, E.; Zhu, S.; Mavris, D.N. Uncertainty Quantification and Management in Engine Conceptual Design. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef]
- Lamorte, N.; Friedmann, P.P.; Dalle, D.J.; Torrez, S.M.; Driscoll, J.F. Uncertainty Propagation in Integrated Airframe–Propulsion System Analysis for Hypersonic Vehicles. J. Propul. Power 2015, 31, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Chang, J.; Ma, J.; Yu, D. Performance uncertainty propagation analysis for control-oriented model of a turbine-based combined cycle engine. Acta Astronaut. 2018, 153, 39–49. [Google Scholar] [CrossRef]
- Montomoli, F. Uncertainty Quantification in Computational Fluid Dynamics and Aircraft Engines; Springer: Cham, Switzerland, 2019; pp. 80–82. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, J.; Tang, H. Interval analysis of the standard of adaptive cycle engine component performance deviation. Aerosp. Sci. Technol. 2018, 81, 179–191. [Google Scholar] [CrossRef]
- Fu, C.; Xu, Y.; Yang, Y.; Lu, K.; Gu, F.; Ball, A. Response analysis of an accelerating unbalanced rotating system with both random and interval variables. J. Sound Vib. 2019, 466. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnsom, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.C.; Helton, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef] [Green Version]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Currin, C.; Mitchell, T.; Morris, M.; Ylvisaker, D. Bayesian prediction of deterministic functions, with applications to the design and analysis of computer experiments. J. Am. Stat. Assoc. 1991, 86, 953–963. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003; pp. 1–3, 27–37. [Google Scholar]
- Chapman, J.W.; Lavelle, T.M.; May, R.; Litt, J.S.; Guo, T.H. Propulsion System Simulation Using the Toolbox for the Modeling and Analysis of Thermodynamic Systems (T-MATS). In Proceedings of the 50th AIAA/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar] [CrossRef] [Green Version]
- Chapman, J.W.; Lavelle, T.M.; Litt, J.S. Practical techniques for modeling gas turbine engine performance. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef] [Green Version]
- Al-Hamdan, Q.Z.; Ebaid, M.S.Y. Modeling and Simulation of a Gas Turbine Engine for Power Generation. J. Eng. Gas. Turbines Power 2006, 128, 302–311. [Google Scholar] [CrossRef]
- Chen, M.; Tang, H.L.; Zhu, Z.L. Goal Programming for Stable Mode Transition in Tandem Turbo-ramjet Engine. Chin. J. Aeronaut. 2009, 22, 486–492. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.L.; Chen, M.; Jin, D.H.; Zou, Z.P. High altitude low Reynolds number effect on the matching performance of a turbofan engine. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2013, 227, 455–466. [Google Scholar] [CrossRef]
- Chen, M.; Tang, H.L.; Zhang, K.; Hui, O.Y.; Wang, Y.J. Turbine-based combined cycle propulsion system integration concept design. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2012, 227, 1068–1089. [Google Scholar] [CrossRef]
- Zheng, J.C.; Tang, H.L.; Chen, M.; Yin, F.J. Equilibrium running principle analysis on an adaptive cycle engine. Appl. Therm. Eng. 2018, 132, 393–409. [Google Scholar] [CrossRef] [Green Version]
- Ghani, F.; Fernandez, E.F.; Almonacid, F.; O’Donovan, T.S. The numerical computation of lumped parameter values using the multi-dimensional Newton-Raphson method for the characterisation of a multi-junction CPV module using the five-parameter approach. Sol. Energy 2017, 149, 302–313. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, UK, 2005; pp. 81–83. [Google Scholar] [CrossRef] [Green Version]
- Marrel, A.; Iooss, B.; Laurent, B.; Roustant, O. Calculations of sobol indices for the Gaussian process metamodel. Reliab. Eng. Syst. Saf. 2008, 94, 742–751. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.H.Y. Robust Parameter design with computer experiments using orthonormal polynomials. Technometrics 2015, 57, 468–478. [Google Scholar] [CrossRef]
- Roshanian, J.; Ebrahimi, M. Latin hypercube sampling applied to reliability-based multidisciplinary design optimization of a launch vehicle. Aerosp. Sci. Technol. 2013, 28, 297–304. [Google Scholar] [CrossRef]
- Mckay, M.D.; Conover, W.J.; Beckman, R.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2004, 66, 751–769. [Google Scholar] [CrossRef] [Green Version]
- Janon, A.; Klein, T.; Lagnoux, A.; Nodet, M. Asymptotic normality and efficiency of two Sobol index estimators. ESAIM Prob. Stat. 2014, 18, 342–364. [Google Scholar] [CrossRef] [Green Version]
- Naeem, M.; Singh, R.; Probert, D. Consequences of aero-engine deteriorations for military aircraft. Appl. Energy 2001, 70, 103–133. [Google Scholar] [CrossRef]
- Brown, H.; Elgin, J.A. Aircraft Engine Control Mode Analysis. J. Eng. Gas. Turbines Power 1985, 107, 838–844. [Google Scholar] [CrossRef]
- Loeppky, J.L.; Sacks, J.; Welch, W.J. Choosing the sample size of a computer experiment: A practical guide. Technometrics 2009, 51, 366–376. [Google Scholar] [CrossRef] [Green Version]


| No. | Notation | Undetermined Parameters |
|---|---|---|
| 1 | The location of the operating point of compressor | |
| 2 | The location of the operating point of HPT | |
| 3 | The location of the operating point of LPT | |
| 4 | The fuel flow |
| Parameter | Value | Unit |
|---|---|---|
| Ambient temperature | 288.15 | K |
| Ambient pressure | 101,325 | Pa |
| Height | 0 | km |
| Mach number | 0 | -- |
| Relative spool speed of HPR (control variable) | 0.97 | -- |
| Relative spool speed of LPT (control variable) | 1 | -- |
| Component | Uncertain Parameter | Notation | High Level | Low Level | Probabilistic Distribution |
|---|---|---|---|---|---|
| Compressor | Flow capacity | 0.02 | −0.02 | Truncated Gaussian distribution | |
| Adiabatic efficiency | 0.02 | −0.02 | Truncated Gaussian distribution | ||
| HPT | Flow capacity | 0.02 | −0.02 | Truncated Gaussian distribution | |
| Adiabatic efficiency | 0.02 | −0.02 | Truncated Gaussian distribution | ||
| LPT | Flow capacity | 0.02 | −0.02 | Truncated Gaussian distribution | |
| Adiabatic efficiency | 0.02 | −0.02 | Truncated Gaussian distribution |
| LHD Size | T45 | Pe | SFC | |||
|---|---|---|---|---|---|---|
| NRMSE | Q2 | NRMSE | Q2 | NRMSE | Q2 | |
| 60 | 0.000508 | 0.999573 | 0.001237 | 0.999121 | 0.000761 | 0.997458 |
| 90 | 0.000451 | 0.99966 | 0.001118 | 0.999278 | 0.000696 | 0.997864 |
| 120 | 0.000417 | 0.999686 | 0.000999 | 0.999427 | 0.000620 | 0.998322 |
| 150 | 0.000398 | 0.999705 | 0.000900 | 0.999536 | 0.00059 | 0.998464 |
| 180 | 0.000378 | 0.999715 | 0.000826 | 0.999609 | 0.000538 | 0.998723 |
| Performance Parameters | Distribution Parameters | Relative Deviation (σ = 0.002) | Relative Deviation (σ = 0.003) | Relative Deviation (σ = 0.004) |
|---|---|---|---|---|
| T45 | Mean | −0.000175% | −0.000876% | −0.001247% |
| Std * | −2.337830% | −4.218916% | −3.548779% | |
| Pe | Mean | 0.001091% | 0.002451% | 0.003923% |
| Std * | −6.624252% | −8.693671% | −8.350732% | |
| SFC | Mean | −0.000679% | −0.001874% | −0.003072% |
| Std * | 3.716896% | 2.997669% | 3.738209% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Tang, H.; Zhang, X.; Chen, M. Gaussian Process Model-Based Performance Uncertainty Quantification of a Typical Turboshaft Engine. Appl. Sci. 2021, 11, 8333. https://doi.org/10.3390/app11188333
Liu X, Tang H, Zhang X, Chen M. Gaussian Process Model-Based Performance Uncertainty Quantification of a Typical Turboshaft Engine. Applied Sciences. 2021; 11(18):8333. https://doi.org/10.3390/app11188333
Chicago/Turabian StyleLiu, Xuejun, Hailong Tang, Xin Zhang, and Min Chen. 2021. "Gaussian Process Model-Based Performance Uncertainty Quantification of a Typical Turboshaft Engine" Applied Sciences 11, no. 18: 8333. https://doi.org/10.3390/app11188333





