Hybrid Equivalent Circuit/Finite Element/Boundary Element Modeling for Effective Analysis of an Acoustic Transducer Array with Flexible Surrounding Structures
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Impedance Matrix Equation
2.1.1. Single Transducer
2.1.2. Array of Transducers
2.2. Acoustic Radiation Impedance
2.3. Transfer Matrix for Field Point Pressure Calculation
3. Validation
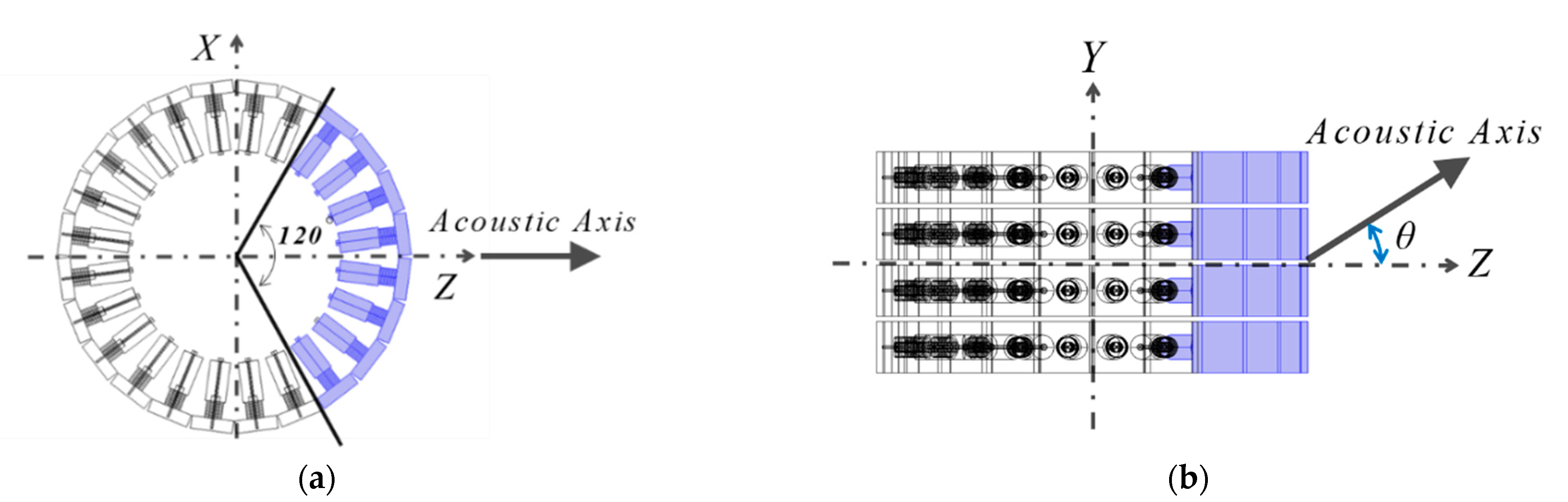
3.1. Analysis Model
3.2. Analysis Condition
3.3. Analysis Result
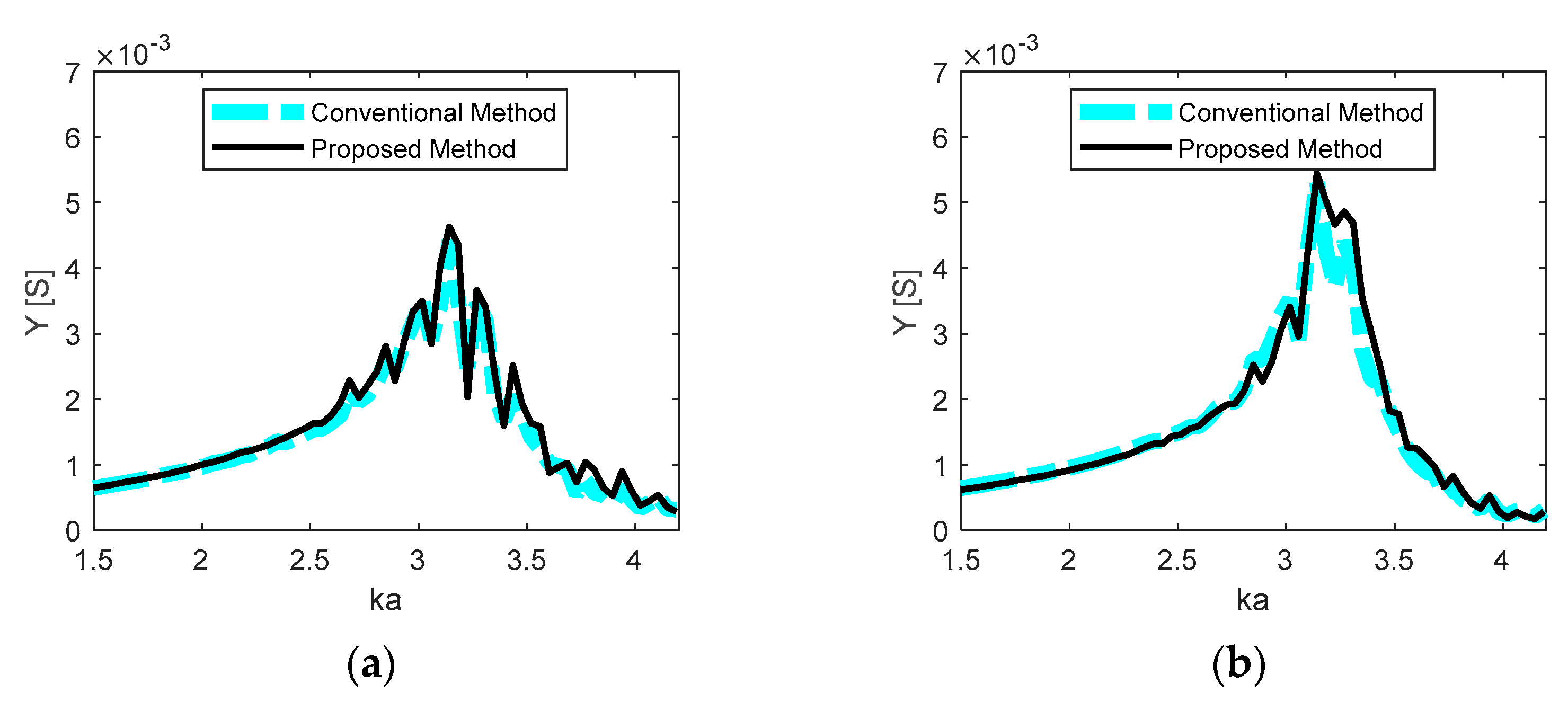
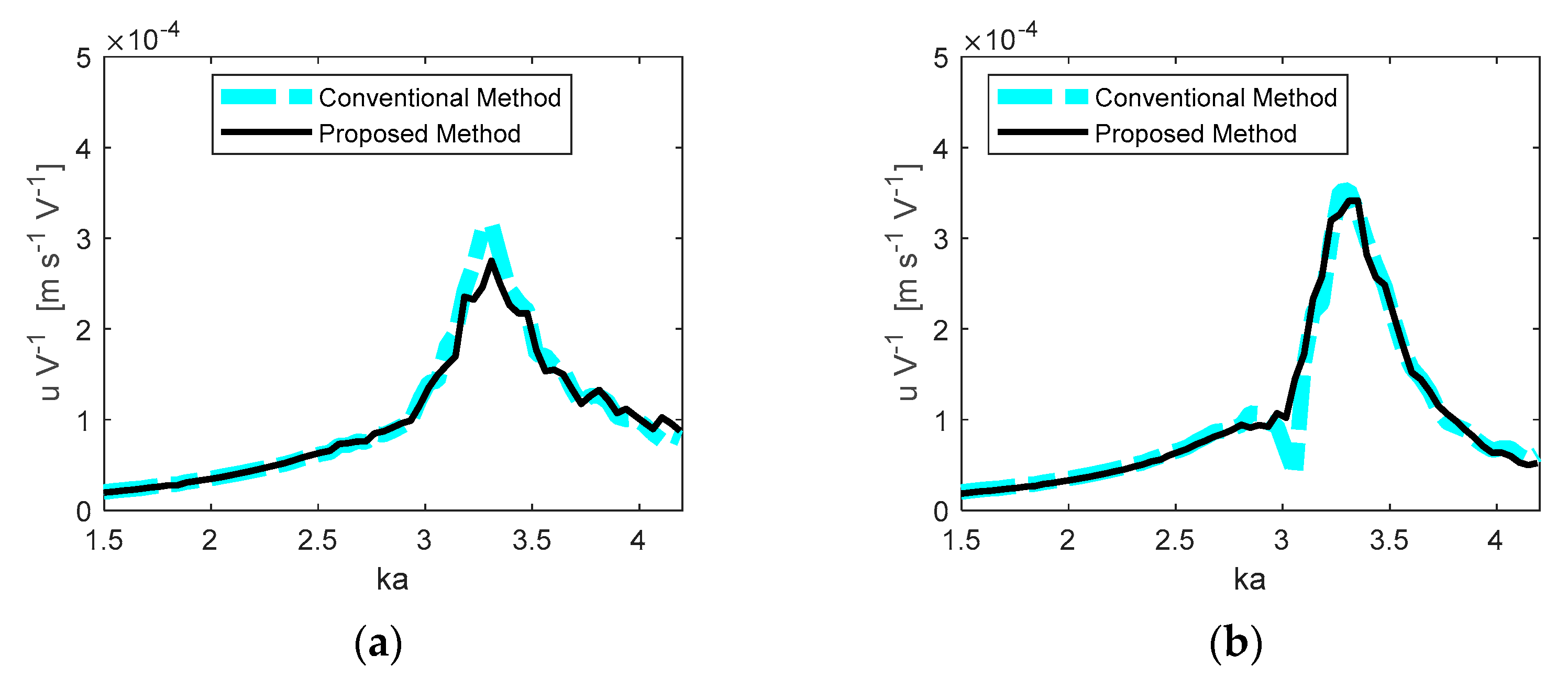
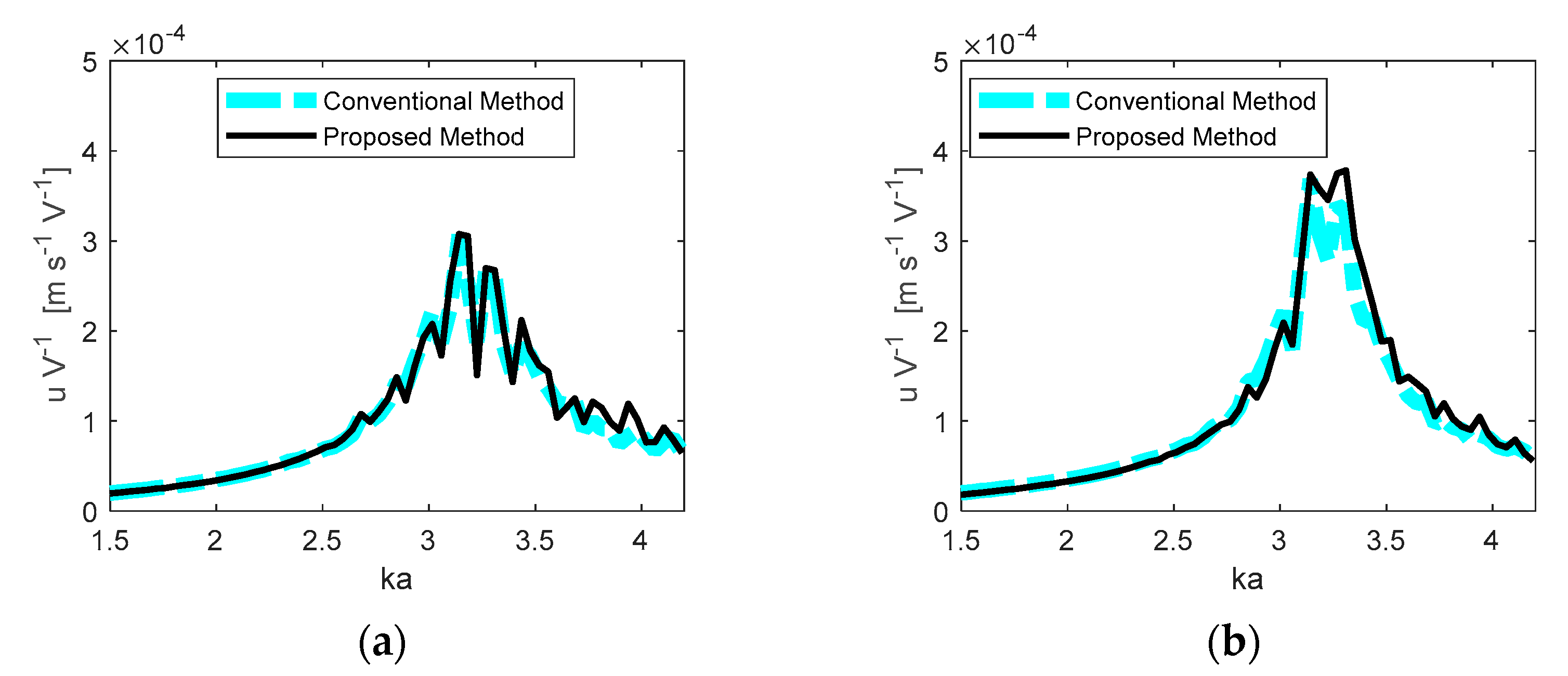
3.3.1. Response of Each Transducer
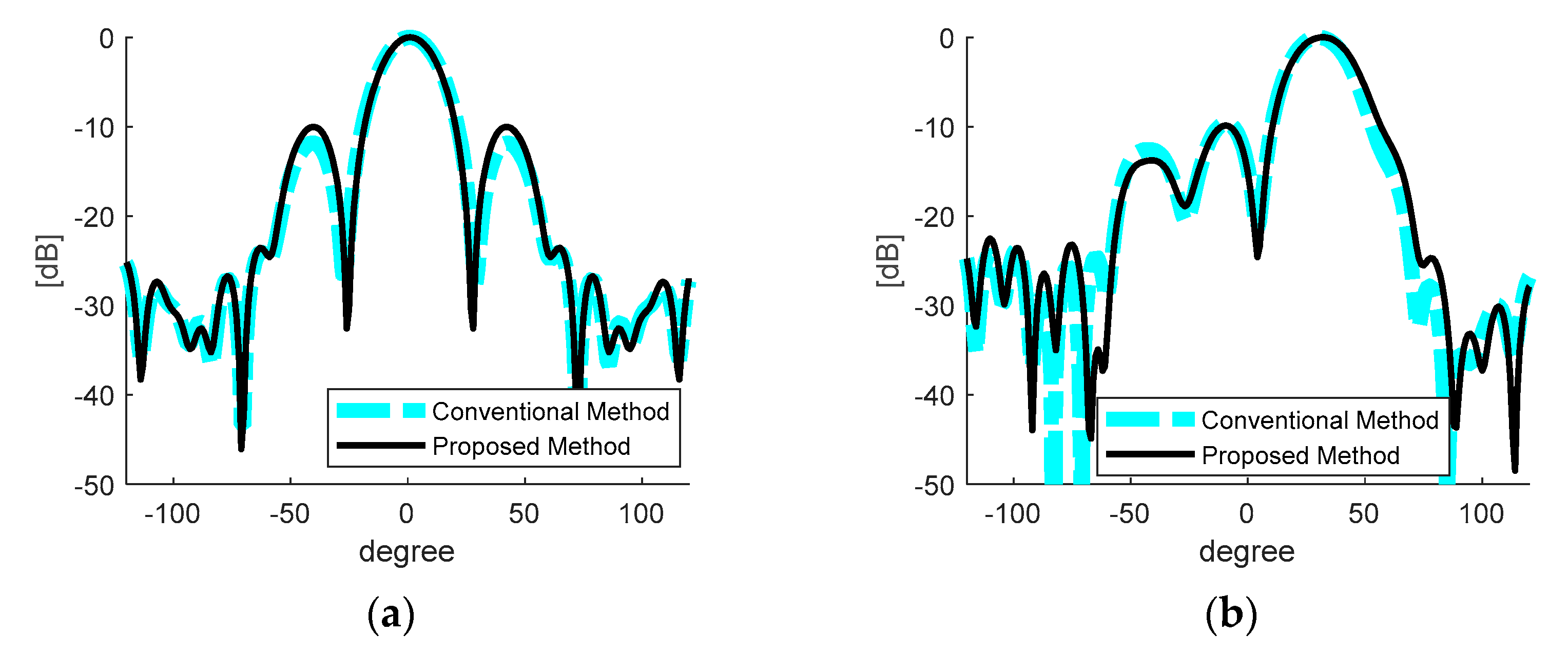
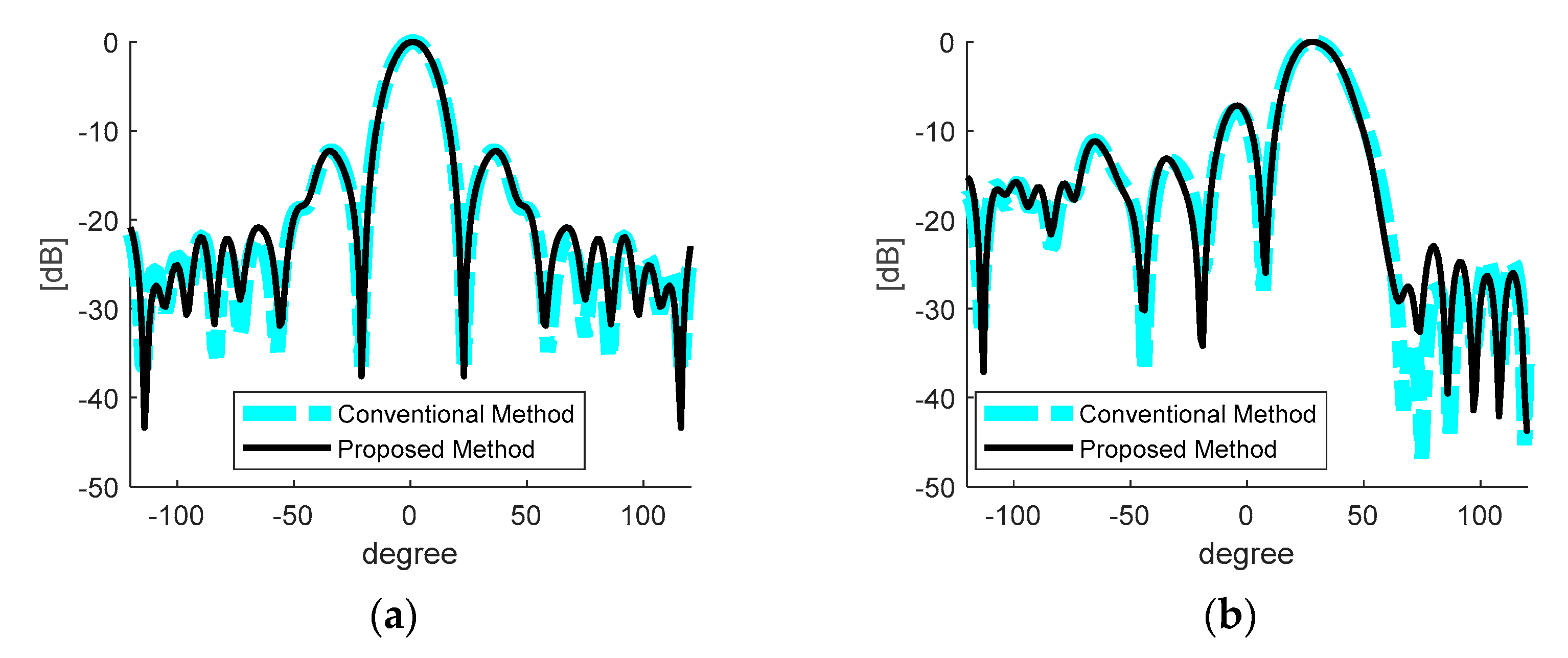
3.3.2. Array Performance
3.4. Evaluation of Numerical Performance (in Terms of DOFs Reduction)
- The size of one side of the acoustic element is set to about [37].
- The FE of the structure should be generated so that the mode shapes that are within 2 times the maximum analysis frequency can be well represented.
- The shape of the acoustic window is assumed to be an oblate spheroid, and its size is set to increase in proportion to the array size. Here, the sizes of the half-length of the principal axes are assumed to be and . is the radius of the array.
- For the conventional full FEM, an adequate amount of space is required between the array and the outer surface in order to apply an open boundary condition to the surface of the acoustic region. The free space of the open boundary is assumed to be set to 300% of the size of the structure. Thus, the radius of the open boundary is three times the half-length of the principal axes.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rizwan, M.K.; Laureti, S.; Mooshofer, H.; Goldammer, M.; Ricci, M. Ultrasonic Imaging of Thick Carbon Fiber Reinforced Polymers through Pulse-Compression-Based Phased Array. Appl. Sci. 2021, 11, 1508. [Google Scholar] [CrossRef]
- Peralta, L.; Ramalli, A.; Reinwald, M.; Eckersley, R.J.; Hajnal, J.V. Impact of Aperture, Depth, and Acoustic Clutter on the Performance of Coherent Multi-Transducer Ultrasound Imaging. Appl. Sci. 2020, 10, 7655. [Google Scholar] [CrossRef] [PubMed]
- Angerer, M.; Zapf, M.; Leyrer, B.; Ruiter, N.V. Model-Guided Manufacturing of Transducer Arrays Based on Single-Fibre Piezocomposites. Appl. Sci. 2020, 10, 4927. [Google Scholar] [CrossRef]
- Go, D.; Kang, J.; Song, I.; Yoo, Y. Efficient Transmit Delay Calculation in Ultrasound Coherent Plane-Wave Compound Imaging for Curved Array Transducers. Appl. Sci. 2019, 9, 2752. [Google Scholar] [CrossRef] [Green Version]
- Bae, S.; Song, T.-K. Methods for Grating Lobe Suppression in Ultrasound Plane Wave Imaging. Appl. Sci. 2018, 8, 1881. [Google Scholar] [CrossRef] [Green Version]
- Mestouri, H.; Loussert, A.; Keryer, G. Finite Element Modeling of 2-D Transducer Arrays. J. Acoust. Soc. Am. 2008, 123, 3116. [Google Scholar] [CrossRef]
- Yamamoto, M.; Inoue, T.; Shiba, H.; Kitamura, Y. Finite-Element Method Analysis of Low-Frequency Wideband Array Composed of Disk Bender Transducers with Differential Connections. Jpn. J. Appl. Phys. 2009, 48, 07GL06. [Google Scholar] [CrossRef]
- Tilmans, H.A. Equivalent circuit representation of electromechanical transducers: I. Lumped-parameter systems. J. Micromech. Microeng. 1996, 6, 157–176. [Google Scholar] [CrossRef]
- Tilmans, H.A. Equivalent circuit representation of electromechanical transducers: II. Distributed-parameter systems. J. Micromech. Microeng. 1997, 7, 285–309. [Google Scholar] [CrossRef]
- Lee, J.; Seo, I.; Han, S.M. Radiation power estimation for sonar transducer arrays considering acoustic interaction. Sens. Actuator A Phys. 2001, 90, 1–6. [Google Scholar] [CrossRef]
- Oguz, H.K.; Atalar, A.; Köymen, H. Equivalent circuit-based analysis of CMUT cell dynamics in arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 1016–1024. [Google Scholar] [CrossRef] [PubMed]
- Hwang, Y.; Moon, W.; Je, Y.; Kim, W.; Lee, S. A Precise Equivalent-Circuit Model for a Circular Plate Radiator. Acta Acust. United Acust. 2018, 104, 79–86. [Google Scholar] [CrossRef]
- Audoly, C. Some aspects of acoustic interactions in sonar transducer arrays. J. Acoust. Soc. Am. 1991, 89, 1428–1433. [Google Scholar] [CrossRef]
- Yokoyama, T.; Henmi, M.; Hasegawa, A.; Kikuchi, T. Effects of mutual interactions on a phased transducer array. Jpn. J. Appl. Phys. 1998, 37, 3166–3171. [Google Scholar] [CrossRef]
- Meynier, C.; Teston, F.; Certon, D. A multiscale model for array of capacitive micromachined ultrasonic transducers. J. Acoust. Soc. Am. 2010, 128, 2549–2561. [Google Scholar] [CrossRef]
- Rudgers, A.J. A correlation technique for determining the self-and mutual-radiation impedances of transducers in an array. J. Acoust. Soc. Am. 1974, 55, 759–765. [Google Scholar] [CrossRef]
- Sherman, C.H.; Butler, J.L. Chapter 7. Transducer Models. In Transducers and Arrays for Underwater Sound, 4th ed.; Springer: New York, NY, USA, 2007; pp. 338–350. [Google Scholar]
- Klapman, S.J. Interaction impedance of a system of circular pistons. J. Acoust. Soc. Am. 1940, 11, 289–295. [Google Scholar] [CrossRef]
- Robey, D.H. On the radiation impedance of an array of finite cylinders. J. Acoust. Soc. Am. 1955, 27, 706–710. [Google Scholar] [CrossRef]
- Sherman, C.H. Mutual radiation impedance of sources on a sphere. J. Acoust. Soc. Am. 1959, 31, s947–s952. [Google Scholar] [CrossRef]
- Pritchard, R.L. Mutual acoustic impedance between radiators in an infinite rigid plane. J. Acoust. Soc. Am. 1960, 32, 730–737. [Google Scholar] [CrossRef]
- Greenspon, J.E.; Sherman, C.H. Mutual-Radiation Impedance and Nearfield Pressure for Pistons on a Cylinder. J. Acoust. Soc. Am. 1964, 36, 149–153. [Google Scholar] [CrossRef]
- Arase, E.M. Mutual radiation impedance of square and rectangular pistons in a rigid infinite baffle. J. Acoust. Soc. Am. 1964, 36, 1521–1525. [Google Scholar] [CrossRef]
- Mangulis, V. Nearfield Pressure for an Infinite Phased Array of Circular Pistons. J. Acoust. Soc. Am. 1967, 41, 412–418. [Google Scholar] [CrossRef]
- Schenck, H.A. Improved integral formulation for acoustic radiation problems. J. Acoust. Soc. Am. 1968, 44, 41–58. [Google Scholar] [CrossRef]
- Thompson, W., Jr. The computation of self-and mutual-radiation impedances for annular and elliptical pistons using Bouwkamp’s integral. J. Sound Vib. 1971, 17, 221–233. [Google Scholar] [CrossRef]
- Stepanishen, P.R. The radiation impedance of a rectangular piston. J. Sound Vib. 1977, 55, 275–288. [Google Scholar] [CrossRef]
- Lee, J.; Seo, I. Radiation impedance computations of a square piston in a rigid infinite baffle. J. Sound Vib. 1996, 198, 299–312.a. [Google Scholar] [CrossRef]
- Rdzanek, W.; Rdzanek, W.; Różycka, A. The Green function for the Neumann boundary value problem at the semiinfinite cylinder and the flat infinite baffle. Arch. Acoust. 2014, 32, 7–12. [Google Scholar]
- Rdzanek, W.P.; Rdzanek, W.J.; Pieczonka, D. The acoustic impedance of a vibrating annular piston located on a flat rigid baffle around a semi-infinite circular rigid cylinder. Arch. Acoust. 2012, 37, 411–422. [Google Scholar] [CrossRef] [Green Version]
- Pyo, S.; Roh, Y. Analysis of the crosstalk in an underwater planar array transducer by the equivalent circuit method. Jpn. J. Appl. Phys. 2017, 56, 07JG01-1–07JG01-6. [Google Scholar]
- Costabel, M. Symmetric methods for the coupling of finite elements and boundary elements (invited contribution). In Mathematical and Computational Aspects, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 411–420. [Google Scholar]
- Amini, S.; Harris, P.J.; Wilton, D.T. Coupled Boundary and Finite Element Methods for the Solution of the Dynamic Fluid-Structure Interaction Problem; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hong, C.S.; Shin, K.K. Applications of General-purpose Packages for Fluid-structure Interaction Problems. Trans. Korean Soc. Noise Vib. Eng. 1997, 7, 571–578. [Google Scholar]
- Atalla, N.; Sgard, F. Chapter 8. Problem of exterior coupling. In Finite Element and Boundary Methods in Structural Acoustics and Vibration; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Sherman, C.H.; Butler, J.L. Chapter 5. Projector Arrays. In Transducers and Arrays for Underwater Sound, 4th ed.; Springer: New York, NY, USA, 2007; pp. 223–228. [Google Scholar]
- Marburg, S. Six boundary elements per wavelength: Is that enough? J. Comput. Acoust. 2002, 10, 25–51. [Google Scholar] [CrossRef]
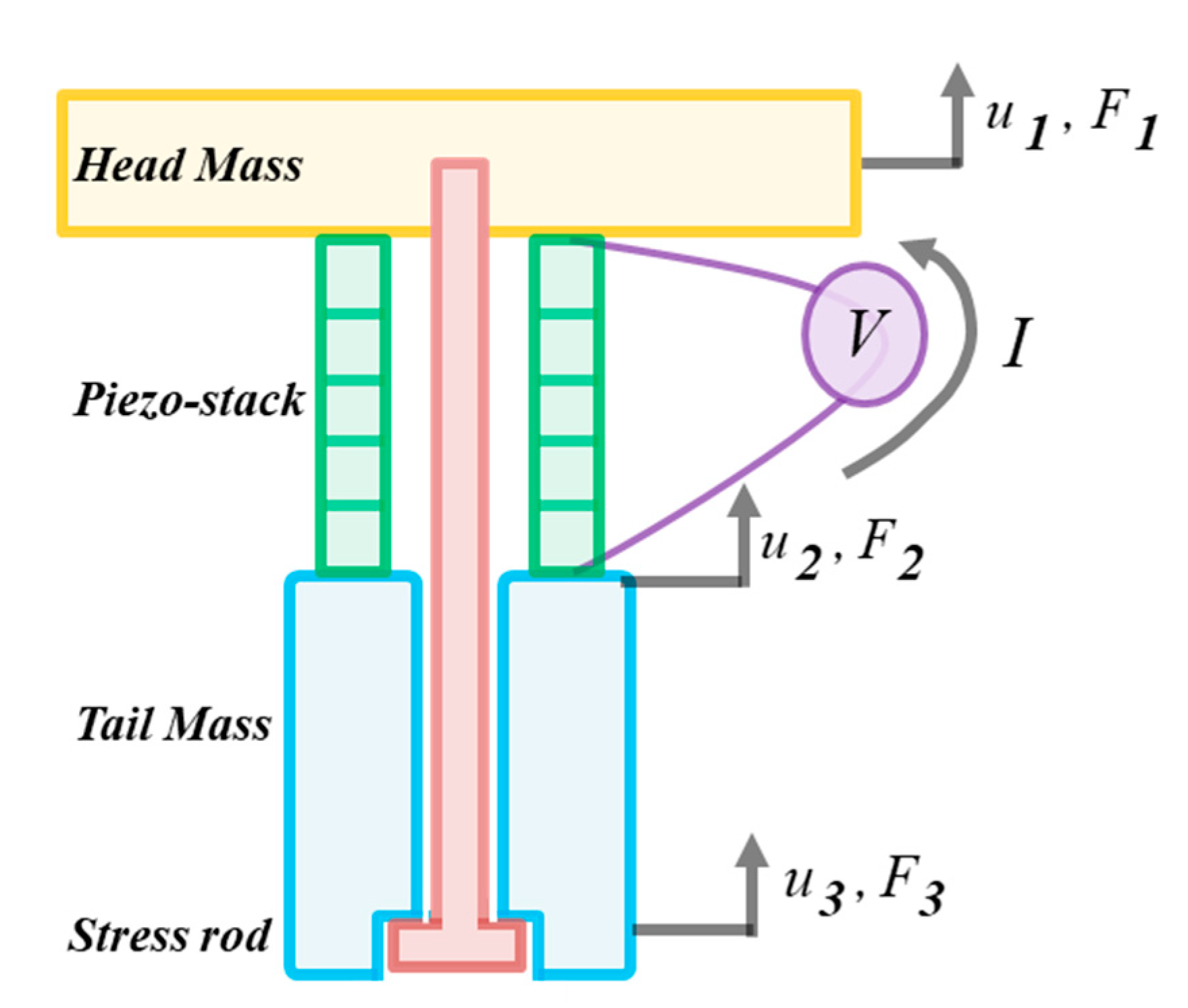
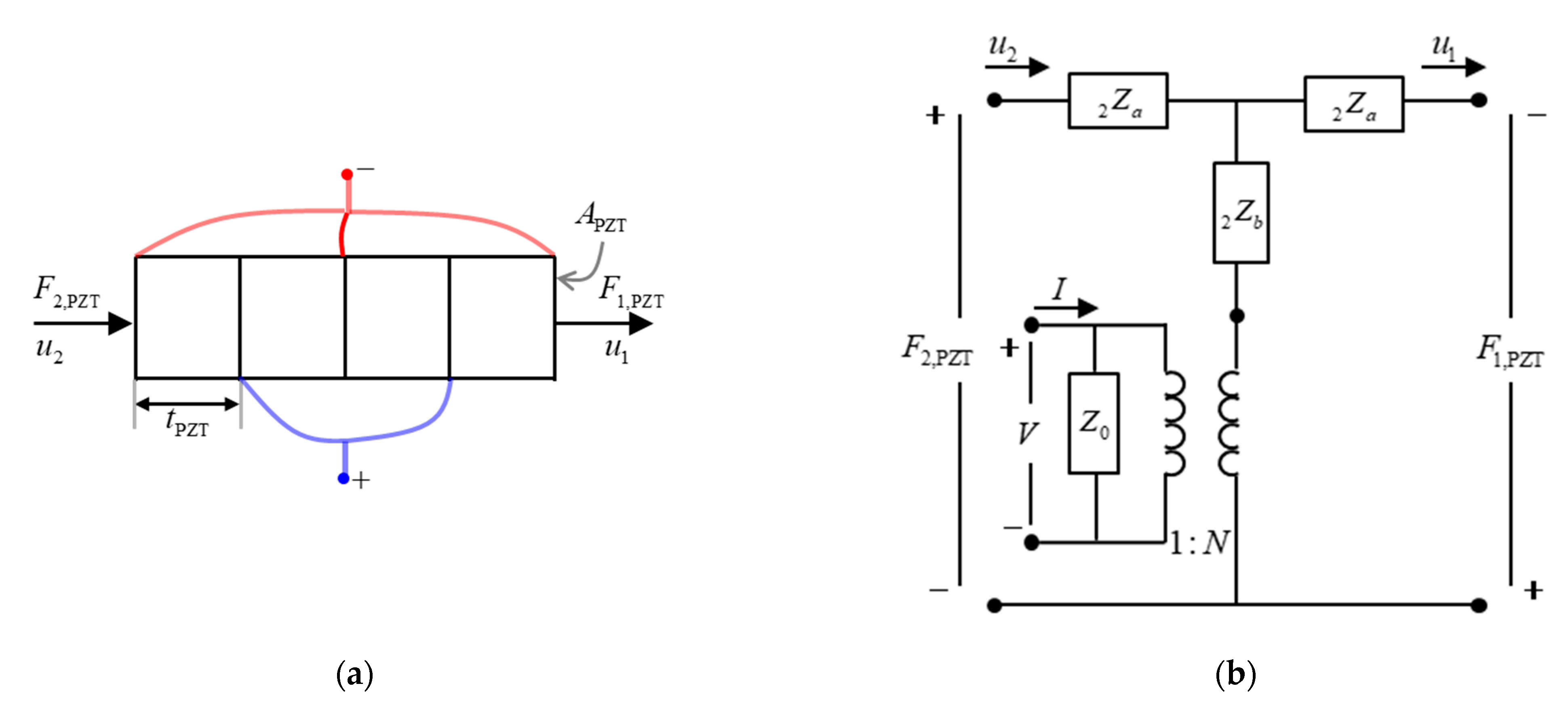


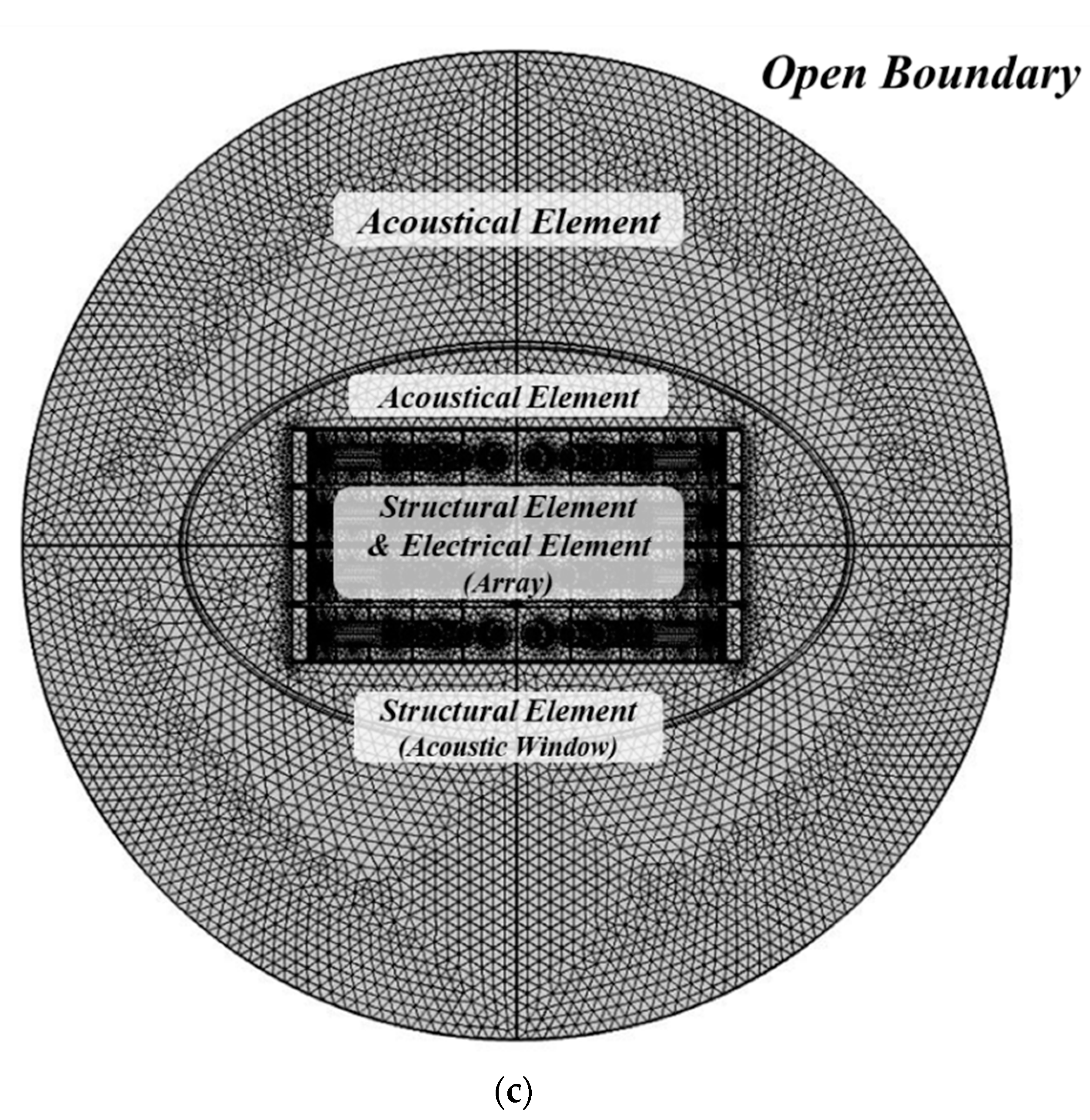
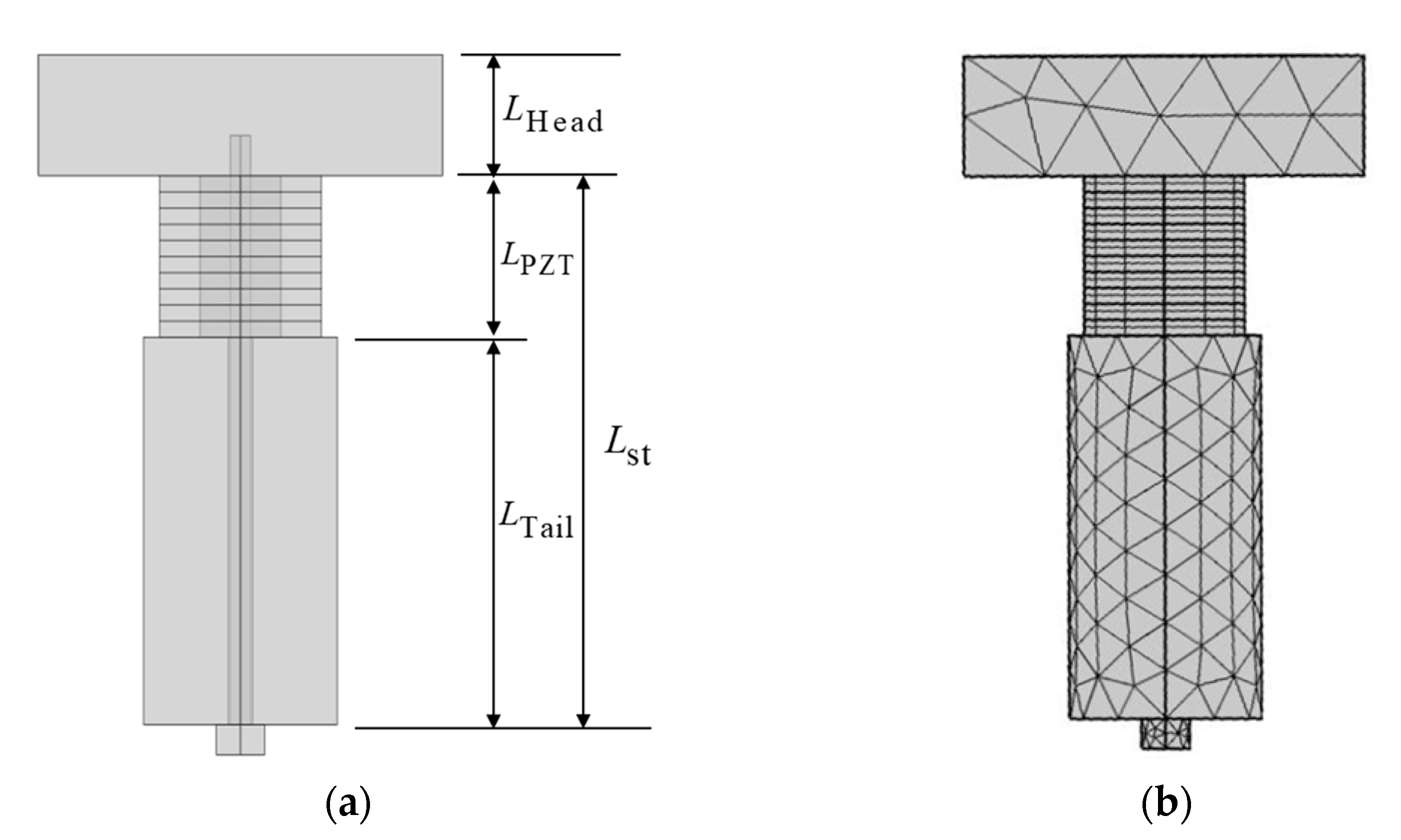





| Component | Property | Symbol | Value |
|---|---|---|---|
| Piston Head (Rigid) | Density | 2700 [kg/m3] | |
| PZT Ceramic (PZT-4) | Compliance coefficient | 1.55 × 10−11 [1/Pa] | |
| 1.23 × 10−11 [1/Pa] | |||
| −4.05 × 10−12 [1/Pa] | |||
| −5.31 × 10−12 [1/Pa] | |||
| 3.90 × 10−11 [1/Pa] | |||
| Piezoelectric coefficient | 2.89 × 10−10 [C/N] | ||
| −1.23 × 10−10 [C/N] | |||
| 4.96 × 10−10 [C/N] | |||
| Relative permittivity coefficient | 1300 | ||
| 1475 | |||
| Density | 7500 [kg/m3] | ||
| Tail Mass & Stress Rod (Steel AISI 4340) | Density | 7850 [kg/m3] | |
| Young’s Modulus | 205 × 109 [Pa] | ||
| Poisson’s Ratio | 0.28 | ||
| Acoustic Window | Density | 1500 [kg/m3] | |
| Longitudinal wave speed | 2400 [m/s] | ||
| Shear wave speed | 1230 [m/s] |
| Component | Dimensions | Symbol | Value |
|---|---|---|---|
| Piston Head | Cross-sectional area | 0.04 [m2] | |
| Longitudinal length | 0.06 [m] | ||
| PZT Ceramic | Cross-sectional area | 3.77 × 10−3 [m2] | |
| Longitudinal length | 0.08 [m] | ||
| Number of rings | 10 | ||
| Thickness of each ring | 8.00 × 10−3 [m] | ||
| Tail Mass | Cross-sectional area | 7.12 × 10−3 [m2] | |
| Longitudinal length | 0.192 [m] | ||
| Stress Rod | Cross-sectional area | 7.80 × 10−5 [m2] | |
| Longitudinal length | 0.272 [m] | ||
| Array | Height | 0.88 [m] | |
| Diameter | 1.68 [m] | ||
| Acoustic Window | Thickness | 0.025 [m] | |
| 1.25 [m] | |||
| half-length of the principal axes | 1.25 [m] | ||
| 0.75 [m] |
| ka = 2.0 | ka = 3.0 | ka = 4.0 | ka = 5.0 | |||||
|---|---|---|---|---|---|---|---|---|
| Array Size | ||||||||
| NC = 24, NR = 4 | 105 | 107 | 105 | 107 | 105 | 107 | 105 | 107 |
| NC = 36, NR = 6 | 105 | 107 | 105 | 107 | 105 | 107 | 105 | 107 |
| NC = 48, NR = 8 | 105 | 107 | 105 | 107 | 105 | 107 | 105 | 107 |
| NC = 60, NR = 10 | 105 | 107 | 105 | 107 | 105 | 107 | 105 | 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, M.-J.; Hong, C.; Jeong, W.-B. Hybrid Equivalent Circuit/Finite Element/Boundary Element Modeling for Effective Analysis of an Acoustic Transducer Array with Flexible Surrounding Structures. Appl. Sci. 2021, 11, 2702. https://doi.org/10.3390/app11062702
Sim M-J, Hong C, Jeong W-B. Hybrid Equivalent Circuit/Finite Element/Boundary Element Modeling for Effective Analysis of an Acoustic Transducer Array with Flexible Surrounding Structures. Applied Sciences. 2021; 11(6):2702. https://doi.org/10.3390/app11062702
Chicago/Turabian StyleSim, Min-Jung, Chinsuk Hong, and Weui-Bong Jeong. 2021. "Hybrid Equivalent Circuit/Finite Element/Boundary Element Modeling for Effective Analysis of an Acoustic Transducer Array with Flexible Surrounding Structures" Applied Sciences 11, no. 6: 2702. https://doi.org/10.3390/app11062702







