Consensus Cooperative Encirclement Interception Guidance Law for Multiple Vehicles against Maneuvering Target
Abstract
:1. Introduction
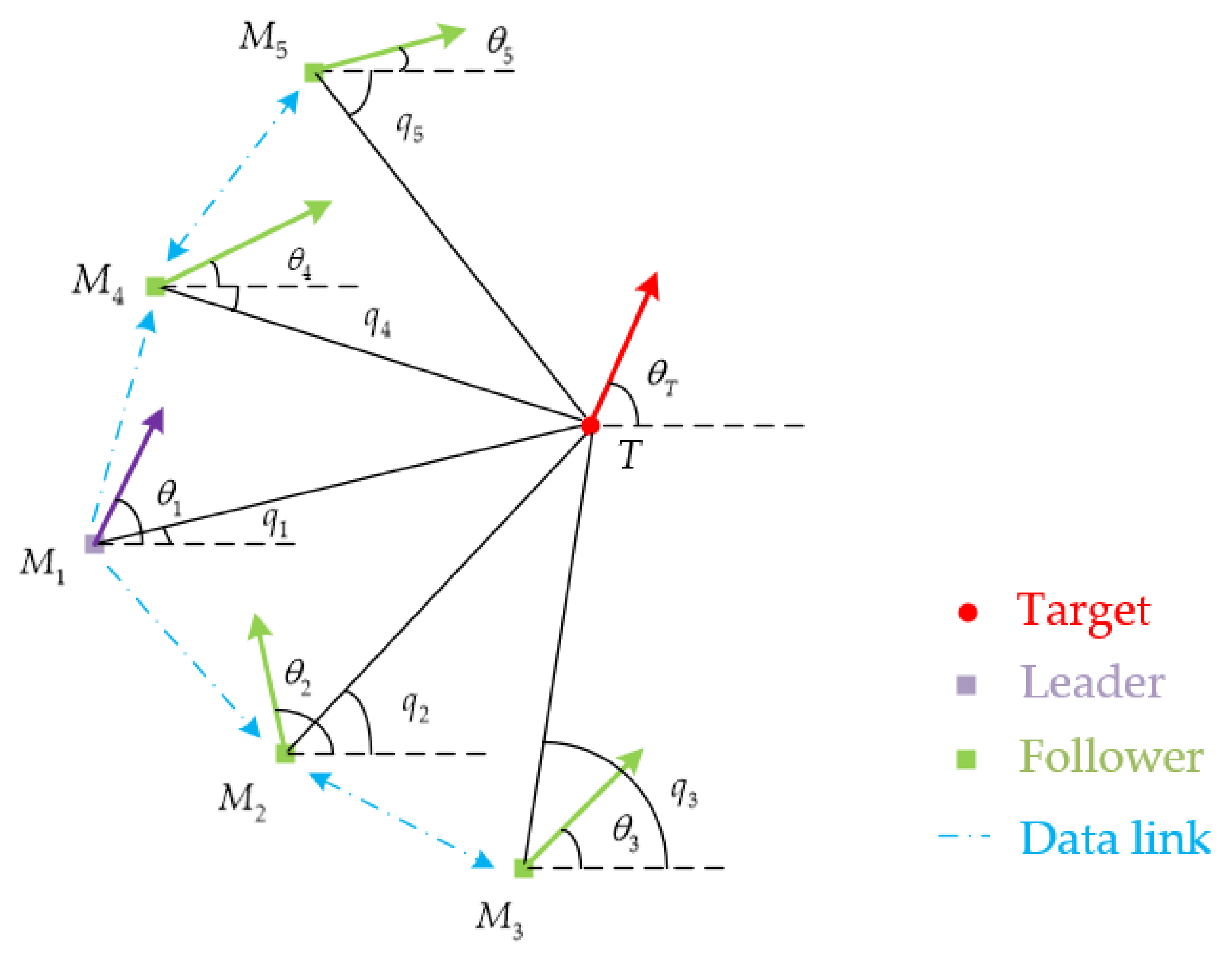
- Compared with other cooperative-guidance laws [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] and encirclement-interception methods [27] that are aimed at a stationary target, this paper presents a new way to realize encirclement interception against a maneuvering target by utilizing a leader–follower topology. During the interception, the followers are arranged around the leader. The vehicles are separated by fixed LOS angles. The guidance law for the leaders is designed to intercept the target at a certain impact angle. Meanwhile, the cooperative guidance law for the followers is designed with variable LOS-angle constraints;
- A fixed-time distributed disturbance observer (DDOB) was designed to compensate for the insufficient target-maneuver information involved in the guidance law. Compared with the traditional disturbance observer in [22], our distributed disturbance observer has a better performance in distributed cooperative interception;
- A predefined-time consensus guidance (PTCG) law was designed to control the impact angle of the vehicles. Compared with [22,23,24,25], the proposed PTCG introduces the communication-consistency control into the guidance law in the normal direction of the LOS, which improves the adaptive-control ability. Furthermore, the proposed PTCG can ensure that the LOS angles of the followers converge to the desired values in the prescribed time. The convergence time is set as the total flight time, which reduces the control input saturation.
2. Preliminaries
2.1. Some Key Definitions
2.2. Graph Theory
2.3. ESO Theory
2.4. Finite-Time Convergence Theory
2.5. Fixed-Time Convergence Theory
3. Problem Formulation
4. Main Results
4.1. Flight-Time Control Part
4.2. Impact-Angle Control Part
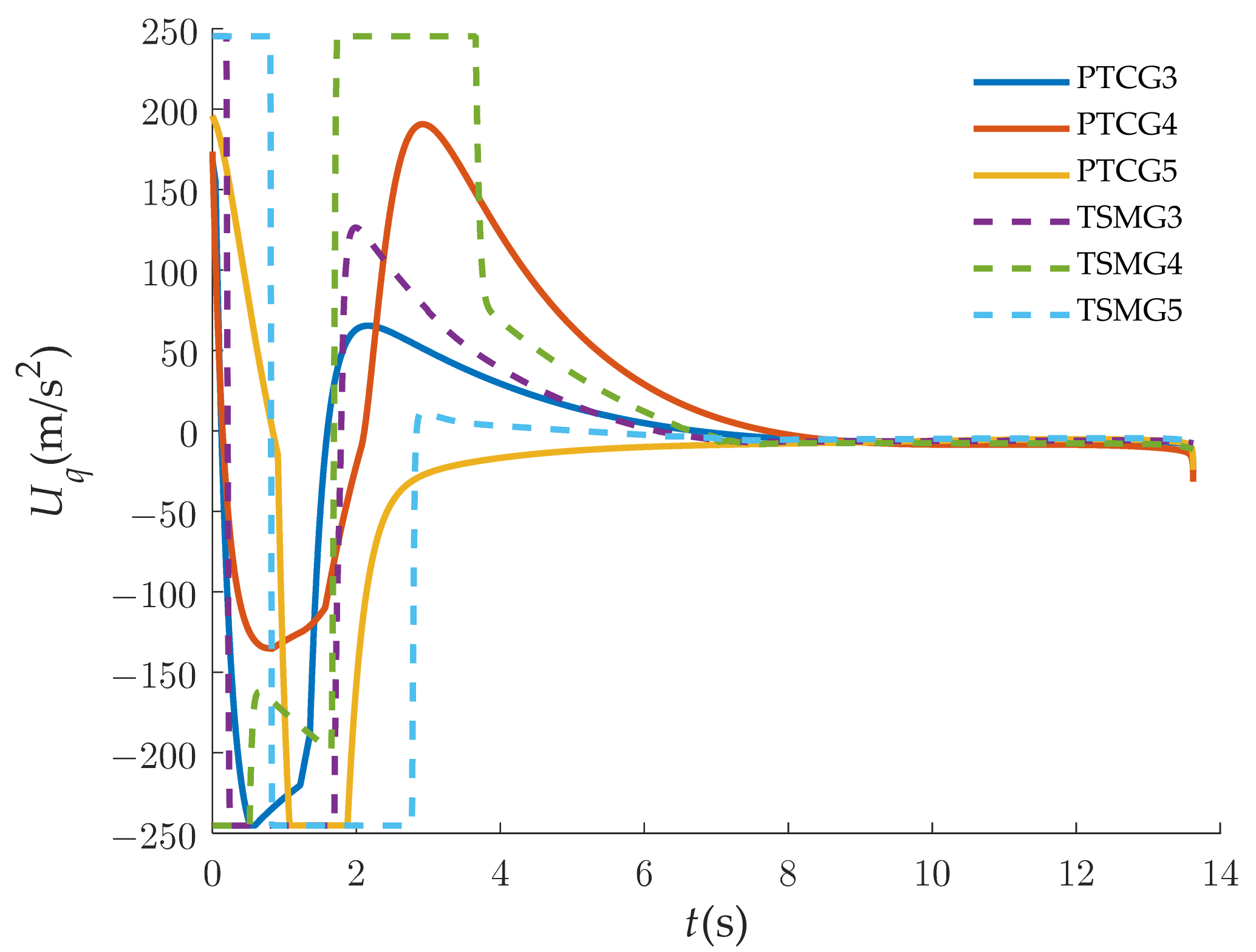
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Zhu, C.H.; Xu, G.D.; Wei, C.Z.; Cai, D.Y.; Yu, Y. Impact-Time-Control Guidance Law for Hypersonic Missiles in Terminal Phase. IEEE Access 2020, 8, 44611–44621. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, X.P.; Zhou, Z.; Yan, F. Two-phase guidance law for impact time control under physical constraints. Chin. J. Aeronaut. 2020, 33, 2946–2958. [Google Scholar] [CrossRef]
- Cho, N.; Kim, Y. Modified Pure Proportional Navigation Guidance Law for Impact Time Control. J. Guid. Control Dyn. 2016, 39, 852–872. [Google Scholar] [CrossRef]
- Song, J.; Song, S.; Xu, S. Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence. Aerosp. Sci. Technol. 2017, 67, 193–205. [Google Scholar] [CrossRef]
- An, K.; Guo, Z.-Y.; Huang, W.; Xu, X.-P. A Cooperative Guidance Approach Based on the Finite-Time Control Theory for Hypersonic Vehicles. Int. J. Aeronaut. Space Sci. 2022, 23, 169–179. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Homing Guidance Law for Cooperative Attack of Multiple Missiles. J. Guid. Control Dyn. 2010, 33, 275–280. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation. J. Guid. Control Dyn. 2016, 39, 1885–1890. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R. Terminal Guidance for a Hypersonic Vehicle with Impact Time Control. J. Guid. Control Dyn. 2018, 41, 1790–1798. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, S.; Guo, J. Two-stage cooperative guidance strategy using a prescribed-time optimal consensus method. Aerosp. Sci. Technol. 2020, 100, 105641. [Google Scholar] [CrossRef]
- He, S.; Wang, W.; Lin, D.; Lei, H. Consensus-Based Two-Stage Salvo Attack Guidance. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1555–1566. [Google Scholar] [CrossRef]
- Zhao, Q.; Dong, X.; Liang, Z.; Bai, C.; Chen, J.; Ren, Z. Distributed cooperative guidance for multiple missiles with fixed and switching communication topologies. Chin. J. Aeronaut. 2017, 30, 1570–1581. [Google Scholar] [CrossRef]
- Zeng, J.; Dou, L.; Xin, B. A joint mid-course and terminal course cooperative guidance law for multi-missile salvo attack. Chin. J. Aeronaut. 2018, 31, 1311–1326. [Google Scholar] [CrossRef]
- Hu, Q.L.; Han, T.; Xin, M. New Impact Time and Angle Guidance Strategy via Virtual Target Approach. J. Guid. Control Dyn. 2018, 41, 1755–1765. [Google Scholar] [CrossRef]
- Ai, X.; Wang, L.; Yu, J.; Shen, Y. Field-of-view constrained two-stage guidance law design for three-dimensional salvo attack of multiple missiles via an optimal control approach. Aerosp. Sci. Technol. 2019, 85, 334–346. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, S. Integrated cooperative guidance framework and cooperative guidance law for multi-missile. Chin. J. Aeronaut. 2018, 31, 546–555. [Google Scholar] [CrossRef]
- Dhananjay, N.; Ghose, D. Accurate Time-to-Go Estimation for Proportional Navigation Guidance. J. Guid. Control Dyn. 2014, 37, 1378–1383. [Google Scholar] [CrossRef]
- Jia, S.; Wang, X.; Li, F.; Wang, Y. Distributed Analytical Formation Control and Cooperative Guidance for Gliding Vehicles. Int. J. Aerosp. Eng. 2020, 2020, 8826968. [Google Scholar] [CrossRef]
- Sun, G.; Wen, Q.; Xu, Z.; Xia, Q. Impact time control using biased proportional navigation for missiles with varying velocity. Chin. J. Aeronaut. 2020, 33, 956–964. [Google Scholar] [CrossRef]
- Lin, M.; Ding, X.; Wang, C.; Liang, L.; Wang, J. Three-Dimensional Fixed-Time Cooperative Guidance Law With Impact Angle Constraint and Prespecified Impact Time. IEEE Access 2021, 9, 29755–29763. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, X.; Lv, Y.; Wen, G. Terminal-time synchronization of multiple vehicles under discrete-time communication networks with directed switching topologies. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2532–2536. [Google Scholar] [CrossRef]
- Dong, X.; Ren, Z. Impact angle constrained distributed cooperative guidance against maneuvering targets with undirected communication topologies. IEEE Access 2020, 8, 117867–117876. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Liu, Z.; Wang, S.; Hu, X. Finite-Time Cooperative Guidance Strategy for Impact Angle and Time Control IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 806–819. [Google Scholar] [CrossRef]
- Jing, L.; Wei, C.; Zhang, L.; Cui, N. Cooperative Guidance Law with Predefined-Time Convergence for Multimissile Systems. Math. Probl. Eng. 2021, 2021, 9940240. [Google Scholar] [CrossRef]
- Cong, M.; Cheng, X.; Zhao, Z.; Li, Z. Studies on Multi-Constraints Cooperative Guidance Method Based on Distributed MPC for Multi-Missiles. Appl. Sci. 2021, 11, 10857. [Google Scholar] [CrossRef]
- Yu, J.; Dong, X.; Li, Q.; Ren, Z. Distributed cooperative encirclement hunting guidance for multiple flight vehicles system. Aerosp. Sci. Technol. 2019, 95, 105475. [Google Scholar] [CrossRef]
- Yan, P.P.; Fan, Y.H.; Liu, R.F.; Wang, M.G. Distributed target-encirclement guidance law for cooperative attack of multiple missiles. Int. J. Adv. Robot. Syst. 2020, 17, 1–15. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Kumar, S.R.; Mukherjee, D. Deviated pursuit-based nonlinear cooperative salvo guidance using finite-time consensus. Nonlinear Dyn. 2021, 106, 605–630. [Google Scholar] [CrossRef]
- Yang, F.; Wei, C.-Z.; Wu, R.; Cui, N.-G. Non-recursive fixed-time convergence observer and extended state observer. IEEE Access 2018, 6, 62339–62351. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Zhang, X. Multiple missiles fixed-time cooperative guidance without measuring radial velocity for maneuvering targets interception. ISA Trans. 2022, 126, 388–397. [Google Scholar] [CrossRef]
- Yang, F.; Xia, G. A finite-time 3D guidance law based on fixed-time convergence disturbance observer. Chin. J. Aeronaut. 2020, 33, 1299–1310. [Google Scholar] [CrossRef]
- Pal, A.K.; Kamal, S.; Yu, X.; Nagar, S.K.; Xiong, X. Free-Will Arbitrary Time Consensus for Multiagent Systems. IEEE Trans. Cybern. 2020, 52, 4636–4646. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, W.; Fang, Y.; Zhu, S.; Wu, Z.; Wang, M. Prescribed-time cooperative guidance law against maneuvering target based on leader-following strategy. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Polyakov, A.; Fridman, L. Stability notions and Lyapunov functions for sliding mode control systems. J. Frankl. Inst. 2014, 351, 1831–1865. [Google Scholar] [CrossRef] [Green Version]
- Wu, R.; Wei, C.; Yang, F.; Cui, N.; Zhang, L. FxTDO-based non-singular terminal sliding mode control for second-order uncertain systems. IET Control Theory Appl. 2018, 12, 2459–2467. [Google Scholar] [CrossRef]
- Basin, M.; Yu, P.; Shtessel, Y. Finite-and fixed-time differentiators utilising HOSM techniques. IET Control Theory Appl. 2017, 11, 1144–1152. [Google Scholar] [CrossRef]


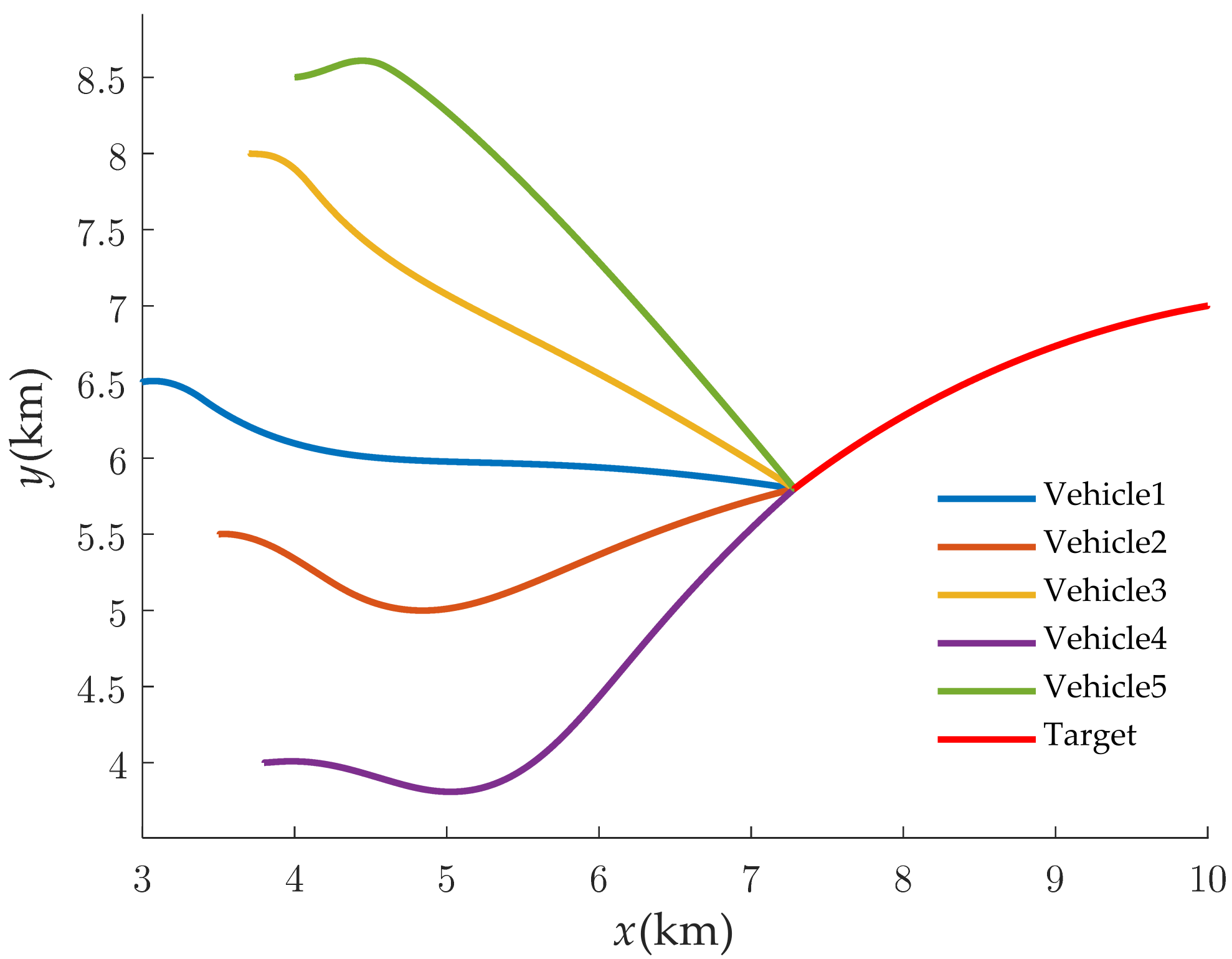


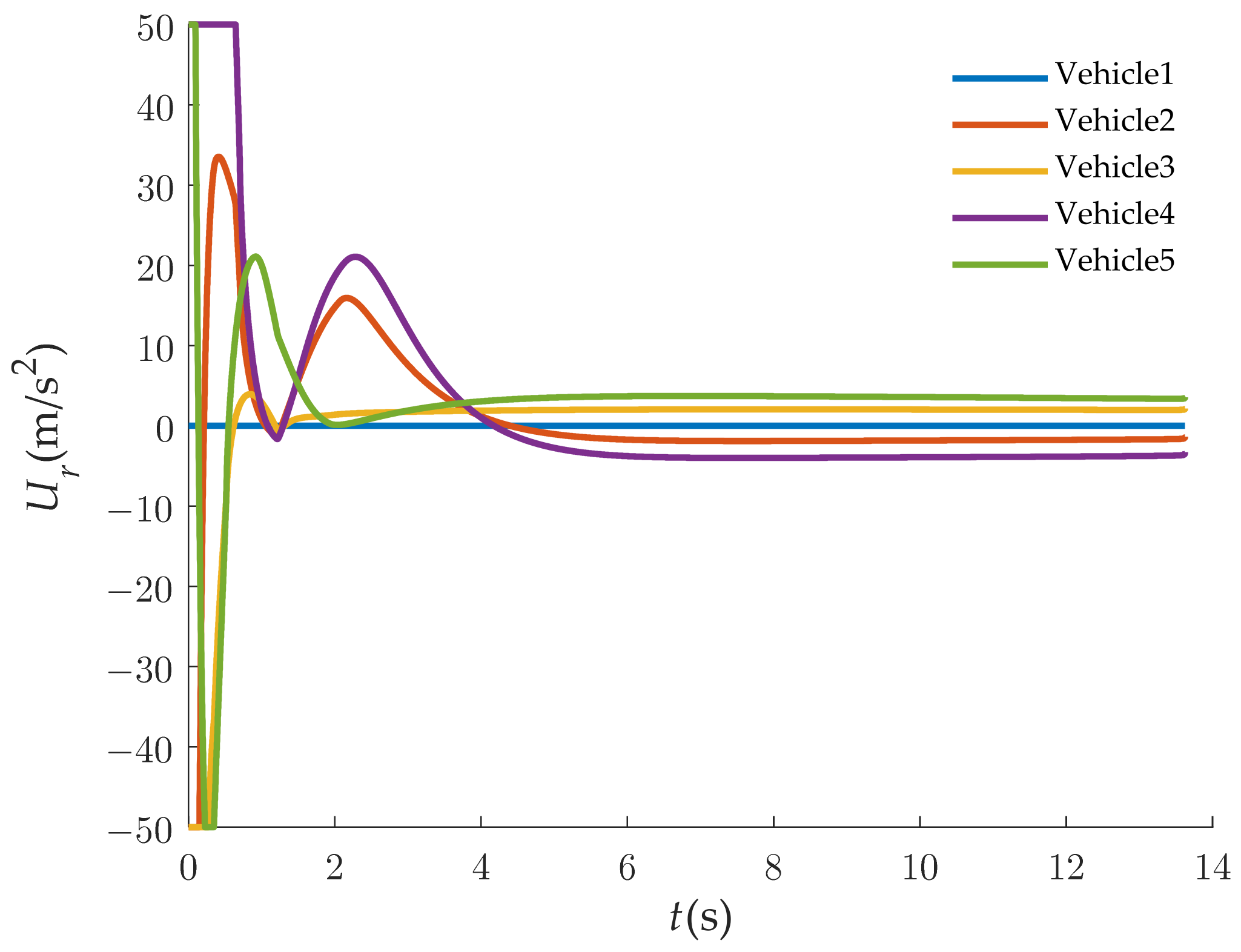

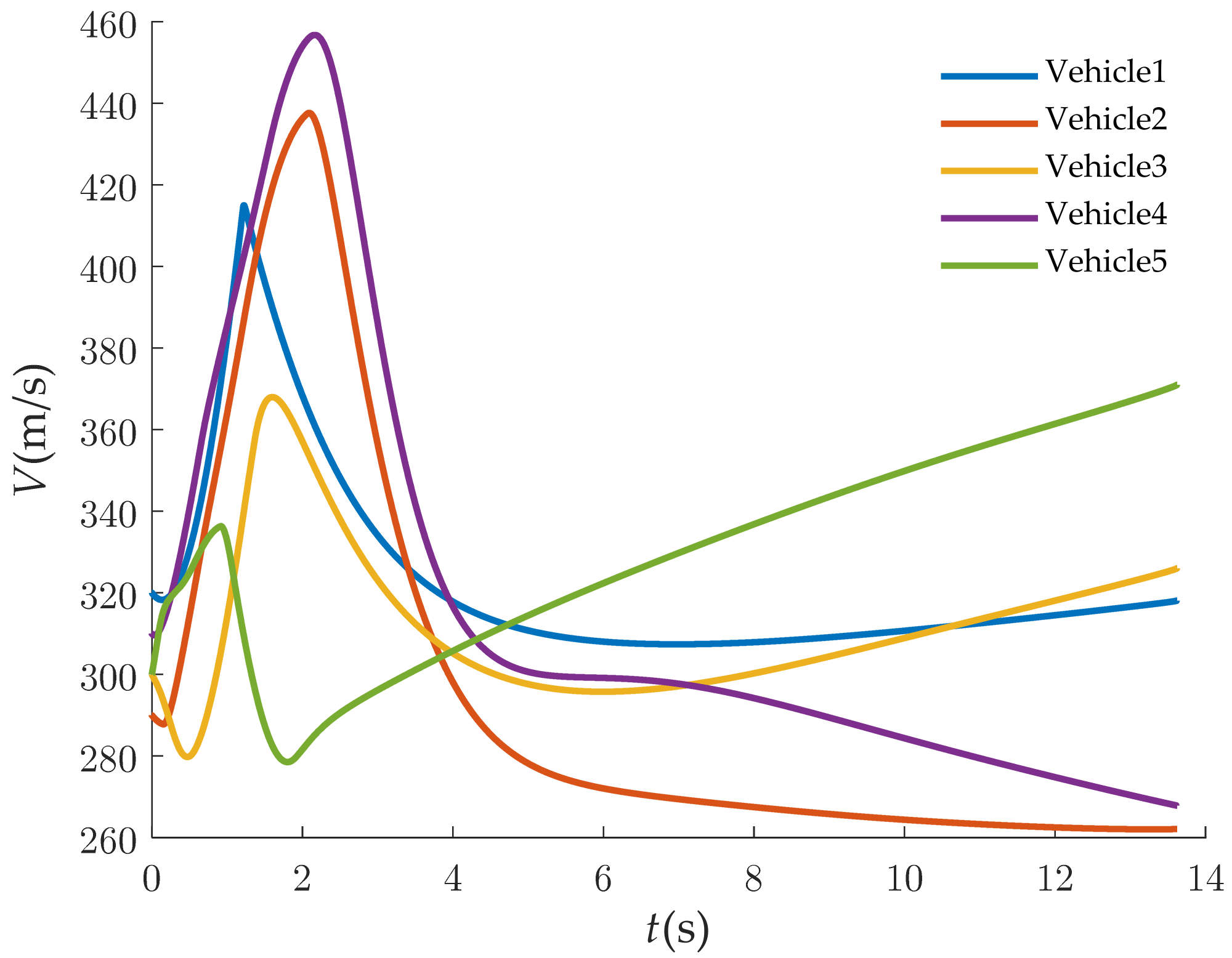
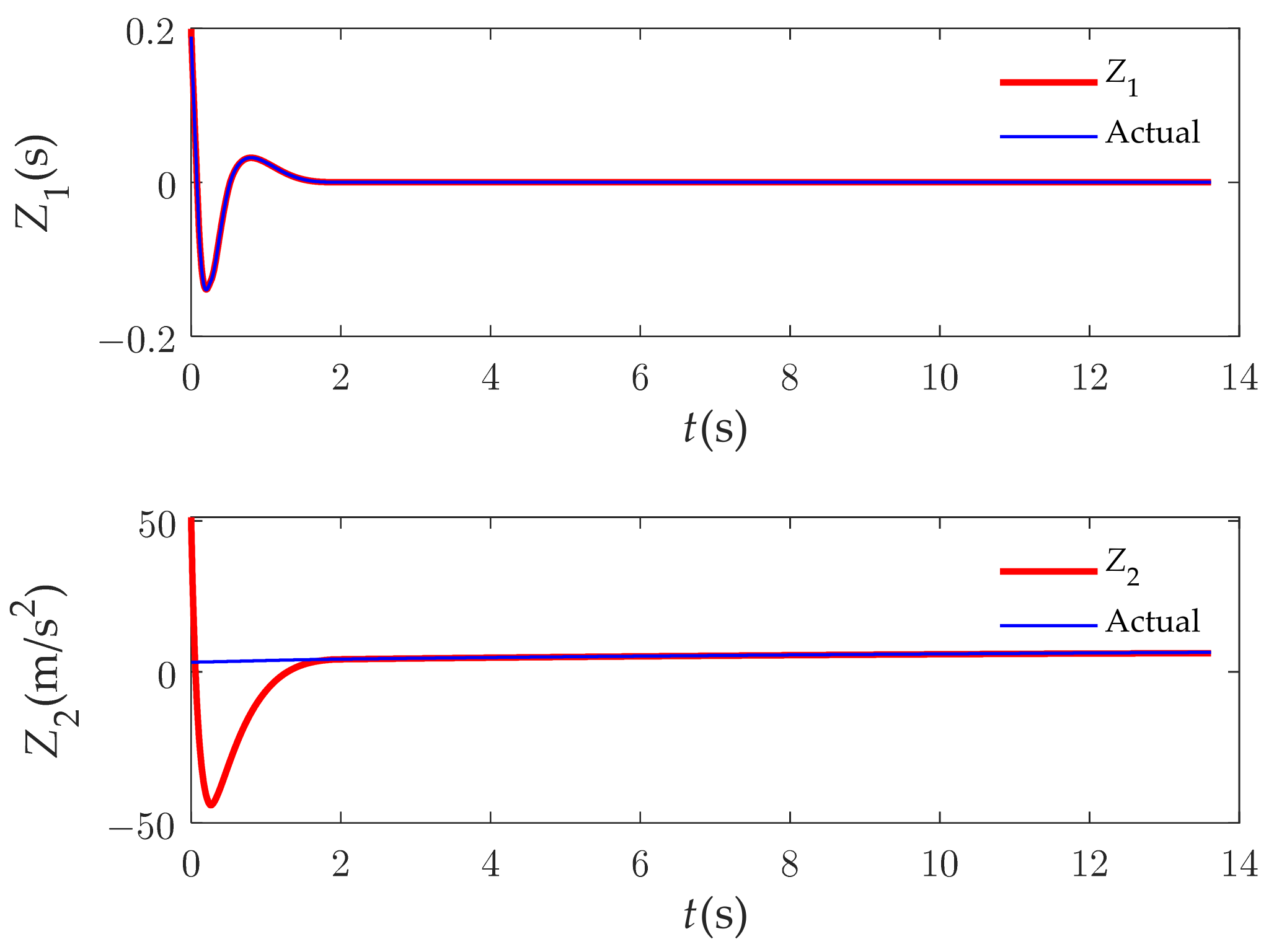
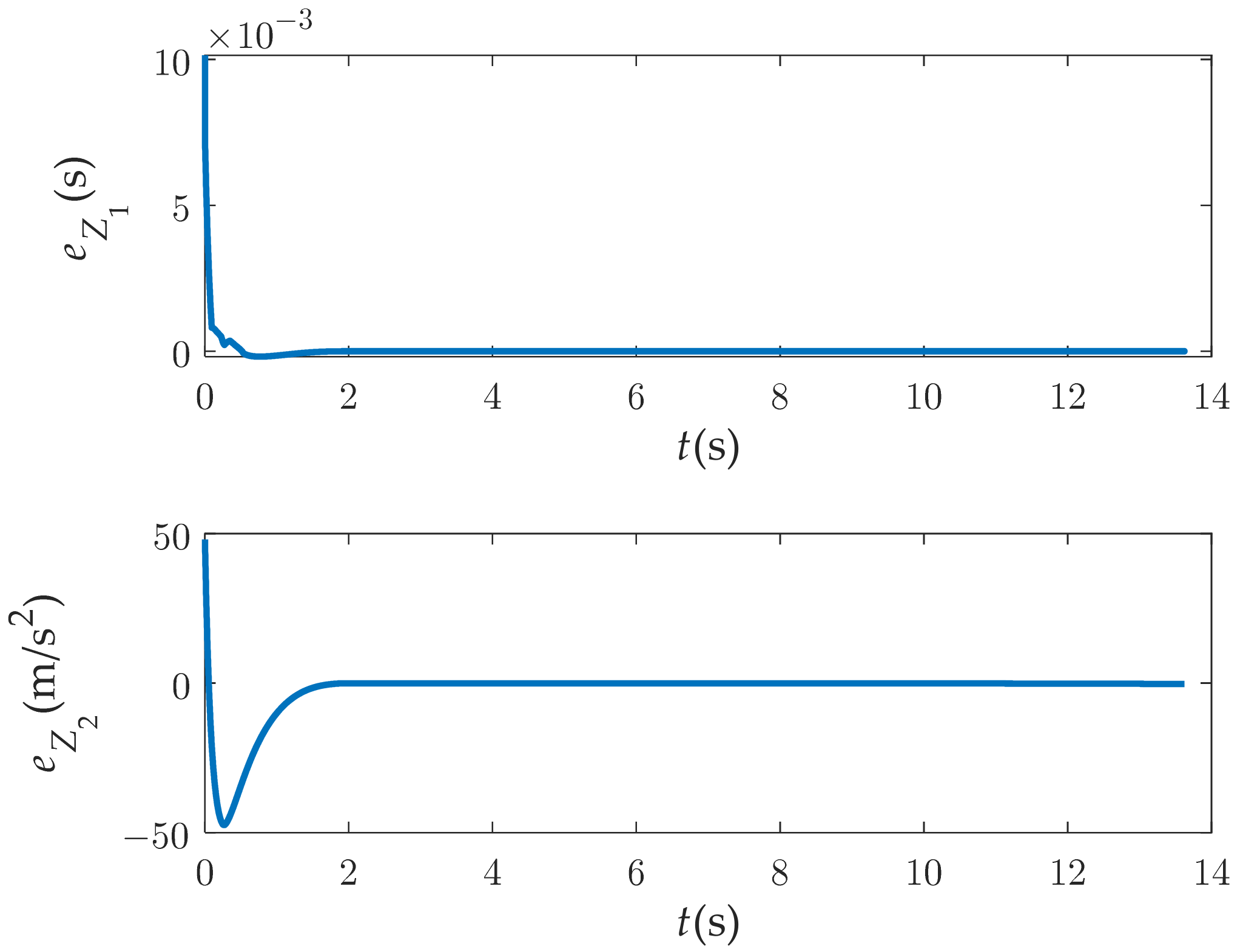
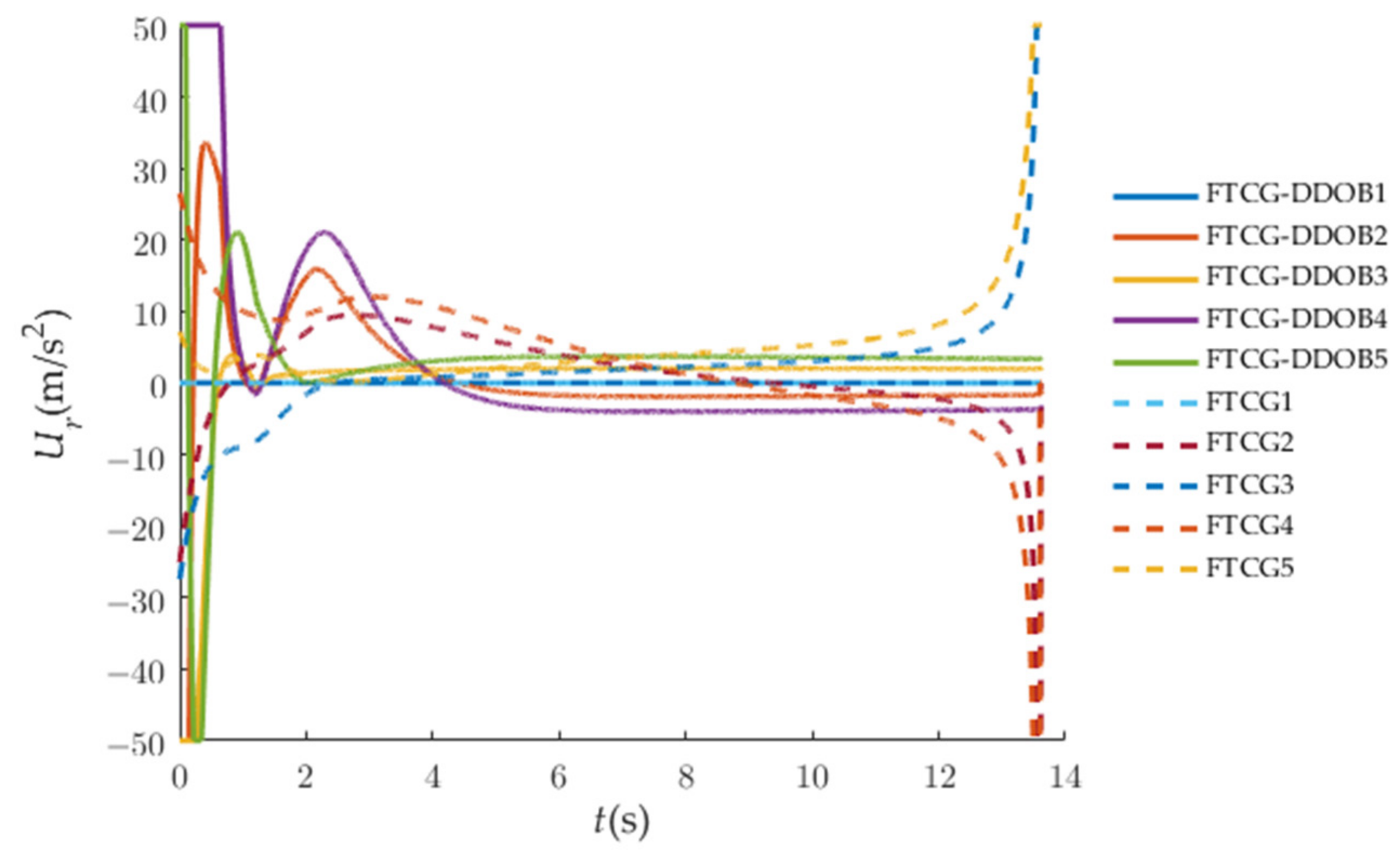

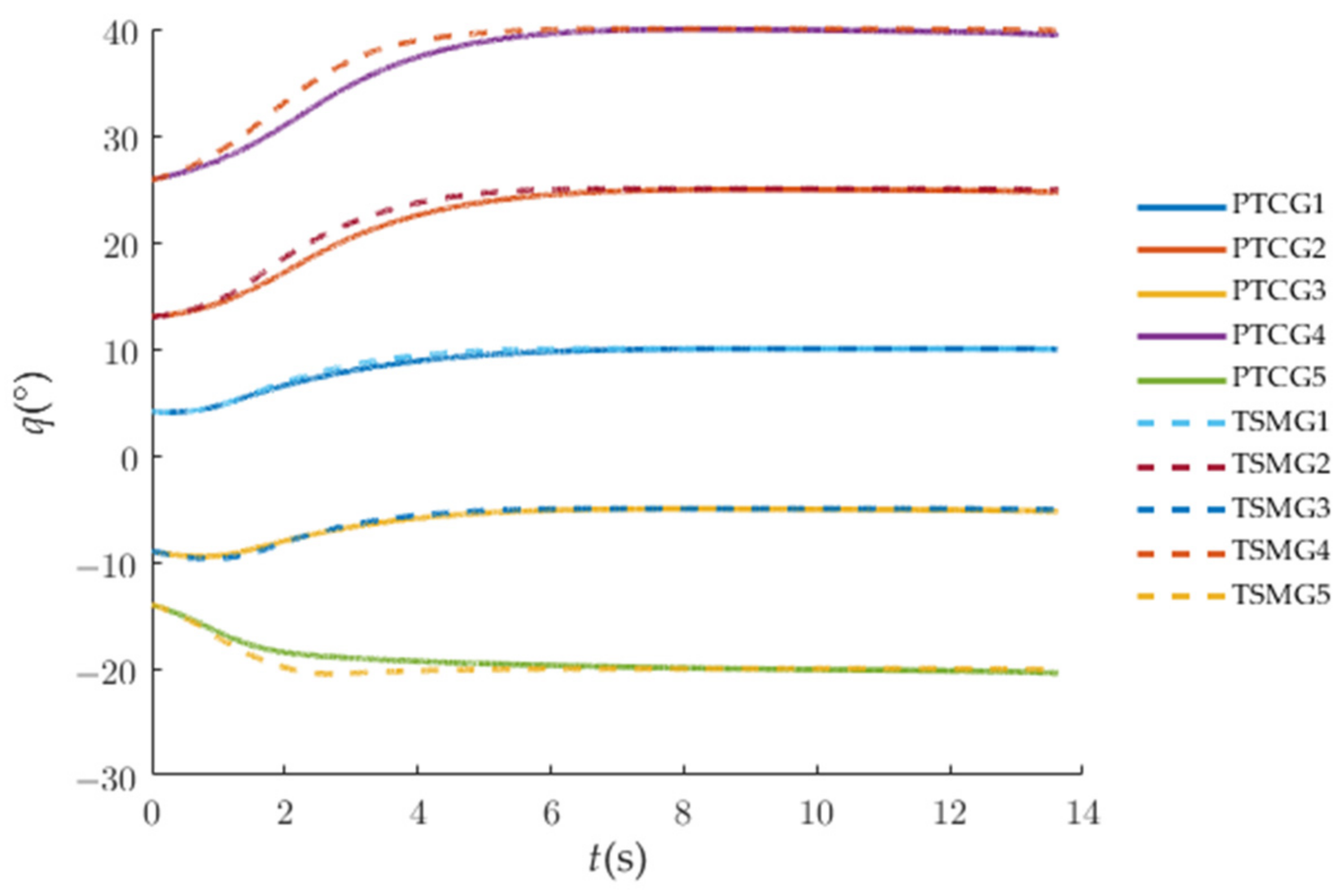
| Vehicle | Initial Position (m, m) | Initial Heading Angle (°) | Initial Velocity (m/s) |
|---|---|---|---|
| M1 (leader) | (3000, 6500) | 10 | 320 |
| M2 | (3500, 5500) | 6 | 290 |
| M3 | (3700, 8000) | −5 | 300 |
| M4 | (3800, 4000) | 2 | 310 |
| M5 | (4000, 8500) | 5 | 300 |
| Initial Position | Initial Heading Angle (°) | Initial Velocity (m/s) | Accelerated Velocity (m/s2) |
|---|---|---|---|
| (10,000, 7000) | −170 | 220 | 0.8 g cos(t) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Xia, G.; Yang, F.; Liu, C.; Liu, K.; Yang, J. Consensus Cooperative Encirclement Interception Guidance Law for Multiple Vehicles against Maneuvering Target. Appl. Sci. 2022, 12, 7307. https://doi.org/10.3390/app12147307
Guo M, Xia G, Yang F, Liu C, Liu K, Yang J. Consensus Cooperative Encirclement Interception Guidance Law for Multiple Vehicles against Maneuvering Target. Applied Sciences. 2022; 12(14):7307. https://doi.org/10.3390/app12147307
Chicago/Turabian StyleGuo, Mingkun, Guangqing Xia, Feng Yang, Cong Liu, Kai Liu, and Jingnan Yang. 2022. "Consensus Cooperative Encirclement Interception Guidance Law for Multiple Vehicles against Maneuvering Target" Applied Sciences 12, no. 14: 7307. https://doi.org/10.3390/app12147307






