Parametric Analysis of Cylinder Drying Process in Association with Various Materials
Abstract
:1. Introduction
2. Methodology
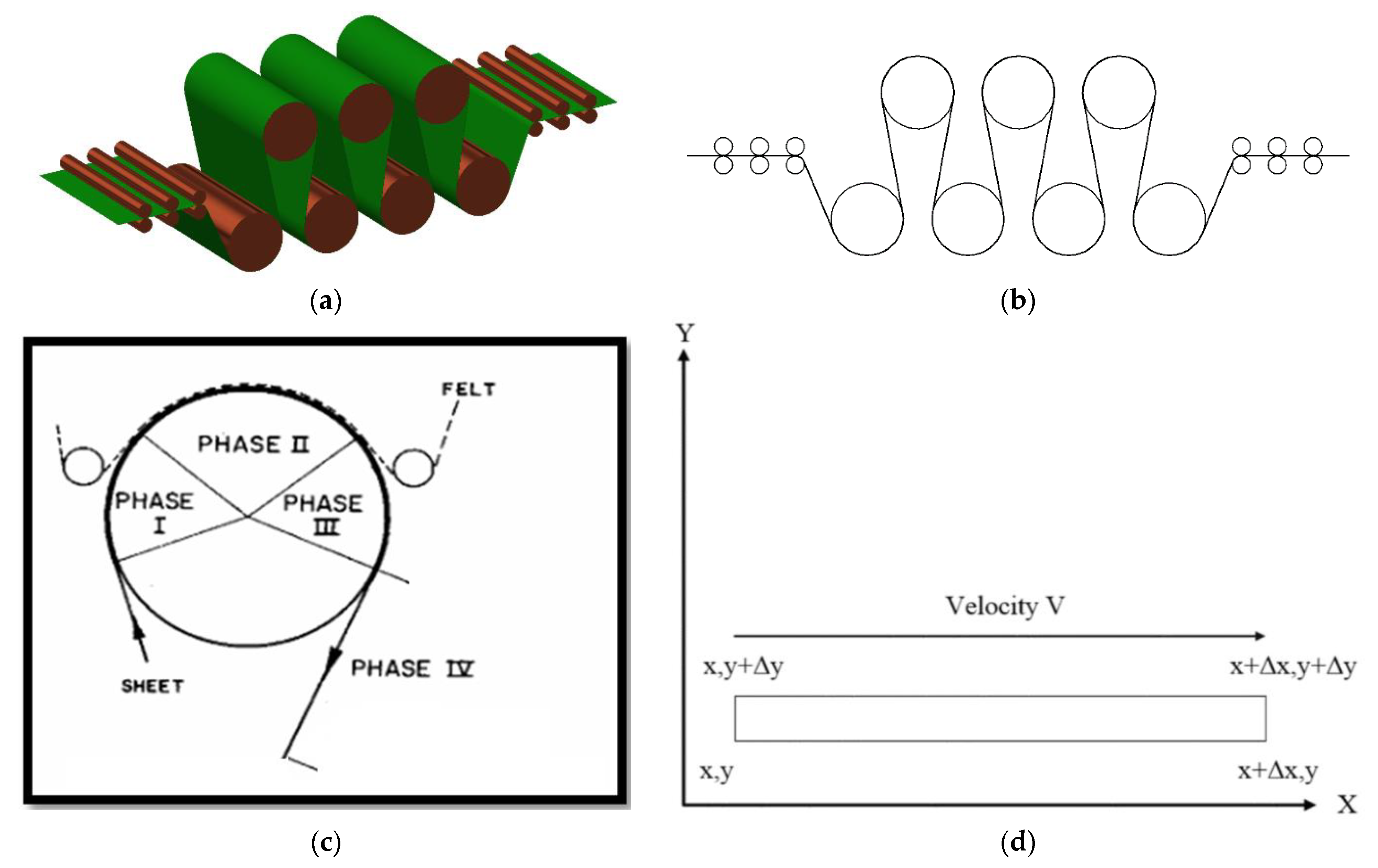
2.1. Work Description
2.2. Computational Model
2.3. Mathematical Model
- There is no heat loss between the cylinder and the ambient environment;
- The temperature of the heated moisture is equal to that of the drying material at the local points;
- The vapor, which is evaporated from the drying material in the drying process, is removed by the cold air of the ambient environment;
- The relative humidity of the ambient environment is constant;
- The temperature of the ambient environment is constant;
- The convection heat transfers between the drying material and the ambient environment in phases I, III, and IV are constant.
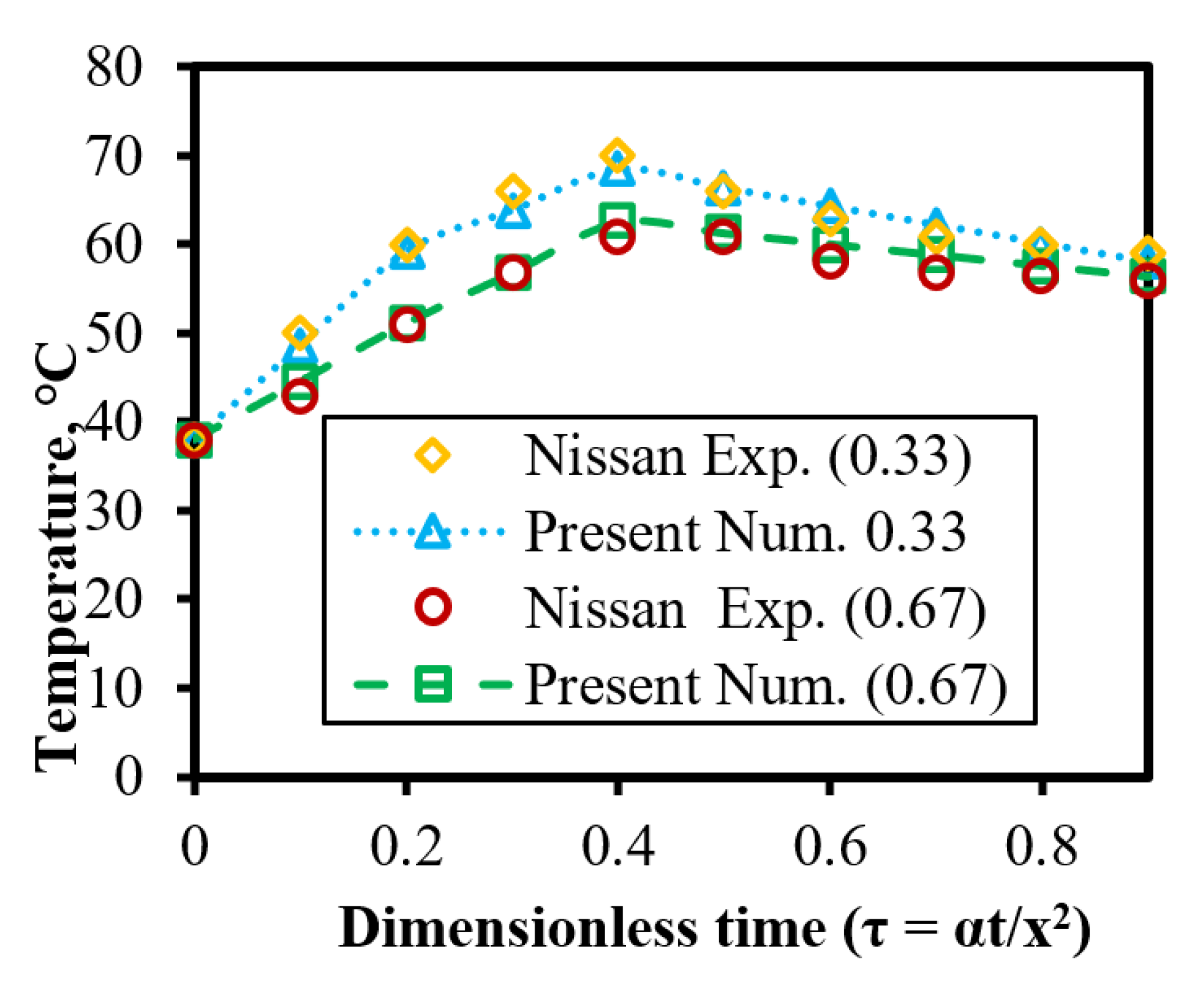
2.4. Computational Model Validation
3. Results and Discussion
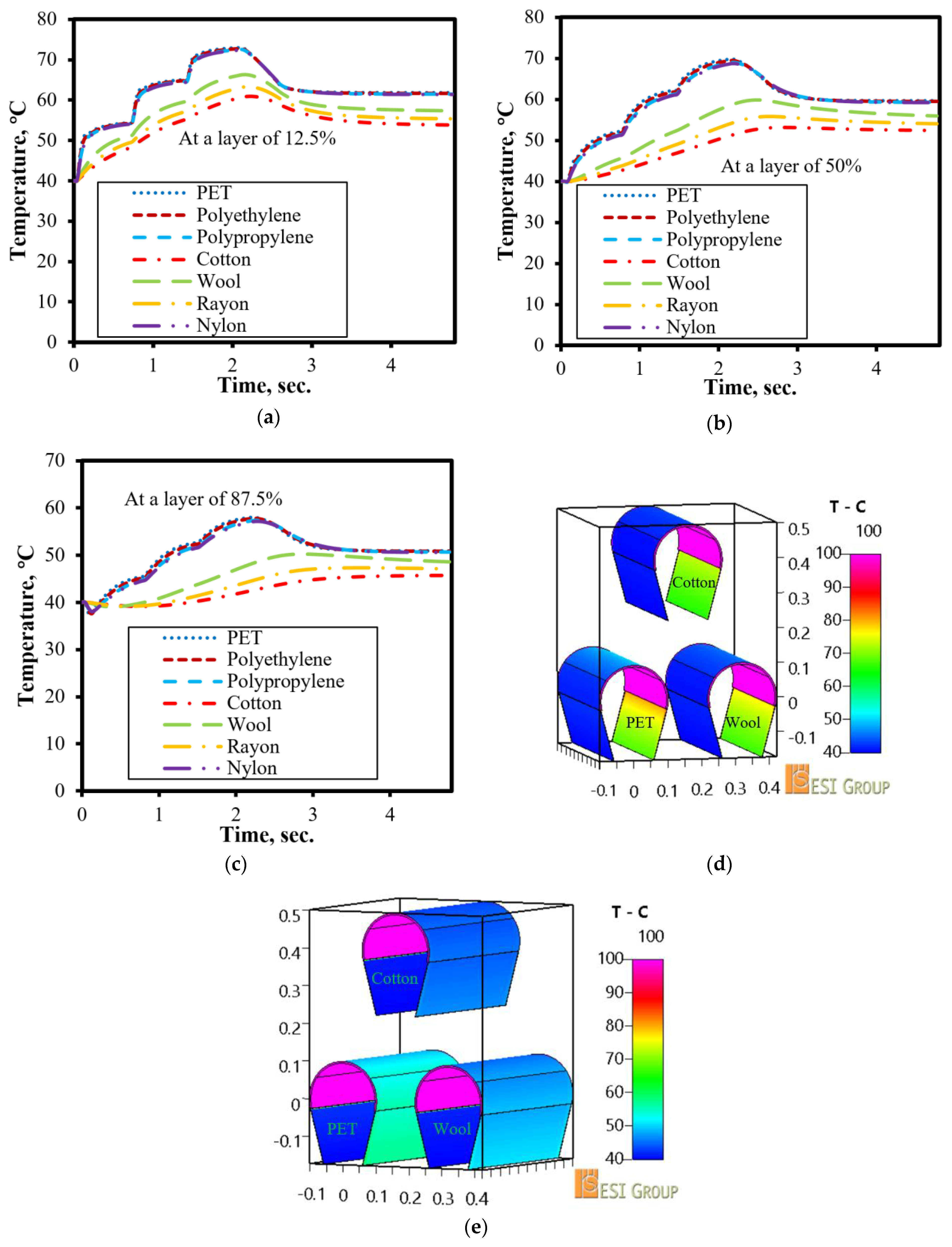
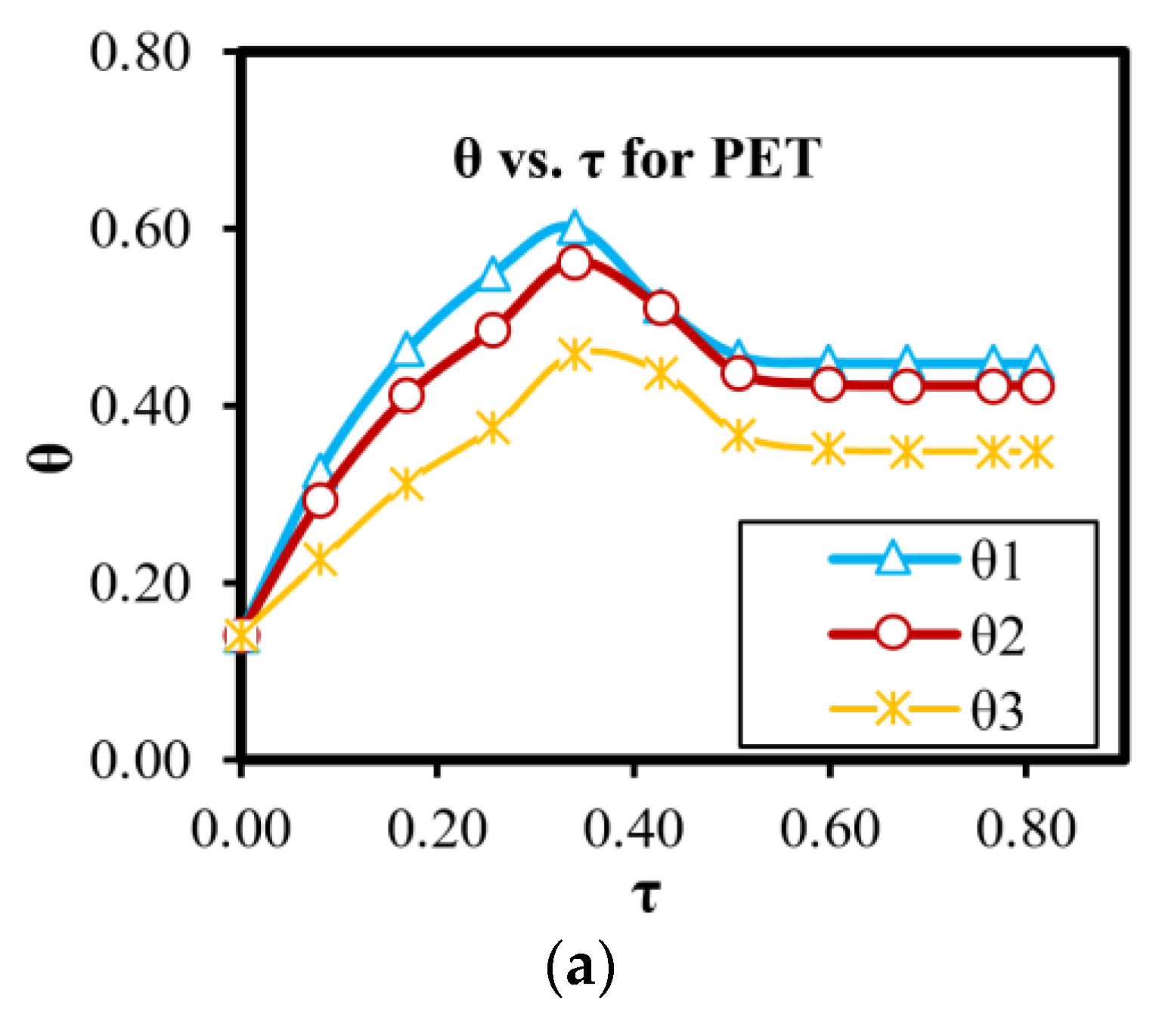
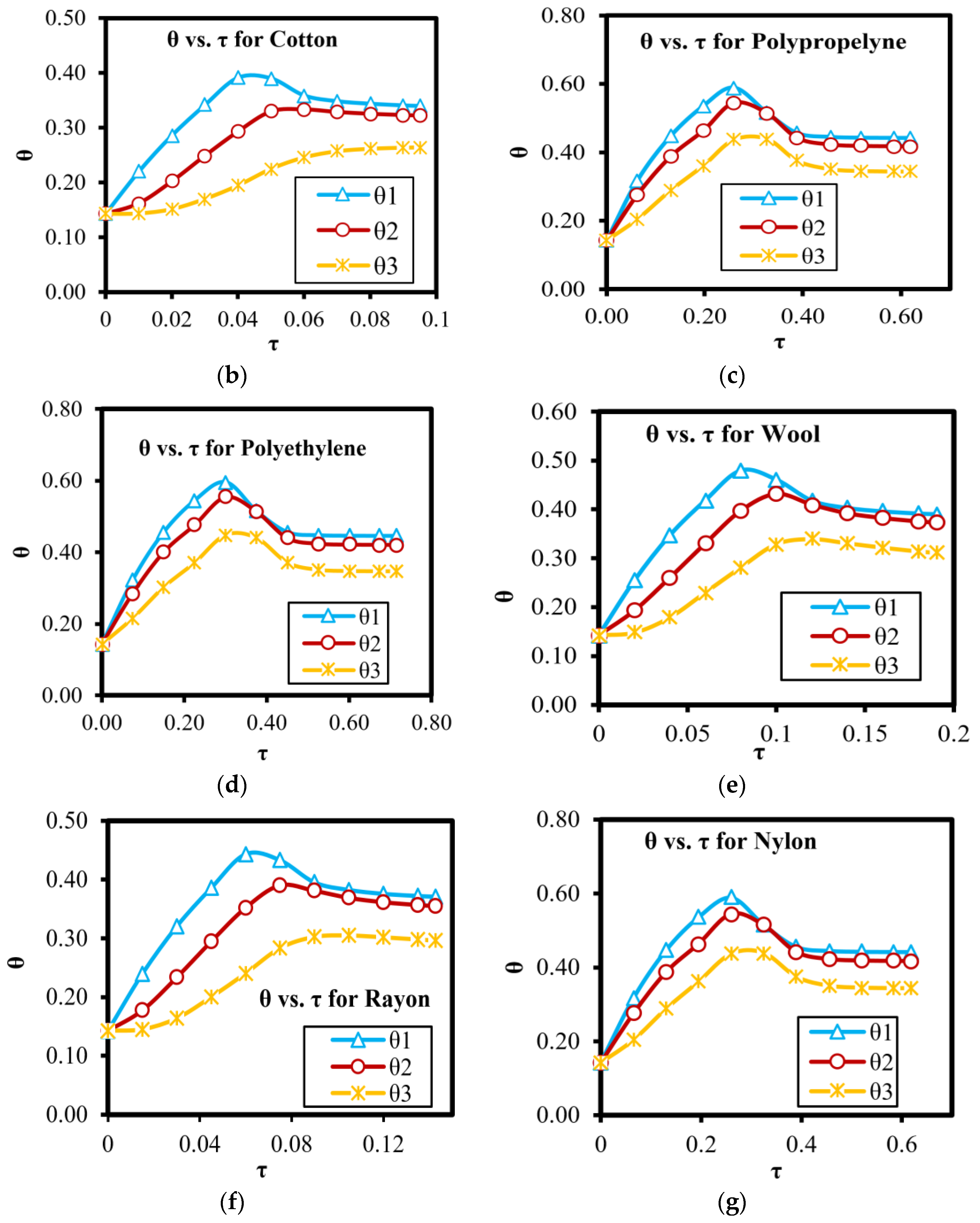
3.1. Effects of Transport Materials
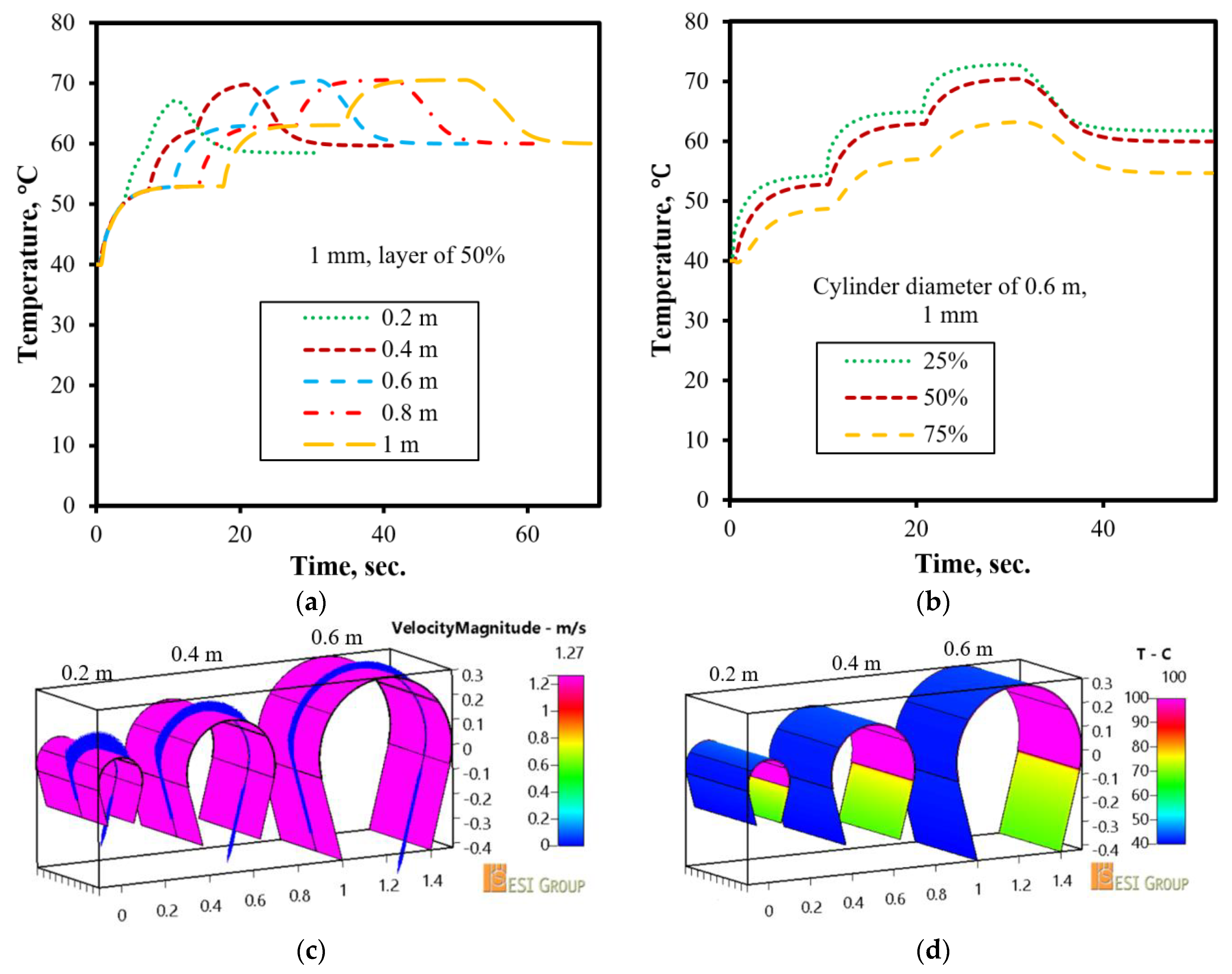
3.2. Effects of the Contacting Percentage
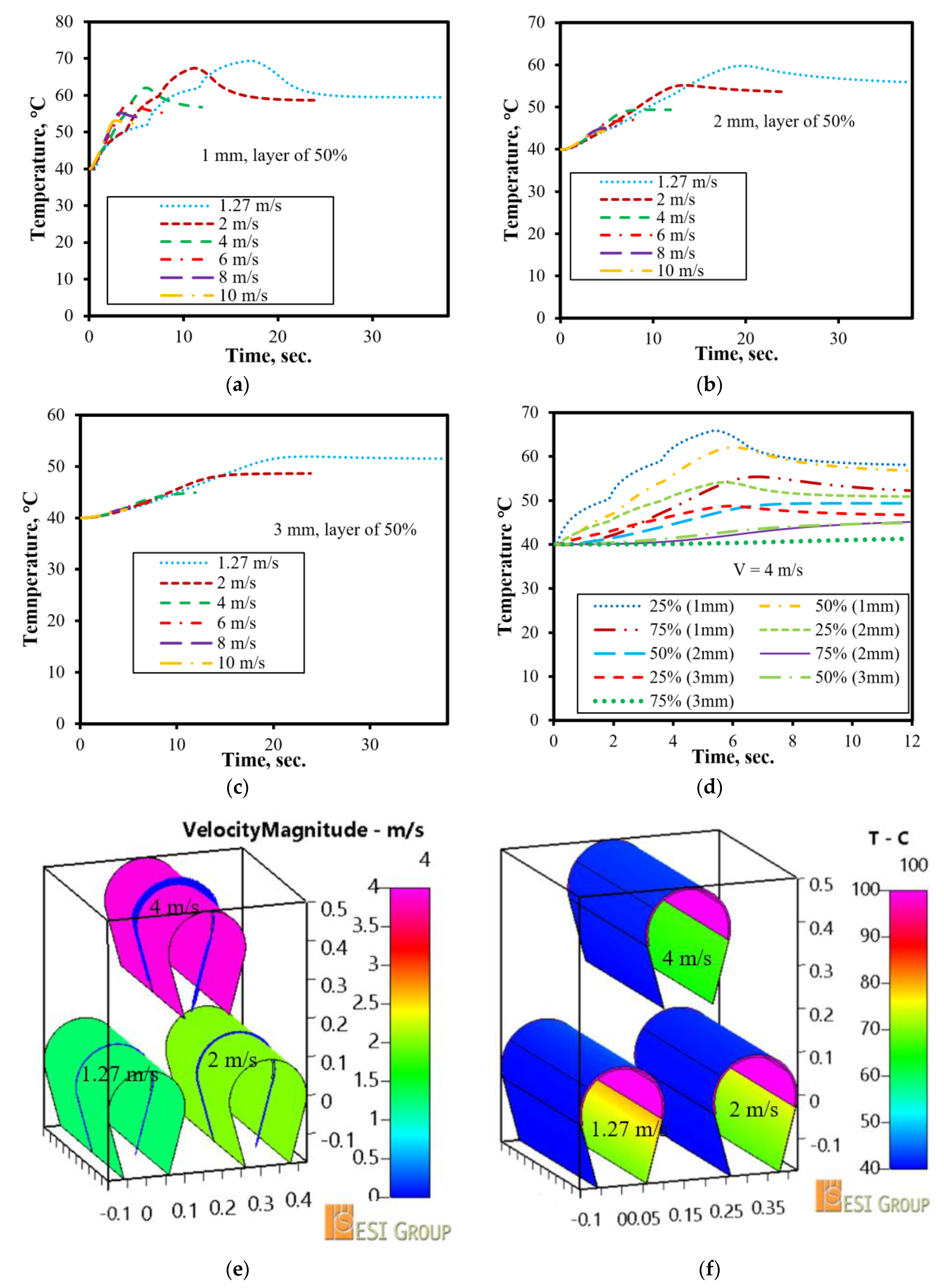
3.3. Effects of the Feeding Velocity
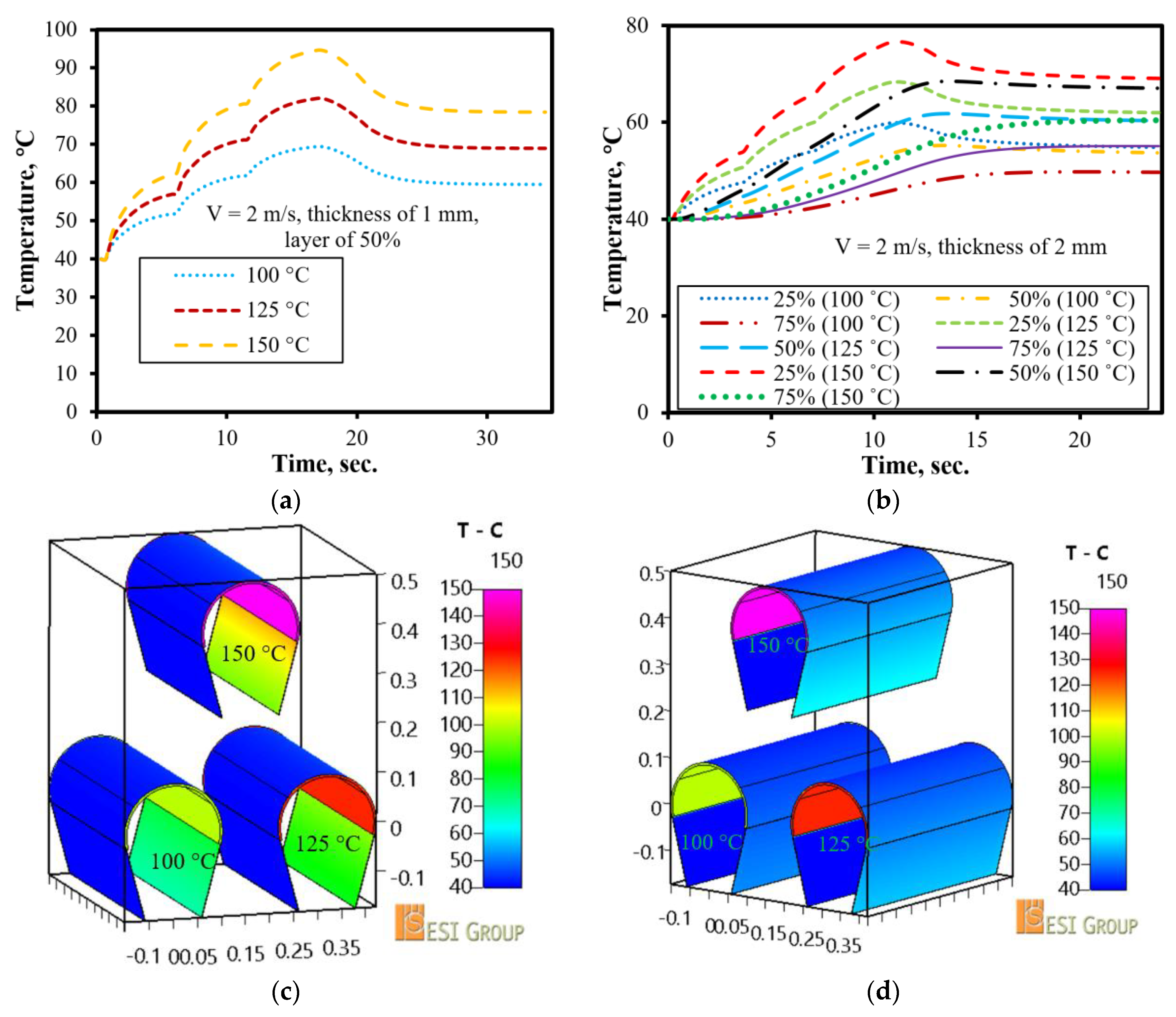
3.4. Effects of the Cylinder Temperature
3.5. Effects of the Cylinder Diameter
3.6. θ versus τ for Different Drying Materials
4. Conclusions
- The drying process of a drying material with higher thermal diffusivity is faster than that with lower thermal diffusivity.
- The peak temperature of the drying material in a cylinder dryer with a larger contact percentage is higher than that of a smaller one. At the same contacting percentage, the peak temperature of the drying material decreases with the rise in drying material thickness.
- At the same examining layer and the same drying material thickness, the temperature of the examining layer with higher feeding velocity is increased faster than those of the lower feeding velocities; however, the peak temperature of a transport material with lower velocity is higher than those of the higher velocities.
- The decrease in temperature of the drying material at the examining layer of 50% of phase IV seems to be independent of the cylinder temperature, and the heat transfer between the central layer of the drying material to the ambient environment is limited by the thermal diffusivity of the drying material.
- The peak temperature of the drying material increases with the increase in cylinder diameter; however, when the cylinder diameter reaches a certain value, the peak temperature of the drying material is constant. Specifically, the maximum temperature is almost unchanged with the increase in the diameter from 0.4 m to 1 m.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dinçer, I.; Zamfirescu, C. Drying Phenomena: Theory and Applications; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Haghi, A.K. Transport phenomena in porous media: A review. Theor. Found. Chem. Eng. 2006, 40, 14–26. [Google Scholar] [CrossRef]
- Fourt, L.; Sookne, A.M.; Frishman, D.; Harris, M. The Rate of Drying of Fabrics. Text. Res. J. 1951, 21, 26–33. [Google Scholar] [CrossRef]
- Majumder, A.S. (Ed.) Handbook of Industrial Drying, 4th ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Bejan, A.; Dincer, I.; Lorente, S.; Miguel, A.F.; Reis, A.H. Porous and Complex Flow Structures in Modern Technologies; Springer: New York, NY, USA, 2004. [Google Scholar]
- Chen, B.X.; Man, Y.; Zheng, Q.F.; Hu, Y.S.; Li, J.G.; Hong, M.N. Industrial verification of energy saving for the single-tier cylinder based paper drying process. Energy 2019, 170, 261–272. [Google Scholar] [CrossRef]
- Roonprasang, K. Thermal Analysis of Multi-Cylinder Drying Section with Variant Geometry. Ph.D. Thesis, Technischen Universität Dresden, Dresden, Germany, 2008. [Google Scholar]
- Ghosh, A.K. Fundamentals of Paper Drying—Theory and Application from Industrial Perspective. In Evaporation, Condensation and Heat transfer, 1st ed.; IntechOpen: London, UK, 2011. [Google Scholar]
- Kong, L.; Liu, H. A Static Energy Model of Conventional Paper Drying for Multicylinder Paper Machines. Dry. Technol. 2012, 30, 276–296. [Google Scholar] [CrossRef]
- Nissan, A.H.; Hansen, D. Heat and mass transfer transients in cylinder drying: Part, I. Unfelted cyclinders. AIChE J. 1960, 6, 606–611. [Google Scholar] [CrossRef]
- Hii, C.L.; Ong, S.P.; Yap, J.Y.; Putranto, A.; Mangindaan, D. Hybrid drying of food and bioproducts: A review. Dry. Technol. 2021, 39, 1554–1576. [Google Scholar] [CrossRef]
- Putranto, A.; Chen, X.D. A new model to predict diffusive self-heating during composting incorporating the reaction engineering approach (REA) framework. Bioresour. Technol. 2017, 232, 211–221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Putranto, A.; Chen, X.D. Reaction engineering approach modeling of intensified drying of fruits and vegetables using microwave, ultrasonic and infrared-heating. Dry. Technol. 2020, 38, 747–757. [Google Scholar] [CrossRef]
- Putranto, A.; Chen, X.D. Vacuum drying of food materials modeled and explored using the reaction engineering approach (REA) framework. Dry. Technol. 2021, 40, 2519–2527. [Google Scholar] [CrossRef]
- Compaore, A.; Dissa, A.O.; Rogaume, Y.; Putranto, A.; Chen, X.D.; Mangindaan, D.; Zoulalian, A.; Rémond, R.; Tiendrebeogo, E. Application of the reaction engineering approach (REA) for modeling of the convective drying of onion. Dry. Technol. 2016, 35, 500–508. [Google Scholar] [CrossRef]
- Yang, S.; Liu, T.; Fu, N.; Xiao, J.; Putranto, A.; Chen, X.D. Convective drying of highly shrinkable vegetables: New method on obtaining the parameters of the reaction engineering approach (REA) framework. J. Food Eng. 2021, 305, 110613. [Google Scholar] [CrossRef]
- Heo, C.H.; Cho, H.; Yeo, Y.K. Dynamic modeling of paper drying processes. Korean J. Chem. Eng. 2011, 28, 1651–1657. [Google Scholar] [CrossRef]
- Keränen, J. Increasing the Drying Efficiency of Cylinder Drying. PhD. Thesis, University of Jyväskylä, Jyväskylä, Finland, 2011. [Google Scholar]
- Wilhelmsson, B.; Nilsson, L.; Stenstram, S.; Wimmerstedt, R. Simulation Models of Multi-Cylinder Paper Drying. Dry. Technol. 2007, 11, 1177–1203. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Holm, R.A. Analysis of heat and mass transfer during drying of paper/board. Dry. Technol. 1999, 17, 49–72. [Google Scholar] [CrossRef]
- The Institute of Paper Chemsitry. A Review of the State of the Art in Paper Drying; Progress Report; The Institute of Paper Chemsitry: Appleton, WI, USA, 29 February 1980; pp. 1–29. [Google Scholar]
- Ghodbanan, S.; Alizadeh, R.; Shafiei, S. Steady-State Modeling of Multi-Cylinder Dryers in a Corrugating Paper Machine AU—Ghodbanan, Shaaban. Dry. Technol. 2015, 33, 1474–1490. [Google Scholar] [CrossRef]
- Helena, L.; Sousa, C.D.; Lima, O.C.M.; Pereira, N.C. Analysis of drying kinetics and moisture distribution in convective textile fabric drying. Dry. Technol. 2006, 24, 485–497. [Google Scholar]
- Ryan, M.; Modak, A.; Zuo, H.; Ramaswamy, S.; Worry, G. Through air drying. Dry. Technol. 2003, 21, 719–734. [Google Scholar] [CrossRef]
- Hsieh, Y.-L. Chemical structure and properties of cotton. In Cotton: Science and Technology; Woodhead Publishing: Cambridge, UK, 2007; pp. 3–34. [Google Scholar]
- Bradbury, J. The Morphology And Chemical Structure Of Wool. Pure Appl. Chem. 1976, 46, 247–253. [Google Scholar] [CrossRef]
- Ward, I.M. The Molecular Structure and Mechanical Properties of Polyethylene Terephthalate Fibers. Text. Res. J. 1961, 31, 650–664. [Google Scholar] [CrossRef]
- Du, X.; Li, Z.; Tong, T.; Li, B.; Liu, H. Isothermal Drying Process and its Effect on Compressive Strength of Concrete in Multiscale. Appl. Sci. 2019, 9, 4015. [Google Scholar] [CrossRef] [Green Version]
- Rzig, R.; Khedher, N.B.; Nasrallah, S.B. Three-Dimensional Simulation of Mass and Heat Transfer in Drying Unsaturated Porous Medium. Heat Transf. Res. 2017, 48, 985–1005. [Google Scholar] [CrossRef]
- Momen, A.M.; Patel, V.K.; Gluesenkamp, K.R.; Erdman, D., III; Kiggans, J., Jr.; Ormston, G. Fabric properties and electric efficiency limits of mechanical moisture extraction from fabrics. Dry. Technol. 2021, 1–17. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, N.; Sengupta, A.; Liaw, J.-S.; Wang, C.-C. Parametric Analysis of Cylinder Drying Process in Association with Various Materials. Appl. Sci. 2022, 12, 10489. https://doi.org/10.3390/app122010489
Tran N, Sengupta A, Liaw J-S, Wang C-C. Parametric Analysis of Cylinder Drying Process in Association with Various Materials. Applied Sciences. 2022; 12(20):10489. https://doi.org/10.3390/app122010489
Chicago/Turabian StyleTran, Ngoctan, Akash Sengupta, Jane-Sunn Liaw, and Chi-Chuan Wang. 2022. "Parametric Analysis of Cylinder Drying Process in Association with Various Materials" Applied Sciences 12, no. 20: 10489. https://doi.org/10.3390/app122010489




