Advanced Prediction for Cyclic Bending Behavior of RC Columns Based on the Idealization of Reinforcement of Bond Properties
Abstract
:1. Introduction
2. Experimental Programs
2.1. Design of Specimen with Densely Arranged, Small Diameter Reinforcements
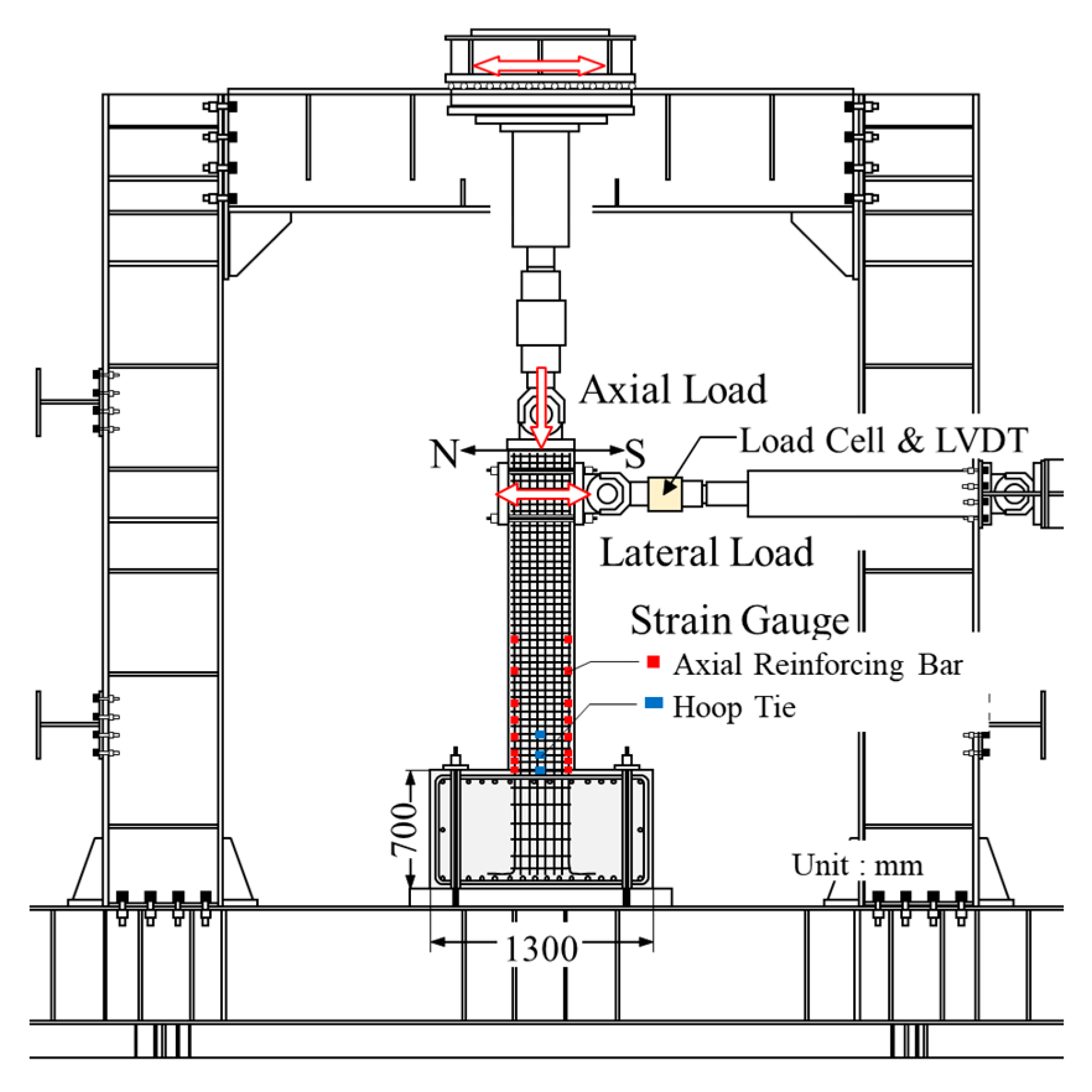
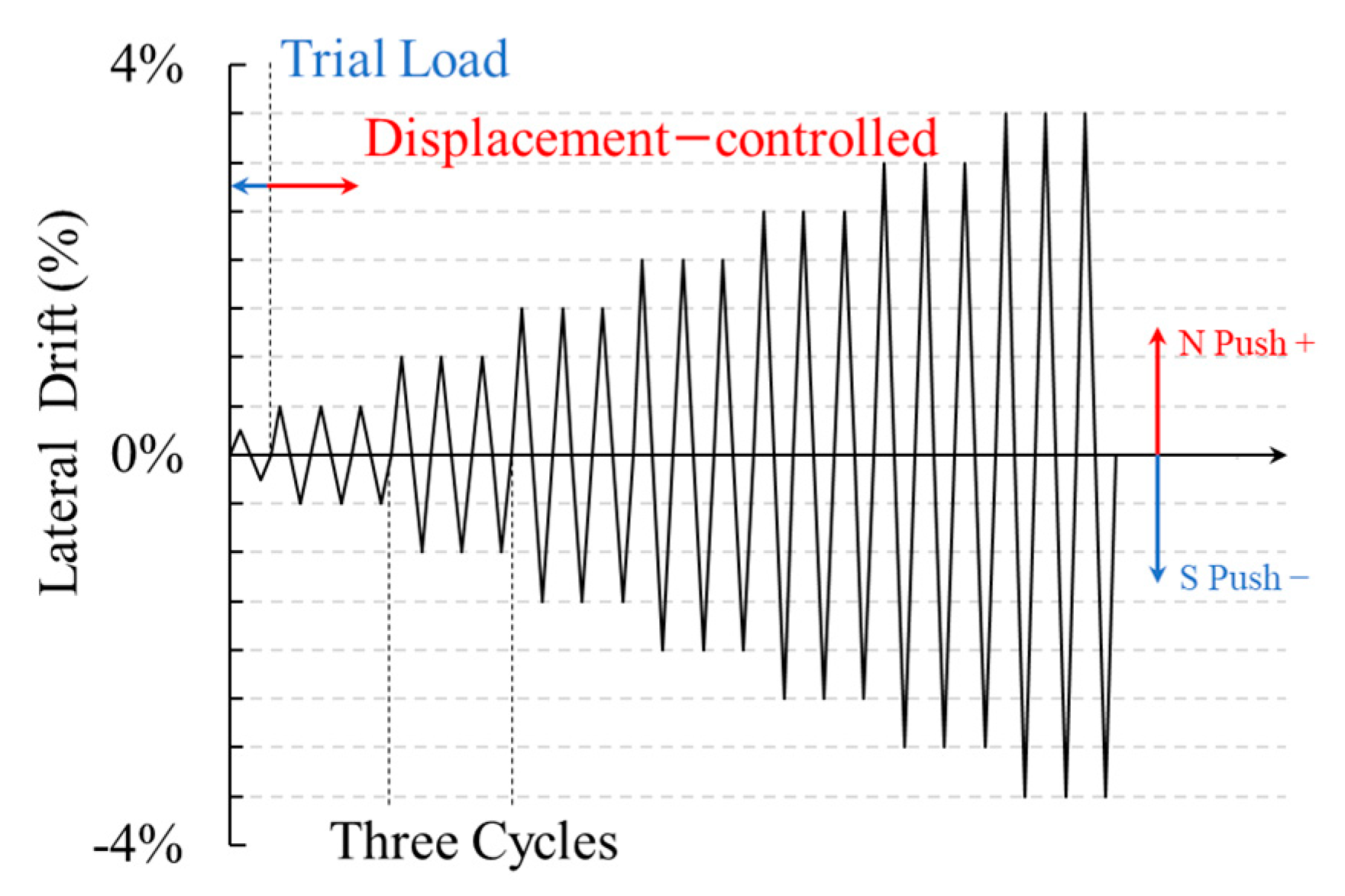
2.2. Test Setup, Loading Protocol, and Instrumentation
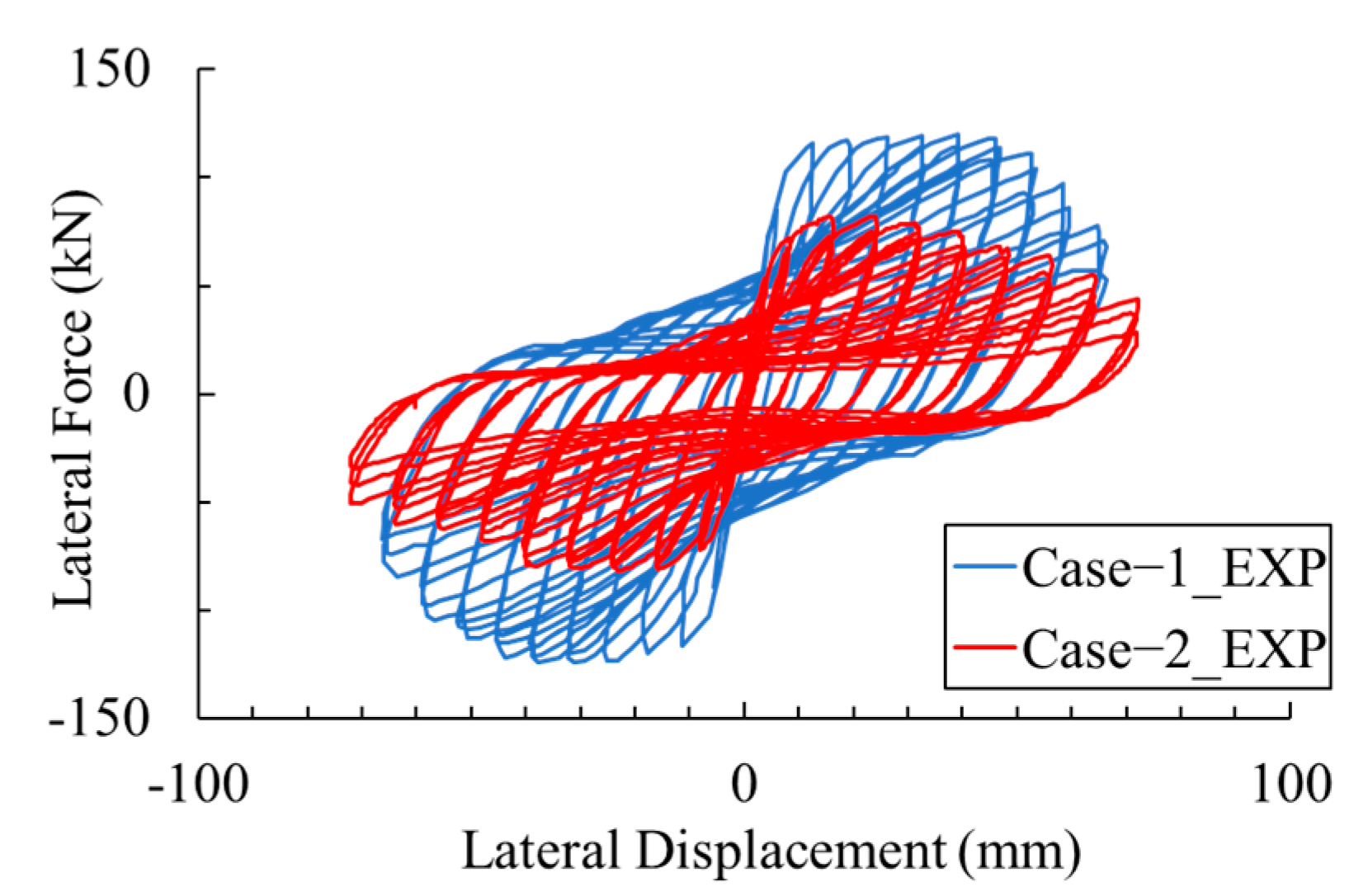
2.3. Cyclic Behaviors of Specimens
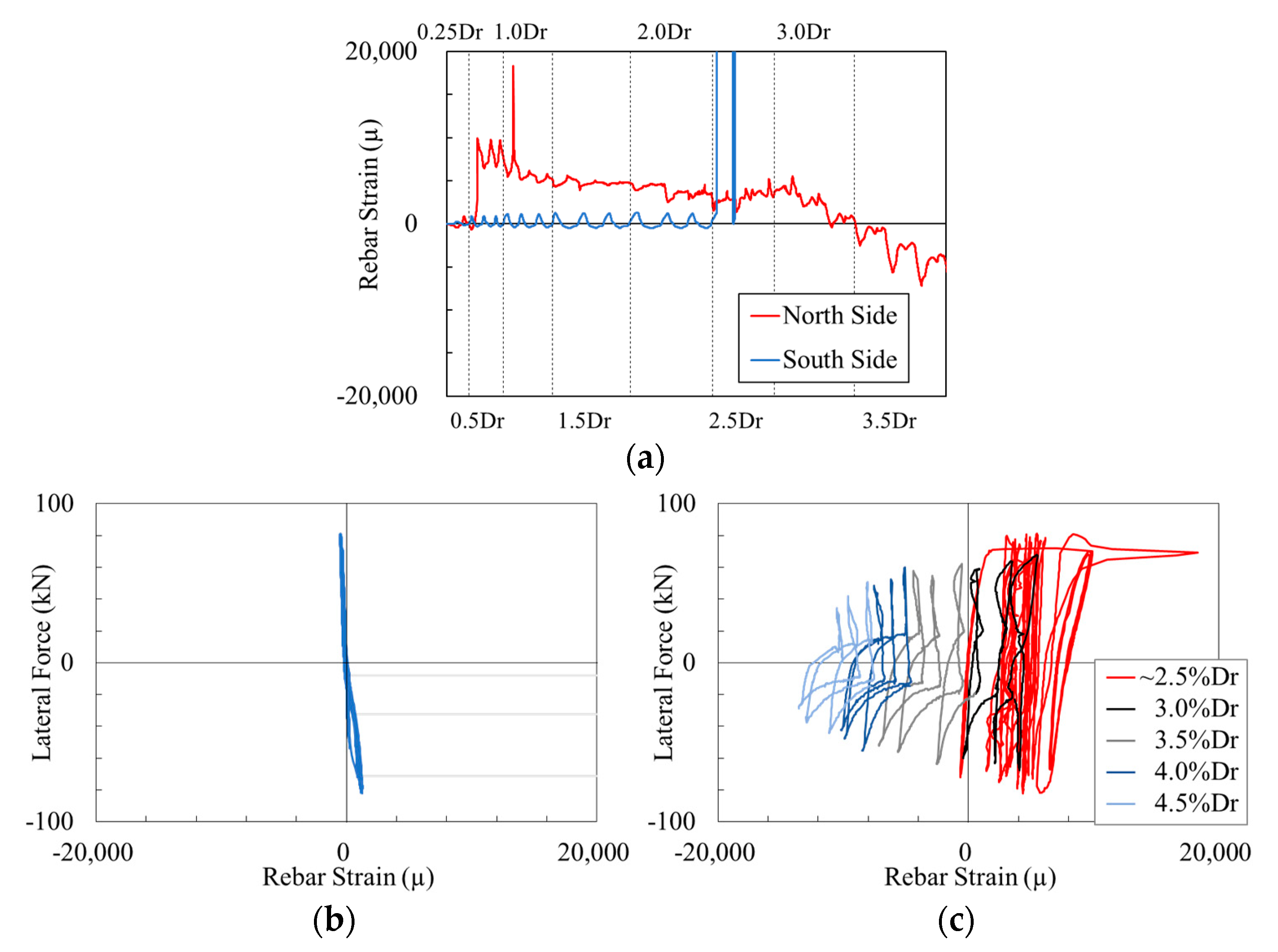
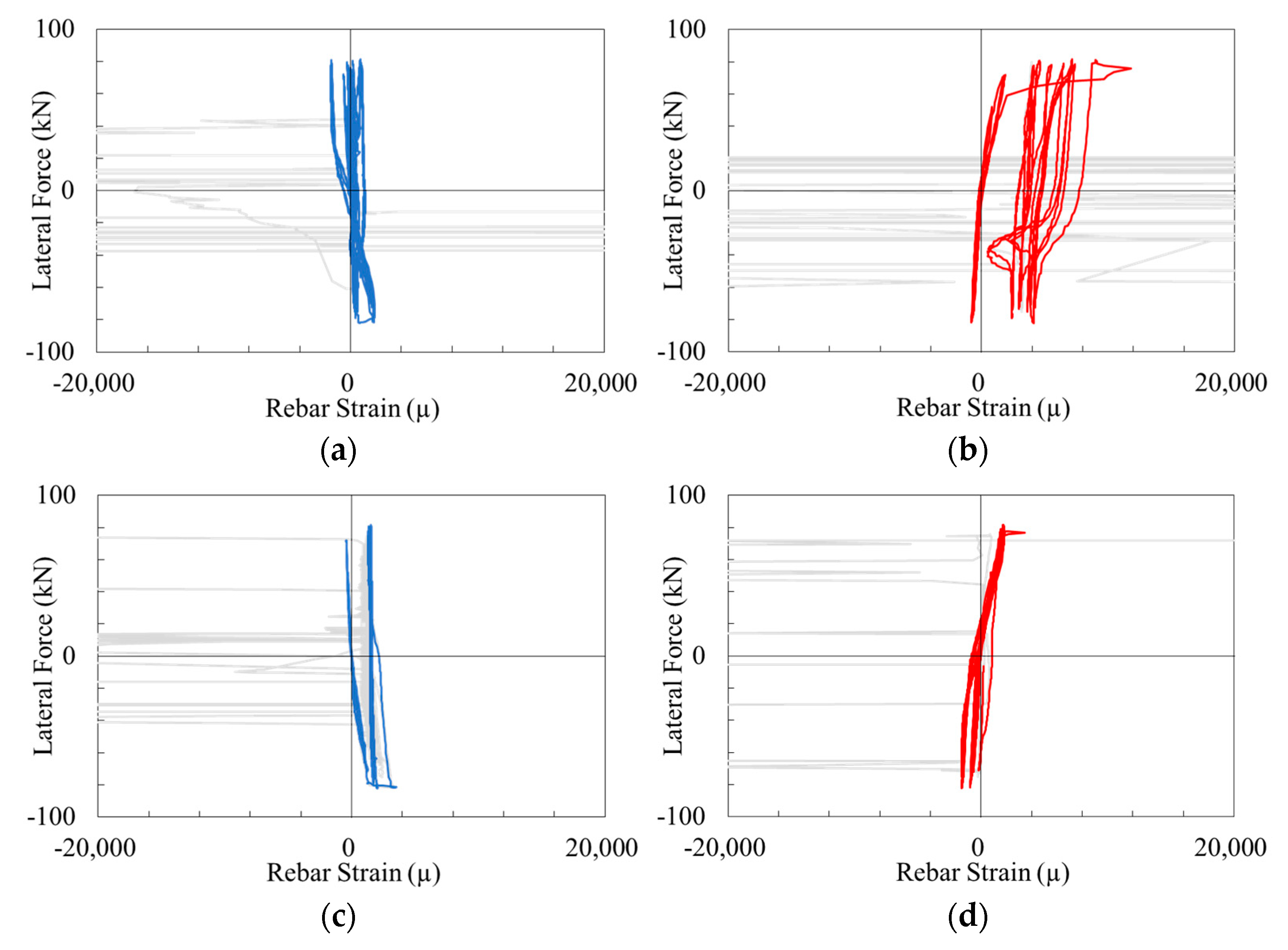
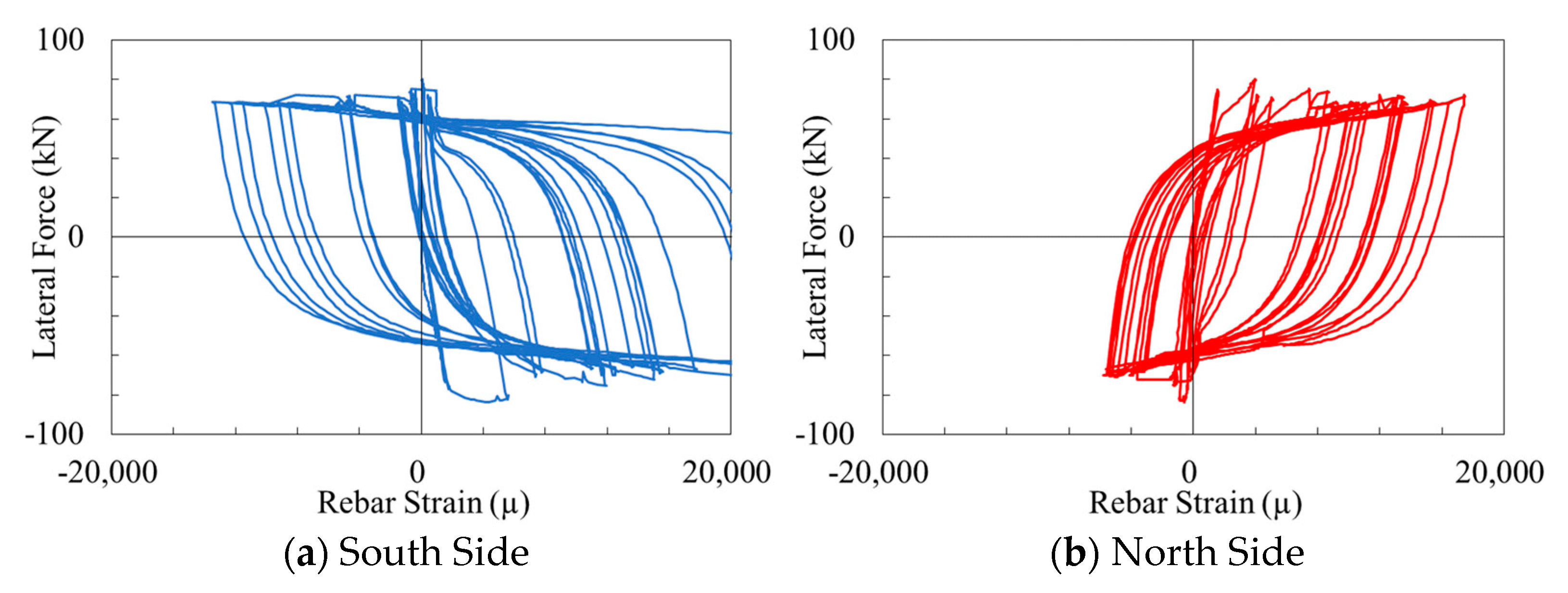
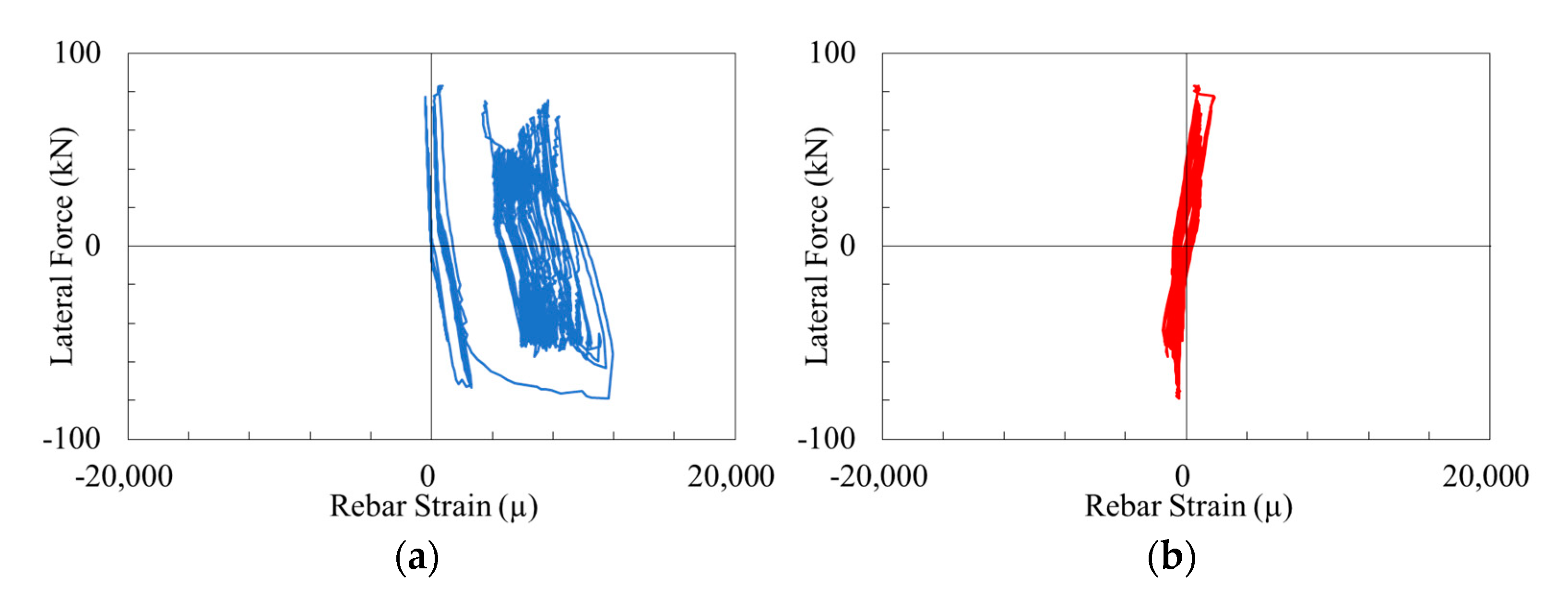
2.4. Damage to Longitudinal Reinforcements
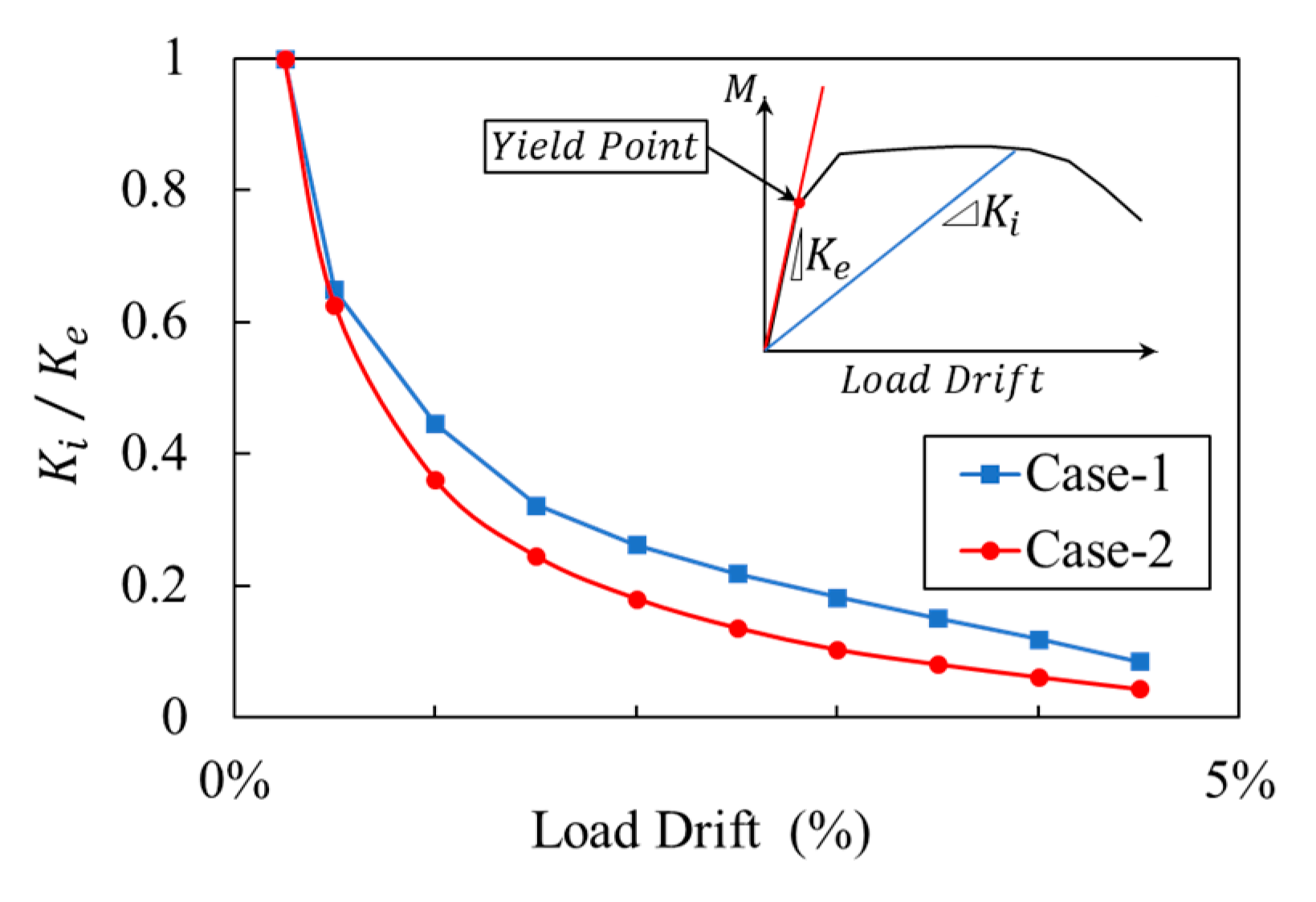
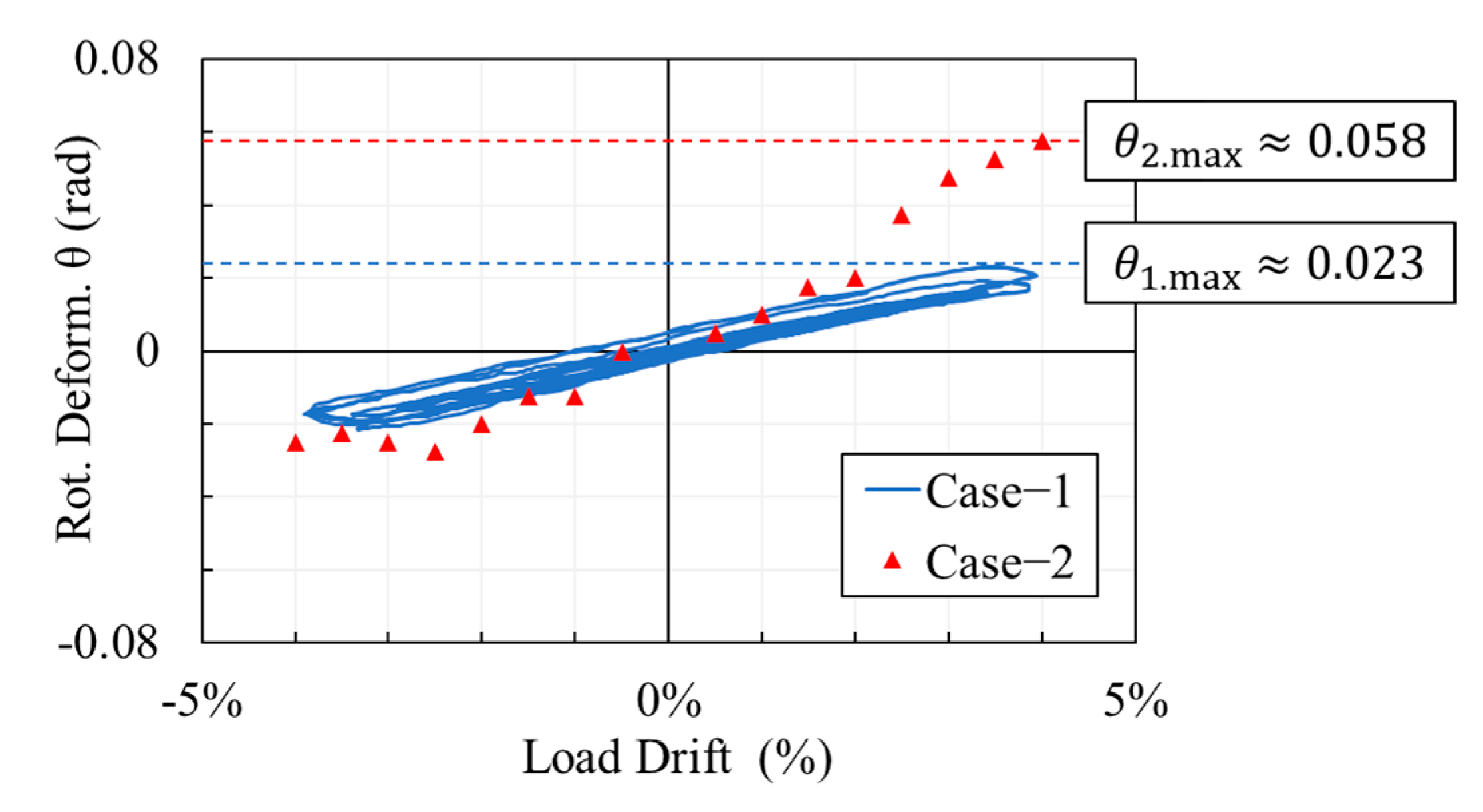
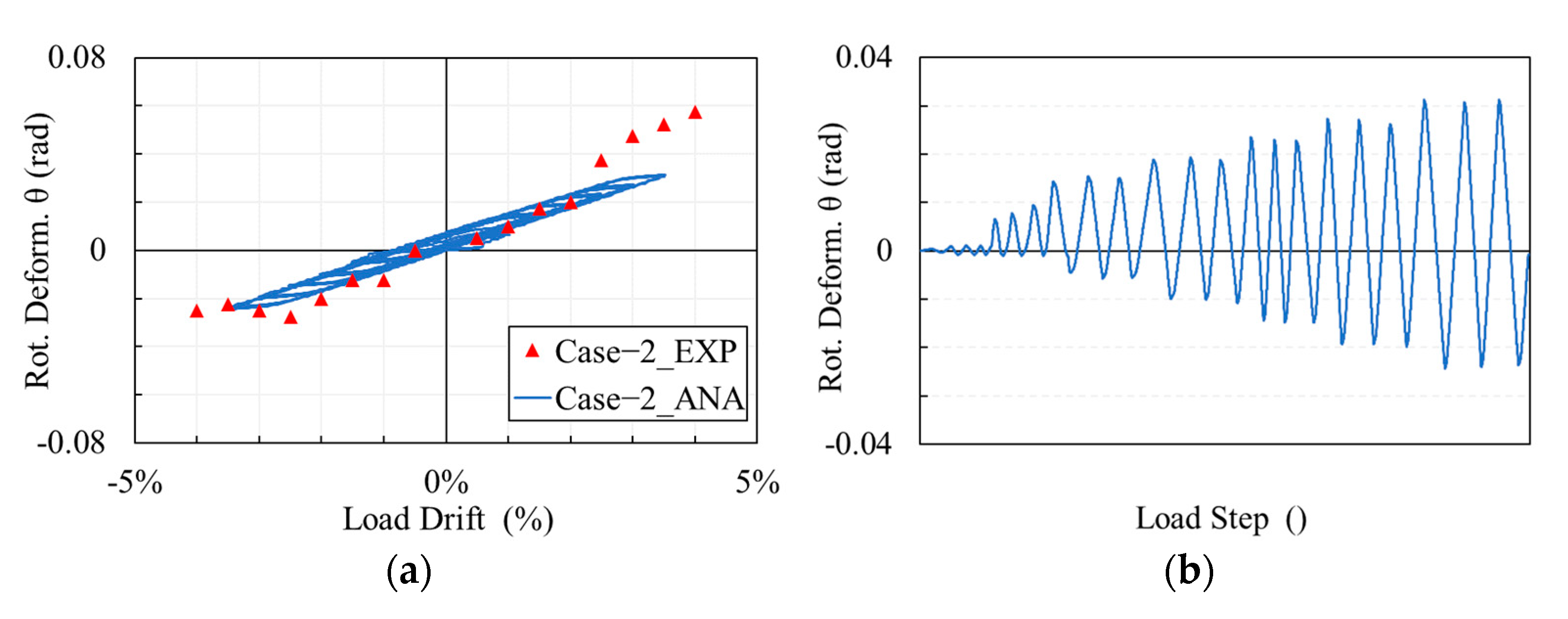
2.5. Rotational Deformation at the Base of Columns
3. FEA Results without Bond-Slip
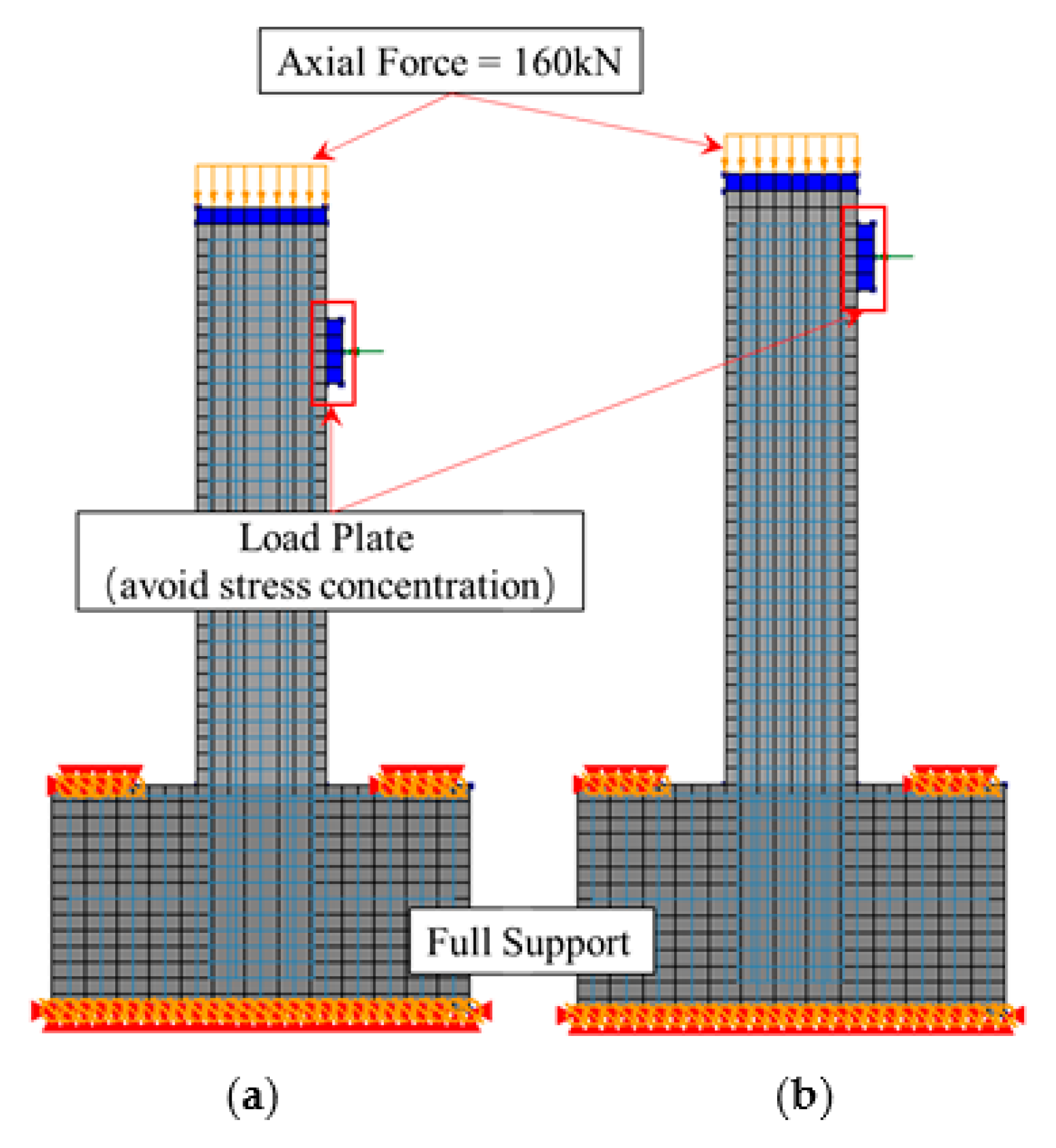
3.1. Structure Modeling
3.2. Material Modeling of Concrete
3.3. Material Modeling of Reinforcements
3.4. Discussion of Analysis Results without Bond-Slip
4. Effects of Different Mode Bond-Slip Fracture
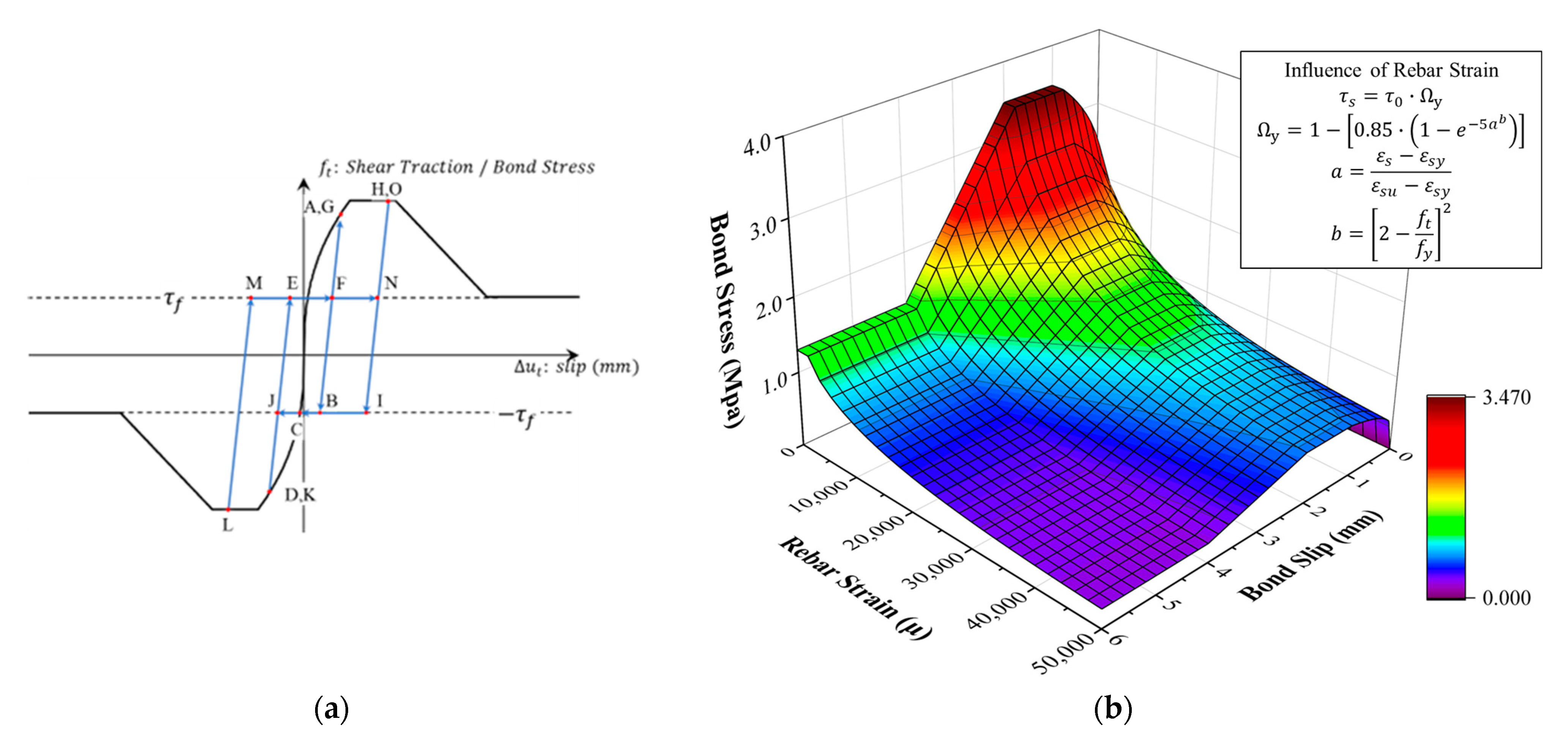
4.1. Research Review on Modeling of Bond-Slip Phenomena
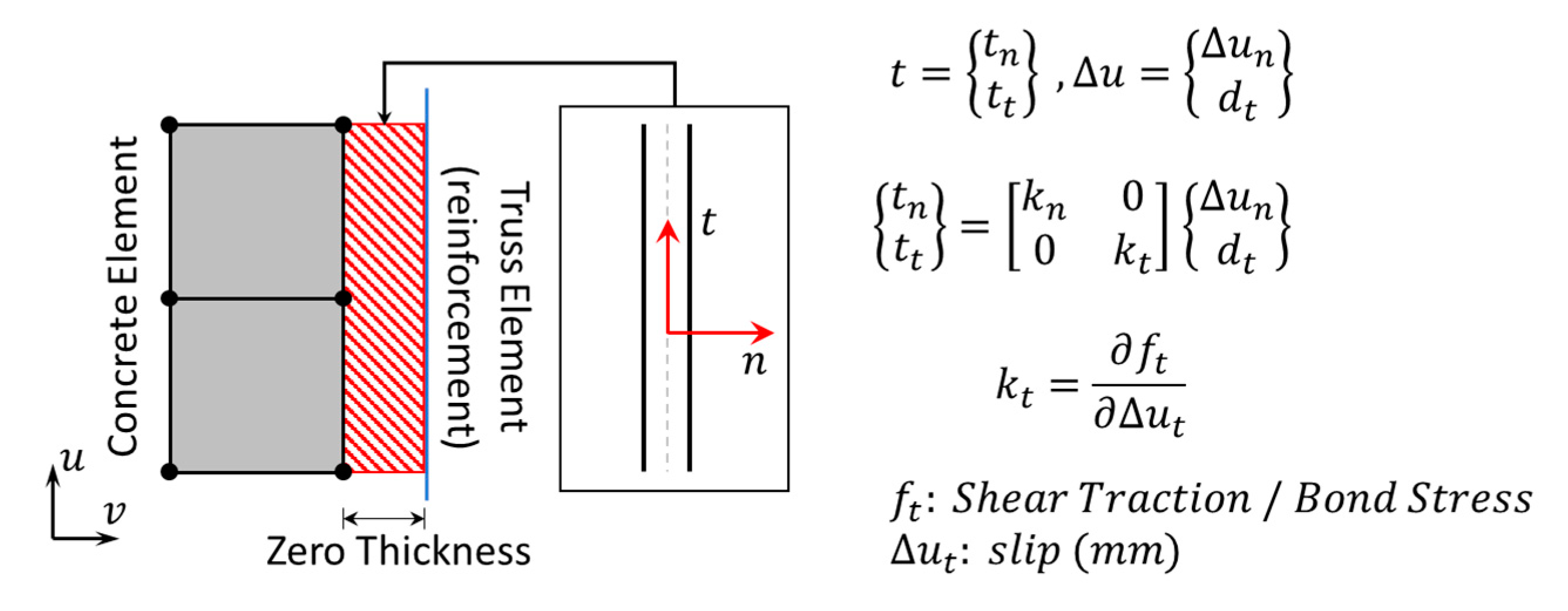
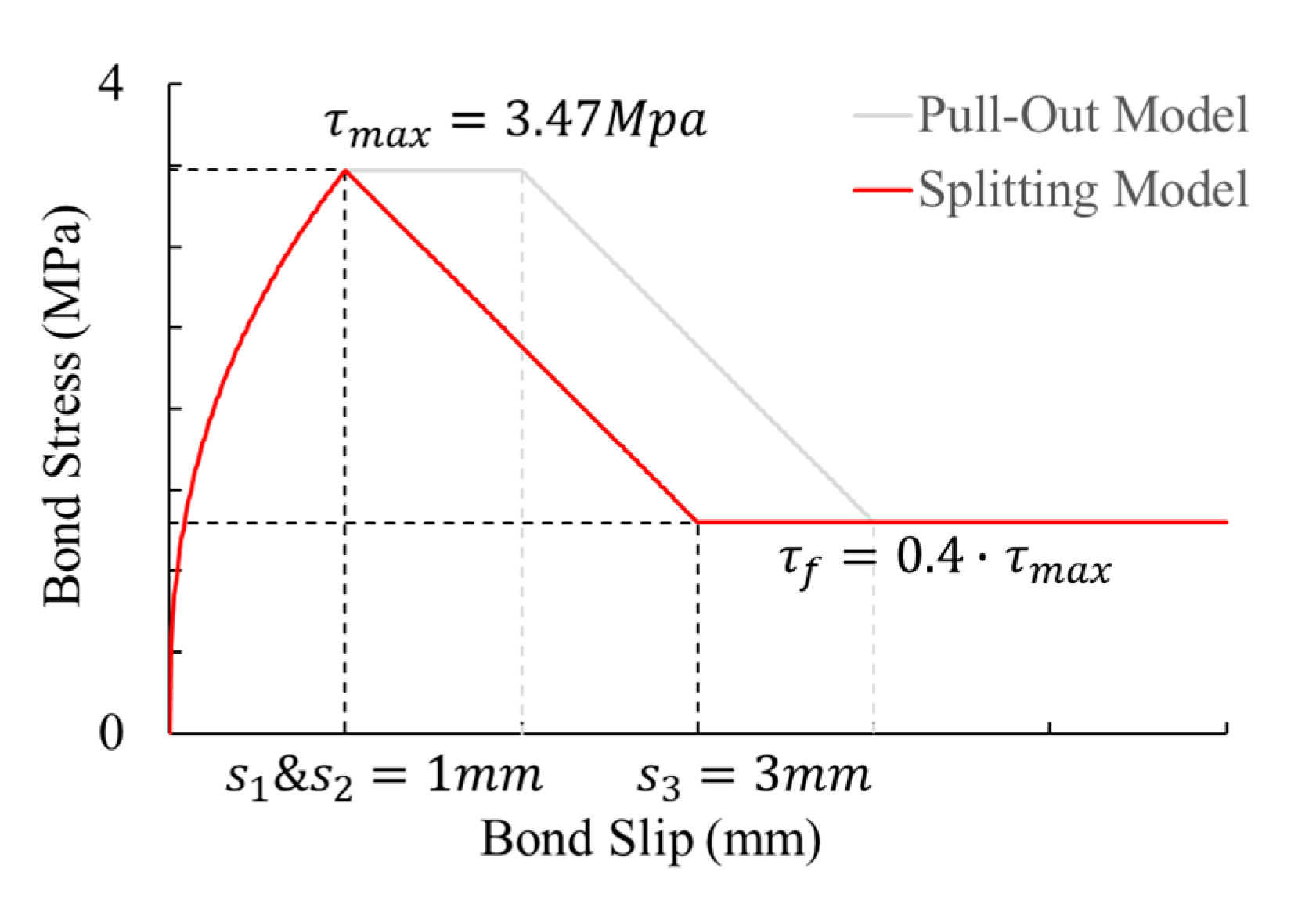
4.2. Numerical Model of Bond-Slip
4.3. Investigation of Different Bond-Slip Failure Modes Based on FEA
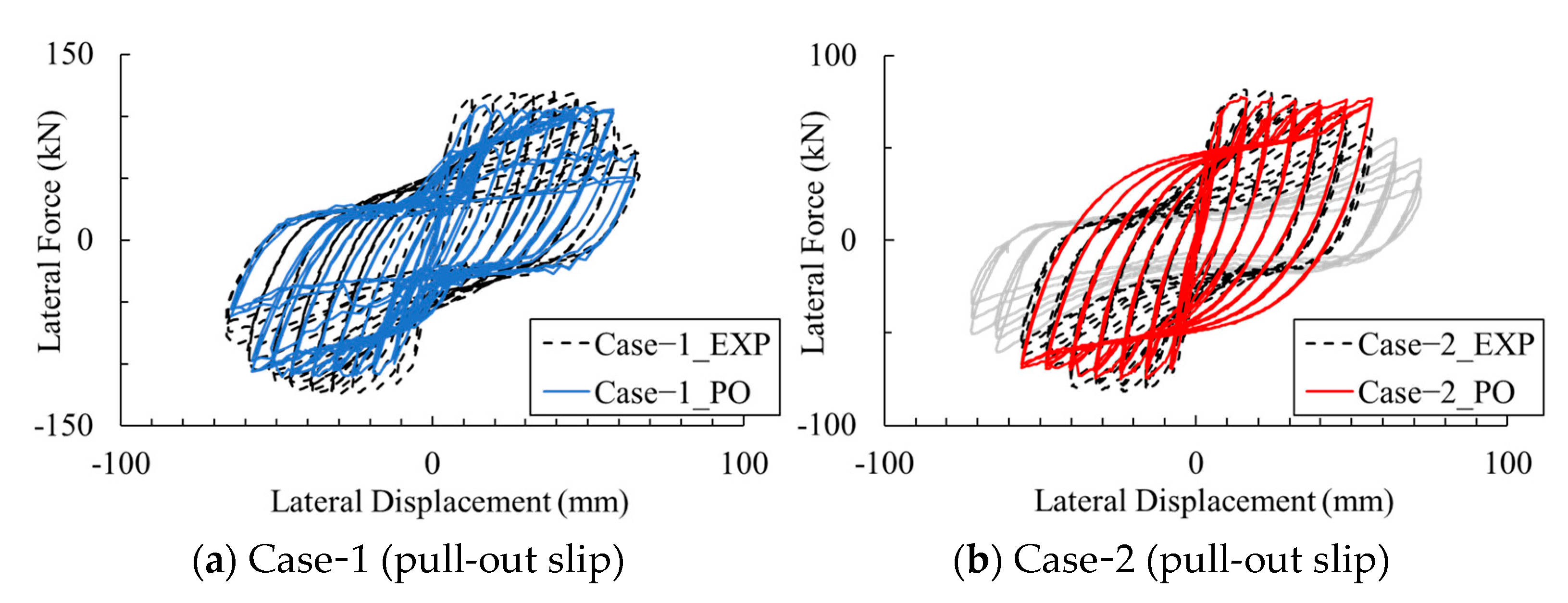
4.3.1. Pull-Out Failure Mode
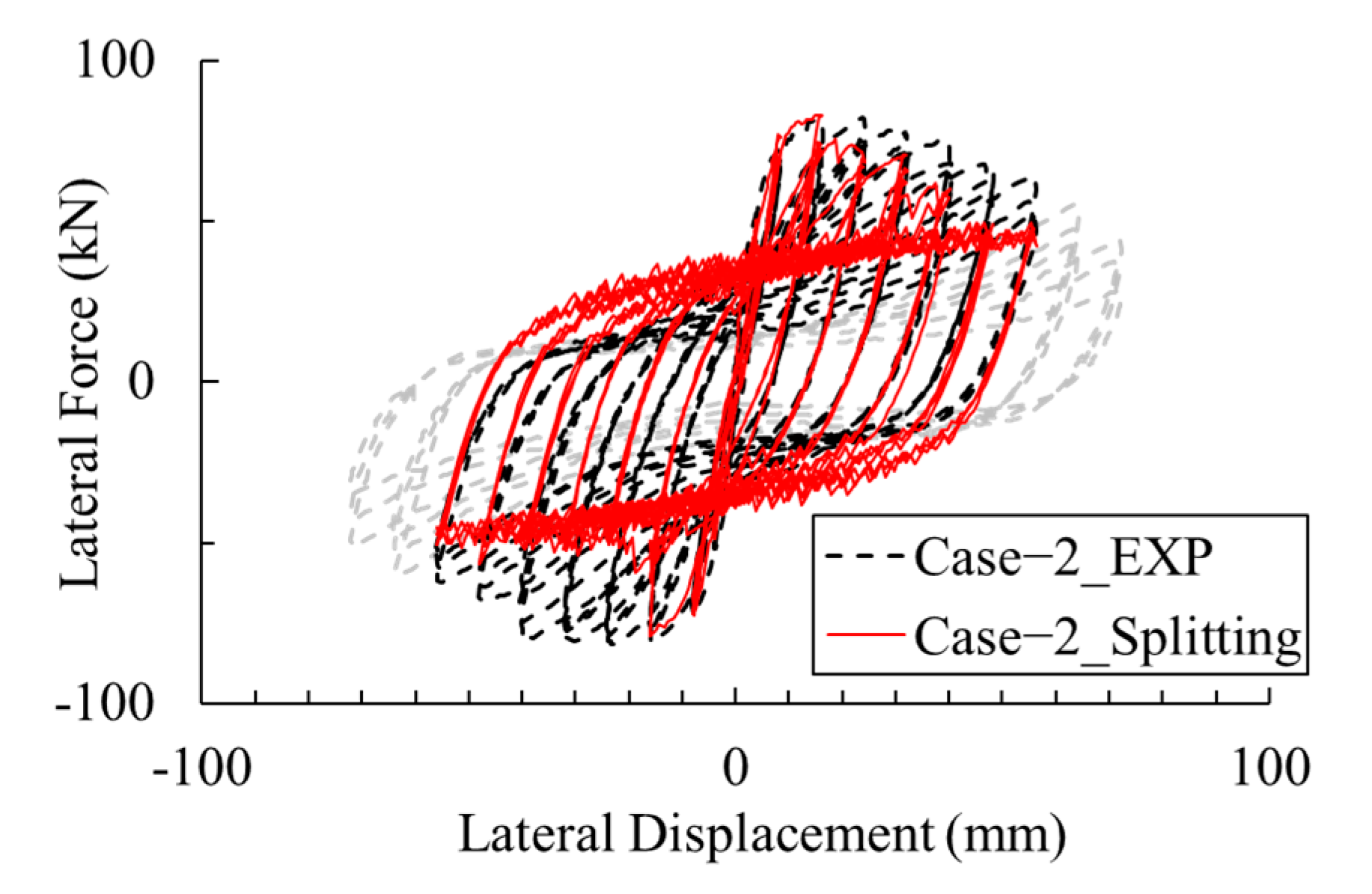
4.3.2. Splitting Failure Mode
5. Conclusions
- ▪
- The load-bearing capacity and deformation performance of reinforced concrete columns is significantly affected by the diameter and arrangement of reinforcing bars, despite the longitudinal reinforcement ratios are same. The reinforced concrete column showed a 3.5% drift of high deformation capacity when using large-diameter and low-density bar arrangements. However, significant degradation of the deformation capacity to a 1.5% drift was observed in the reinforced concrete column with the small-diameter and high-density bar arrangements.
- ▪
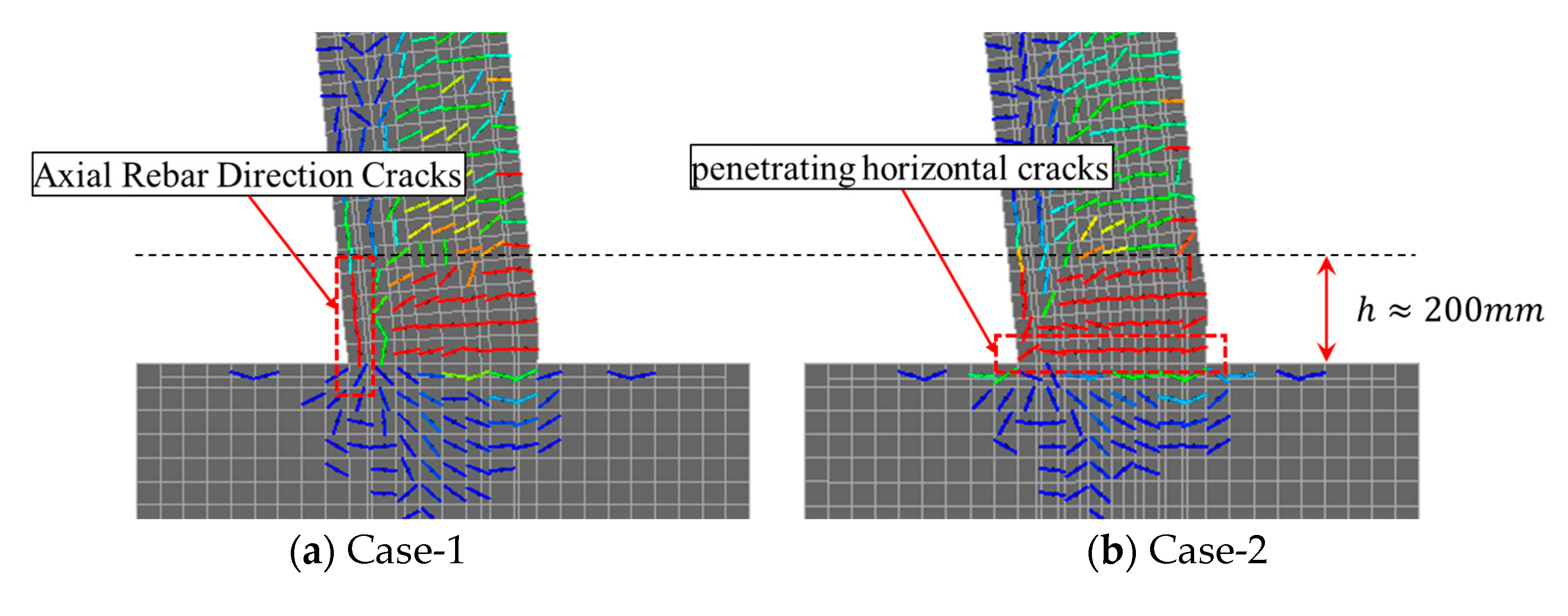
- In the cyclic loading test, despite being subjected to symmetrical hysteretic loadings, the RC column with small-diameter and high-density bar arrangements results in the splitting bond failure of the reinforcements. And in the loading directions it results in pronounced asymmetrical damage induced in the longitudinal reinforcements, ultimately leading in localized damage within the RC columns.
- ▪
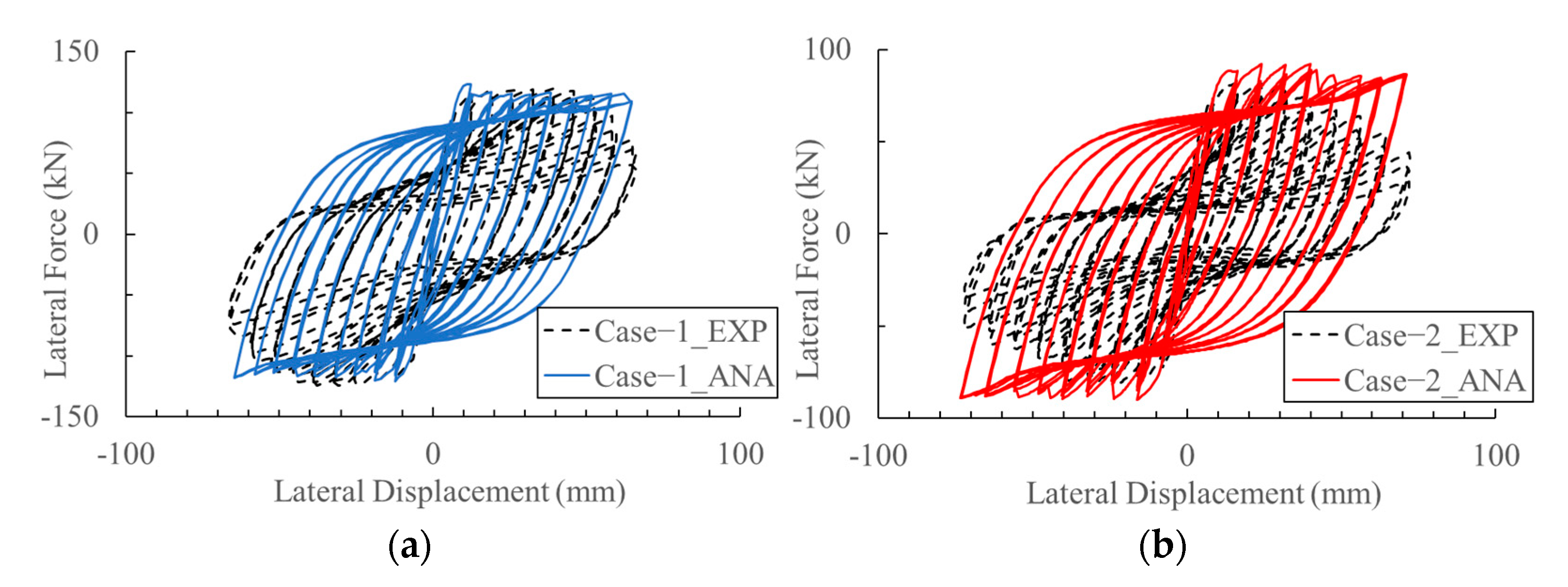
- By employing the bond-slip model proposed in this study in finite element analysis, the load-bearing capacity of RC columns can be reproduced with high precision. When using the pull-out model, the analytical error for the maximum load capacity of Case-1 is approximately 8% to 11%. In contrast, when using the splitting model, the analytical error for the maximum load capacity of Case-2 is less than 3%. Moreover, the damage condition of the reinforcement is also replicated.
- ▪
- Furthermore, pinching phenomena observed in unloading hysteresis curve of force-displacement relationship also can be reproduced by employing an appropriate bond-slip model. Thus, it enables to verify the energy dissipation during earthquakes.
- ▪
- The RC column with small-diameter and high-density bar arrangements result in the splitting bond failure along the longitudinal reinforcement bars, which leads the RC column to change the failure mode from the bending deformation mode to the rocking deformation mode.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.N.; Wu, J.C.; Kawashima, K.; Unjoh, S. Hybrid control of seismic-excited bridge structures. Earthq. Eng. Struct. Dyn. 1995, 24, 1437–1451. [Google Scholar] [CrossRef]
- Penzien, J.; Clough, R.W. Observations on the Damages of Highway Bridge Structures, San Fernando, California, Earthquake, February 9, 1971; Report to Division of Structural Engineers, Federal Highway Administration; University of California: Berkeley, CA, USA, 1971. [Google Scholar]
- Schoettler, M.; Restrepo, J.; Guerrini, G.; Duck, D.E.; Carrea, F. A Full-Scale, Single-Column Bridge Bent Tested by Shake-Table Excitation (Report No. 258); Center for Civil Engineering Earthquake Research, Department of Civil Engineering, University of Nevada: Reno, NV, USA, 2012. [Google Scholar]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations (Report No. UCB/EERC-83/23); Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Lv, X.; Yu, Z.; Shan, Z. Bond stress-slip model for rebar-concrete interface under monotonic and cyclic loading. Structures 2021, 34, 498–506. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, J.; Zhao, H. Experimental study on bond performance between corroded reinforcement and concrete in bridge piers. Constr. Build. Mater. 2019, 223, 581–594. [Google Scholar] [CrossRef]
- Shao, P.; Watanabe, G.; Kosa, K. Evaluation of bending behavior of RC column under the cyclic force based on the non-linear finite element analysis focusing on the bond-strain-slip relationship between rebars and concrete at the column base. J. Jpn. Soc. Civ. Eng. 2021, 77, 23–38. (In Japanese) [Google Scholar] [CrossRef]
- Kawashima, K.; Hosoiri, K.; Shoji, G.; Sakai, J. Effect of unbonding of main reinforcements at plastic hinge region for enhancing ductility of reinforced concrete bridge columns. J. Jpn. Soc. Civ. Eng. 2001, 2001, 67–76. (In Japanese) [Google Scholar] [CrossRef]
- Haselton, C.B.; Deierlein, G.G. Assessing seismic collapse safety of modern reinforced concrete moment-frame buildings. J. Struct. Eng. 2008, 134, 709–728. [Google Scholar] [CrossRef]
- Abtahi, S.; Li, Y. Bond-slip model uncertainty quantification and effect on nonlinear behavior simulations of reinforced concrete columns. Eng. Struct. 2022, 266, 114525. [Google Scholar] [CrossRef]
- Xu, F.; Zhi-min, W.; Zheng, J.; Hu, Y.; Li, Q.; Xu, F.; Zhi-min, W.; Zheng, J.; Hu, Y.; Li, Q. Bond behavior of plain round bars in concrete under complex lateral pressures. ACI Struct. J. 2014, 111, 883–892. [Google Scholar] [CrossRef]
- Ahmad, S.; Rafi, M.M.; Pilakoutas, K.; Khan, Q.U.Z.; Shabbir, F.; Tahir, M.F. Bond-slip behaviour of steel bars in low-strength concrete. Proc. Inst. Civ. Eng. Struct. Build. 2016, 169, 581–594. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Zhang, X. A mechanical bond model for reinforcing bar in concrete subjected to monotonic and reversed cyclic loading. J. Build. Eng. 2021, 44, 102912. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, Y.; Liu, J. Bond behavior of concrete reinforced with high-strength and high-toughness steel bars. Constr. Build. Mater. 2023, 370, 130433. [Google Scholar] [CrossRef]
- Ertzibengoa, D.; Matthys, S.; Taerwe, L. Bond behaviour of flat stainless steel rebars in concrete. Mater. Struct. 2012, 45, 1639–1653. [Google Scholar] [CrossRef]
- Chapman, R.A.; Shah, S.P. Early-age bond strength in reinforced concrete. ACI Mater. J. 1987, 84, 501–510. [Google Scholar] [CrossRef]
- Khaksefidi, S.; Ghalehnovi, M.; de Brito, J. Bond behaviour of high-strength steel rebars in normal (NSC) and ultra-high performance concrete (UHPC). J. Build. Eng. 2021, 33, 101592. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Li, H.; Gu, X. Experimental investigation of fatigue bond behavior between deformed steel bar and concrete. Cem. Concr. Compos. 2020, 108, 103515. [Google Scholar] [CrossRef]
- Japan Road Association. Specifications for Highway Bridges, Part V: Seismic Design; Japan Road Association: Tokyo, Japan, 1996. [Google Scholar]
- Hayakawa, R.; Kawashima, K.; Watanabe, G. Effect of bilateral loadings on the flexural strength and ductility of reinforced concrete bridge columns. J. Jpn. Soc. Civ. Eng. 2004, 759, 79–98. (In Japanese) [Google Scholar] [CrossRef]
- Shao, P.; Watanabe, G.; Kosa, K. Study on the Enhancement of Bending Deformation Performance of Concrete Column by Winding up the Ultra-thin PCM and Reinforcements. Proc. Concr. Struct. Scenar. JSMS 2020, L6941B, 411–416. (In Japanese) [Google Scholar]
- Kwak, H.-G.; Kim, J.-K. Implementation of bond-slip effect in analyses of RC frames under cyclic loads using layered section method. Eng. Struct. 2006, 28, 1715–1727. [Google Scholar] [CrossRef]
- Li, Y.; Yongbin, L.; Junwu, D.; Tao, J. Novel uniaxial concrete constitutive model considering bond-slip effect. Earthq. Eng. Eng. Vib. 2020, 19, 649–668. [Google Scholar] [CrossRef]
- FEA Software DIANA; DIANA User’s Manual 10.6; TNO DIANA BV: Delft, The Netherlands, 2021.
- Tadokoro, T.; Sato, Y.; Ueda, T. Influences of crack and reinforcement modeling on tensile behavior of RC members. J. Struct. Eng. 2002, 48A, 43–50. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Cormeau, I.C. Viscoplasticity, plasticity and creep in elastic solids—A unified numerical solution approach. Int. J. Numer. Methods Eng. 1974, 8, 821–845. [Google Scholar] [CrossRef]
- Maekawa, K.; Fukuura, N. Nonlinear Modeling of 3D Structural Reinforced Concrete and Seismic Performance Assessment. In Advances in Engineering Structures, Mechanics & Construction; Hsu, T.T.C., Wu, C.L., Xu, S.X., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 495–529. [Google Scholar] [CrossRef]
- Maekawa, K.; Okamura, H.; Pimanmas, A. Nonlinear Mechanics of Reinforced Concrete; Spon Press: London, UK, 2003. [Google Scholar]
- Japan Society of Civil Engineers. JSCE Guidelines for Concrete No. 15: Standard Specifications for Concrete Structures—2007 “Design”; Japan Society of Civil Engineers: Tokyo, Japan, 2010. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and nonelastic behavior of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973; pp. 15–22. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints (Tech. Rep. EERC 83-19); Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Nilson, H.A. Internal measurement of bond slip. ACI J. 1972, 69, 192–196. [Google Scholar]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behavior and modeling of bond of FRP rebars to concrete. J. Compos. Constr. 1997, 1, 40–51. [Google Scholar] [CrossRef]
- Fib—International Federation for Structural Concrete. Fib Model Code for Concrete Structures 2010; Ernst & Sohn: Berlin, Germany, 2013. [Google Scholar]
- Orangun, C.O.; Jirsa, J.O.; Breen, J.E. A reevaluation of test data on development length and splice strength. ACI J. Proc. 1977, 74, 114–122. [Google Scholar]
- Rizkalla, S.; El-Hacha, R.; Elagroudy, H. Bond characteristics of high-strength steel reinforcement. ACI Struct. J. 2006, 103, 794–802. [Google Scholar]
- Al-Shura, M.F.; Al-Zaid, R.Z. Bond failure of deformed reinforcing bars based on the longitudinal splitting effect of the bars. ACI Mater. J. 1991, 88, 381–390. [Google Scholar]







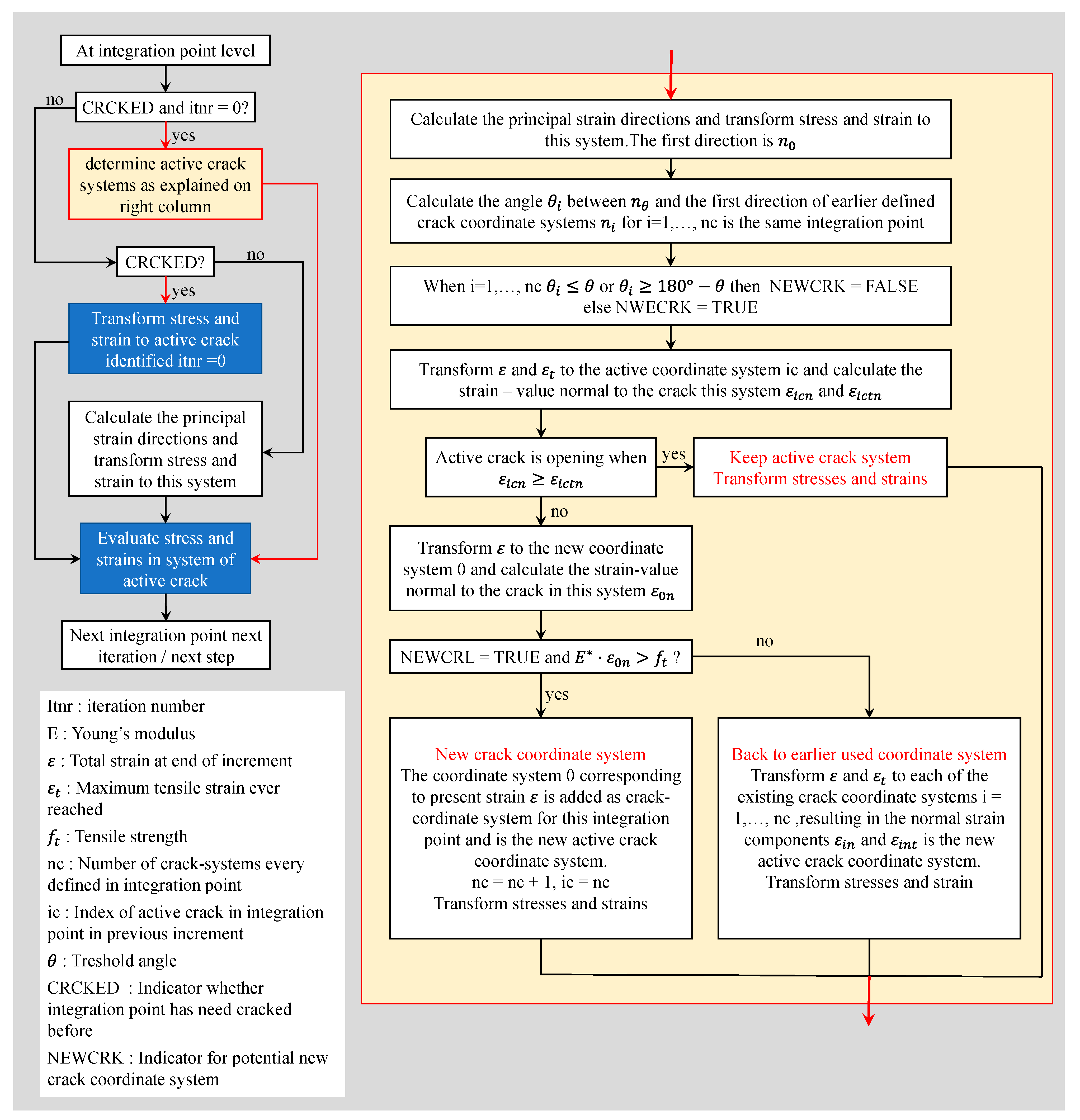
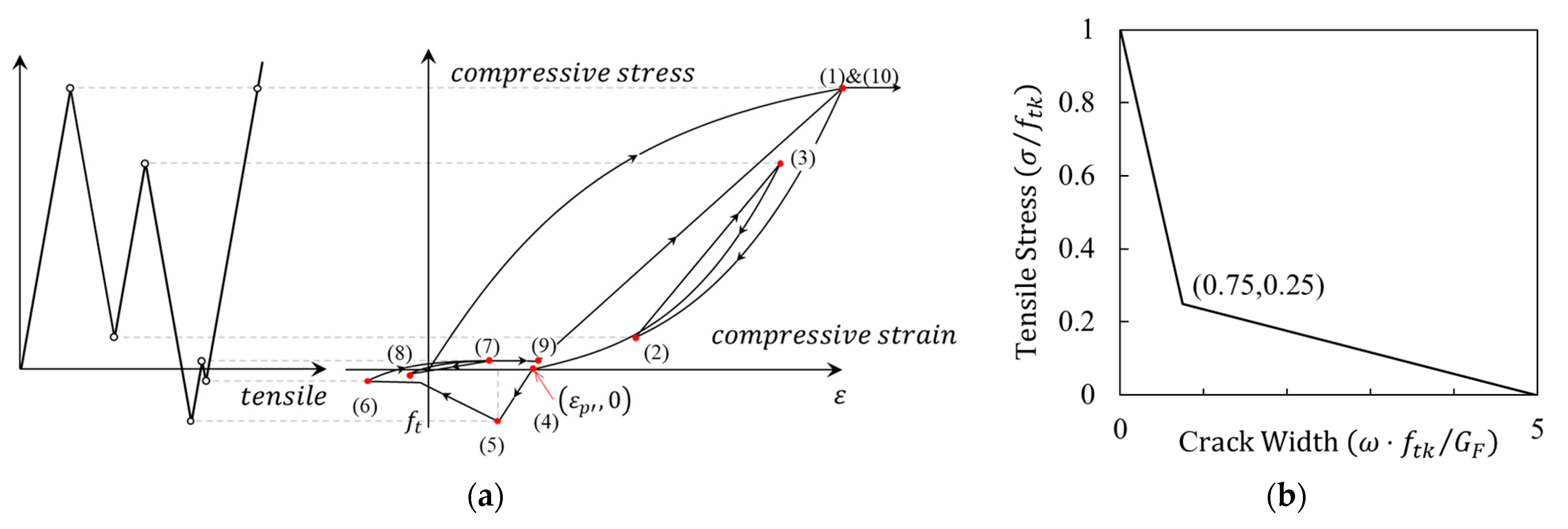
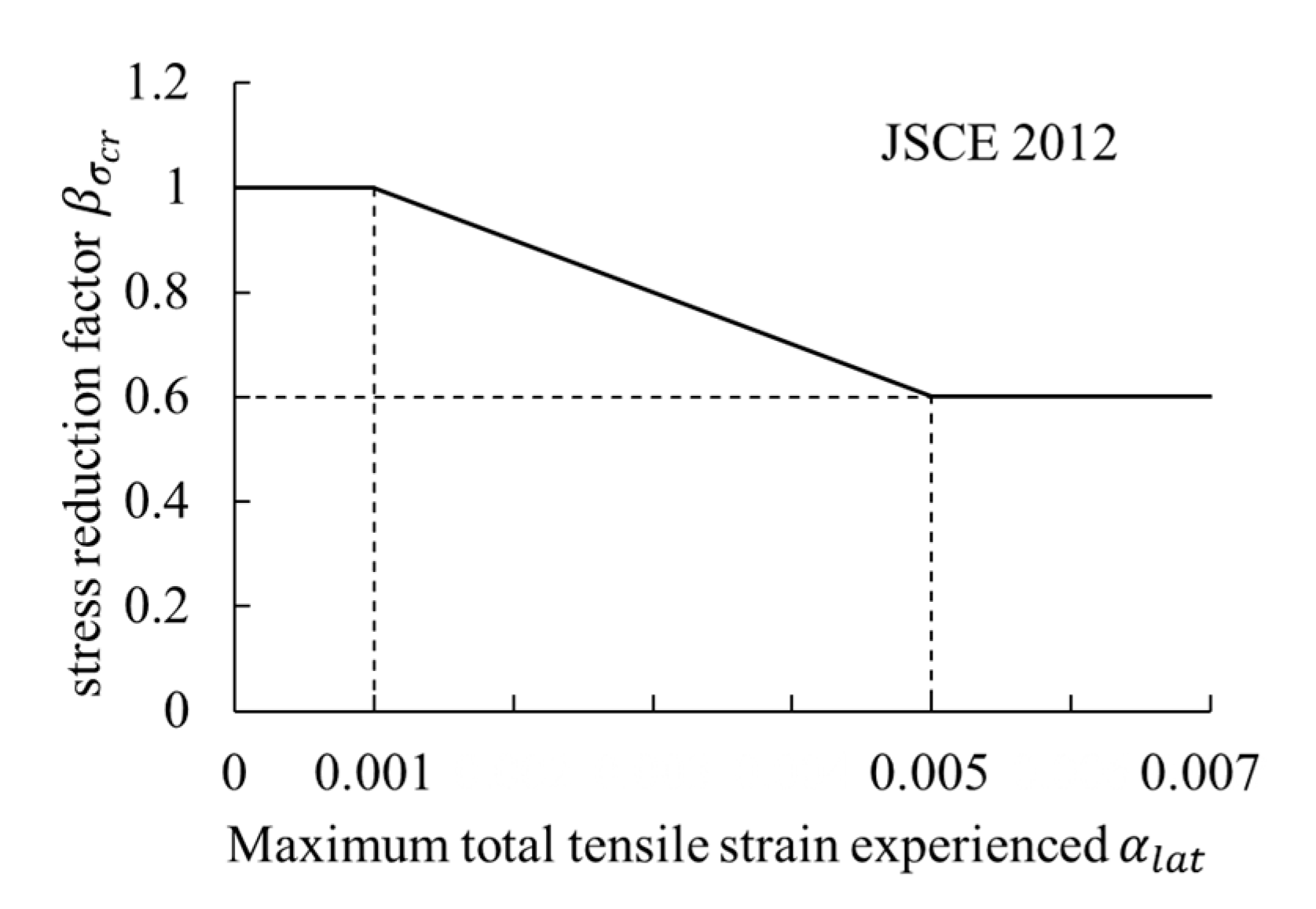
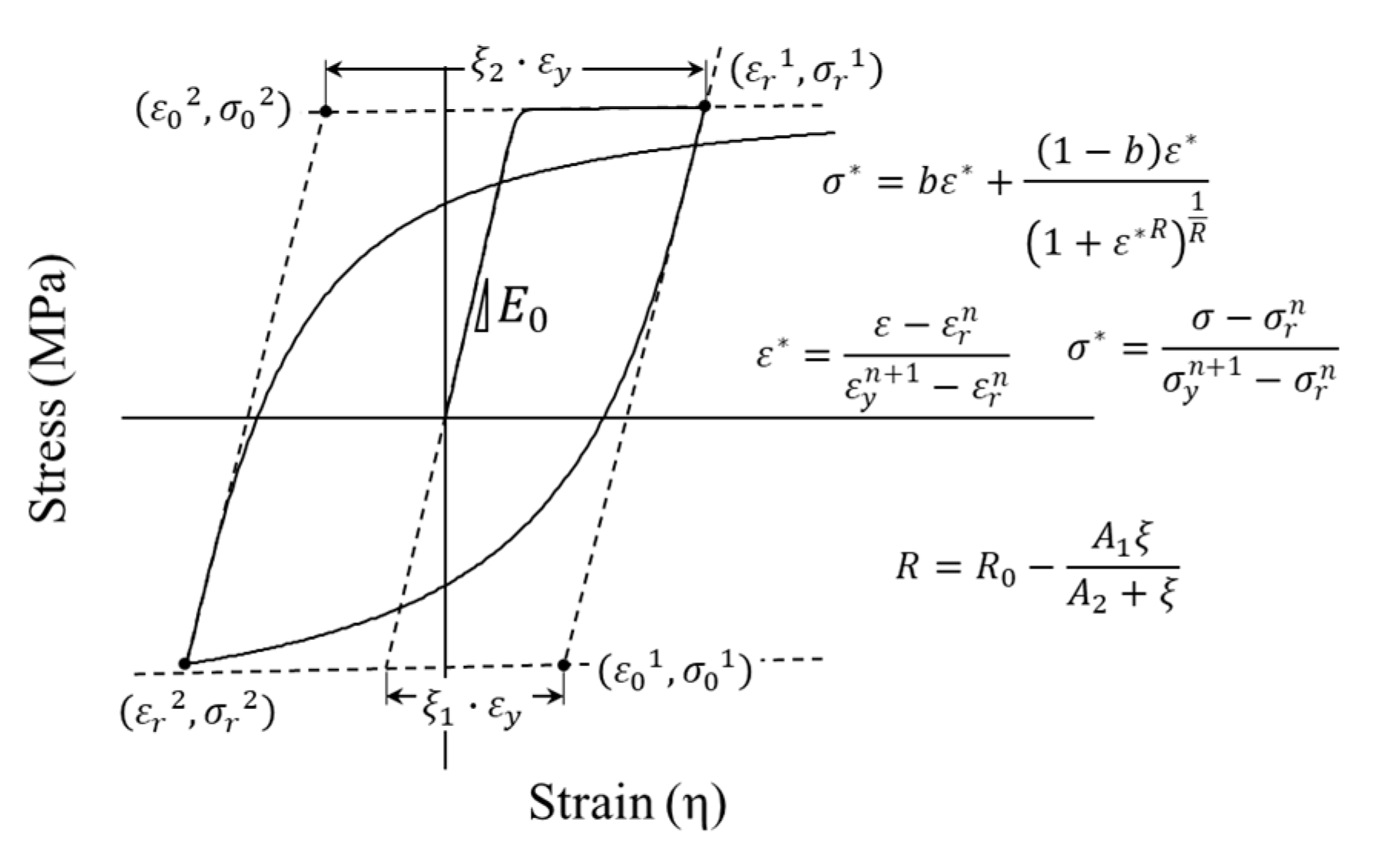


| Strength Parameters (Mpa) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case-1 | 30.1 | 357 | 486 | 321 | 492 | D13 (12.7 mm) | 1.27% | 0.79% | |
| Case-2 | 27.6 | 351 | 483 | 332 | 500 | D10 (9.53 mm) | 1.25% | 0.79% | |
| 1 mm | 2 mm | 4 mm | 3.47 Mpa | 1.38 Mpa |
| 1 mm | 1 mm | 3 mm | 3.47 Mpa | 1.38 Mpa |
| Case-1 (PULL-OUT) | Case-2 (SPLITTING) | |||||
|---|---|---|---|---|---|---|
| EXP | ANA | ERRO | EXP | ANA | ERRO | |
| + | 119.81 kN | 109.30 kN | 8.77% | 82.20 kN | 83.09 kN | 1.08% |
| − | −124.21 kN | −110.36 kN | 11.16% | −81.43 kN | −78.92 kN | 3.08% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, P.; Watanabe, G.; Tita, E.E. Advanced Prediction for Cyclic Bending Behavior of RC Columns Based on the Idealization of Reinforcement of Bond Properties. Appl. Sci. 2023, 13, 6379. https://doi.org/10.3390/app13116379
Shao P, Watanabe G, Tita EE. Advanced Prediction for Cyclic Bending Behavior of RC Columns Based on the Idealization of Reinforcement of Bond Properties. Applied Sciences. 2023; 13(11):6379. https://doi.org/10.3390/app13116379
Chicago/Turabian StyleShao, Peilun, Gakuho Watanabe, and Elfrido Elias Tita. 2023. "Advanced Prediction for Cyclic Bending Behavior of RC Columns Based on the Idealization of Reinforcement of Bond Properties" Applied Sciences 13, no. 11: 6379. https://doi.org/10.3390/app13116379





