Precision and Accuracy Assessment of Cephalometric Analyses Performed by Deep Learning Artificial Intelligence with and without Human Augmentation

Abstract

The aim was to assess the precision and accuracy of cephalometric analyses performed by artificial intelligence (AI) with and without human augmentation. Four dental professionals with varying experience levels identified 31 landmarks on 30 cephalometric radiographs twice. These landmarks were re-identified by all examiners with the aid of AI. Precision and accuracy were assessed by using intraclass correlation coefficients (ICCs) and mean absolute errors (MAEs). AI revealed the highest precision, with a mean ICC of 0.97, while the dental student had the lowest (mean ICC: 0.77). The AI/human augmentation method significantly improved the precision of the orthodontist, resident, dentist, and dental student by 3.26%, 2.17%, 19.75%, and 23.38%, respectively. The orthodontist demonstrated the highest accuracy with an MAE of 1.57 mm/°. The AI/human augmentation method improved the accuracy of the orthodontist, resident, dentist, and dental student by 12.74%, 19.10%, 35.69%, and 33.96%, respectively. AI demonstrated excellent precision and good accuracy in automated cephalometric analysis. The precision and accuracy of the examiners with the aid of AI improved by 10.47% and 27.27%, respectively. The AI/human augmentation method significantly improved the precision and accuracy of less experienced dental professionals to the level of an experienced orthodontist.

1. Introduction

Since the development of cephalometric radiography by Broadbent and Hofrath in 1931 [1], a multitude of lateral cephalometric analyses have been developed for the purpose of orthodontic diagnosis and treatment planning. These analyses allow orthodontists to quantify and analyze relationships in the craniofacial region between the skeleton, dentition, and soft tissue. However, an accurate orthodontic diagnosis derived from a cephalometric radiograph requires accurate identification of key landmarks. Current methods of landmark identification include hand tracing with acetate paper or the use of computer software to manually mark digitized cephalometric radiographs, both of which have been shown to be equally reliable [2].

Regardless of the method of cephalometric tracing, manual identification of anatomical structures presents inherent challenges. Factors such as differences in training and radiograph quality can cause variations in intra-examiner and inter-examiner reliability [3]. Additionally, reliability varies depending on the landmark being identified. The landmarks condylion, gnathion, orbitale, and anterior nasal spine tended to have the lowest inter-examiner reliability among experienced dental radiologists and orthodontists [4]. Computing technology demonstrates the potential to automate this process through artificial intelligence (AI).

AI refers to the development of computer systems that can perform tasks that would typically require human intelligence. These tasks include but are not limited to: learning, reasoning, problem-solving, perception, and language understanding. AI systems often employ algorithms and models to process and interpret data, enabling them to make informed decisions or predictions. In dentistry, AI has been used in a variety of applications, such as to assist in the diagnosis of vertical root fractures, diagnosis of proximal caries and localization of root canals [5]. One area in which AI has been used in orthodontics is automatic lateral cephalometric landmark identification. Pioneered by Cohen in 1984, preliminary attempts to locate landmarks using AI were limited to easily identifiable landmarks such as sella and menton [6]. Since Cohen’s attempt to automate landmark identification, several AI methods have been developed to increase accuracy and precision. Success rates of these methods, defined as a deviation of less than 2 mm between the distance measured from the AI-marked landmark and the expert-marked landmark, have varied from 35 to 84.7% depending on the methodology [5]. Convolutional neural networks (CNNs), a type of deep-learning algorithm, have demonstrated some of the highest accuracy in automatic lateral cephalometric landmark identification [7]. The CNN You-Only-Look-Once version 3 (YOLOv3) is a frontrunner in this aspect [8,9].

More recent studies have attempted to improve upon the precision and accuracy of the YOLOv3 algorithm, albeit with limited success. Yao used a customized CNN using PyTorch software (Facebook Artificial Intelligence Research; Facebook, Menlo Park, CA, USA) and found a mean radial error of about 1 mm, averaged among 37 landmarks [10]. However, the mean radial errors varied significantly, ranging from 0.5 mm for pronasale to 2 mm for pogonion [10]. Jeon utilized a CNN using CephX software and found significant differences between AI and manual measurements for saddle angle, U1-NA (mm), and L1-NB (mm) measurements [11]. Manual adjustment of landmarks identified by AI was recommended for further improvement in accuracy [11]. A systematic review conducted to evaluate the accuracy of automatic cephalometric landmark identification concluded that most CNNs demonstrated accuracy that matched the accuracy of an experienced orthodontist for many measurements [12].

In addition to two-dimensional landmark identification, studies have been conducted to evaluate the accuracy of AI in landmark identification in three dimensions. Bao evaluated the accuracy of cephalometric landmark identification with AI on lateral cephalometric radiographs generated from 3D cone-beam computed tomography (CBCT) images. It was discovered that 15 of 23 cephalometric measurements were within the clinically acceptable range, or within 2 mm or degrees from the gold standard [13]. A meta-analysis by Serafin evaluated the accuracy of 3D landmark identification on CBCT images using only recent studies (from 2020 to 2022). As technology advanced, the mean error improved by over 2 mm over the 2-year period [14]. Despite the improvements, AI has fared better in 2D landmark identification compared to 3D, likely due to smaller sample sizes and increased computational complexity in CBCT studies [12].

Although cephalometric landmark identification with AI has improved in the last few decades, a few limitations still exist. Most studies have used far below the recommended 2300 images to train the AI in order to achieve the same level of accuracy as human examiners [15]. Additionally, few studies have used AI trained from multiple types of x-ray machines, which limits real-world clinical application of the software [16]. A study by Silva et al. addressed these limitations by training a CNN named CEFBOT (RadioMemory Ltd., Belo Horizonte, Brazil) with over 250,000 images from various x-ray sources to automatically perform Arnett’s analysis measurements [17].

AI-based fully automated decision-making processes put machines in the driver’s seat and aim to replace human decisions. However, can machines and humans work together in making better decisions? This new concept is defined as AI/human augmentation, where the goal is to improve human decision-making with machine insights and recommendations. Although previous studies show a promising future for AI-based automatic cephalometric landmark identification and analysis, machines have not yet shown the ability to outperform humans. On average, 80% of landmarks are accurately identified by AI alone within 2 mm of the ideal location [18]. The errors in the remaining 20% of landmarks can drastically affect cephalometric angular and linear measurements to the point that the results are not of diagnostic value. The ability to manually alter the location of the inaccurate landmarks could result in significantly improved accuracy levels. However, there is a lack of studies in the literature that specifically evaluate the extent to which clinicians with different levels of experience can benefit from this collaborative approach. To the best of our knowledge, this study will be the first to assess the impact of AI on the precision and accuracy of cephalometric analyses conducted by examiners with varying levels of experience. The objective of this study was to evaluate the precision and accuracy of cephalometric analyses performed using AI alone and in combination with human augmentation, and to determine whether this collaboration leads to varying levels of improvement among examiners with different levels of experience. Our hypothesis is that the least experienced clinicians would derive the greatest benefit from the AI/human augmentation in cephalometric analyses.

2. Materials and Methods

This study was reviewed and marked as IRB exempt by Indiana University Institutional Review Board (Protocol:14334) on 14 March 2022.

2.1. Sample Size Justification

Prior to the start of the study, a power analysis was conducted to determine the sample size. With a sample size of 30 images, the width of the 95% confidence interval for the intraclass correlation coefficients (ICCs) ranged from 0.08 and 0.28 from the estimated ICC, assuming the ICC is between 0.8 and 0.95. In addition, the width of the 95% confidence interval for the percentage of measurements within 1.5 mm of the ideal ranged between 20% and 30% from the estimated percentage, assuming the percentage is between 75% and 95%.

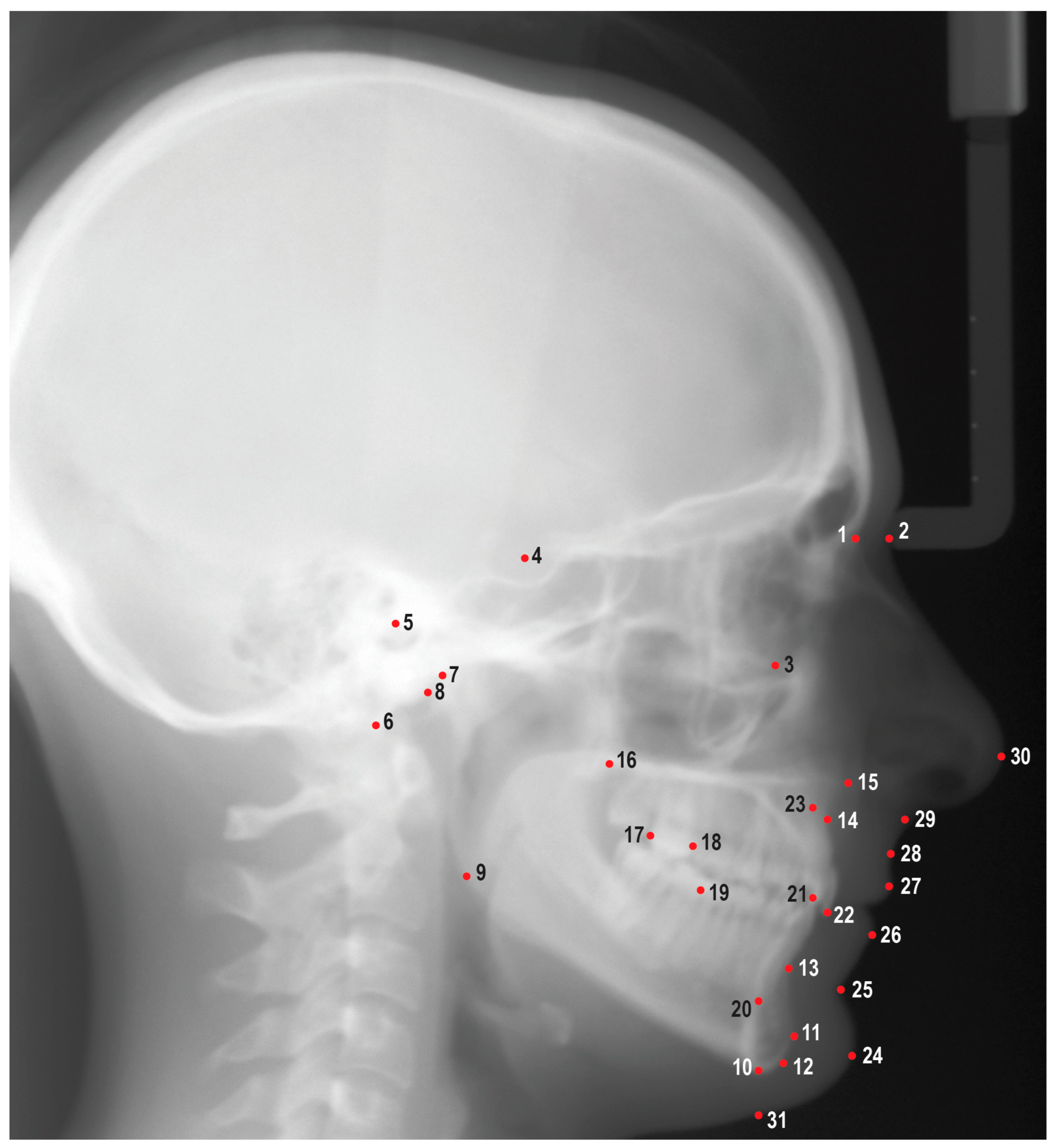
2.2. Data Collection

Thirty lateral cephalograms were randomly selected from a pool of adult (age 18 or older) orthodontic patients treated in the Indiana University School of Dentistry (IUSD). Inclusion criteria included patients with a class I skeletal relationship (defined as ANB between 0.5 to 5.0°) and an angle class I dental relationship. Patients were excluded if they had craniofacial anomalies, missing or unerupted permanent incisors, missing or unerupted permanent molars, or poor quality initial cephalometric radiographs. The cephalometric radiographs were saved as JPEG files at a resolution of 200 dpi.

A calibration session led by an orthodontist with 25 years of experience was conducted to clarify the cephalometric landmark identification process and to define each of the landmarks. Four examiners, including an orthodontist with two years of experience, a second-year orthodontics resident, a fourth-year dental student, and a general dentist with one year of experience, each separately and manually identified 31 cephalometric landmarks on the 30 radiographs (Figure 1). The same examiners retraced all radiographs after a period of one week in a randomized order. After completion of the manual tracings, the examiners traced the same cephalometric radiographs with the aid of a deep-learning AI (AI/human augmentation method). For these tracings, AI first located all of the landmarks, and the examiners later adjusted points as needed. The AI/human augmentation method tracings were completed again after one week in a randomized order. Additionally, AI alone identified each of the landmarks without any adjustments and repeated the process one week later.

The gold standard for landmark positions was identified with the collaboration of an orthodontist and dental radiologist, each with 25 years of experience within their respective fields. Any disagreements resulted in the point being located at the midpoint both vertically and horizontally between the two points.

2.3. Software

RadioCef software v.3 (RadioMemory Ltd., Belo Horizonte, Brazil) with CEFBOT module was used for automated cephalometric landmark identification. This software uses four subsystems to locate cephalometric landmarks. Subsystem 1 is a convolutional neural network (CNN) that processes radiographs into probability maps of cephalometric landmark positions. Subsystem 2 is another CNN that partitions radiographs by vectorizing skeletal and soft tissue borders and estimates the positions of cranial landmarks. Subsystem 3 combines the two CNN subsystems to estimate the position of landmarks, whereas subsystem 4 acts as a quality check to validate the previous results [17]. The CEFBOT was trained with substantial cephalometric data comprising over 250,000 cephalometric images from multiple X-ray sources and providers [17].

2.4. Data Analyses

Using the traced landmarks, 26 cephalometric measurements were measured for each of the traced radiographs (Supplementary Table S1). Precision was evaluated by comparing the initial tracing to the final tracing completed after a period of one week for each of the examiners, with and without the aid of AI. The accuracy of each of these measurements was evaluated by comparing each examiner’s values, with and without the aid of AI, to the gold standard values through mean absolute error (MAE). MAEs were expressed as millimeters or degrees depending on whether it was a linear or angular measurement.

2.5. Statistical Analyses

For both precision and accuracy analyses, MAEs with 95% confidence intervals were provided for differences between the gold standard and each measurement. For precision analysis, ICCs and Bland–Altman plots were used to measure the agreement between initial and final measurements. One-way analysis of variance (ANOVA) with a random effect was used to test for the differences between the 9 examiner groups. All the analyses were done using SAS 9.4 (Cary, NC, USA) software.

3. Results

3.1. Precision Analysis

Table 1. Precision of the examiners with and without the aid of AI given by the intraclass correlation coefficients (ICCs).

Measurements	Orthodontist	Orthodontist AI	Resident	Resident AI	Dentist	Dentist AI	Student	Student AI	AI	Mean without AI	Mean with AI
SNA (°)	0.92	0.93	0.91	0.93	0.71	0.98	0.39	0.94	0.97	0.73	0.95
SN-Palatal Plane (°)	0.93	0.93	0.89	0.98	0.62	0.96	0.74	0.96	0.92	0.80	0.96
SNB (°)	0.96	0.94	0.92	0.98	0.77	0.98	0.92	0.96	0.99	0.89	0.97
FMA (°)	0.95	0.93	0.94	0.98	0.88	0.97	0.88	0.98	0.99	0.91	0.97
SN-MP (°)	0.99	0.95	0.95	0.99	0.88	0.98	0.95	0.99	1.00	0.94	0.98
Y-Axis (°)	0.97	0.96	0.92	0.98	0.79	0.98	0.93	0.97	0.99	0.90	0.97
ANB (°)	0.81	0.91	0.84	0.73	0.60	1.00	0.13	0.89	0.91	0.60	0.88
ANS-PNS (mm)	0.78	0.92	0.86	0.91	0.58	0.98	0.65	0.93	0.99	0.72	0.94
Co-Gn (mm)	0.95	0.96	0.96	0.99	0.82	0.98	0.88	0.97	1.00	0.90	0.98
Ba-S-N (°)	0.97	0.96	0.94	0.98	0.87	0.94	0.87	0.96	1.00	0.91	0.96
U1-SN (°)	0.95	0.96	0.93	0.95	0.91	0.93	0.90	0.95	0.98	0.92	0.95
U1-NA (°)	0.93	0.96	0.96	0.94	0.92	0.93	0.90	0.95	0.97	0.93	0.95
U1-NA (mm)	0.88	0.92	0.90	0.81	0.71	0.96	0.22	0.91	0.91	0.68	0.90
L1-MP (°)	0.94	0.96	0.95	0.96	0.96	0.98	0.90	0.93	0.99	0.94	0.96
L1-NB (°)	0.92	0.98	0.94	0.94	0.93	0.97	0.84	0.88	0.99	0.91	0.94
L1-NB (mm)	0.94	0.96	0.96	0.98	0.94	1.00	0.92	0.97	0.99	0.94	0.98
Interincisal Angle (°)	0.96	0.98	0.96	0.96	0.96	0.96	0.90	0.94	0.99	0.95	0.96
Upper Lip to E-Plane (mm)	0.99	0.99	0.99	0.99	0.99	0.98	0.96	0.98	1.00	0.98	0.99
Lower Lip to E-Plane (mm)	1.00	0.99	0.99	0.99	0.99	0.99	0.97	0.99	1.00	0.99	0.99
N′-Sn′ (mm)	0.75	0.93	0.85	0.97	0.67	0.98	0.85	0.97	0.99	0.78	0.96
Sn′-Me′ (mm)	0.95	0.97	0.97	0.96	0.95	0.82	0.85	0.94	1.00	0.93	0.92
N-ANS (mm)	0.94	0.92	0.75	0.98	0.56	0.99	0.81	0.94	0.89	0.77	0.96
ANS-Me (mm)	0.98	0.99	0.99	0.99	0.99	1.00	0.98	0.99	0.98	0.99	0.99
Ar-Go (mm)	0.96	0.92	0.93	0.99	0.81	0.97	0.91	0.99	0.98	0.90	0.97
NA-Apo (°)	0.83	0.87	0.84	0.70	0.59	1.00	0.13	0.90	0.91	0.60	0.87
FH-Npo (°)	0.81	0.95	0.88	0.95	0.71	0.94	0.65	0.94	0.96	0.76	0.95
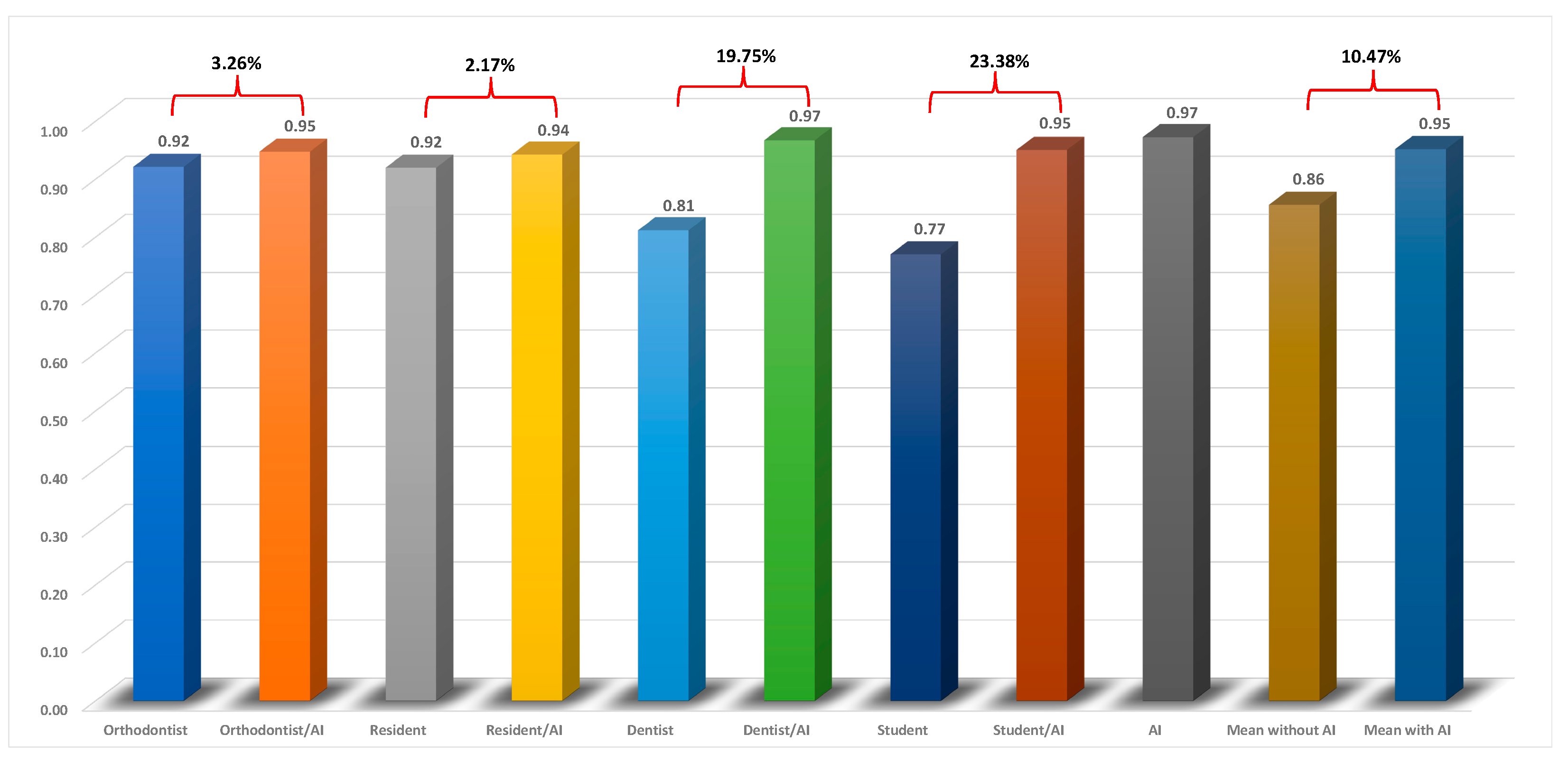
Mean	0.92	0.95	0.92	0.94	0.81	0.97	0.77	0.95	0.97	0.86	0.95

shows the ICCs of the cephalometric measurements for each group. Mean ICC values were also calculated for all groups of examiners by averaging the individual cephalometric measurement ICC values. According to the results, AI showed excellent precision (ICCs > 0.90). The precision of the examiners without the aid of AI generally followed their level of experience and exposure to the cephalometric analyses. The orthodontist, resident, dentist, and dental student had a mean ICC of 0.92, 0.92, 0.81, and 0.77, respectively. With the aid of AI, the precision of the orthodontist, resident, dentist, and dental student improved by 3.26%, 2.17%, 19.75%, and 23.38%, respectively (Figure 2). Overall, the precision of the examiners improved by 10.47% with the aid of AI. As we expected, the least experienced clinicians benefitted the most from the help of AI.

Without the aid of AI, the cephalometric measurements that yielded moderate precision were maxillary length, U1-NA (mm), SNA, ANB, and convexity angles. With the AI/human augmentation method, 23 out of 26 measurements showed excellent precision, while U1-NA (mm), ANB, and convexity angles improved to good precision (Table 1).

Table 2. The results of the one-way ANOVA analysis with a random effect used to test for the differences in precision between the methods.

Measurements	F-Value	p-Value	Pairwise Comparison
SNA (°)	1.31	0.24
SN-Palatal Plane (°)	1.97	0.05
SNB (°)	3.98	<0.01	1 < 5, 2 < 5, 3 < 5, 4 < 5, 7 < 5, 8 < 5, 5 > 6, 5 > 9
FMA (°)	9.18	<0.01	1 > 7, 2 > 7, 3 > 7, 4 > 7, 7 < 8, 7 < 5, 7 < 6, 7 < 9
SN-MP (°)	5.51	<0.01	1 > 3, 1 > 5, 2 < 5, 3 < 4, 3 < 8, 3 > 5, 3 < 6, 3 < 9, 4 > 5, 7 > 5, 8 > 5, 5 < 6, 5 < 9
Y-Axis (°)	6.83	<0.01	1 > 5, 2 > 5, 3 > 5, 4 > 5, 7 > 5, 8 > 5, 5 < 6, 5 < 9
ANB (°)	2348.9	<0.01	1 < 8, 2 < 7, 2 < 8, 3 < 8, 4 < 8, 7 < 8, 8 > 5, 8 > 6, 8 > 9
ANS-PNS (mm)	2.71	0.01	1 < 2, 2 > 3, 2 > 7, 2 > 8, 2 > 5, 3 > 7, 4 > 7, 7 < 5, 7 < 6, 7 < 9
Co-Gn (mm)	2.4	0.02	1 < 2, 1 < 5, 2 > 7, 3 < 5, 4 < 5, 7 < 5, 5 > 6, 5 > 9
Ba-S-N (°)	3.04	<0.01	1 > 5, 2 > 5, 3 < 7, 4 > 5, 7 > 5, 8 > 5, 5 < 6, 5 < 9
U1-SN (°)	1.25	0.27
U1-NA (°)	1.59	0.13
U1-NA (mm)	0.9	0.52
L1-MP (°)	2.12	0.03	1 < 3, 1 < 7, 3 > 4, 3 > 5, 4 < 7, 7 > 5, 5 < 6, 5 < 9
L1-NB (°)	0.65	0.74
L1-NB (mm)	1.14	0.34
Interincisal Angle (°)	0.42	0.9101
Upper Lip to E-Plane (mm)	1.05	0.4
Lower Lip to E-Plane (mm)	1.68	0.1
N′-Sn′ (mm)	7.27	<0.01	1 < 2, 1 < 3, 1 < 4, 1 < 7, 1 < 8, 1 > 5, 1 < 6, 1 < 9, 2 > 5, 3 > 5, 4 > 5, 7 > 5, 8 > 5, 5 < 6, 5 < 9
Sn′-Me′ (mm)	0.89	0.53
N-ANS (mm)	6.21	<0.01	1 > 5, 2 > 5, 3 > 5, 4 > 5, 7 > 5, 8 > 5, 5 < 6, 5 < 9
ANS-Me (mm)	3.87	0.0003	1 > 3, 1 > 7, 1 > 5, 1 > 9, 2 > 3, 2 > 7, 2 > 5, 2 > 9, 3 < 4, 3 < 8, 4 > 7, 4 > 5, 4 > 9, 7 < 8, 7 < 6
Ar-Go (mm)	1.18	0.31
NA-Apo (°)	1.3	0.24
FH-Npo (°)	1.98	0.05	2 < 7, 3 < 7, 4 < 7, 7 > 6, 7 > 9, 5 > 6

1: Orthodontist, 2: orthodontist/AI, 3: resident, 4: resident/AI, 5: dentist, 6: dentist/AI, 7: student, 8: student/AI, 9: AI.

shows the results of the one-way ANOVA analysis, with a random effect used to test for the differences in precision between the methods. A statistically significant difference was found in 13 out of 26 measurements (p < 0.05). In general, the dentist and student, both without the aid of AI, had more significant differences in precision compared to the rest of the examiner groups.

3.2. Accuracy Analysis

To compare each examiner’s overall accuracy with and without AI’s aid, an average of the MAEs was calculated for each group (

Table 3. Accuracy of the examiners with and without the aid of AI given by the mean absolute errors (MAEs) from the gold standard.

Measurements	Orthodontist	Orthodontist AI	Resident	Resident AI	Dentist	Dentist AI	Student	Student AI	AI	Mean without AI	Mean with AI
SNA (°)	1.67	1.20	1.69	1.66	3.24	1.61	3.57	1.77	1.86	2.54	1.56
SN-Palatal Plane (°)	1.50	1.18	1.66	1.10	2.87	1.51	1.76	1.47	1.58	1.95	1.32
SNB (°)	1.17	0.86	1.38	1.22	2.93	1.31	1.42	1.24	1.49	1.73	1.16
FMA (°)	1.41	1.65	3.00	2.91	1.81	1.52	3.05	2.21	3.18	2.32	2.07
SN-MP (°)	1.20	1.36	1.44	2.51	2.98	1.33	2.00	1.62	2.99	1.91	1.71
Y-Axis (°)	0.83	0.77	1.26	0.92	3.29	1.12	1.36	0.94	1.09	1.69	0.94
ANB (°)	0.97	0.71	1.07	0.66	1.21	0.78	2.90	0.91	0.70	1.54	0.77
ANS-PNS (mm)	2.21	1.78	3.44	2.36	3.35	1.88	2.56	1.58	2.06	2.89	1.90
Co-Gn (mm)	2.49	1.66	1.68	1.30	2.99	1.38	2.44	1.48	1.37	2.40	1.46
Ba-S-N (°)	3.03	2.76	3.36	2.38	5.74	3.39	3.89	3.17	1.99	4.01	2.93
U1-SN (°)	2.19	1.84	3.25	1.94	5.78	2.99	4.69	3.48	2.39	3.98	2.56
U1-NA (°)	2.62	1.75	3.24	2.42	4.24	3.17	5.36	3.28	2.52	3.87	2.66
U1-NA (mm)	1.05	0.84	1.35	0.85	1.53	1.04	3.78	1.04	0.80	1.93	0.94
L1-MP (°)	1.96	2.19	2.88	2.60	2.38	2.04	3.18	2.61	3.08	2.60	2.36
L1-NB (°)	1.87	1.86	2.70	1.98	2.28	2.21	4.37	2.56	2.16	2.81	2.15
L1-NB (mm)	0.55	0.46	0.56	0.49	0.52	0.56	0.84	0.58	0.58	0.62	0.52
Interincisal Angle (°)	2.60	1.96	4.16	2.86	4.21	3.82	7.12	4.47	2.73	4.52	3.28
Upper Lip to E-Plane (mm)	0.33	0.40	0.43	0.35	0.37	0.34	0.30	0.57	0.85	0.36	0.42
Lower Lip to E-Plane (mm)	0.47	0.47	0.44	0.39	0.45	0.47	0.38	0.49	0.83	0.44	0.46
N′-Sn′ (mm)	1.92	1.38	1.48	1.38	2.33	1.75	1.39	1.44	2.60	1.78	1.49
Sn′-Me′ (mm)	1.72	1.74	1.81	1.59	1.15	1.64	1.84	1.63	1.81	1.63	1.65
N-ANS (mm)	0.94	1.21	1.73	1.08	2.80	1.45	1.11	1.10	1.49	1.65	1.21
ANS-Me (mm)	1.16	1.32	1.38	1.07	1.60	1.13	1.25	0.82	1.49	1.35	1.09
Ar-Go (mm)	1.76	1.63	1.91	3.10	1.97	1.65	2.77	2.60	3.11	2.10	2.25
NA-Apo (°)	1.63	1.31	1.82	1.17	2.45	1.38	4.27	1.42	1.26	2.54	1.32
FH-Npo (°)	1.60	1.31	2.51	1.60	1.83	1.20	2.20	1.47	1.66	2.04	1.40
Mean	1.57	1.37	1.99	1.61	2.55	1.64	2.68	1.77	1.83	2.20	1.60

). The average MAE of CEFBOT was 1.83 (in mm/°), which was within the clinically acceptable range (MAEs < 2 mm/°). The examiners’ accuracy without AI generally followed their level of experience and exposure to the cephalometric analyses. The orthodontist and resident both had MAEs within the clinically acceptable range (1.57 and 1.99 mm/°, respectively) while the accuracy of the dentist and dental student were out of the range, with MAEs of 2.55 and 2.68 mm/°, respectively. With the aid of AI, the accuracy of the orthodontist, resident, dentist, and dental student improved by 12.74%, 19.10%, 35.69%, and 33.96%, respectively (Figure 3). The AI/human augmentation method revealed clinically acceptable accuracies for all of the examiner groups. Although the examiners’ accuracy improved by 27.27% with the aid of AI, the least experienced clinicians benefitted the most from the AI/human augmentation method of cephalometric landmark identification.

Without the aid of AI, 13 out of 26 cephalometric measurements (maxillary and mandibular lengths, posterior face height, SNA, FMA, cranial base, U1-SN, L1-MP, L1-NB, interincisal, convexity, and facial angles) yielded MAEs out of the clinically acceptable range (Table 3). With the AI/human augmentation method, five of these measurements (SNA, maxillary and mandibular lengths, convexity, and facial angles) improved to be in the clinically acceptable range, while others remained out of the range although they showed some improvement in their accuracies (Table 3).

Table 4. The results of the one-way ANOVA analysis with a random effect used to test for the differences in accuracies between the methods.

Measurements	F-Value	p-Value	Pairwise Comparison
SNA (°)	4.4	<0.0001	1 < 7, 1 < 5, 2 < 7, 2 < 5, 3 < 5, 4 < 7, 4 < 5, 7 > 6, 7 > 9, 8 < 5, 8 > 9, 5 > 6, 5 > 9
SN-Palatal Plane (°)	6.82	<0.0001	1 > 5, 2 > 5, 3 < 4, 3 > 5, 4 > 7, 4 > 8, 4 > 5, 4 > 6, 7 > 5, 7 < 9, 8 > 5, 8 < 9, 5 < 6, 5 < 9, 6 < 9
SNB (°)	22.21	<0.0001	1 < 3, 1 < 7, 1 < 5, 1 > 9, 2 < 3, 2 < 7, 2 < 5, 2 > 9, 3 > 4, 3 < 5, 3 > 6, 3 > 9, 4 < 7, 4 < 8, 4 < 5, 7 < 5, 7 > 6, 7 > 9, 8 < 5, 8 > 6, 8 > 9, 5 > 6, 5 > 9, 6 > 9
FMA (°)	11.92	<0.0001	1 < 3, 1 < 4, 1 > 7, 1 < 9, 2 < 3, 2 < 4, 2 > 7, 2 < 8, 2 < 9, 3 > 7, 3 > 5, 3 > 6, 4 > 7, 4 > 5, 4 > 6, 7 < 8, 7 < 5, 7 < 6, 7 < 9, 8 > 5, 5 < 9, 6 < 9
SN-MP (°)	27	<0.0001	1 < 4, 1 < 8, 1 > 5, 1 < 9, 2 < 4, 2 < 8, 2 > 5, 2 < 9, 3 < 4, 3 < 8, 3 > 5, 3 < 9, 4 > 7, 4 > 8, 4 > 5, 4 > 6, 7 > 5, 7 < 9, 8 > 5, 8 < 9, 5 < 6, 5 < 9, 6 < 9
Y-Axis (°)	23.89	<0.0001	1 > 7, 1 > 5, 1 < 9, 2 > 7, 2 > 5, 2 < 9, 3 < 4, 3 > 5, 3 < 9, 4 > 7, 4 > 8, 4 > 5, 4 > 6, 7 < 8, 7 > 5, 7 < 6, 7 < 9, 8 > 5, 8 < 9, 5 < 6, 5 < 9, 6 < 9
ANB (°)	0.4	0.9209
ANS-PNS (mm)	12.8	<0.0001	1 > 3, 1 > 4, 1 > 5, 2 > 3, 2 > 4, 2 > 5, 3 < 4, 3 < 7, 3 < 8, 3 < 6, 3 < 9, 4 < 7, 4 < 8, 4 > 5, 4 < 6, 4 < 9, 7 > 5, 8 > 5, 5 < 6, 5 < 9
Co-Gn (mm)	16.56	<0.0001	1 > 2, 1 > 3, 1 > 4, 1 > 7, 1 > 8, 1 > 6, 1 > 9, 2 > 4, 2 > 7, 2 > 8, 2 < 5, 2 > 6, 2 > 9, 3 > 7, 3 < 5, 4 > 7, 4 < 5, 7 < 5, 8 < 5, 5 > 6, 5 > 9
Ba-S-N (°)	11.69	<0.0001	1 > 5, 1 < 9, 2 > 5, 2 < 9, 3 < 4, 3 > 5, 3 < 9, 4 > 5, 4 > 6, 4 < 9, 7 > 5, 7 < 9, 8 > 5, 8 < 9, 5 < 6, 5 < 9, 6 < 9
U1-SN (°)	30.85	<0.0001	1 < 3, 1 < 7, 1 < 8, 1 < 5, 1 < 6, 1 > 9, 2 < 3, 2 < 7, 2 < 8, 2 < 5, 2 < 6, 2 > 9, 3 > 4, 3 < 7, 3 < 5, 3 > 9, 4 < 7, 4 < 8, 4 < 5, 4 < 6, 4 > 9, 7 > 8, 7 < 5, 7 > 6, 7 > 9, 8 < 5, 8 > 6, 8 > 9, 5 > 6, 5 > 9, 6 > 9
U1-NA (°)	12.01	<0.0001	1 < 7, 1 < 5, 1 > 9, 2 < 3, 2 < 7, 2 < 8, 2 < 5, 2 < 6, 3 < 7, 3 > 9, 4 < 7, 4 < 8, 4 < 5, 4 > 9, 7 > 8, 7 > 5, 7 > 6, 7 > 9, 8 > 9, 5 > 9, 6 > 9
U1-NA (mm)	0.43	0.9016
L1-MP (°)	7.38	<0.0001	1 < 7, 1 > 9, 2 < 7, 2 > 9, 3 > 4, 3 > 8, 3 > 9, 4 < 7, 4 > 9, 7 > 8, 7 > 5, 7 > 6, 7 > 9, 8 > 9, 5 > 9, 6 > 9
L1-NB (°)	1.51	0.156
L1-NB (mm)	4.83	<0.0001	1 > 5, 1 < 6, 2 > 7, 2 > 5, 3 > 5, 3 < 6, 3 < 9, 4 > 7, 4 > 5, 7 < 6, 7 < 9, 8 > 5, 8 < 6, 8 < 9, 5 < 6, 5 < 9
Interincisal Angle (°)	7.95	<0.0001	1 > 3, 1 > 7, 1 > 8, 1 > 5, 2 > 3, 2 > 7, 2 > 8, 2 > 5, 2 > 6, 3 > 7, 3 < 9, 4 > 7, 4 > 5, 4 < 9, 7 < 8, 7 < 6, 7 < 9, 7 < 9, 5 < 6, 5 < 9, 6 < 9
Upper Lip to E-Plane (mm)	6.28	<0.0001	1 > 3, 1 > 8, 1 > 9, 2 > 8, 2 > 9, 3 < 7, 3 < 5, 3 < 6, 3 > 9, 4 > 8, 4 > 9, 7 > 8, 7 > 9, 8 < 5, 8 < 6, 5 > 9, 6 > 9
Lower Lip to E-Plane (mm)	4.31	<0.0001	1 < 7, 1 < 6, 1 > 9, 2 < 6, 2 > 9, 3 > 9, 4 < 6, 4 > 9, 7 > 9, 8 < 6, 8 > 9, 5 > 9, 6 > 9
N′-Sn′ (mm)	20.29	<0.0001	1 < 2, 1 < 3, 1 < 4, 1 < 7, 1 < 8, 1 > 5, 1 < 6, 1 < 9, 2 > 5, 2 < 9, 3 > 5, 3 < 6, 3 < 9, 4 > 5, 4 < 9, 7 > 5, 7 < 6, 7 < 9, 8 > 5, 8 < 9, 5 < 6, 5 < 9, 6 < 9
Sn′-Me′ (mm)	7.62	<0.0001	1 > 5, 1 > 6, 2 > 5, 2 > 6, 2 > 9, 3 > 5, 3 > 6, 4 > 5, 4 > 6, 7 > 5, 7 > 6, 8 > 5, 8 > 6, 5 < 9, 6 < 9
N-ANS (mm)	12	<0.0001	1 > 3, 1 > 5, 2 > 3, 2 > 5, 3 < 4, 3 > 5, 3 < 6, 3 < 9, 4 > 5, 7 > 5, 7 < 9, 8 > 5, 5 < 6, 5 < 9
ANS-Me (mm)	4.76	<0.0001	1 < 8, 1 > 5, 2 < 8, 3 < 8, 4 > 5, 7 < 8, 7 > 5, 8 > 5, 8 > 9, 5 < 6, 6 > 9
Ar-Go (mm)	22.38	<0.0001	1 > 3, 1 > 4, 1 > 7, 1 > 8, 1 > 5, 1 > 6, 1 > 9, 2 > 3, 2 > 4, 2 > 7, 2 > 8, 2 > 5, 2 > 6, 2 > 9, 3 > 4, 3 > 7, 3 > 8, 3 > 9, 4 < 5, 4 < 6, 7 < 5, 7 < 6, 8 < 5, 8 < 6, 5 > 9, 6 > 9
NA-APo (°)	0.8	0.6021
FH-NPo (°)	15.05	<0.0001	1 < 3, 1 < 7, 1 > 5, 2 < 3, 2 < 4, 2 < 7, 2 > 5, 2 < 9, 3 > 4, 3 > 8, 3 > 5, 3 > 6, 3 > 9, 4 > 8, 4 > 5, 4 > 6, 7 > 8, 7 > 5, 7 > 6, 8 > 5, 5 < 6, 5 < 9, 6 < 9

1: Orthodontist, 2: orthodontist/AI, 3: resident, 4: resident/AI, 5: dentist, 6: dentist/AI, 7: student, 8: tudent/AI, 9: AI.

shows the results of the one-way ANOVA analysis with a random effect used to test for the differences in accuracies between the methods. A statistically significant difference was found in 23 out of 26 measurements (p < 0.0001). No significant differences between groups were found in the ANB, L1-NB (°), and NA-Apo measurements (p > 0.05).

4. Discussion

Accurate identification of cephalometric landmarks is crucial in orthodontic diagnosis and treatment planning. Approximately 20% of landmarks identified by AI deviate by more than 2 mm from the ideal location [18]. These landmarks are used for angular and linear cephalometric measurements. A slight deviation in the position of a single landmark can significantly alter the resulting measurement and reduce the diagnostic quality of the traced cephalometric radiograph. Manual adjustment of the misidentified landmarks has been suggested to improve accuracy and allow orthodontists to use the radiograph in a diagnostic manner [11]. Currently, there is no literature that compares the precision and accuracy of AI/human modified landmarks to AI alone. Additionally, no studies have evaluated how less experienced examiners, such as dentists and dental students, fare in cephalometric landmark identification, with or without the aid of AI. As the proportion of orthodontic cases treated by general dentists compared to orthodontists increases, it is important to evaluate the accuracy of these less experienced clinicians.

The precision of AI alone obtained in this study was similar to the levels of precision reported in other studies [9,17]. Silva and his colleagues found that the ICC of AI ranged from 0.768 to 0.997 for the 10 Arnett’s measurements. Excluding the lowest ICC measurement of Frankfort plane to true horizontal line (ICC = 0.768), the remaining ICC values were greater than 0.94, indicating excellent precision [17]. This is similar to our study, in that the ICC values of AI traced cephalometric measurements ranging from 0.890 to 1.00 across the 26 cephalometric measurements and demonstrated the greatest precision of all examiners. Furthermore, Hwang found that the YOLOv3 deep-learning software had excellent precision and marked each landmark at the exact same position compared to the human inter-examiner reliability of 0.97 mm [9]. The accuracy of AI-derived cephalometric measurements differed from Silva’s study, which found that there were no statistically significant differences in accuracy of nine of the 10 Arnett’s measurements used, and AI was unable to measure the 10th measurement [9]. In this study, 10 out of 26 AI-derived measurements revealed accuracies out of the clinically acceptable range. An interesting note was that of the four of these measurements involved the gonion landmark (posterior face height, FMA, SN-MP, and L1-MP). Posterior face height and L1-MP were significantly underestimated, whereas SN-MP and FMA were overestimated. These errors were consistent with AI software identifying gonion too superiorly relative to the gold standard, which is a likely source contributing to the mean error. This error was not limited to our study, as Hwang found that the mean error of YOLOv3 was 2.9 mm in the identification of the gonion landmark [9]. Additionally, a meta-analysis conducted by Schwendicke showed that porion, subspinale, gonion, articulare, and anterior nasal spine were the least accurate landmarks identified by AI, although it varied depending on the specific AI software being tested [18].

Of the five cephalometric measurements that demonstrated moderate precision without the aid of AI, four of them (U1-NA distance, SNA, ANB, and convexity angles) involved “Point A” landmark. This suggests “Point A” may pose significant challenges in terms of reproducibility. Possibilities for this include the proximity of this point to the maxillary incisor root, superimposition of nearby structures, blurriness of the curvature in the anterior maxilla, and proximity of the canine fossa. Subspinale, also known as Point A, has shown good reliability in the x-axis but significant variation in the y-axis [19]. Jeon also reported a significant reduction in accuracy in U1-NA (mm) compared to other measurements and theorized it may be due to superimposition of surrounding anatomy [11].

In terms of accuracy averaged among all the examiners, 13 of the 26 measurements demonstrated MAEs greater than 2 mm or degrees without the use of AI. The increased MAEs of FMA and posterior face height may be due to the difficulty of identification of the gonion landmark. Gonion is a constructed point that relies on accurate identification of other landmarks, such as articulare and menton, to create tangent lines to the inferior body of the mandible and posterior border of the ramus. Slight inaccuracies in the tangent lines can dramatically affect the location of gonion. Among the 16 landmarks evaluated by Baumrind and Frantz, gonion was found to be the least reliable landmark in both the x and y-axes in lateral cephalometric films [20]. Additionally, in the case of FMA, it is possible that the orbitale landmark was not accurately identified by all examiners. Orbitale has been shown to have significant variability in lateral cephalometric identification, especially in the y-axis [21]. Inaccuracy of the maxillary length measurement may be due to difficulty of identification of the posterior nasal spine landmark, as it is often superimposed with the third molar germ. Condylion and basion landmarks are also challenging to identify due to the superimposition of other craniofacial structures and thus may explain the higher MAEs of mandibular length and cranial base angle. Basion has shown significant variation in identification in both the x and y-coordinates [21]. The incisor angulation measurements (U1-SN, U1-NA, L1-MP, L1-NB, and interincisal angle) also demonstrated increased MAEs. This could be due to difficulty in the identification of upper and lower incisor apices. Stabrun and Danielson found that upper and lower incisor apices were not reproducibly identified in 75% of cases [22]. Misidentification of the incisor root apices results in alterations of the long axis of the upper and lower incisors, which affects the accuracy of U1-SN, U1-NA, L1-MP, L1-NB, and interincisal angles.

The AI/human augmentation method was a novel aspect of this study. This method demonstrated an increase in the precision and accuracy of all examiner groups compared to the manual landmark identification technique, especially with the less experienced student and dentist examiners. This is likely due to the inherent ability of the AI to predictably locate each landmark in a nearly identical position [9]. The less experienced examiners may not have changed the position of landmarks unless there was a significant discrepancy due to a lack of skill in tracing lateral cephalometric radiographs. Most measurements that showed clinical significance overlapped between AI alone and the AI/human augmentation method (posterior face height, FMA, L1-MP, L1-NB, and interincisal angles). This reinforces the idea that the location of difficult to locate landmarks, such as gonion and incisor apices, may not have been modified by examiners.

Overall, the results from this study show that the human/AI augmentation method demonstrates greater accuracy and precision for all examiner groups compared to manual landmark identification. Additionally, the mean accuracy of every examiner with the aid of AI was greater than the accuracy of AI alone. Therefore, this method improves the diagnostic quality of lateral cephalometric radiographs compared to manual or AI identification alone.

One limitation of this study is that a single examiner represented an entire dental professional group. Ideally, each experience level would comprise multiple examiners. Additionally, we were unable to compare the accuracy or precision of individual landmarks. Future studies with multiple examiners and evaluation of the precision and accuracy of individual landmarks are recommended. Despite significant improvements in computing technology and AI in automatic lateral cephalometric landmark identification, AI alone cannot fully replace experienced clinicians. However, AI can serve as an educational tool and aid in landmark identification through the human/AI augmentation method, especially for less experienced clinicians.

5. Conclusions

Deep learning AI demonstrated excellent precision and good accuracy in automated cephalometric analysis. Overall, the precision and accuracy of the examiners with the aid of AI improved by 10.47% and 27.27%, respectively. The AI/human augmentation method significantly improved the precision and accuracy of less experienced dental professionals and students in comparison to that of an experienced orthodontist. These groups benefited the most from the approach.