Study on Dynamic Uncertainty and Sensitivity of Gear System Considering the Influence of Machining Accuracy
Abstract
:1. Introduction
2. The Original Dynamic Model of Gear System
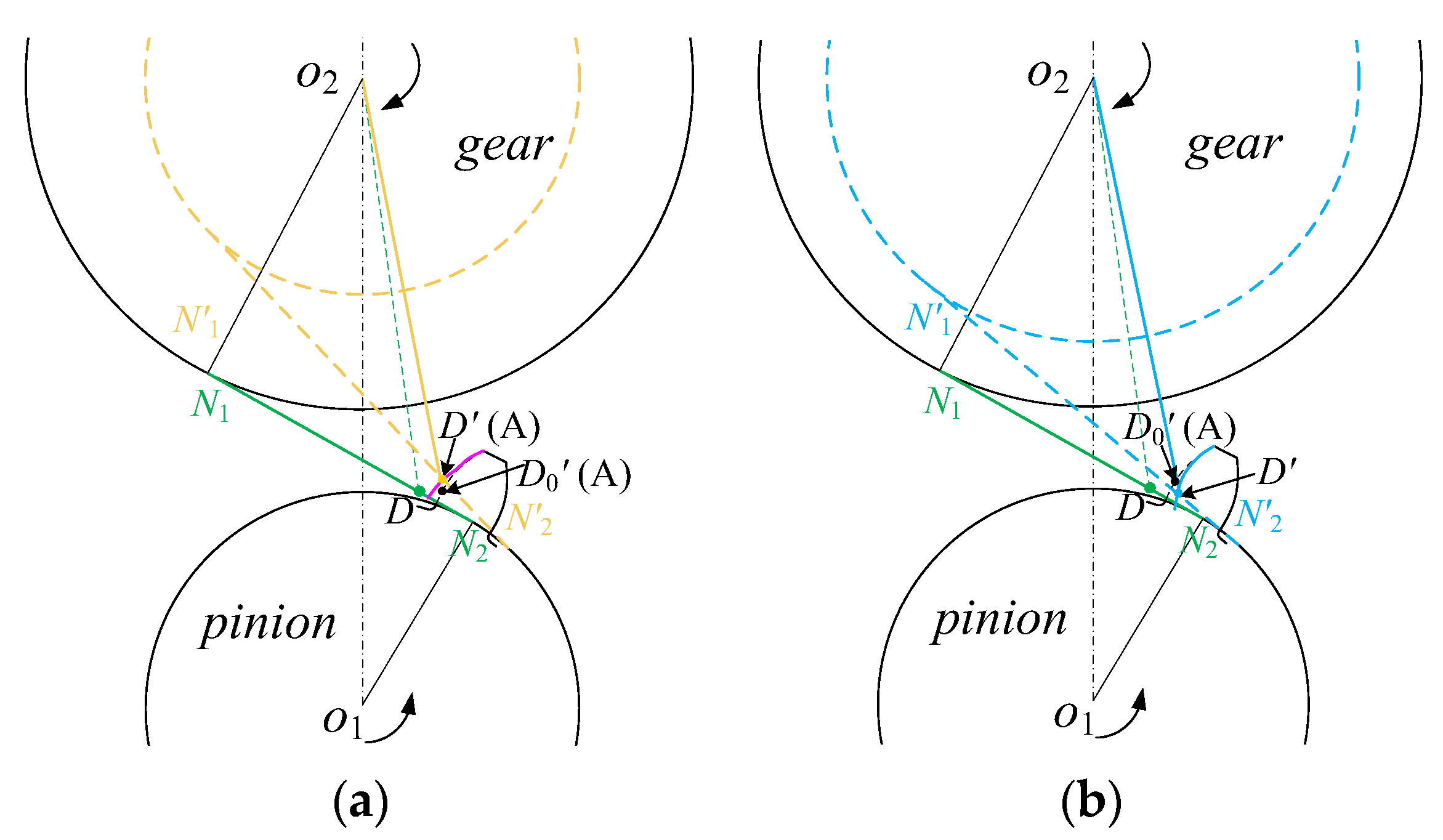
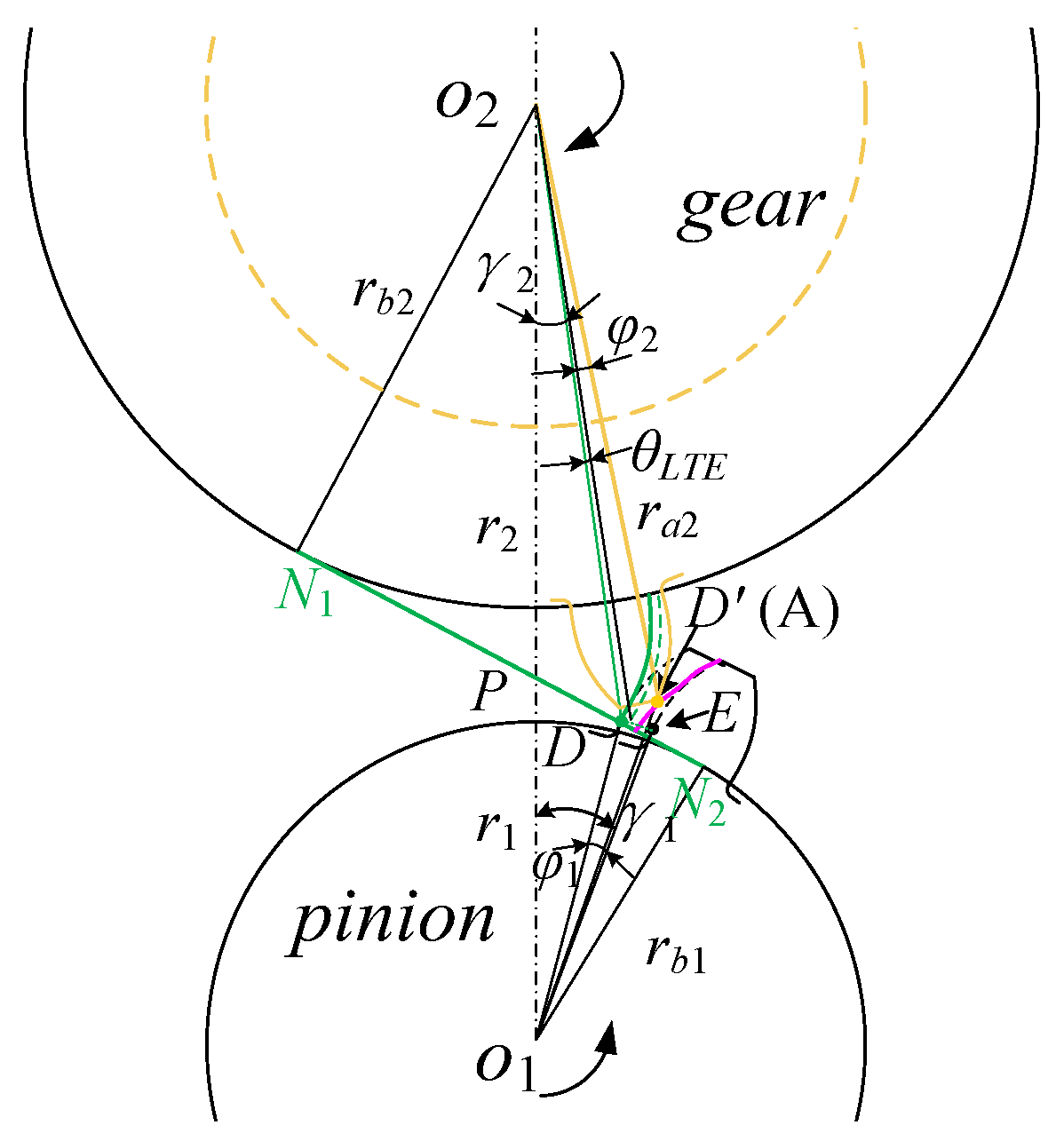
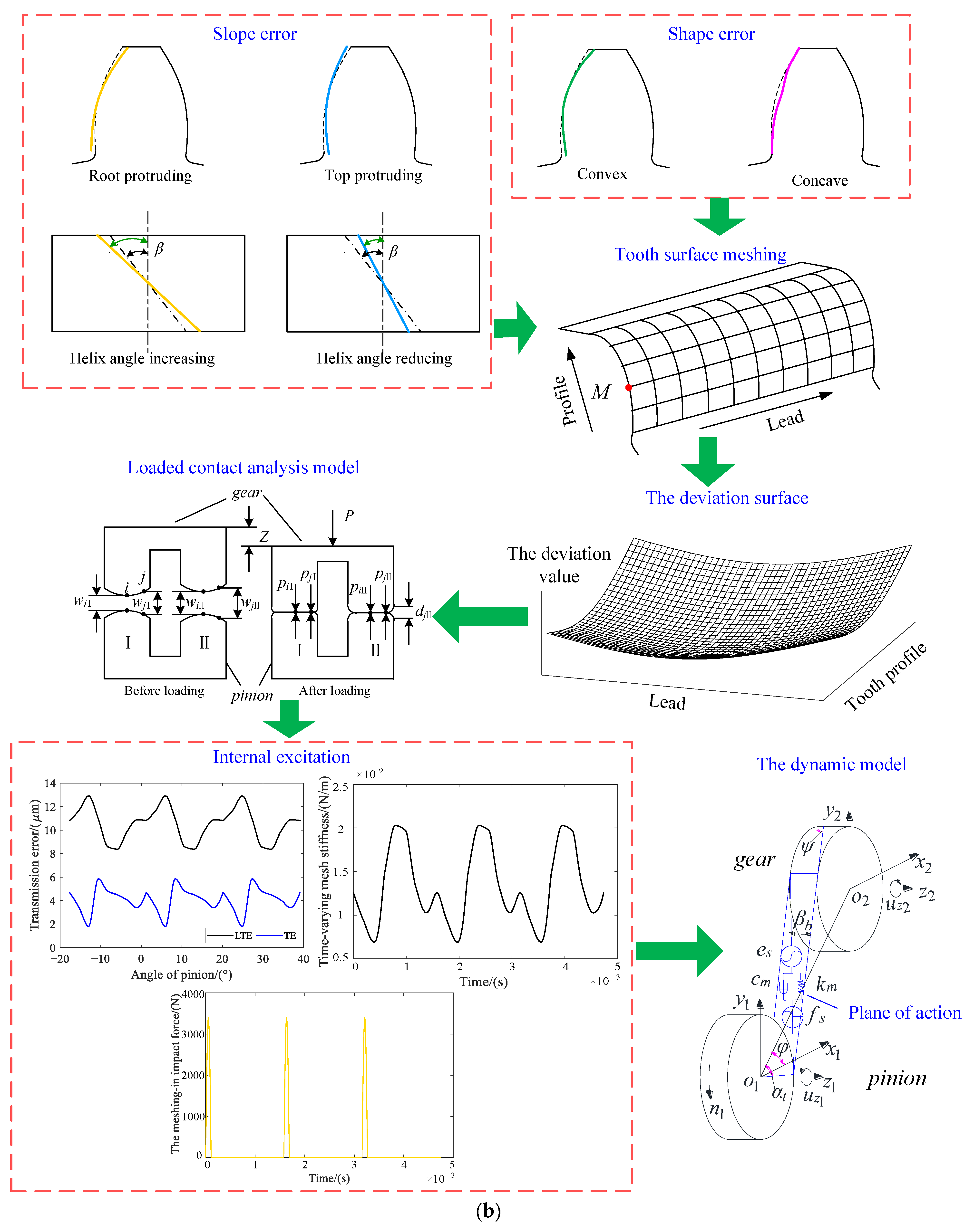
2.1. Actual Tooth Surface Contact Analysis
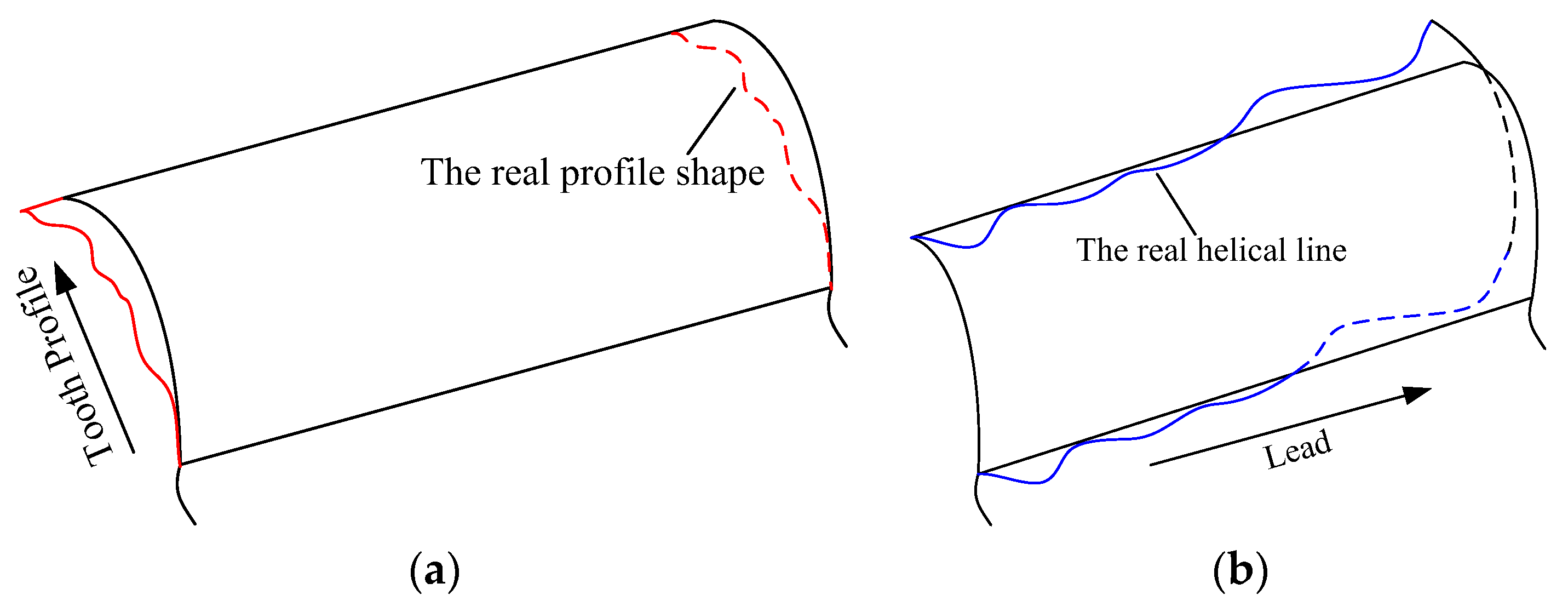
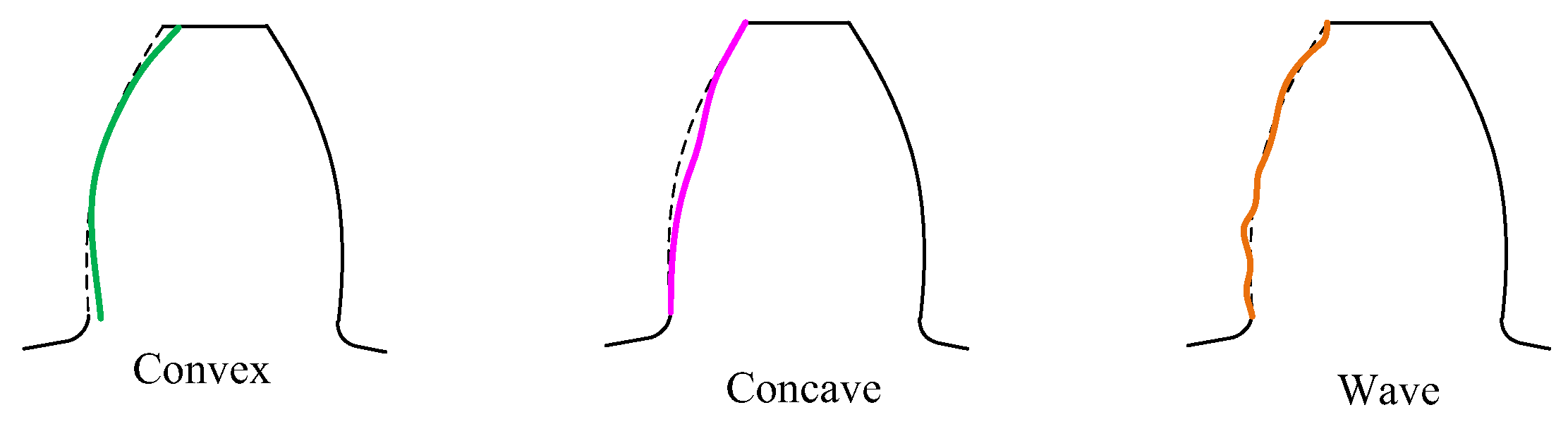
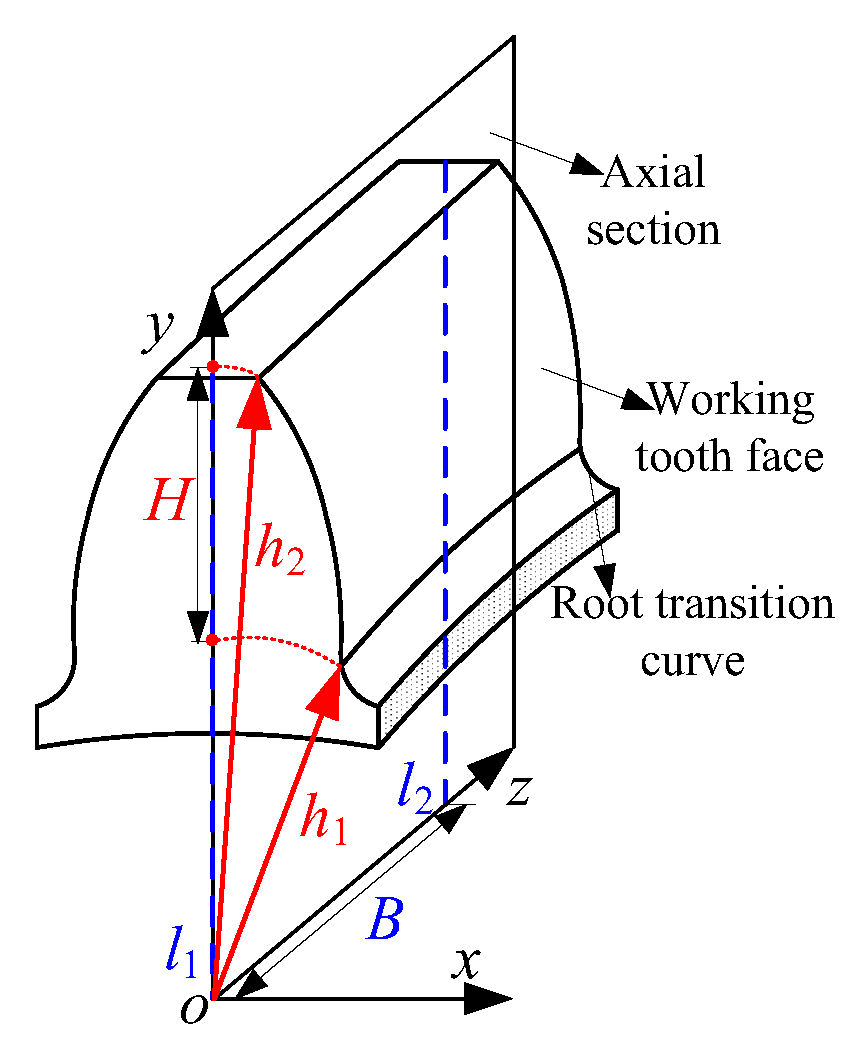
2.1.1. Mathematical Modeling of Typical Manufacturing Errors
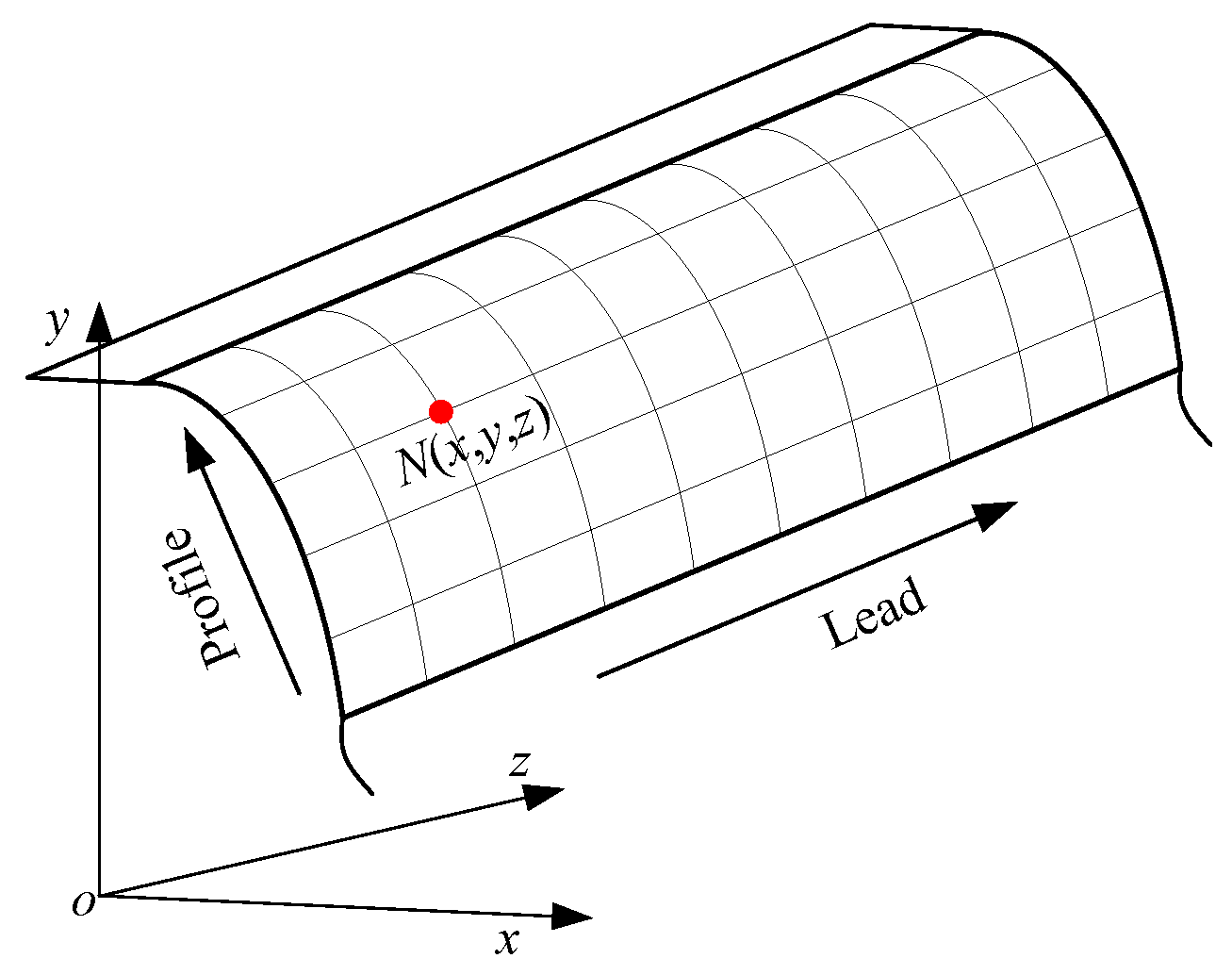
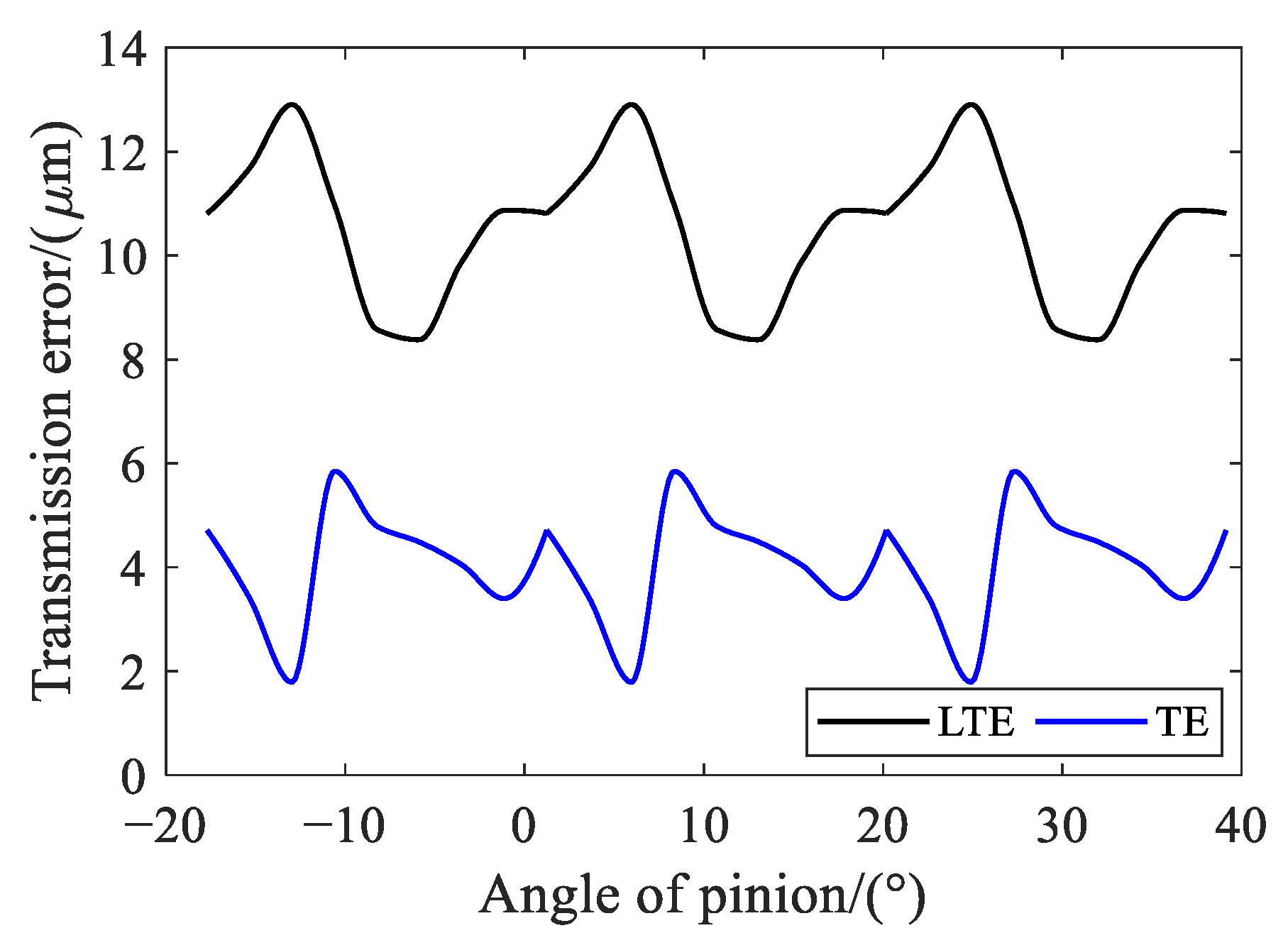
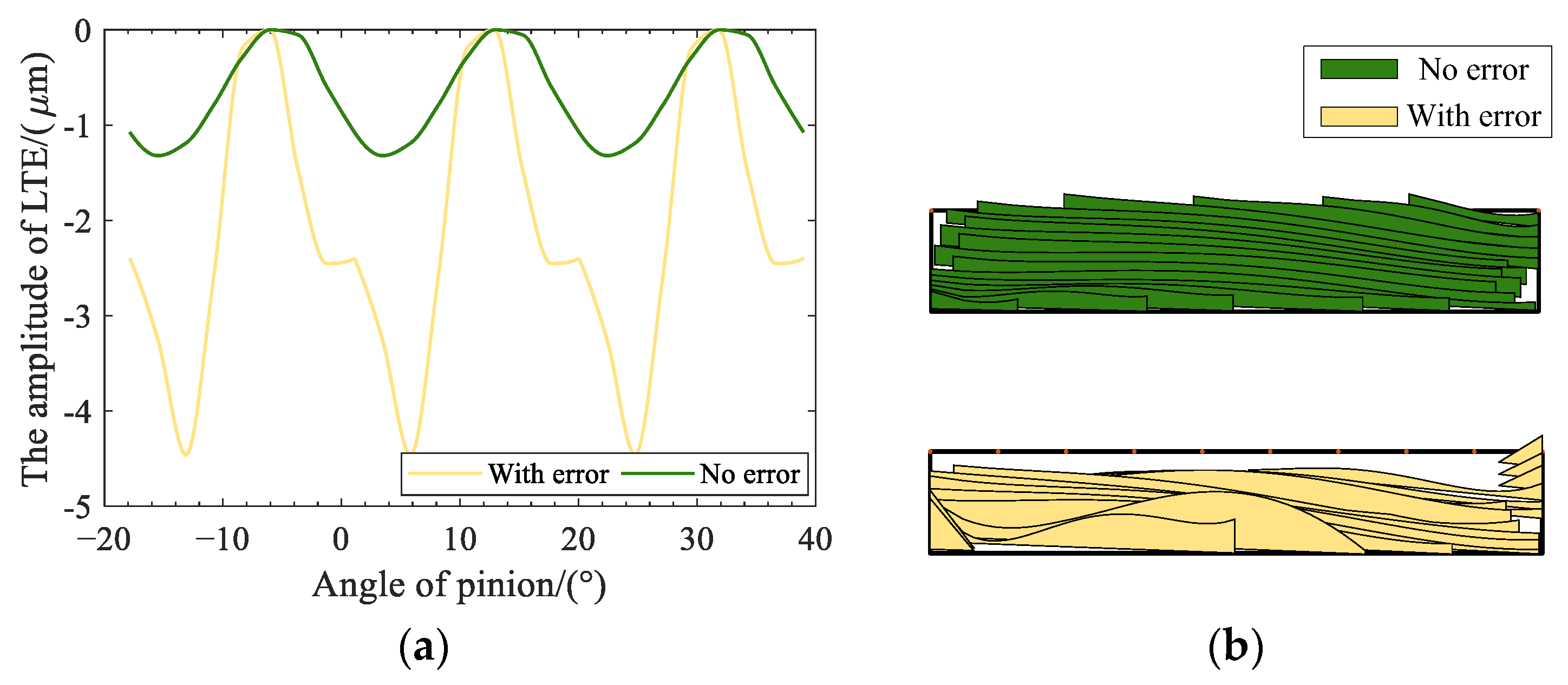
2.1.2. Meshing Performance Analysis of Actual Tooth Surface
2.2. Internal Excitation Calculation Based on Actual Meshing Performance
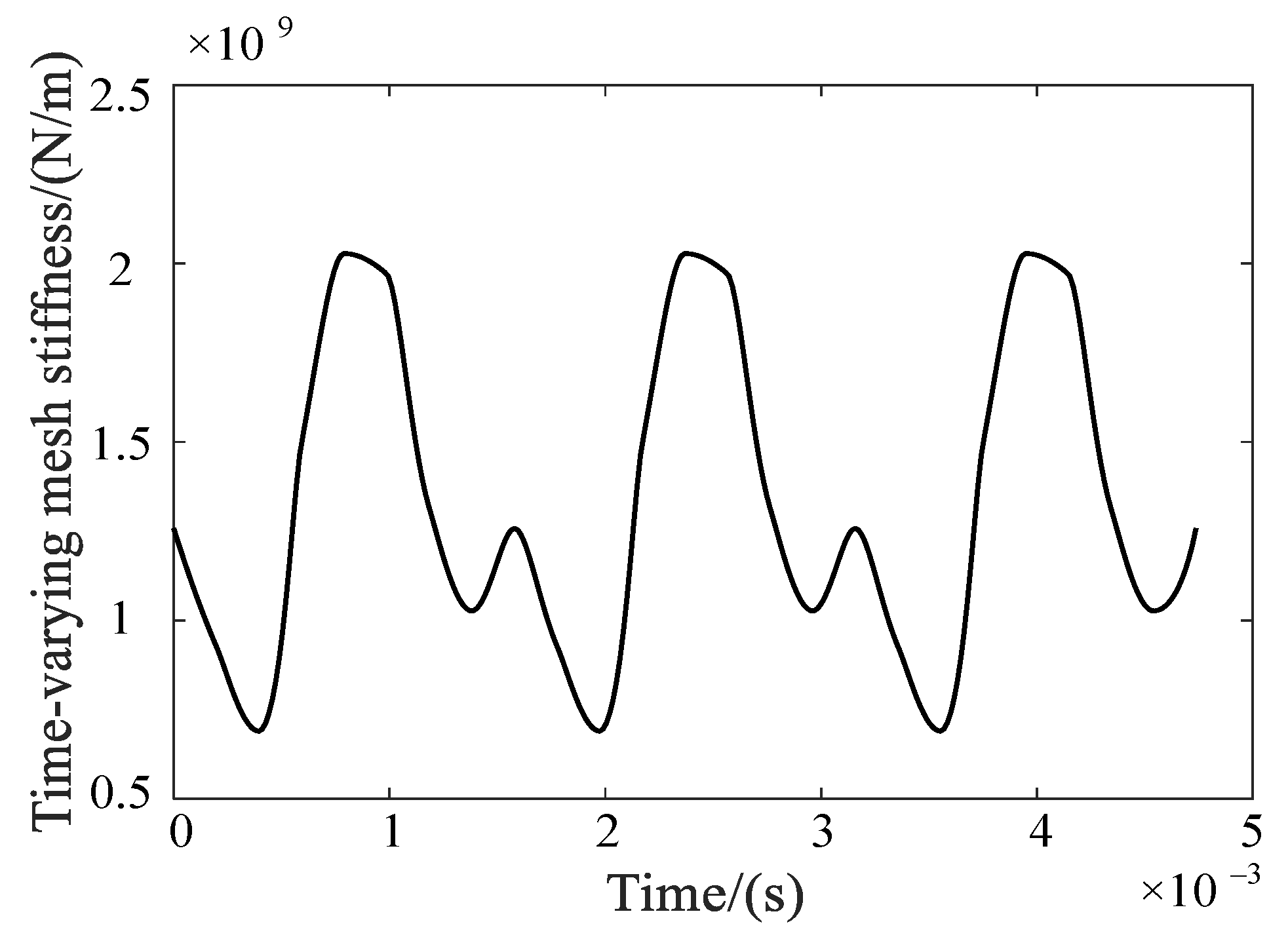
2.2.1. Determination of Time-Varying Mesh Stiffness
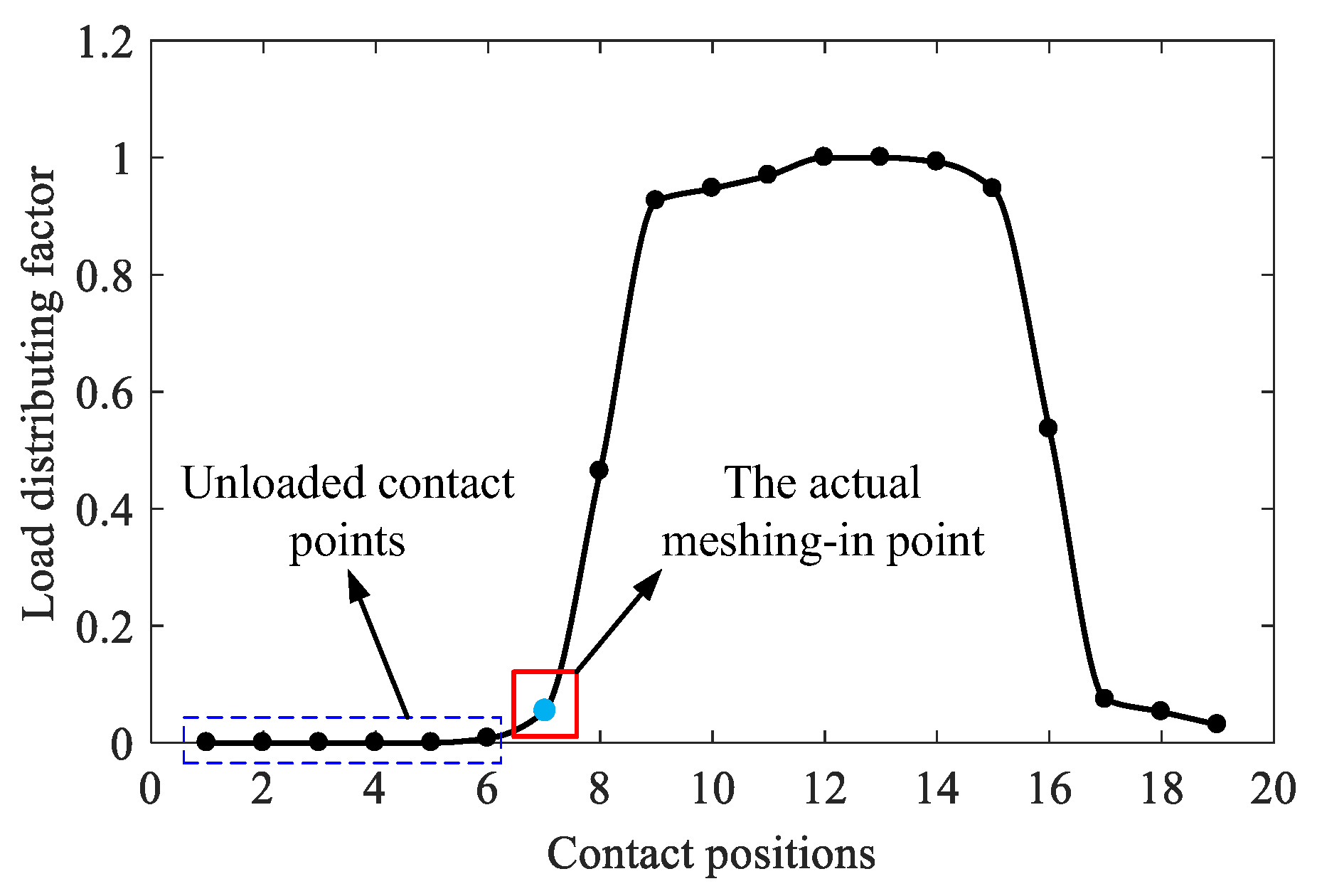
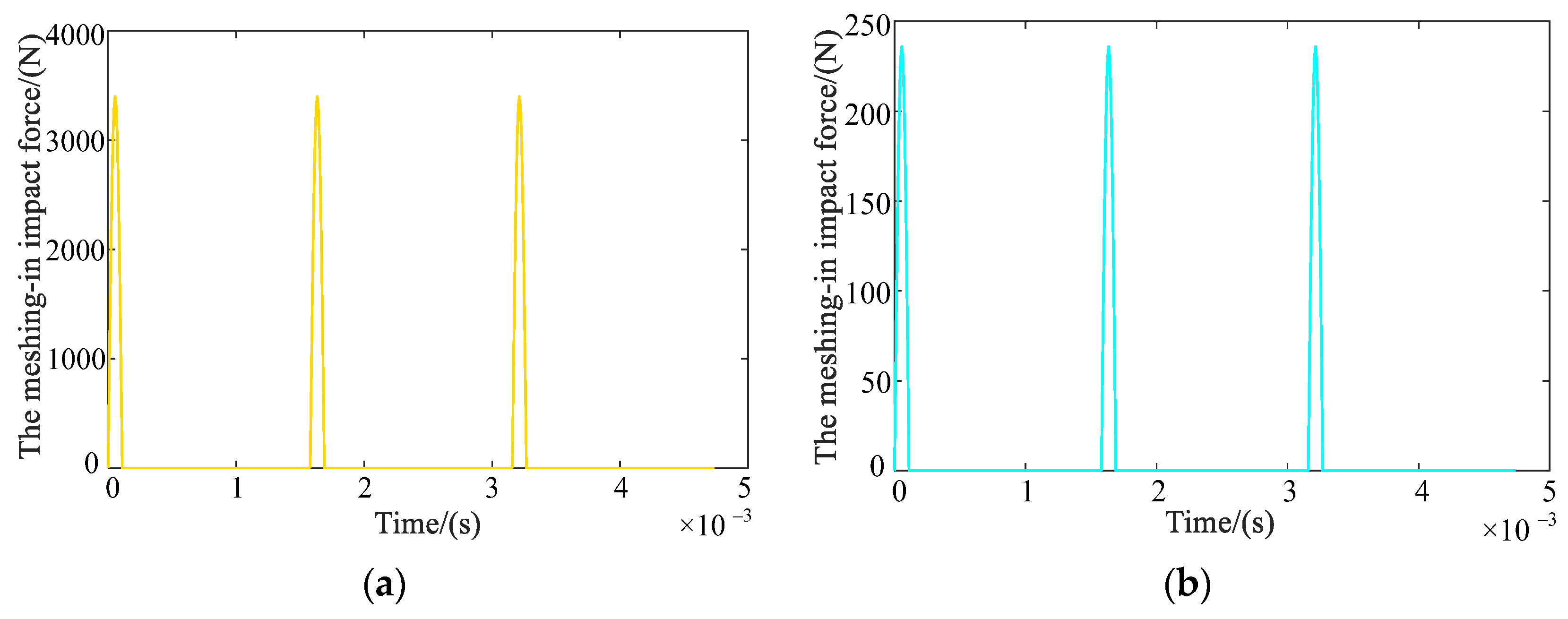
2.2.2. Meshing-In Impact
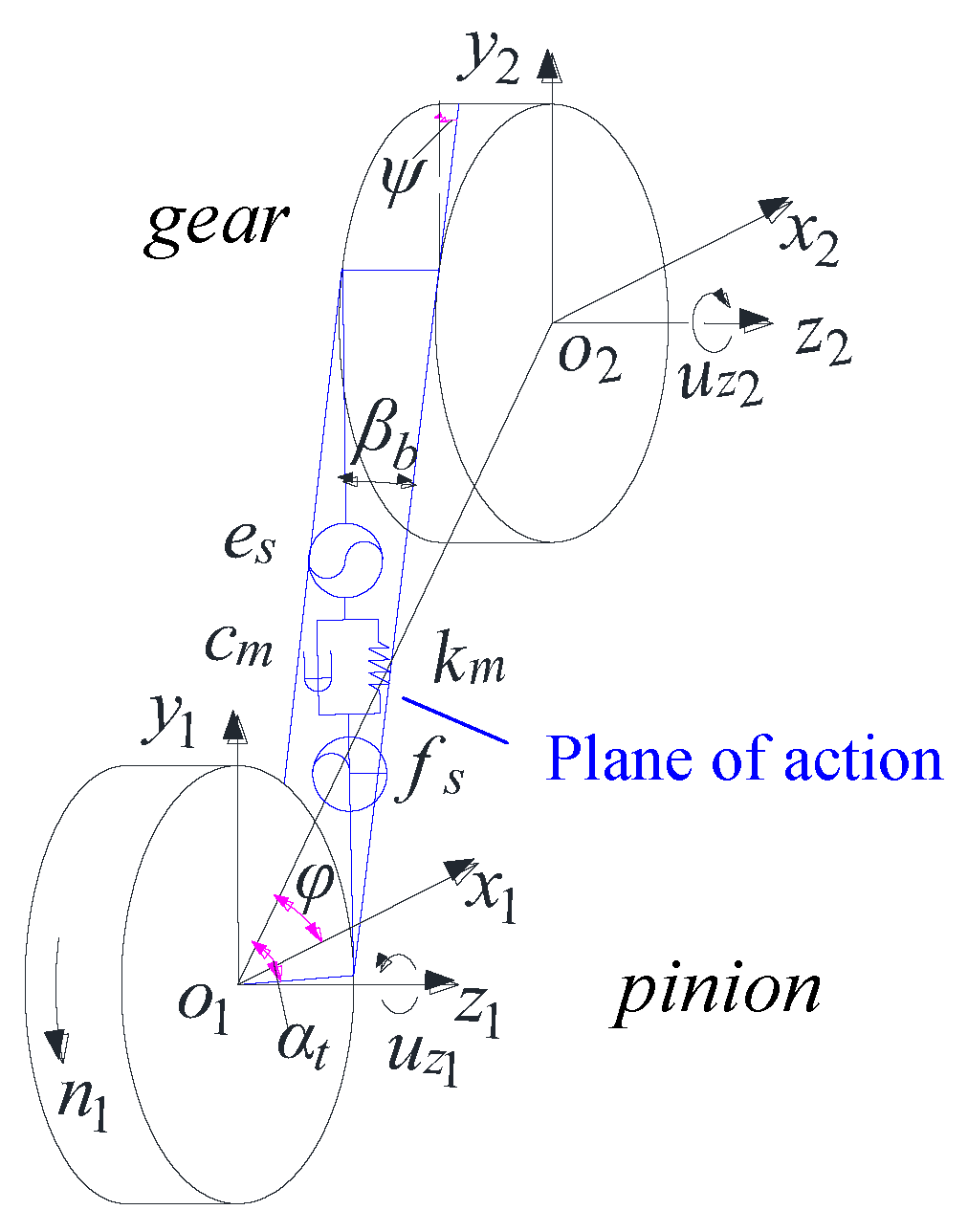
2.3. Dynamic Model of the System
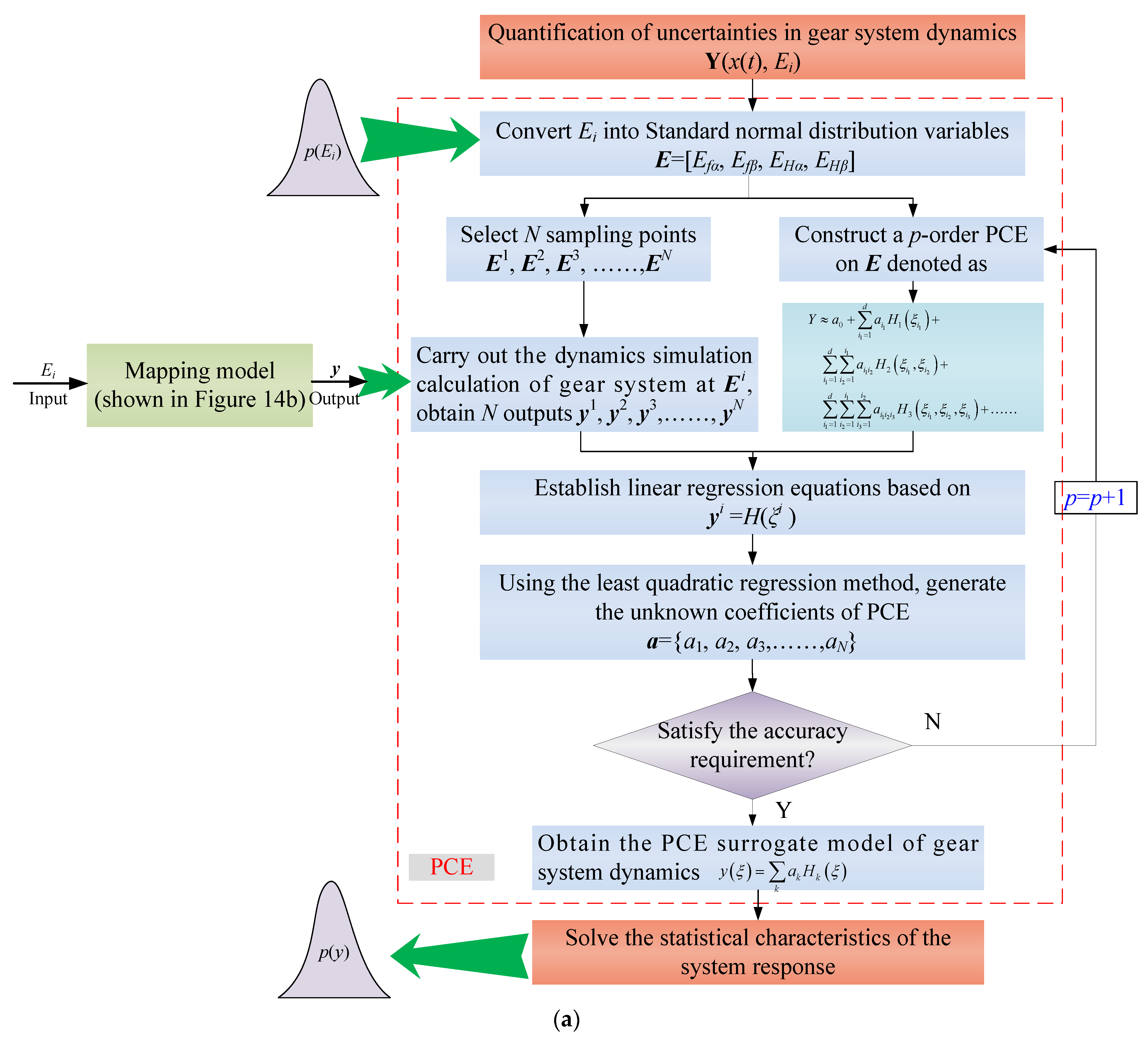
3. Polynomial Chaos Expansion (PCE) for the Gear System with Random Error
3.1. Random Variable and Its Distribution Model
3.2. Polynomial Chaos Expansion (PCE)
3.2.1. Determination of Orthogonal Polynomial Base
3.2.2. The Solution of Polynomial Chaos Expansion Coefficient
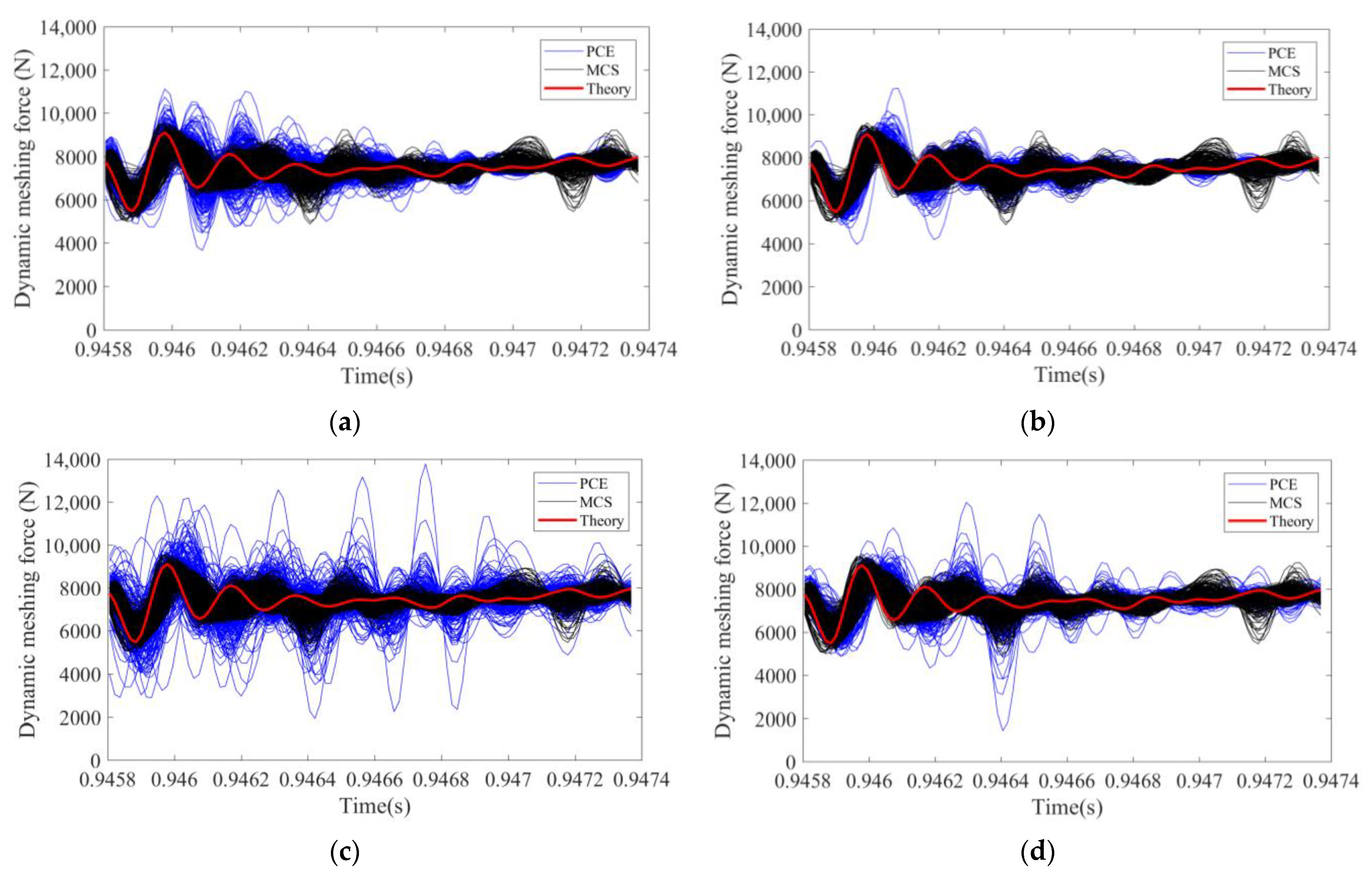
3.3. Precision Analysis of Polynomial Chaotic Expansion Model
4. Error Sensitivity Analysis of the Dynamic Performance Based on the PCE Model of the Gear System
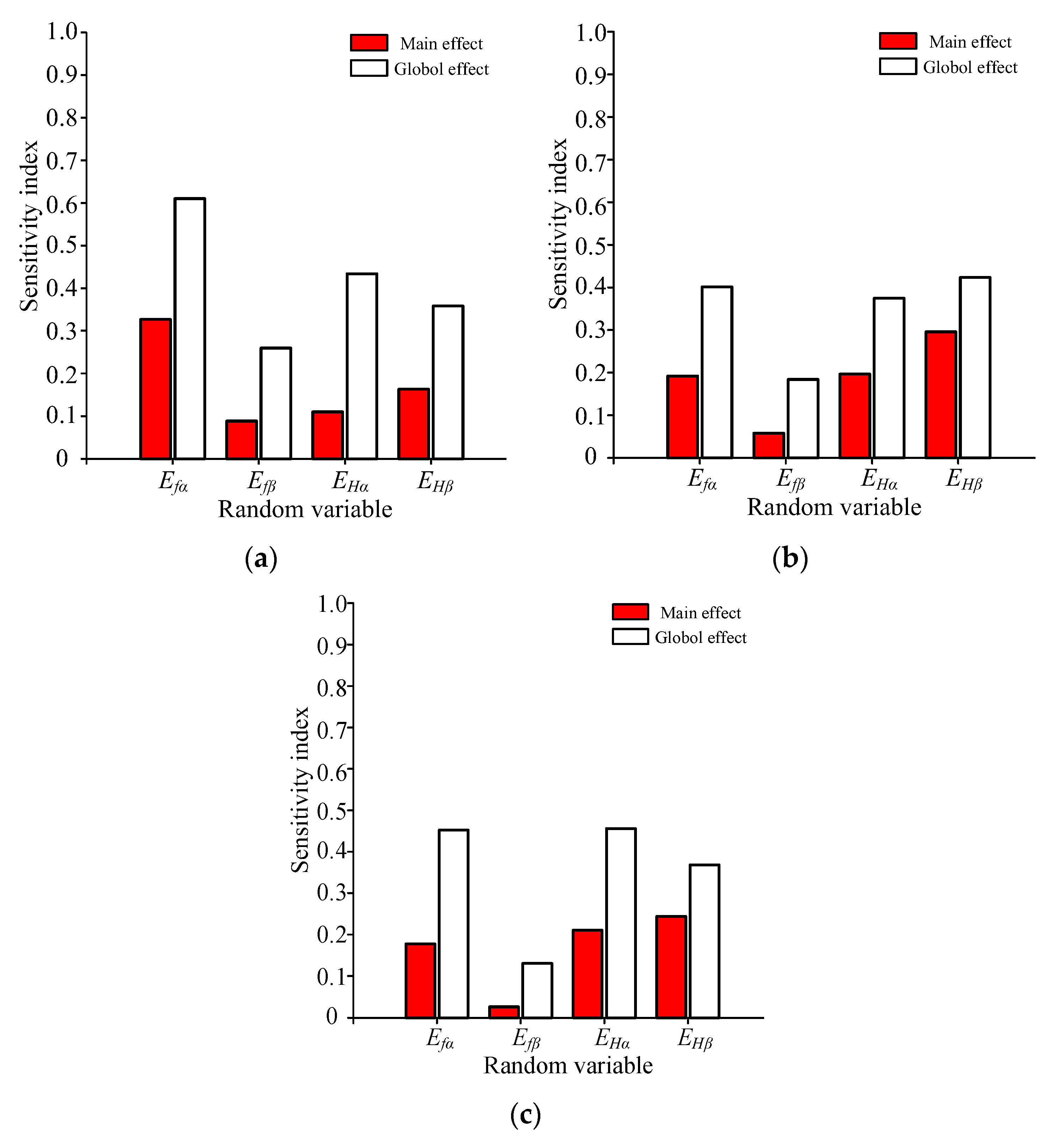
4.1. Global Sensitivity Analysis Method
4.2. Sensitivity Analysis of System Dynamic Response to Random Manufacturing Errors
5. Conclusions
- (1)
- Based on tooth contact analysis (TCA), loaded tooth contact analysis (LTCA), and the system dynamic model, a PCE model with the peak–peak value of the dynamic meshing force as the statistical index of the dynamic response was established. When the polynomial expansion ended at the third order, and the number of sample points was four times the number of polynomial coefficients, the PCE model could not only meet the computational accuracy requirements, it also had high computational efficiency.
- (2)
- The accuracy of the PCE model was compared and verified by using the Monte Carlo method. The results showed that the relative error of the mean of the system response was less than 1%, and the relative error of the standard deviation was less than 2%. When the two methods achieved the same accuracy, the PCE method only called the original system model 140 times, which took 0.4 h. The Monte Carlo method called 1000 times, which took 6 h. The PCE method had a higher efficiency and could provide an efficient and accurate new idea for the quantification of dynamic uncertainty and the reliability design of gear systems.
- (3)
- Based on the PCE model, the Sobol′ index of each error was quickly solved. The influence degree of each error on the dynamic performance of gear systems and the change in the interaction effect between errors were compared and analyzed under different precisions. It provides a reference for the machining precision control in the actual machining and application of batch gears.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Donmez, A.; Kahraman, A. Influence of various manufacturing errors on gear rattle. Mech. Mach. Theory 2022, 173, 104868. [Google Scholar] [CrossRef]
- Zhang, C.P.; Wei, J.; Peng, B.; Cao, M.F.; Hou, S.S.; Lim, T.C. Investigation of dynamic similarity of gear transmission system considering machining error distortion: Theoretical analysis and experiments. Mech. Mach. Theory 2022, 172, 104803. [Google Scholar] [CrossRef]
- Zhou, C.J.; Ning, L.Y.; Wang, H.Y.; Tang, L.W. Effects of centring error and angular misalignment on crack initiation life in herringbone gears. Eng. Fail. Anal. 2021, 120, 105082. [Google Scholar] [CrossRef]
- Vivet, M.; Tamarozzi, T.; Desmet, W.; Mundo, D. On the modelling of gear alignment errors in the tooth contact analysis of spiral bevel gears. Mech. Mach. Theory 2021, 155, 104065. [Google Scholar] [CrossRef]
- Bonori, G.; Pellicano, F. Non-smooth dynamics of spur gears with manufacturing errors. J. Sound Vib. 2007, 306, 271–283. [Google Scholar] [CrossRef]
- Driot, N.; Perret-Liaudet, J. Variability of modal behavior in terms of critical speeds of a gear pair due to manufacturing errors and shaft misalignments. J. Sound Vib. 2006, 292, 824–843. [Google Scholar] [CrossRef]
- Liu, C.; Shi, W.K.; Curá, F.M.; Mura, A. A novel method to predict static transmission error for spur gear pair based on accuracy grade. J. Cent. South Univ. 2020, 27, 3334–3349. [Google Scholar] [CrossRef]
- Guo, F.; Fang, Z.D. The statistical analysis of the dynamic performance of a gear system considering random manufacturing errors under different levels of machining precision. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 3–18. [Google Scholar] [CrossRef]
- Diestmann, T.; Broedling, N.; Götz, B.; Melz, T. Surrogate Model-Based Uncertainty Quantification for a Helical Gear Pair. In ICUME 2021: Uncertainty in Mechanical Engineering; Springer: Cham, Switzerland, 2021; pp. 191–207. [Google Scholar]
- Chen, H.T.; Fan, J.K.; Jing, S.X.; Wang, X.H. Probabilistic design optimization of wind turbine gear transmission system based on dynamic reliability. J. Mech. Sci. Technol. 2019, 33, 579–589. [Google Scholar] [CrossRef]
- Bel Mabrouk, I.; El Hami, A.; Walha, L.; Zghal, B.; Haddar, M. Dynamic response analysis of Vertical Axis Wind Turbine geared transmission system with uncertainty. Eng. Struct. 2017, 139, 170–179. [Google Scholar] [CrossRef]
- Kahnamouei, J.T.; Yang, J. Development and verification of a computationally efficient stochastically linearized planetary gear train model with ring elasticity. Mech. Mach. Theory 2021, 155, 104061. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, F. Statistical modification analysis of helical planetary gears based on response surface method and monte carlo simulation. Chin. J. Mech. Eng. 2015, 28, 1194–1203. [Google Scholar] [CrossRef]
- Hu, C.F.; Geng, G.D.; Spanos, P.D. Stochastic dynamic load-sharing analysis of the closed differential planetary transmission gear system by the Monte Carlo method. Mech. Mach. Theory 2021, 165, 104420. [Google Scholar] [CrossRef]
- Liu, W.Z.; Zhu, R.P.; Zhou, W.G.; Shang, Y.W. Probability distribution model of gear time-varying mesh stiffness with random pitting of tooth surface. Eng. Fail. Anal. 2021, 130, 105782. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, J.S.; Han, Q.K.; Chu, F.L. Dynamic response analysis on torsional vibrations of wind turbine geared transmission system with uncertainty. Renew. Energy 2015, 78, 60–67. [Google Scholar] [CrossRef]
- Xun, C.; Long, X.H.; Hua, H.X. Effects of random tooth profile errors on the dynamic behaviors of planetary gears. J. Sound Vib. 2018, 415, 91–110. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Lu, Z.Z.; Yun, W.Y. Active sparse polynomial chaos expansion for system reliability analysis. Reliab. Eng. Syst. Saf. 2020, 202, 107025. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.H.; Fan, Y.; Li, Y.P. Development of clustered polynomial chaos expansion model for stochastic hydrological prediction. J. Hydrol. 2021, 595, 126022. [Google Scholar] [CrossRef]
- Xiao, H.J.; Song, T.; Jia, B.H.; Lu, X. Uncertainty analysis of MSD crack propagation based on polynomial chaos expansion. Theor. Appl. Fract. Mech. 2022, 120, 103390. [Google Scholar] [CrossRef]
- ISO 1328-1:2013; Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 1: Definitions and Allowable Values of Deviations Relevant to Flanks of Gear Teeth. 2nd ed. International Organization for Standardization: Geneva, Switzerland, 2013; pp. 1–58.
- Litvin, F.L.; Lu, J.; Townsend, D.P.; Howkins, M. Computerized simulation of meshing of conventional helical involute gears and modification of geometry. Mech. Mach. Theory 1999, 34, 123–147. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.D. Tooth contact analysis of helical gears with modification. J. Aerosp. Power 1997, 12, 247–250. (In Chinese) [Google Scholar]
- Wu, B.; Yang, S.; Yao, J. Theoretical analysis on meshing impact of involute gears. Mech. Sci. Technol. 2003, 22, 55–57. (In Chinese) [Google Scholar]
- Guo, F.; Fang, Z.D.; Zhang, X.J.; Cui, Y.M. Influence of the eccentric error of star gear on the bifurcation properties of herringbone star gear transmission with floating sun gear. Shock Vib. 2018, 2018, 6014570. [Google Scholar] [CrossRef] [Green Version]
- Xiu, D.B.; Karniadakis, G.E. The WIENER-ASKEY polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Crestaux, T.; Maître, O.L.; Martinez, J. Polynomial chaos expansion for sensitivity analysis. Reliab. Eng. Syst. Saf. 2009, 94, 1161–1172. [Google Scholar] [CrossRef]


| Parameters | Pinion | Gear |
|---|---|---|
| Number of teeth, Z1/Z2 | 19 | 47 |
| Handedness | left | right |
| Normal modulus, mn (mm) | 6 | |
| Normal pressure angle, α (°) | 20 | |
| Helix angle, β (°) | 9.91 | |
| Tooth width, B (mm) | 79 | 75 |
| Load torque, T2 (N·m) | 1000 | |
| Input speed, n1 (rpm) | 2000 | |
| Tooth Profile (μm) | Lead (μm) | ||
|---|---|---|---|
| Shape Error, Efα | Slope Error, EHα | Shape Error, Efβ | Slope Error, EHβ |
| −3 | −3 | −3 | −4 |
| Method | MCS | PCE | |||
|---|---|---|---|---|---|
| PCE Order and the Sample Size Needed to Determine PCE Coefficient | 2 (M = 15) | 3 (M = 35) | |||
| N = 2M | N = 4M | N = 2M | N = 4M | ||
| Mean value (N) | 3045.86 | 3198.17 | 3045.86 | 3262.95 | 3042.35 |
| Standard deviation (N) | 594.76 | 538.46 | 482.80 | 943.96 | 606.55 |
| Times calling the black-box system model | 1000 | 30 | 60 | 70 | 140 |
| Computing time (h) | 6 | 0.08 | 0.17 | 0.20 | 0.40 |
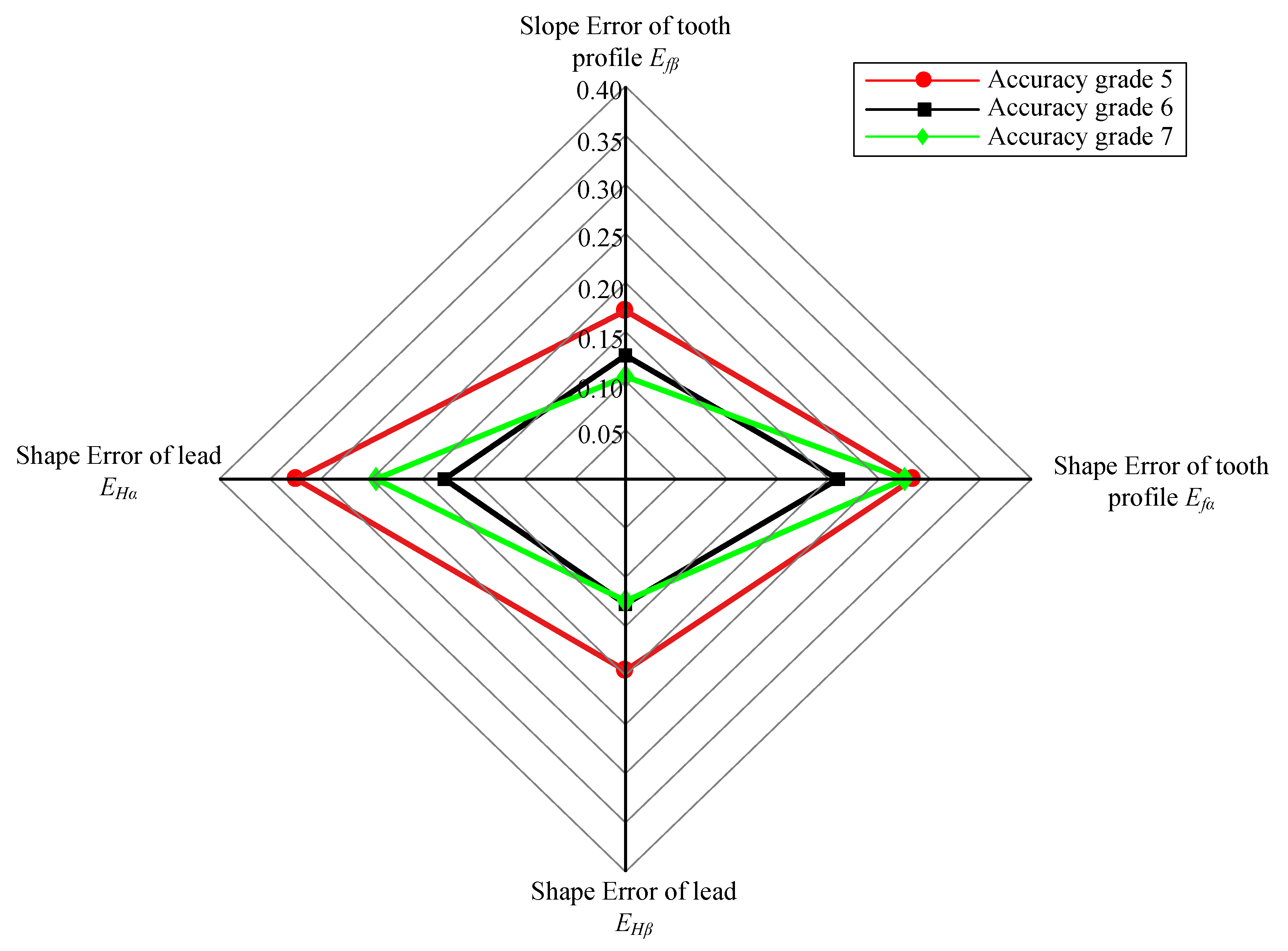
| Accuracy Grade | Tooth Profile | Lead | ||
|---|---|---|---|---|
| Shape Error, Efα | Slope Error, EHα | Shape Error, Efβ | Slope Error, EHβ | |
| 5 | 0.2831 | 0.1714 | 0.3243 | 0.1951 |
| 6 | 0.2095 | 0.1259 | 0.1783 | 0.1274 |
| 7 | 0.2748 | 0.1044 | 0.2457 | 0.1241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Li, C.; Su, J.; Liu, C. Study on Dynamic Uncertainty and Sensitivity of Gear System Considering the Influence of Machining Accuracy. Appl. Sci. 2023, 13, 8011. https://doi.org/10.3390/app13148011
Guo F, Li C, Su J, Liu C. Study on Dynamic Uncertainty and Sensitivity of Gear System Considering the Influence of Machining Accuracy. Applied Sciences. 2023; 13(14):8011. https://doi.org/10.3390/app13148011
Chicago/Turabian StyleGuo, Fang, Chen Li, Jinzhan Su, and Chao Liu. 2023. "Study on Dynamic Uncertainty and Sensitivity of Gear System Considering the Influence of Machining Accuracy" Applied Sciences 13, no. 14: 8011. https://doi.org/10.3390/app13148011





