Acoustic Characteristics Analysis of Double-Layer Liquid-Filled Pipes Based on Acoustic–Solid Coupling Theory
Abstract
:1. Introduction
2. Basic Theory of Acoustic–Solid Coupling
2.1. Basic Assumptions for Establishing the Acoustic Wave Equation
2.2. Pressure-Acoustic Domain Control Equation
2.3. Structural Control Equations
2.4. Acoustic-Structure Boundary Coupling
2.5. Cut-Off Frequency Equation
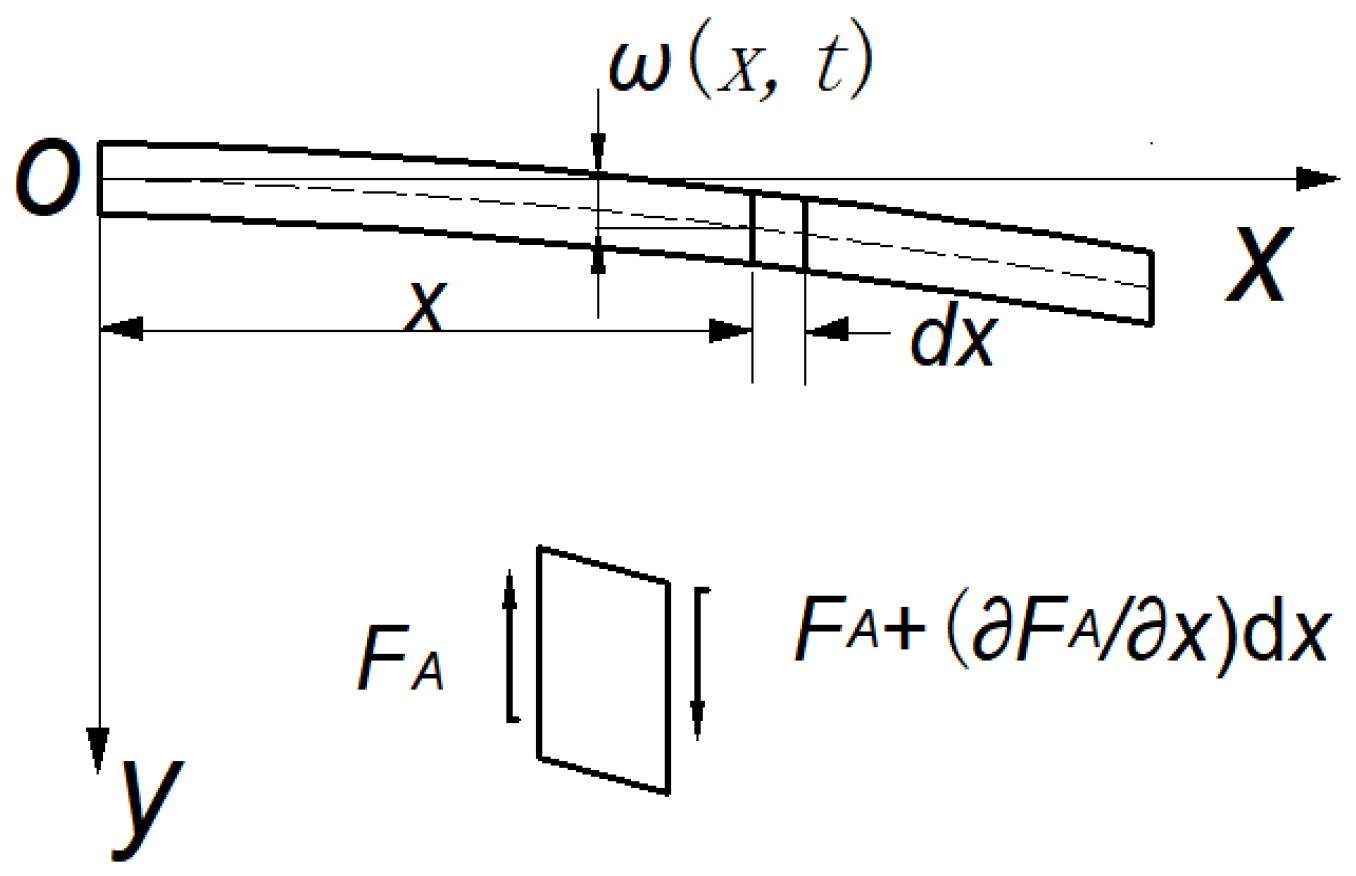
2.6. Timoshenko Beam Model
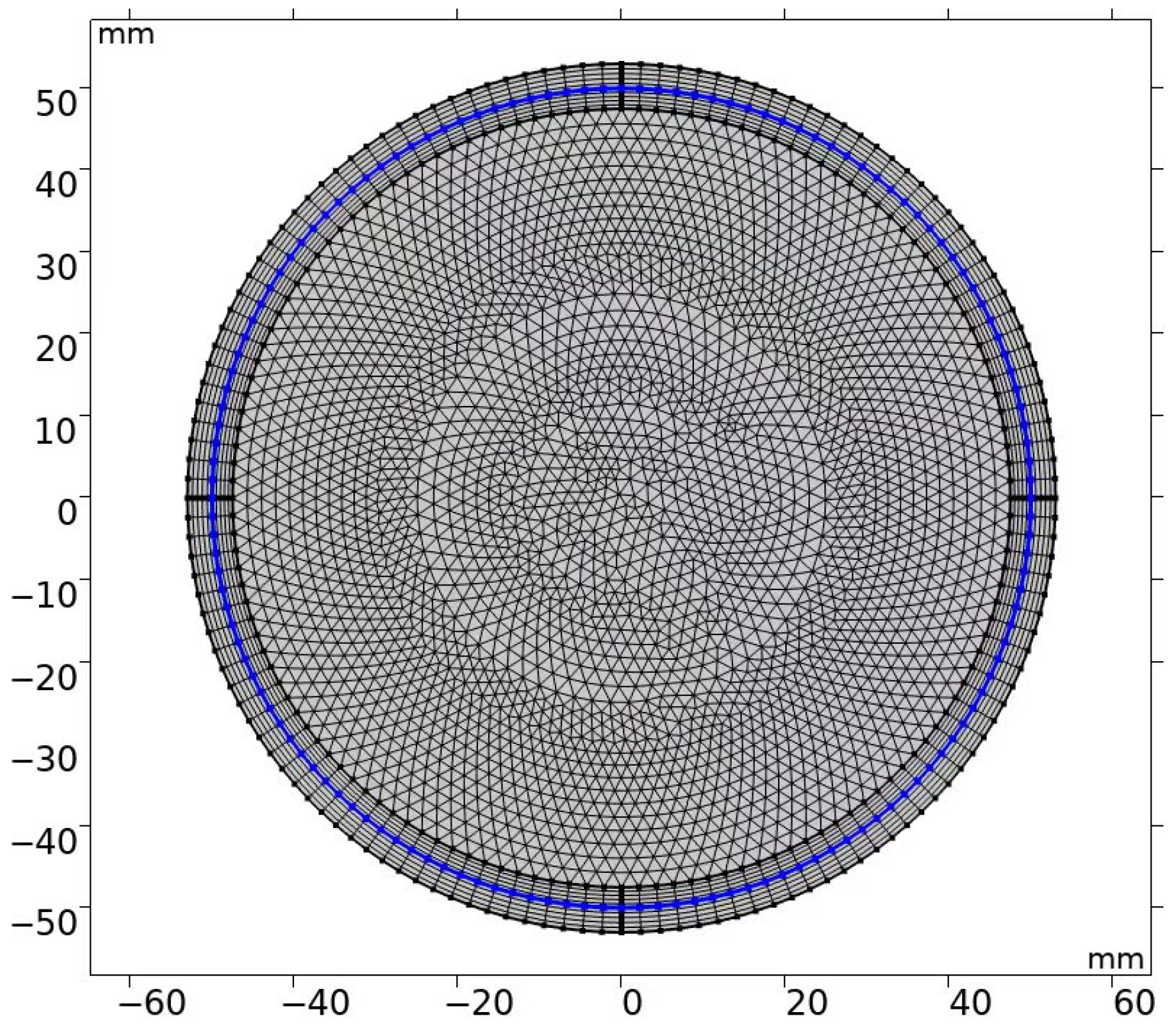
3. Numerical Modeling
4. Simulation and Analysis of the DLLFP
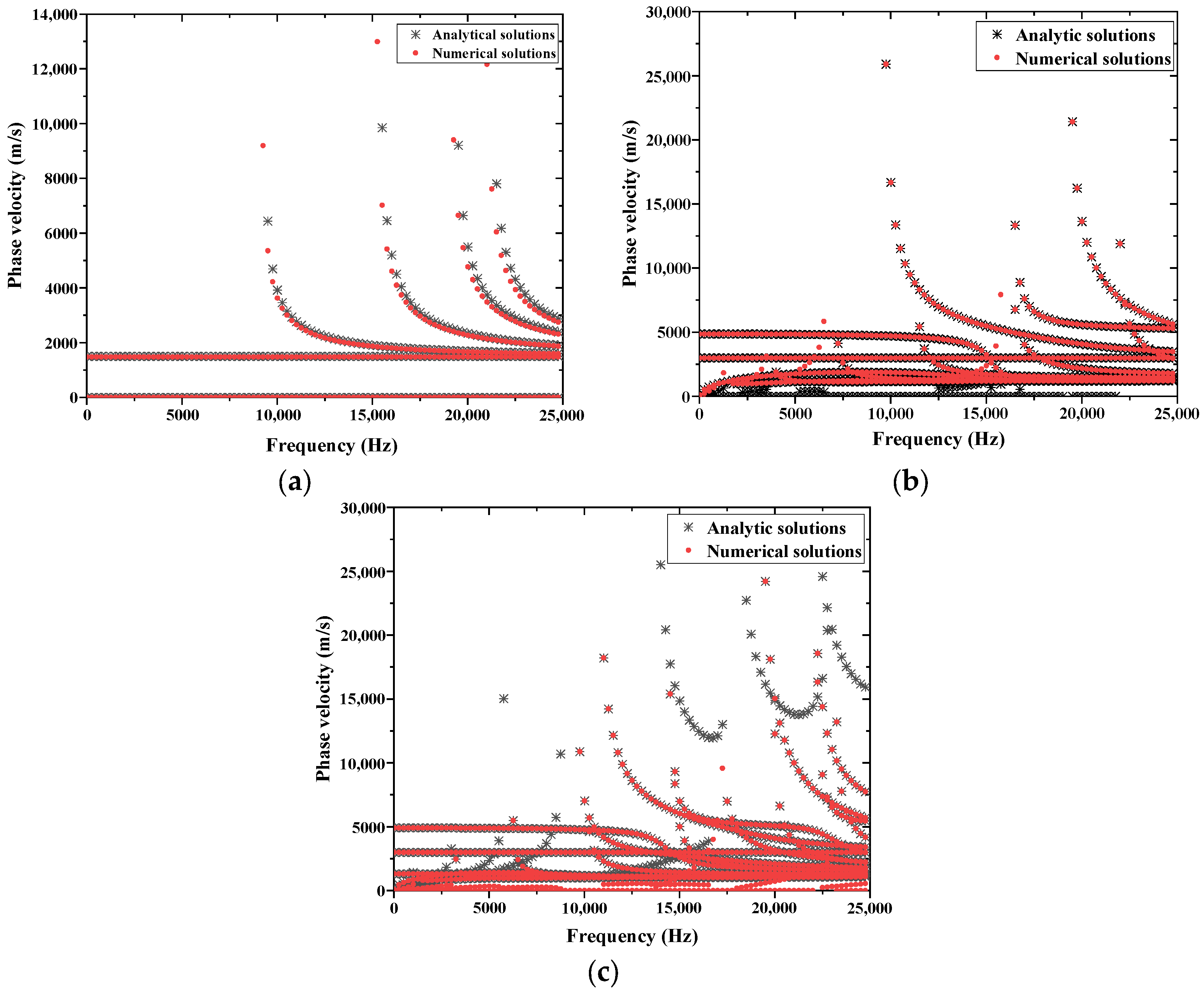
4.1. Comparison of Numerical and Analytical Solutions
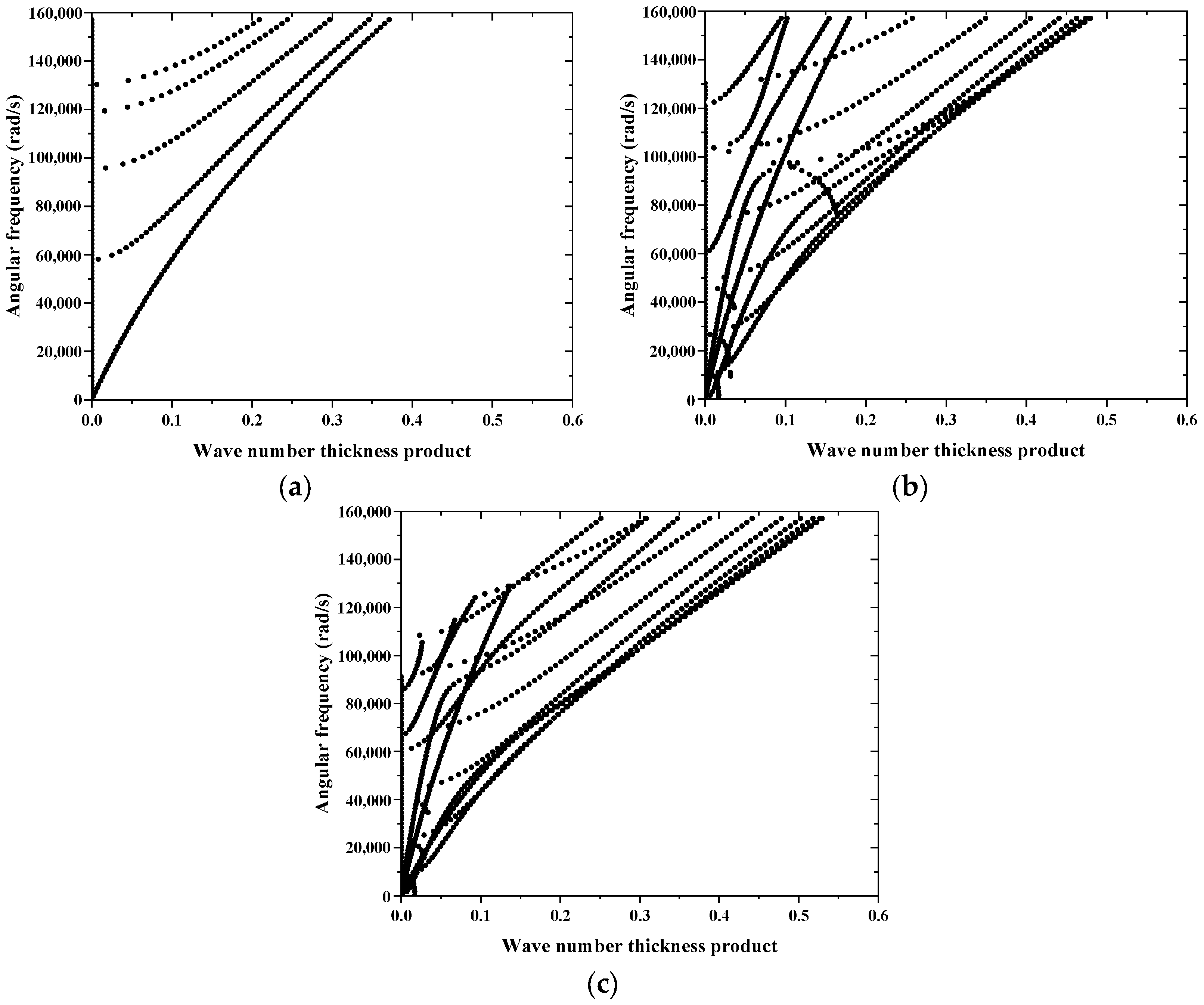
4.2. Dispersion Curves at Different Frequency–Thickness Products
4.3. Wavenumber–Thickness Product Versus Angular Frequency Curve
4.4. DLLFP with Simple Positive Wave Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zakikhani, K.; Nasiri, F.; Zayed, T. A review of failure prediction models for oil and gas pipelines. J. Pipeline Syst. Eng. Pract. 2020, 11, 03119001. [Google Scholar] [CrossRef]
- Lu, H.; Behbahani, S.; Azimi, M.; Matthews, J.C.; Han, S.; Iseley, T. Trenchless construction technologies for oil and gas pipelines: State-of-the-art review. J. Constr. Eng. Manag. 2020, 146, 03120001. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, Z.; Sun, W.; Li, Z. Pipeline leakage localization based on distributed FBG hoop strain measurements and support vector machine. Optik 2019, 176, 1–13. [Google Scholar] [CrossRef]
- Lukman, A.J.A.O.; Emmanuel, A.; Chinonso, N.; Mutiu, A.; James, A.; Jonathan, K. An anti-theft oil pipeline vandalism detection: Embedded system development. Int. J. Eng. Sci. Appl. 2018, 2, 55–64. [Google Scholar]
- Wright, R.F.; Lu, P.; Devkota, J.; Lu, F.; Ziomek-Moroz, M.; Ohodnicki, P.R., Jr. Corrosion sensors for structural health monitoring of oil and natural gas infrastructure: A review. Sensors 2019, 19, 3964. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, X.; Cheng, Y.F.; Shuai, J. Modeling and analysis of a catastrophic oil spill and vapor cloud explosion in a confined space upon oil pipeline leaking. Pet. Sci. 2020, 17, 556–566. [Google Scholar] [CrossRef]
- Reynolds, J.H.; Barrett, M.H. A review of the effects of sewer leakage on groundwater quality. Water Environ. J. 2003, 17, 34–39. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.; Lu, Y.; Sohn, H.; Qing, X. Locating fatigue damage using temporal signal features of nonlinear Lamb waves. Mech. Syst. Signal Process. 2015, 60, 182–197. [Google Scholar] [CrossRef]
- Astaneh, A.V.; Guddati, M.N. Dispersion analysis of composite acousto-elastic waveguides. Compos. Part B Eng. 2017, 130, 200–216. [Google Scholar] [CrossRef]
- Datta, S.; Sarkar, S. A review on different pipeline fault detection methods. J. Loss Prev. Process Ind. 2016, 41, 97–106. [Google Scholar] [CrossRef]
- El Mountassir, M.; Yaacoubi, S.; Dahmene, F. Reducing false alarms in guided waves structural health monitoring of pipelines: Review synthesis and debate. Int. J. Press. Vessel. Pip. 2020, 188, 104210. [Google Scholar] [CrossRef]
- Ma, Q.; Tian, G.; Zeng, Y.; Li, R.; Song, H.; Wang, Z.; Gao, B.; Zeng, K. Pipeline in-line inspection method, instrumentation and data management. Sensors 2021, 21, 3862. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Li, R.; Nie, B.; Liu, S.; Zhao, L.; Zhang, H. Literature review: Theory and application of in-line inspection technologies for oil and gas pipeline girth weld defection. Sensors 2016, 17, 50. [Google Scholar] [CrossRef] [PubMed]
- Guan, R.; Lu, Y.; Duan, W.; Wang, X. Guided waves for damage identification in pipeline structures: A review. Struct. Control Health Monit. 2017, 24, e2007. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wu, B.; Wang, X.Y. Longitudinal mode of ultrasonic guide in a viscoelastic coatin filling duct. Acta Acust. 2007, 7, 316–322. [Google Scholar]
- Yu, B.; Yang, S.; Gan, C.; Lei, H. A new procedure for exploring the dispersion characteristics of longitudinal guided waves in a multi-layered tube with a weak interface. J. Nondestruct. Eval. 2013, 32, 263–276. [Google Scholar] [CrossRef]
- Ebrahiminejad, A.; Mardanshahi, A.; Kazemirad, S. Nondestructive evaluation of coated structures using Lamb wave propagation. Appl. Acoust. 2022, 185, 108378. [Google Scholar] [CrossRef]
- Yu, Y.; Krynkin, A.; Li, Z.; Horoshenkov, K.V. Analytical and empirical models for the acoustic dispersion relations in partially filled water pipes. Appl. Acoust. 2021, 179, 108076. [Google Scholar] [CrossRef]
- Murat, B.I.S. Propagation and Scattering of Guided Waves in Composite Plates with Defects. PhD. Thesis, UCL (University College London), London, UK, 2015. [Google Scholar]
- Su, C.; Jiang, M.; Liang, J.; Tian, A.; Sun, L.; Zhang, L.; Zhang, F.; Sui, Q. Damage identification in composites based on Hilbert energy spectrum and Lamb wave tomography algorithm. IEEE Sens. J. 2019, 19, 11562–11572. [Google Scholar] [CrossRef]
- Mardanshahi, A.; Shokrieh, M.M.; Kazemirad, S. Simulated Lamb wave propagation method for nondestructive monitoring of matrix cracking in laminated composites. Struct. Health Monit. 2022, 21, 695–709. [Google Scholar] [CrossRef]
- Fathi, H.; Kazemirad, S.; Nasir, V. Lamb wave propagation method for nondestructive characterization of the elastic properties of wood. Appl. Acoust. 2021, 171, 107565. [Google Scholar] [CrossRef]
- Kijanka, P.; Urban, M.W. Dispersion curve calculation in viscoelastic tissue-mimicking materials using non-parametric, parametric, and high-resolution methods. Ultrasonics 2021, 109, 106257. [Google Scholar] [CrossRef] [PubMed]
- Viola, E.; Marzani, A. Exact analysis of wave motions in rods and hollow cylinders. In Mechanical Vibration: Where Do We Stand? Springer: Vienna, Austria, 2007; pp. 83–104. [Google Scholar]
- Quintanilla, F.H.; Fan, Z.; Lowe MJ, S.; Craster, R.V. Guided waves’ dispersion curves in anisotropic viscoelastic single-and multi-layered media. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150268. [Google Scholar] [CrossRef]
- Kirby, R.; Duan, W. Guided wave propagation in cylindrical ducts with elastic walls enclosing a fluid moving with a uniform velocity. Wave Motion 2019, 85, 1–9. [Google Scholar] [CrossRef]
- Zheng, M.; He, C.; Lyu, Y.; Wu, B. Guided waves propagation in anisotropic hollow cylinders by Legendre polynomial solution based on state-vector formalism. Compos. Struct. 2019, 207, 645–657. [Google Scholar] [CrossRef]
- Roy, T.; Guddati, M.N. Shear wave dispersion analysis of incompressible waveguides. J. Acoust. Soc. Am. 2021, 149, 972–982. [Google Scholar] [CrossRef] [PubMed]
- Chiappa, A.; Iakovlev, S.; Marzani, A.; Giorgetti, F.; Groth, C.; Porziani, S.; Biancolini, M.E. An analytical benchmark for a 2D problem of elastic wave propagation in a solid. Eng. Struct. 2021, 229, 111655. [Google Scholar] [CrossRef]
- Yu, J.G.; Lefebvre, J.E. Guided waves in multilayered hollow cylinders: The improved Legendre polynomial method. Compos. Struct. 2013, 95, 419–429. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, Y.; Zheng, M.; Liu, M.; Liu, H.; Wu, B.; He, C. Application of state vector formalism and Legendre polynomial hybrid method in the longitudinal guided wave propagation analysis of composite multi-layered pipes. Wave Motion 2021, 100, 102670. [Google Scholar] [CrossRef]
- Yeung, C.; Ng, C.T. Time-domain spectral finite element method for analysis of torsional guided waves scattering and mode conversion by cracks in pipes. Mech. Syst. Signal Process. 2019, 128, 305–317. [Google Scholar] [CrossRef]
- Yeung, C.; Ng, C.T. Nonlinear guided wave mixing in pipes for detection of material nonlinearity. J. Sound Vib. 2020, 485, 115541. [Google Scholar] [CrossRef]
- Fakih, M.A.; Mustapha, S.; Harb, M.; Ng, C.T. Understanding the interaction of the fundamental Lamb-wave modes with material discontinuity: Finite element analysis and experimental validation. Struct. Health Monit. 2022, 21, 640–665. [Google Scholar] [CrossRef]
- Wang, X.; Gao, H.; Zhao, K.; Wang, C. Time-frequency characteristics of longitudinal modes in symmetric mode conversion for defect characterization in guided waves-based pipeline inspection. NDT E Int. 2021, 122, 102490. [Google Scholar] [CrossRef]
- Ahmad, R.; Banerjee, S.; Kundu, T. Pipe wall damage detection in buried pipes using guided waves. J. Press. Vessel. Technol. 2009, 131, 011501. [Google Scholar] [CrossRef]
- Jing, L.; Li, Z.; Li, Y.; Murch, R.D. Channel characterization of acoustic waveguides consisting of straight gas and water pipelines. IEEE Access 2018, 6, 6807–6819. [Google Scholar] [CrossRef]
- Rouze, N.C.; Palmeri, M.L.; Nightingale, K.R. An analytic, Fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources. J. Acoust. Soc. Am. 2015, 138, 1012–1022. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.; Kirby, R. Guided wave propagation in buried and immersed fluid-filled pipes: Application of the semi analytic finite element method. Comput. Struct. 2019, 212, 236–247. [Google Scholar] [CrossRef]
- Brennan, M.J.; Karimi, M.; Muggleton, J.M.; Almeida, F.C.L.; de Lima, F.K.; Ayala, P.C.; Obata, D.; Paschoalini, A.T.; Kessissoglou, N. On the effects of soil properties on leak noise propagation in plastic water distribution pipes. J. Sound Vib. 2018, 427, 120–133. [Google Scholar] [CrossRef]
- Su, N.; Han, Q.; Yang, Y.; Shan, M.; Jiang, J. Analysis of Longitudinal Guided Wave Propagation in a Liquid-Filled Pipe Embedded in Porous Medium. Appl. Sci. 2021, 11, 2281. [Google Scholar] [CrossRef]
- Zhang, H.L. Theoretical Acoustics; Higher Education Press: Beijing, China, 2007; pp. 176–177. (In Chinese) [Google Scholar]
- Zhang, L.Y.; Zhang, M.H. Vibration and Acoustic Foundation; Harbin Engineering University Press: Harbin, China, 2016; pp. 78–85. (In Chinese) [Google Scholar]
- Giordano, J.A.; Koopmann, G.H. State space boundary element–finite element coupling for fluid–structure interaction analysis. J. Acoust. Soc. Am. 1995, 98, 363–372. [Google Scholar] [CrossRef]
- Yang, H.S. Study on the Vibroacoustic Characteristics of Sandwich Plate with Corrugated Cores Based on Structural-Acoustic Coupling Effect. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2017; pp. 23–28. (In Chinese). [Google Scholar]
- Ma, J.Y.; Zhao, M.R.; Huang, X.J. Application of longitudinal guide waves in viscosity measurement. J. Tianjin Univ. Nat. Sci. Eng. Technol. Ed. 2017, 50, 758–766. [Google Scholar]
- Weaver, W., Jr.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Tedesco, J.; McDougal, W.G.; Ross, C.A. Structural Dynamics; Pearson Education: London, UK, 2000. [Google Scholar]
- Liu, H.; Liu, S.; Chen, X.; Lyu, Y.; Liu, Z. Coupled Lamb waves propagation along the direction of non-principal symmetry axes in pre-stressed anisotropic composite lamina. Wave Motion 2020, 97, 102591. [Google Scholar] [CrossRef]
- Chen, D.J.; Yan, J.; Yangyang, L.; Chao, H.; Lülong, Z. Analysis of the acoustic vibration properties of flow pipelines considering the sound-solid coupling effect. Chin. Ship Res. 2021, 16, 137–143. [Google Scholar]
- Sadaf, M.; Perveen, Z.; Zainab, I.; Akram, G.; Abbas, M.; Baleanu, D. Dynamics of unsteady fluid-flow caused by a sinusoidally varying pressure gradient through a capillary tube with Caputo-Fabrizio derivative. Therm. Sci. 2023, 27, 49–56. [Google Scholar] [CrossRef]




| Materials | Wall Thickness [mm] | Density ρ [kg/m3] | Sound Velocity c [m/s] | Young’s Modulus E [pa] | Poisson’s Ratio μ |
|---|---|---|---|---|---|
| Structural steel | 2.5 | 7850 | Disregard | 205 × 109 | 0.30 |
| Titanium beta-21Sl | 3 | 4940 | Disregard | 105× 109 | 0.33 |
| Water | Disregard | 1000 | 1500 | Disregard | Disregard |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Li, J.; Zou, L.; Zhang, D.; Wang, C.; Tang, Z. Acoustic Characteristics Analysis of Double-Layer Liquid-Filled Pipes Based on Acoustic–Solid Coupling Theory. Appl. Sci. 2023, 13, 11017. https://doi.org/10.3390/app131911017
Yan J, Li J, Zou L, Zhang D, Wang C, Tang Z. Acoustic Characteristics Analysis of Double-Layer Liquid-Filled Pipes Based on Acoustic–Solid Coupling Theory. Applied Sciences. 2023; 13(19):11017. https://doi.org/10.3390/app131911017
Chicago/Turabian StyleYan, Jin, Jiangfeng Li, Lvlong Zou, Dapeng Zhang, Cheng Wang, and Zhi Tang. 2023. "Acoustic Characteristics Analysis of Double-Layer Liquid-Filled Pipes Based on Acoustic–Solid Coupling Theory" Applied Sciences 13, no. 19: 11017. https://doi.org/10.3390/app131911017





