Three-Dimensional Stability Analysis of Ridge Slope Using Strength Reduction Method Based on Unified Strength Criterion
Abstract
:1. Introduction
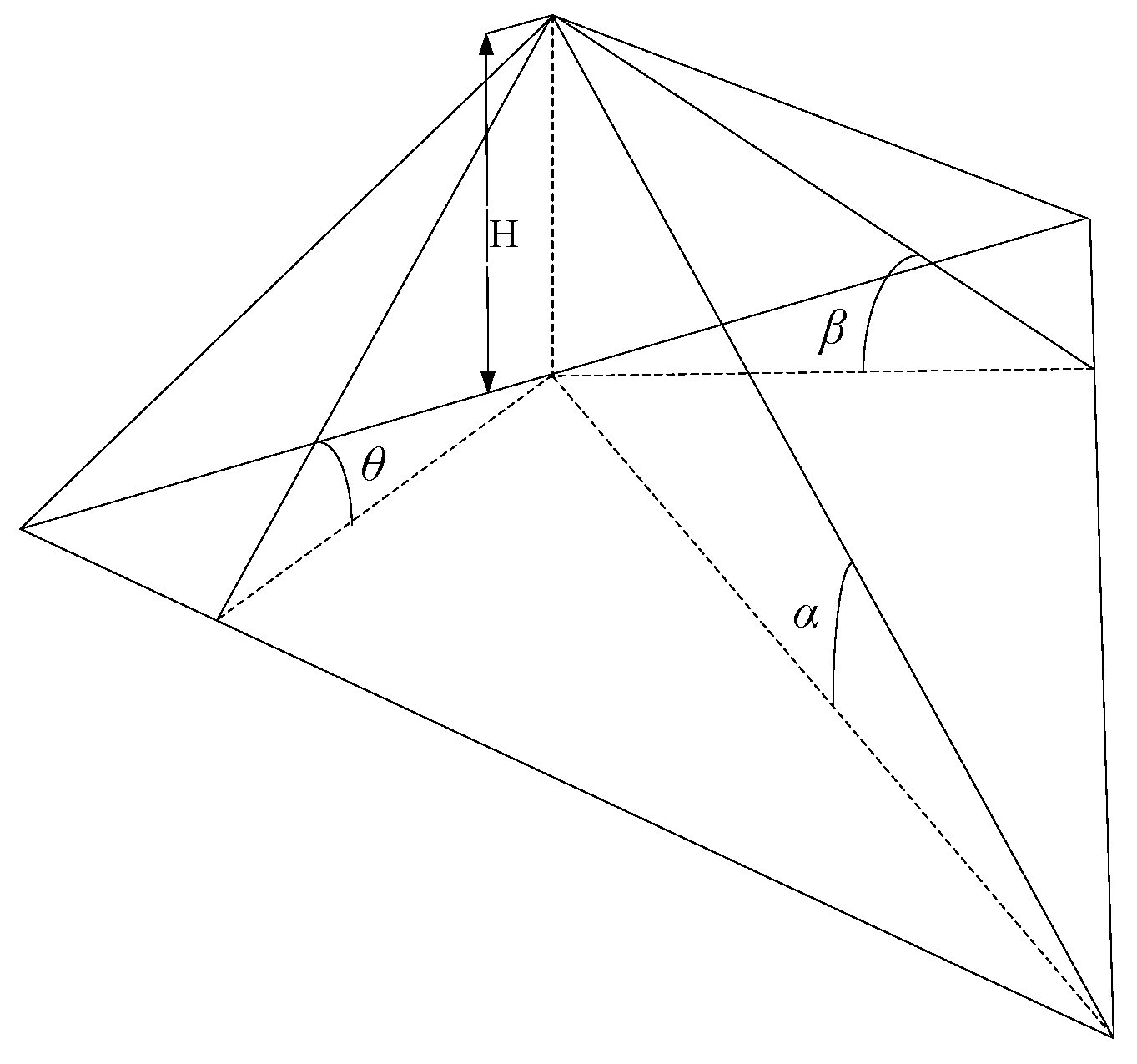
2. Three-Dimensional Model of Natural Ridge Slope
2.1. Establishment of Three-Dimensional Model of Natural Ridge Slope and Wire Frame Model
2.2. Geometric Parameters of Natural Ridge Slope Model
2.3. Physical and Mechanical Parameters of the Ridge and Slope Model
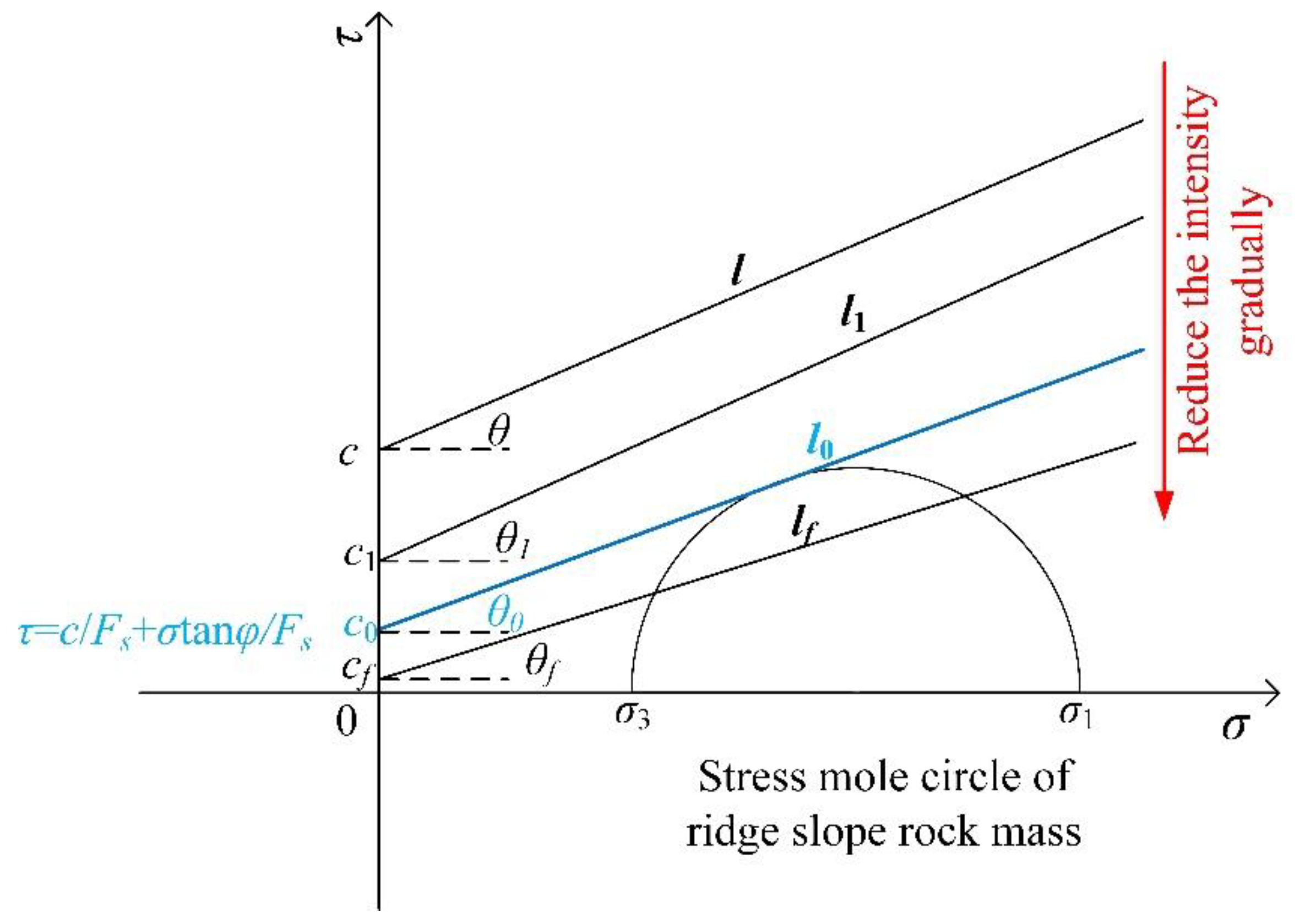
3. Stability Analysis of Ridge Slope
3.1. Deformation and Failure Characteristics of Ridge Slope under Different Ridgeline Dip Angles
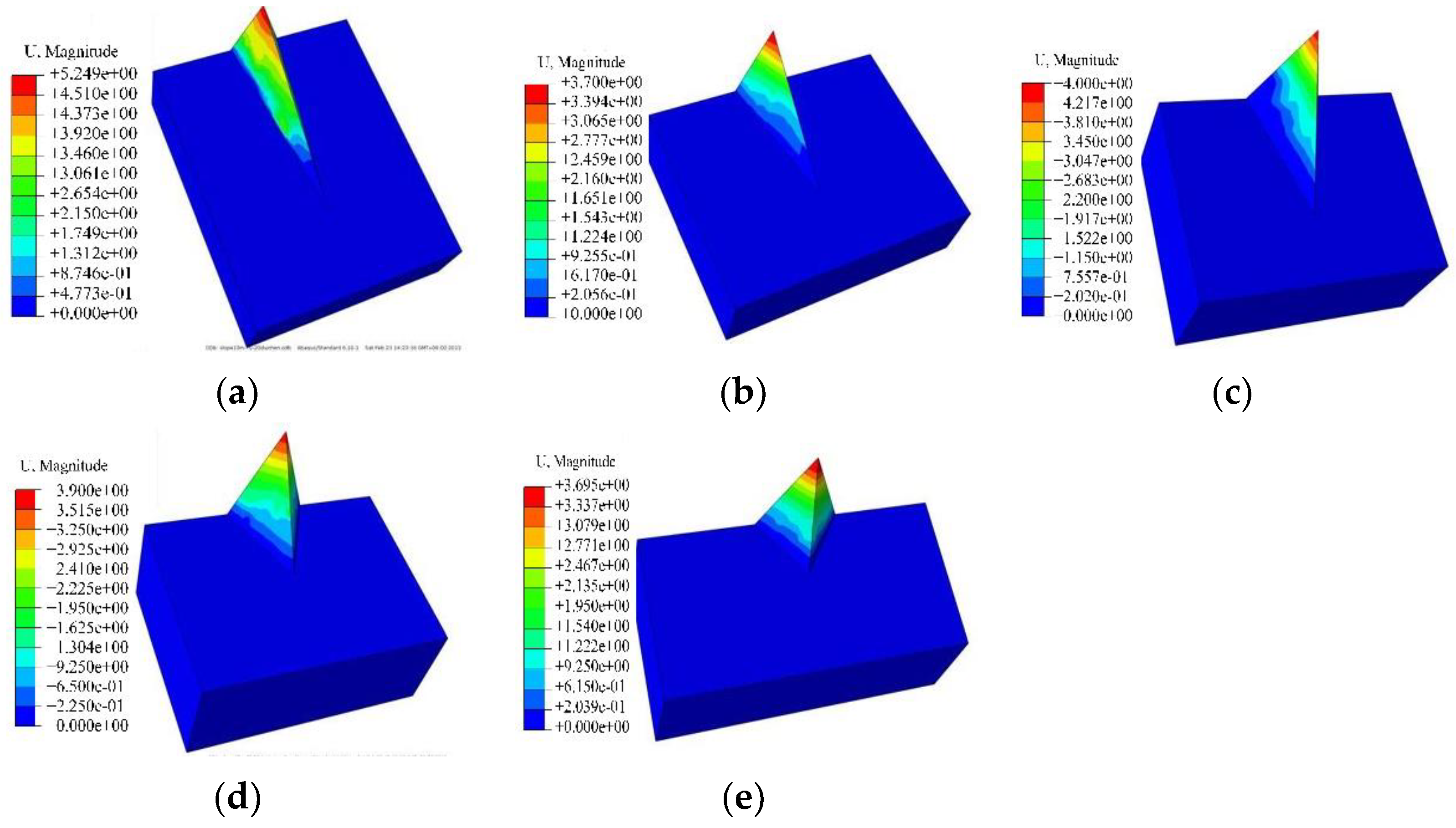
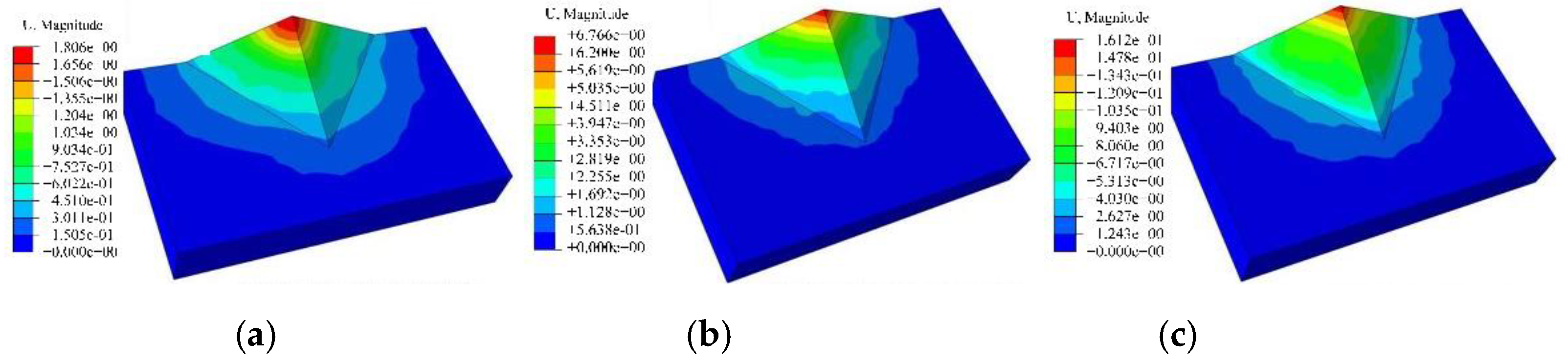
3.1.1. Deformation Characteristics of Ridge Slope under Different Ridgeline Dip Angles
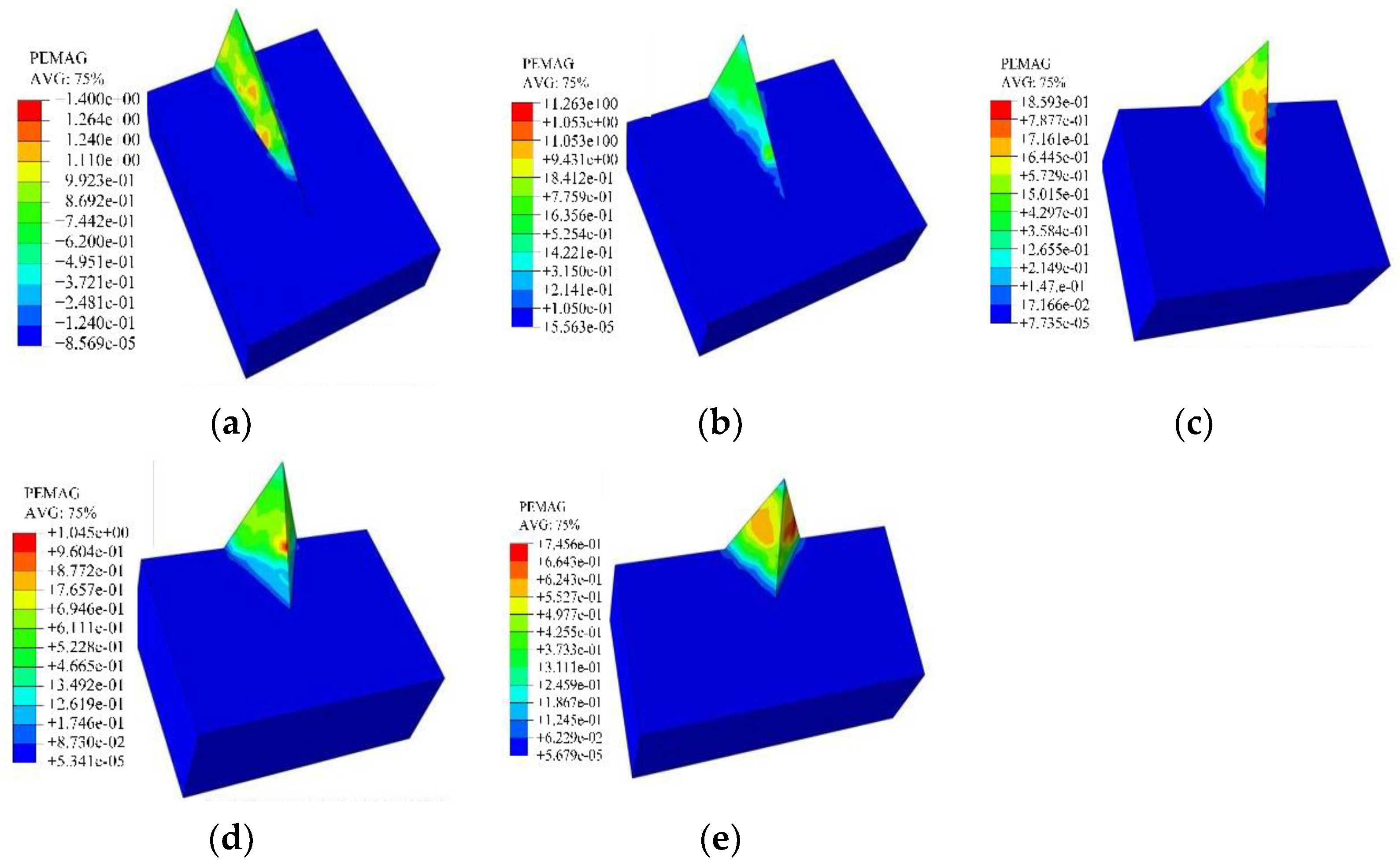
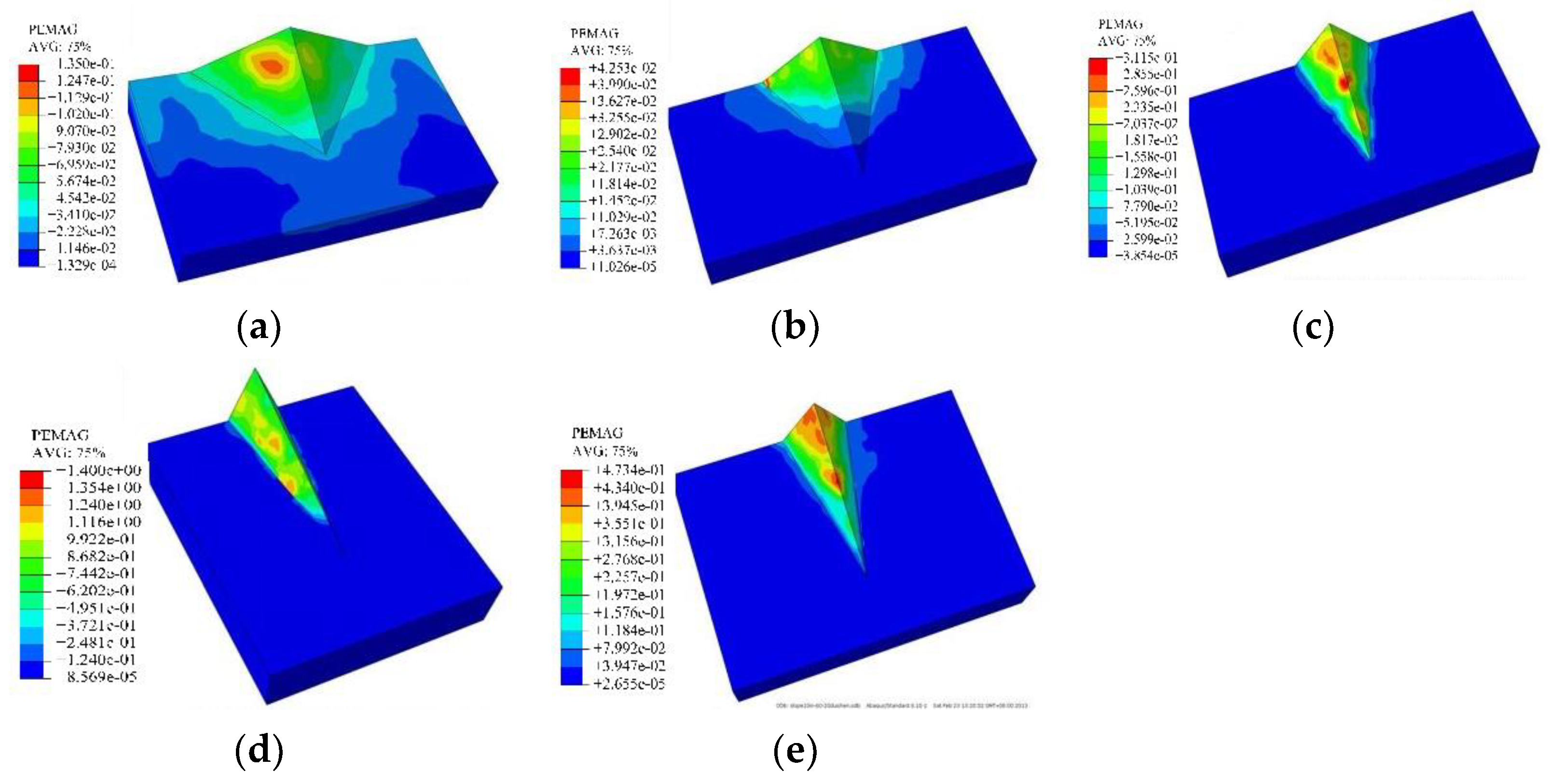
3.1.2. Failure Characteristics of Ridge Slope under Different Ridgeline Dip Angles
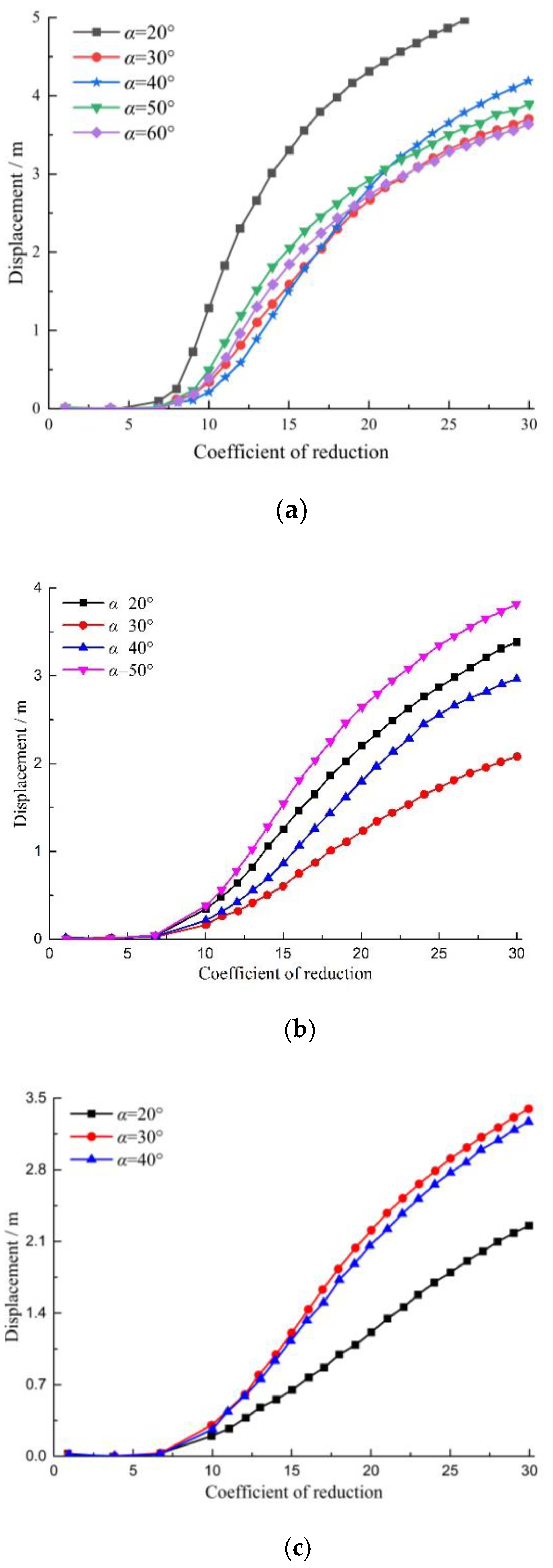
3.1.3. Stability of Ridge Slope under Different Ridgeline Dip Angles
3.2. Deformation and Failure Characteristics of Ridge Slope under Different Flank Angles
3.2.1. Deformation Characteristics of Ridge Slope under Different Flank Slope Angles
3.2.2. Failure Characteristics of Ridge Slope under Different Flank Slope Angles
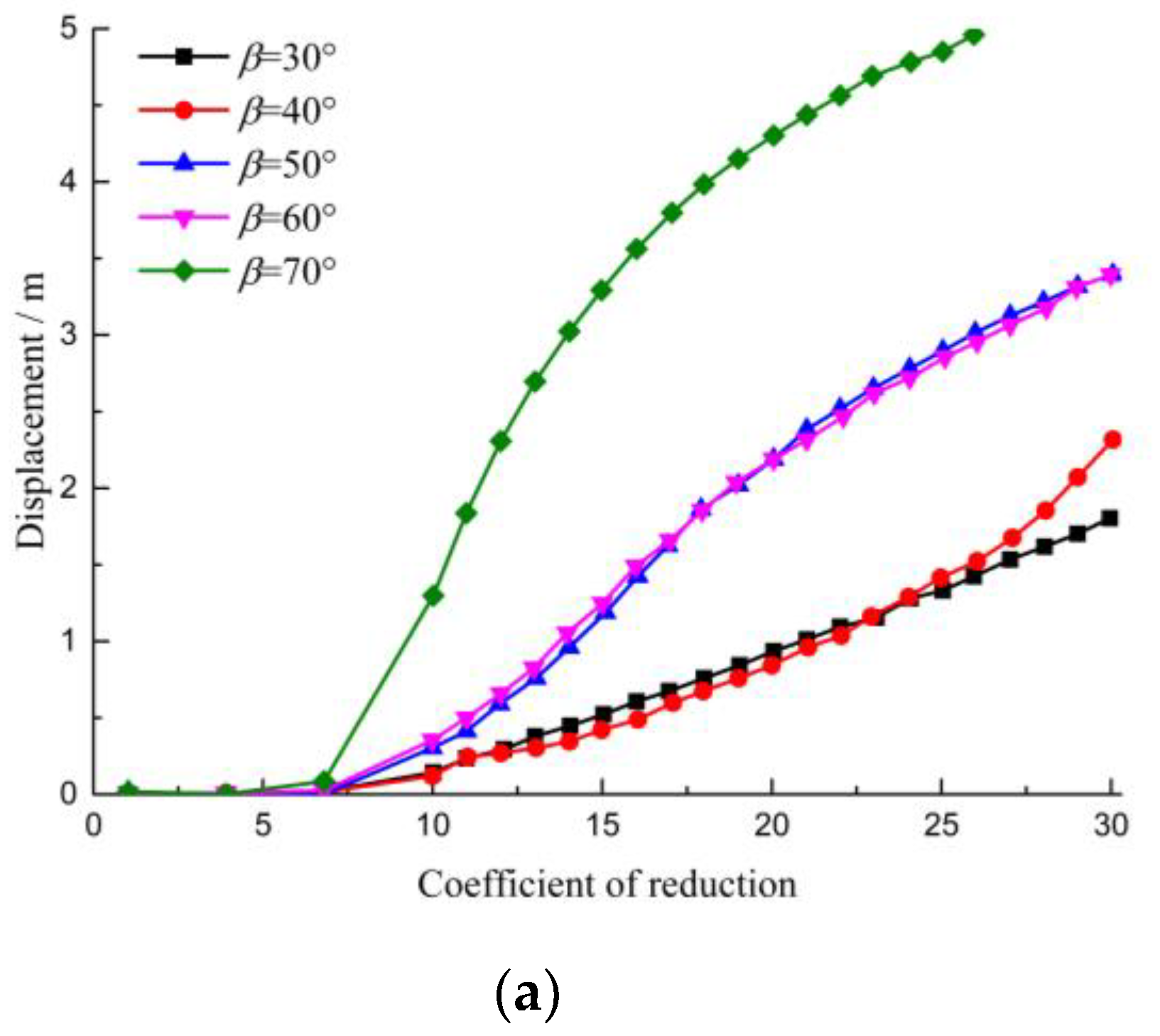
3.2.3. Stability of Ridge Slope under Different Flank Slope Angles
3.3. Deformation and Failure Characteristics of Ridge Slopes with Different Slope Heights
3.3.1. Deformation Characteristics of Ridge Slope under Different Slope Heights
3.3.2. Failure Characteristics of Ridge Slope under Different Slope Heights
3.3.3. Stability of Ridge Slope under different Slope Heights
4. Numerical Simulation Study on Stability of Ridge and Slope after Excavation
4.1. Simulation of Excavation Model
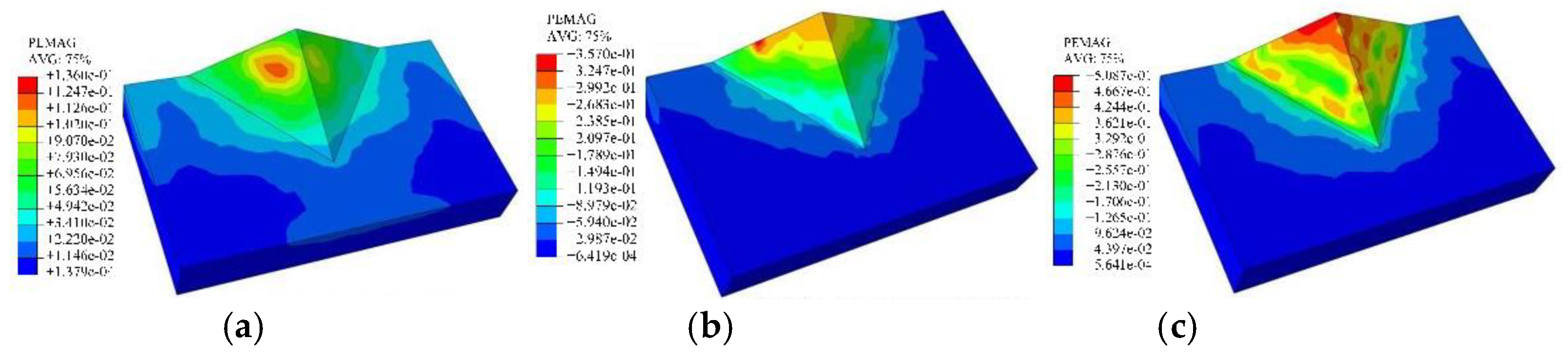
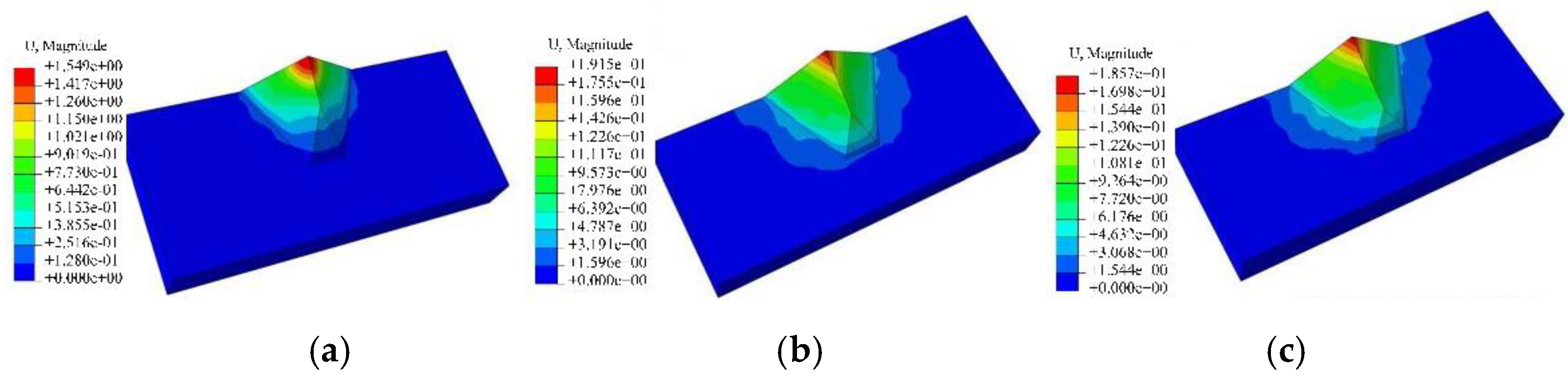
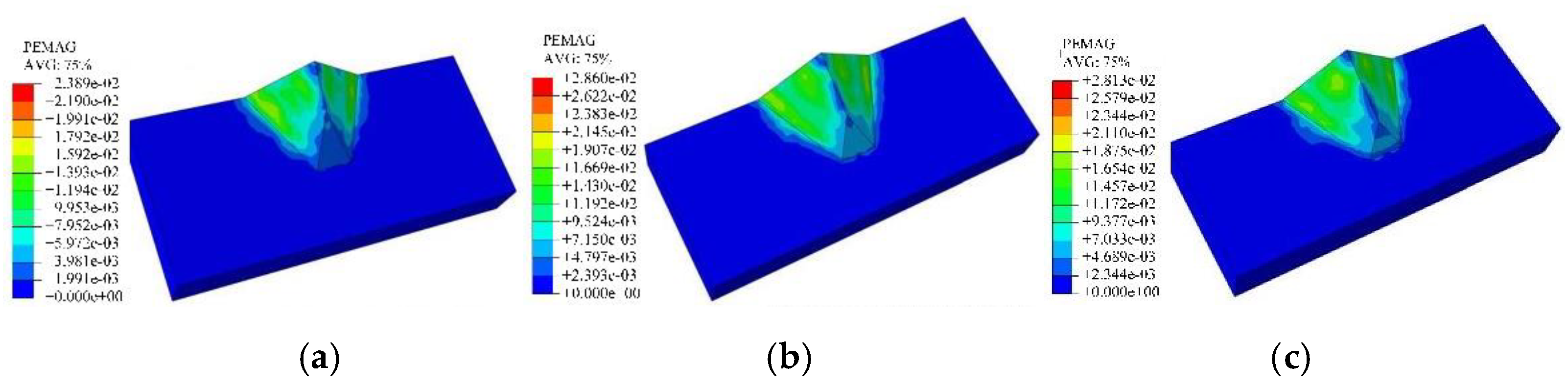
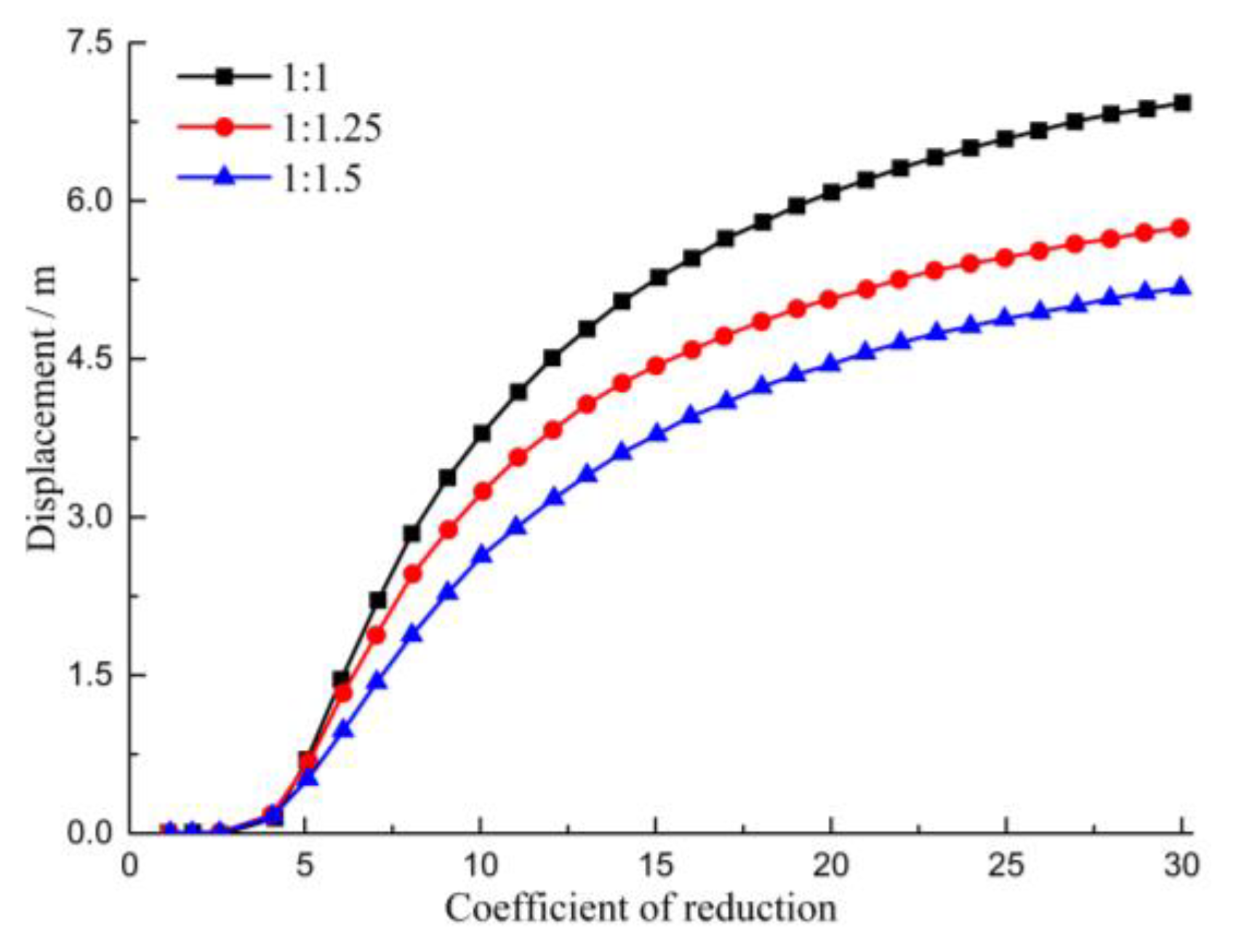
4.2. Stability of Ridge Slope under Different Excavation Slope Ratio
5. Conclusions
- No displacement of the ridge slope occurred under different α values when the reduction factor was less than six. The smaller the α of the ridge slope, the worse its stability. When α = 20°, the stability coefficient of the ridge slope was 8, and when α was greater than 20°, the stability coefficient of the ridge slope increased to 10.
- When the β was small, the plastic area was distributed in a flank slope position, and the plastic area gradually concentrated to the ridge as β increased. When the β was 70 °, the stabilization coefficient of the ridge slope was 7. When the β decreased to 40° and 30°, the stability coefficient of the ridge slope reached 15. Under the same reduction factor, the larger the β of the ridge slope, the larger the displacement, and the ridge slope was more prone to instability.
- The higher the slope height was, the larger the displacement at the top of the slope was. The reduction coefficient of the ridge slope curve increased gently, and the instability phenomenon of the slope hardly occurred. When the slope height increased to 30 m, the displacement at the top of the slope was 14.7 m, and the safety and stability coefficient of the slope was 4.
- When the excavation slope rate was large, the bedrock exhibited a large displacement; the plastic zone and a large displacement began to appear on the excavation slope surface because of the close proximity of the excavation surface position to the back edge of the ridge slope. Therefore, the ridge slope is more prone to instability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Li, X.; Liu, X.; Yang, Z. A combined shear strength reduction and surrogate model method for efficient reliability analysis of slopes. Comput. Geotech. 2022, 152, 105021. [Google Scholar] [CrossRef]
- Chen, X.; Ren, J.; Wang, D.; Lyu, Y.; Zhang, H. A Generalized Strength Reduction Concept and Its Applications to Geotechnical Stability Analysis. Geotech. Geol. Eng. 2019, 37, 2409–2424. [Google Scholar] [CrossRef]
- Xu, Q.; Yin, H.; Cao, X.; Li, Z. A temperature-driven strength reduction method for slope stability analysis. Mech. Res. Commun. 2009, 36, 224–231. [Google Scholar] [CrossRef]
- Li, P.F.; Liu, H.B.; Zhang, Y. Based on The Strength Reduction Slope Stability Finite Element Analysis of Engineering Examples: Progress in Civil Engineering, PTS 1–4[Z]. In Proceedings of the 2nd International Conference on Civil Engineering, Architecture and Building Materials (CEABM 2012), Yantai, China, 25–27 May 2012; Volume 170–173, pp. 885–888. [Google Scholar]
- Illeditsch, M.; Preh, A.; Sausgruber, J.T. Challenges Assessing Rock Slope Stability Using the Strength Reduction Method with the Hoek-Brown Criterion on the Example of Vals (Tyrol/Austria). Geosciences 2022, 12, 255. [Google Scholar] [CrossRef]
- Chen, Q.; Bai, B.; Wang, H.; Li, X. Dissipated Energy as the Evaluation Index for the Double Reduction Method. Int. J. Geomech. 2021, 21, 6021012. [Google Scholar] [CrossRef]
- Yang, Y.; Xia, Y.; Zheng, H.; Liu, Z. Investigation of rock slope stability using a 3D nonlinear strength-reduction numerical manifold method. Eng. Geol. 2021, 292, 106285. [Google Scholar] [CrossRef]
- An, X.; Li, N. Non-Equal Strength Reduction Analysis of Soil Slopes Considering Progressive Failure. Soil Mech. Found. Eng. 2021, 58, 273–279. [Google Scholar] [CrossRef]
- Hu, L.; Takahashi, A.; Kasama, K. Effect of spatial variability on stability and failure mechanisms of 3D slope using random limit equilibrium method. Soils Found. 2022, 62, 101225. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Hu, B.; Yin, T.; Chen, G.; Chen, G. Hazard Classification and Stability Analysis of High and Steep Slopes from Underground to Open-Pit Mining. Int. J. Environ. Res. Public Health 2022, 19, 11679. [Google Scholar] [CrossRef]
- Ding, Q.L.; Peng, Y.Y.; Cheng, Z.; Wang, P. Numerical Simulation of Slope Stability during Underground Excavation Using the Lagrange Element Strength Reduction Method. Minerals 2022, 12, 1054. [Google Scholar] [CrossRef]
- Li, Y.; Qian, C.; Fu, Z.; Li, Z. On Two Approaches to Slope Stability Reliability Assessments Using the Random Finite Element Method. Appl. Sci. 2019, 9, 4421. [Google Scholar] [CrossRef] [Green Version]
- Dyson, A.P.; Tolooiyan, A. Optimisation of strength reduction finite element method codes for slope stability analysis. Innov. Infrastruct. Solut. 2018, 3, 38. [Google Scholar] [CrossRef]
- Luan, M.; Wu, Y.; Nian, T. An Alternative Criterion for Evaluating Slope Stability Based on Development of Plastic Zone by Shear Strength Reduction FEM. J. Disaster Prev. Mitig. Eng. 2003, 23, 1–8. [Google Scholar]
- Shi, B.T.; Zhang, Y.; Zhang, W. Strength reduction material point method for slope stability. Chin. J. Geotech. Eng. 2016, 38, 1678–1684. [Google Scholar]
- Ahangari Nanehkaran, Y.; Pusatli, T.; Chengyong, J.; Chen, J.; Cemiloglu, A.; Azarafza, M.; Derakhshani, R. Application of Machine Learning Techniques for the Estimation of the Safety Factor in Slope Stability Analysis. Water 2022, 14, 3743. [Google Scholar] [CrossRef]
- Nanehkaran, Y.A.; Licai, Z.; Chen, J.; Azarafza, M.; Yimin, M. Application of artificial neural networks and geographic information system to provide hazard susceptibility maps for rockfall failures. Environ. Earth Sci. 2022, 81, 475. [Google Scholar] [CrossRef]
- Azarafza, M.; Nanehkaran, Y.A.; Rajabion, L.; Akgün, H.; Rahnamarad, J.; Derakhshani, R.; Raoof, A. Application of the modified Q-slope classification system for sedimentary rock slope stability assessment in Iran. Eng. Geol. 2020, 264. [Google Scholar] [CrossRef]
- Bai, B.; Yuan, W.; Li, X. A new double reduction method for slope stability analysis. J. Cent. South Univ. 2014, 21, 1158–1164. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Sun, G.; Zheng, H. A stability analysis of rock slopes using a nonlinear strength reduction numerical manifold method. Comput. Geotech. 2021, 129, 103864. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Mei, G.; Xu, N. A statistics-based discrete element modeling method coupled with the strength reduction method for the stability analysis of jointed rock slopes. Eng. Geol. 2020, 264, 105247. [Google Scholar] [CrossRef]
- Deng, D.; Li, L.; Zhao, L. Limit equilibrium method (LEM) of slope stability and calculation of comprehensive factor of safety with double strength-reduction technique. J. Mt. Sci. 2017, 14, 2311–2324. [Google Scholar] [CrossRef]
- Yuan, W.; Bai, B.; Li, X.C.; Wang, H.B. A strength reduction method based on double reduction parameters and its application. J. Cent. South Univ. 2013, 20, 2555–2562. [Google Scholar] [CrossRef]
- Wei, Y.; Jiaxin, L.; Zonghong, L.; Wei, W.; Xiaoyun, S. A strength reduction method based on the Generalized Hoek-Brown (GHB) criterion for rock slope stability analysis. Comput. Geotech. 2020, 117, 103240. [Google Scholar] [CrossRef]
- Chen, Z.; Lei, J.; Huang, J. Finite element limit analysis of slope stability considering spatial variability of soil strengths. Chin. J. Geotech. Eng. 2018, 40, 985–993. [Google Scholar]
- Xu, Z.; Li, C.; Fang, F.; Wu, F. Study on the Stability of Soil-Rock Mixture Slopes Based on the Material Point Strength Reduction Method. Appl. Sci. 2022, 12, 11595. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, T.; Wu, W.; Zheng, H. Modelling the stability of a soil-rock-mixture slope based on the digital image technology and strength reduction numerical manifold method. Eng. Anal. Bound. Elem. 2021, 126, 45–54. [Google Scholar] [CrossRef]
- Zhang, W.L.; Sun, X.Y.; Chen, Y. Slope stability analysis method based on compressive strength reduction of rock mass. Rock Soil Mech. 2022, 43, 607–615. [Google Scholar]
- Lin, H.; Wang, W.; Li, A. Investigation of dilatancy angle effects on slope stability using the 3D finite element method strength reduction technique. Comput. Geotech. 2020, 118, 103295. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Lansivaara, T.; Wei, W.B. Reply to “Comments on ‘Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods’ by Y.M. Cheng, T. Lansivaara and W.B. Wei,” by J. Bojorque, G. De Roeck and J. Maertens. Comput. Geotech. 2008, 35, 309–311. [Google Scholar] [CrossRef]
- Nie, Z.; Zhang, Z.; Zheng, H. Slope stability analysis using convergent strength reduction method. Eng. Anal. Bound. Elem. 2019, 108, 402–410. [Google Scholar] [CrossRef]
- Sarkar, S.; Chakraborty, M. Stability analysis for two-layered slopes by using the strength reduction method. Int. J. Geo-Eng. 2021, 12, 24. [Google Scholar] [CrossRef]
- Wei, W.B.; Cheng, Y.M. Stability Analysis of Slope with Water Flow by Strength Reduction Method. Soils Found. 2010, 50, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Qiao, S.F.; Wang, C. Study on safety factor calculation and stability evaluation of dynamic slope based on strength reduction method. Fresenius Environ. Bull. 2019, 28, 5301–5311. [Google Scholar]
- Sun, G.; Lin, S.; Zheng, H.; Tan, Y.; Sui, T. The virtual element method strength reduction technique for the stability analysis of stony soil slopes. Comput. Geotech. 2020, 119, 103349. [Google Scholar] [CrossRef]
- Ding, Z.J.; Zheng, J.; Lu, Q.; Deng, J.; Tong, M. Discussion on calculation methods of quality index of slope engineering rock mass in Standard for engineering classification of rock mass. Rock Soil Mech. 2019, 40, 275–280. [Google Scholar]
- Wu, X.; Jia, Z.X.; Chen, Z.Y.; Wang, X.G.; Yang, J. Research of a synthetical method GMEM on ascertaining shear strength for engineering rock mass. Chin. J. Rock Mech. Eng. 2005, 24, 246–251. [Google Scholar]
- Wang, J.Q. Study on Slope Stability Analysis Based on Double Strength Reduction Method. Master’s Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]








| Method | Advantage | Disadvantage |
|---|---|---|
| Limit equilibrium method | The physical meaning of parameters and structures is very clear; the formula is simple and easy to understand intuitively. | Without considering the relationship between material stress and material strain, the obtained safety factor is only the average safety degree on the assumed sliding surface. |
| Probability analysis method | The reliability analysis method can objectively and quantitatively reflect the safety of a slope to a certain extent. | The probability model of each factor and its numerical characteristics cannot be reasonably selected, and the calculation process is relatively complex. |
| Fuzzy mathematical method | It is convenient to obtain objective and fair evaluation conclusions with strong uncertain information processing ability. | There is strong subjectivity when determining attribute weight. The problem of information overlap between evaluation reference levels cannot be solved. The calculation process is complicated. |
| Neural network method | It has obvious advantages in solving nonlinear problems and excellent performance in modeling nonlinear multivariate problems. | It shows excessive reliance on a large number of data samples, and the computer performance requirements are relatively high, which can easily lead to precision damage. |
| Grey analysis theory | The calculated workload is relatively small. Samples do not need to be distributed regularly. | The mechanism of connotative mechanics is unclear and there is no clear quantitative description. |
| Normal finite element reduction method | The stability factor can be calculated. The instability mechanism can be analyzed. | The calculation is time consuming and expensive. Failure mode has been determined before calculation. |
| Finite element reduction method of unified strength criterion | The stability factor can be calculated. The instability mechanism can be analyzed. Failure mode can be determined through calculation. | The calculation is time consuming and expensive. |
| H (m) | α (°) | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|
| β (°) | |||||||
| 10 | 30 | 10-30-20 | - | - | - | - | |
| 40 | 10-40-20 | 10-40-30 | - | - | - | ||
| 50 | 10-50-20 | 10-50-30 | 10-50-40 | - | - | ||
| 60 | 10-60-20 | 10-60-30 | 10-60-40 | 10-60-50 | - | ||
| 70 | 10-70-20 | 10-70-30 | 10-70-40 | 10-70-50 | 10-70-60 | ||
| 20 | 30 | 20-30-20 | - | - | - | - | |
| 40 | 20-40-20 | 20-40-30 | - | - | - | ||
| 50 | 20-50-20 | 20-50-30 | 20-50-40 | - | - | ||
| 60 | 20-60-20 | 20-60-30 | 20-60-40 | 20-60-50 | - | ||
| 70 | 20-70-20 | 20-70-30 | 20-70-40 | 20-70-50 | 20-70-60 | ||
| 30 | 30 | 30-30-20 | - | - | - | - | |
| 40 | 30-40-20 | 30-40-30 | - | - | - | ||
| 50 | 30-50-20 | 30-50-30 | 30-50-40 | - | - | ||
| 60 | 30-60-20 | 30-60-30 | 30-60-40 | 30-60-50 | - | ||
| 70 | 30-70-20 | 30-70-30 | 30-70-40 | 30-70-50 | 30-70-60 | ||
| Parameter | c (kPa) | φ (°) | ν | E (GPa) | γ (kN/m3) |
|---|---|---|---|---|---|
| Numerical | 1400 | 50.2 | 0.35 | 5.0 | 22.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, P.; Si, P.; Li, H.; Wu, F.; Su, Y.; Long, Y.; Cao, A.; Sun, Y.; Zhang, Q. Three-Dimensional Stability Analysis of Ridge Slope Using Strength Reduction Method Based on Unified Strength Criterion. Appl. Sci. 2023, 13, 1580. https://doi.org/10.3390/app13031580
Wang J, Liu P, Si P, Li H, Wu F, Su Y, Long Y, Cao A, Sun Y, Zhang Q. Three-Dimensional Stability Analysis of Ridge Slope Using Strength Reduction Method Based on Unified Strength Criterion. Applied Sciences. 2023; 13(3):1580. https://doi.org/10.3390/app13031580
Chicago/Turabian StyleWang, Jianxiu, Pengfei Liu, Pengfei Si, Huboqiang Li, Fan Wu, Yuxin Su, Yanxia Long, Ansheng Cao, Yuanwei Sun, and Qianyuan Zhang. 2023. "Three-Dimensional Stability Analysis of Ridge Slope Using Strength Reduction Method Based on Unified Strength Criterion" Applied Sciences 13, no. 3: 1580. https://doi.org/10.3390/app13031580





