Experimental Investigation of Enhancement of Natural Convective Heat Transfer in Air Using Ultrasound
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments
2.2. Mathematical Model
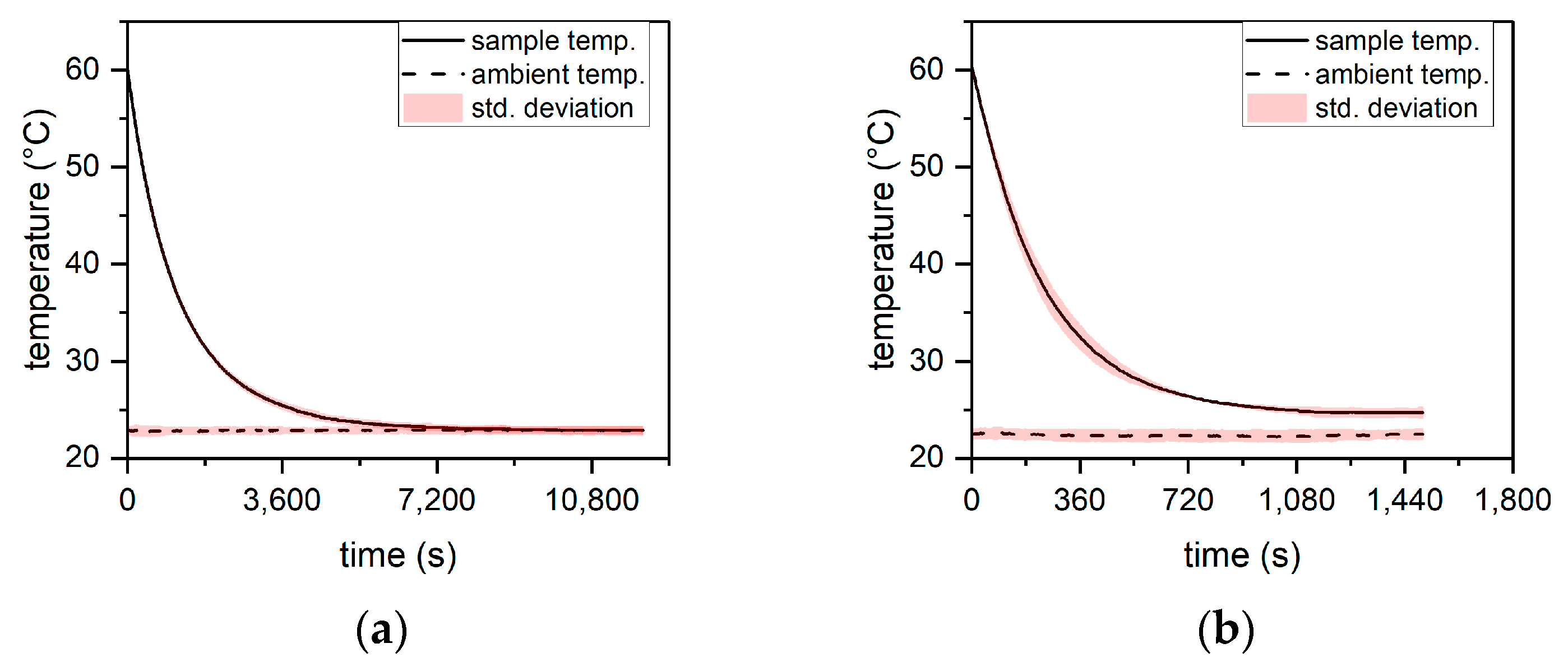
- The heat exchanged by the sample with the environment consists of two fluxes: heat transferred to the air by convection and the energy of ultrasound absorbed by the sample. The heat exchange between the sample and the PTFE mesh is negligibly small.
- The convective heat flux between a sample and the surrounding air is described by Newton’s law, i.e., it is proportional to the difference in the temperature of the sample surface and the temperature of the surrounding air.
- The resistance to heat conduction inside the sample is much lower than the convective resistance to heat transport to the outside of the sample.
2.3. Statistical Analysis
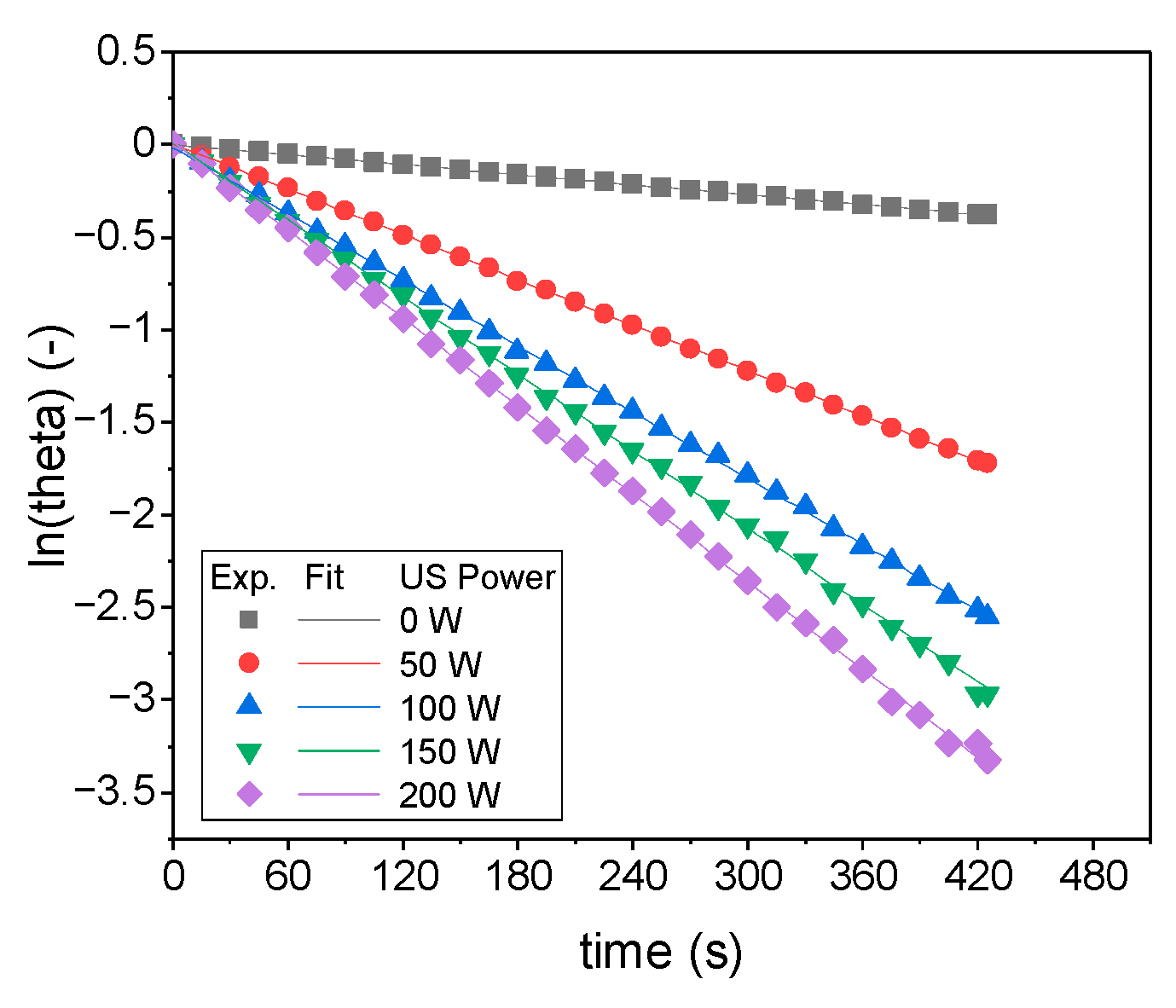
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, Y.; Ding, R. Analysis of Heat Transfer and Flow Characteristics of a Helically Coiled Tube with Twisted Elliptical in a Low Reynolds Number Flow. Processes 2022, 10, 2229. [Google Scholar] [CrossRef]
- Gómez-Villarejo, R.; Estellé, P.; Navas, J. Boron nitride nanotubes-based nanofluids with enhanced thermal properties for use as heat transfer fluids in solar thermal applications. Sol. Energy Mater. Sol. Cells 2020, 205, 110266. [Google Scholar] [CrossRef]
- Lin, W.; Shi, R.; Lin, J. Heat Transfer and Pressure Drop of Nanofluid with Rod-like Particles in Turbulent Flows through a Curved Pipe. Entropy 2022, 24, 416. [Google Scholar] [CrossRef]
- Tusar, M.; Noman, A.; Islam, M.; Yarlagadda, P.; Salam, B. CFD study of heat transfer enhancement and fluid flow characteristics of turbulent flow through tube with twisted tape inserts. Energy Procedia 2019, 160, 715–722. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Soleimani, S.; Ganji, D.D. Effect of electric field on hydrothermal behavior of nanofluid in a complex geometry. J. Mol. Liq. 2016, 213, 153–161. [Google Scholar] [CrossRef]
- Ijaz Khan, M.; Waqas, M.; Hayat, T.; Imran Khan, M.; Alsaedi, A. Behavior of stratification phenomenon in flow of Maxwell nanomaterial with motile gyrotactic microorganisms in the presence of magnetic field. Int. J. Mech. Sci. 2017, 131–132, 426–434. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Qiu, S.; Poh, H.J.; Mujumdar, A.S. Turbulent impinging jet heat transfer enhancement due to intermittent pulsation. Int. J. Therm. Sci. 2010, 49, 1247–1252. [Google Scholar] [CrossRef]
- Kaood, A.; Elhagali, I.O.; Hassan, M.A. Investigation of high-efficiency compact jet impingement cooling modules for high-power applications. Int. J. Therm. Sci. 2023, 184, 108006. [Google Scholar] [CrossRef]
- Singh, M.R.; Giri, A.; Lingfa, P. Enhancing heat transfer in phase change material-based cooling: A review. AIP Conf. Proc. 2022, 2421, 060008. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, J.; Barker, R.; Wang, C.; Neville, A.; Pessu, F. Effect of thermal cycling on the corrosion behaviour of stainless steels and Ni-based alloys in molten salts under air and argon. Sol. Energy 2022, 238, 248–257. [Google Scholar] [CrossRef]
- Zhou, W.; Therdthai, N. Section IV. Bakery Products: Manufacturing of Bread and Bakery Products. In Handbook of Food Products Manufacturing; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 1, pp. 257–278. ISBN 978-0-470-11355-4. [Google Scholar]
- Kowalski, S.J.; Szadzińska, J.; Pawłowski, A. Ultrasonic-Assisted Osmotic Dehydration of Carrot Followed by Convective Drying with Continuous and Intermittent Heating. Dry. Technol. 2015, 33, 1570–1580. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Szadzińska, J.; Łechtańska, J. Non-stationary drying of carrot: Effect on product quality. J. Food Eng. 2013, 118, 393–399. [Google Scholar] [CrossRef]
- Yu, H.; Mei, J.; Xie, J. New ultrasonic assisted technology of freezing, cooling and thawing in solid food processing: A review. Ultrason. Sonochem. 2022, 90, 106185. [Google Scholar] [CrossRef] [PubMed]
- Pagnossa, J.P.; Rocchetti, G.; Ribeiro, A.C.; Piccoli, R.H.; Lucini, L. Ultrasound: Beneficial biotechnological aspects on microorganisms-mediated processes. Curr. Opin. Food Sci. 2020, 31, 24–30. [Google Scholar] [CrossRef]
- Yu, X.; Bao, X.; Zhou, C.; Zhang, L.; Yagoub, A.E.-G.A.; Yang, H.; Ma, H. Ultrasound-ionic liquid enhanced enzymatic and acid hydrolysis of biomass cellulose. Ultrason. Sonochem. 2018, 41, 410–418. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Yan, L.; Ma, X.; Wang, W.; Zou, M.; Zhong, J.; Ding, T.; Ye, X.; Liu, D. Ultrasound promotes enzymatic reactions by acting on different targets: Enzymes, substrates and enzymatic reaction systems. Int. J. Biol. Macromol. 2018, 119, 453–461. [Google Scholar] [CrossRef]
- Sergeev, A.; Shilkina, N.; Tarasov, V.; Mettu, S.; Krasulya, O.; Bogush, V.; Yushina, E. The effect of ultrasound treatment on the interaction of brine with pork meat proteins. Ultrason. Sonochem. 2020, 61, 104831. [Google Scholar] [CrossRef]
- Franco, R.R.; Ojeda, G.A.; Rompato, K.M.; Sgroppo, S.C. Effects of short-wave ultraviolet light, ultrasonic and microwave treatments on banana puree during refrigerated storage. Food Sci. Technol. Int. 2023, 29, 50–61. [Google Scholar] [CrossRef]
- Yeoh, W.K.; Ali, A. Ultrasound treatment on phenolic metabolism and antioxidant capacity of fresh-cut pineapple during cold storage. Food Chem. 2017, 216, 247–253. [Google Scholar] [CrossRef]
- Alenyorege, E.A.; Ma, H.; Ayim, I.; Lu, F.; Zhou, C. Efficacy of sweep ultrasound on natural microbiota reduction and quality preservation of Chinese cabbage during storage. Ultrason. Sonochem. 2019, 59, 104712. [Google Scholar] [CrossRef]
- Arghavani-Beydokhti, S.; Rajabi, M.; Asghari, A. Coupling of two centrifugeless ultrasound-assisted dispersive solid/liquid phase microextractions as a highly selective, clean, and efficient method for determination of ultra-trace amounts of non-steroidal anti-inflammatory drugs in complicated matrices. Anal. Chim. Acta 2018, 997, 67–79. [Google Scholar] [CrossRef] [PubMed]
- Roohinejad, S.; Koubaa, M.; Sant’Ana, A.S.; Greiner, R. Chapter 4—Mechanisms of Microbial Inactivation by Emerging Technologies. In Innovative Technologies for Food Preservation; Barba, F.J., Sant’Ana, A.S., Orlien, V., Koubaa, M., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 111–132. ISBN 978-0-12-811031-7. [Google Scholar]
- Dehbani, M.; Rahimi, M.; Rahimi, Z. A review on convective heat transfer enhancement using ultrasound. Appl. Therm. Eng. 2022, 208, 118273. [Google Scholar] [CrossRef]
- Musielak, G.; Mierzwa, D.; Kroehnke, J. Food drying enhancement by ultrasound—A review. Trends Food Sci. Technol. 2016, 56, 126–141. [Google Scholar] [CrossRef]
- Lam, F.; Avramidis, S.; Lee, G. Effect of Ultrasonic Vibration on Convective Heat Transfer Between Water and Wood Cylinders. Wood Fiber Sci. 1992, 24, 154–160. [Google Scholar]
- Baffigi, F.; Bartoli, C. Influence of the ultrasounds on the heat transfer in single phase free convection and in saturated pool boiling. Exp. Therm. Fluid Sci. 2012, 36, 12–21. [Google Scholar] [CrossRef]
- Setareh, M.; Saffar-Avval, M.; Abdullah, A. Experimental and numerical study on heat transfer enhancement using ultrasonic vibration in a double-pipe heat exchanger. Appl. Therm. Eng. 2019, 159, 113867. [Google Scholar] [CrossRef]
- Hotrum, N.E.; de Jong, P.; Akkerman, J.C.; Fox, M.B. Pilot scale ultrasound enabled plate heat exchanger—Its design and potential to prevent biofouling. J. Food Eng. 2015, 153, 81–88. [Google Scholar] [CrossRef]
- Zhou, D.; Hu, X.; Liu, D. Local convective heat transfer from a horizontal tube in an acoustic cavitation field. J. Therm. Sci. 2004, 13, 338–343. [Google Scholar] [CrossRef]
- Cai, J.; Huai, X.; Liang, S.; Li, X. Augmentation of natural convective heat transfer by acoustic cavitation. Front. Energy Power Eng. China 2010, 4, 313–318. [Google Scholar] [CrossRef]
- Bartoli, C.; Franco, A.; Macucci, M. Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment. Acoustics 2020, 2, 279–292. [Google Scholar] [CrossRef]
- Martínez-Ramos, T.; Corona-Jiménez, E.; Ruiz-López, I.I. Analysis of ultrasound-assisted convective heating/cooling process: Development and application of a Nusselt equation. Ultrason. Sonochem. 2021, 74, 105575. [Google Scholar] [CrossRef] [PubMed]
- Azimy, H.; Meghdadi Isfahani, A.H.; Farahnakian, M. Investigation of the effect of ultrasonic waves on heat transfer and nanofluid stability of MWCNTs in sono heat exchanger: An experimental study. Heat Mass Transf. 2022, 58, 467–479. [Google Scholar] [CrossRef]
- Shen, G.; Ma, L.; Zhang, S.; Zhang, S.; An, L. Effect of ultrasonic waves on heat transfer in Al2O3 nanofluid under natural convection and pool boiling. Int. J. Heat Mass Transf. 2019, 138, 516–523. [Google Scholar] [CrossRef]
- Loh, B.-G.; Hyun, S.; Ro, P.I.; Kleinstreuer, C. Acoustic streaming induced by ultrasonic flexural vibrations and associated enhancement of convective heat transfer. J. Acoust. Soc. Am. 2002, 111, 875–883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Abatzoglou, N. Review: Fundamentals, applications and potentials of ultrasound-assisted drying. Chem. Eng. Res. Des. 2020, 154, 21–46. [Google Scholar] [CrossRef]
- Lee, D.-R.; Loh, B.-G. Smart Cooling Technology Utilizing Acoustic Streaming. IEEE Trans. Compon. Packag. Technol. 2007, 30, 691–699. [Google Scholar] [CrossRef]
- Uhlenwinkel, V.; Meng, R.; Bauckhage, K. Investigation of heat transfer from circular cylinders in high power 10 kHz and 20 kHz acoustic resonant fields. Int. J. Therm. Sci. 2000, 39, 771–779. [Google Scholar] [CrossRef]
- Musielak, G.; Mierzwa, D. Enhancement of Convection Heat Transfer in Air Using Ultrasound. Appl. Sci. 2021, 11, 8846. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Pawłowski, A.; Szadzińska, J.; Łechtańska, J.; Stasiak, M. High power airborne ultrasound assist in combined drying of raspberries. Innov. Food Sci. Emerg. Technol. 2016, 34, 225–233. [Google Scholar] [CrossRef]
- Stasiak, M.; Musielak, G.; Mierzwa, D. Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes. Energies 2020, 13, 6577. [Google Scholar] [CrossRef]
- Help Online—Origin Help—Theory of Nonlinear Curve Fitting. Available online: https://www.originlab.com/doc/origin-help/nlfit-theory (accessed on 5 December 2022).
- Help Online—Origin Help—Additional Information of R-Square. Available online: https://www.originlab.com/doc/en/Origin-Help/Details_of_R_square (accessed on 5 December 2022).




| Sample | Dimensions | ||
|---|---|---|---|
| Length (mm) | Width (mm) | Height (mm) | |
| Cube | 30 | 30 | 30 |
| Cuboid | 120 | 30 | 40 |
| Diameter (mm) | Height (mm) | ||
| Cylinder | 30 | 30 | |
| Small cylinder | 20 | 20 | |
| Sample | US Power | ||||
|---|---|---|---|---|---|
| 0 [W] | 50 [W] | 100 [W] | 150 [W] | 200 [W] | |
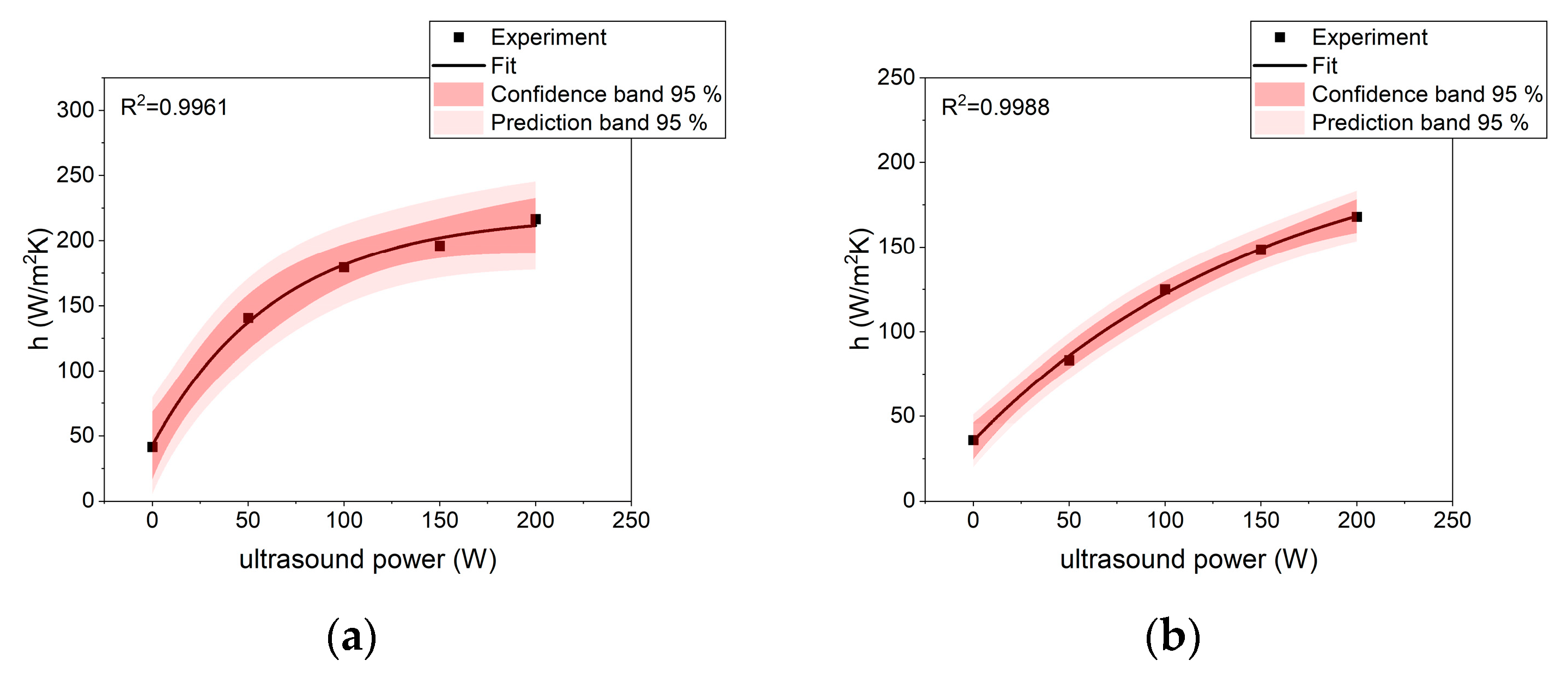
| cube | 41.64 ± 0.76 | 140.60 ± 3.02 | 179.50 ± 4.53 | 1926.20 ± 6.04 | 216.50 ± 6.04 |
| cuboid | 36.09 ± 0.31 | 83.28 ± 1.17 | 124.90 ± 4.53 | 148.50 ± 1.13 | 167.90 ± 1.13 |
| cylinder | 45.27 ± 0.76 | 150.80 ± 1.22 | 188.80 ± 1.51 | 230.10 ± 10.6 | 239.70 ± 6.80 |
| small cylinder | 52.43 ± 0.50 | 238.70 ± 4.53 | 396.50 ± 6.55 | 418.20 ± 3.24 | 487.90 ± 10.60 |
| Sample | a | b | c |
|---|---|---|---|
| cube | 219.9 ± 8.1 | 177.4 ± 9.3 | 9.85 × 10−1 ± 2.10 × 10−3 |
| cuboid | 219.8 ± 14.6 | 184.4 ± 13.8 | 9.94 × 10−1 ± 8.84 × 10−4 |
| cylinder | 256.5 ± 14.0 | 210.0 ± 14.6 | 9.87 × 10−1 ± 2.25 × 10−3 |
| small cylinder | 519.3 ± 38.6 | 466.3 ± 39.1 | 9.88 × 10−1 ± 2.50 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musielak, G.; Mierzwa, D.; Łechtańska, J. Experimental Investigation of Enhancement of Natural Convective Heat Transfer in Air Using Ultrasound. Appl. Sci. 2023, 13, 2516. https://doi.org/10.3390/app13042516
Musielak G, Mierzwa D, Łechtańska J. Experimental Investigation of Enhancement of Natural Convective Heat Transfer in Air Using Ultrasound. Applied Sciences. 2023; 13(4):2516. https://doi.org/10.3390/app13042516
Chicago/Turabian StyleMusielak, Grzegorz, Dominik Mierzwa, and Joanna Łechtańska. 2023. "Experimental Investigation of Enhancement of Natural Convective Heat Transfer in Air Using Ultrasound" Applied Sciences 13, no. 4: 2516. https://doi.org/10.3390/app13042516






