A Coordinated Supply Contract for a Two-Echelon Supply Chain Considering Learning Effects

Abstract

In a supply chain composed of multiple members, supply chain coordination plays a crucial role in achieving overall optimization and efficiency. Various supply contract forms have been studied in the existing literature to facilitate supply chain coordination. However, most existing literature has established coordination models assuming constant production costs. In reality, per-unit production costs often decrease as production quantity increases, which is called the learning effect. This paper underscores the significance of considering this learning effect in decision-making processes for coordinated supply contracts. We propose a supply contract scheme for channel coordination that incorporates the learning effect within a supply chain comprising a single manufacturer and a single retailer. In this framework, the manufacturer acts as a Stackelberg leader, initiating the process by designing and presenting the contract. The supply contract scheme is designed to ensure that the retailer’s order quantity aligns with the global solution. We also demonstrate how the contract parameters are determined when the relative bargaining powers of the supply chain members are given exogenously in the market. Our findings reveal that contracts with a learning curve can generate additional profits for both the manufacturer and the retailer compared to the existing coordinated contracts with static production costs. This study provides valuable insights into the impact of the learning effect on supply chain efficiency and offers practical implications for supply chain practitioners.

1. Introduction

Supply chain coordination is crucial for optimizing operational efficiency and enhancing overall performance, especially in today’s rapidly changing business environment [1]. Effective supply chain coordination can achieve a balance of interests among the various participants in the supply chain and drive collaborative efforts [2], i.e., the total profit of the decentralized supply chain is equal to that achieved under a centralized system. Supply contracts serve as key tools widely applied to establish cooperative relationships among the parties involved in the supply chain and ensure the realization of mutual benefits. Several channel coordination schemes have been introduced, including revenue-sharing contracts [3,4], cost-sharing contracts [5,6], and option contracts [7,8], etc. It is important to note that these supply contracts assume constant production costs throughout a production period. However, in real-world industries, the per-unit production cost is often reduced as production quantity increases or over time due to learning from repetitive activities [9,10,11]. This phenomenon is known as the learning curve (LC) effect. The LC effect has been widely observed in such industries as assembly tasks, aircraft manufacturing, apparel manufacturing, transportation, and semiconductor industries [1,8,9,10,11,12,13,14]. Wright [9] is regarded as the first to address the operations management (OM) problems under LC effects. Since then, a substantial body of literature has emerged, incorporating the LC effects as a crucial concept applied to achieve cost efficiency and optimize operational efficiency in OM problems [12,13]. The existing literature has addressed problems in pricing strategy [3,15,16,17], lot size [18,19,20,21], outsourcing decisions [22,23,24,25], scheduling [26,27,28,29,30], and supplier selection strategy [31,32], to name a few. Their findings demonstrate the effectiveness of implementing learning curve effects across various domains, showcasing improvements in system performance. However, few studies exist on coordinated supply-contract-design models in situations where LC effects are present. This study aims to fill the research gap by integrating the learning effects into the development of supply contracts. Specifically, we aim to provide a coordinated supply contract scheme for a two-stage supply chain with decreasing production costs due to the LC effects. The supply chain under consideration consists of two independent parties, a single manufacturer and a single retailer. It is assumed that the manufacturer acts as a Stackelberg game leader who takes the first move by designing and offering the contract. The contract is designed in a way that the retailer orders a quantity amount that aligns with the globally optimal solution.

This paper contributes to the literature twofold: (1) We develop a coordinated contract scheme for the manufacturer under LC effects. The scheme includes a procedure to determine a globally optimal order quantity for the supply chain under LC effects. Then, the revenue-sharing contract is applied for channel coordination. Our findings reveal that the contract with LC effects can provide additional profits for manufacturers and retailers compared to the existing coordinated contracts with static production costs. (2) We address the problems related to bargaining powers among supply chain members. We present how the contract parameters are chosen for different bargaining-power structures. The relationships between bargaining-power structures and revenue-sharing ratios are identified in the coordinated contracts.

This article is organized as follows. Section 2 reviews the related literature. In Section 3, we present basic supply-contract models for the centralized and decentralized system under static production costs, which are used as benchmarks. Section 4 presents the supply contract scheme that incorporates the LC effect in a supply-contract-design process. Section 5 presents numerical illustrations to demonstrate the performance of the proposed model compared to the existing benchmark models. We also show how the contract parameters affect the bargaining structure of each supply-chain member. Section 6 concludes our study with some findings and suggestions for future research directions.

2. Literature Review

This section reviews the relevant literature, summarizing existing research findings on the impact of learning effects on supply-chain management. It provides insights into how learning effects influence contract design, pricing strategy, supplier selection, outsourcing decisions, scheduling, and overall production strategy.

2.1. The Development of the Learning Effect

The learning effect or LC effect is an economic concept that signifies an increase in a worker’s efficiency as the task progresses, indicating a faster pace of task completion. In the context of manufacturing, the learning effect refers to the phenomenon where unit production time decreases as production volume increases. Study on the learning effect dates back to Wright [9], who investigated the LC effect in the aircraft industry. Within the realm of learning curves, various models have been developed. Among them, the log-linear model expressed below stands out as a widely used and straightforward type of LC model [9,27]:

$$c_x=c_1{x}^{-b}$$

(1)

where x is the total number of units made, $c_x$ is the cumulative average per-unit production cost for the first x units, and b is the exponent measuring the strength of learning. It is usually expressed as $b={-log}_{2}r$, where r is the learning rate. For example, if the production cost for the first product is 100, i.e., $c_1=100$, with the learning rate r = 0.8, then we have $c_2=80$, $c_4=64$, $c_8=51.2$, etc. Wright [9] found that the learning rate is about 80% in aircraft manufacturing, meaning that the per-unit production cost decreases by 20% for every doubling of total units made. The simplicity of the log-linear model caused many researchers to apply it when examining the learning effect in OM problems [10,14,33]. However, the log-linear model has the limitation that the cumulative average per-unit production cost, $c_x$, converges to zero as x approaches infinity. To address this problem, plateaued log-linear models are introduced by incorporating an additive constant c that accounts for the steady-state worker’s performance. This constant reflects the performance level attained when learning is completed or when workers’ improvement is constrained by machinery limitations [10,34,35]. Some researchers combine the log-linear model with the exponential upturn function [36,37], i.e., $c_x=c_1{x}^{-b}{e}^{-vx}$, where v is a positive parameter leading to an upturn for the large values of x. The exponential model may enhance predictions in extended production runs to offer improved predictions for long-duration production processes. Various models suitable for a range of tasks and manufacturing environments have been studied in addition to the learning-effect models mentioned above. For comprehensive learning-curve models, refer to [28,38,39,40,41].

2.2. The Application of Learning Effect to Supply-Chain Management

Understanding the application of LC models would offer numerous benefits, spanning both operational and strategic levels. Operational-level issues encompass inventory management, lot sizing, supplier selection, scheduling, capacity planning, etc. In contrast, strategic-level issues involve the optimal timing of new product introductions, competitive pricing decisions, determining investment levels, and vertical integration decisions [42]. Our review in this section mainly focuses on the application of the LC effects on supply chain operational problems, with the overarching objective of enhancing operational efficiency while minimizing costs.

2.2.1. Inventory Management and Lot Sizing

In supply-chain management and production decision-making, incorporating learning effects in production decisions leads to cost reductions and operational improvements. Jaber and Bonney [43] review the impact of learning on lot-size issues and explore the possibility of incorporating learning effects and JIT concepts. Keachie and Fontana [33] and Jaber and Bonney [44] modified the economic manufacture quantity model to integrate learning in production, revealing that increased production rates lead to reduced costs and rapid inventory accumulation, influencing production policies. Chand [19] introduces a mathematical model to determine optimal lot sizes and setup frequencies in a system with reduced setup costs attributed to worker learning. Anzanello [12] and Jaber and Bonney [45] examine LC models’ structural aspects, modifications to suit specific applications, and limitations in modeling workers’ learning processes. Timothy et al. [18] revised the models on optimal lot sizes with decreasing production costs, suggesting longer production runs based on learning and forgetting effects.

2.2.2. Supplier Selection and Outsourcing

Supplier selection is a multifaceted process that requires a consideration of learning effects for optimizing procurement, negotiations, and understanding shared supplier dynamics. Heese [46] underscores the significant influence of learning effects on buyer decisions when selecting suppliers, emphasizing the need to consider how learning reduces production costs and the ability to negotiate with the supplier over residual value. Agrawal et al. [47] explore the interaction between spillover effects, competition, and investment returns from shared suppliers on investment thresholds and leader investment time, further emphasizing the importance of considering these factors comprehensively in the supplier-selection process. Basu et al. [31] examine factors leading to single-sourcing, dual-sourcing, or hybrid-sourcing strategies under production learning and process improvement to determine the optimal purchasing strategy. Meanwhile, Silbermayr and Minner [32] analyze the optimal order decisions considering supplier characteristics, learning effects, and disruption factors in a dual-sourcing scenario.

Integrating learning effects into outsourcing decisions is crucial for understanding cost dynamics and competitive scenarios. Production learning and process improvement can help to determine the optimal outsourcing strategy and supplier configuration decision [24]. The impact of cost-learning effects on strategic manufacturers’ outsourcing decisions is examined within a two-period game, underscoring the significance of cost-learning effects in the outsourcing decision-making process [23,24]. Deng et al. [25] build a two-period model to investigate the competition effect of learning-by-doing in a supply chain with two competing manufacturers.

2.2.3. Scheduling and Line-Balancing Decisions

Scheduling is the process of arranging and organizing tasks within a defined timeframe. The decrease in production time due to the learning effect has a significant impact on the efficiency of scheduling. Azzouz et al. [27] extensively review scheduling problems under the learning effects. They classify the learning curve models into two main categories: position-based learning effects and sum-of-processing-time-based learning effects. Koltai and Kalló [28] propose scheduling classification schemes under different learning effect models. Their studies highlight how learning effects significantly optimize scheduling in various production scenarios, emphasizing efficiency gains in low-volume, high-mix production and addressing challenges in simple assembly lines. Learning effects play a vital role in assembly lines during the new product launch or the start of production [30]. Otto [30] and Silbermayr [32] examine the operation and balancing problems of simple assembly lines by considering learning effects.

2.2.4. Pricing

The learning effect and pricing strategy are closely intertwined. Xu et al. [15] examine the impacts of the learning effect on pricing strategies and channel efficiency in a decentralized supply chain consisting of a manufacturer and a retailer. It is assumed in their model that the demand is certain, only dependent on the sales price. They investigate two pricing strategies: open-loop (with given wholesale prices) and feedback pricing (with dynamic wholesale pricing) strategies. It is shown that the channel efficiency with the feedback pricing strategy is higher than that with the open-loop strategy. However, their models do not lead to supply chain coordination. Shum et al. [16] examine the impact of learning effects under dynamic pricing, price commitment, and price matching. They present a different perspective, suggesting that production-learning effects may only sometimes be beneficial for companies due to increased expected cost reductions and significant incentives for strategic customer waiting.

The existing literature has emphasized the significant role of learning effects in supply-chain management and production decision making, investigating the implications of these effects on supplier selection, procurement strategies, outsourcing decisions, production and scheduling decisions, and pricing strategies. However, few studies exist on coordinated supply-contract-design models in situations where LC effects exist. Tsao and Sheen [5] investigate a supplier–retailer supply chain where the retailer’s promotional efforts affect the sales amount, and sales-learning effects exist on the retailer side. They present a model featuring the promotion costs shared between the supplier and retailer while considering the time-based sales-learning effect. It is demonstrated that the promotion-cost-sharing strategy increases profits for all parties, leading to channel coordination. However, their study pertains to sales costs, not the production costs that are the focus of our study. Li et al. [3] address channel coordination problems for a two-period supply chain under learning effects. They examine the impact of the learning rate on the pricing strategies of the channel members, on the manufacturer’s production decisions, and on the retailer’s procurement decisions. They demonstrate that the double marginalization problem becomes more severe as the learning rate increases. They present a coordinated contract scheme by using the concept of revenue sharing within each period. They assume that learning effects on production costs occur only between two periods and not within a period.

This study addresses the research gap by incorporating the learning effect in developing supply contracts. We address channel coordination contracts in supply chain situations where production costs decrease as production volume increases. Specifically, we aim to provide a coordinated supply contract scheme for a two-stage supply chain under LC effects. The supply chain under consideration consists of two independent parties, a single manufacturer, and a single retailer. It is assumed that the manufacturer acts as a Stackelberg game leader who takes the first move by designing and offering the contract. The contract is designed in a way that the retailer orders a quantity amount that aligns with the globally optimal solution.

Our work differs from the existing literature in three aspects:

(1)

We investigate the coordination of supply contracts by integrating the learning effect in revenue-sharing contracts. By integrating the learning effect into the design of supply contracts, our aim is to pinpoint strategies that enhance the profitability of individual stakeholders while also bolstering the overall profitability of the entire supply chain;

(2)

We consider the bargaining power between the manufacturer and the retailer in contract-building processes. This consideration is essential in understanding how the distribution of profits is affected by the negotiation strength of each party, further enhancing the real-world applicability of our findings;

(3)

We use a numerical method, Newton–Raphson method, to find the optimal order quantity in the system with learning-curve effects. We will demonstrate that this approach is a simple and efficient solution method for the problem in this study.

3. Basic Supply-Chain Models without Learning-Curve Effects

We consider a two-echelon supply chain with one manufacturer and one retailer in which the manufacturer distributes its products through the retailer to the single-selling season market. The market demand is subject to high demand uncertainty and can be characterized by a stochastic variable X that follows a probability density function f(x) and a cumulative distribution function F(x). The product requires a long production lead time, and the order quantity must be determined well before the sale season. Any products unsold until the end of the selling season are salvaged at discounted prices. In our research, we have chosen model Equation (1) as the learning curve, with $b=-{log}_{2}r$, where r represents the learning rate. Then, the learning curve model is as follows:

$$c_Q=c_1{Q}^{-b}=c_1{Q}^{lo{g}_{2}r}$$

(2)

where Q is the production quantity and $c_Q$ is the cumulative average per-unit production cost for the Q units produced.

This model is relatively easy to comprehend and interpret. The model facilitates intuitive and convenient data fitting and analysis. The supply contract scheme in our study is based on a Stackelberg game framework, with the manufacturer acting as the leader, determining the supply contract and offering it to the retailer, and the retailer as the follower, deciding on order quantity based on the offered contract. The manufacturer anticipates the retailer’s decisions and tries to coordinate the supply chain by setting the contract parameters, including wholesale price and revenue-sharing fractions, so it is optimal for the retailer to determine the order quantities that are parallel to the decision in the centralized system. The notations in Nomenclature are used throughout this article. It is assumed that the sales price is greater than the production cost, and the excess inventory is sold at a lower price than the production cost, i.e., p > c > s.

To begin with, we discuss contract models for a supply chain with static production costs (without learning effects). These models are used as benchmarks for our model, which will be presented in the upcoming section. In a two-tier supply chain composed of a manufacturer and a retailer, the optimal production quantity for the overall supply chain in the face of uncertain demand can be obtained by treating these two tiers as a single organization and making decisions accordingly [41]. If the supply chain produces Q products and x is a realized demand, the sales quantity will be min (Q, x), and the excess inventory will be max (Q − x, 0). It is straightforward to have $S\left(Q\right)=E[\mathit{min}(Q,x)]=Q-{\int }_0^{Q}F\left(x\right)dx$ and $I\left(Q\right)={\int }_0^{Q}F\left(x\right)dx=Q-S\left(Q\right)$. Then, the expected profit of the supply chain is as follows:

$${\pi }_{Nc}=pS\left(Q\right)-cQ+sI\left(Q\right)=(p-c)Q-(p-s){\int }_0^{Q}F\left(x\right)dx$$

(3)

The first term is sales revenue, the second term is production cost, and the final term is salvage value from unsold products. The first and second derivatives of ${\pi }_{Nc}$ with respect to Q are as follows:

$$\frac{d{\pi }_{Nc}}{dQ}=(p-c)-(p-s)F\left(Q\right)$$

(4)

$$\frac{d^2{\pi }_{Nc}}{d{Q}^2}=-(p-s)f\left(Q\right)<0$$

(5)

We can determine that ${\pi }_{Nc}$ is a concave function in Q because its second derivative is negative. The optimal production quantity giving the maximum expected profit is obtained by the first order condition. Let $Q_{Nc}^{*}$ denote the optimal production supply quantity that maximizes the overall profit of the supply chain, then the following relationship holds.

$$Q_{Nc}^{*}=F^{-1}\left(\frac{p-c}{p-s}\right)$$

(6)

From the system’s perspective, it is optimal to produce $Q_{Nc}^{*}$, to maximize the whole supply-chain profit. When each member of the supply chain makes decisions independently, it is natural for them to make decisions to maximize their individual benefits. A commonly employed strategy in decentralized decision-making systems is wholesale contracts. In this strategy, the manufacturer sets the wholesale price, w, considering production costs and their desired profit margin. It is well known that the wholesale contract cannot lead to channel coordination due to the double marginalization problems. (The coordination can be achieved only for the case of w = c, which is not reasonable in real industries). Double marginalization occurs when each entity in the supply chain makes decisions to maximize its own profit, without considering the overall supply chain’s welfare. In wholesale contracts, the manufacturer sets the wholesale price to maximize its profit, and the retailer, in turn, determines the order quantity to maximize its profit. This sequential decision making leads to reduced total supply-chain profit and decreased consumer welfare. To overcome the double marginalization problems, various coordinated supply contracts have been proposed, among which revenue-sharing contracts are one of the most prominent contract models. In the revenue-sharing contract, the sales revenue is shared between the retailer and the manufacturer. Two parameters need to be designed by the manufacturer: wholesale price, w, and the revenue sharing, ϕ. At the end of the season, the retailer disposes of unsold products for a salvage price, s. It has been well known that channel coordination can be achieved by the revenue-sharing contract with the parameter set of w and s if the relationship $\frac{\varnothing p-w}{\varnothing p-s}=\frac{p-c}{p-s}$ holds [4]. Existing revenue-sharing contracts assume that the per-unit production cost is constant regardless of the production quantity. Supply contracts based on such static assumptions fail to provide channel-coordinated solutions when production costs dynamically vary with increases in production quantity. It will be seen in the forthcoming numerical illustration section that additional benefits can be realized for both manufacturers and retailers when we design supply contracts considering production cost dynamics due to learning-curve effects.

4. Coordinated Supply Contract under the Learning Curve (LC)

This section outlines a procedure for achieving overall supply chain optimization in the presence of learning effects. The manufacturer acts as a Stackelberg leader, initiating the process by designing and presenting the contract. Based on the contract terms, the retailer determines its order quantity to maximize expected profits. The contract employs revenue sharing with two key parameters: the wholesale price (w) and the revenue-sharing ratio (ϕ). The supply contract parameters are determined to ensure that the retailer’s order quantity aligns with the global solution.

The sequence of events in our supply-contract scheme under learning effects is as follows:

• The manufacturer predicts production costs, $c_Q$, depending on the production amount and determines $Q_{Lc}^{*}$ so that the SC profit can be maximized. The production costs are assumed to follow the log-linear function given in expression (2);
• The manufacturer designs the revenue-sharing contract with the wholesale price w and the profit-share ratio ϕ, and presents the contract to the retailer;
• The retailer determines the order quantity $Q_{Lr}$ to maximize the profit based on the uncertain demand, and places an order to the manufacturer;
• The manufacturer produces and delivers a quantity Q and receives payment from the retailer.
• The retailer sells the product at a given selling price during the sales season and gives a portion of the revenue to the manufacturer (revenue sharing);
• At the end of the season, the retailer disposes of unsold products for a salvage price.

In the following subsections, we introduce how the manufacturer can determine the optimal production quantity when the learning effects exist and set the contract parameters that lead to the retailer’s order quantity aligning with the global solution.

4.1. Model Construction with LC Effects for Maximizing SC Profit

The key problem here is finding the optimal level of production in a situation where production costs are reduced through learning effects. As previously discussed, the optimal production quantity can be found when we assume the system is centrally integrated. A central decision-maker will determine the production quantity in a way in which the overall profit of the supply chain is maximized. If the production supply quantity is Q, the expected value of the supply-chain profit, ${\pi }_{Lc}$, can be obtained as follows:

$${\pi }_{Lc}=pS\left(Q\right)+sI\left(Q\right)-c_{Q}Q=(p-c_1{Q}^{lo{g}_{2}r})Q-(p-s){\int }_0^{Q}F\left(x\right)dx$$

(7)

The first and second derivatives of Equation (7) with respect to Q are as follows:

$$\frac{d{\pi }_{Lc}}{dQ}=p-c_1(lo{g}_{2}r+1)Q^{lo{g}_{2}r}-(p-s)F\left(Q\right)$$

(8)

$$\frac{d^2{\pi }_{Lc}}{d{Q}^2}=-c_1(lo{g}_{2}r+1)lo{g}_{2}r{Q}^{(lo{g}_{2}r-1)}-(p-s)f\left(Q\right)$$

(9)

Based on the assumption p > s, Equation (9) follows that $\frac{d^2{\pi }_{Lc}}{d{Q}^2}<0$. Therefore, to maximize the profit of the supply chain, it is necessary to satisfy the condition $\frac{d{\pi }_{Lc}}{dQ}=0$, as stated below.

$$p-c_1(lo{g}_{2}r+1)Q^{lo{g}_{2}r}-(p-s)F\left(Q\right)=0$$

(10)

Equation (10) involves a nonlinear function, making it challenging to find an analytical solution directly.

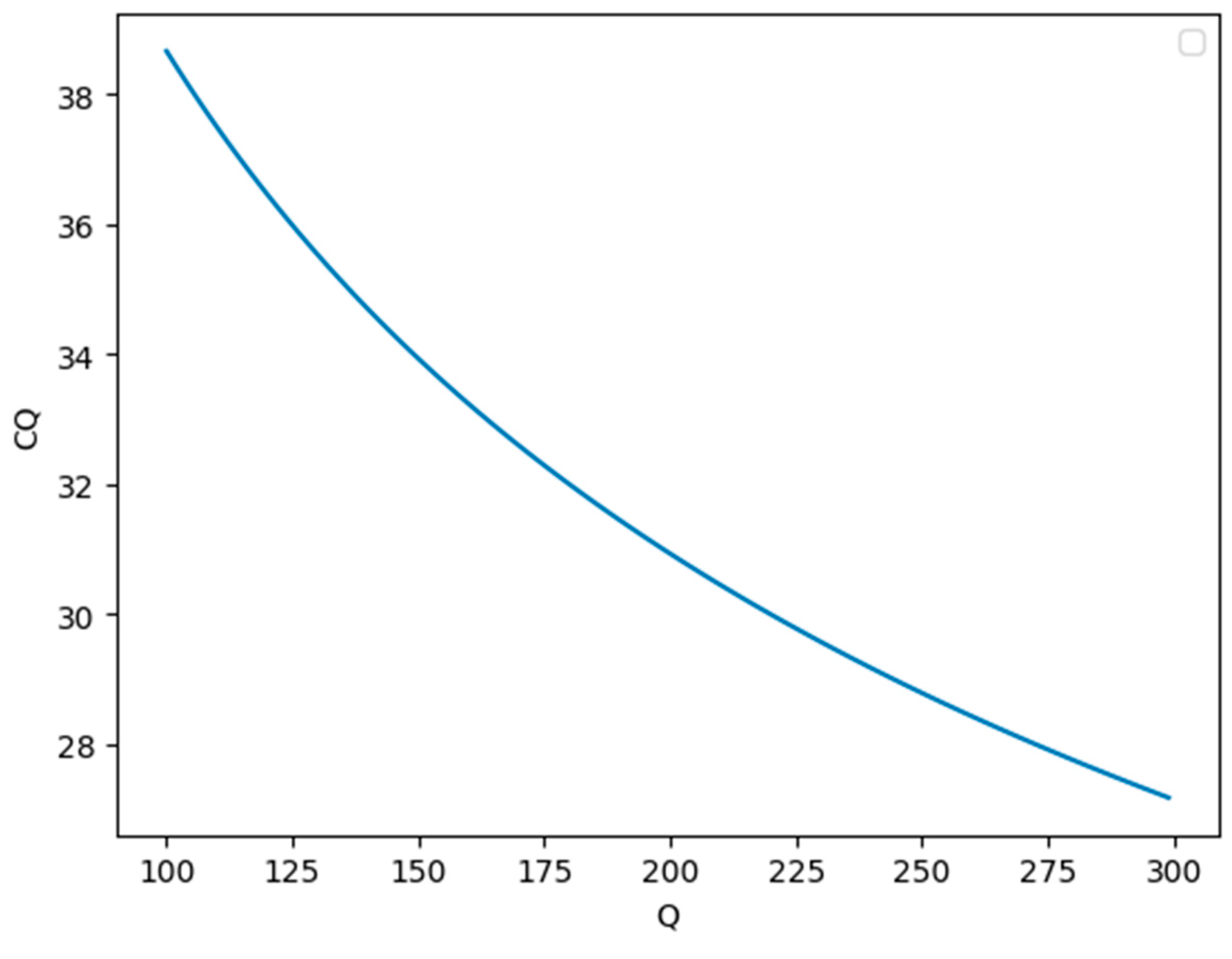
4.2. The Determination of Optimal Order Quantity by Using the Newton–Raphson Method

We employ a numerical method, the Newton–Raphson method, to find the optimal order quantity, $Q_{Lc}^{*}$, that satisfies Equation (10). The Newton–Raphson method is an iterative process that can approximate solutions to an equation with fast speed and good accuracy. The procedure is outlined as follows.

Step 1. Initialization: Set n = 0. Commence with an initial approximation, denoted as $Q_0$.

Step 2. Evaluate objective function and its derivatives: Obtain the first two derivatives of ${\pi }_{Lc}$ in terms of $Q_n$, ${\pi }_{Lc}^{\prime }\left(Q_n\right)$ and ${\pi }_{Lc}^{″}\left(Q_n\right)$.

Step 3. Update approximation: Update the approximation using the Newton–Raphson formula:

$$Q_{n+1}\leftarrow Q_n-\frac{{\pi }_{Lc}^{\prime }\left(Q_n\right)}{{\pi }_{Lc}^{″}\left(Q_n\right)}$$

(11)

Step 4. Iteration: Repeat Steps 2 and 3 iteratively until the desired level of accuracy is attained. Set $Q_{Lc}^{*}=Q_n$ in the final iteration.

4.3. The Development of Coordinated Contract Parameters

Now, given the optimal order quantity $Q_{Lc}^{*}$ under the learning-curve effects, we establish a supply contract to enable the retailer to order $Q_{Lc}^{*}$ units by applying the revenue-sharing contract. The supply contract includes the wholesale price and the revenue-sharing ratio to ensure the fulfillment of the given bargaining power. If the production supply quantity is Q, the expected profits of the retailer and manufacturer with the learning curve can be obtained as follows:

$${\pi }_{Lr}=(\varphi p-w)Q-(\varphi p-s){\int }_0^{Q}F\left(x\right)dx$$

(12)

$${\pi }_{Lm}=(w-c_1{Q}^{lo{g}_{2}r})Q+(1-\varphi )p(Q-{\int }_0^{Q}F\left(x\right)dx)$$

(13)

It is evident that ${\pi }_{Lr}$ is concave in Q. Hence, to maximize the profit of the retailer, it is necessary to satisfy the condition $\frac{dE{\pi }_{Lr}}{dQ}=0$, giving the following equations:

$$F\left(Q_{Lr}^{*}\right)=\frac{\varphi p-w}{\varphi p-s}$$

(14)

$$Q_{Lr}^{*}=F^{-1}\left(\frac{\varphi p-w}{\varphi p-s}\right)$$

(15)

The channel coordination can be achieved in the condition that $Q_{Lr}^{*}=Q_{Lc}^{*}$. This condition leads to $\frac{\varnothing p-w}{\varnothing p-s}={\mathrm{z}}^{*}$ where ${\mathrm{z}}^{*}=F\left(Q_{Lc}^{*}\right)$. Then, the following equations must hold for the channel coordination:

$$w=(1-z^{*})\varphi p+s{z}^{*}$$

(16)

4.4. The Identification of the Feasible Range of ϕ with Bargaining Power α

By observing the equation, it can be deduced that an increase in ϕ leads to an increase in w in the coordinated contract. The optimal set of (w*, ϕ*) can have infinite combinations, and each combination affects the profit structure of both the manufacturer and the retailer. As the values of (w*, ϕ*) increase, the retailer’s profit increases while the manufacturer’s profit decreases. The selection of appropriate (w, ϕ) can be determined based on the bargaining power of supply-chain members. The total profit generated in the supply chain is distributed among the members based on their relative bargaining power. Let α represent the expected retailer’s profit share in the total supply-chain profit, i.e., $\alpha =\frac{{\pi }_{Lr}}{{\pi }_{Lc}}$. From expressions (7) and (12), we can derive the following (note that $I\left(Q\right)={\int }_0^{Q}F\left(x\right)dx$):

$$\alpha =\frac{(\varphi p-w)Q-(\varphi p-s)I\left(Q\right)}{(p-c_Q)Q-(p-s)I\left(Q\right)}$$

(17)

When we restate Equation (17) for ϕ, we have the following expression.

$$\varphi =\frac{s}{p}+\alpha \frac{(p-c_Q)Q-(p-s)I\left(Q\right)}{p[z^{*}Q-I(Q\left)\right]}$$

(18)

From expression (18), we can see that ϕ increases as α increases in the coordinated contract. Similarly, from Equation (16), w also increases as α increases. To be feasible in industries, α should lie between zero and one, and so should ϕ. When α = 0 (all the SC profit goes to the manufacturer), we have:

$${\varphi }_{\alpha =0}=\frac{s}{p}$$

(19)

Since p > s is assumed, the range of ϕ, $\varphi \in (0,1)$ is feasible. Equation (19) indicates that the revenue-sharing ratio ϕ should be at least $\frac{s}{p}$ for the channel coordination. In case of α = 1 (all the SC profit goes to the retailer), we have:

$${\varphi }_{\alpha =1}=\frac{s}{p}+\frac{(p-c_Q)Q-(p-s)I\left(Q\right)}{p[z^{*}Q-I(Q\left)\right]}$$

(20)

We prove that ${\varphi }_{\alpha =1}<1$ (the proof is given in Appendix A). Since ϕ is an increasing function in terms of α, we can have the possible range of ϕ under the coordinated supply contract as follows:

$$\frac{s}{p}\le \varphi \le \frac{s}{p}+\frac{(p-c_Q)Q-(p-s)I\left(Q\right)}{p[z^{*}Q-I(Q\left)\right]}$$

(21)

Expression (21) shows that all bargaining-power structures, that is, 0 ≤ α ≤ 0, can be satisfied under the presented coordinated supply-contract scheme.

5. Numerical Illustrations

In this section, we provide numerical illustrations to demonstrate the performance of our proposed model compared to the existing benchmark models. Additionally, we demonstrate how the contract parameters affect the bargaining structure of each member in the supply chain. We use specific parameter values, p = 60, s = 10, w = 40 (under wholesale contract), $c_1=170.3$, and r = 0.8 (under learning effect case). We assume that the demand variable X follows a uniform distribution, X ~ Uniform (100, 300). To visually represent and analyze these results, we leverage an open-source ‘matplotlib.pyplot’ library (https://matplotlib.org/) in Python version 3.10. Figure 1 shows the production cost over production quantity under learning-curve effects.

First, we consider a supply-chain system where LC effects are not considered. Here, we assume that the per-unit production cost remains constant at 30.0 (i.e., c = 30.0). (This corresponds to the average production cost when 220 items are produced in the system under learning-curve effects, i.e., $c_{220}=170.3\times {220}^{{\log }_{2}0.8}=30.0$). In the centralized system without learning effects, we can derive the optimal production quantity ($Q_{Nc}^{\mathrm{*}}$) using expression (6): $Q_{Nc}^{\mathrm{*}}=F^{-1}\left(\frac{p-c}{p-s}\right)=F^{-1}\left(0.6\right)=220$. The total expected supply-chain profit, calculated from Equation (3), is 4800. In a decentralized system with independent supply-chain members considering a wholesale contract (w = 40), the retailer’s optimal order quantity ($Q_{Nw}^{\mathrm{*}}$) is derived as follows: $Q_{Nw}^{\mathrm{*}}=F^{-1}\left(\frac{p-w}{p-s}\right)=F^{-1}\left(0.4\right)=180$, resulting in the total expected supply-chain profit of 4600. The finding shows that the wholesale contract yields a supply-chain profit that falls short by 200 compared to the centralized system due to the double marginalization problem. To address the double marginalization problem in the decentralized system, a revenue-sharing contract can be adopted with appropriate parameters, wholesale price (w), and revenue-sharing ratio (ϕ). For example, if we set ϕ = 0.5 in the revenue-sharing contract, we can obtain w = 17.2 by the channel coordination relationship $\frac{\varnothing p-w}{\varnothing p-s}=\frac{p-c}{p-s}$. With the revenue-sharing contract with parameters (w, ϕ) = (17.2, 0.5), it is possible to achieve the same overall optimal profit of 4800 as would be attained in a centralized decision-making scenario. In Figure 2, the orange-color curve shows supply-chain performance over different order quantities without the consideration of learning-curve effects. It is seen that the maximum supply-chain profit is realized when 220 products are ordered for the system under static production costs.

Now, let us consider the proposed contract for a supply-chain system under learning-curve effects with r = 0.8. The first step in the proposed contract is to find the optimal production (order) quantity, considering the learning effects. The proposed iteration method (the Newton–Raphson method) in Section 4.2 provides the optimal order quantity of 263.2. (In this scenario, only five iterations are enough to find the optimal quantity.) This yields the corresponding production cost, $c_{263}=c_1{Q}^{{\log }_{2}r}=170.3\times {263.2}^{{\log }_{2}0.8}=28.32$, and $z^{*}=F\left(263.2\right)=0.816$. (Refer to expressions (2) and (6) for the calculations.) According to Equation (7), the resulting total expected supply-chain profit is 5011. It should be noted that the resulting profit is increased by 211, compared with the profit from the optimal decision without the consideration of LC effects. The blue-color curve in Figure 2 illustrates the total expected profit of the supply chain with LC effects. This observation emphasizes that considering learning effects during the formulation of supply-contract designs is crucial for achieving overall optimization.

The primary goal of our study is for the manufacturer to design the supply contract that achieves channel coordination for the system with LC effects. Two contract parameters are involved in decision processes, w and ϕ. All the (w, ϕ) sets satisfying expression (16) in Section 4.3 lead to channel coordination. For example, a specific parameter (w, ϕ) = (13.681, 0.5) that satisfies expression (16) is one of the possible coordinated solutions. In this case, from the perspective of the retailer, ordering 263.2 units maximizes its expected profit. This decision ultimately yields an expected profit of 2964 for the retailer and 2047 for the manufacturer. (Refer to expressions (12) and (13) for this mathematics in Section 4.3) As a result, the expected total profit becomes 5011, the same as in the centralized system. It is noted that in this scenario, 59.1% of the total supply-chain profit goes to the manufacturer, while the remaining 40.9% goes to the retailer.

The profit distributions between the manufacturer and retailer are often determined based on the relative bargaining power of each supply-chain member. One distinct feature of the proposed contract scheme is that any bargaining-power structure can be satisfied with the appropriate manipulation of contract parameters.

Table 1. Feasible profit distribution given the revenue-sharing with LC effects.

$\mathit{\varphi }$	w*	${\mathit{\pi }}_{\mathit{L}\mathit{r}}$	${\mathit{\pi }}_{\mathit{L}\mathit{m}}$	${\mathit{\pi }}_{\mathit{L}\mathit{c}}$	α
0.167	8.161	0	5011	5011	0.000
0.200	10.368	296	4714	5011	0.059
0.300	11.472	1185	3825	5011	0.237
0.400	12.576	2074	2936	5011	0.414
0.500	13.681	2964	2047	5011	0.591
0.600	14.785	3853	1158	5011	0.769
0.700	15.889	4742	269	5011	0.946
0.730	16.224	5011	0	5011	1.000

w*: the optimal wholesale price when a specific ϕ is given.

illustrates a set of contract parameters satisfying different bargaining-power structures in the new revenue-sharing contracts in which LC effects are integrated. (Refer to Section 4.3 and Section 4.4 for the mathematics.) When all the supply-chain profits are allocated to the manufacturer with α = 0, the revenue-sharing ratio for the coordinated supply contract is ϕ = 0.167, which is calculated from expression (19). Then, the corresponding wholesale price for the coordinated contract is w = 8.161. On the other hand, if all the supply-chain profits were to go to the retailer with α = 1, the revenue-sharing ratio for the coordinated supply contract would be ϕ = 0.730, which is obtained from expression (20). The corresponding wholesale price for the coordinated contract is w = 16.224. For the range of 0 ≤ α ≤ 0, the parameter sets in the coordinated contract, w and ϕ, are obtained from expression (18). It is observed that the value of ϕ has a lower limit, ϕ = 0.617, and an upper limit, ϕ = 0.730 in the coordinated contract. The results show that that all the profit split structures with different values of α can be satisfied with appropriate contract parameters. It is also seen that the revenue-sharing ratio, ϕ, and the wholesale price, w, increase as the retailer’s profit ratio increases. This finding can be explained by the natural tendency for retailers to retain a significant portion of the profit when the wholesale price is high.

Additional Discussions

Table 2. The optimal solution of wholesale contract and revenue-sharing contracts with and without LC effects.

	Wholesale	Revenue-Sharing without LC	Revenue-Sharing with LC
$Q^{*}$	180	220	263
w	40	22.17	13.79
ϕ	-	0.6739	0.5101
${\pi }_r$	2800	2922	3053
${\pi }_m$	1800	1878	1958
${\pi }_c$	4600	4800	5011

Q*: the optimal order quantity when a set of w and ϕ is given.

compares the performance of the wholesale contract and revenue-sharing contracts with and without considering the LC effects. Under the wholesale contract, the expected profit of the supply chain is ${\pi }_{Nc}=4600$ as discussed previously, with the retailer’s expected profit at 2800 (60.9% of the total profit) and the manufacturer’s expected profit at 1800 (39.1% of the total profit). We adjusted the contract parameters, w and ϕ, for the revenue-sharing contracts to achieve the same profit-sharing ratio, α, as the wholesale contract. Under the revenue-sharing contract without LC effects, the expected profit of the supply chain is ${\pi }_{Nc}=4800$, with retailer’s profit at 2922 and manufacturer’s profit at 1878. It is observed that the revenue-sharing contract generates more profit compared to the wholesale contract. Under the revenue-sharing contract with LC effects, the expected profit of the supply chain is ${\pi }_{Lc}=5011$, with the retailer’s profit at 3049 and the manufacturer’s profit at 1962. It is evident that the coordinated contract results in even greater profit when LC effects are considered in the contract-design process. The proposed contract scheme not only maximizes the overall total expected profit but also ensures a win–win situation for both the manufacturer and retailer.

Our investigation explores the integration of learning-curve (LC) effects within revenue-sharing contracts, revealing a mechanism conducive to supply-chain coordination across various bargaining-power dynamics between manufacturers and retailers. The adaptability of the proposed contract parameters (w, ϕ) to diverse profit distribution scenarios has been illustrated in Table 1. Our findings indicate a notable enhancement in supply-chain profitability with the inclusion of LC effects, surpassing the efficacy of traditional contracts reliant on static production costs. Through the new contract scheme, supply-chain profits can be distributed fairly, motivating all parties to leverage LC effects and enhance system efficiency. This coordination mechanism optimizes individual profits and culminates in mutual advantages, underscoring the strategic value of such adaptive contractual frameworks in supply-chain management.

6. Conclusions

The reduction in production costs due to learning effects is a widely observed phenomenon across various industries. However, the majority of existing supply contracts are based on static production costs, thus missing out on the potential benefits derived from learning effects within the supply chain. This paper has explored a two-echelon supply chain, taking into account the impact of the learning effects. We have introduced a coordinated supply contract where learning effects are integrated into the contract-building process. Our findings reveal that the proposed contract with the learning effects can generate additional profits for both the manufacturer and the retailer compared to the existing coordinated contracts with static production costs. Furthermore, our study addresses the complexities arising from diverse bargaining powers among supply chain members, illustrating how contract parameters are determined for different profit-distribution cases. The results reveal that the new supply contract with learning effects can accommodate any profit distribution structure through the appropriate manipulation of contract parameters.

The current study is subject to several limitations, which pave the way for potential future research avenues:

−

The proposed contract is based on the log-linear learning-curve model. Further research is needed to explore the implications of other learning-curve models, as various alternative models also exist;

−

Our study only considers risk-neutral supply-chain participants. Investigating risk-averse and risk-seeking participants would be an interesting research avenue;

−

While we examine revenue-sharing contracts to coordinate the supply chain under learning-curve effects, exploring other contract types like option contracts and buyback contracts with learning effects is warranted;

−

We solely consider learning effects, neglecting forgetting effects. Future research incorporating both learning and forgetting effects would provide a more comprehensive understanding of production efficiencies over time;

−

This study focuses on the two-echelon supply-chain structure. Investigating the impact of the learning effects on various supply-chain structures, especially those involving multiple echelons or complex network relationships, could provide deeper insights into the applicability of coordination strategies across different supply-chain models;

−

Further analyses could also be conducted, incorporating psychological factors such as retailers’ overconfidence in supply-chain decisions for enhanced supply-chain coordination.

In conclusion, our study offers valuable insights into the impact of learning effects on supply-chain efficiency and provides practical implications for supply-chain practitioners. Addressing the identified limitations in future research endeavors would contribute to advancing the field of supply-chain management.