The Advanced Assessment of Nanoindentation-Based Mechanical Properties of a Refractory MoTaNbWV High-Entropy Alloy: Metallurgical Considerations and Extensive Variable Correlation Analysis
Abstract
:1. Introduction
- (a)
- High-Entropy Alloys and Nanoindentation-based mechanical properties
- (b)
- Analysis of Input Importance on Mechanical Properties Using Various Models
2. Experimental Procedure
2.1. Materials and Methods
2.2. Creep Assessment Calculation Framework
3. Results and Discussion
3.1. Brief Discussion on the System’s Microstructure
3.2. Nanoindentation-Based Basic Mechanical Property Assessment
3.2.1. Obtained Data and Metallurgical–Microstructural Evaluation
- (a)
- The indentation hardness values lie within a broad range of roughly 800–1000 HV and are, in general, in good agreement with other experimental efforts dealing with this refractory high-entropy alloy [25]. The two different input parameters, i.e., preset depth and loading speed, seem to have, in general, the opposite effect: the higher the preset depth, the lower the hardness values, whereas the lower the loading speed, the higher the hardness. Concerning the effect of the preset depth, the observed trend is expected since (a) according to the Oliver–Pharr approach [26,27], the contribution of the load P and the indentation depth h in calculating the hardness is not analogous (hardness is a function of P/h2), and as such, as the indentation depth increases, the hardness values decrease; (b) furthermore, if we recall that hardness is practically the resistance to plastic deformation, the observed trend shows that at higher indentation depths, the plastic deformation can be expressed more easily. This is attributed to the fact that at higher indentation depths, the affected material volume underneath the indenter increases, which implies that the number of dislocations to accommodate the plastic deformation increases, which, in this way, increases the capability for the plastic flow to be expressed. The effect of the loading speed, as already stated, is, in general, the opposite. Hardness values decrease as the loading speed increases. It must be mentioned, however, that the effect of the loading speed is not as severe as the effect of the indentation depth. The trend concerning the effect of the loading speed is also associated with the availability for plastic deformation dislocations. As the loading speed increases, the rate of dislocation generation increases, ensuring that there are enough dislocations to contribute to the plastic flow of the alloy. The effect is more profound at lower indentation depths and seems to fade as the indentation depths increase. This is attributed to the fact that the affected material volume where dislocations can generate increases, and this increase gradually compensates for the restriction of dislocations at the lower depths.
- (b)
- The analysis of the indentation modulus of elasticity (Eit) presents a nuanced picture, particularly when considering the effect of preset depth. Identifying a clear trend in Eit values in relation to preset depth proves challenging. However, an observable influence is noted with changes in loading speed; a decrease in loading speed generally leads to a reduction in Eit, an effect that becomes more pronounced at preset depths of 1500 and 2000 nm. Several critical factors contribute to this behavior. Firstly, Eit and elasticity (E), more broadly, are intrinsically linked to the elastic strain field within the lattice and the bond energy among atoms. This fundamental relationship underscores the mechanical response of materials under indentation. Secondly, the concept of Local Chemical Order (LCO), as discussed in studies [28,29,30,31,32], highlights the degree of atomic ordering within alloys. Li et al. [28] illustrate that alloys, when subjected to high heat treatment temperatures, tend to resemble a fully disordered solid solution characterized by a random atomic distribution within the lattice. This state is associated with high configurational entropy and minimal ordering. In contrast, at lower temperatures or in the as-cast condition, there is invariably some presence of LCO, leading to the regional formation of ordered atomic clusters. Such conditions lower configurational entropy and elevate LCO values. The manifestation of LCO, where atomic movement and organization into ordered clusters occur, serves to alleviate the elastic strain energy in highly disordered structures, consequently reducing elastic moduli. Thirdly, the impact of LCO extends beyond temperature influences, encompassing potential stress fields induced during mechanical loading. For instance, Kang et al. [10] observed in their nanoindentation study of a CoCrFeMnNi high-entropy alloy that a stress gradient between dislocations and the bulk material promotes the segregation of elements from the distorted lattice to dislocation lines. This process aims to mitigate the intense lattice stress field and foster the formation of thermodynamically stable atomic clusters driven by enthalpy of formation. Notably, the propensity for atomic migration, leading to enhanced LCO, is greater when dislocations show low mobility or are stationary. Considering these insights, it is logical to deduce that at reduced loading speeds, the diminished mobility of dislocations augments atomic movement and LCO formation. Consequently, this results in a more effectively relieved lattice stress field, reflected in decreased Eit values.
- (c)
- Regarding the nit factor, which denotes the ratio of energy observed in the elastic region to the total absorbed energy, it exhibits trends analogous to hardness as detailed in study [33]. This parallel suggests a consistent relationship between the material’s hardness and its ability to absorb and release energy during indentation, highlighting the nit factor as a crucial parameter for understanding material behavior under mechanical stress.
3.2.2. Statistical Analysis
- For the relationship between Input Initial Indentation Depth and Output HV (hardness value), correlation analysis reveals a strong negative correlation of −0.90, while Random Forest analysis assigns a high importance score to indentation depth. ANOVA underscores this with a statistically significant effect, and Partial Dependence Plots illustrate a decreasing trend in HV as indentation depth increases. The unified conclusion from all methods is that indentation depth significantly and negatively impacts hardness value, indicating lower hardness at greater indentation depths.
- Regarding Input Initial Indentation Depth and Output nIt (%), there is a strong negative correlation of −0.86 from correlation analysis and a high importance score from Random Forest, slightly lower than that for HV. ANOVA shows a statistically significant effect, whereas Partial Dependence Plots suggest an increasing trend in nIt (%) with deeper indentations. Despite the negative correlation, the increasing trend in nIt (%) indicated by PDPs points to a potential increase in nIt (%) with indentation depth, highlighting possible non-linear relationships not captured by the correlation coefficient.
- In the case of Input Loading Speed and Output EIt (GPa), correlation analysis shows a moderate positive correlation of 0.67. Random Forest assigns a lower importance score to loading speed compared to indentation depth, and ANOVA does not find a statistically significant effect. However, Partial Dependence Plots depict an increasing trend in EIt with higher loading speeds. This suggests a generally positive effect of loading speed on EIt, although the lack of statistical significance in ANOVA indicates a potentially weaker or more complex relationship.
- For the correlation between Output HV and Output nIt (%), a strong positive correlation of 0.78 suggests that these outputs tend to increase or decrease in tandem, hinting at an underlying material property that influences both. Lastly, the moderate negative correlation of −0.50 between Output EIt (GPa) and Output nIt (%) suggests an inverse relationship, possibly reflecting different material responses under elastic and plastic deformations.
3.3. Creep Assessment
3.3.1. Creep Behaviour Assessment—Metallurgical Approach
- (1)
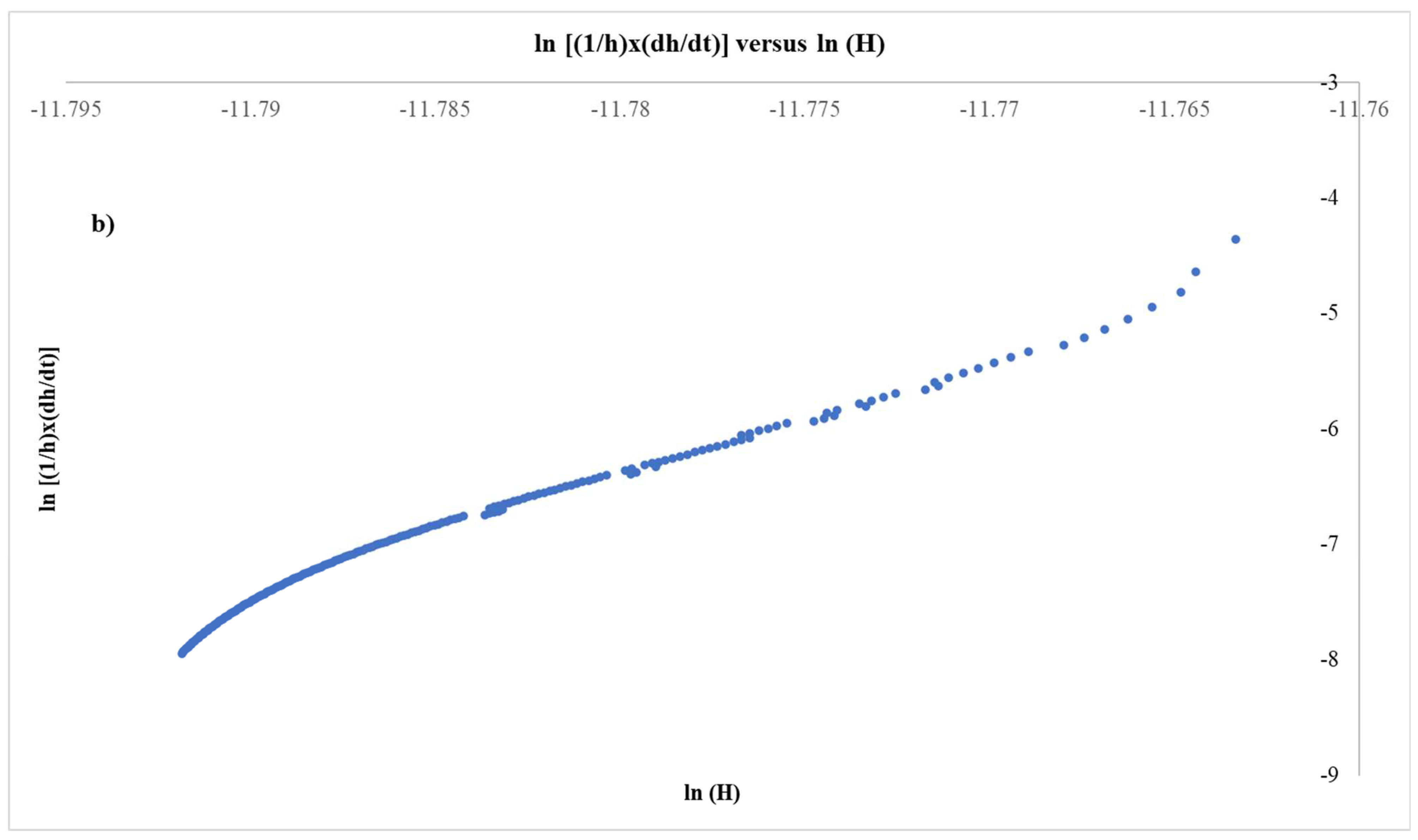
- Figure 10a presents a typical indentation displacement (Δh) vs. time (t) curve for the holding stage (creep stage) along with the typical correlation parameters. These correlation parameters were obtained by applying a power law fitting. This observation is very important. It has been proposed by many researchers that a power law fitting of the creep displacement as a function of the holding time suggests a dislocation-driven creep deformation and, more specifically, a dislocation glide mode [2,5,9,11,12,34]. Despite the fact that Li et al. [4], in their early work, pointed out that a power law creep behavior is mainly associated with dislocation climb and/or dislocation climb–glide mixed mode at intermediate to high temperatures, in their concluding remarks, they admit that at low temperatures, dislocation glide-induced plasticity must be the predominant mechanism due to the high stresses being developed within the elastic–plastic zone. As such, in the present effort, since a power law of extremely good fitting was observed, dislocation glide is considered the main creep deformation mechanism.
- (2)
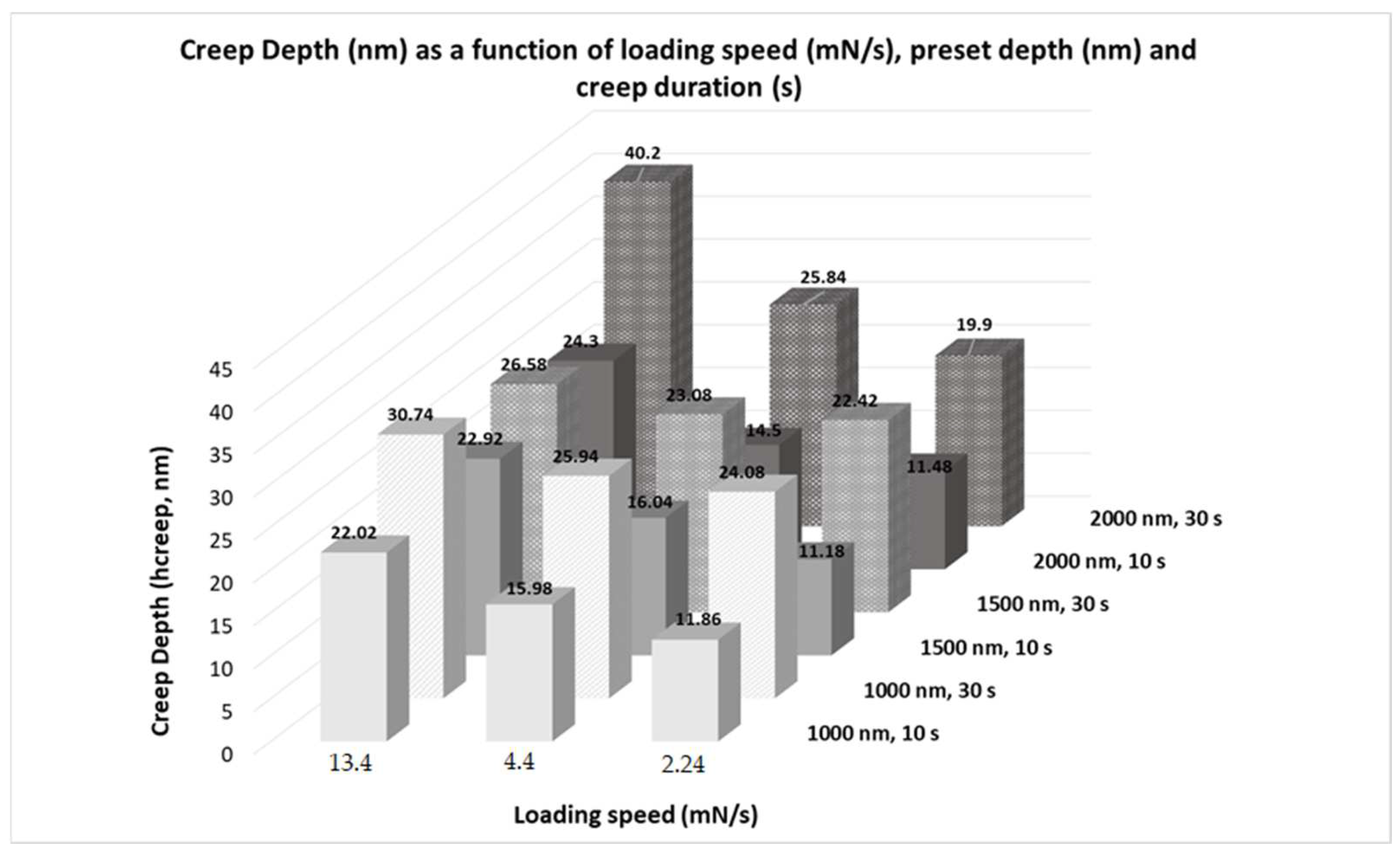
- Net Creep deformation (hcreep): The first important observation is the fact that, irrespective of the testing conditions, creep deformation increases as the creep period increases. This is expected since the more prolonged the time, the more time for the available dislocations to move and provide plastic flaws, i.e., plastic deformation. Similar observations can also be found in other experimental efforts [8,9,22].
- (3)
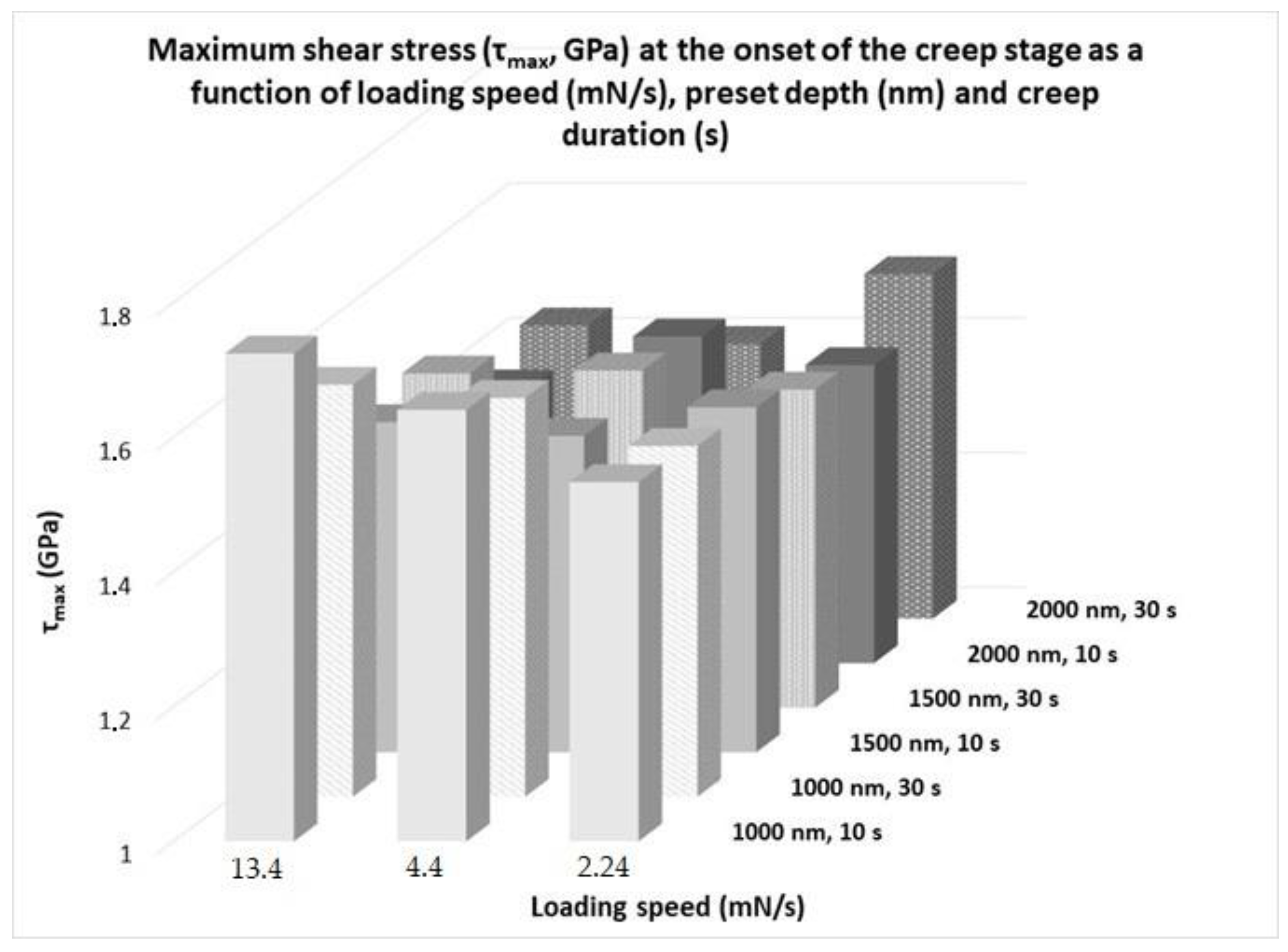
- For a more thorough assessment of creep behavior, it is important to take into consideration other parameters in addition to the net creep deformation obtained from the previous paragraphs. Maximum shear stress (τmax): τmax is the stress that practically drives the deformation process since it is the stress that makes the dislocation move and provide the plastic flow of the material. It can be seen from the data of Table 3 and Figure 12 that τmax decreases, in general, as the preset depth increases. This is expected since, according to the calculation sequence, τmax is directly related to the hardness, which, as shown and explained previously, is also reduced as the indentation depth increases. What is significant is that this trend is more profound for the lower creep periods (10 s). Additionally, it appears that τmax is also slightly affected by the loading speed, with this effect being more significant for the lower preset depths. It could be thus postulated that in general lines, τmax follows similar trends as the net creep depth but in reverse order. According to the comments of Karantzalis et al. [23], this behavior and inter-relation are expected and are exactly associated with the extent of the dislocation mobility the τmax provides.
- (4)
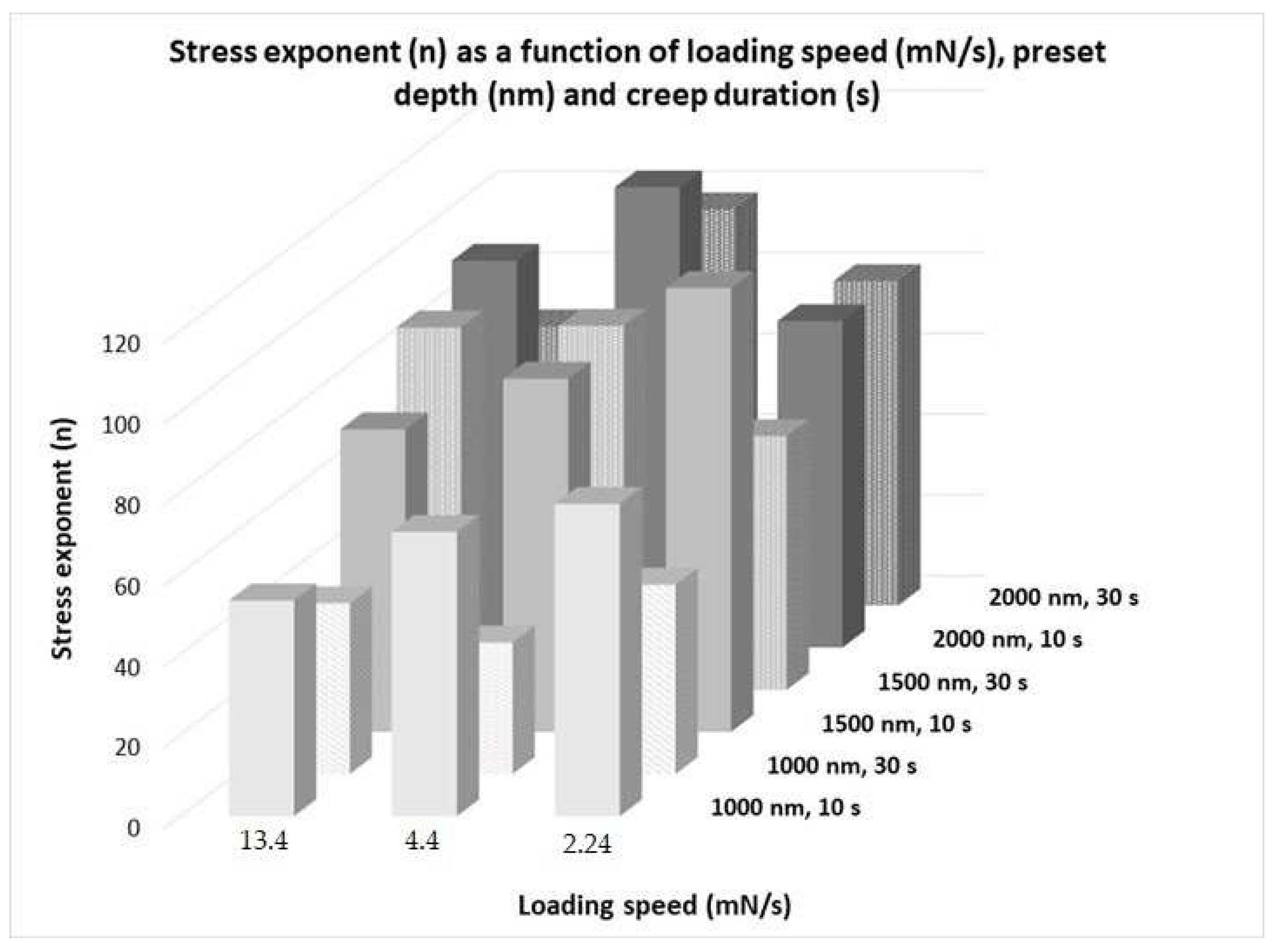
- Stress exponent n: Stress exponent n is an indirect measure of how easily the creep deformation is achieved, and, as a general rule, the higher its values, the more restrained the creep deformation. The stress exponent n, in many cases, dictates the mode and the type of creep behavior [5,6,7,8,9,10,11]. As previously mentioned, in the present effort, the type of creep is a power law creep, which imposes a dislocation glide creep mechanism. The values of n obtained in the present effort also support this type and are in agreement with other experimental efforts [6,7,8,9,10,22]. According to the data of Table 3 and Figure 13, it can be observed that the stress exponent n is reduced with creep duration time, in general. The second important observation is that the stress exponent n increases as the preset depth increases. The last important observation is that n increases as the loading speed decreases, especially in the case of lower loading speeds. As far as the effect of the creep period is concerned, the reduction in time implies that once the primary stage of creep (the stage where the greater portion of the creep deformation is achieved) is met, the creep deformation is not that affected by the applied stress. This is due to the fact that a considerable number of dislocations, as the period increases, are generated that can lead to plastic flow of the material irrespective of the applied stresses. The second effect to be discussed is the effect of the loading speed. It is observed that stress exponent n increases as the loading speed decreases. This behaviour is associated with the dislocations generated at the initial loading stage. The lower the loading speed, the less the generated dislocations; and the fewer the overall number of dislocations available at the creep stage, the more restricted the deformation they provide, and thus the higher the stress exponent n. Despite these effects, the most important—and obscure, in a sense—is the fact that stress exponent n increases as the preset depth increases. This trend, as reported in many experimental efforts [7,8,9], is a trend mainly associated with FCC high-entropy alloy systems. On the contrary, Ma et al. [9] reported that in the BCC nanocrystalline coatings, the stress exponent remained unaffected by the indentation depth, and recently, Karantzalis et al. [22] reported that stress exponent n in the MoTaNbVxTi systems they examined was reduced upon increasing the preset depth. It must be mentioned, nevertheless, that during the last effort, the systems consisted of a combination of BCC and HCP phases and not solely of a BCC structure. What also must be mentioned at this point is the fact that the treatment and the discussion of Ma et al. [9] when comparing BCC and FCC structures, are somehow different compared to the present case. Ma et al. [9] compared the BCC structure, which was formed by the addition of Al to a system (Co, Cr, Fe, Ni, and Cu) that, at its equi-atomic composition, possesses FCC structure. In the present effort, the BCC structure is formed solely by BCC refractory metals. The net characteristics between the two BCC structures can be significantly different. The addition of Al creates a more significant lattice distortion, whereas, in the pure BBC refractory high-entropy alloy, the lattice can be undergo further changes. The same trend may occur as far as the stress–elastic strain field within the lattice is concerned. Additionally, lattice defects that can accommodate, incubate, and eventually grow dislocation loops may also be significantly different. If such is the case, this different dislocation sequence may severely affect the critical volume for dislocation nucleation, Vcr, which is a crucial factor, as will be presented later, for the creep behavior. These hints suggest that in the present effort, at higher preset depths, there must be mechanisms that are activated that obstruct the dislocation movement to provide plastic flow. Possible mechanisms can be (a) dislocation entanglement either at the loading stage or between the dislocations generated at the creep stage, (b) reduced number of dislocations available to accommodate plastic deformation, or (c) a lack of mechanisms such as dislocation climb that will assist the continuance of their movement. The authors recognize, nevertheless, that further experimentation is required in order to clarify this behavior. It must be mentioned, however, that the critical volume for dislocation generation Vcr, presented in Figure 14, also contributes toward the postulate of the low number of available dislocations. Indeed, it can be seen from Table 3 and Figure 14 that this volume increases with the preset depth. This practically means that at higher preset depths, the volume of the system underneath the indenter and within the plastic zone, which has to be activated in order for new and fresh dislocations to be generated, increases. According to Ma et al. [9], dislocation loops are generated and grow at lattice defects from atomic-sized regions. A higher activation volume practically means that the flow unit is hard to activate, reducing in such terms the number of glissile dislocations. A very important parameter that influences the extent of Vcr is the type of dislocation type and movement. In BCC structures, the movement of screw dislocations by climbing is severely restrained, causing the continuance of the plastic flow to be even more difficult to sustain. This behavior could also be a cause for the increased values of Vcr. Nevertheless, Vcr should not be treated independently of τmax: τmax directly affects Vcr in a reversed manner. It was observed in Figure 12 that τmax reduces with preset depth, and this has a direct opposite effect of Vcr, which increases.
3.3.2. Creep Response—Statistical Analysis
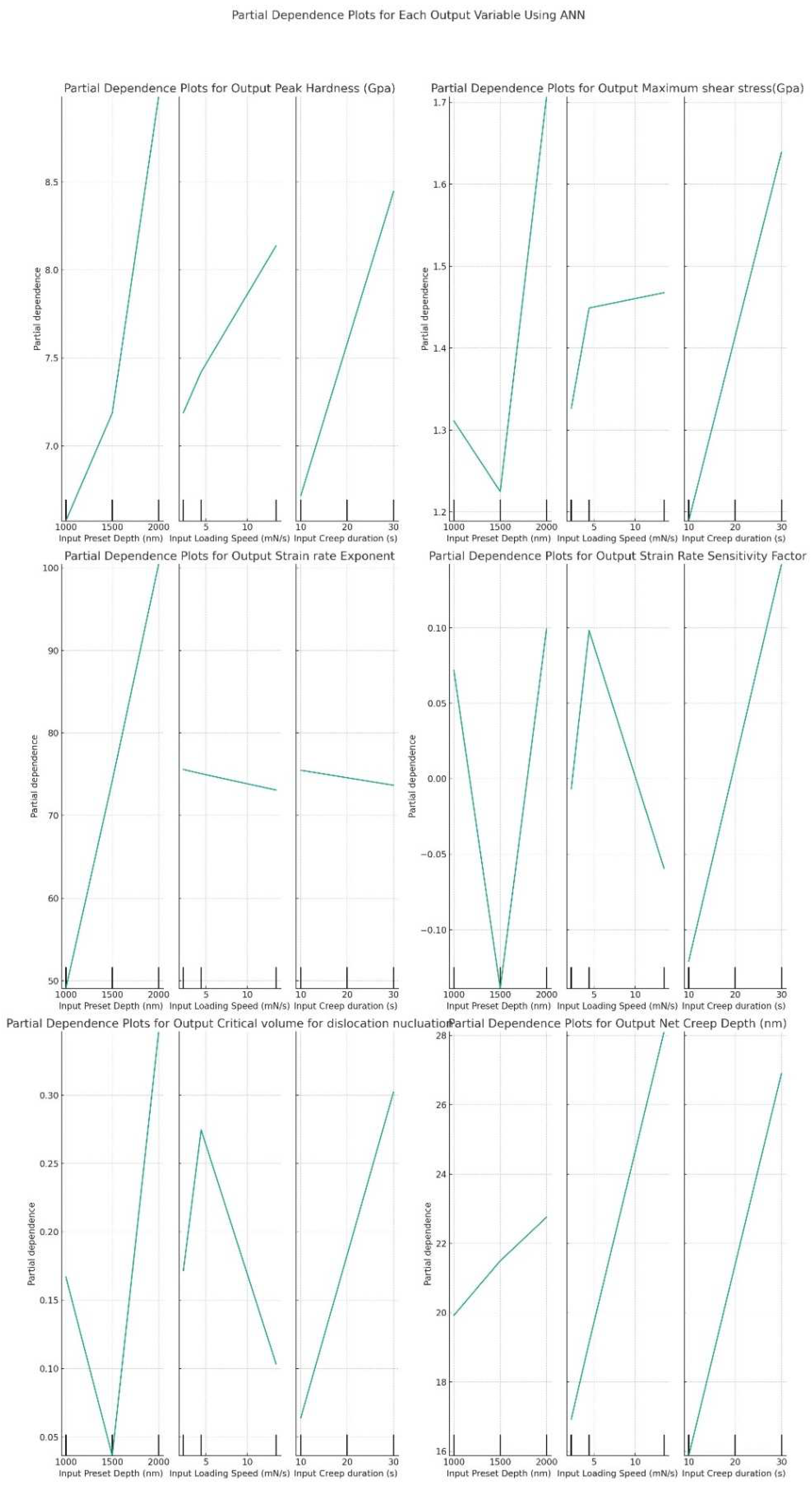
- For the output variable Peak Hardness (Gpa), the PDP indicates a consistent rise in predicted hardness with an increase in “Input Preset Depth (nm)”. This upward trend is also observed for “Input Loading Speed (mN/s)” and “Input Creep duration (s)”, suggesting that increases in these input values are associated with higher predicted hardness values.
- The analysis of Maximum Shear Stress (Gpa) via PDPs reveals a strong positive correlation with “Input Preset Depth (nm)” and “Input Creep duration (s)”, indicating that higher values of these inputs predict greater shear stress. Conversely, the plot for “Input Loading Speed (mN/s)” displays a slight upward trend that eventually plateaus, suggesting a more nuanced relationship with predicted shear stress.
- Regarding the Output Strain Rate Exponent, the PDP underscores a marked increase in the predicted exponent with a rise in “Input Preset Depth (nm),” while the trends for the other inputs are more subdued.
- The PDPs for the Output Strain Rate Sensitivity Factor exhibit erratic behavior, pointing to potentially complex or non-linear interactions between these inputs and the output, hinting at the intricacies of the underlying relationships.
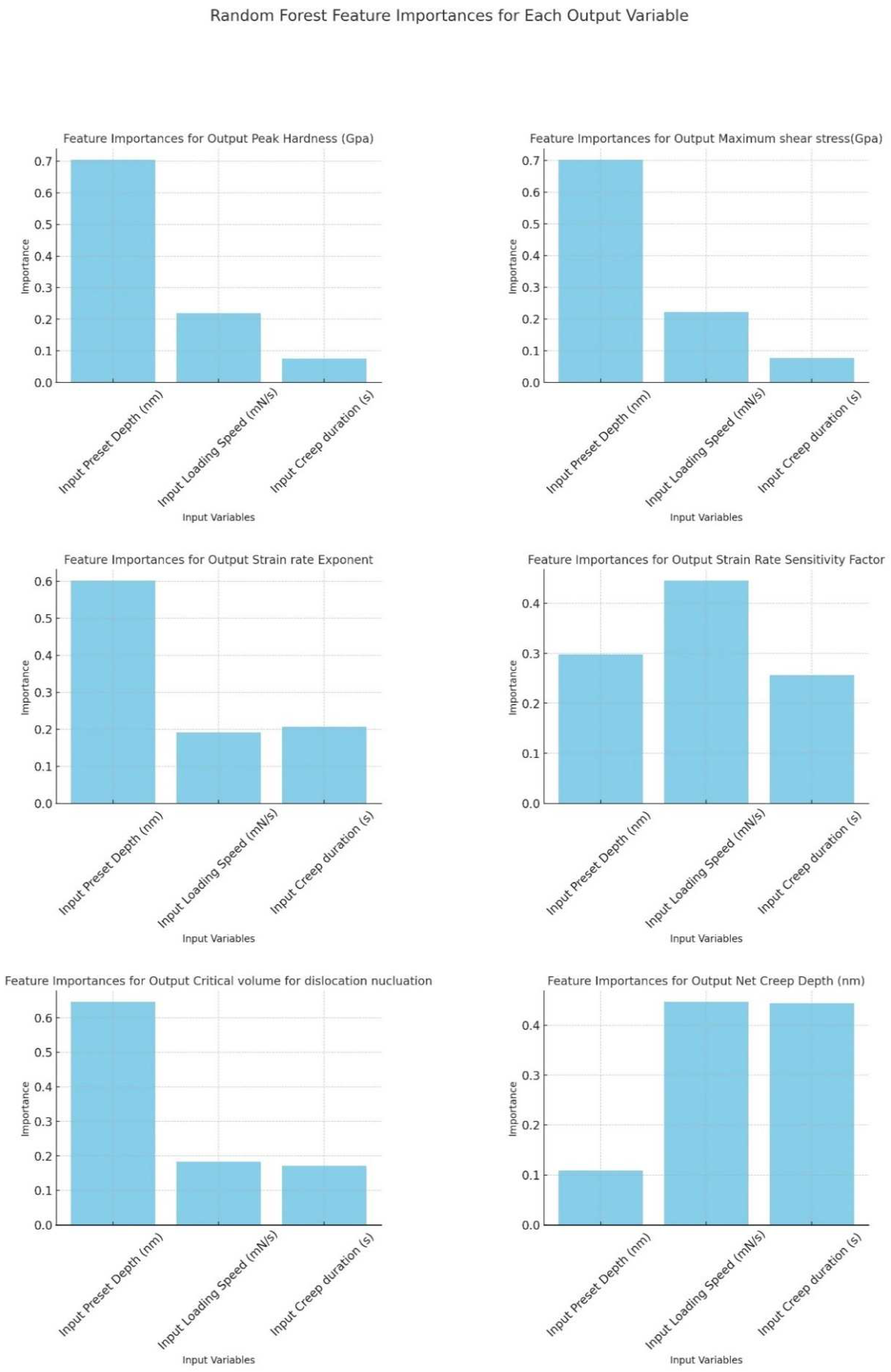
- For Output Critical Volume for Dislocation Nucleation, the plots for “Input Preset Depth (nm)” and “Input Loading Speed (mN/s)” reveal sharp peaks, highlighting specific input values that correspond to drastic changes in the predicted response. In contrast, the plot for “Input Creep duration (s)” shows a smoother, more gradual relationship, indicating a different pattern of influence on the predicted outcome.
- Lastly, the PDPs for Output Net Creep Depth (nm) illustrate increasing trends for all three input variables, with notably steep slopes for “Input Loading Speed (mN/s)” and “Input Creep duration (s)”. This indicates a strong positive relationship between these inputs and the predicted net creep depth, suggesting that higher input values lead to greater predicted creep depths.
- Regarding Input Preset Depth (nm), ANOVA highlights its significant effect on both “Output Peak Hardness (GPa)” and “Output Maximum Shear Stress (GPa)”. The Random Forest analysis identifies it as an important feature for several outputs, while PDPs suggest a positive impact on the outputs. However, the correlation matrix reveals a negative correlation between “Output Peak Hardness (GPa)” and “Output Maximum Shear Stress (GPa)”. This consensus indicates that while ANOVA and Random Forest recognize the significance of this input, the negative correlation observed in the correlation matrix contrasts with the positive relationship indicated by PDPs and the significant effects noted in ANOVA, hinting at possible non-linear effects that may not be captured in linear analyses.
- For Input Loading Speed (mN/s), ANOVA shows a significant effect on “Output Net Creep Depth (nm)”, which is echoed by its noted importance for “Output Strain Rate Sensitivity Factor” and “Output Net Creep Depth (nm)” in Random Forest analysis. PDPs also depict a positive relationship with “Output Net Creep Depth (nm)”, a finding supported by a moderate positive correlation in the correlation matrix. The consensus across all methods underscores the importance and positive impact of this input on “Output Net Creep Depth (nm)”, indicating a uniform agreement on its role.
- Input Creep duration (s) is identified by ANOVA as having a significant effect on “Output Net Creep Depth (nm)”, with Random Forest attributing some importance to it for this output. PDPs and the correlation matrix further affirm a positive relationship with “Output Net Creep Depth (nm)”, marked by a strong positive correlation. This general agreement among all methods on the significant and positive relationship between this input and “Output Net Creep Depth (nm)” highlights a clear consensus on its impact.
4. Conclusions
- (1)
- An in-depth examination of the mechanical properties of a refractory MoTaNbVW high-entropy alloy was conducted, and the effects of the different testing parameters were assessed.
- (2)
- The hardness of the alloy was affected by the two input parameters, i.e., the preset depth and the loading speed. It was found that these two factors have opposite effects. A clear trend of the preset depth on the modulus of elasticity Eit was not ascertained. On the contrary, it was shown that a reduction in the loading speeds leads to lower Eit values, especially for higher indentation depths (1500 and 2000 nm, respectively). The ratio of the absorbed elastic energy, nit, seems to follow the same trend as hardness.
- (3)
- The four different statistical analysis techniques verified the preset indentation depth as the most crucial parameter for the obtained hardness values. Additionally, and even though three of the four techniques showed some relation between the loading speed and the Eit, this relation is characterized as weak, and more complex approaches should be taken into consideration. This outcome is also in alignment with the related metallurgical and microstructural postulates.
- (4)
- The pre-creep loading stage revealed the presence of serrations, especially at the lower preset depths and the lower loading speeds. These serrations manifest premature creep behaviour at the loading stage.
- (5)
- The net creep deformation was found to be affected by all the different testing variables: the creep deformation increases as the present depth increases, the creep duration increases, and the loading speed increases. The maximum shear stress, τmax, i.e., the stress which is directly associated with the dislocation mobility to provide the plastic deformation during creep, shows a similar behaviour as the net creep deformation in reversed order. The stress exponent n was reduced as the creep duration decreased, the preset depth increased, and the loading speed decreased. The Vcr was also taken into consideration since it is also associated with the number of the associated with the deformation dislocations.
- (6)
- The correlation analysis methods showed the importance of the loading speed and the creep duration on the output values, such as the net creep depth, and verified the tendencies expressed in metallurgical and microstructural terms. Correlation analysis also revealed, in some cases, that the involved phenomena governing individual input–output inter-relations may have an extensive degree of complexity, and as such, more sophisticated modeling approaches may be required.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miracle, D.B.; Senkov, O.N.; Wilks, J. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Choi, I.-C.; Yoo, B.-G.; Kim, Y.-J.; Jang, J.-I. Indentation creep revisited. J. Mater. Res. 2011, 27, 3–11. [Google Scholar] [CrossRef]
- Bull, S.J. Nanoindentation of coatings. J. Phys. D Appl. Phys. 2005, 38, R393–R413. [Google Scholar] [CrossRef]
- Li, W.; Henshall, J.; Hooper, R.; Easterling, K. The mechanisms of indentation creep. Acta Met. Mater. 1991, 39, 3099–3110. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, P.; Cheng, H.; Zhang, H.; Diao, H.; Shi, Y.; Chen, B.; Chen, P.; Feng, R.; Bai, J.; et al. Nanoindentation Creep Behavior of an Al0.3CoCrFeNi High-Entropy Alloy. Met. Mater. Trans. A 2016, 47, 5871–5875. [Google Scholar] [CrossRef]
- Ding, Z.Y.; Song, Y.X.; Ma, Y.; Huang, X.W.; Zhang, T.H. Nanoindentation Investigation on the Size-Dependent Creep Behavior in a Zr-Cu-Ag-Al Bulk Metallic Glass. Metals 2019, 9, 613. [Google Scholar] [CrossRef]
- Lin, P.; Chou, H.; Huang, J.; Chuang, W.; Jang, J.; Nieh, T. Elevated-temperature creep of high-entropy alloys via nanoindentation. MRS Bull. 2019, 44, 860–866. [Google Scholar] [CrossRef]
- Ma, Z.; Long, S.; Zhou, Y.; Pan, Y. Indentation scale dependence of tip-in creep behavior in Ni thin films. Scr. Mater. 2008, 59, 195–198. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, Y.; Debela, T.T.; Peng, G.; Zhang, T. Nanoindentation study on the creep characteristics of high-entropy alloy films: Fcc versus bcc structures. Int. J. Refract. Met. Hard Mater. 2016, 54, 395–400. [Google Scholar] [CrossRef]
- Bin Kang, Y.; Shim, S.H.; Lee, K.H.; Hong, S.I. Dislocation creep behavior of CoCrFeMnNi high entropy alloy at intermediate temperatures. Mater. Res. Lett. 2018, 6, 689–695. [Google Scholar] [CrossRef]
- Jiao, Z.M.; Chu, M.Y.; Yang, H.J.; Wang, Z.H.; Qiao, J.W. Nanoindentation characterised plastic deformation of a Al0.5CoCrFeNi high entropy alloy. Mater. Sci. Technol. 2015, 31, 1244–1249. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, S.; Wang, Q.; Liu, Z.; Wang, J.; Yang, Y.; Liu, C. Nanoindentation characterized initial creep behavior of a high-entropy-based alloy CoFeNi. Intermetallics 2014, 53, 183–186. [Google Scholar] [CrossRef]
- Kaufmann, J.; Schering, A.G. Analysis of Variance ANOVA; Wiley: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Available online: https://scikit-learn.org/0.24/modules/generated/sklearn.inspection.plot_partial_dependence.html (accessed on 15 November 2023).
- Reed, S. Artificial Neural Networks. In Encyclopedia of Structural Health Monitoring; Boller, C., Chang, F.-K., Fujino, Y., Eds.; Wiley: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Hüsser, A.P. Correlation Analysis. In The International Encyclopedia of communication Research Methods; Matthes, J., Davis, C.S., Potter, R.F., Eds.; Wiley: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Available online: https://docs.scipy.org/doc/scipy/reference/stats.html (accessed on 15 November 2023).
- Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html (accessed on 15 November 2023).
- Available online: https://www.tensorflow.org/about/bib (accessed on 15 November 2023).
- Available online: https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.corr.htm (accessed on 15 November 2023).
- Karantzalis, A.E.; Sioulas, D.; Poulia, A.; Mathiou, C.; Georgatis, E. A first approach on the assessment of the creep behavior of MoTaNbVxTi high entropy alloys by indentation testing. SN Appl. Sci. 2020, 2, 950. [Google Scholar] [CrossRef]
- Wang, D.; Tan, J.; Li, C.J.; Qin, X.M.; Guo, S.F. Enhanced creep resistance of Ti30Al25Zr25Nb20 high-entropy alloy at room temperature. J. Alloy. Compd. 2021, 885, 161038. [Google Scholar] [CrossRef]
- Yu, P.F.; Feng, S.D.; Xu, G.S.; Guo, X.L.; Wang, Y.Y.; Zhao, W.; Qi, L.; Li, G.; Liaw, P.K.; Liu, R.P. Room-temperature creep resistance of Co-based metallic glasses. Scr. Mater. 2014, 90, 45–48. [Google Scholar] [CrossRef]
- Poulia, A.; Georgatis, E.; Lekatou, A.; Karantzalis, A. Microstructure and wear behavior of a refractory high entropy alloy. Int. J. Refract. Met. Hard Mater. 2016, 57, 50–63. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in under-standing and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Li, Q.-J.; Sheng, H.; Ma, E. Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 2019, 10, 3563. [Google Scholar] [CrossRef]
- Jian, W.-R.; Xie, Z.; Xu, S.; Su, Y.; Yao, X.; Beyerlein, I.J. Effects of lattice distortion and chemical short-range order on the mechanisms of deformation in medium entropy alloy CoCrNi. Acta Mater. 2020, 199, 352–369. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, F.; Yuan, X.; Huang, H.; Wen, X.; Wang, Y. Short-range ordering and its effects on mechanical properties of high-entropy alloys. J. Mater. Sci. Technol. 2021, 62, 214–220. [Google Scholar] [CrossRef]
- Antillon, E.; Woodward, C.; Rao, S.I.; Akdim, B.; Parthasarathy, T.A. Chemical short range order strengthening in a model FCC high entropy Alloy. Acta Mater. 2020, 190, 29–42. [Google Scholar] [CrossRef]
- Yang, X.; Xi, Y.; He, C.; Chen, H.; Zhang, X.; Tu, S. Chemical short-range order strengthening mechanism in CoCrNi medium-entropy alloy under nanoindentation. Scr. Mater. 2022, 209, 114364. [Google Scholar] [CrossRef]
- Mathiou, C.; Kyrtsidou, K.; Georgatis, E.; Karantzalis, A.E. Primary nano-indentation assessment of low entropy NiAl-Cr alloys. SOJ Mater. Sci. Eng. 2022, 10, 1–15. [Google Scholar]
- Zhao, J.; Wang, F.; Huang, P.; Lu, T.; Xu, K. Depth dependent strain rate sensitivity and inverse indentation size effect of hardness in body-centered cubic nanocrystalline metals. Mater. Sci. Eng. A 2014, 615, 87–91. [Google Scholar] [CrossRef]


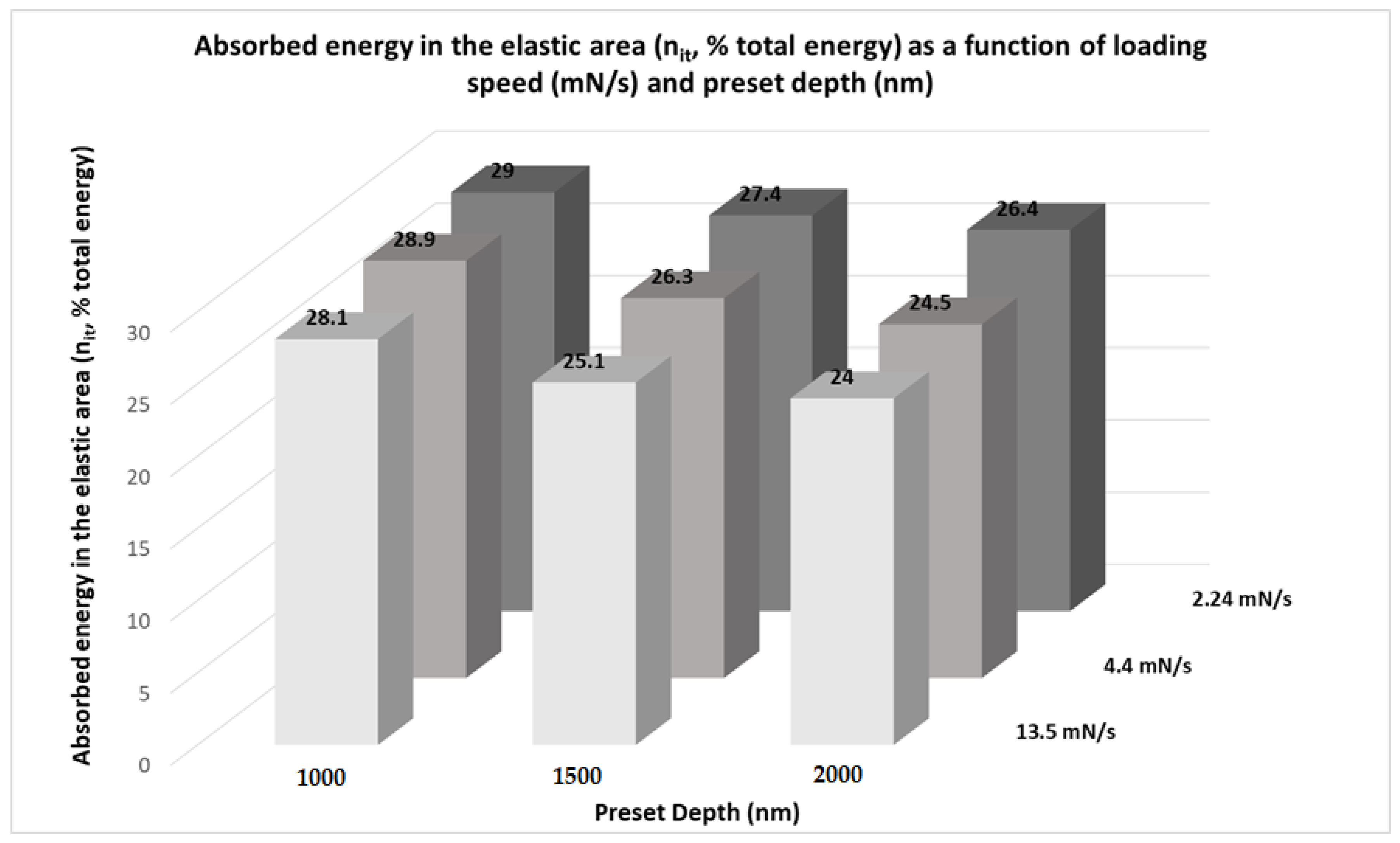

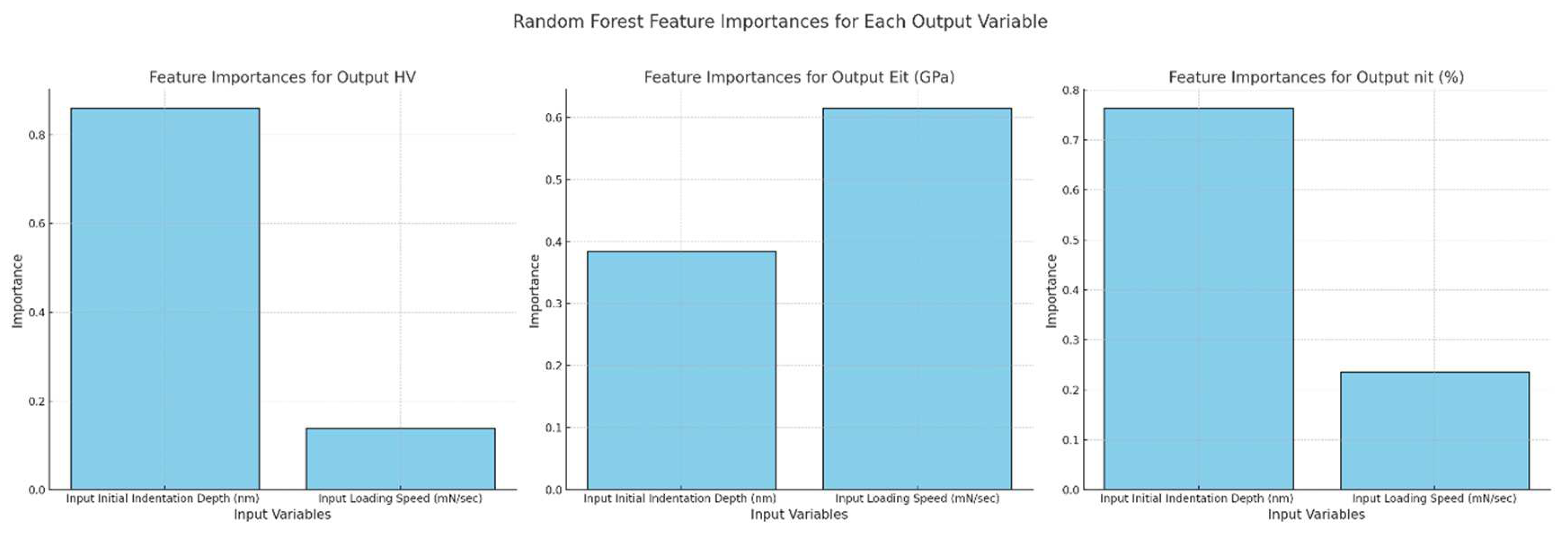

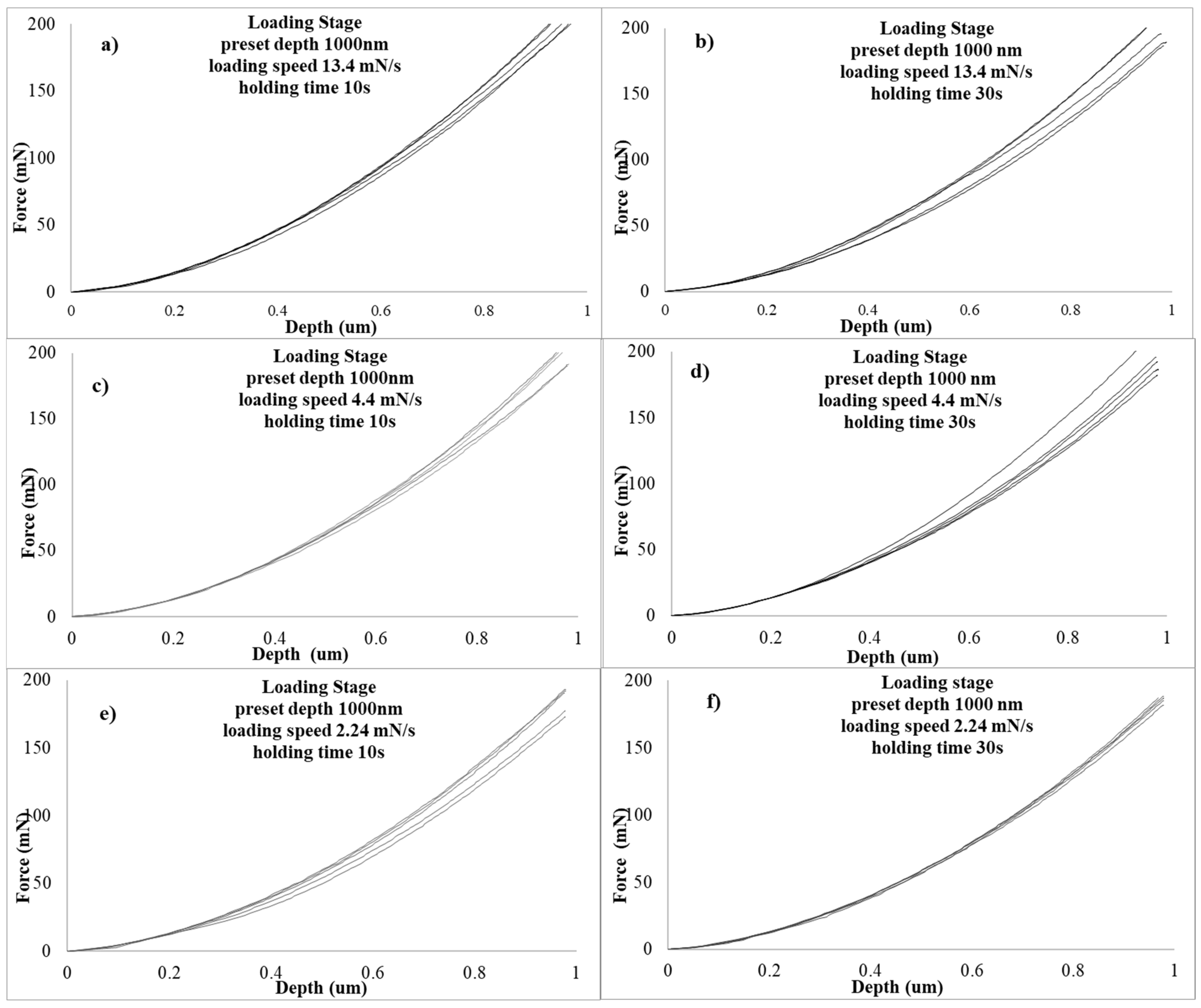


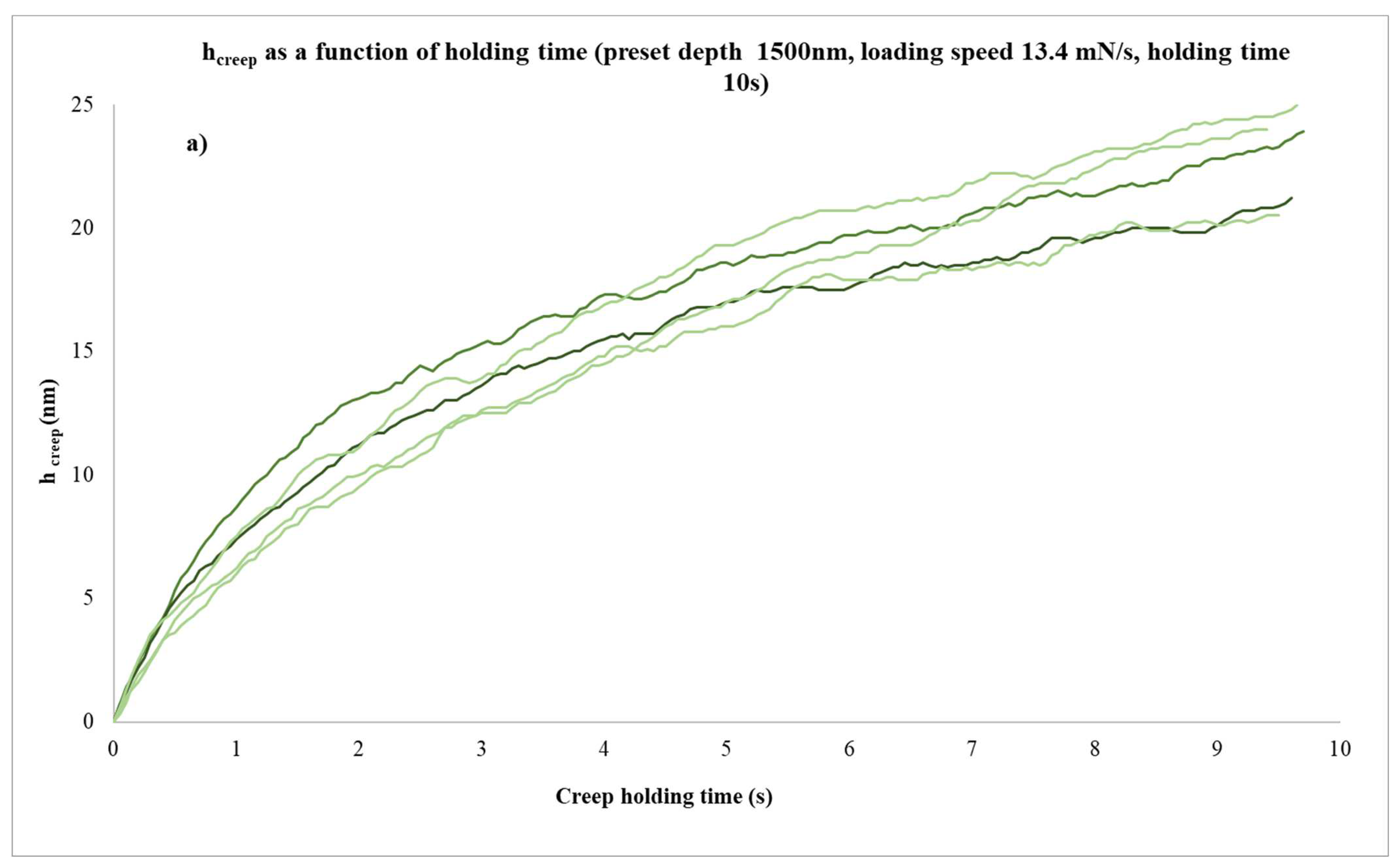


| Input Variables | Outcome Parameters | |||
|---|---|---|---|---|
| Overall Hardness Hit | Indentation Modulus of Elasticity Eit | Fraction of the Elastic Absorbed Energy nit | ||
| Initial Indentation Depth (nm) | Loading Speed (mN/s) | HV | Eit (GPa) | nit (%) |
| 13.5 | 929 | 244 | 28.1 | |
| 1000 | 4.4 | 949 | 235 | 28.9 |
| 2.24 | 963 | 245 | 29 | |
| 13.5 | 864 | 267 | 25.1 | |
| 1500 | 4.4 | 895 | 255 | 26.3 |
| 2.24 | 799 | 227 | 27.4 | |
| 13.5 | 800 | 255 | 24 | |
| 2000 | 4.4 | 797 | 246 | 24.5 |
| 2.24 | 826 | 227 | 26.4 | |
| Output Variable | Input Feature Category | F-Value | p-Value | Significant | |
|---|---|---|---|---|---|
| 1 | Output Eit (GPa) | Loading Speed Category | 3.306 | 0.108 | No |
| 2 | Output Eit (GPa) | Indentation Depth Category | 0.275 | 0.769 | No |
| 3 | Output HV | Indentation Depth Category | 15.443 | 0.004 | Yes |
| 4 | Output HV | Loading Speed Category | 0.048 | 0.953 | No |
| 5 | Output nit (%) | Indentation Depth Category | 10.003 | 0.012 | Yes |
| 6 | Output nit (%) | Loading Speed Category | 0.708 | 0.530 | No |
| Testing Variables | Measured Parameters (Outcomes) | |||||||
|---|---|---|---|---|---|---|---|---|
| Preset Depth (nm) | Loading Speed (mN/s) | Creep Duration (s) | Peak Hardness (GPa) | Maximum Shear Stress (GPa) | Strain Rate Exponent | Strain Rate Sensitivity Factor | Critical Volume for Dislocation Nucluation | Net Creep Depth (nm) |
| H (GPa) | τmax (GPa) | n | m | V (nm3) | h creep | |||
| 13.5 | 10 | 8.9618 | 1.7244 | 53.34 | 0.01914 | 0.12564 | 22.02 | |
| 30 | 8.3752 | 1.6118 | 42.242 | 0.0259 | 0.10508 | 30.74 | ||
| 1000 | 4.4 | 10 | 8.5262 | 1.6406 | 70.302 | 0.34636 | 0.17384 | 15.98 |
| 30 | 8.2728 | 1.59224 | 32.506 | 0.06186 | 0.08324 | 25.94 | ||
| 2.24 | 10 | 7.9672 | 1.5334 | 77.208 | 0.01328 | 0.20406 | 11.86 | |
| 30 | 7.904 | 1.5208 | 46.826 | 0.0225 | 0.12366 | 24.08 | ||
| 13.5 | 10 | 7.7442 | 1.49 | 74.812 | 0.01474 | 0.20356 | 22.92 | |
| 30 | 7.6842 | 1.4962 | 89.56 | 0.01164128 | 0.24192 | 26.58 | ||
| 1500 | 4.4 | 10 | 7.637 | 1.4696 | 87.32 | 0.011642313 | 0.24036 | 16.04 |
| 30 | 7.7992 | 1.5006 | 89.98 | 0.013049941 | 0.24166 | 23.08 | ||
| 2.24 | 10 | 7.859 | 1.5122 | 109.772 | 0.01022261 | 0.29012 | 11.18 | |
| 30 | 7.6522 | 1.4722 | 62.708 | 0.02174 | 0.163868 | 22.42 | ||
| 13.5 | 10 | 7.3248 | 1.4094 | 95.636 | 0.010500209 | 0.27564 | 24.3 | |
| 30 | 7.4602 | 1.4352 | 68.996 | 0.015363658 | 0.19396 | 40.2 | ||
| 2000 | 4.4 | 10 | 7.7166 | 1.4848 | 113.804 | 0.008797107 | 0.31024 | 14.5 |
| 30 | 7.3168 | 1.4076 | 97.938 | 0.010973542 | 0.2781 | 25.84 | ||
| 2.24 | 10 | 7.4968 | 1.4424 | 80.704 | 0.015591584 | 0.225 | 11.48 | |
| 30 | 7.8544 | 1.5112 | 80.184 | 0.016451501 | 0.21466 | 19.9 | ||
| Output Variable | Input Variable | Sum of Squares | Degrees of Freedom | F-Statistic | p-Value |
|---|---|---|---|---|---|
| Output Critical volume for dislocation nucleation | Input Creep duration (s) | 0.004 | 1 | 3.717 | 0.112 |
| Output Critical volume for dislocation nucleation | Input Loading Speed (mN/s) | 0.003 | 1 | 2.550 | 0.171 |
| Output Critical volume for dislocation nucleation | Input Preset Depth (nm) | 0.017 | 1 | 15.745 | 0.011 |
| Output Maximum shear stress (Gpa) | Input Creep duration (s) | 0.002 | 1 | 1.282 | 0.309 |
| Output Maximum shear stress (Gpa) | Input Loading Speed (mN/s) | 0.000 | 1 | 0.151 | 0.714 |
| Output Maximum shear stress (Gpa) | Input Preset Depth (nm) | 0.020 | 1 | 11.348 | 0.020 |
| Output Net Creep Depth (nm) | Input Creep duration (s) | 99.552 | 1 | 21.260 | 0.006 |
| Output Net Creep Depth (nm) | Input Loading Speed (mN/s) | 247.741 | 1 | 52.908 | 0.001 |
| Output Net Creep Depth (nm) | Input Preset Depth (nm) | 1.591 | 1 | 0.340 | 0.585 |
| Output Peak Hardness (Gpa) | Input Creep duration (s) | 0.060 | 1 | 1.291 | 0.307 |
| Output Peak Hardness (Gpa) | Input Loading Speed (mN/s) | 0.007 | 1 | 0.150 | 0.714 |
| Output Peak Hardness (Gpa) | Input Preset Depth (nm) | 0.527 | 1 | 11.307 | 0.020 |
| Output Strain Rate Sensitivity Factor | Input Creep duration (s) | 0.000 | 1 | 0.012 | 0.917 |
| Output Strain Rate Sensitivity Factor | Input Loading Speed (mN/s) | 0.001 | 1 | 0.127 | 0.736 |
| Output Strain Rate Sensitivity Factor | Input Preset Depth (nm) | 0.007 | 1 | 1.447 | 0.283 |
| Output Strain rate Exponent | Input Creep duration (s) | 475.580 | 1 | 3.479 | 0.121 |
| Output Strain rate Exponent | Input Loading Speed (mN/s) | 499.093 | 1 | 3.651 | 0.114 |
| Output Strain rate Exponent | Input Preset Depth (nm) | 1853.284 | 1 | 13.557 | 0.014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokoli, V.; Kamnis, S.; Delibasis, K.; Georgatis, E.; Kiape, S.; Karantzalis, A.E. The Advanced Assessment of Nanoindentation-Based Mechanical Properties of a Refractory MoTaNbWV High-Entropy Alloy: Metallurgical Considerations and Extensive Variable Correlation Analysis. Appl. Sci. 2024, 14, 2752. https://doi.org/10.3390/app14072752
Sokoli V, Kamnis S, Delibasis K, Georgatis E, Kiape S, Karantzalis AE. The Advanced Assessment of Nanoindentation-Based Mechanical Properties of a Refractory MoTaNbWV High-Entropy Alloy: Metallurgical Considerations and Extensive Variable Correlation Analysis. Applied Sciences. 2024; 14(7):2752. https://doi.org/10.3390/app14072752
Chicago/Turabian StyleSokoli, Vassiliki, Spyros Kamnis, Konstantinos Delibasis, Emmanuel Georgatis, Stavros Kiape, and Alexander E. Karantzalis. 2024. "The Advanced Assessment of Nanoindentation-Based Mechanical Properties of a Refractory MoTaNbWV High-Entropy Alloy: Metallurgical Considerations and Extensive Variable Correlation Analysis" Applied Sciences 14, no. 7: 2752. https://doi.org/10.3390/app14072752





