Numerical Analysis of Mice Carotid Arteries’ Response Emphasizing the Importance of Material Law Constants’ Validation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Approach to Analysis
2.2. Material Laws Subjected to Validation
2.3. Geometrical Properties of the Artery
2.4. The Computational Domain and Meshing
2.5. The Analysis and Validation
2.6. New Constants Sets Proposals
3. Results
3.1. Necessary Model Checks
3.2. Validation of Selected Material Laws
3.2.1. Fung Law for Wild-Type, Sgcd−/−, and Mdx Mice
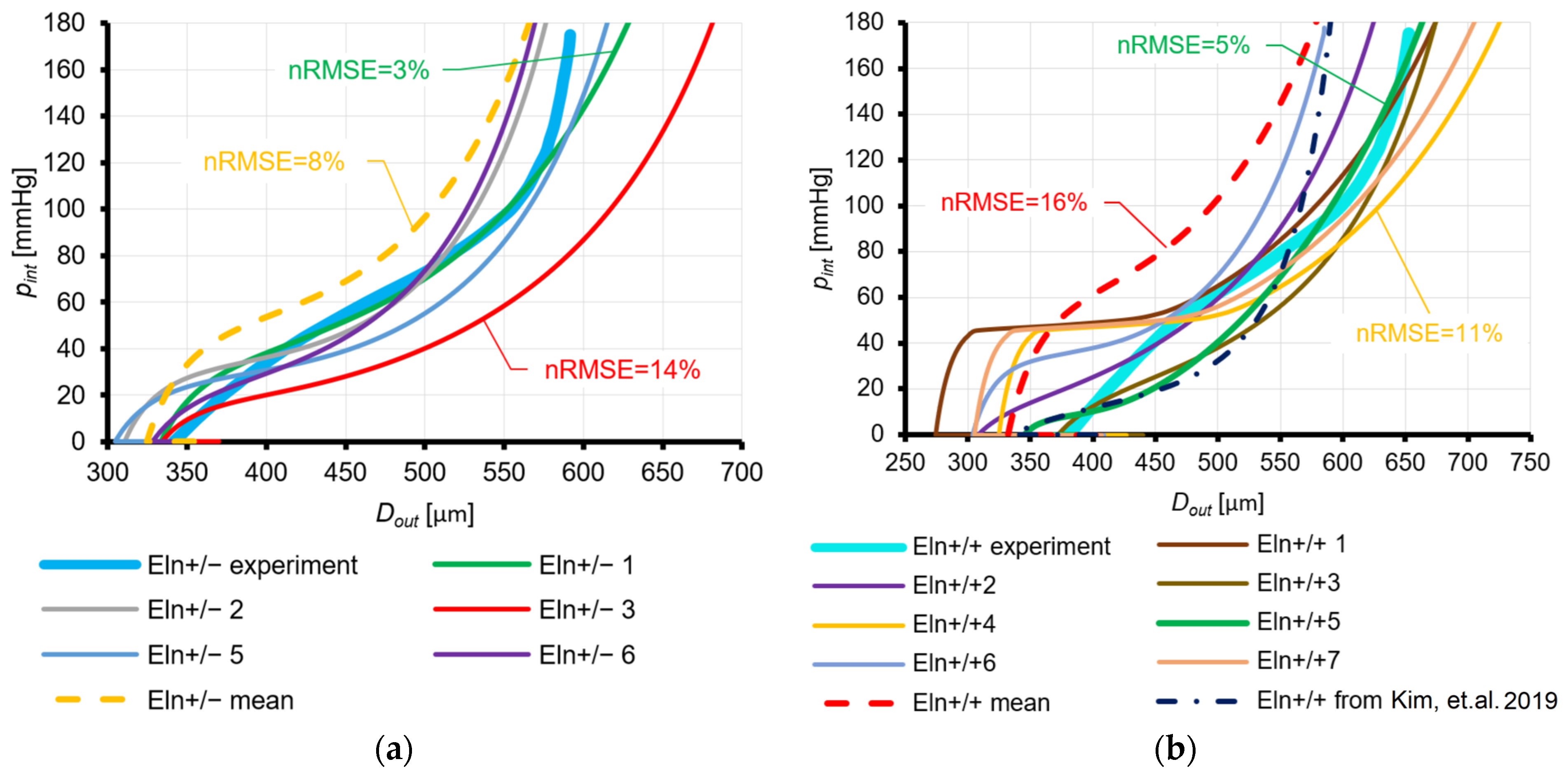
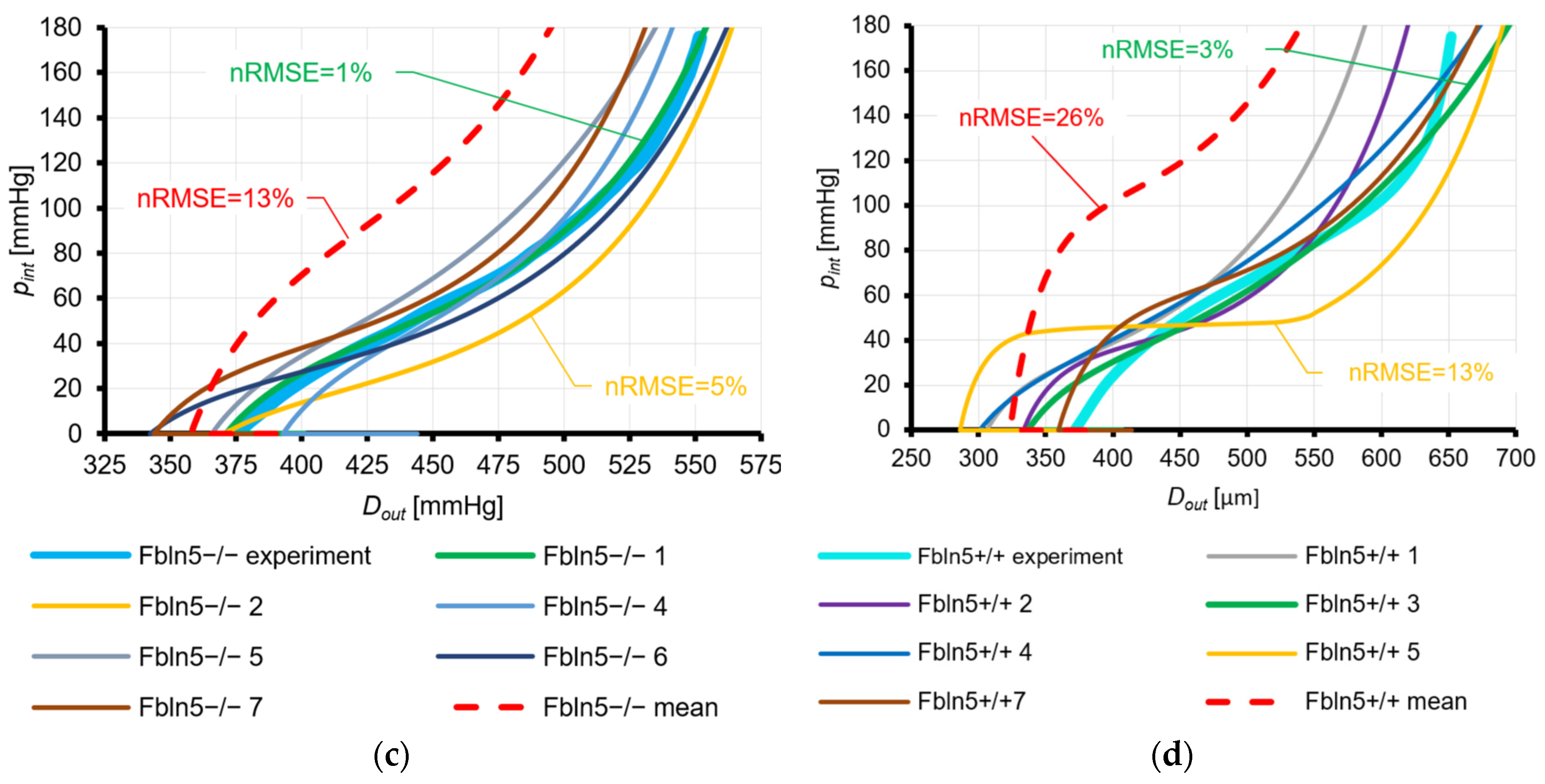
3.2.2. Fung Law for Eln+/−, Eln+/+, FBln5−/−, and Fbln5+/+ Mice and Holzapfel Law for Eln+/+ Mice
3.3. Proposals of New Constants Sets
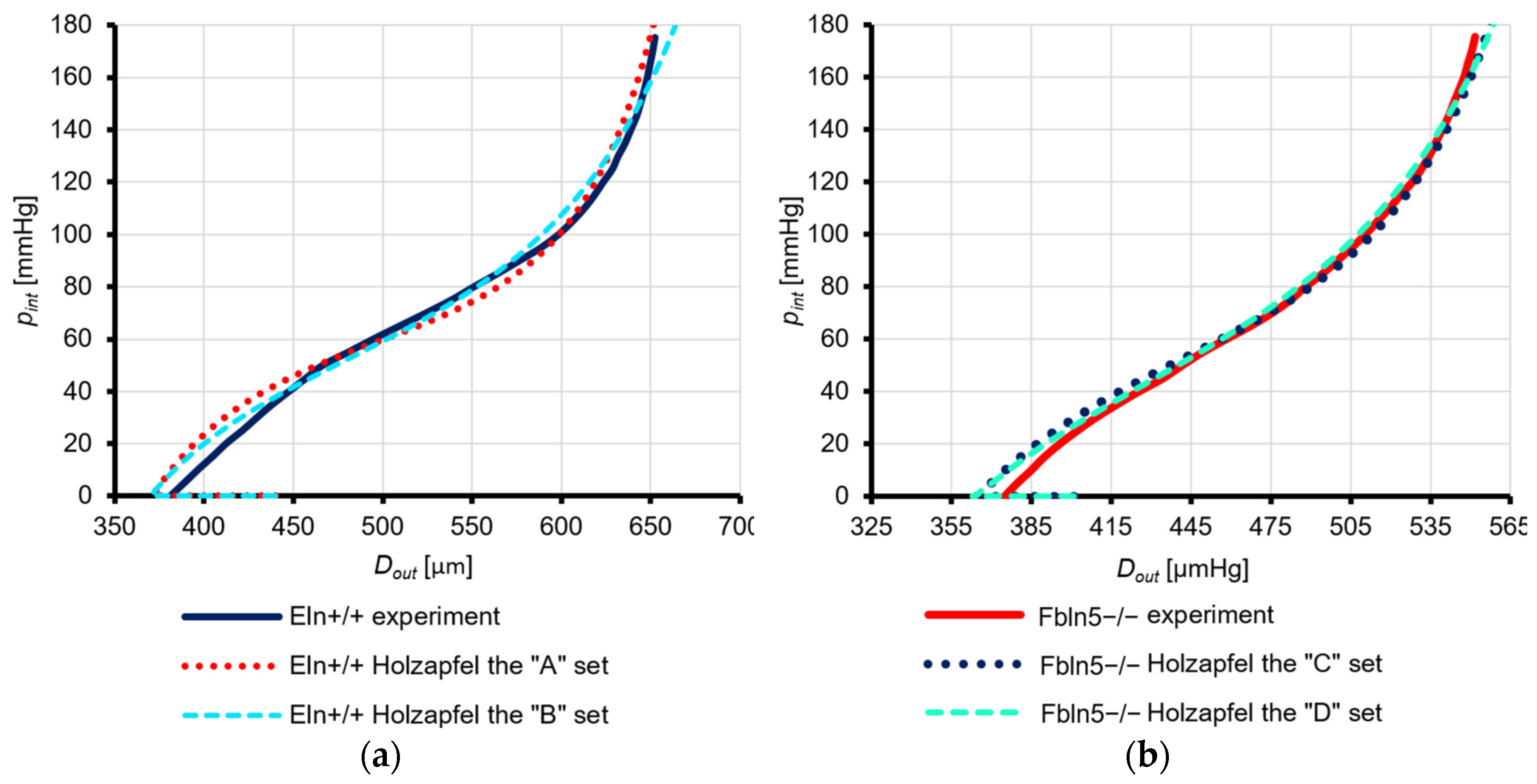
3.3.1. Eln+/+ Mice
3.3.2. Fbln5−/− Mice
3.4. Buckling Analysis
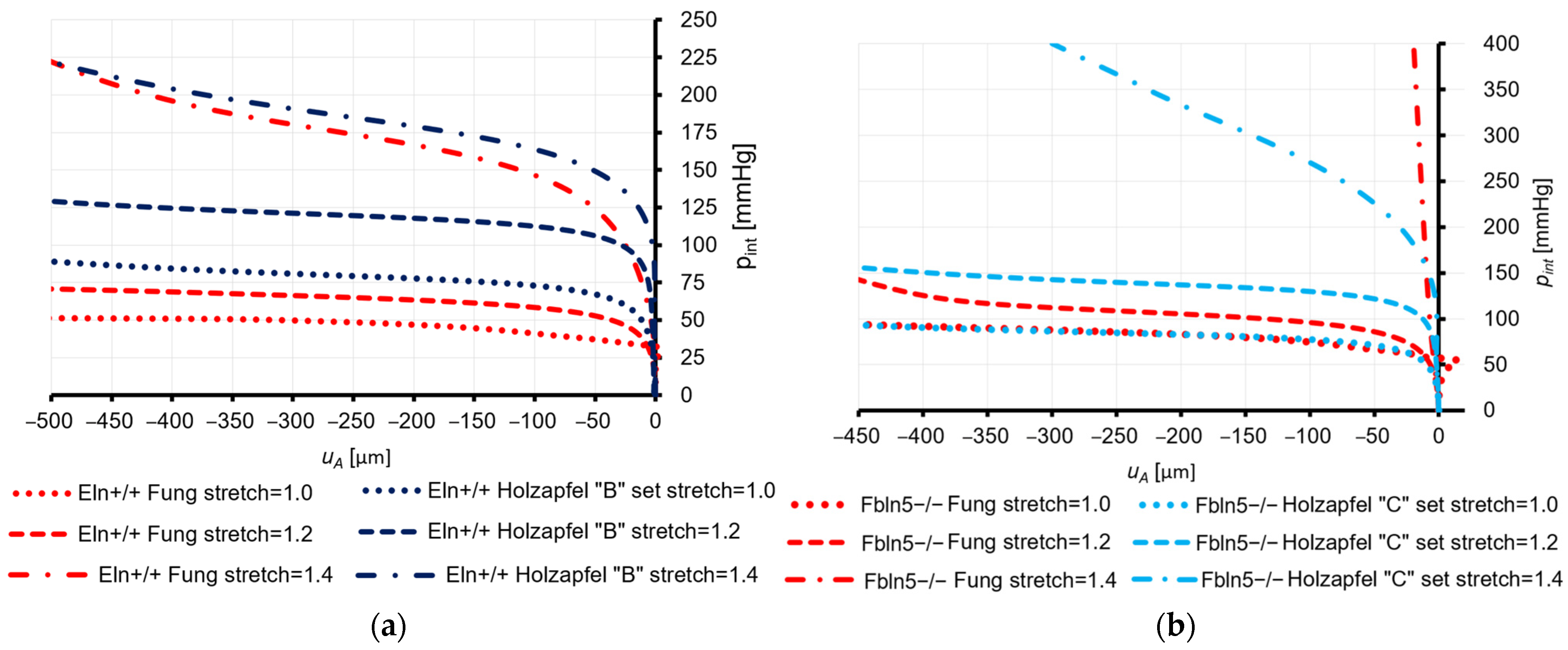
3.4.1. Eln+/+ Mice
3.4.2. Fbln5−/− Mice
4. Discussion
4.1. Validation of Selected Material Laws
4.1.1. Fung Law for Wild-Type, Sgcd−/−, and Mdx Mice
4.1.2. Fung Law for Eln+/−, Eln+/+, FBln5−/−, and Fbln5+/+ Mice and Holzapfel Law for Eln+/+ Mice
4.1.3. Summary of Validation
4.2. Proposals of New Constants Sets
4.2.1. Eln+/+ Mouse Model
4.2.2. Fbln5−/− Mouse Model
4.2.3. Summary
4.3. Buckling
4.3.1. Eln+/+ Mouse Model
4.3.2. Fbln5−/− Mouse Model
4.3.3. Summary of Buckling Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| 11305 | 1.032 | 0.018 | 0.250 | 0.185 | 0.019 | 0.308 | 202 |
| 12705 | 0.474 | 0.041 | 0.113 | 0.149 | 0.044 | 0.234 | 400 |
| 102704 | 0.873 | 0.000 | 0.182 | 0.208 | 0.022 | 0.341 | 171 |
| 110104 | 0.130 | 0.000 | 0.099 | 0.000 | 0.007 | 0.184 | 232 |
| 110304 | 1.339 | 0.189 | 0.282 | 0.284 | 0.071 | 0.384 | 110 |
| 110504 | 0.662 | 0.074 | 0.224 | 0.114 | 0.033 | 0.197 | 303 |
| mean | 0.752 | 0.054 | 0.192 | 0.157 | 0.033 | 0.275 | 236 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| 12505 | 5.381 | 0.437 | 0.551 | 1.233 | 0.216 | 1.038 | 33 |
| 20105 | 3.940 | 0.000 | 0.340 | 0.895 | 0.059 | 0.845 | 49 |
| 112204 | 3.039 | 0.268 | 0.543 | 0.637 | 0.140 | 0.793 | 41 |
| 121404 | 2.111 | 0.000 | 0.594 | 0.387 | 0.137 | 0.939 | 31 |
| 121504 | 1.708 | 0.241 | 0.445 | 0.416 | 0.154 | 0.702 | 67 |
| 12505 | 5.381 | 0.437 | 0.551 | 1.233 | 0.216 | 1.038 | 33 |
| mean | 3.236 | 0.189 | 0.494 | 0.714 | 0.141 | 0.864 | 44 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| 011405 | 3.638 | 0.075 | 0.253 | 0.993 | 0.088 | 0.994 | 42 |
| 011905 | 1.946 | 0.000 | 0.226 | 0.554 | 0.080 | 0.642 | 67 |
| 012005 | 0.482 | 0.000 | 0.391 | 0.079 | 0.056 | 0.476 | 102 |
| 111704 | 2.211 | 0.207 | 0.401 | 0.511 | 0.128 | 0.623 | 82 |
| 120304 | 1.665 | 0.116 | 0.344 | 0.385 | 0.099 | 0.494 | 97 |
| 122104 | 1.943 | 0.119 | 0.302 | 0.473 | 0.089 | 0.757 | 63 |
| mean | 1.981 | 0.086 | 0.319 | 0.499 | 0.09 | 0.664 | 76 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| Eln+/+ - 1 | 0.338 | 0.030 | 0.090 | 0.000 | 0.056 | 0.148 | 323 |
| Eln+/+ - 2 | 0.249 | 0.000 | 0.197 | 0.027 | 0.109 | 0.387 | 125 |
| Eln+/+ - 3 | 1.269 | 0.000 | 0.467 | 0.523 | 0.270 | 0.557 | 59 |
| Eln+/+ - 4 | 4.908 | 0.000 | 0.421 | 1.171 | 0.272 | 1.052 | 26 |
| Eln+/+ - 5 | 0.168 | 0.111 | 0.170 | 0.000 | 0.068 | 0.118 | 328 |
| Eln+/+ - 6 | 2.522 | 0.000 | 0.636 | 0.140 | 0.130 | 0.579 | 38 |
| Eln+/+ - 7 | 0.376 | 0.000 | 0.135 | 0.179 | 0.091 | 0.383 | 252 |
| mean | 1.404 | 0.020 | 0.302 | 0.292 | 0.143 | 0.461 | 165 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| Eln+/− - 1 | 0.515 | 0.000 | 0.107 | 0.213 | 0.074 | 0.306 | 180 |
| Eln+/− - 2 | 3.49 | 0.000 | 0.330 | 0.793 | 0.126 | 0.99 | 31 |
| Eln+/− - 3 | 0.439 | 0.041 | 0.156 | 0.000 | 0.085 | 0.19 | 125 |
| Eln+/− - 4 | 4.436 | 0.000 | 0.380 | 1.299 | 0.231 | 1.142 | 32 |
| Eln+/− - 5 | 3.359 | 0.000 | 0.353 | 0.990 | 0.083 | 1.117 | 48 |
| Eln+/− - 6 | 1.937 | 0.000 | 0.442 | 0.620 | 0.177 | 0.862 | 41 |
| mean | 2.363 | 0.007 | 0.295 | 0.653 | 0.129 | 0.768 | 76 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| Fbln5+/+ - 1 | 1.076 | 0.000 | 0.213 | 0.396 | 0.132 | 0.559 | 88 |
| Fbln5+/+ - 2 | 4.455 | 0.000 | 0.360 | 1.488 | 0.160 | 1.367 | 39 |
| Fbln5+/+ - 3 | 0.148 | 0.000 | 0.093 | 0.055 | 0.061 | 0.164 | 490 |
| Fbln5+/+ - 4 | 0.045 | 0.000 | 0.031 | 0.052 | 0.035 | 0.137 | 737 |
| Fbln5+/+ - 5 | 4.639 | 0.023 | 0.218 | 0.203 | 0.000 | 1.186 | 27 |
| Fbln5+/+ - 6 | 1.061 | 0.000 | 0.086 | 0.719 | 0.136 | 0.632 | 171 |
| Fbln5+/+ - 7 | 2.547 | 0.000 | 0.181 | 1.036 | 0.196 | 0.819 | 117 |
| Fbln5+/+ - 8 | 5.052 | 0.000 | 0.185 | 2.624 | 0.402 | 1.955 | 50 |
| mean | 2.378 | 0.003 | 0.171 | 0.822 | 0.140 | 0.852 | 215 |
| Designation Number | b1111 | b1122 | b2222 | b1133 | b2233 | b3333 | c [kPa] |
|---|---|---|---|---|---|---|---|
| Fbln5−/− - 1 | 7.860 | 0.000 | 0.971 | 3.796 | 0.505 | 3.877 | 25 |
| Fbln5−/− - 2 | 3.964 | 0.692 | 1.192 | 2.627 | 0.555 | 2.724 | 34 |
| Fbln5−/− - 3 | 21.41 | 0.000 | 0.446 | 9.765 | 0.491 | 7.595 | 11 |
| Fbln5−/− - 4 | 17.325 | 0.612 | 2.258 | 3.797 | 0.000 | 4.247 | 9 |
| Fbln5−/− - 5 | 1.338 | 0.353 | 0.604 | 0.552 | 0.285 | 0.830 | 161 |
| Fbln5−/− - 6 | 1.605 | 0.0000 | 0.598 | 0.239 | 0.029 | 1.912 | 45 |
| Fbln5−/− - 7 | 8.528 | 0.146 | 0.956 | 3.095 | 0.265 | 3.366 | 19 |
| mean | 8.861 | 0.258 | 1.003 | 3.410 | 0.304 | 3.507 | 43 |
References
- Mojarab, A.; Kamali, R. Design, Optimization and Numerical Simulation of a MicroFlow Sensor in the Realistic Model of Human Aorta. Flow Meas. Instrum. 2020, 74, 101791. [Google Scholar] [CrossRef]
- Pasta, S.; Catalano, C.; Cannata, S.; Guccione, J.M.; Gandolfo, C. Numerical Simulation of Transcatheter Mitral Valve Replacement: The Dynamic Implication of LVOT Obstruction in the Valve-in-Ring Case. J. Biomech. 2022, 144, 111337. [Google Scholar] [CrossRef] [PubMed]
- Uesaka, K.; Oka, H.; Kato, R.; Kanie, K.; Kojima, T.; Tsugawa, H.; Toda, Y.; Horinouchi, T. Bioinformatics in Bioscience and Bioengineering: Recent Advances, Applications, and Perspectives. J. Biosci. Bioeng. 2022, 134, 363–373. [Google Scholar] [CrossRef] [PubMed]
- Heydarian, A.; Darvishi, P.; Mortazavi, H.; Mortazavy Beni, H. Experimental and Numerical Responses of Fibroblast and Epithelial Cells to the Frequency of Electric Toothbrush. J. Mech. Behav. Biomed. Mater. 2023, 140, 105697. [Google Scholar] [CrossRef]
- Knutsen, A.K.; Vidhate, S.; McIlvain, G.; Luster, J.; Galindo, E.J.; Johnson, C.L.; Pham, D.L.; Butman, J.A.; Mejia-Alvarez, R.; Tartis, M.; et al. Characterization of Material Properties and Deformation in the ANGUS Phantom during Mild Head Impacts Using MRI. J. Mech. Behav. Biomed. Mater. 2023, 138, 105586. [Google Scholar] [CrossRef]
- Mondal, S.; MacManus, D.B.; Bonatti, A.F.; De Maria, C.; Dalgarno, K.; Chatzinikolaidou, M.; De Acutis, A.; Vozzi, G.; Fiorilli, S.; Vitale-Brovarone, C.; et al. A Computational Analysis of a Novel Therapeutic Approach Combining an Advanced Medicinal Therapeutic Device and a Fracture Fixation Assembly for the Treatment of Osteoporotic Fractures: Effects of Physiological Loading, Interface Conditions, and Fracture. Med. Eng. Phys. 2023, 114, 103967. [Google Scholar] [CrossRef] [PubMed]
- Motchon, Y.D.; Sack, K.L.; Sirry, M.S.; Kruger, M.; Pauwels, E.; Van Loo, D.; De Muynck, A.; Van Hoorebeke, L.; Davies, N.H.; Franz, T. Effect of Biomaterial Stiffness on Cardiac Mechanics in a Biventricular Infarcted Rat Heart Model with Microstructural Representation of in Situ Intramyocardial Injectate. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3693. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Ronan, W.; Teh, I.; Schneider, J.E.; Varela, C.E.; Whyte, W.; McHugh, P.; Leen, S.; Roche, E. A Comparison of Two Quasi-static Computational Models for Assessment of Intra-myocardial Injection as a Therapeutic Strategy for Heart Failure. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3213. [Google Scholar] [CrossRef] [PubMed]
- Ortún-Terrazas, J.; Cegoñino, J.; Santana-Penín, U.; Santana-Mora, U.; Pérez del Palomar, A. A Porous Fibrous Hyperelastic Damage Model for Human Periodontal Ligament: Application of a Microcomputerized Tomography Finite Element Model. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3176. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Dong, X.; Guan, Y.; Kang, Y. Design and Mechanical Properties Analysis of Heterogeneous Porous Scaffolds Based on Bone Slice Images. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3673. [Google Scholar] [CrossRef]
- Johnston, R.D.; Ghasemi, M.; Lally, C. Inverse Material Parameter Estimation of Patient-specific Finite Element Models at the Carotid Bifurcation: The Impact of Excluding the Zero-pressure Configuration and Residual Stress. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3663. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Harvey, T.; Begiristain, E.; Domínguez, C.; Sánchez-Abella, L.; Browne, M.; Cook, R.B. Measuring the Elastic Modulus of Soft Biomaterials Using Nanoindentation. J. Mech. Behav. Biomed. Mater. 2022, 133, 105329. [Google Scholar] [CrossRef]
- Weizel, A.; Distler, T.; Detsch, R.; Boccaccini, A.R.; Bräuer, L.; Paulsen, F.; Seitz, H.; Budday, S. Hyperelastic Parameter Identification of Human Articular Cartilage and Substitute Materials. J. Mech. Behav. Biomed. Mater. 2022, 133, 105292. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cocciolone, A.J.; Staiculescu, M.C.; Mecham, R.P.; Wagenseil, J.E. Passive Biaxial Mechanical Behavior of Newborn Mouse Aorta with and without Elastin. J. Mech. Behav. Biomed. Mater. 2022, 126, 105021. [Google Scholar] [CrossRef] [PubMed]
- Cavinato, C.; Murtada, S.-I.; Rojas, A.; Humphrey, J.D. Evolving Structure-Function Relations during Aortic Maturation and Aging Revealed by Multiphoton Microscopy. Mech. Ageing Dev. 2021, 196, 111471. [Google Scholar] [CrossRef]
- Patel, M.; Savvopoulos, F.; Berggren, C.C.; Aslanidou, L.; Timmins, L.H.; de Silva, R.; Pedrigi, R.M.; Krams, R. Considerations for Analysis of Endothelial Shear Stress and Strain in FSI Models of Atherosclerosis. J. Biomech. 2021, 128, 110720. [Google Scholar] [CrossRef]
- Eberth, J.F.; Taucer, A.I.; Wilson, E.; Humphrey, J.D. Mechanics of Carotid Arteries in a Mouse Model of Marfan Syndrome. Ann. Biomed. Eng. 2009, 37, 1093–1104. [Google Scholar] [CrossRef] [PubMed]
- Bellini, C.; Bersi, M.R.; Caulk, A.W.; Ferruzzi, J.; Milewicz, D.M.; Ramirez, F.; Rifkin, D.B.; Tellides, G.; Yanagisawa, H.; Humphrey, J.D. Comparison of 10 Murine Models Reveals a Distinct Biomechanical Phenotype in Thoracic Aortic Aneurysms. J. R. Soc. Interface 2017, 14, 20161036. [Google Scholar] [CrossRef]
- Luetkemeyer, C.M.; James, R.H.; Devarakonda, S.T.; Le, V.P.; Liu, Q.; Han, H.-C.; Wagenseil, J.E. Critical Buckling Pressure in Mouse Carotid Arteries with Altered Elastic Fibers. J. Mech. Behav. Biomed. Mater. 2015, 46, 69–82. [Google Scholar] [CrossRef]
- Amin, M.; Le, V.P.; Wagenseil, J.E. Mechanical Testing of Mouse Carotid Arteries: From Newborn to Adult. J. Vis. Exp. 2012, 60, e3733. [Google Scholar] [CrossRef]
- Wan, W.; Dixon, J.B.; Gleason, R.L. Constitutive Modeling of Mouse Carotid Arteries Using Experimentally Measured Microstructural Parameters. Biophys. J. 2012, 102, 2916–2925. [Google Scholar] [CrossRef]
- Badel, P.; Avril, S.; Lessner, S.; Sutton, M. Mechanical Identification of Layer-Specific Properties of Mouse Carotid Arteries Using 3D-DIC and a Hyperelastic Anisotropic Constitutive Model. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Gleason, R.L.; Dye, W.W.; Wilson, E.; Humphrey, J.D. Quantification of the Mechanical Behavior of Carotid Arteries from Wild-Type, Dystrophin-Deficient, and Sarcoglycan-δ Knockout Mice. J. Biomech. 2008, 41, 3213–3218. [Google Scholar] [CrossRef]
- Dye, W.W.; Gleason, R.L.; Wilson, E.; Humphrey, J.D. Altered Biomechanical Properties of Carotid Arteries in Two Mouse Models of Muscular Dystrophy. J. Appl. Physiol. 2007, 103, 664–672. [Google Scholar] [CrossRef]
- Guo, X.; Kassab, G.S. Variation of Mechanical Properties along the Length of the Aorta in C57bl/6 Mice. Am. J. Physiol. Circ. Physiol. 2003, 285, H2614–H2622. [Google Scholar] [CrossRef]
- Vargas-Vargas, H.; Sáez-Landete, J.; Siegmann, P.; Camacho-Bello, C. Validation of Solid Mechanics Models Using Modern Computation Techniques of Zernike Moments. Mech. Syst. Signal Process. 2022, 173, 109019. [Google Scholar] [CrossRef]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Texts in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10, ISBN 978-3-642-33286-9. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9781856176330. [Google Scholar]
- Luczkiewicz, P.; Daszkiewicz, K.; Witkowski, W.; Chróścielewski, J.; Ferenc, T.; Baczkowski, B. The Influence of a Change in the Meniscus Cross-Sectional Shape on the Medio-Lateral Translation of the Knee Joint and Meniscal Extrusion. PLoS ONE 2018, 13, e0193020. [Google Scholar] [CrossRef]
- Nowak, M.; Divo, E.; Adamczyk, W.P. Multiscale Model for Blood Flow after a Bileaflet Artificial Aortic Valve Implantation. Comput. Biol. Med. 2023, 158, 106805. [Google Scholar] [CrossRef]
- Chuong, C.J.; Fung, Y.C. On Residual Stresses in Arteries. J. Biomech. Eng. 1986, 108, 189–192. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C.; Fronek, K.; Patitucci, P. Pseudoelasticity of Arteries and the Choice of Its Mathematical Expression. Am. J. Physiol. Circ. Physiol. 1979, 237, H620–H631. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef] [PubMed]
- Abaqus 2019 Documentation; Dassault Systèmes: Providence, RI, USA, 2019.
- Sutton, M.A.; Ke, X.; Lessner, S.M.; Goldbach, M.; Yost, M.; Zhao, F.; Schreier, H.W. Strain Field Measurements on Mouse Carotid Arteries Using Microscopic Three-Dimensional Digital Image Correlation. J. Biomed. Mater. Res. Part A 2008, 84A, 178–190. [Google Scholar] [CrossRef] [PubMed]
- Teter, A.; Kolakowski, Z. On Using Load-Axial Shortening Plots to Determine the Approximate Buckling Load of Short, Real Angle Columns under Compression. Compos. Struct. 2019, 212, 175–183. [Google Scholar] [CrossRef]
- Rozylo, P.; Teter, A.; Debski, H.; Wysmulski, P.; Falkowicz, K. Experimental and Numerical Study of the Buckling of Composite Profiles with Open Cross Section under Axial Compression. Appl. Compos. Mater. 2017, 24, 1251–1264. [Google Scholar] [CrossRef]
- Sun, W.; Sacks, M.S. Finite Element Implementation of a Generalized Fung-Elastic Constitutive Model for Planar Soft Tissues. Biomech. Model. Mechanobiol. 2005, 4, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Bhat, S.K.; Yamada, H. Mechanical Characterization of Dissected and Dilated Human Ascending Aorta Using Fung-Type Hyperelastic Models with Pre-Identified Initial Tangent Moduli for Low-Stress Distensibility. J. Mech. Behav. Biomed. Mater. 2022, 125, 104959. [Google Scholar] [CrossRef] [PubMed]
- Rivera, C.P.; Li, L.; Cai, S.; Pei, N.; McAlear, G.E.; Bollavaram, K.; Ariyo, O.V.; Omojola, V.O.; Song, H.; Alfonso, A.L.; et al. Age-Dependent Characterization of Carotid and Cerebral Artery Geometries in a Transgenic Mouse Model of Sickle Cell Anemia Using Ultrasound and Microcomputed Tomography. Blood Cells Mol. Dis. 2020, 85, 102486. [Google Scholar] [CrossRef]
- Chan, J.M.; Park, S.-J.; Ng, M.; Chen, W.C.; Garnell, J.; Bhakoo, K. Predictive Mouse Model Reflects Distinct Stages of Human Atheroma in a Single Carotid Artery. Transl. Res. 2022, 240, 33–49. [Google Scholar] [CrossRef]
- Das Neves Borges, P.; Forte, A.E.; Vincent, T.L.; Dini, D.; Marenzana, M. Rapid, Automated Imaging of Mouse Articular Cartilage by MicroCT for Early Detection of Osteoarthritis and Finite Element Modelling of Joint Mechanics. Osteoarthr. Cartil. 2014, 22, 1419–1428. [Google Scholar] [CrossRef]
- Niestrawska, J.A.; Spronck, B.; Cavinato, C.; Humphrey, J.D. Tempol Improves Aortic Mechanics in a Mouse Model of Hypertension. J. Biomech. 2024, 162, 111911. [Google Scholar] [CrossRef] [PubMed]
- Riou, L.M.; Broisat, A.; Ghezzi, C.; Finet, G.; Rioufol, G.; Gharib, A.M.; Pettigrew, R.I.; Ohayon, J. Effects of Mechanical Properties and Atherosclerotic Artery Size on Biomechanical Plaque Disruption—Mouse vs. Human. J. Biomech. 2014, 47, 765–772. [Google Scholar] [CrossRef] [PubMed]
- Saba, L.; Sanfilippo, R.; Suri, J.S.; Cademartiri, F.; Corrias, G.; Mannelli, L.; Zucca, S.; Senis, I.; Montisci, R.; Wintermark, M. Does Carotid Artery Tortuosity Play a Role in Stroke? Can. Assoc. Radiol. J. 2021, 72, 789–796. [Google Scholar] [CrossRef] [PubMed]





| Reference Paper | Mouse Model | Outer Carotid Diameter [μm] | Carotid Wall Thickness [μm] | Inner to Outer Diameter Ratio |
|---|---|---|---|---|
| [19] | Eln+/+ | 402 | 58.5 | 0.71 |
| Eln+/− | 354 | 55 | 0.69 | |
| Fbln5+/+ | 379 | 59 | 0.69 | |
| Fbln5−/− | 390 | 57 | 0.71 | |
| [22] | unknown | 343 | 71.2 | 0.58 |
| [23] | wild-type | 424 | 63.3 | 0.70 |
| mdx | 432 | 63.6 | 0.71 | |
| sgcd−/− | 416 | 62.9 | 0.70 |
| Stretch | Experiment from [19] | FEM Predictions | |||||
|---|---|---|---|---|---|---|---|
| Analysis of the Post-Buckling Response | The Pressure at uA = Dout/2 | ||||||
| Fung Constants from [19] | Holzapfel, Set “B” | Fung Constants from [19] | Holzapfel, Set “B” | ||||
| λz | pexp [mmHg] | pbuck,FEM [mmHg] | pbuck,FEM [mmHg] | puA,FEM [mmHg] | Relative Error [%] | puA,FEM [mmHg] | Relative Error [%] |
| 1.0 | 67 | 40 | 71 | 47 | 29.9 | 77 | 14.9 |
| 1.2 | 111 | 61 | 107 | 64 | 42.3 | 118 | 6.3 |
| 1.4 | 180 | 142 | 152 | 168 | 6.7 | 181 | 0.6 |
| Stretch | Experiment from [19] | FEM Predictions | |||||
|---|---|---|---|---|---|---|---|
| Analysis of the Post-Buckling Response | The Pressure at uA = Dout/2 | ||||||
| Fung Constants from [19] | Holzapfel, Set “B” | Fung Constants from [19] | Holzapfel, Set “B” | ||||
| λz | pexp [mmHg] | pbuck,FEM [mmHg] | pbuck,FEM [mmHg] | puA,FEM [mmHg] | Relative Error [%] | puA,FEM [mmHg] | Relative Error [%] |
| 1.0 | 58 | 52 | 81 | 83 | 43.1 | 82 | 41.4 |
| 1.2 | 115 | 135 | 135 | 105 | 8.7 | 136 | 18.3 |
| 1.4 | 227 * | >400 | 205 | >400 | >100 | 330 | 45.4 |
| Carotid Artery Type | Set | C10 [kPa] | k1 [kPa] | k2 [kPa] | γmedia [°] | γadventitia [°] |
|---|---|---|---|---|---|---|
| Eln+/+ | A | 19 | 3 | 0.53 | 30 | 75 |
| B | 12 | 10 | 0.23 | 30 | 75 | |
| Fbln5−/− | C | 15 | 8 | 0.7 | 30 | 75 |
| D | 10 | 15 | 0.42 | 30 | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobczyk, B.; Chróścielewski, J.; Wilde, K. Numerical Analysis of Mice Carotid Arteries’ Response Emphasizing the Importance of Material Law Constants’ Validation. Appl. Sci. 2024, 14, 3571. https://doi.org/10.3390/app14093571
Sobczyk B, Chróścielewski J, Wilde K. Numerical Analysis of Mice Carotid Arteries’ Response Emphasizing the Importance of Material Law Constants’ Validation. Applied Sciences. 2024; 14(9):3571. https://doi.org/10.3390/app14093571
Chicago/Turabian StyleSobczyk, Bartosz, Jacek Chróścielewski, and Krzysztof Wilde. 2024. "Numerical Analysis of Mice Carotid Arteries’ Response Emphasizing the Importance of Material Law Constants’ Validation" Applied Sciences 14, no. 9: 3571. https://doi.org/10.3390/app14093571





