X-ray Chirped Pulse Amplification: towards GW Soft X-ray Lasers

Abstract

Extensive modeling of the seeding of plasma-based soft X-ray lasers is reported in this article. Seminal experiments on amplification in plasmas created from solids have been studied in detail and explained. Using a transient collisional excitation scheme, we show that a 18 µJ, 80 fs fully coherent pulse is achievable by using plasmas pumped by a compact 10 Hz laser. We demonstrate that direct seeding of plasmas created by nanosecond lasers is not efficient. Therefore, we propose and fully study the transposition to soft X-rays of the Chirped Pulse Amplification (CPA) technique. Soft X-ray pulses with energy of 6 mJ and 200 fs duration are reachable by seeding plasmas pumped by compact 100 J, sub-ns, 1 shot/min lasers. These soft X-ray lasers would reach GW power, corresponding to an increase of 100 times as compared to the highest peak power achievable nowadays in the soft X-ray region (30 eV–1 keV). X-ray CPA is opening new horizon for soft x-ray ultra-intense sources.

1. Introduction

Over the last decade, ultra-intense X-ray sources have opened new avenues in physics, creating new states of matter, probing or imaging the most intimate components of living [1] or inert matter or realizing movies of samples excited by ultra-fast sources [2]. Within the panorama of available ultra-intense X-ray sources, free-electron lasers (FEL) have a strong leadership, as they deliver pulses combining femtosecond duration and 10s of microjoules to millijoule energy [3,4].

Considering the applications developed so far or under consideration, pump (infrared laser)-probe (FEL) experiments attract a lot of interest. Although such technique has been widely used on other X-ray sources like synchrotrons or high harmonic generation (HHG, high order harmonics of infrared lasers), free-electron lasers are just opening new horizons by freezing during a few femtoseconds the non-reproducible evolution of samples excited by an external source. As an example, we may cite the work of Wang and co-authors [5] that imaged using X-ray holography the local deformation of nano-domains of a magnetic multilayer after being heated up by a femtosecond laser. This experiment raised two key issues. First, simpler techniques like X-ray diffraction suffer from information loss, being incapable of catching the tiniest change of the magnetic structure observed by X-ray holography as it averages the size and shape over all the nano-domains. Second, X-ray holography, even using the most efficient techniques, requires extreme energies of few mJ per pulse. Indirectly, this energy range has been confirmed by B. Vodungbo et al [6]. who accumulated 0.1 mJ, corresponding to nearly a million high harmonic pulses for producing a high quality soft X-ray diffraction image (at 60 eV) of a magnetic sample similar to those used by Wang et al. [5]. The list can be extended to many imaging experiments and beyond to other fields, of which we would like to draw the attention on the study of Mancuso and collaborators on imaging of biological samples [7]. Here, 1500 FEL pulses needed to be accumulated for reaching a total of 15 mJ on target, to produce high-resolution image of algae by soft X-ray holography (at 8 nm). Nowadays, milli-Joule energy in a single pulse is only achieved at the LCLS free-electron laser that combines a high number of photons, several 10¹²/pulse, and photon energies up to 12 keV. For the rest of the article, we differentiate the soft x-ray domain that extends from typically 30 eV to 1 keV from hard X-ray (photon energy above 1 keV).

In parallel, laser-pumped soft X-ray lasers (SXRL) show exciting promise having demonstrated the most energetic monochromatic soft X-ray pulse, up to 12 mJ but with poor coherence and long (200 ps) pulses [8]. Increasing the coherence of plasma-based SXRL has been a subject of active research during the last two decades. Many techniques have been tested, like the use of a half or full cavity, all being far from producing fully coherent pulses. The first ground-breaking step forward was realized by T. Ditmire and collaborators who seeded a plasma with an external ultrafast (200 fs) and fully coherent high harmonic pulse [9]. Results were not at the level of expectations: the seed was amplified only 3 times reaching less than 1 µJ while the amplified spontaneous emission, ASE, i.e., stochastic incoherent noise, reached 5 mJ. Analysis of the experiment by T. Ditmire et al. pointed out the problem of refraction in plasmas created from solid targets as well as several technical problems. Based on their conclusions, we realized the first successful demonstration of amplification of high harmonic pulses in plasma created from gas targets [10]. Gas amplifiers present negligible refraction effects and due to the pumping technique (longitudinal pumping) they eased the location of the gain region in space and time. This work was followed in 2008 by the strong amplification, up to 600 times, of a high harmonic pulse in plasma created from solid target [11]. Although very successful, this experiment exhibited two unexpected results: the output energy of 0.1 µJ was lower or similar to those measured with gas amplifiers over our different experiments. In addition to this, the pulse duration was still limited at about 1 ps. Indeed, solid amplifiers, having in general much higher electron density and temperature than gas amplifiers, are expected to present larger values of both spectral bandwidth, Δλ, (τ 1/Δλ, τ being the pulse duration) and saturation fluence, leading to shorter pulses.

Considering the different unexplained issues described above and considering that plasmas emitting spontaneously millijoule of energy (ASE) are driven by low repetition-rate lasers (1 shot/20 mn at best), we considered it essential to precisely model the full seeding experiment prior to the shift from well-known gas amplifiers to solid ones.

Using a Maxwell-Bloch time-dependant code, we have previously shown [12] that the key to extracting the energy from long pulse X-ray lasers is to stretch the seed, to accommodating the fast gain recovery time in higher density plasmas. Noticing that a high level of seed was necessary, we anticipated that plasma pre-amplifier, producing a µJ-level pulse with a bandwidth matched to the long pulse amplifier, should yield the highest final energy at the shortest pulse duration (>10 mJ, sub 200 fs at 21 nm). In this paper, we give the conditions for the pre-amplifier optimization through full hydrodynamic and radiation simulations, and show the working conditions for a Chirped Pulse Amplification (CPA) X-ray laser chains.

2. Numerical Section

We have first used ARWEN 2D hydrodynamic code [13] developed by P. Velarde, Spain, to clarify and then optimize the plasma amplifier conditions [14]. This code is a 2D hydrodynamic code with radiation-transport that solves radiation hydrodynamics equations enhanced with the treatment of electron thermal conduction. Navier-Stokes equations are solved with Eulerian scheme using a high-order Godunov type method with a real gas approximated Riemann solver. Electron thermal conduction and radiation transport are solved with matrix-free solvers and Sn multigroup methods respectively. Equations of State and opacities are obtained from the QEOS and BigBART programs. This code is based on the Adaptive Mesh Refinement technique, saving computational time by refining the mesh only in a small part of the simulation domain. Since Wang et al. [11] was the sole successful seeding experiment with a solid amplifier, we benchmarked our numerical codes against it. They used the so-called Transient Collisional Excitation Scheme (TCE), combining a long infrared pulse that creates the plasma at the right ionization stage followed after a variable delay by a short (ps) pulse that produces the population inversion. All modeling showed in this article is done using this scheme: the plasma is created by a 100 ps infrared pulse (I = 1.2 × 10¹² W/cm²) preceded by a 1 ns pre-pulse (I = 1.2 × 10¹¹ W/cm²); free-electrons are heated up directly by the short infrared pulse (0.5 ps, I = 1.1 × 10¹⁵ W/cm²) and later by thermal conductivity. Then, they collide with the lasing ions populating both the lower (1) and upper (2) lasing levels. On a simplified but realistic description, population inversion is created because the upper level is metastable (the radiative transition between the fundamental and the upper level is forbidden) and the lower level is coupled to the ground-state (0) by a very fast E2 transition. Lasing ions considered in this article are either neonlike (10 bound electrons) or nickellike (28 bound electrons). Einstein’s coefficients for the different transitions involved on this scheme are A₂₁ = 1.3 × 10¹⁰ s⁻¹ and A₁₀ = 8.3 × 10¹¹ s⁻¹ for the 2p ⁵ 3s J = 1 → 2p⁵ 3p, J = 0 neonlike Fe transition occurring at λ = 25.5 nm; A₂₁ = 1.8 × 10¹⁰ s⁻¹ and A₁₀ = 1.0 × 10¹² s⁻¹ for the 2p ⁵ 3s J = 1 → 2p⁵ 3p, J = 0 neonlike Zn transition at λ = 21.2 nm and A₂₁ = 4.4 × 10¹¹ s⁻¹ and A₁₀ = 4.2 × 10¹¹ s⁻¹ for the 4p¹ J = 1 → 4d¹ J = 0 nickellike Mo transition occurring at λ = 18.9 nm.

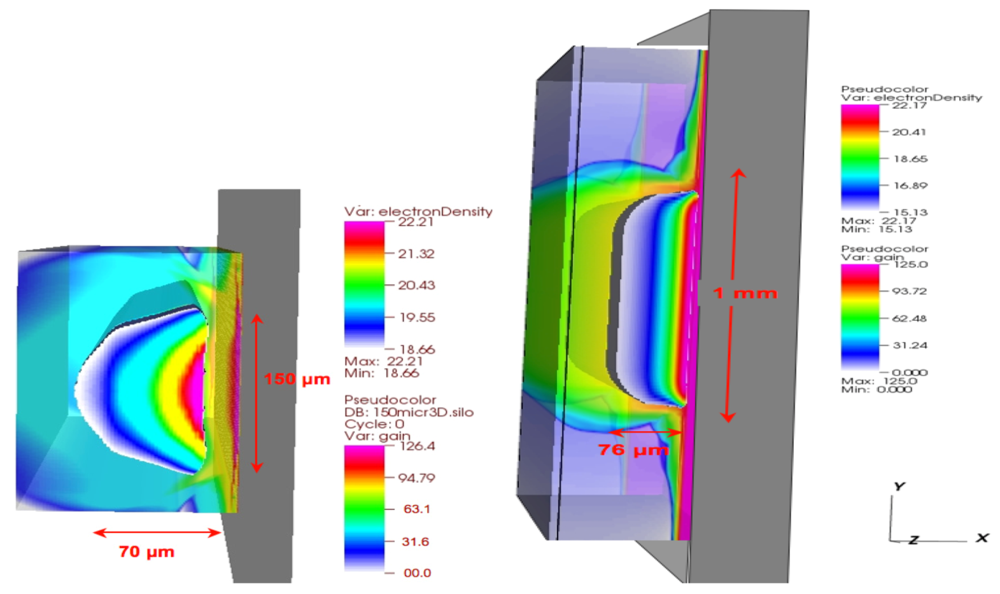
On Figure 1, a 3D map of the plasma and of the gain region is displayed. This plasma is assumed to be homogeneous along the longer (Z) dimension. In Wang et al.’s experiment [11], the pump laser was focused over a 30 µm × 5 mm line. At first glance, we may observe that the plasma is almost three times the size of the focal width along the target surface (Y). Such a strong plasma flow was not expected, leading to a larger gain region, about 50 µm wide. It is interesting to observe that the gain zone extends only over 10 µm along the pump laser axis (X). The gain peaks at about 62 cm⁻¹ agreeing very well with Wang et al.’s data. It decreases very fast when the distance from the target surface increases.

Figure 1. Image in false colors of plasma created by two laser pulses and the gain region. This modeling has been used to benchmark ARWEN code against Wang et al.’s experiment. [11].

Figure 1. Image in false colors of plasma created by two laser pulses and the gain region. This modeling has been used to benchmark ARWEN code against Wang et al.’s experiment. [11].

The saturation fluence calculated over the gain region is roughly stable at 2.3 mJ/cm² agreeing well with Wang’s article (fluence of 1.8 mJ/cm²). These two results are striking. Although most plasma-based soft X-ray lasers are running at about 10 times the saturation fluence, in order to break the mJ threshold, one needs to produce a gain region of 0.1 cm² (to be compared to 5 × 10⁻⁶ cm⁻² for Wang et al. [11]). We therefore explored the possibility of enlarging the gain region. The most accessible solution consists in enlarging the focal width while keeping the intensity constant. We modeled plasmas created with focal widths from 30 µm up to 2 mm (Figure 2). It is striking to observe that peak gain increases very quickly from 62 to 126 cm⁻¹ when enlarging the focal width from 30 µm to 100 µm. Then, peak gain remains constant for widths larger than 100 µm [15]. Note that the gain region increases nearly 8 times along the X direction from 10 µm to 76 µm while the vertical flow becomes negligible maintaining the gain region near the focal width size. When the focal width is larger than 100 µm, the gain zone is rather homogeneous. These changes are due to a reduction of the thermal losses by lateral conduction and radiation cooling as well as the inhibition of the lateral expansion when increasing the focal width [16].

Figure 2. Image in false colors of plasmas created by 100 µm (left) and 1 mm (right) focal width. For 1 mm large width, the plasma flow along the target surface is very weak.

Figure 2. Image in false colors of plasmas created by 100 µm (left) and 1 mm (right) focal width. For 1 mm large width, the plasma flow along the target surface is very weak.

Considering a 1 mm large plasma that may be created with a sub-PW laser, about 0.4 mJ is stored on the population inversion. This value, although too low for the most demanding experiments like biological imaging, represents a huge step forward. However, using only a hydrodynamic code is not sufficient to give a precise estimate of the output energy when seeding this amplifier with high harmonics. Several issues still remain to be studied numerically to define the best seeding conditions and thus the highest output energy and shortest duration achievable.

In the second step, we used a time-dependent Maxwell-Bloch model as a post-processor for the plasma conditions, enabling us to answer the remaining questions by describing accurately the temporal structure of the soft X-ray pulse all along its amplification. In brief, the model describes the evolution of the electromagnetic field of the soft X-ray radiation (seed and spontaneous emission) during its amplification (Maxwell equations) coherently coupled to the time-dependent evolution of the population of the energy levels of the lasing ion (Bloch equations). The model includes a stochastic source term to mimic the spontaneous emission as well as a depolarization term due to electron-ion collisions. A thorough description of the model can be found in [17,18,19]. Our model is coupled to ARWEN output while previous similar models used ab initio plasma conditions. It is worth noting that since HHG are linearly polarized, our Maxwell-Bloch model does not take into account the degeneracy of the lower level. If circularly polarized HHG were seeded (created using polarizing mirrors [20] or mixing two-color fields [21,22]), the magnetic sub-levels must be taken into account since left polarized HHG induces transitions to the m = −1 level whereas right polarized HHG induces transitions to the m = 1 level. 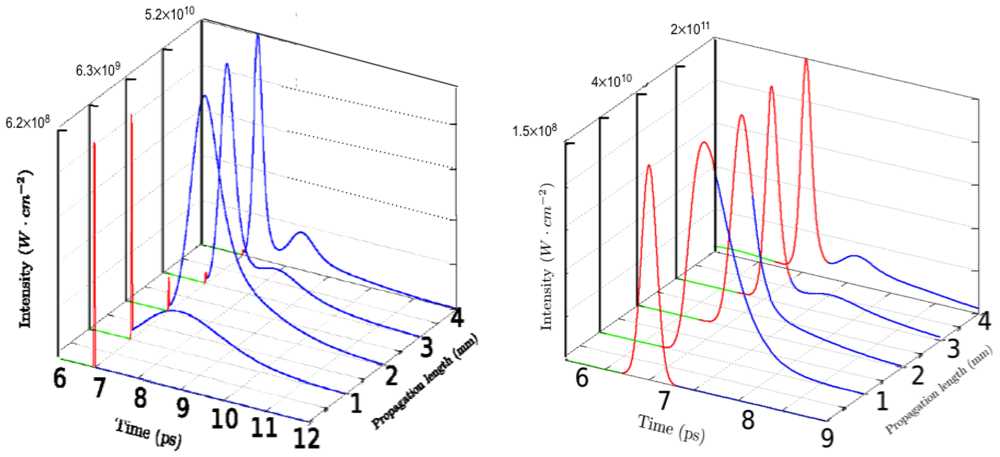When modeling Wang et al.’s experiment, we observed the well-known weak amplification of the HHG seed followed by a wake field that is amplified [23,24] and contains most of the energy in a 2 ps pulse (Figure 3). As explained by E. Oliva and collaborators, the incapacity of such plasma in amplifying the seed comes from the mismatch between the polarization characteristic time (~0.1–0.2 ps) and the HHG duration (30 fs). Also, the long lasting (several picosecond) wake originates from the long duration of the polarization induced by the seed. Indeed, depolarization mainly occurs through electron-ion collisions that have a characteristic time of several picoseconds. Therefore, E. Oliva and collaborators proposed and tested to seed a longer HHG beam (200 fs) in high-density plasma that presents a faster depolarization timescale and thus a shorter wake [18]. ARWEN modeling showed that plasmas larger than 100 µm have the adequate conditions. Seeding with this parameters (and 50 nJ energy to maintain the seeding intensity) a 100 µm wide plasma enhances the coupling HHG-plasma. The combination of the fast depolarization of the plasma (due to electron collisions) and the strong saturation of the population inversion by the HHG field inhibits the creation and amplification of the wake, conserving the femtosecond duration of the seed. Furthermore, as observed on classical lasers [25,26], amplification in this deep-saturation regime is only efficient during the first part of the high harmonic pulse while the second half of the pulse encountering a reduced population inversion is weakly amplified. This phenomenon results in the pulse shortening observed for lengths above 2 mm (Figure 3 right). This scheme leads to the generation of a 1.4 µJ, 80 fs pulse after passing through a 2.5 mm length plasma (Figure 3). It is not worth to use longer plasmas as the ASE and the wake are strongly developed after this optimal length.

Figure 3. Evolution of the intensity versus time along the 30 µm (left, high harmonic generation (HHG) = 30 fs) and 100 µm width (right, HHG = 200 fs) plasma columns. The green, red and blue lines stand for the ASE, seed and wake fields. The vertical scales are not constant to account for amplification.

Figure 3. Evolution of the intensity versus time along the 30 µm (left, high harmonic generation (HHG) = 30 fs) and 100 µm width (right, HHG = 200 fs) plasma columns. The green, red and blue lines stand for the ASE, seed and wake fields. The vertical scales are not constant to account for amplification.

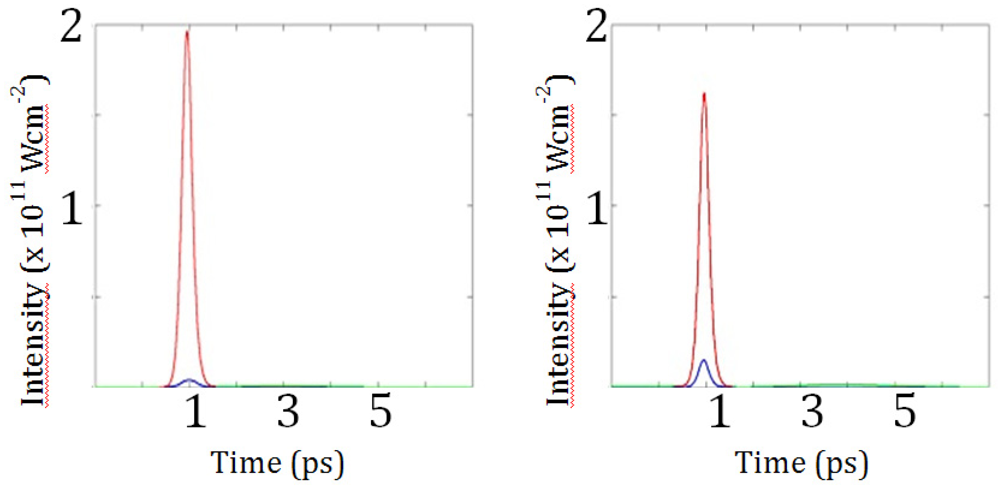
When considering direct amplification in a 1 mm large plasma, we observe that optimal seeding conditions require using 1 µJ seed. However, even for this high-density plasma, the spectral width of the soft X-ray laser is about 30 times narrower than the spectral width of the HHG, meaning that we need a 30 µJ HHG beam. Such energy is currently unrealistic. However, 100 µm plasma seeded with HHG delivers a beam with optimal properties (1.4 µJ, 80 fs and similar bandwidth) as the input of the 1 mm one (Figure 4). At the end of the main amplifier (1.5 mm long, 1 mm large), the pulse is totally dominated by the amplified coherent HHG seed, reaching at best 18 µJ in 80 fs (Figure 5). About 10 J is necessary to create the main plasma, which is achievable using commercial, 10 Hz lasers.

Figure 4. Artistic view of an amplification chain starting, from left to right, with the HHG source, focusing optics, pre and main amplifiers.

Figure 4. Artistic view of an amplification chain starting, from left to right, with the HHG source, focusing optics, pre and main amplifiers.

Figure 5. Left, temporal evolution of the HHG intensity at the first plasma entrance (blue) and at its exit (red) (cf Figure 3). Right, same image but at the entrance and exit of the main amplifier. One can observe although ASE exists in both cases, the optimized seeding conditions allow it to be kept at a negligible level.

Figure 5. Left, temporal evolution of the HHG intensity at the first plasma entrance (blue) and at its exit (red) (cf Figure 3). Right, same image but at the entrance and exit of the main amplifier. One can observe although ASE exists in both cases, the optimized seeding conditions allow it to be kept at a negligible level.

Although a complete study of seeding soft x-ray lasers in a transient collisional scheme opened very interesting paths for delivering beams of interest to users, the highest energy achievable is still far from our goal of several millijoules. We thus studied the seminal experiment of Ditmire et al.’s [9]. This experiment was using kilojoule class laser with nanosecond duration to create a plasma emitting ASE soft X-ray laser during about 1.2 ns. Such modeling is particularly delicate due to the very different time-scales under consideration, from 20 fs for the HHG, to 100s of ps for the spontaneous emission and ns for the plasma hydrodynamic. We first benchmarked our Maxwell-Bloch model against Ditmire et al.’s experiment [9]. The plasma was seeded with 200 fs, 0.5 nJ in-band HHG. 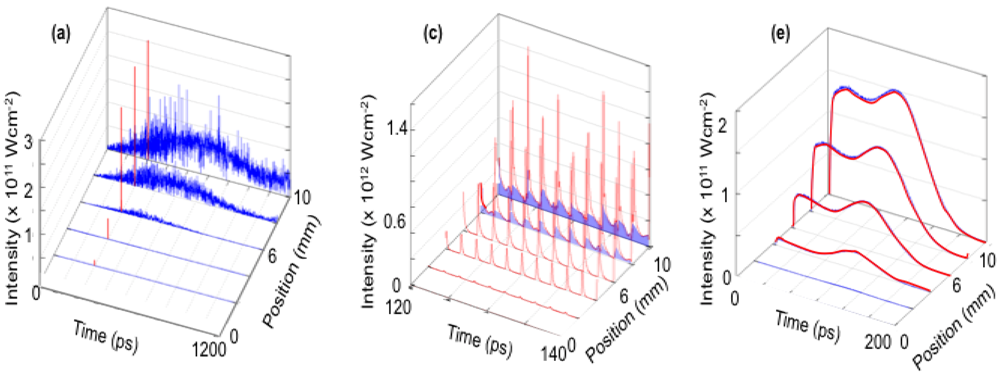Figure 6a displays the temporal evolution of the emitted beam at different plasma lengths. The same features shown in Ditmire et al.’s [9] article have been observed. The HHG is barely amplified and is preceded and followed by strong ASE. Most of the output energy is contained on the post-HHG ASE. The duration of each spike (about 150 fs) is physical while for Ditmire’s experiment it was convolved by the streak camera resolution (40 ps). Such behavior (very strong post-HHG ASE) was not observed on previous seeding experiments (Zeitoun et al. [10] and Wang et al. [11] experiments).

Figure 6. Intensity of the amplified HHG (red) and ASE (blue) at different plasma lengths in (a) Ditmire’s experiment; (b) when seeding a train of 100 HHG (only ten HHG are shown); and (c) when a stretched HHG matching the duration of the gain is seeded into the plasma.

Figure 6. Intensity of the amplified HHG (red) and ASE (blue) at different plasma lengths in (a) Ditmire’s experiment; (b) when seeding a train of 100 HHG (only ten HHG are shown); and (c) when a stretched HHG matching the duration of the gain is seeded into the plasma.

In order to clarify this issue, we concentrated our attention on the interaction of the HHG with the amplifier. As expected, the HHG saturates the amplification (gain drops to near zero). However, the gain is recovered extremely fast, in about 2 ps, allowing spontaneous emission to be amplified. To maintain the coherent amplification inhibiting spontaneous emission, the simplest solution would be to seed a new HHG pulse every 2 ps (or less). In this case, modeling shows a very different picture from the original experiment (Figure 6b). The amplified HHG pulses contain 5 mJ while the ASE drops to 0.1 mJ. Although it is possible to generate a HHG pulse train [27], it seems barely realistic to consider synchronizing over 100s of pulses. We then shifted from a discrete multiple-pulse seed to a single-pulse but continuous seed by seeding a 100s of ps HHG pulses. In this case, we consider as amplifier the plasma reported in a recent experiment on zinc soft X-ray laser (21.2 nm) since it exhibited the highest energy beam (12 mJ) reached to-date. In this case the gain lasts about 200 ps, meaning that the seed must have a duration of 200 ps (and an energy of 1 µJ in-band). The result is very positive: the coherent amplified pulse has 12 mJ after 10 mm of plasma while the ASE remains negligible at 0.1 µJ (Figure 6c). Still, the problem with this scheme is the realization of a seed with a duration of hundreds of picosecond, as it is well-known that HHG pulses are produced by using ultra-short infrared pulses from few fs to 1 ps, leading to sub-ps duration at maximum. We thus propose to transpose the Chirped Pulse Amplification technique [28] to the soft X-rays. The full architecture is displayed in Figure 7 showing the seed HHG, a pre-amplifier followed by a soft X-ray stretcher (grating pair + telescope) the main plasma and the soft X-ray compressor (grating pair). Compressor efficiency as high as 50% is realistic if using a single-pass compressor and off-axis gratings [12,29].

Figure 7. Schematic description of a high energy X-ray Chirped Pulse Amplification (CPA) chain. The same laser is split into three beams to generate the HHG, to pump the pre-amplifier using the Transient Collisional Excitation Scheme (TCE) scheme and to pump the main amplifier with ns duration. Note that the stretcher is placed after the pre-amplifier to keep the intensity high enough for efficiently seeding the different plasmas. This scheme is fully scalable to higher or lower energies. In that last case, pre-amplifier is not necessary.

Figure 7. Schematic description of a high energy X-ray Chirped Pulse Amplification (CPA) chain. The same laser is split into three beams to generate the HHG, to pump the pre-amplifier using the Transient Collisional Excitation Scheme (TCE) scheme and to pump the main amplifier with ns duration. Note that the stretcher is placed after the pre-amplifier to keep the intensity high enough for efficiently seeding the different plasmas. This scheme is fully scalable to higher or lower energies. In that last case, pre-amplifier is not necessary.

After recompression, a 6 mJ, 200 fs, fully coherent in space and in time soft X-ray laser may be produced. The pulse duration has been estimated considering the spectral narrowing as well as the chirp acquired during the amplification. Compensation of quadratic phase terms by the compressor is not included. The required IR pump laser energy reaches 100 J but in sub-ns pulses, that is commercially available with repetition-rate of 1 shot per minute.

3. Conclusions

We presented here an extensive study of the amplification of high harmonics in different laser-created plasmas. Hydrodynamic simulations showed that millimeter-wide plasmas stock hundreds of microjoules of energy in the population inversion, presenting a large and homogeneous gain zone. Time-dependent Maxwell-Bloch simulations allowed us to optimize the coupling between seed and amplifier. If correctly seeded, the harmonic extracts the energy available in the plasma maintaining its femtosecond duration. As these plasma amplifiers can be created using compact lasers, seeding these plasmas with high harmonics will deliver 18 µJ, 80 fs fully coherent pulse at a repetition-rate of 10 Hz.

Seeding plasmas that naturally emit several milijoules raises new problems. The mismatch between the seed duration (hundreds of femtoseconds) and the gain duration (hundreds of picoseconds) is responsible for the powerful Amplified Spontaneous Emission that these plasmas emit, even when seeded. Stretching a high harmonic until its duration matches the gain duration is proposed and simulated in this paper. By coupling the X-ray CPA and sub-ns infrared laser to create the amplifying plasma, a seeded soft X-ray laser may reach the unprecedented (in the soft X-ray region) energy of 6 mJ in 200 fs duration.