Auralization of Accelerating Passenger Cars Using Spectral Modeling Synthesis
Abstract
:1. Introduction
2. Model Development
2.1. Overview


2.2. Emission Module
2.2.1. Sound of Tires
2.2.2. Driving Dynamics

2.2.3. Sound of Propulsion

2.3. Propagation Filtering
- Propagation delay
- Doppler effect (frequency shift and amplification)
- Convective amplification
- Geometrical spreading
- Ground reflection
- Air absorption
2.3.1. Effects Due to Source Motion and Propagation Delay


2.3.2. Ground Effect

2.3.3. Air Absorption
2.4. Reproduction Rendering
3. Model Parameter Estimation
3.1. Tire Noise


3.2. Propulsion Noise

3.2.1. Resampling

3.2.2. Order Analysis



3.2.3. Noise Analysis



3.2.4. Background Noise Corrections
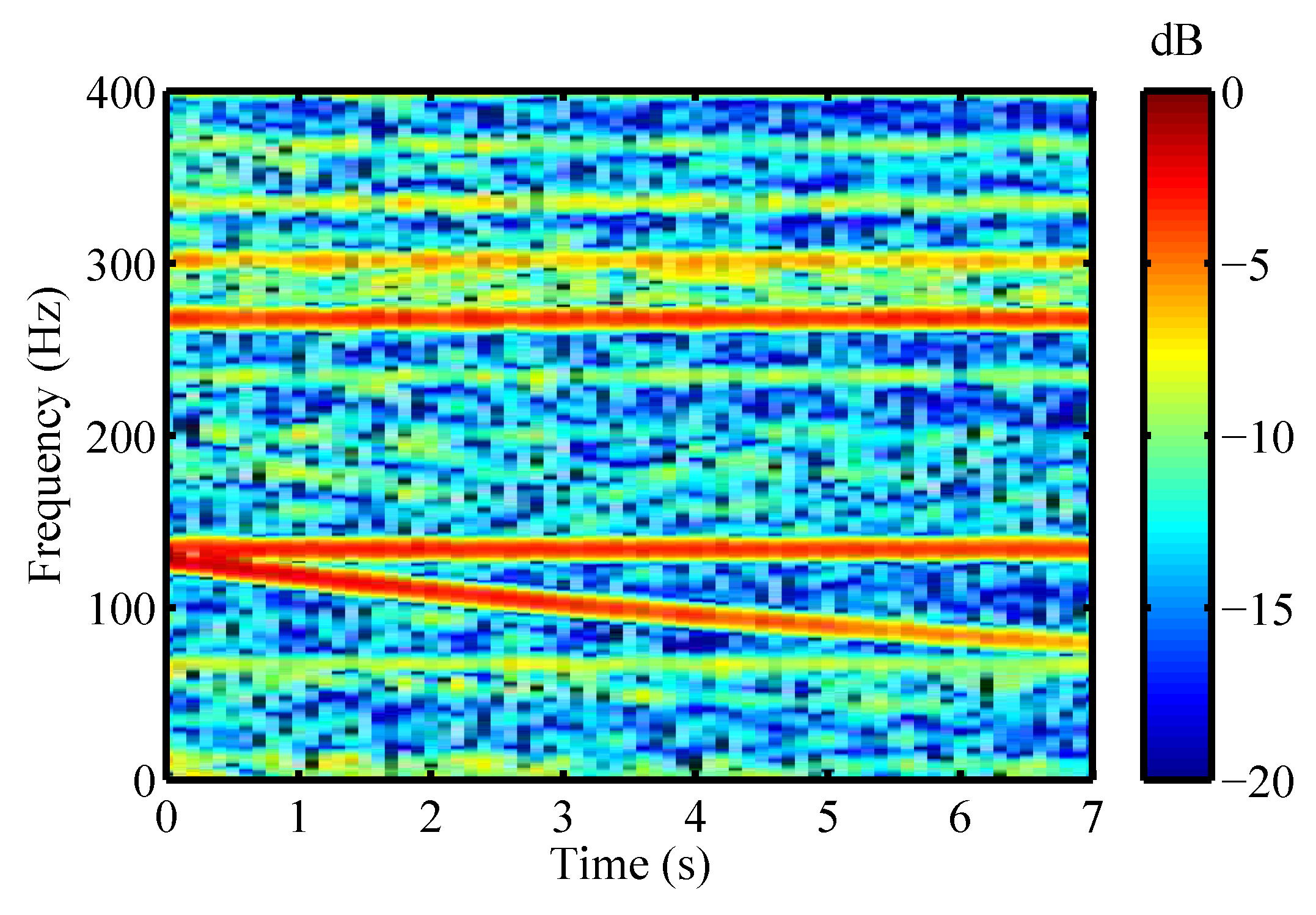
3.2.5. Backpropagation
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
Appendix Code of the Frequency Tracking Algorithm
| M = size (q,1) ; |
| N = size (q,2) ; |
| Q(1 ,:) = q(1 ,:) ; |
| for m = 2:M |
| for k = 1:N |
| kb = max(k−c,1) |
| kt = min(k+c,N) |
| [max Val, maxIdx] = max(Q(m−1,kb:kt)) |
| Q(m,k) = q(m,k) + maxVal; |
| B(m,k) = kb + maxVal − 1; |
| end |
| end |
| [~, P(M)] = max(Q(M,:)); |
| for m = M:−1:2 |
| P(m−1) = B(m,P(m)); |
| end |
References
- Kleiner, M.; Dalenbäck, B.I.; Svensson, P. Auralization—An Overview. J. Audio Eng. Soc. 1993, 41, 861–875. [Google Scholar]
- Vorländer, M. Auralization: Fundamentals of Acoustics, Modelling, Simulation, Algorithms and Acoustic Virtual Reality; Springer: Berlin, Germany, 2008. [Google Scholar]
- Savioja, L.; Svensson, U. Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 2015, 138, 708–730. [Google Scholar] [CrossRef] [PubMed]
- Klemenz, M. Sound Synthesis of Starting Electric Railbound Vehicles and the Influence of Consonance on Sound Quality. Acta Acust. United Acust. 2005, 91, 779–788. [Google Scholar]
- Jagla, J.; Maillard, J.; Martin, N. Sample-based engine noise synthesis using an enhanced pitch-synchronous overlap-and-add method. J. Acoust. Soc. Am. 2012, 132, 3098–3108. [Google Scholar] [CrossRef] [PubMed]
- Pieren, R.; Heutschi, K.; Müller, M.; Manyoky, M.; Eggenschwiler, K. Auralization of Wind Turbine Noise: Emission Synthesis. Acta Acust. United Acust. 2014, 100, 25–33. [Google Scholar] [CrossRef]
- Arntzen, M.; Simons, D. Modeling and synthesis of aircraft flyover noise. Appl. Acoust. 2014, 84, 99–106. [Google Scholar] [CrossRef]
- Sahai, A.; Wefers, F.; Pick, P.; Stumpf, E.; Vorländer, M.; Kuhlen, T. Interactive simulation of aircraft noise in aural and visual virtual environments. Appl. Acoust. 2016, 101, 24–38. [Google Scholar] [CrossRef]
- Rizzi, S.; Sullivan, B.; Sondridge, C. A three-dimensional virtual simulator for aircraft flyover presentation. In Proceedings of the 2003 International Conference on Auditory Display, Boston, MA, USA, 6–9 July 2003; pp. 87–90.
- Rietdijk, F.; Heutschi, K.; Zellmann, C. Determining an empirical emission model for the auralization of jet aircraft. In Proceedings of the 10th European Conference on Noise Control, Maastricht, The Netherlands, 31 May–3 June 2015; pp. 781–784.
- Manyoky, M.; Hayek Wissen, U.; Klein, T.; Pieren, R.; Heutschi, K.; Grêt-Regamey, A. Concept for collaborative design of wind farms facilitated by an interactive GIS-based visual-acoustic 3D simulation. In Proceedings of the Digital Landscape Architecture, Bernburg, Germany, 31 May 2012; pp. 297–306.
- Manyoky, M.; Hayek Wissen, U.; Heutschi, K.; Pieren, R.; Grêt-Regamey, A. Developing a GIS-Based Visual-Acoustic 3D Simulation for Wind Farm Assessment. ISPRS Int. J. Geo-Inf. 2014, 3, 29–48. [Google Scholar]
- Forssén, J.; Kaczmarek, T.; Alvarsson, J.; Lundén, P.; Nilsson, M.E. Auralization of traffic noise within the LISTEN project—Preliminary results for passenger car pass-by. In Proceedings of the Eighth European Conference on Noise Control, Edinburgh, UK, 26–28 October 2009.
- Peplow, A.; Forssén, J.; Lundén, P.; Nilsson, M.E. Exterior Auralization of Traffic Noise within the LISTEN project. In Proceedings of the European Conference on Acoustics (Forum Acusticum 2011), Aalborg, Denmark, 27 June–1 July 2011; pp. 665–669.
- Maillard, J.; Jagla, J. Real Time Auralization of Non-Stationary Traffic Noise—Quantitative and Perceptual Validation in an Urban Street. In Proceedings of the AIA-DAGA Conference on Acoustics, Merano, Italy, 18–21 March 2013.
- McDonald, P.; Rice, H.; Dobbyn, S. Auralisation and Dissemination of Noise Map Data Using Virtual Audio. In Proceedings of the Eighth European Conference on Noise Control, Edinburgh, UK, 26–28 October 2009.
- Fiebig, A.; Genuit, K. Development of a synthesis tool for soundscape design. In Proceedings of the Eighth European Conference on Noise Control, Edinburgh, UK, 26–28 October 2009.
- Heutschi, K. SonRoad: New Swiss Road Traffic Noise Model. Acta Acust. United Acust. 2004, 90, 548–554. [Google Scholar]
- Havelock, D.; Kuwano, S.; Vorländer, M. Handbook of Signal Processing in Acoustics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Pieren, R.; Bütler, T.; Heutschi, K. Auralisation of accelerating passenger cars. In Proceedings of the 10th European Conference on Noise Control, Maastricht, The Netherlands, 31 May–3 June 2015; pp. 757–762.
- Jonasson, H.G. Acoustical Source Modelling of Road Vehicles. Acta Acust. United Acust. 2007, 93, 173–184. [Google Scholar]
- Sandberg, U.; Ejsmont, J. Tyre/Road Noise Reference Book; INFORMEX, Harg: Kisa, Sweden, 2002. [Google Scholar]
- Zeller, P. Handbuch Fahrzeugakustik—Grundlagen, Auslegung, Berechnung, Versuch, 2nd ed.; Vieweg Teubner Verlag: Wiesbaden, Geramny, 2012. [Google Scholar]
- United Nations. UN/ECE Regulation No. 117: Uniform Provisions Concerning the Approval of Tyres with Regard to Rolling Sound Emissions and/or to Adhesion on Wet Surfaces and/or to Rolling Resistance. Off. J. Eur. Union 2011, 54, 3–63. [Google Scholar]
- International Organization of Standardization. ISO 11819-1: Acoustics—Measurement of the Influence of Road Surfaces on Traffic Noise—Part 1: Statistical Pass-By Method; ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Schutte, J.; Wijnant, Y.; de Boer, A. The Influence of the Horn Effect in Tyre/Road Noise. Acta Acust. United Acust. 2015, 101, 690–700. [Google Scholar] [CrossRef]
- European Commission. Commission Directive (EU) 2015/996 of 19 May 2015 establishing common noise assessment methods according to Directive 2002/49/EC of the European Parliament and of the Council. Off. J. Eur. Union 2015, 58, 1–823. [Google Scholar]
- Roads, C. The Computer Music Tutorial; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Rossing, T. Springer Handbook of Acoustics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Smith, J., III. Spectral Audio Signal Processing; W3K Publishing: Standford, UK, 2011. [Google Scholar]
- Serra, X.; Smith, J., III. Spectral Modeling Synthesis: A Sound Analysis/Synthesis System Based on a Deterministic Plus Stochastic Decomposition. Comput. Music J. 1990, 14, 12–24. [Google Scholar] [CrossRef]
- Serra, X. Musical Sound Modeling with Sinusoids plus Noise. In Musical Signal Processing; Swets & Zeitlinger: Lisse, The Netherlands, 1997. [Google Scholar]
- International Electrotechnical Commission. IEC 1260:1995: Electroacoustics—Octave-Band and Franctional-Octave-Band Filters; IEC: Geneva, Switzerland, 1995. [Google Scholar]
- Reif, K. Bosch Automotive Handbook, 8th ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- United Nations. UN/ECE/TRANS/WP.29/2014/27: Proposal for a New Global Technical Regulation on the Worldwide harmonized Light vehicles Test Procedure (WLTP); UNECE: Geneva, Switzerland, 2014. [Google Scholar]
- International Organization of Standardization. ISO 15031-5: Road Vehicles—Communication between Vehicle and External Equipment for Emissions-Related Diagnostics—Part 5: Emissions-related Diagnostic Services; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Maekawa, Z. Noise reduction by screens. Appl. Acoust. 1968, 1, 157–173. [Google Scholar] [CrossRef]
- International Organization of Standardization. ISO 9613-2: Acoustics—Attenuation of Sound during Propagation Outdoors—Part 2: General Method of Calculation; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- Van Maercke, D.; Defrance, J. Development of an Analytical Model for Outdoor Sound Propagation within the Harmonoise Project. Acta Acust. United Acust. 2007, 93, 201–212. [Google Scholar]
- Daigle, G.; Embleton, T.; Piercy, J. Propagation of sound in the presence of gradients and turbulence near the ground. J. Acoust. Soc. Am. 1986, 79, 613–627. [Google Scholar] [CrossRef]
- Hofmann, J.; Heutschi, K. An engineering model for sound pressure in shadow zones based on numerical simulations. Acta Acust. United Acust. 2005, 91, 661–670. [Google Scholar]
- Wunderli, J.; Pieren, R.; Heutschi, K. The Swiss shooting sound calculation model sonARMS. Noise Control Eng. J. 2012, 90, 224–235. [Google Scholar]
- Heutschi, K. Calculation of Reflections in an Urban Environment. Acta Acust. United Acust. 2009, 95, 644–652. [Google Scholar] [CrossRef]
- Wunderli, J. An Extended Model to Predict Reflections from Forests. Acta Acust. United Acust. 2012, 98, 263–278. [Google Scholar] [CrossRef]
- Pieren, R.; Wunderli, J. A Model to Predict Sound Reflections from Cliffs. Acta Acust. United Acust. 2011, 97, 243–253. [Google Scholar] [CrossRef]
- Heutschi, K.; Pieren, R.; Müller, M.; Manyoky, M.; Hayek Wissen, U.; Eggenschwiler, K. Auralization of Wind Turbine Noise: Propagation Filtering and Vegetation Noise Synthesis. Acta Acust. United Acust. 2014, 100, 13–24. [Google Scholar] [CrossRef]
- Lighthill, M. On sound generated aerodynamically. I. General Theory. Proc. R. Soc. Lond. Ser. A 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Morse, P.; Ingard, K. Theoretical Acoustics; Mc Gray-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Lighthill, M. The Bakerian Lecture, 1961: Sound Generated Aerodynamically. Proc. R. Soc. Lond. Ser. A 1962, 267, 147–182. [Google Scholar] [CrossRef]
- Smith, J.; Serafin, S.; Abel, J.; Berners, D. Doppler Simulation and the Leslie. In Proceedings of the 5th International Conference on Digital Audio Effects, Hamburg, Germany, 26–28 September 2002; pp. 932–937.
- Laakso, T.I.; Välimäki, V.; Karjalainen, M.; Laine, U.K. Splitting the unit delay—Tools for fractional delay filter design. IEEE Signal Process. Mag. 1996, 13, 30–60. [Google Scholar] [CrossRef]
- Bruneau, M. Fundamentals of Acoustics; ISTE Ltd: London, UK, 2006. [Google Scholar]
- Delany, M.E.; Bazley, E.N. Acoustical properties of fibrous absorbent materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- International Organization of Standardization. ISO 9613-1: Acoustics—Attenuation of Sound During Propagation Outdoors—Part 1: Calculation of the Absorption of Sound by the Atmosphere; ISO: Geneva, Switzerland, 1993. [Google Scholar]
- Gerzon, M. Periophony: With-Height Sound Reproduction. J. Audio Eng. Soc. 1973, 21, 2–10. [Google Scholar]
- Gerzon, M. Ambisonics in Multichannel Broadcasting and Video. J. Audio Eng. Soc. 1985, 33, 859–871. [Google Scholar]
- Pulkki, V. Virtual Sound Source Positioning Using Vector Base Amplitude Panning. J. Audio Eng. Soc. 1997, 45, 456–466. [Google Scholar]
- Pulkki, V. Uniform spreading of amplitude panned virtual sources. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 17–20 October 1999.
- Ballou, G. Handbook for Sound Engineers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Dickreiter, M.; Dittel, V.; Hoeg, W.; Wöhr, M. Handbuch der Tonstudiotechnik—Band 1, 7th ed.; ARD.ZDF medienakademie: Nürnberg, Geramny, 2008. [Google Scholar]
- Rabiner, L.; Cheng, M.; Rosenberg, A.; McGonegal, C. A comparative performance study of several pitch detection algorithms. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 399–418. [Google Scholar] [CrossRef]
- De la Cuadra, P.; Master, A. Efficient pitch detection techniques for interactive music. In Proceedings of the International Computer Music Conference, Havana, Cuba, 17–23 September 2001; pp. 87–90.
- Gerhard, D. Pitch Extraction and Fundamental Frequency: History and Current Techniques, Technical Report TR-CS 2003-06; Department of Computer Scinece, University of Regina: Regina, SK, Canada, 2003. [Google Scholar]
- Dreuw, P.; Deselaers, T.; Rybach, D.; Keysers, D.; Ney, H. Tracking Using Dynamic Programming for Appearance-Based Sign Language Recognition. In Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, Southampton, UK, 2–6 April 2006; pp. 293–298.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieren, R.; Bütler, T.; Heutschi, K. Auralization of Accelerating Passenger Cars Using Spectral Modeling Synthesis. Appl. Sci. 2016, 6, 5. https://doi.org/10.3390/app6010005
Pieren R, Bütler T, Heutschi K. Auralization of Accelerating Passenger Cars Using Spectral Modeling Synthesis. Applied Sciences. 2016; 6(1):5. https://doi.org/10.3390/app6010005
Chicago/Turabian StylePieren, Reto, Thomas Bütler, and Kurt Heutschi. 2016. "Auralization of Accelerating Passenger Cars Using Spectral Modeling Synthesis" Applied Sciences 6, no. 1: 5. https://doi.org/10.3390/app6010005
APA StylePieren, R., Bütler, T., & Heutschi, K. (2016). Auralization of Accelerating Passenger Cars Using Spectral Modeling Synthesis. Applied Sciences, 6(1), 5. https://doi.org/10.3390/app6010005





