A Novel Mobile Communications Authentication Scheme with Roaming Service and User Anonymity
Abstract
:1. Introduction
2. Preliminaries
2.1. Li’s Scheme
2.1.1. Registration Phase
2.1.2. Authentication Phase
2.1.3. Roaming Phase
2.2. Advantages of Li’s Scheme
2.3. Weaknesses of Li’s Scheme
3. Proposed Scheme
3.1. Notations
3.2. Registration Phase
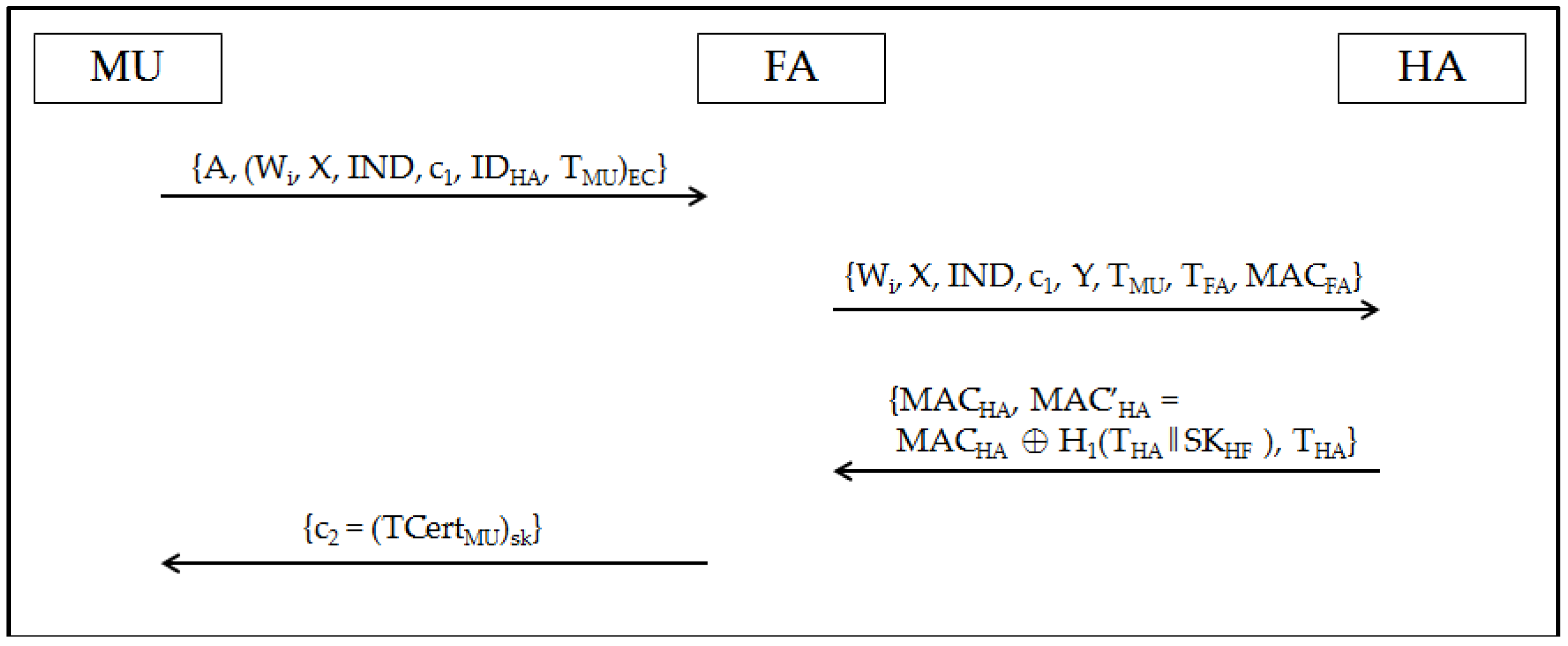
3.3. Authentication Phase
3.4. Roaming Phase
4. BAN-Logic Analysis
4.1. Introduction to BAN-Logic
- MU believes the session key: MU←-SK-→FA
- MU believes that FA believed the session key: MU←-SK-→FA
- A believes the session key: MU←-SK-→FA
- FA believes that MU believed the session key: MU←-SK-→FA
- (X, Y): X or Y is one part of the parameter (X, Y).
- <X>Y: X can be obtained through the secret parameter Y.
- {X}K: X is encrypted under the key K.
- P←-K-→Q: P and Q may use the shared secret key K to communicate. The third party does not know the secret key K.
- P<=S=>Q: S is only known between P and Q. P and Q must use S to prove the identity of each other.
4.2. Rules of BAN-Logic
4.3. Authentication Proof Based on BAN-logic
- mV1. MU→FA: {(<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi), Wi, X, IDHA)}EC
- mV2. FA→HA: (<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi), Wi, X, Y){Ri}SKHF
- mV3. HA→FA: {(Wi, X, Y, IDHA, IDFA)} SKHF
- mV4. FA→MU:{TCertMU}<MU←-SK-→FA>
- A1:
- MU believes X.
- A2:
- MU believes X1.
- A3:
- MU believes A.
- A4:
- FA believes Y.
- A5:
- FA believes Ri.
- A6:
- HA believes Wi.
- A7:
- MU believes MU<=H(N)=>HA.
- A8:
- HA believes MU<=H(N)=>HA.
- A9:
- FA believes FA <=SKHF=>HA.
- A10:
- HA believes FA <=SKHF=>HA.
- A11:
- MU believes MU←-SK-→FA.
- A12:
- FA believes (MU controls MU←-SK-→FA).
- A13:
- HA believes (MU controls MU←-SK-→FA).
- A14:
- HA believes (MU controls IDMU).
- A15:
- IDMU is known only to user.
- A16:
- MU believes TCertMU.
- A17:
- MU believes IDMU.
- A18:
- FA believes IDFA.
- A19:
- HA believes IDHA.
- By mV1, A3, and A4, we apply the freshness rule to deriveFA believes (<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi), Wi, X, IDHA).
- By mV1, A1, and A6, we apply the nonce verification rule to deriveFA believes that MU said (<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi), IDHA).
- By mV2 and A10, we apply the message meaning rule to deriveHA believes that FA said (<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi), Wi, X, Y){Ri}.
- By mV2, A1, A4, A5, and A6, we apply the nonce verification rule to deriveHA believes that FA believes (<IDMU>H1(X1||TMU), <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi)).
- By Statement 4, we break the conjunction to obtainHA believes that FA believes <IDMU>H1(X1||TMU).HA believes that FA believes <X1, H1(IDMU||N||Wi)>H2(PWMU⊕rn), H3(Wi).
- By Statement 5 and A2, we apply the message meaning rule and nonce verification rule to deriveHA believes that MU believes IDMU.
- By Statement 7 and A14, we apply the jurisdiction rule to obtainHA believes IDMU.
- By Statement 8 and A15, we break the conjunction to obtainHA believes MU<=IDMU=>HA.
- By mV3 and A9, we apply the message meaning rule to deriveFA believes that HA said (Wi, X, Y, IDHA, IDFA).
- By Statement 10, A1, A4, A5, and A6, we apply the nonce verification rule to deriveFA believes that HA believes (IDHA, IDFA).
- By Statement 11 and A18, we break the conjunction to obtainFA believes that HA believes IDHA.
- By Statement 12, we apply the jurisdiction rule to obtainFA believes IDHA.
- By mV3, A1, A4, and A12, we break the conjunction to obtainFA believes that MU believes <MU←-SK-→FA>.
- By Statement 14, we apply the jurisdiction rule to obtainFA believes <MU←-SK-→FA>.
- By mV4 and A16, we break the conjunction to obtainMU believes that FA believes <MU←-SK-→FA>.
- By Statement 14, 15, 16, and A11, we prove that the process of setting the session key is safe between the MU and the FA.
5. Security Analysis
5.1. Resist Replay Attack
5.2. Resist Distributed Denial-of-Service Attack
5.3. Achieve High Level of Anonymity
5.4. Solve Corresponding Problem of Session Key in Roaming Phase
5.5. Balanced Calculation of Session Key
6. Comparison with Related Works
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, K.H.; Li, J.S.; Wang, C.Y.; Chilamkurti, N.; Vasilakos, A.V. Minimizing multiplayer interactive delay in multihop wireless networks. Int. J. Commun. Syst. 2012, 25, 1330–1349. [Google Scholar] [CrossRef]
- Vavoulas, A.; Vaiopoulos, N.; Varoutas, D.A.; Chipouras, A.; Stefanou, G. Performance improvement of fixed wireless access networks by conjunction of dual polarization and time domain radio resource allocation technique. Int. J. Commun. Syst. 2011, 24, 483–491. [Google Scholar] [CrossRef]
- Li, J.S.; Liu, K.H. A hidden mutual authentication protocol for low-cost RFID tags. Int. J. Commun. Syst. 2011, 24, 1196–1211. [Google Scholar] [CrossRef]
- Tang, H.B.; Liu, X.S. Cryptanalysis of a dynamic ID-based remote user authentication with key agreement scheme. Int. J. Commun. Syst. 2012, 25, 1639–1644. [Google Scholar] [CrossRef]
- Buttyan, L.; Gbaguidi, C.; Staamann, S.; Wilhelm, U. Extensions to an authentication technique proposed for the global mobility network. IEEE Trans. Commun. 2000, 48, 373–376. [Google Scholar] [CrossRef]
- Hwang, K.F.; Chang, C.C. A self-encryption mechanism for authentication of roaming and teleconference services. IEEE Trans. Wirel. Commun. 2003, 2, 400–407. [Google Scholar] [CrossRef]
- Tzeng, Z.J.; Tzeng, W.G. Authentication of mobile users in third generation mobile system. Wirel. Pers. Commun. 2001, 16, 35–50. [Google Scholar] [CrossRef]
- Suzukiz, S.; Nakada, K. An authentication technique based on distributed security management for the global mobility network. IEEE J. Sel. Areas Commun. 1997, 15, 1608–1617. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R. A logic of authentication. ACM Trans. Comput. Syst. 1990, 8, 18–36. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chang, C.C.; Lin, C.H. User authentication with anonymity for global mobility networks. In Proceedings of the IEEE Mobility Conference 2005: The Second Asia Pacific Conference on Mobile Technology, Applications and Systems, Guangzhou, China, 15–17 November 2005.
- Lin, C.H.; Lee, C.Y. Cryptanalysis of a new authentication scheme with anonymity for wireless environments. In Proceedings of the Second International Conference on Advances in Mobile Multimedia, Bali, Indonesia, 22–24 September 2004; pp. 399–402.
- Li, C.T. Secure smart card based password authentication scheme with user anonymity. Inf. Technol. Control 2011, 40, 157–162. [Google Scholar] [CrossRef]
- Wan, Z.; Ren, K.; Preneel, B. A secure privacy-preserving roaming protocol based on hierarchical identity-based encryption for mobile networks. In Proceedings of the First ACM Conference on Wireless Network Security, Alexandria, VA, USA, 31 March–2 April 2008; pp. 62–67.
- Chen, C.L.; Lee, C.C.; Hsu, C.Y. Mobile device integration of a fingerprint biometric remote authentication scheme. Int. J. Commun. Syst. 2012, 25, 585–597. [Google Scholar] [CrossRef]
- Chuang, Y.H.; Tseng, Y.M. Towards generalized ID-based user authentication for mobile multi-server environment. Int. J. Commun. Syst. 2012, 25, 447–460. [Google Scholar] [CrossRef]
- Xie, Q. A new authenticated key agreement for session initiation protocol. Int. J. Commun. Syst. 2012, 25, 47–54. [Google Scholar] [CrossRef]
- Argyroudis, P.G.; Verma, R.; Tewari, H.; O’Mahony, D. Performance analysis of cryptographic protocols on handheld devices. In Proceedings of the 3rd IEEE International Symposium on Network Computing and Applications (NCA2004), Cambridge, MA, USA, 2004; pp. 169–174.
- Chen, B.L.; Kuo, W.C.; Wuu, L.C. Robust smart-card-based remote user password authentication scheme. Int. J. Commun. Syst. 2014, 27, 377–389. [Google Scholar] [CrossRef]
- Doomun, M.R.; Soyjaudah, K.S.; Bundhoo, D. Energy consumption and computational analysis of Rijndael-AES. In Proceedings of the Third IEEE International Conference in Central Asia on Internet the Next Generation of Mobile, Wireless and Optical Communications Networks (ICI 2007), Tashkent, Uzbekistan, 26–28 September 2007; pp. 1–6.
- Passing, M.; Dressler, F. Experimental performance evaluation of cryptographic algorithms. In Proceedings of the 3rd IEEE International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Vancouver, BC, Canada, 9–12 June 2006; pp. 882–887.
- Passing, M.; Dressler, F. Practical evaluation of the performance impact of security mechanisms in sensor networks. In Proceedings of the 31st IEEE Conference on Local Computer Networks, Tampa, FL, USA, 14–17 November 2006; pp. 623–629.
- Syverson, P. A taxonomy of replay attacks. In Proceedings of the 7th IEEE Computer Security Foundations Workshop, Franconia, NH, USA, 14–16 June 1994; pp. 131–136.
- Wong, D.S.; Fuentes, H.H.; Chan, A.H. The performance measurement of cryptographic primitives on palm devices. In Proceedings of the 17th Annual Computer Security Applications Conference (ACSAC 2001), New Orleans, LA, USA, 10–14 December 2001; pp. 92–101.
- Zhu, J.; Ma, J. A new authentication scheme with anonymity for wireless environments. IEEE Trans. Consum. Electron. 2004, 50, 230–234. [Google Scholar]
- Lee, C.C.; Hwang, M.S.; Liao, I.E. Security enhancement on a new authentication scheme with anonymity for wireless environments. IEEE Trans. Ind. Electron. 2006, 53, 1683–1687. [Google Scholar] [CrossRef]
- Lee, J.S.; Chang, J.H.; Lee, D.H. Security flaw of authentication scheme with anonymity for wireless communications. IEEE Commun. Lett. 2009, 13, 292–293. [Google Scholar]
- Li, C.T. A more secure and efficient authentication scheme with roaming service and user anonymity for mobile communications. Inf. Technol. Control 2012, 41, 69–76. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Deng, Y. Based on BAN logic analysis otway-rees protocol. Chaohu Coll. J. 2006, 78, 36–37. [Google Scholar]
- Li, T.; Liu, X.; Qin, Z. Formal analysis for security of otway-rees protocol with BAN-logic. In Proceedings of the First International Workshop on Database Technology and Applications, Wuhan, Hubei, 25–26 April 2009; pp. 590–593.
- Li, T.; Liu, X.; Qin, Z.; Zhang, X. An improved security protocol formal analysis with BAN-logic. In Proceedings of the International Conference on Electronic Commerce and Business Intelligence, Beijing, China, 6–7 June 2009; pp. 102–105.

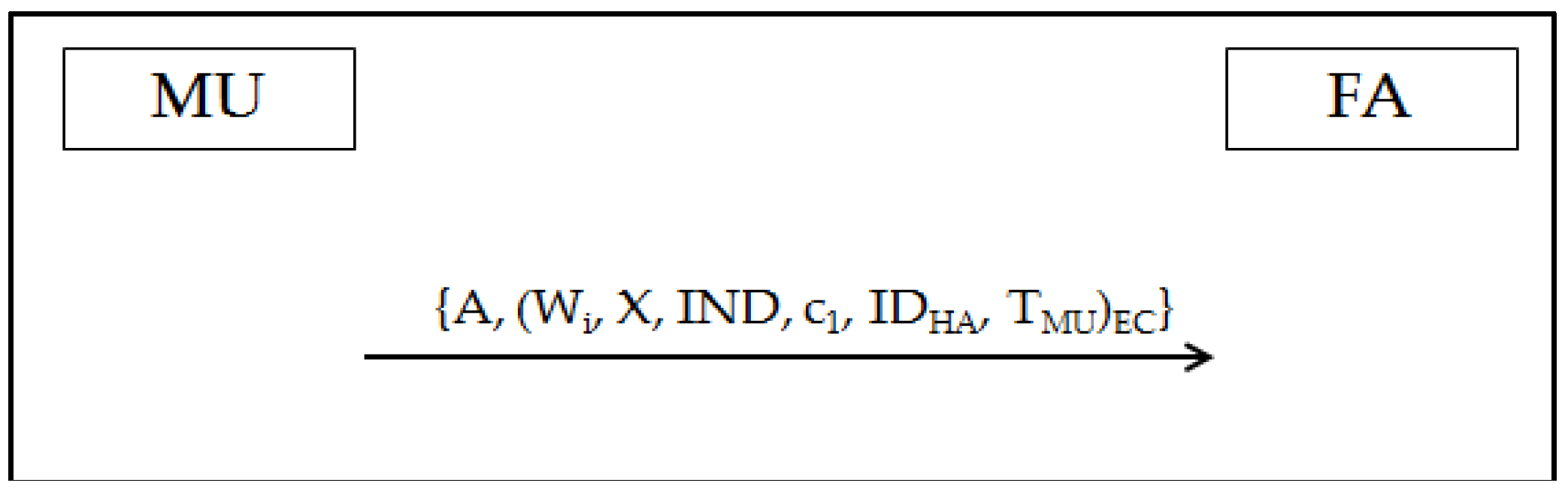
| Notations | Descriptions |
|---|---|
| MU | A mobile user |
| HA | The home agent of a mobile user |
| FA | The foreign agent of the network |
| IDMU | The MU’s identity |
| PWMU | The MU’s password |
| N | A strong secret key of the HA |
| TA | Timestamp generated by an entity A |
| CertA | Certificate of an entity A |
| (X)K | Encryption of a message X using a symmetric key K |
| (PA,SA) | The asymmetric public key and private key pair of an entity A based on Elliptic curve cryptography (ECC) |
| EP | An elliptic curve equation, over a finite field p: y2 = x3 + ax + b mod p, where p > 216°, n > 2160, a and b are two integer elements and 4a3 + 27b2 mod p≠0 |
| E | An elliptic curve equation of HA choose |
| p, n | Two large prime numbers |
| P | A base point with the order n over E |
| SKHF | A pre-shared symmetric key between HA and FA |
| ⊕ | Exclusive-OR (XOR) operation |
| H(.) | A collision-free one-way hash function |
| || | Concatenation |
| Step | Phase | Descriptions |
|---|---|---|
| V1 | Authentication phase | Because IDHA is transmitted in plaintext, the attacker can intercept messages and determine the relationship among the MU, FA, and HA. Then, the attacker can use a replay attack and target a specific object, namely the HA, by a distributed denial-of-service attack. |
| L2 | Roaming phase | Li’s scheme does not clearly explain how to obtain corresponding session keys and the relationship between different users. So FA is impossible for a user to calculate the specific session key, and decrypt mi. Therefore, this scheme lacks integrity. |
| Notations | Descriptions |
|---|---|
| PFA = b | A public key of the FA based on ECC |
| G1 | Additive group on ECC |
| G2 | Multiplicative group on ECC |
| H1 | H1 = {0,1}*→Z*q |
| H2 | H2 = {0,1}n→Znq |
| H3 | H3 = G1→{0,1}* |
| Sender | Receiver |
|---|---|
| V1: MU calculates X = xP and EC = aPFA = abP | V2: FA calculates Y = yP and EC = bA = abP |
| V2: FA calculates MACFA | V3: HA calculates MACFA |
| V3: HA calculates MACHA | V4: FA calculates MACHA |
| V4: FA calculates ski = xY and c2 | V5: MU calculates ski = xY and c2 |
| Secure Item | Li [27] | Lee et al. [25] | Zhu-Ma [24] | Our Scheme |
|---|---|---|---|---|
| Resist internal attack | Yes | No | No | Yes |
| Resist replay attack | No | Yes | Yes | Yes |
| Resist distributed denial-of-service attack for specific object | No | Yes | Yes | Yes |
| Achieve a high level of anonymity | No | No | No | Yes |
| Session key providing anonymity and authentication | No | No | No | Yes |
| Balanced calculation of the session key | Yes | No | No | Yes |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chain, K.; Kuo, W.-C.; Cheng, J.-C. A Novel Mobile Communications Authentication Scheme with Roaming Service and User Anonymity. Appl. Sci. 2016, 6, 393. https://doi.org/10.3390/app6120393
Chain K, Kuo W-C, Cheng J-C. A Novel Mobile Communications Authentication Scheme with Roaming Service and User Anonymity. Applied Sciences. 2016; 6(12):393. https://doi.org/10.3390/app6120393
Chicago/Turabian StyleChain, Kai, Wen-Chung Kuo, and Jiin-Chiou Cheng. 2016. "A Novel Mobile Communications Authentication Scheme with Roaming Service and User Anonymity" Applied Sciences 6, no. 12: 393. https://doi.org/10.3390/app6120393
APA StyleChain, K., Kuo, W.-C., & Cheng, J.-C. (2016). A Novel Mobile Communications Authentication Scheme with Roaming Service and User Anonymity. Applied Sciences, 6(12), 393. https://doi.org/10.3390/app6120393





