Parallel Dynamic Analysis of a Large-Scale Water Conveyance Tunnel under Seismic Excitation Using ALE Finite-Element Method
Abstract
:1. Introduction
2. Methodologies for Parallel Numerical Computation
2.1. Arbitrary Lagrangian-Eulerian Based Fluid–Structure Interaction

2.2. Nonlinear Contact Algorithm
2.3. Explicit Finite Element Time Integration
2.4. Domain Decomposition Technique

2.5. Modified Domain Decomposition Method (DDM) Considering Contact and Fluid–Structure Interaction (FSI) Load Balance

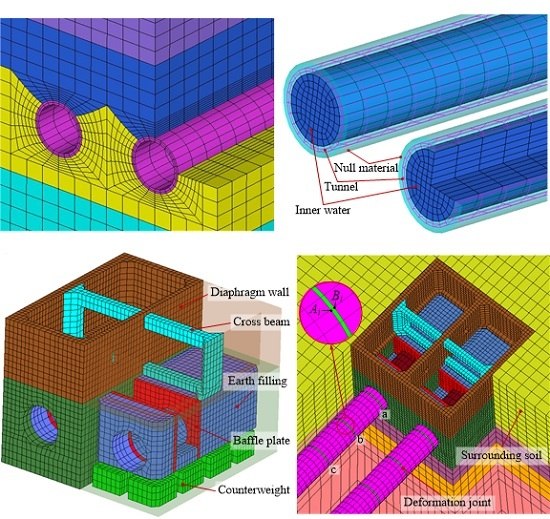
3. Model Description for Water Conveyance Tunnel
3.1. Tunnel Project


3.2. Finite Element Model Overview




3.3. Material Nonlinearity and Constitutive Model
| Layers | Density (kg/m3) | Young’s Modulus (MPa) | Poisson Ratio | Damping Ratio | Dominant Excitation Frequency (Hz) | Shear Wave Velocity (m/s) |
|---|---|---|---|---|---|---|
| 1 | 1897.96 | 37.98 | 0.26 | 0.055 | 3.5 | 89.11 |
| 2 | 1908.16 | 68.94 | 0.28 | 0.063 | 3.5 | 118.80 |
| 3 | 1795.92 | 67.40 | 0.33 | 0.078 | 3.5 | 118.78 |
| 4 | 1714.29 | 116.13 | 0.35 | 0.078 | 3.5 | 158.40 |
| 5 | 1836.73 | 230.00 | 0.32 | 0.070 | 3.5 | 217.79 |
| 6 | 1887.76 | 371.30 | 0.28 | 0.054 | 3.5 | 277.18 |
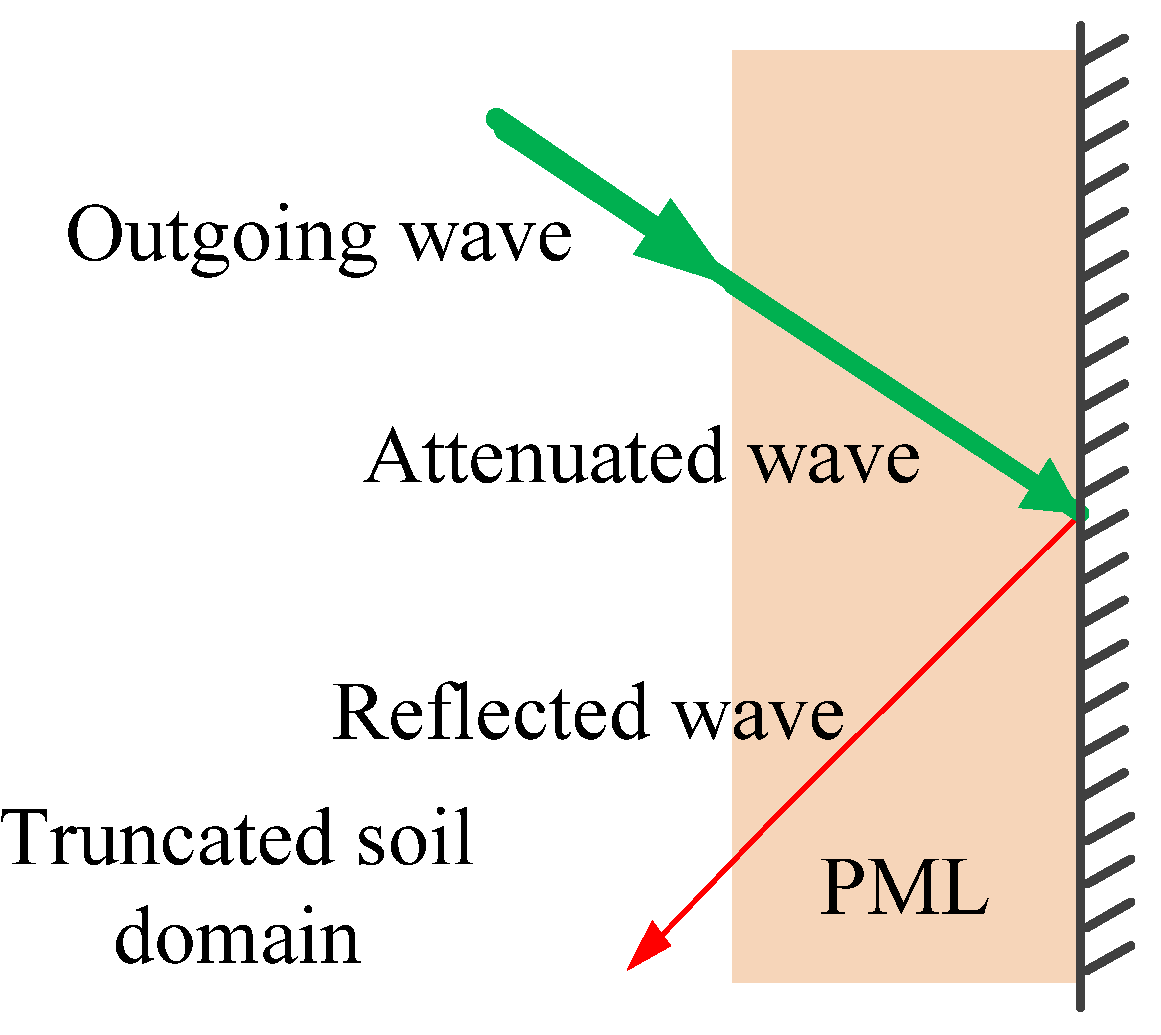
3.4. Boundary Conditions and Input Seismic Wave

3.5. Parallel Computing Environment
| Parameters | Value |
|---|---|
| Cores | 30720 |
| CPU | quad-core Opteron 8347 HE 1.9 GHz |
| Memory capacity | 95 TB |
| Storage capacity | 500TB SAN |
| Network | Infiniband connectX DDR |
| Operating system | SuSE-10.2 |
| Workload management platform | LSF 7.0 |
4. Results and Discussion
4.1. Results Comparison and Method Validation


4.2. Dynamic Response Analysis







| Control Sections | IS1 | IS2 | IS3 | IS4 | IS5 | IS6 | IS7 | IS8 | IS9 | RS1 | RS2 | RS3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum compressive stress | 4.00 | 1.99 | 1.89 | 1.83 | 3.91 | 5.69 | 2.07 | 1.88 | 3.80 | 4.76 | 4.20 | 2.95 |
| Maximum tensile stress | 3.14 | 2.38 | 2.24 | 1.85 | 3.52 | 3.57 | 1.99 | 1.87 | 1.61 | 5.32 | 3.95 | 3.15 |
| Control sections | RS4 | RS5 | RS6 | RS7 | RS8 | RS9 | RS10 | LS1 | LS2 | LS3 | LS4 | LS5 |
| Maximum compressive stress | 4.05 | 4.55 | 4.58 | 4.65 | 5.39 | 5.27 | 8.36 | 6.17 | 5.52 | 4.09 | 3.82 | 1.71 |
| Maximum tensile stress | 3.29 | 3.76 | 3.71 | 3.07 | 2.04 | 2.92 | 5.20 | 4.22 | 3.47 | 1.77 | 3.09 | 2.11 |


4.3. Domain Decomposition Comparison and Parallel Performance Evaluation

| Subdomain | RCB Method | MRCB Method | ||||
|---|---|---|---|---|---|---|
| Ntol | Ncon | Nfsi | Ntol | Ncon | Nfsi | |
| SD1 | 120,880 | 8828 | 5515 | 120,037 | 11,252 | 5790 |
| SD2 | 122,157 | 11,548 | 6188 | 121,002 | 11,067 | 5736 |
| SD3 | 117,797 | 17,873 | 10,480 | 119,524 | 11,133 | 5736 |
| SD4 | 116,319 | 0 | 0 | 119,577 | 11,074 | 5736 |
| SD5 | 121,399 | 14,339 | 6200 | 119,399 | 11,159 | 5736 |
| SD6 | 120,709 | 11,708 | 7334 | 119,378 | 10,871 | 5736 |
| SD7 | 118,680 | 14,120 | 6580 | 119,355 | 11,062 | 5735 |
| SD8 | 122,386 | 11,596 | 7206 | 119,342 | 11,059 | 5736 |
| SD9 | 121,623 | 12,545 | 6240 | 119,217 | 11,059 | 5736 |
| SD10 | 118,561 | 7497 | 4197 | 119,106 | 11,060 | 5735 |
| SD11 | 120,636 | 19,267 | 9257 | 118,645 | 11,058 | 5736 |
| SD12 | 116,330 | 0 | 0 | 119,413 | 11,059 | 5734 |
| SD13 | 118,108 | 11,736 | 5740 | 119,657 | 11,058 | 5736 |
| SD14 | 121,415 | 12,996 | 5514 | 120,054 | 11,063 | 5736 |
| SD15 | 120,924 | 16,128 | 8800 | 121,230 | 11,071 | 5739 |
| SD16 | 115,600 | 6719 | 2578 | 118,588 | 10,795 | 5736 |
| Number of Cores | RCB Method | MRCB Method | ||||
|---|---|---|---|---|---|---|
| Ti (s) | Su | Ef (%) | Ti (s) | Su | Ef (%) | |
| 1 | 3,299,460 | 1 | 100 | 3,299,460 | 1 | 100 |
| 2 | 1,729,320 | 1.91 | 95.4 | 1,693,620 | 1.95 | 97.4 |
| 4 | 900,240 | 3.67 | 91.6 | 882,720 | 3.74 | 93.4 |
| 8 | 523,920 | 6.3 | 78.7 | 505,500 | 6.53 | 81.6 |
| 16 | 322,056 | 10.24 | 64 | 282,352 | 11.69 | 73 |
| 32 | 182,210 | 18.11 | 56.6 | 159,923 | 20.63 | 64.5 |

4.4. Parametric Study


| Location | Largest Tensile Stress | Largest Compressive Stress | ||||
|---|---|---|---|---|---|---|
| Without | With | Change (%) | Without | With | Change (%) | |
| S1RI | 1.698 | 1.548 | −8.83 | 1.716 | 1.610 | −6.18 |
| S2LE | 1.208 | 1.125 | −6.87 | 1.222 | 1.157 | −5.32 |
| S2RI | 1.266 | 1.176 | −7.11 | 1.526 | 1.429 | −6.36 |
| S3LE | 1.894 | 1.718 | −9.29 | 2.861 | 2.538 | −11.29 |
| S3RI | 2.634 | 2.194 | −16.7 | 2.793 | 2.349 | −15.9 |
| S4LE | 3.027 | 2.661 | −12.09 | 2.841 | 2.383 | −16.12 |
| S4RI | 2.548 | 2.278 | −10.6 | 2.838 | 2.568 | −9.51 |
| S5LE | 2.589 | 2.348 | −9.31 | 2.730 | 2.487 | −8.9 |
5. Conclusions
- (1)
- The ALE based FSI method can be used to deal with the interaction between tunnel lining and inner water. The approaches and the established model in this study are suitable for the seismic analyses of the large-scale water conveyance tunnel and can be used as an effective way for performing seismic analyses of analogous tunnels.
- (2)
- The proposed MRCB domain decomposition method considers the features of the underground tunnel and the balance between time-consuming contact and FSI coupling loads. The proposed MRCB based parallel computing method has a higher speedup and a better parallel efficiency than that of the RCB based method. The proposed MRCB based parallel computing method can accelerate the calculation process of the nonlinear dynamic analyses for large-scale water conveyance tunnels under seismic excitation. The proposed parallel technique makes the simulation of large-scale models more efficient and provides an effective approach for numerical simulation of large-scale underground infrastructure.
- (3)
- The water conveyance tunnel fulfills the design requirements under seven degree seismic intensity. The results for axial forces, moments, stresses and deformations show its earthquake resistance. The simulation results can be used as references for the anti-seismic design of large-scale water conveyance tunnels. Specifically, the internal forces and moments obtained during and after the earthquake can be used to aid the design of connections for different rings, connections of different segments in a ring and water-proof measures, and the stresses and deformations obtained can be employed to evaluate the strength and stiffness of the tunnel structures.
- (4)
- The tunnel with filled water suffers higher stresses compared to the empty tunnel. The amount of inner water should be considered during the design and analyses of water conveyance tunnels. The deformation joints can partially release the stresses of the tunnel linings near work shafts caused by the sharp changes of structure and stiffness during earthquakes.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cheng, X.; Xu, W.; Yue, C.; Du, X.; Dowding, C.H. Seismic response of fluid–structure interaction of undersea tunnel during bidirectional earthquake. Ocean Eng. 2014, 75, 64–70. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Kumar, J. Seismic stability of a long unsupported circular tunnel. Comp. Geotech. 2012, 44, 109–115. [Google Scholar] [CrossRef]
- Yue, Q.; Ang, A.H.-S. Nonlinear response and reliability analysis of tunnels under strong earthquakes. Struct. Infrastruct. Eng. 2015, in press. [Google Scholar]
- Wang, Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Menkiti, C.; Mair, R.; Miles, R. Highway tunnel performance during the 1999 duzce earthquake. In Proceedings of the 15th International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul, Turkey, 28–31 August 2001.
- Wang, J.N. Seismic Design of Tunnels: A Simple State-of-the-Art Design Approach; Parsons Brinckerhoff Quade & Douglas: New York, NY, USA, 1993. [Google Scholar]
- Stamos, A.; Beskos, D. 3-D seismic response analysis of long lined tunnels in half-space. Soil Dyn. Earthq. Eng. 1996, 15, 111–118. [Google Scholar] [CrossRef]
- Ding, J.-H.; Jin, X.-L.; Guo, Y.-Z.; Li, G.-G. Numerical simulation for large-scale seismic response analysis of immersed tunnel. Eng. Struct. 2006, 28, 1367–1377. [Google Scholar] [CrossRef]
- Hashash, Y.M.; Hook, J.J.; Schmidt, B.; John, I.; Yao, C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Carter, J.P.; Desai, C.S.; Potts, D.M.; Schweiger, H.F.; Sloan, S.W. Computing and computer modelling in geotechnical engineering. In Proceedings of the ISRM International Symposium, Melbourne, Australia, 12–14 November 2000.
- Westergaard, H.M. Water pressures on dams during earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–432. [Google Scholar]
- Housner, G.W. Dynamic pressures on accelerated fluid containers. Bull. Seismol. Soc. Am. 1957, 47, 15–35. [Google Scholar]
- Ruiz, R.; Lopez-Garcia, D.; Taflanidis, A. An efficient computational procedure for the dynamic analysis of liquid storage tanks. Eng. Struct. 2015, 85, 206–218. [Google Scholar] [CrossRef]
- Budiansky, B. Sloshing of liquids in circular canals and spherical tanks. J. Aerosp. Sci. 1958, 27, 161–173. [Google Scholar] [CrossRef]
- Karamanos, S.A.; Patkas, L.A.; Platyrrachos, M.A. Sloshing effects on the seismic design of horizontal-cylindrical and spherical industrial vessels. J. Press. Vessel Technol. 2006, 128, 328–340. [Google Scholar] [CrossRef]
- Karamanos, S.A.; Papaprokopiou, D.; Platyrrachos, M.A. Finite element analysis of externally-induced sloshing in horizontal-cylindrical and axisymmetric liquid vessels. J. Press. Vessel Technol. 2009, 131. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, P.Y.; Jin, X.L. Dynamic analysis of flexible container under wind actions by ALE finite-element method. J. Wind Eng. Ind. Aerodyn. 2010, 98, 881–887. [Google Scholar]
- Zhao, C.; Chen, J.; Xu, Q. Fsi effects and seismic performance evaluation of water storage tank of AP1000 subjected to earthquake loading. Nucl. Eng. Des. 2014, 280, 372–388. [Google Scholar] [CrossRef]
- Razzaq, M.; Damanik, H.; Hron, J.; Ouazzi, A.; Turek, S. FEM multigrid techniques for fluid–structure interaction with application to hemodynamics. Appl. Numer. Math. 2012, 62, 1156–1170. [Google Scholar] [CrossRef]
- Turek, S.; Hron, J.; Madlik, M.; Razzaq, M.; Wobker, H.; Acker, J.F.; Bungartz, H.; Mehl, M.; Schäfer, M. Numerical simulation and benchmarking of a monolithic multigrid solver for fluid–structure interaction problems with application to hemodynamics. In Fluid–Structure Interaction II: Modelling, Simulation, Optimization; Barth, T.J., Griebel, M., Keyes, D.E., Nieminen, R.M., Roose, D., Schlick, T., Eds.; Springer: Berlin, Germany, 2010; pp. 193–220. [Google Scholar]
- Turek, S.; Hron, J.; Razzaq, M.; Schäfer, M.; Bungartz, H.; Mehl, M.; Schäfer, M. Numerical benchmarking of fluid–structure interaction: A comparison of different discretization and solution approaches. In Fluid–Structure Interaction II: Modelling, Simulation, Optimization; Barth, T.J., Griebel, M., Keyes, D.E., Nieminen, R.M., Roose, D., Schlick, T., Eds.; Springer: Berlin, Germany, 2010; pp. 413–424. [Google Scholar]
- Dupros, F.; de Martin, F.; Foerster, E.; Komatitsch, D.; Roman, J. High-performance finite-element simulations of seismic wave propagation in three-dimensional nonlinear inelastic geological media. Parallel Comput. 2010, 36, 308–325. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Liu, J.-Y. Fluid–structure coupling analysis of water conveyance tunnel subjected to seismic excitation. Rock Soil Mech. 2006, 27, 1077. (In Chinese) [Google Scholar]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid–structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Razzaq, M. Finite Element Simulation Techniques for Incompressible Fluid–Structure Interaction with Applications to Bio-Engineering and Optimization. Ph.D. Thesis, TU Dortmund University, North Rhine-Westphalia, Germany, 16 February 2011. [Google Scholar]
- Sedarat, H.; Kozak, A.; Hashash, Y.M.; Shamsabadi, A.; Krimotat, A. Contact interface in seismic analysis of circular tunnels. Tunn. Undergr. Space Technol. 2009, 24, 482–490. [Google Scholar] [CrossRef]
- Kouretzis, G.P.; Sloan, S.W.; Carter, J.P. Effect of interface friction on tunnel liner internal forces due to seismic s-and p-wave propagation. Soil Dyn. Earthq. Eng. 2013, 46, 41–51. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures; John Wiley & Sons Ltd.: New York, NY, USA, 2013. [Google Scholar]
- Xu, J.; Zou, J. Some nonoverlapping domain decomposition methods. SIAM Rev. 1998, 40, 857–914. [Google Scholar] [CrossRef]
- Bamford, T. An implementation of domain decomposition by recursive bisection. Available online: https://static.ph.ed.ac.uk/dissertations/hpc-msc/2006-2007/6547365-27d-d07rep1.2.pdf (accessed on 30 March 2015).
- Bernaud, D.; Maghous, S.; de Buhan, P.; Couto, E. A numerical approach for design of bolt-supported tunnels regarded as homogenized structures. Tunn. Undergr. Space Technol. 2009, 24, 533–546. [Google Scholar] [CrossRef]
- Felhös, D. Dry Sliding and Rolling Tribotests of Carbon Black Filled Epdm Elastomers and Their FE Simulations. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 16 December 2008. [Google Scholar]
- Spanos, P.D.; Tsavachidis, S. Deterministic and stochastic analyses of a nonlinear system with a biot visco-elastic element. Earthq. Eng. Struct. Dyn. 2001, 30, 595–612. [Google Scholar] [CrossRef]
- Pinto, P.A. Study of Constitutive Models for Soils under Cyclic Loading. Master’s Thesis, Universidade Técnica de Lisboa, Lisbon, Portugal, 12 November 2012. [Google Scholar]
- Livermore Software Technology Corporation. LS-DYNA Theory Manual. Available online: http://www.lstc.com/download/manuals (accessed on 5 November 2014).
- Zhu, J.; Taylor, Z.; Zienkiewicz, O. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Basu, U. Explicit finite element perfectly matched layer for transient three-dimensional elastic waves. Int. J. Numer. Methods Eng. 2009, 77, 151. [Google Scholar] [CrossRef]
- Platyrrachos, M.; Karamanos, S. Finite element analysis of sloshing in horizontal-cylindrical industrial vessels under earthquake loading. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005.
- Abramson, H.N. The Dynamic Behavior of Liquids in Moving Containers; Report NASA-SP-106; Southwest Research Institute: San Antonio, TX, USA, 1966. [Google Scholar]
- Mircevska, V.; Bulajić, I.; Manova, K. Comparison of added mass method with sophisticated analytical BEM-FEM approach using ADAD-IZIIS software. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012.
- Shanghai Urban Construction and Communications Commission. Foundation Design Code (DGJ08–11–1999); Shanghai Urban Construction and Communications Commission: Shanghai, China, 1999. (In Chinese) [Google Scholar]
- Westfall, D.E. Water Conveyance Tunnels. In Tunnel Engineering Handbook; Springer: New York, NY, USA, 1996; pp. 298–310. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jin, X.; Wang, P.; Yang, Z. Parallel Dynamic Analysis of a Large-Scale Water Conveyance Tunnel under Seismic Excitation Using ALE Finite-Element Method. Appl. Sci. 2016, 6, 36. https://doi.org/10.3390/app6020036
Wang X, Jin X, Wang P, Yang Z. Parallel Dynamic Analysis of a Large-Scale Water Conveyance Tunnel under Seismic Excitation Using ALE Finite-Element Method. Applied Sciences. 2016; 6(2):36. https://doi.org/10.3390/app6020036
Chicago/Turabian StyleWang, Xiaoqing, Xianlong Jin, Puyong Wang, and Zhihao Yang. 2016. "Parallel Dynamic Analysis of a Large-Scale Water Conveyance Tunnel under Seismic Excitation Using ALE Finite-Element Method" Applied Sciences 6, no. 2: 36. https://doi.org/10.3390/app6020036
APA StyleWang, X., Jin, X., Wang, P., & Yang, Z. (2016). Parallel Dynamic Analysis of a Large-Scale Water Conveyance Tunnel under Seismic Excitation Using ALE Finite-Element Method. Applied Sciences, 6(2), 36. https://doi.org/10.3390/app6020036