Supercooled Water Droplet Impacting Superhydrophobic Surfaces in the Presence of Cold Air Flow

Abstract

In the present work, an investigation of stagnation flow imposed on a supercooled water drop in cold environmental conditions was carried out at various air velocities ranging from 0 (i.e., still air) to 10 m/s along with temperature spanning from −10 to −30 °C. The net effect of air flow on the impacting water droplet was investigated by controlling the droplet impact velocity to make it similar with and without air flow. In cold atmospheric conditions with temperatures as low as −30 °C, due to the large increase of both internal and contact line viscosity combined with the presence of ice nucleation mechanisms, supercooled water droplet wetting behavior was systematically affected. Instantaneous pinning for hydrophilic and hydrophobic surfaces was observed when the spread drop reached the maximum spreading diameter (i.e., no recoiling phase). Nevertheless, superhydrophobic surfaces showed a great repellency (e.g., contact time reduction up to 30% where air velocity was increased up to 10 m/s) at temperatures above the critical temperature of heterogeneous ice nucleation (i.e., −24 °C). However, the freezing line of the impacting water droplet was extended up to 2-fold at air velocity up to 10 m/s where substrate temperature was maintained below the aforementioned critical temperature (e.g., −30 °C).

1. Introduction

Nano-micro topography of solid surfaces exhibits different characteristics when interaction of solid-liquid ranging from severe adhesion to strong repellency is taken into consideration [1]. They have shown different outcomes when a hot [2] or cold surface [3] has been used for heat transfer and wetting dynamics evaluation. Cloud droplets leading to icing are supercooled water droplets in metastable equilibrium, a better understanding of the mechanism of phase change is essential for numerous applications. These applications range from electrical transmission power line, wind turbine to aerospace industries [4,5,6]. It was shown that having a surface with low wettability is a key prerequisite for ice formation mitigation [7] which is related to the substrates receding contact angle [8]. Kulinich et al. [7] defined a correlation between ice adhesion strength and contact angle hysteresis (the difference between advancing and receding contact angle) for different solid surfaces with various wettabilities. An extremely low wettable surface, namely superhydrophobic surface, typically has a static and hysteresis contact angle larger than 150° and 10°, respectively [9,10]. These surfaces exhibit a tremendous water repellency whether in room or low temperature conditions above the critical temperature of freezing (i.e., −24 °C) [11]. Indeed, superhydrophobicity is produced by combing rough surfaces coated with low surface-energy materials. Entrapped air underneath of an impacting water drop on rough surface changes the thermal transport property by increasing thermal resistance due to the low thermal conductivity of entrapped air [12,13,14]. This unique features of superhydrophobic surfaces act as a good insulator [15] used for decreasing solid–liquid interface temperature during the impact of the supercooled water droplet.

Solid-liquid interface temperature plays a critical role in cthe rystallization process. It generally plays a dual role when a supercooled water droplet impacts on cold substrates. Larger solid-liquid interfacial area of impacting drop causes a significant increase in the heat transfer cooling rate [15]. Furthermore, both induced homogeneous nucleation [16] (i.e., due to evaporation cooling) and heterogeneous nucleation (solid-liquid interaction) [17] are related to liquid interface temperature. In fact, in real atmospheric cold conditions, induced homogeneous nucleation can happen even above the critical temperature of homogeneous nucleation (i.e., −37 °C) [18,19] due to the presence of air flow which systematically increases the rate of evaporation cooling at low and high humidity environments [16]. Therefore, gas-liquid interface temperature becomes as important as solid-liquid interface temperature (i.e., Gibbs free surface energy is related to interface temperature whether gas-liquid or solid-liquid) when evaluation of both nucleation mechanisms on wetting dynamics of an impacting supercooled water drop are taken into account.

When a supercooled water drop impacts on a substrate the interface temperature becomes very close to the substrate temperature. Analysis of heat penetration length [1] showed that liquid water drop viscosity increases several times depending on substrate temperature. Dramatic changes in near wall viscosity results in rapid increase of viscous dissipation rate during drop impact, particularly at recoiling phase [20]. For moderate and high inertia impact conditions, partial meniscus penetration also happens which promotes viscous dissipation rate owing to contact line friction. Therefore, droplet receding velocity is reduced [21] which is the main reason for an increase in droplet contact time up to almost 75% and 20% for droplet Weber number (i.e., ratio of inertia to surface tension force) up to 236 and 100, respectively. However, for low Weber number, impact conditions up to 10 and 52 [20,22] contact time remain completely unaffected while the restitution coefficient was decreased down to 27% (supercooled condition) that of the room temperature water drop impact condition [22].

Reducing contact time of the bouncing droplet is a systematic way for prevention of ice formation on superhydrophobic surfaces [23]. However, due to the large increase of viscosity of a supercooled water droplet, the contact time increases, which leads to higher probability of ice formation through the classical ice nucleation theory [24]. It was reported that droplet contact time can be reduced by increasing the receding contact angle [25] or by switching recoiling dynamics from an axisymmetric retraction to a nonaxisymmetric one [23] up to about 50% (based on inertia—capillary time scale [26]: ${\left(\mathsf{\rho }{D}_o^3/8\mathsf{\sigma }\right)}^{1/2}$) through breaking up the droplets and also through the pancake bouncing mechanism [27]. Although the aforementioned techniques were used to reduces droplet adhesion with a surface by minimizing droplet contact time or by shedding the droplet by airflow [16,28], the effect of stagnation air flow on an impacting water drop [29] whether in room or super cooling conditions has not been fully addressed yet. In the present study, the influence of stagnation flow on a spreading water droplet is evaluated through classical Homann flow approach [30]. Incoming air flow changes wetting dynamics of a supercooled water drop on solid surfaces with different wettabilities ranging from hydrophilic to superhydrophobic surfaces. Indeed, combination of both induced homogeneous nucleation through an evaporation cooling mechanism and imposing extra dynamic pressure of air flow on impacting drop totally changes the behavior of conventional drop impact dynamics on a superhydrophobic surface. Unlike the phenomenology of static pressure on wetting behavior of impacting drop on hydrophilic [31,32,33] and superhydrophobic surfaces [34], here the effect of extra pressure buildup due to incoming air flow on substrates such as superhydrophobic surface is evaluated, which might result in variation of droplet contact time below and above the critical temperature of heterogeneous ice nucleation (i.e., −24 °C).

2. Materials and Methods

Experiments were performed on different substrates. Polished aluminum, Teflon and superhydrophobic surface made of a polished aluminum sample coated with WX2100. This spray is commercially available by Cytonix (Beltsville, MD, USA). Regarding the surface morphology, a laser confocal microscopy (VK-X200, Keyence, Japan) was carried out to capture surface topography of different surfaces (see Supplementary Materials).

In fact, three surfaces with almost comparable differences in wettability (i.e., ${90}^{\mathrm{o}}<{\mathsf{\theta }}_{adv}<{160}^{\mathrm{o}},{50}^{\mathrm{o}}<{\mathsf{\theta }}_{rec}<{150}^{\mathrm{o}}$ and $8^{\mathrm{o}}<{\mathsf{\theta }}_{hys}<{40}^{\mathrm{o}})$were served in this study to illustrate effect of surface wetting on droplet pinning/freezing in cold environment conditions. The difference between advancing and receding contact angle is called contact angle hysteresis. The smallest hysteresis contact angle is referred to as a superhydrophobic surface. The high mobility of these surfaces can be demonstrated (see Supplementary Materials).

Experiments were conducted in cold air conditions at different temperatures ranging from −10 °C to −30 °C with negligible relative humidity ratio below 0.1%. The novelty of this study is related to presence of airflow (i.e., stagnation flow) toward the impacting water drop. In order to generate stagnation flow, a multi-components device, named the droplet accelerator, is added to the typical set up of drop generators in the still air. The droplet accelerator provides a co-flow at various air speeds. Air velocity was measured by using Dwyer Pitot tube (MS-351-LCD) at the outlet of the droplet accelerator. However characterization of airflow at the nozzle outlet was performed using numerical simulation (see Supplementary Materials). 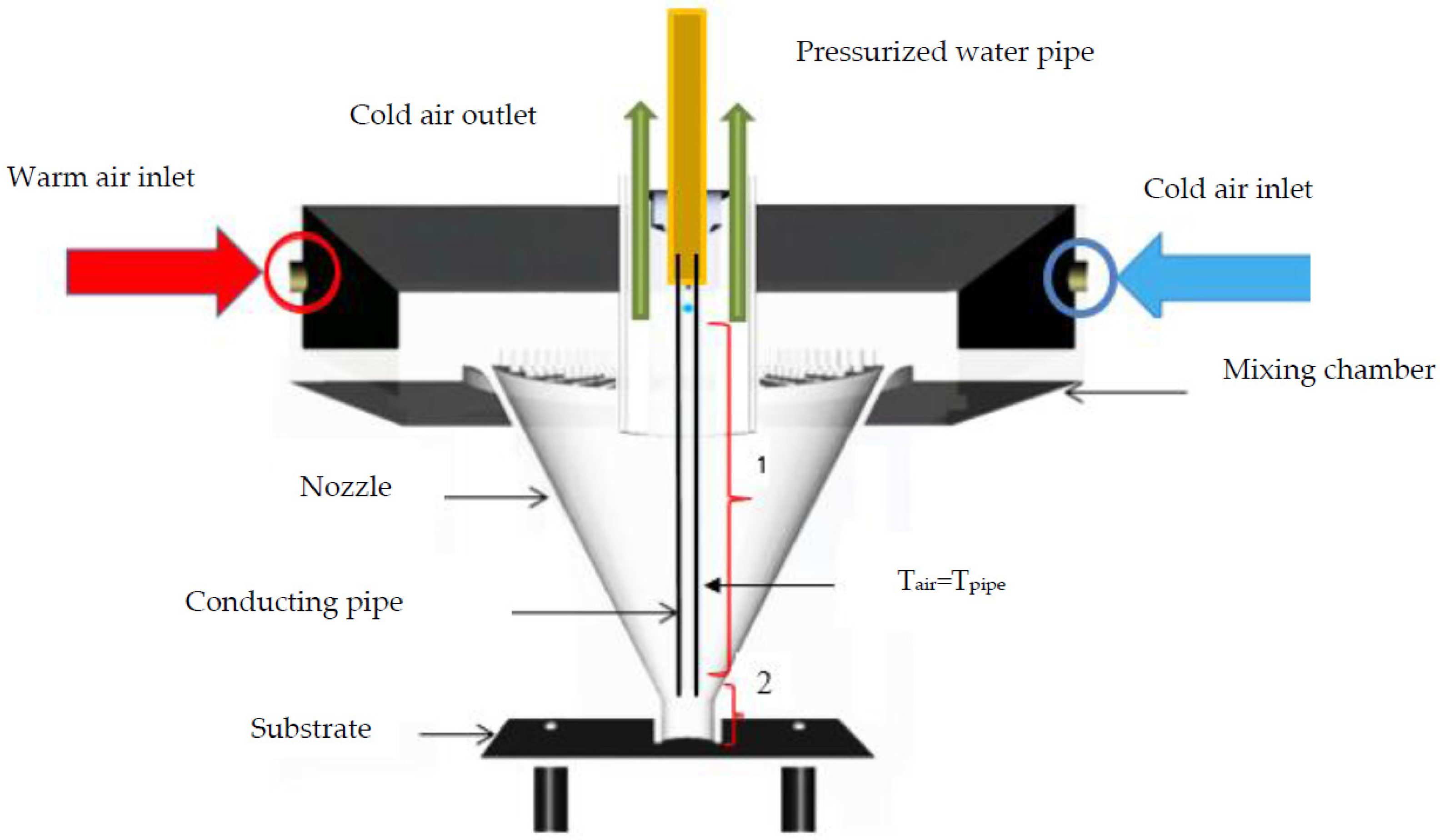A schematic of the droplet accelerator is illustrated in Figure 1.

Current study is focused on observing the net effect of air flow on an impacting water droplet the impact velocities of which are similar with and without air flow. In order to reach this aim we provide a small clear cellulose (Butyrate) tube, 3/8″ OD, 1/4″ ID which is connected to the droplet generator system (i.e., it is connected to the end of the copper pipe where the needle is installed). As depicted in Figure 1, pipe length was chosen based on the distance from needle location to 1 mm above the entrance of the nozzle throat. The distance from the end of the conducting pipe to the substrate was about 15 mm. Based on the numerical simulation, the droplet is exposed to air flow almost close to the substrate. Imposed associated drag force is negligible (see Supplementary Materials), which results in the same droplet impact velocity. The measured impact velocity, based on few sequential images above substrate recorded with high speed camera, shows that imposed drag force between two domains (i.e., domain 1 and 2 illustrated in Figure 1) cancel each other out, so the droplet impact velocity becomes almost identical, and is even in a lower range of impact velocity (1% compared with still air) (see Supplementary Materials).

An experimental setup for producing cold air flow along with generation of supercooled water drop has a relatively complex design. A large volume flow rate of dry room temperature is cooled down by an immediate cooling through a designed heat exchanger. Cold air flow is mixed with room temperature air with controllable flow rate in the mixing chamber of the droplet accelerator. Temperature measurements at the internal part of the nozzle shows a uniform and constant temperature at nozzle throats which demonstrates an effective mixing through the nozzle and mixing chamber of the droplet accelerator (see Supplementary Materials).

It is worth mentioning that measuring surface temperature of a different substrate and super cooled water drop has been carried out by the non-intrusive IR thermography method [15]. Due to the fact that aluminum substrate is very shiny, spectral reflectivity is high enough to read a misleading temperature. Therefore, aluminum substrate was covered by a very thin black conductive thermal tape (i.e., 0.008 inch thickness). This method has been used for two other surfaces. However, the reflectivity of Teflon and superhydrophobic surfaces is much less than that for a polished mirror like aluminum.

Gas temperature can be monitored by measuring surface temperature of an opaque small pipe which was inserted inside of the nozzle (i.e., droplet conductor pipe, see Figure 1). The small pipe is an opaque object and it is long enough to reach the final part of nozzle throat. In this case, assumption of thermal equilibrium between the surrounding gas and small pipe is valid, as it was monitored by IR camera. We did not observe any temperature gradient between the internal wall of the nozzle and the small pipe surface.

While many important parameters are involved in wetting dynamics of an impacting water drop, namely different droplet sizes and velocities, in this study only one impact velocity and droplet size were taken into account due to the extremely challenging experimental test conditions. On the other hand, different air velocities with different temperatures were used to evaluate the effect of stagnation flow on droplet spreading and retraction behavior. This process was imaged using a high-speed camera. Imaging equipment used in this study includes a Photron SA1.1 (Photron, San Diego, CA, USA) high speed camera, an LED light, and a high magnification zoom macro lens (Nikon AF-S Micro nikkor lens with focal length of 105 mm). Spatial resolution for the presented temporal spreading diameter 19–21 µm for 1 pixel. Different recording rates were used to trace the impact behavior of the water drop. For measuring droplet contact time of the water drop on SHS (i.e., superhydrophobic surface), the recording rate should not be less than 9000 fps [35].

3. Results and Discussion

Wetting dynamics of an impacting supercooled water droplet on a cold substrate combined with cold stagnation flow is evaluated in the current study. In order to evaluate the net effect of airflow on an impacting supercooled water drop, the maximum air velocity was chosen based on the conception of no droplet deformation of a free falling drop exposed to gas flow. The dimensionless number describing this phenomenon is the relative Weber number, $\frac{{\mathsf{\rho }}_{air}{(U_g-U_d)}^2{D}_d}{{\mathsf{\sigma }}_{lv}}$, which is defined based on density of the gas, which is air in this experiment (${\mathsf{\rho }}_{air}$), relative velocity of impinging water drop and air jet velocity, ($U_g-U_d)$, water droplet size $D_d,$ and surface tension of water drop (${\mathsf{\sigma }}_{lv}$). For air velocity up to 10 m/s and with constant droplet diameter up to 2.6 mm the evaporation effect on droplet size during free falling (at height of 0.15 m in the current study) is negligible (1% of initial droplet size) [36]. Calculation of relative Weber number shows that it becomes close to the suggested value (i.e., 3) for having a non-deformed drop [37]. Deformation of the water drop is almost negligible and the droplet remains spherical.

Dynamics of a water drop in supercooling conditions fundamentally changes that of room temperature. When drop impact condition is no longer isothermal, phase change might happen based on the difference between droplet and target surface temperature [38]. 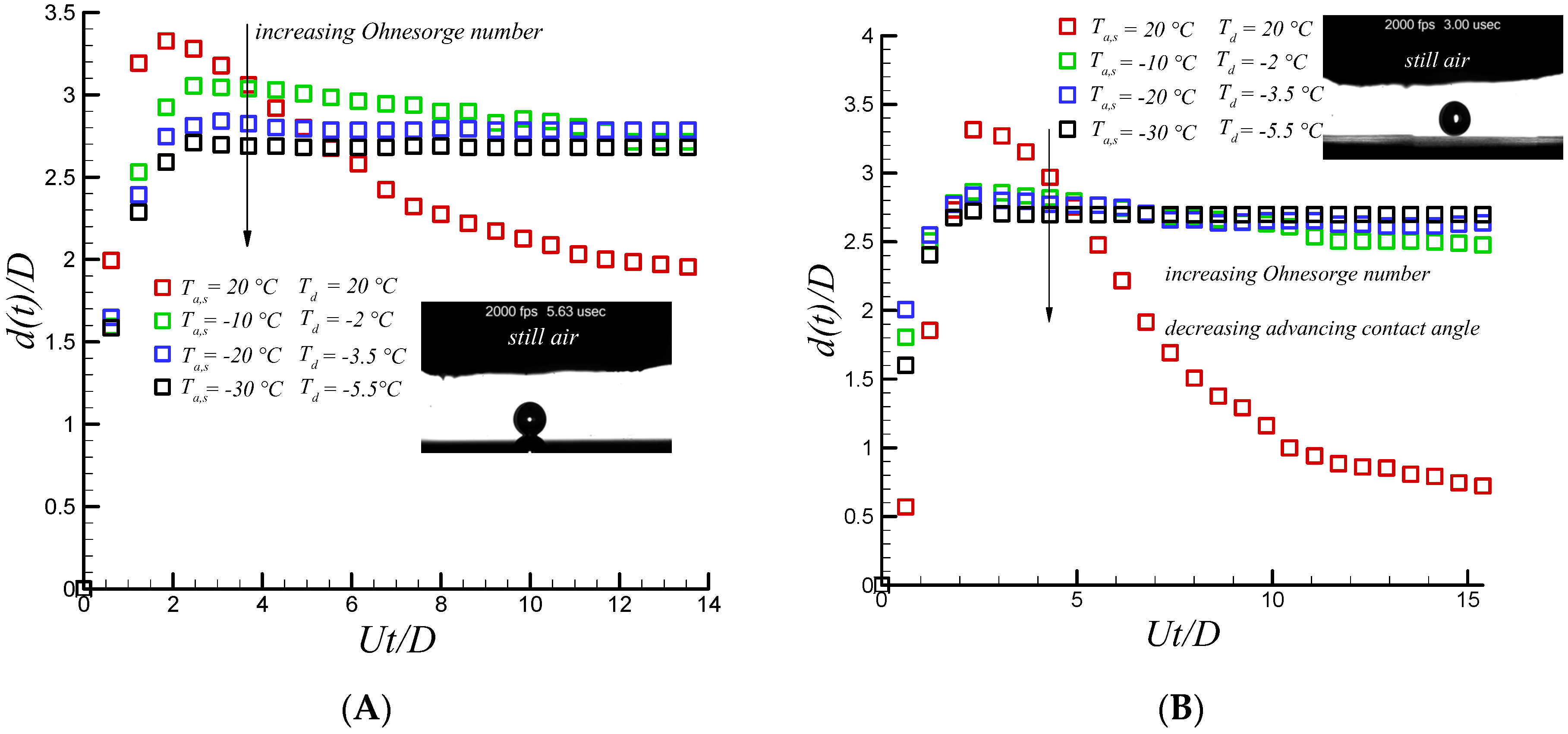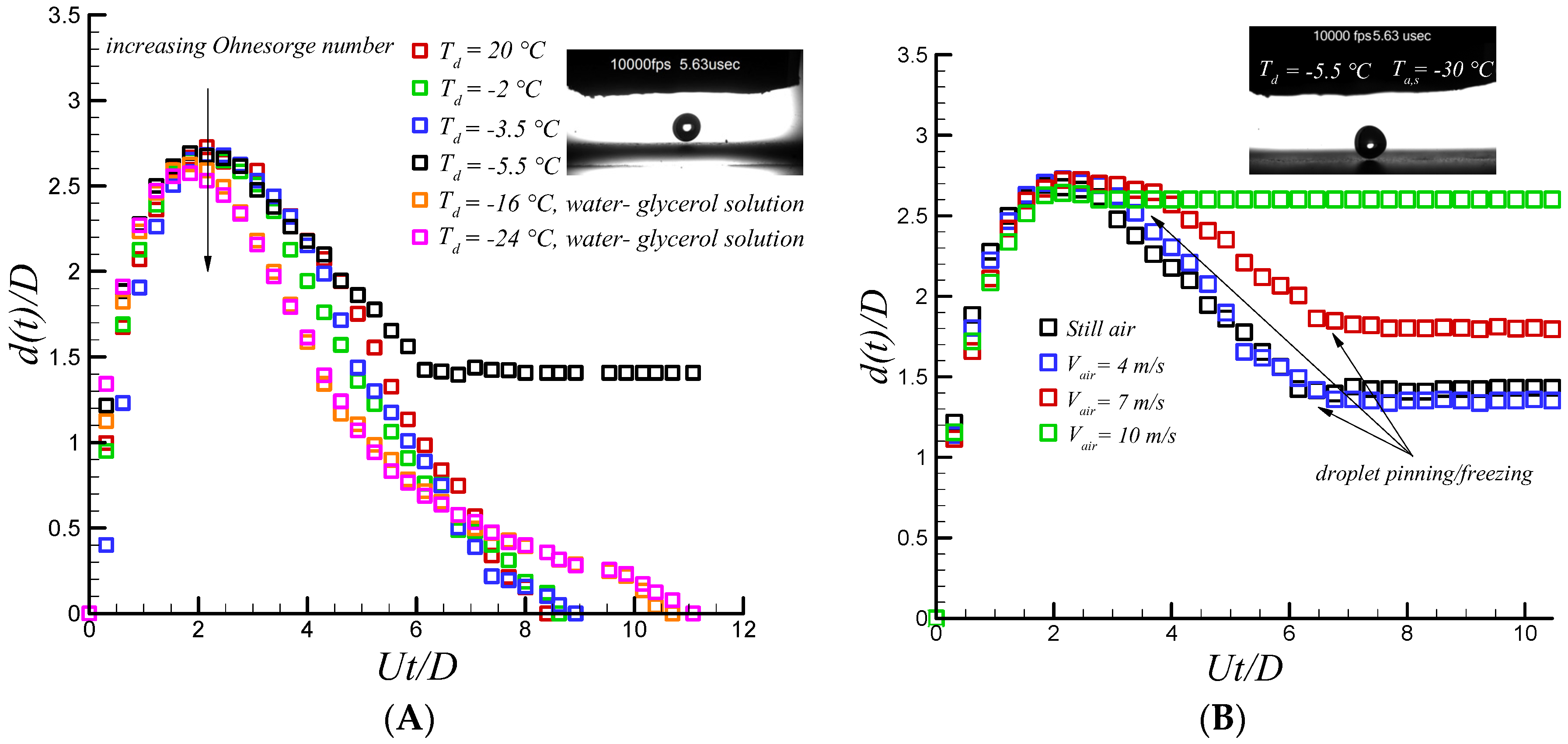In order to demonstrate the effect of droplet degree of super cooling conditions on wetting dynamics behavior, temporal spreading factor versus dimensionless time is illustrated in Figure 2 for both aluminum and Teflon substrates. Increasing relaxing phase time rapidly increases rate of heat transfer within the drop through the substrate. Large interfacial area results in significant decrease in receding velocity compared to the room temperature one due to the increase in heat transfer cooling rate. As depicted in Figure 2, it is clear that at the maximum spreading diameter, instantaneous freezing (i.e., no retraction, pinning) was observed for coldest droplet and substrate temperature condition (i.e., −5.5 °C and −30 °C, respectively). However, slight retraction was observed at the initial stage of the retraction phase for the remaining scenarios. In fact, due to both the liberation of latent heat of fusion and molecular diffusivity [15] there is a sufficient freezing delay time when droplet and substrate temperature are not sufficiently cold, resulting in retraction initiations. However, after 25 ms, due to the large heat transfer cooling rate (i.e., large contact area which is almost not varied by time), the retraction force becomes almost zero, signaling the presence of heterogeneous ice nucleations between the impacting water drop and underneath the substrate. It becomes strong enough so that the droplet is pinned on the surface.

This phenomenon can be further elaborated through classical ice nucleation theory combined with thermal transport analysis. As shown in Equation (1), nucleation rate [39,40] is related to the multiplication of kinetic rate (i.e., activation energy of diffusion) to the exponential function of Gibbs free surface energy and interface temperature of an impacting water drop on substrates along with solid-liquid interfacial area and Boltzmann constant (i.e., $k_B$).

$$J\left(T\right)=K\left(T\right)A_{s-l}\exp \left(\frac{-\Delta G_{Het}\left(T,{\mathsf{\theta }}_{wI}\right)}{k_B{T}_{Interace}}\right)$$

(1)

where A_s−l is the solid-liquid surface area.

Additionally Gibbs free surface energy is defined based on the melting temperature of water, $T_m$, water-ice surface tension,${\mathsf{\gamma }}_{wI}$, latent heat of fusion, $H_f$, solid-liquid or gas-liquid interface temperature,$T_{Interface}$, and geometrical factor,$f_{({\mathsf{\theta }}_{wI})},$ as illustrated in Equations (2) and (3) [17,40].

$$\Delta G_{Het}\left(T,{\mathsf{\theta }}_{wI}\right)=\frac{T_m^{2}16{\mathsf{\pi }\mathsf{\gamma }}_{wI}^3}{3H_f^2{\left(T_m-T_{Interface}\right)}^2}f({\mathsf{\theta }}_{wI})$$

(2)

$$f({\mathsf{\theta }}_{wI})=\left[\frac{\left(2+cos{\mathsf{\theta }}_{wI}\right){\left(1-cos{\mathsf{\theta }}_{wI}\right)}^2}{4}\right]$$

(3)

Interface temperature of a liquid drop on a surface with various roughness is predicted by solving two transient conduction equations through the drop and coated (i.e., rough surface) domain. It is given by Equation (4).

$$T_{w-interface}\left(h,t_c\right)=T_{drop}+[\left(T_{sub}-T_d\right)]erfc\left(\frac{h_{pa}}{2\sqrt{{\mathsf{\alpha }}_{pa}{t}_c}}\right)$$

(4)

Furthermore, temperature distribution inside of spread water can be predicted from Equation (5) (see Supplementary Materials).

$$T_w\left(x_w,t_c\right)=T_{drop}+\left[T_{sub}-T_d\right)]\frac{erfc\left(\frac{h_{pa}}{2\sqrt{{\mathsf{\alpha }}_{pa}{t}_c}}\right)}{erfc\left(\frac{h_w}{2\sqrt{{\mathsf{\alpha }}_w{t}_c}}\right)}.erfc\left(\frac{x_w>h}{2\sqrt{{\mathsf{\alpha }}_w{t}_c}}\right)$$

(5)

In equation above, $T_{sub}$, is the temperature of semi post-air domain (i.e., coated surface) and $T_w$ is water temperature, $t_c$ is the total contact time of liquid drop on surface, and $h_{pa}$ represents average or root mean square roughness of substrate. ${\mathsf{\alpha }}_{pa}$ and ${\mathsf{\alpha }}_w$ are thermal diffusivity of post-air domain and water respectively. Composite thermal diffusivity of air-pillar domain, ${\mathsf{\alpha }}_{pa}$, is found through equivalent thermal conductivity and specific heat of coated (i.e., semi air-pillar) domain [17].

At cooler conditions (T ≤ −30 °C) due to the presence of extreme cold interface temperature, which become close to substrate temperature, nucleation rate increases exponentially, resulting in instantaneous pinning when drop reaches its maximum spreading diameter on both aluminum and Teflon substrates. The change in the maximum spreading diameter is due to an increase of droplet internal bulk viscosity up to 8-fold [41,42]. It was shown that an increase in viscous dissipation results in a decrease in the maximum spreading diameter, as can be inferred from droplet viscous dissipation function, $\mathsf{\phi }\approx \mathsf{\mu }{\left(\frac{U}{L}\right)}^2$ [43] where U and L are droplet impact velocity and near wall boundary layer thicknesses [44].

However, in order to show that reduction in droplet maximum spreading diameter is only related to viscosity variation and not by phase change and crystallization process, a classical energy-based model of maximum spreading diameter prediction derived by Passandideh-Fard et al. [45] is presented by Equation (6). In this equation, the effect of phase change and solidification is also considered by assumption of all the kinetic energy stored in ice layer being lost.

$$\mathsf{\zeta }=\frac{D}{D_{\max }}=\sqrt{\frac{We+12}{\frac{3}{8}We{s}^{*}+3\left(1-cos{\mathsf{\theta }}_a\right)+4\frac{We}{\sqrt{Re}}}}$$

(6)

where $s^{*}=\sqrt{2t^{*}\frac{Ste}{Pe}}$ is dimensionless growth rate of freezing front which follows from the Stefan problem soultion. It was showed that where $\sqrt{\frac{Ste}{Pr}}$ << 1 the effect of formed ice nuclei on the maximum spreading dimeter is negligeble. The dimensionless Stefan number, $\frac{C_{p,l}\left(T_m-T_s\right)}{H_{f,l}}$, is increased by increasing the degree of sub cooling of surface (i.e., temperature difference between substrate and melting point of water, $(T_m-T_s$)). On the other hand, the ratio of droplet specific heat and latent heat of fusion is also increased when water droplet temperature is decreased. However, both the supercooled water droplet specific heat and latent heat of fusion are weak functions of temperature within the range of the present work (i.e., −10 °C and −30 °C). In the current study the ratio ($\sqrt{\frac{Ste}{Pr}}$) in lowest temperature conditions becomes as low as 0.15, stressing that the wetting dynamics during the spreading phase are not much affected by phase change mechanism. Therefore, comparison of the maximum spreading diameter with that of hydrodynamic energy balance models at specfic temperatures can be performed.

After analysis of the impacting supercooled water drop in the still air, the effect of stagnation flow on the impacting water drop seems an interesting topic. The resulting shear and normal force of the air flow might lead to important changes in wetting dynamics of an impacting water drop. Furthermore, it significantly changes thermal transport properties of air-liquid interface by evaporation cooling [16]. However, quantitative analysis of temporal evolution of spreading diameter, illustrated in Figure 3, shows that the effect of incoming cold air flow has an insignificant effect on wetting dynamics on hydrophilic and hydrophobic surfaces which arise from strong crystallization process at solid-liquid interface combined with sever increase in contact line viscosity up to 8 and 4.3 fold at −30 °C and −20 °C , respectively [41,42]. Furthermore, the effect of the capillary ridge become important where exposed air flow on thin film of super cooled water comes into contact with solid material [46]. On the other hand, due to the fact that both homogeneous nucleation, which weakens surface tension, and heterogeneous nucleation, which results in an increase in hydrophilicity by changing contact angle [17], enhances the chance of pinning on a polished aluminum surface and the resulting normal and shear force of stagnation flow cannot overcome the formed capillary ridge. However, incoming air flow has an observable and important outcome on the superhydrophobic surface.

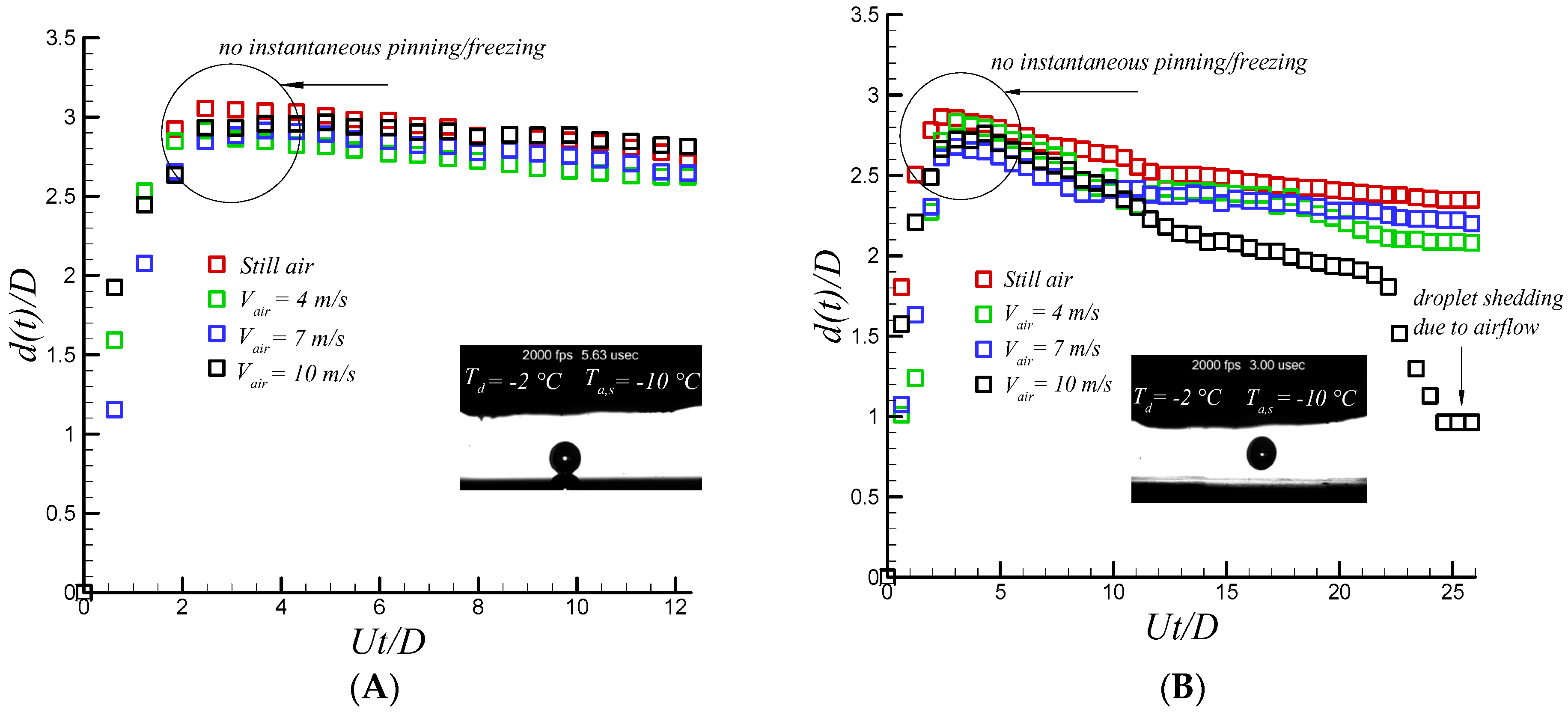
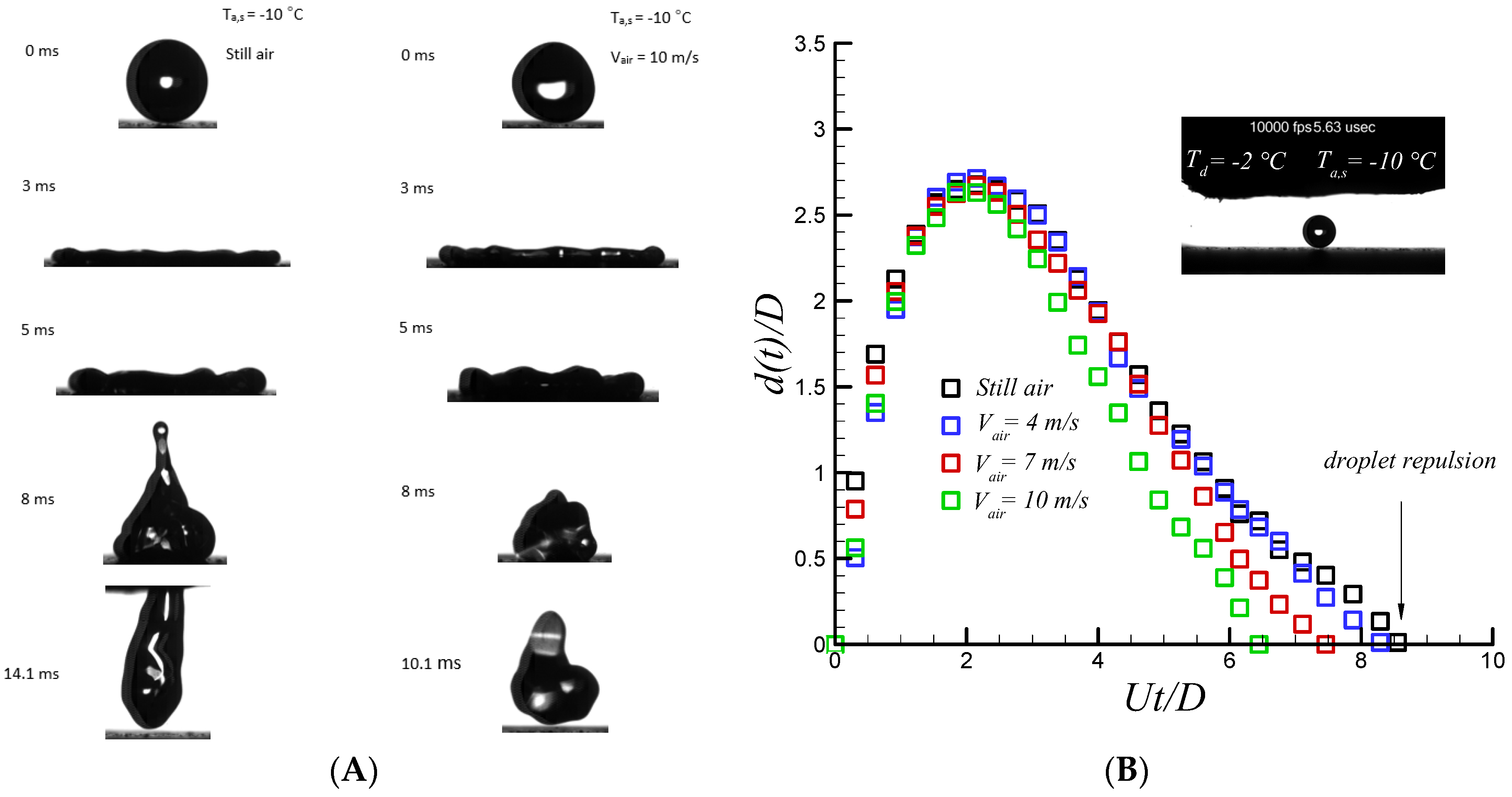
Figure 4 shows the sequential images of supercooled water droplet impacting on a coated superhydrophobic substrate along with quantitative analysis of temporal spreading diameter. The droplet diameter, impact velocity, Weber and Reynolds, Stefan, and Prandtl number are 2.6 mm, 1.6 m/s, 88, 2170, 0.128, 14.83, respectively. Droplet sphericity is changed after impact due to rapid raise in pressure and gets flattened cylindrical shape at 3 ms with no differences between the cases with and without air flow. However, at recoiling phase when the air jet velocity is increased (i.e., an increase in dynamic pressure), droplet bouncing and jet formation is dramatically suppressed, as depicted in Figure 4.

The recoiling phase is almost initiated right after finishing the relaxation phase and lasts up to 0.2 ms. Strong retraction force due to high receding contact angle and partial slip velocity [47,48] results in droplet detachment at 14 ms. Droplet contact time is not a function of impact velocity when it is sufficiently higher than the critical velocity of drop repulsion (i.e., $V_c={\left(g{R}_o^3/l{c}^2\right)}^{1/2}$, where $lc$ is capillary length of water drop, $lc=\sqrt{\mathsf{\gamma }/\rho g}$) and it varies with $R^{2/3}$ [49]. On the other hand, quantitative analysis of the impacting supercooled water drop on superhydrophobic substrate accompanied with different air speeds shows different phenomena, as depicted in Figure 4. Striking results were observed when air velocity was increased. A droplet detached from the surface in a considerably smaller time than that of the still air case as a function of air speed. Contact time is reduced up to almost 30% at air velocity up to 10 m/s highlighting the effect of another physical factor. Recent study of droplet impact on dry ice shows that there is rapid generation of gas vapor formed beneath of the impacting droplet on a dry ice surface [50]. Therefore, the droplet moves on a compressed layer of vapor and not the surface. Consequently, occurrence of full slip condition rather than partial one promotes capillary force (i.e., ideally no contact line viscous dissipation is present at full slip condition) and leads to the achievement of complete repellency as observed on superhydrophobic surfaces. Therefore, it can be inferred that stagnation flow may result in the presence of a thin moving layer of air underneath the impacting water drop and superhydrophobic surface. By increasing incoming air velocity, the accelerated flowing thin air layer in the viscous region helps to reduce the droplet contact time by two mechanisms. First, the generated rim of the droplet in contact with the thin layer of air underneath promotes the ligament of the impacting water droplet to spread without significant viscous dissipation compared to the still air case. In fact, near the wall boundary layer thickness is not same as still air conditions. Secondly, K-H instability [31] which is promoted by increasing air speeds at either interface (solid-air or air-liquid) results in a more unstable spreading ligament. In fact, contribution of the full slip boundary condition along with K-H instability results in faster detachment of the water droplet during the recoiling phase.

Furthermore, impacting the water drop in the presence of air flow is not fully axisymmetrical as the drop might not impact exactly at the stagnant point. In fact, numerical simulation of the impinging air flow shows that the stagnation domain has a diameter of about 1 mm where air radial velocity in this area is negligible (i.e., below 2% of air jet velocity (see Supplementary Materials). Therefore, the spread drop might face the nonaxisymmetric shear and normal force of the air flow. Similarly to the study of Birds et al. [23], droplet contact time is reduced significantly when receding velocity is no longer axisymmetric for normal drop impacts. However, it was shown to be independent of surface inclination for oblique drop impact [51]. To this end, the same results was observed for an impacting supercooled water drop with temperature as low as −3.5 °C on superhydrophobic surfaces maintained at temperature as cold as −20 °C. 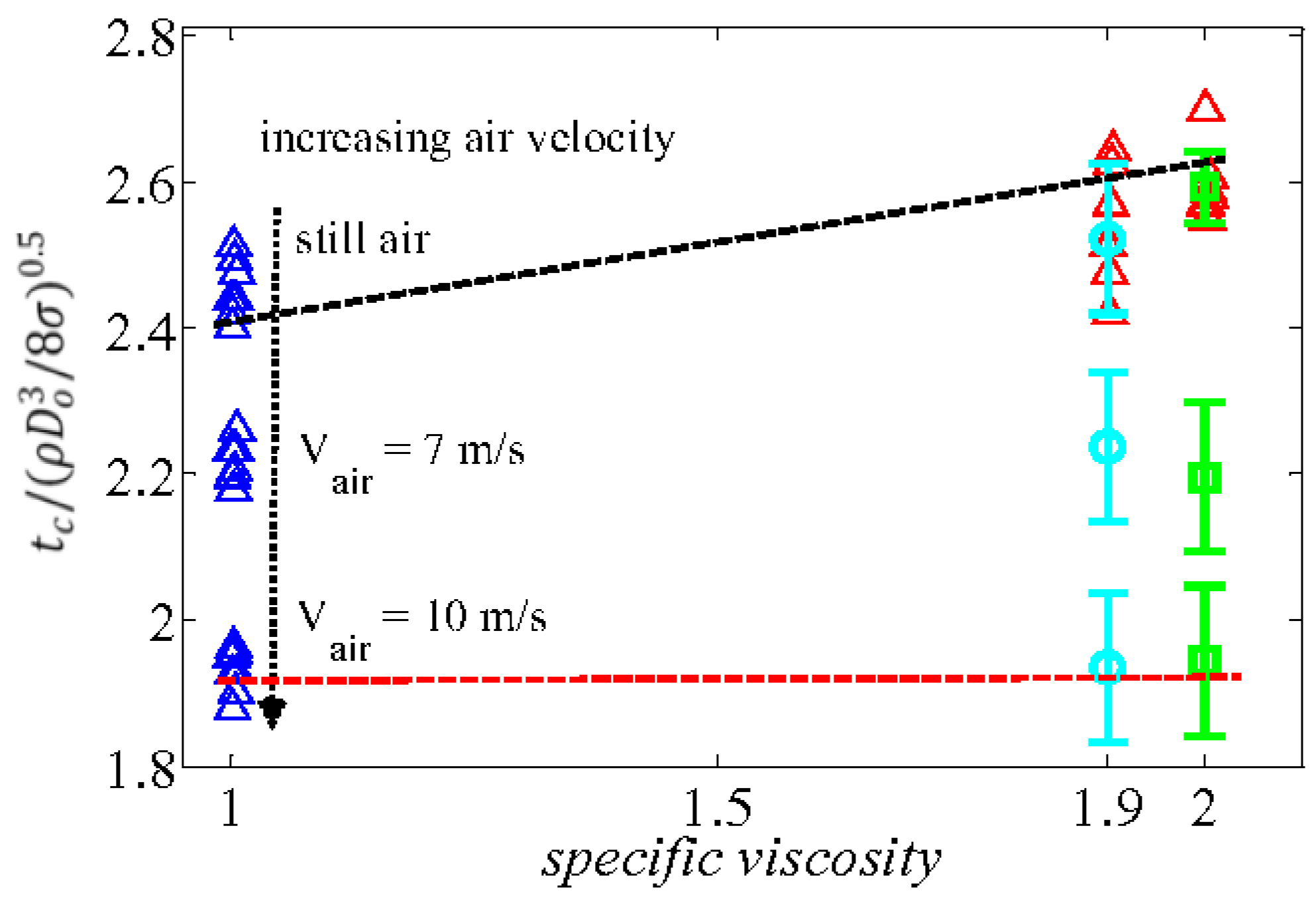In Figure 5, dimensionless contact time based on capillary-inertia time scale versus specific viscosity ($\frac{{\mathsf{\mu }}_{sd}}{{\mathsf{\mu }}_d}),$ for various supercooled water droplet temperatures is presented where ${\mathsf{\mu }}_{sd}$ is the viscosity of supercooled water and ${\mathsf{\mu }}_d$ is the viscosity of water at room temperature. In addition, we have added results of water-glycerol solution having the same viscosity as that of a supercooled water drop to properly evaluate the net effect of increasing viscosity on the detachment time of an impacting supercooled water drop [51].

On the other hand, supercooled water droplet dynamics on superhydrophobic substrate maintained at −30 °C which is below critical temperature of heterogeneous nucleation (i.e., −24 °C) has a systematically different behavior (see Supplementary Materials). Although the spreading phase remains unaffected (e.g., measuring both advancing dynamic contact angle and maximum spreading diameter, along with calculation of ratio of Stefan to Prandtl ratio (i.e., 0.15)) by both ice nucleation mechanisms and sever increase in contact line viscosity with and without air flow, dramatic changes were observed in the relaxation and receding phases. Time at the maximum spreading diameter (i.e., relaxation time) was significantly increased up to 2 ms causing a significant increase in heat transfer cooling rate due to the large wetting area. A faster heterogeneous nucleation rate is also promoted, due to the fact that interface temperature becomes almost as cold as substrate temperature which dramatically changes the receding dynamics contact angle. In fact, complete superhydrophobicity break down was observed at 5 ms (see Supplementary Materials) due to the aforementioned factors. Reduction of the dynamic receding contact angle and rapid increases in viscosity, especially at the contact line up to 8-fold, results in a significant reduction in capillary force which is a function of receding contact angle and liquid drop surface tension, $\mathsf{\pi }\mathsf{\gamma }{D}_{\max }\left(1-cos{\mathsf{\theta }}_{rec}\right)$. Experimental observation shows that (see Figure 6A) the effect of increased viscosity slightly changes the maximum spreading diameter of an impacting drop (i.e., within the current study) while significantly changing the droplet contact time through reduction of receding velocity. Therefore, by reducing the receding velocity, the chance of heat transfer cooling and the heterogeneous nucleation process is even further increased due to the larger interfacial area. Quantitative analysis of an impacting water drop on superhydrophobic surface in still air, as illustrated in Figure 6B, shows that the capillary force become zero, corresponding to a receding velocity of about 11 ms (i.e., corresponding dimensionless time is 7).

On the other hand, when droplet is under the effect of cold air flow it becomes an even further complicated process due to the presence of another type of nucleation mechanism such as homogeneous nucleation and crystallization induced nucleation from inside-out [52]. Due to the presence of forced convective evaporation cooling, which results in the presence of aforementioned nucleation mechanism, the gas-liquid interface temperature becomes even lower than air temperature, which is a function of air velocity and air humidity [16]. It was observed that, when relative humidity is negligible and the chance of superhydrophobicity degradation is small [53], which is the case in the present study, the effect of evaporation cooling becomes significant and homogeneous nucleation happens at the air-liquid interface. This phenomenon has a further adverse effect on wetting dynamics of an impacting droplet by reducing surface tension force. Likewise, heterogeneous ice nucleation, which changes wetting dynamics by reducing receding dynamic contact angle, the effect of homogeneous nucleation can affect the wetting dynamics by changing the droplet surface tension value. In fact, surface tension of the mixture of ice-water is about 20 mN/m [17] which shows a reduction in liquid surface tension of up to 3.5-fold that of the room temperature droplet. Therefore, after formation of ice nuclei on the gas-liquid interface, it gradually changes the surface tension or capillary force of impacting water drop, especially at the time of maximum spreading diameter where the droplet is exposed to utmost evaporation cooling due to the larger interfacial area. To this end, the capillary force experience largely decreases (i.e., due to combination of both surface tension and apparent receding contact angle reduction, $\mathsf{\pi }\mathsf{\gamma }{D}_{\max }\left(1-{\cos \mathsf{\theta }}_{rec}\right)$) where cooled stagnation flow is present. As illustrated in Figure 6B, aforementioned factors result in droplet pinning at 4.5 ms which is slightly after the initiation of the retraction phase. Furthermore, the solidified wetting diameter becomes considerably larger compared to the still air case. It increases up to almost 2-fold at 10 m/s air velocity, which highlights a significant difference on impacting drop dynamics on a superhydrophobic surface where stagnation flow is present.

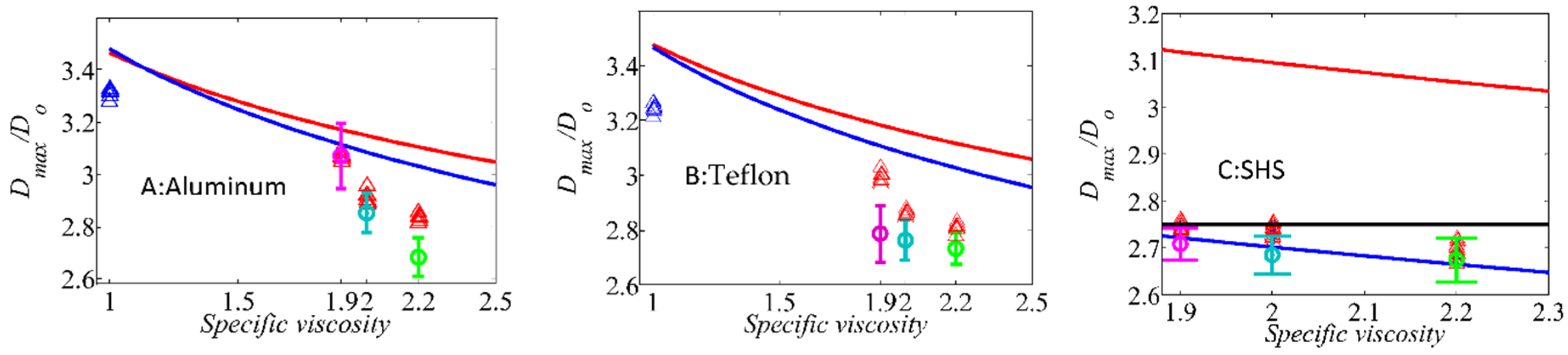
In Figure 7, comparison of the maximum spreading diameters was carried out by three different approaches. The first is the energy based model proposed by Passandideh-Fard et al. [44] which is based on the balance of all energies before and after impacts, and the second model is an analytical hydrodynamic model proposed by Roisman [54] derived from continuity and momentum equations. Both the hydrodynamic and energy based model were used to compare with experimental data. For a superhydrophobic surface, a scaling law analysis proposed by Clanet et al. [55] is used for proper evaluation. As depicted in Figure 7C, for supercooling conditions, the scaling law predicts very well the supercooled water drop at −2 °C. However, it overestimates the maximum spreading diameter for the lowest temperature supercooled water drop (i.e., −5.5 °C) with mean value deviation up 3%. The best agreement was observed for the energy balanced model at supercooling condition. This model fits very well with experimental data with mean value deviation of up to 1%. However, the analytical hydrodynamic model predicts relatively well the mean value deviation up to 14% for supercooled water drop at −5.5 °C. In addition to supercooled water droplet experiments, the droplet impact of water-glycerol solution with various specific viscosity ranging from 1.9 (corresponding supercooled water at −2 °C) to 2.2 (corresponding −5.5 °C supercooled water) were carried out to mimic an increased viscosity in supercooled water due to temperature reduction. The results show a very good agreement with that of supercooled water drop experiments.

The same comparison was carried out for aluminum and Teflon substrates, as depicted in Figure 7. Both the energy based model and hydrodynamic model agree very well with experimental results. Associated errors for the energy based model become slightly larger than those of the hydrodynamic model for room temperature conditions on an aluminum substrate with mean value deviation of 4.6% and 3.5%, respectively. The same results were found for Teflon substrate for both models with almost the same mean value deviation up to 8% for room temperature conditions. However, when viscosity is increased, the difference between experimental results and the two aforementioned models becomes larger. For a higher water drop degree of subcooling (i.e., −5.5 °C), the mean value deviation for energy based and hydrodynamic models for aluminum substrates become 12% and 15%, and 10% and 14% for Teflon substrates, respectively. The difference between experimental results with that of the aforementioned models stems from water drop interface temperature moving through cold air before impacting on the substrates. Thermal transport analysis (see Supplementary Materials) shows that the Biot number becomes larger than 0.1 when air flow is present. Furthermore, the Fourier number becomes as small as 0.00045. Therefore, we can expect an interfacial temperature change. Calculation of heat penetration lengths [1], ${\mathsf{\delta }}_h\approx {\left({\mathsf{\alpha }}_w{t}_c\right)}^{\frac{1}{2}}$, shows that this length varies up to 0.1 mm (${\mathsf{\alpha }}_w=0.1310-6\left(\frac{m^2}{s}\right)$ and $t_c\approx$ 85 ms). It is evident that interface temperature of impacting supercooled condition becomes as cold as −30 °C. Consequently, there is a viscosity jump of up to 8 and 3.6 fold higher than that of room temperature and water drop temperature at −5.5 °C, respectively. Therefore, viscous dissipation should be represented by a combination of internal bulk of impacting water and that of an interface one. Further justification is carried out by using different water-glycerol solutions having the same viscosity as that of an impacting supercooled water drop. In all experimental results, supercooled water droplet impact shows lower mean value maximum spreading diameter compared with water-glycerol mixture at the same bulk viscosity, as illustrated in Figure 7 for all target surfaces. Therefore, the aforementioned increased viscosity in droplet contact line competes with droplet inertia leading to a slightly larger decrease on the maximum spreading diameter compared to water-glycerol solution at the same internal bulk viscosity.

4. Conclusions

The effect of stagnation air flow on an impacting supercooled water drop at various air velocities and temperatures were experimentally evaluated. Various target surfaces covering a wide range of wettability spanning from hydrophilic to superhydrophobic surfaces were used in the current study. Controllable air temperature as low as −30 °C was produced by designing a heat exchanger which works with liquid nitrogen. In addition, a droplet accelerator was added to the experimental set up to provide controlled stagnation flow at velocities ranging from 0 (i.e., still air) to 10 m/s. The limitation of imposing higher air velocity stems from having spherical drop with and without air flow based on the definition of critical relative Weber number below 3. The current study highlights the net effect of air flow on an impacting supercooled water drop at various air velocities and temperatures. Droplet impact velocity was independent of incoming air jet velocity. Analysis of stagnation air flow analysis was carried out by using the classical Homann flow approach. Imposed stagnation flow on the impacting water drop results in a produced shear and normal force on the gas-liquid interface of the spread drop. For hydrophilic and hydrophobic substrates, non-instantaneous pinning at the maximum spreading diameter was observed at temperature above −20 °C, and complete water drop repellency was shown for the superhydrophobic surface. A striking phenomenon was observed: droplet contact time was reduced by up to about 30% for air velocity up to 10 m/s that of still air. This phenomenon was attributed to the transition of partial slip conditions to full slip ones, which eliminates the contact line viscous dissipation. Furthermore, slight nonaxisymmetric receding velocity reduces droplet contact time. Nevertheless, for substrate temperatures below the critical temperature of heterogeneous nucleation on bouncing droplets (i.e., −24 °C), instantaneous pinning (i.e., no recoiling phase) was observed for hydrophilic and hydrophobic surfaces. In contrast, for superhydrophobic surfaces, the recoiling phase is subjected to a severe reduction in receding contact angle and surface tension due to the presence of ice nuclei at the solid-liquid and gas-liquid interface. This results in transition from superhydrophobicity to hydrophilicity due to the rapid crystallization process. Further decreases in receding contact angle occurred by imposing higher stagnation flow up to 10 m/s which results in an almost non-recoiling phase of the supercooled droplet impacts on a superhydrophobic surface.