Guided Self-Accelerating Airy Beams—A Mini-Review
Abstract
:1. Introduction
2. Results and Discussion
2.1. Nonlinear Guidance
2.1.1. Kerr Medium
2.1.2. Saturable Medium
2.1.3. Soliton and Kerr Case
2.2. Harmonic Potential Guidance
2.2.1. One-Dimensional Airy Beams
- (i)
- (ii)
- Perform the convolution of the two Fourier transforms in Equations (19) and (20), and using the definition [72]find the inverse Fourier transform:
- (i)
- When , we have —an initial beam recurrence.
- (ii)
- When , we have —an inversion of the initial beam.
- (iii)
- When , by directly solving Equation (18) for the FT of the initial beam, we havewhere if m is even and if m is odd. This field is unrelated to the initial Airy beam—that is, it represents a new “phase” of the propagating beam.
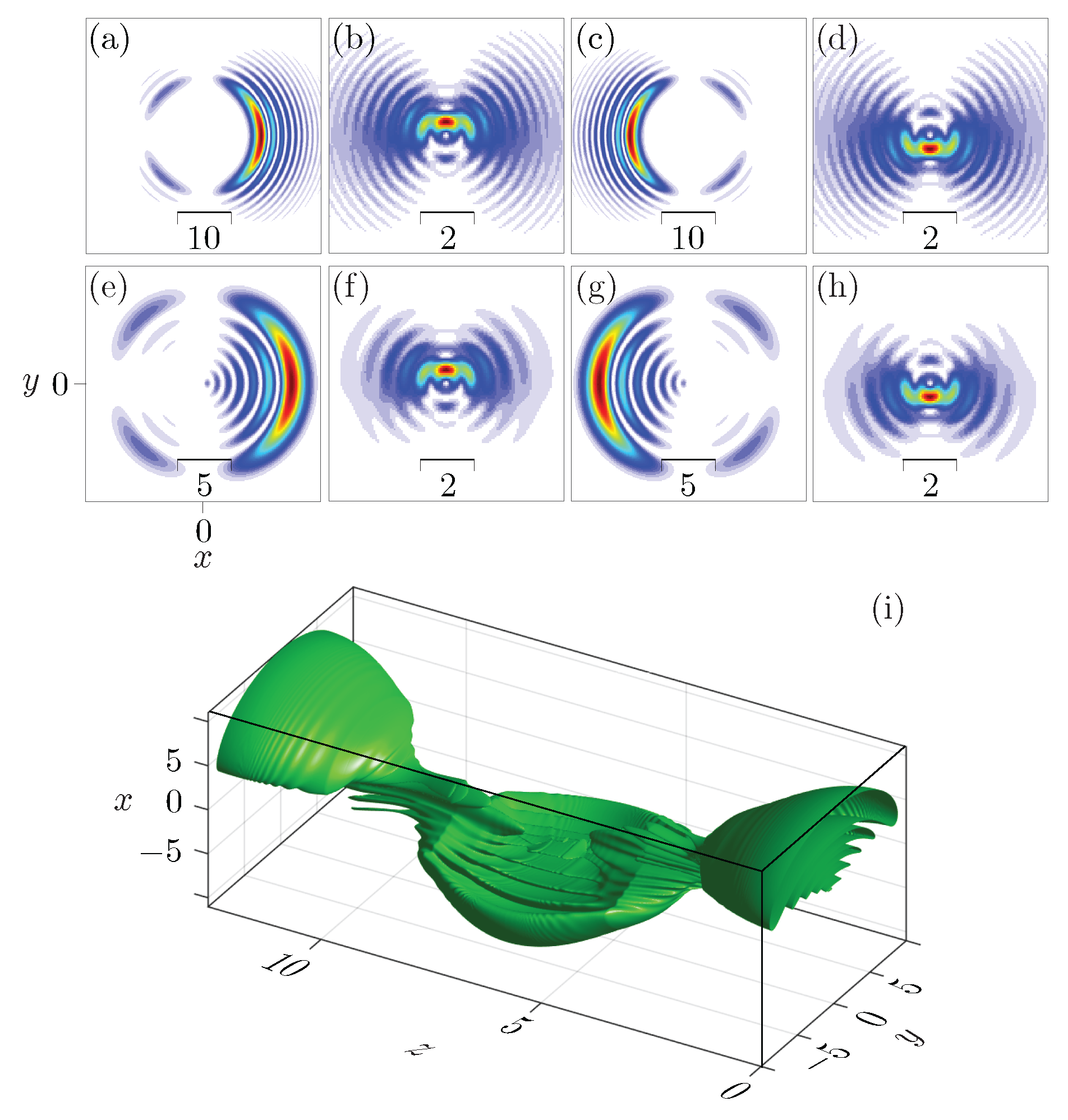
2.2.2. Two-Dimensional Case
2.3. Dynamic Linear Potential Guidance
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Ballistic dynamics of Airy beams. Opt. Lett. 2008, 33, 207–209. [Google Scholar] [CrossRef] [PubMed]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and Near-Field Imaging of Airy Surface Plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Li, T.; Wang, S.M.; Zhang, C.; Zhu, S.N. Plasmonic Airy Beam Generated by In-Plane Diffraction. Phys. Rev. Lett. 2011, 107, 126804. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Guo, X.; Tu, J.; Ma, Q.; Wu, J.; Zhang, D. Acoustic non-diffracting Airy beam. J. Appl. Phys. 2015, 117, 104503. [Google Scholar] [CrossRef]
- Fu, S.; Tsur, Y.; Zhou, J.; Shemer, L.; Arie, A. Propagation Dynamics of Airy Water-Wave Pulses. Phys. Rev. Lett. 2015, 115, 034501. [Google Scholar] [CrossRef] [PubMed]
- Bar-Ziv, U.; Postan, A.; Segev, M. Observation of shape-preserving accelerating underwater acoustic beams. Phys. Rev. B 2015, 92, 100301. [Google Scholar] [CrossRef]
- Siviloglou, G.; Broky, J.; Dogariu, A.; Christodoulides, D. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved plasma channel generation using ultraintense Airy beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Salandrino, A.; Christodoulides, D.N. Airy plasmon: A nondiffracting surface wave. Opt. Lett. 2010, 35, 2082–2084. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Hu, Y.; Song, D.; Lou, C.; Zhang, X.; Chen, Z.; Xu, J. Image signal transmission with Airy beams. Opt. Lett. 2015, 40, 5686–5689. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Vaughan, J.C.; Zhuang, X. Isotropic three-dimensional super-resolution imaging with a self-bending point spread function. Nat. Photon. 2014, 8, 302–306. [Google Scholar] [CrossRef] [PubMed]
- Polynkin, P.; Kolesik, M.; Moloney, J. Filamentation of Femtosecond Laser Airy Beams in Water. Phys. Rev. Lett. 2009, 103, 123902. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Zhang, B.F.; Chen, H.; Ding, J.; Wang, H.T. Optical trapping with focused Airy beams. Appl. Opt. 2011, 50, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Yang, Y.; Wang, J.; Bu, J.; Wang, M.; Yuan, X.C. Microfabricated continuous cubic phase plate induced Airy beams for optical manipulation with high power efficiency. Appl. Phys. Lett. 2011, 99, 261106. [Google Scholar] [CrossRef]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photon. 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Zhang, P.; Prakash, J.; Zhang, Z.; Mills, M.S.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Trapping and guiding microparticles with morphing autofocusing Airy beams. Opt. Lett. 2011, 36, 2883–2885. [Google Scholar] [CrossRef] [PubMed]
- Schley, R.; Kaminer, I.; Greenfield, E.; Bekenstein, R.; Lumer, Y.; Segev, M. Loss-proof self-accelerating beams and their use in non-paraxial manipulation of particles’ trajectories. Nat. Commun. 2014, 5, 5189. [Google Scholar] [CrossRef] [PubMed]
- Vettenburg, T.; Dalgarno, H.I.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Meth. 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Abdollahpour, D.; Suntsov, S.; Papazoglou, D.G.; Tzortzakis, S. Spatiotemporal Airy Light Bullets in the Linear and Nonlinear Regimes. Phys. Rev. Lett. 2010, 105, 253901. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Airy-Bessel wave packets as versatile linear light bullets. Nat. Photon. 2010, 4, 103–106. [Google Scholar] [CrossRef]
- Ament, C.; Polynkin, P.; Moloney, J.V. Supercontinuum Generation with Femtosecond Self-Healing Airy Pulses. Phys. Rev. Lett. 2011, 107, 243901. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.Y.; Hwang, C.Y.; Lee, B. Slow non-dispersing wavepackets. Opt. Express 2011, 19, 2286–2293. [Google Scholar] [CrossRef] [PubMed]
- Voloch-Bloch, N.; Lereah, Y.; Lilach, Y.; Gover, A.; Arie, A. Generation of electron Airy beams. Nature 2013, 494, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Gbur, G. Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Čižmár, T.; Mazilu, M.; Chan, V.C.; Carruthers, A.E.; Capron, B.A.; McNeely, W.; Wright, E.M.; Dholakia, K. Optical path clearing and enhanced transmission through colloidal suspensions. Opt. Express 2010, 18, 17130–17140. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Chremmos, I.D.; Song, D.; Christodoulides, D.N.; Efremidis, N.K.; Chen, Z. Curved singular beams for three-dimensional particle manipulation. Sci. Rep. 2015, 5, 12086. [Google Scholar] [CrossRef] [PubMed]
- Libster-Hershko, A.; Epstein, I.; Arie, A. Rapidly Accelerating Mathieu and Weber Surface Plasmon Beams. Phys. Rev. Lett. 2014, 113, 123902. [Google Scholar] [CrossRef] [PubMed]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photon. 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Lotti, A.; Faccio, D.; Couairon, A.; Papazoglou, D.G.; Panagiotopoulos, P.; Abdollahpour, D.; Tzortzakis, S. Stationary nonlinear Airy beams. Phys. Rev. A 2011, 84, 021807. [Google Scholar] [CrossRef]
- Fattal, Y.; Rudnick, A.; Marom, D.M. Soliton shedding from Airy pulses in Kerr media. Opt. Express 2011, 19, 17298–17307. [Google Scholar] [CrossRef] [PubMed]
- Rudnick, A.; Marom, D.M. Airy-soliton interactions in Kerr media. Opt. Express 2011, 19, 25570–25582. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Belić, M.; Wu, Z.K.; Zheng, H.B.; Lu, K.Q.; Li, Y.Y.; Zhang, Y.P. Soliton pair generation in the interactions of Airy and nonlinear accelerating beams. Opt. Lett. 2013, 38, 4585–4588. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Belić, M.R.; Zheng, H.B.; Chen, H.X.; Li, C.B.; Li, Y.Y.; Zhang, Y.P. Interactions of Airy beams, nonlinear accelerating beams, and induced solitons in Kerr and saturable nonlinear media. Opt. Express 2014, 22, 7160–7171. [Google Scholar] [CrossRef] [PubMed]
- Kaminer, I.; Segev, M.; Christodoulides, D.N. Self-Accelerating Self-Trapped Optical Beams. Phys. Rev. Lett. 2011, 106, 213903. [Google Scholar] [CrossRef] [PubMed]
- Panagiotopoulos, P.; Abdollahpour, D.; Lotti, A.; Couairon, A.; Faccio, D.; Papazoglou, D.G.; Tzortzakis, S. Nonlinear propagation dynamics of finite-energy Airy beams. Phys. Rev. A 2012, 86, 013842. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, S.; Zhang, P.; Lou, C.; Xu, J.; Chen, Z. Persistence and breakdown of Airy beams driven by an initial nonlinearity. Opt. Lett. 2010, 35, 3952–3954. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Yin, C.F.; Chu, X.X.; Wang, H. Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 2010, 82, 043832. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.Y.; Kim, K.Y.; Lee, B. Dynamic Control of Circular Airy Beams With Linear Optical Potentials. IEEE Photon. J. 2012, 4, 174–180. [Google Scholar] [CrossRef]
- Hwang, C.Y.; Kim, K.Y.; Lee, B. Bessel-like beam generation by superposing multiple Airy beams. Opt. Express 2011, 19, 7356–7364. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.; Efremidis, N.K.; Christodoulides, D.N. Pre-engineered abruptly autofocusing beams. Opt. Lett. 2011, 36, 1890–1892. [Google Scholar] [CrossRef] [PubMed]
- Papazoglou, D.G.; Efremidis, N.K.; Christodoulides, D.N.; Tzortzakis, S. Observation of abruptly autofocusing waves. Opt. Lett. 2011, 36, 1842–1844. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.; Zhang, P.; Prakash, J.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Fourier-space generation of abruptly autofocusing beams and optical bottle beams. Opt. Lett. 2011, 36, 3675–3677. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.D.; Efremidis, N.K. Band-specific phase engineering for curving and focusing light in waveguide arrays. Phys. Rev. A 2012, 85, 063830. [Google Scholar] [CrossRef]
- Hu, Y.; Siviloglou, G.A.; Zhang, P.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Self-accelerating Airy Beams: Generation, Control, and Applications. In Nonlinear Photonics and Novel Optical Phenomena; Chen, Z., Morandotti, R., Eds.; Springer: New York, NY, USA, 2012; Volume 170, pp. 1–46. [Google Scholar]
- Bandres, M.A.; Kaminer, I.; Mills, M.; Rodriguez-Lara, B.M.; Greenfield, E.; Segev, M.; Christodoulides, D.N. Accelerating Optical Beams. Opt. Phot. News 2013, 24, 30–37. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Hu, Y.; Song, D.; Zhang, Z.; Zhao, J.; Liang, Y. Control and novel applications of self-accelerating beams. Acta Opt. Sin. 2016, 36, 1026009. (In Chinese) [Google Scholar] [CrossRef]
- Levy, U.; Derevyanko, S.; Silberberg, Y. Light Modes of Free Space. In Progress in Optics; Visser, T.D., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 61, pp. 237–281. [Google Scholar]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Zhang, Y.; Zhang, Z.; Li, C.; Zhang, D.; Zhang, Y.; Belić, M.R. Nonparaxial self-accelerating beams in an atomic vapor with electromagnetically induced transparency. Opt. Lett. 2016, 41, 5644–5647. [Google Scholar] [CrossRef] [PubMed]
- Makris, K.G.; Kaminer, I.; El-Ganainy, R.; Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Accelerating diffraction-free beams in photonic lattices. Opt. Lett. 2014, 39, 2129–2132. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Gao, J.; Ge, L. Solitons shedding from Airy beams and bound states of breathing Airy solitons in nonlocal nonlinear media. Sci. Rep. 2015, 5, 9814. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Li, W.; Lee, R.K. Control on the anomalous interactions of Airy beams in nematic liquid crystals. Opt. Express 2016, 24, 8501–8511. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, N.; Marsal, N.; Sciamanna, M.; Wolfersberger, D. Spatiotemporal dynamics of counterpropagating Airy beams. Sci. Rep. 2015, 5, 13463. [Google Scholar] [CrossRef] [PubMed]
- Diebel, F.; Bokić, B.M.; Timotijević, D.V.; Savić, D.M.J.; Denz, C. Soliton formation by decelerating interacting Airy beams. Opt. Express 2015, 23, 24351–24361. [Google Scholar] [CrossRef] [PubMed]
- Driben, R.; Hu, Y.; Chen, Z.; Malomed, B.A.; Morandotti, R. Inversion and tight focusing of Airy pulses under the action of third-order dispersion. Opt. Lett. 2013, 38, 2499–2501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, K.; Zhong, H.; Zhang, J.; Li, Y.; Fan, D. Effect of initial frequency chirp on Airy pulse propagation in an optical fiber. Opt. Express 2015, 23, 2566–2576. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Tehranchi, A.; Wabnitz, S.; Kashyap, R.; Chen, Z.; Morandotti, R. Improved Intrapulse Raman Scattering Control via Asymmetric Airy Pulses. Phys. Rev. Lett. 2015, 114, 073901. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Hu, W.; Zheng, Y.; Liang, Y.; Cao, L.; Lan, S.; Guo, Q. Self-induced fractional Fourier transform and revivable higher-order spatial solitons in strongly nonlocal nonlinear media. Phys. Rev. A 2008, 78, 043815. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Ru, G. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys. Lett. 2014, 11, 105001. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liu, X.; Belić, M.R.; Zhong, W.P.; Petrović, M.S.; Zhang, Y.P. Automatic Fourier transform and self-Fourier beams due to parabolic potential. Ann. Phys. 2015, 363, 305–315. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Belić, M.R.; Zhang, L.; Zhong, W.P.; Zhu, D.Y.; Wang, R.M.; Zhang, Y.P. Periodic inversion and phase transition of finite energy Airy beams in a medium with parabolic potential. Opt. Express 2015, 23, 10467–10480. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.; Simon, R. A simple realization of fractional Fourier transform and relation to harmonic oscillator Green’s function. Opt. Commun. 1994, 110, 23–26. [Google Scholar] [CrossRef]
- Bernardini, C.; Gori, F.; Santarsiero, M. Converting states of a particle under uniform or elastic forces into free particle states. Eur. J. Phys 1995, 16, 58–62. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform with Applications in Optics and Signal Processing; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Bandres, M.A.; Gutiérrez-Vega, J.C. Airy-Gauss beams and their transformation by paraxial optical systems. Opt. Express 2007, 15, 16719–16728. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Zaskanov, S.G. Diffraction integral and propagation of Hermite-Gaussian modes in a linear refractive index medium. J. Opt. Soc. Am. A 2014, 31, 914–919. [Google Scholar] [CrossRef] [PubMed]
- Mendlovic, D.; Ozaktas, H.M. Fractional Fourier transforms and their optical implementation: I. J. Opt. Soc. Am. A 1993, 10, 1875–1881. [Google Scholar] [CrossRef]
- Mendlovic, D.; Ozaktas, H.M.; Lohmann, A.W. Graded-index fibers, Wigner-distribution functions, and the fractional Fourier transform. Appl. Opt. 1994, 33, 6188–6193. [Google Scholar] [CrossRef] [PubMed]
- Vallée, O.; Soares, M. Airy Functions and Applications to Physics, 2nd ed.; Imperial College Press: Singapore, 2010. [Google Scholar]
- Hu, Y.; Zhang, P.; Lou, C.; Huang, S.; Xu, J.; Chen, Z. Optimal control of the ballistic motion of Airy beams. Opt. Lett. 2010, 35, 2260–2262. [Google Scholar] [CrossRef] [PubMed]
- Caola, M.J. Self-Fourier functions. J. Phys. A Math. Gen. 1991, 24, L1143–L1144. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Belić, M.; Zheng, H.B.; Chen, H.; Li, C.B.; Song, J.P.; Zhang, Y.P. Nonlinear Talbot effect of rogue waves. Phys. Rev. E 2014, 89, 032902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Belić, M.R.; Petrović, M.S.; Zheng, H.B.; Chen, H.X.; Li, C.B.; Lu, K.Q.; Zhang, Y.P. Two-dimensional linear and nonlinear Talbot effect from rogue waves. Phys. Rev. E 2015, 91, 032916. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Zhong, W.P.; Belić, M.R. Self-Similar Hermite-Gaussian Spatial Solitons in Two-Dimensional Nonlocal Nonlinear Media. Commun. Theor. Phys. 2010, 53, 937–942. [Google Scholar]
- Panagiotopoulos, P.; Papazoglou, D.G.; Couairon, A.; Tzortzakis, S. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets. Nat. Commun. 2013, 4, 2622. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Liu, X.; Belić, M.R.; Zhong, W.P.; Wen, F.; Zhang, Y.P. Anharmonic propagation of two-dimensional beams carrying orbital angular momentum in a harmonic potential. Opt. Lett. 2015, 40, 3786–3789. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Zhang, Y.; Belić, M.R.; Li, C.; Wen, F.; Zhang, Z.; Zhang, Y. Controllable circular Airy beams via dynamic linear potential. Opt. Express 2016, 24, 7495–7506. [Google Scholar] [CrossRef] [PubMed]
- Efremidis, N.K. Airy trajectory engineering in dynamic linear index potentials. Opt. Lett. 2011, 36, 3006–3008. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.D.; Chen, Z.; Christodoulides, D.N.; Efremidis, N.K. Abruptly autofocusing and autodefocusing optical beams with arbitrary caustics. Phys. Rev. A 2012, 85, 023828. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, J.J.; Zhang, P.; Ni, P.G.; Prakash, J.; Hu, Y.; Jiang, D.S.; Christodoulides, D.N.; Chen, Z.G. Generation of autofocusing beams with multi-Airy beams. Acta Phys. Sin. 2013, 62, 034209. [Google Scholar]








© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhong, H.; Belić, M.R.; Zhang, Y. Guided Self-Accelerating Airy Beams—A Mini-Review. Appl. Sci. 2017, 7, 341. https://doi.org/10.3390/app7040341
Zhang Y, Zhong H, Belić MR, Zhang Y. Guided Self-Accelerating Airy Beams—A Mini-Review. Applied Sciences. 2017; 7(4):341. https://doi.org/10.3390/app7040341
Chicago/Turabian StyleZhang, Yiqi, Hua Zhong, Milivoj R. Belić, and Yanpeng Zhang. 2017. "Guided Self-Accelerating Airy Beams—A Mini-Review" Applied Sciences 7, no. 4: 341. https://doi.org/10.3390/app7040341
APA StyleZhang, Y., Zhong, H., Belić, M. R., & Zhang, Y. (2017). Guided Self-Accelerating Airy Beams—A Mini-Review. Applied Sciences, 7(4), 341. https://doi.org/10.3390/app7040341




