Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber
Abstract
:1. Introduction
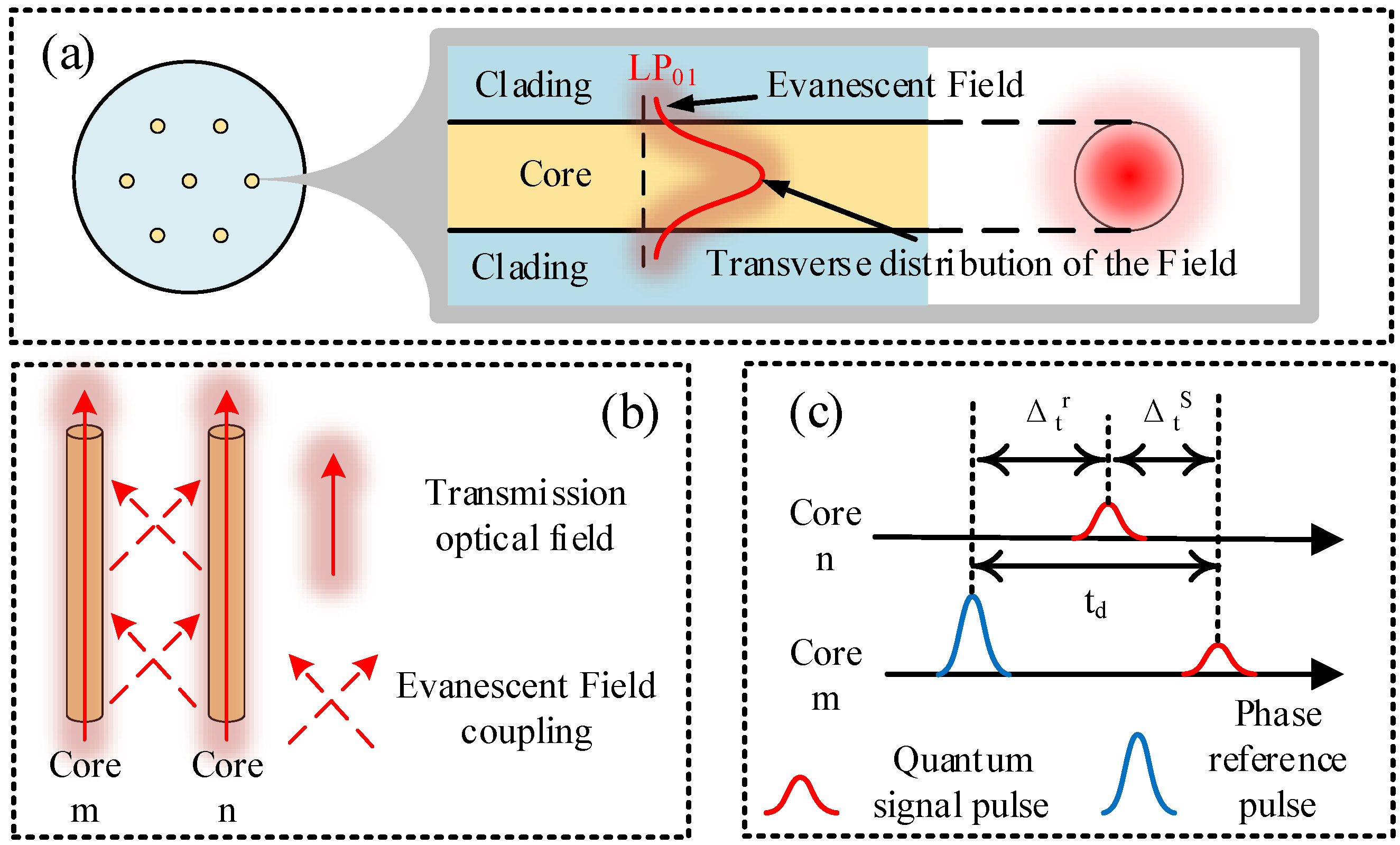
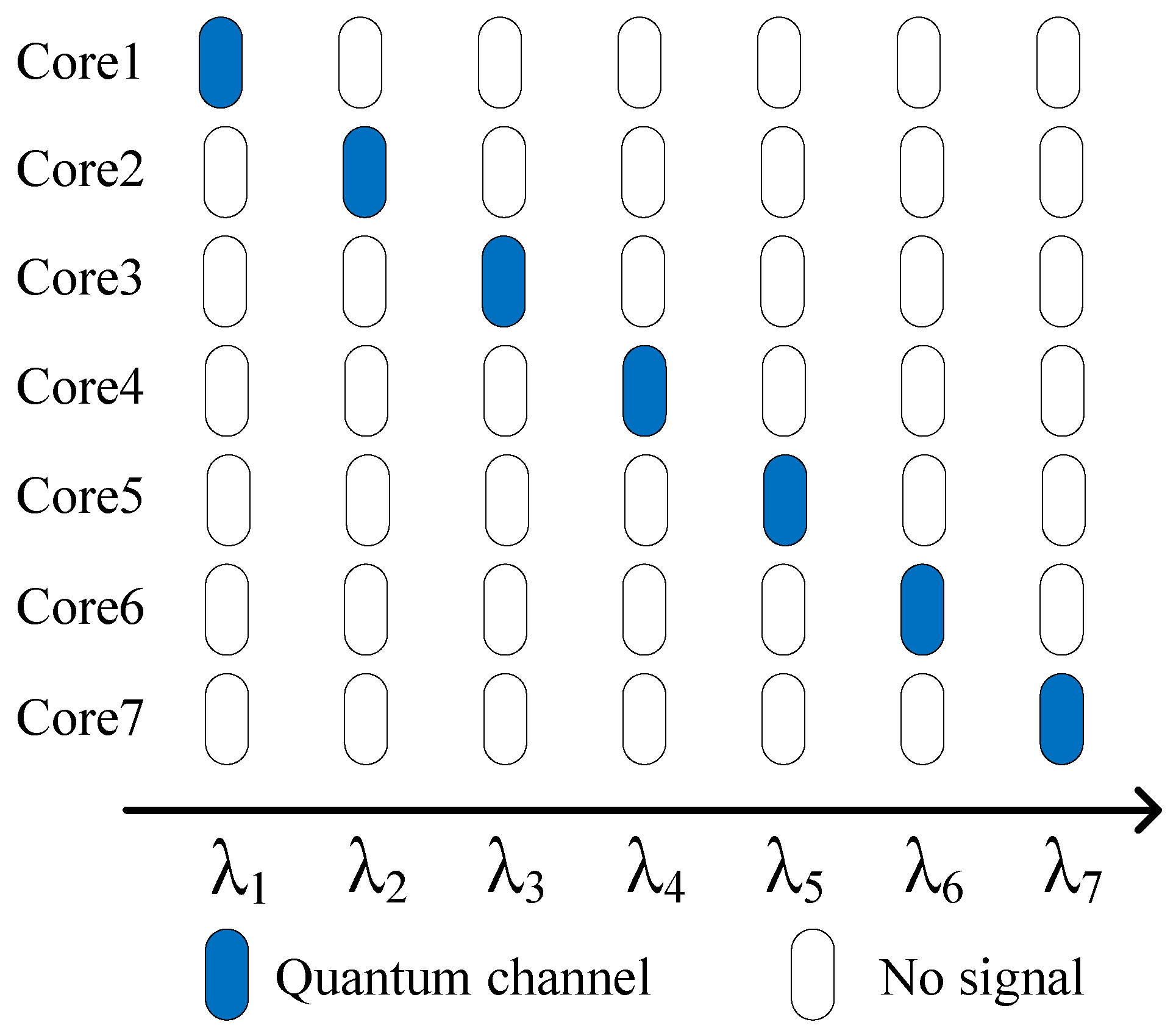
2. The MCF-Based CVQKD
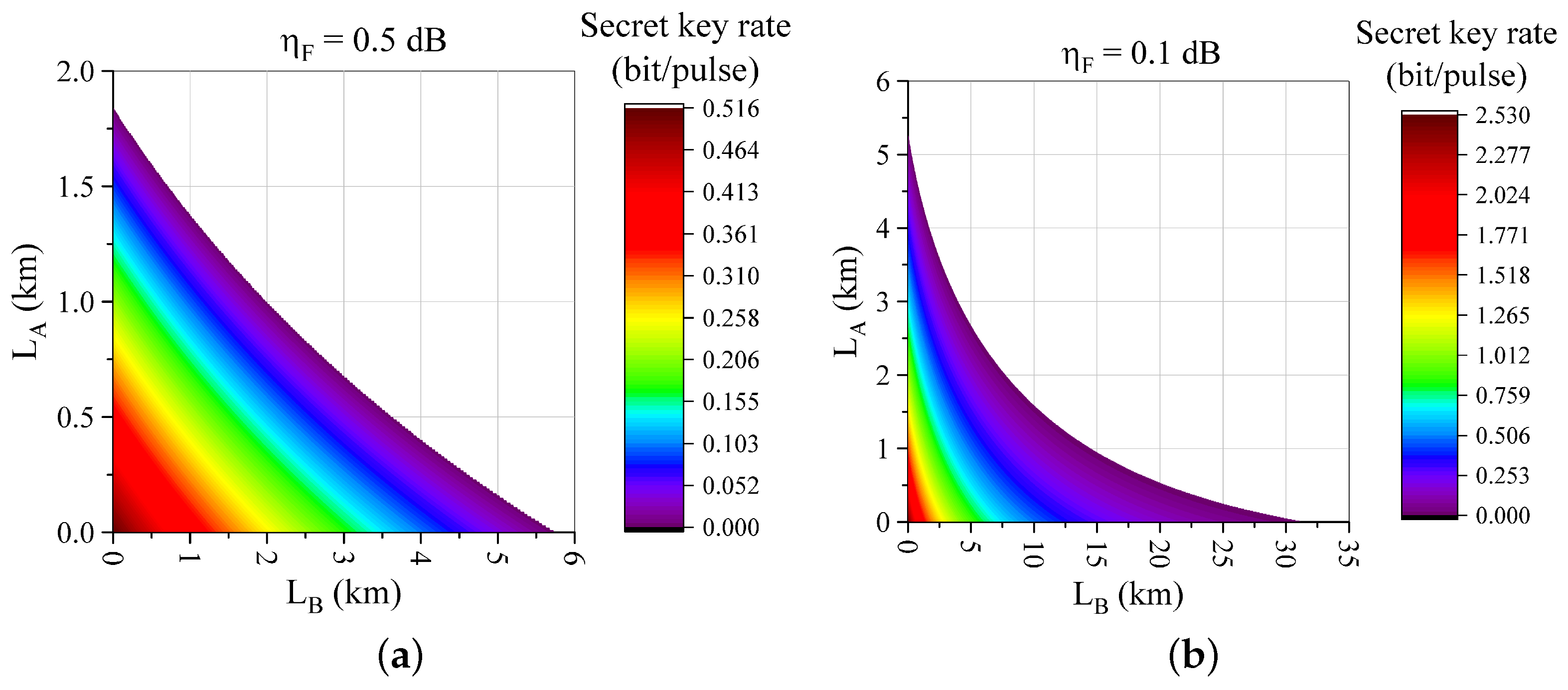
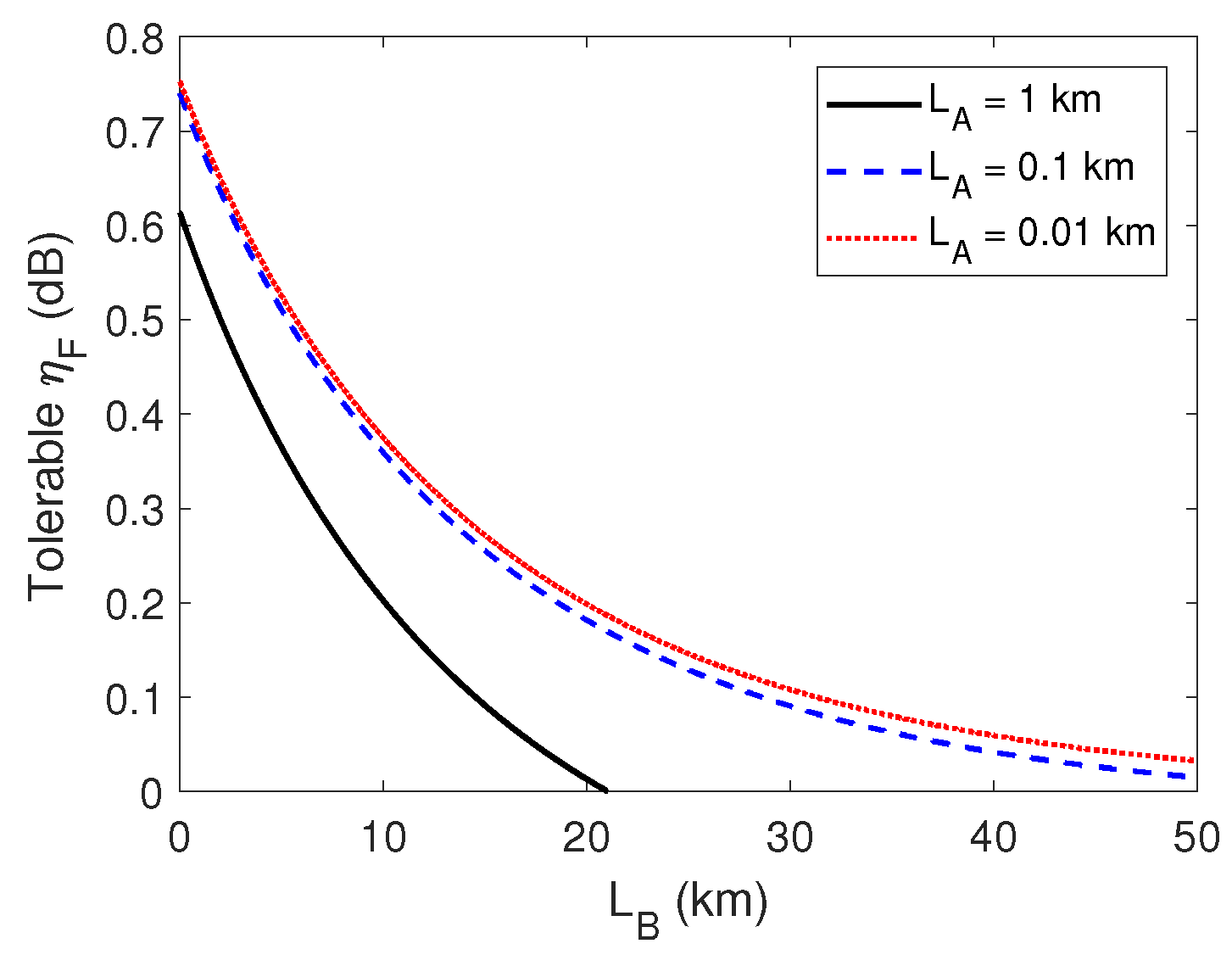
3. Performance Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Secret Key Rate Calculation of the One-Way Protocol
References
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- García-Patrón, R.; Cerf, N.J. Unconditional Optimality of Gaussian Attacks against Continuous-Variable Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Grosshans, F.; Acín, A. Optimality of Gaussian Attacks in Continuous-Variable Quantum Cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef]
- Furrer, F.; Franz, T.; Berta, M.; Leverrier, A.; Scholz, V.B.; Tomamichel, M.; Werner, R.F. Continuous Variable Quantum Key Distribution: Finite-Key Analysis of Composable Security against Coherent Attacks. Phys. Rev. Lett. 2012, 109, 100502. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Composable Security Proof for Continuous-Variable Quantum Key Distribution with Coherent States. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Soh, D.B.S.; Brif, C.; Coles, P.J.; Lütkenhaus, N.; Camacho, R.M.; Urayama, J.; Sarovar, M. Self-Referenced Continuous-Variable Quantum Key Distribution Protocol. Phys. Rev. X 2015, 5, 041010. [Google Scholar] [CrossRef]
- Qi, B.; Lougovski, P.; Pooser, R.; Grice, W.; Bobrek, M. Generating the Local Oscillator “Locally” in Continuous-Variable Quantum Key Distribution Based on Coherent Detection. Phys. Rev. X 2015, 5, 041009. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.; Wang, C.; Zeng, G. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695–3698. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, Y.C.; Xu, F.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052301. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Gui, M.; Liang, L.M. Gaussian-modulated coherent-state measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 042335. [Google Scholar] [CrossRef]
- Wu, Y.D.; Zhou, J.; Gong, X.B.; Guo, Y.; Zhang, Z.M.; He, G.Q. Continuous-variable measurement-device-independent multipartite quantum communication. Phys. Rev. A 2016, 93, 022325. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.; Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 2016, 6, 19201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, Z.; Djordjevic, I.B.; Neifeld, M.A. RF-subcarrier-assisted four-state continuous-variable QKD based on coherent detection. Opt. Lett. 2016, 41, 5507–5510. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photon. 2015, 9, 397. [Google Scholar] [CrossRef] [Green Version]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B 2009, 42, 114014. [Google Scholar] [CrossRef] [Green Version]
- Huang, P.; He, G.; Fang, J.; Zeng, G. Performance improvement of continuous-variable quantum key distribution via photon subtraction. Phys. Rev. A 2013, 87, 012317. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Wang, X.; Xu, B.; Peng, X.; Guo, H. Non-Gaussian postselection and virtual photon subtraction in continuous-variable quantum key distribution. Phys. Rev. A 2016, 93, 012310. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Liao, Q.; Wang, Y.; Huang, D.; Huang, P.; Zeng, G. Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction. Phys. Rev. A 2017, 95, 032304. [Google Scholar] [CrossRef]
- Liao, Q.; Guo, Y.; Huang, D.; Huang, P.; Zeng, G. Long-distance continuous-variable quantum key distribution using non-Gaussian state-discrimination detection. New J. Phys. 2018, 20, 023015. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Li, R.; Liao, Q.; Zhou, J.; Huang, D. Performance improvement of eight-state continuous-variable quantum key distribution with an optical amplifier. Phys. Lett. A 2018, 382, 372–381. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, X.D.; Huang, D.; Guo, Y. Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier. Entropy 2018, 20, 461. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, Y.; Wang, X.; Liao, Q.; Wu, X.; Guo, Y. Enhancing of Self-Referenced Continuous-Variable Quantum Key Distribution with Virtual Photon Subtraction. Entropy 2018, 20, 578. [Google Scholar] [CrossRef]
- Fang, J.; Huang, P.; Zeng, G. Multichannel parallel continuous-variable quantum key distribution with Gaussian modulation. Phys. Rev. A 2014, 89, 022315. [Google Scholar] [CrossRef]
- Huang, D.; Lin, D.; Wang, C.; Liu, W.; Fang, S.; Peng, J.; Huang, P.; Zeng, G. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511–17519. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Djordjevic, I.B. High-speed free-space optical continuous-variable quantum key distribution enabled by three-dimensional multiplexing. Opt. Express 2017, 25, 7919–7928. [Google Scholar] [CrossRef] [PubMed]
- Dynes, J.F.; Kindness, S.J.; Tam, S.W.B.; Plews, A.; Sharpe, A.W.; Lucamarini, M.; Fröhlich, B.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Quantum key distribution over multicore fiber. Opt. Express 2016, 24, 8081–8087. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bacco, D.; Ding, Y.; Dalgaard, K.; Rottwitt, K.; Oxenløwe, L.K. Space division multiplexing chip-to-chip quantum key distribution. Sci. Rep. 2017, 7, 12459. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, Y.; Bacco, D.; Dalgaard, K.; Cai, X.; Zhou, X.; Rottwitt, K.; Oxenløwe, L.K. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. NPJ Quantum Inf. 2017, 3, 25. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, T.; Taru, T.; Shimakawa, O.; Sasaki, T.; Sasaoka, E. Design and fabrication of ultra-low crosstalk and low-loss multi-core fiber. Opt. Express 2011, 19, 16576–16592. [Google Scholar] [CrossRef] [PubMed]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Analytical Expression of Average Power-Coupling Coefficients for Estimating Intercore Crosstalk in Multicore Fibers. IEEE Photonics J. 2012, 4, 1987–1995. [Google Scholar] [CrossRef] [Green Version]
- Fujisawa, T.; Amma, Y.; Sasaki, Y.; Matsuo, S.; Aikawa, K.; Saitoh, K.; Koshiba, M. Crosstalk Analysis of Heterogeneous Multicore Fibers Using Coupled-Mode Theory. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Qi, B.; Huang, L.L.; Qian, L.; Lo, H.K. Experimental study on the Gaussian-modulated coherent-state quantum key distribution over standard telecommunication fibers. Phys. Rev. A 2007, 76, 052323. [Google Scholar] [CrossRef]
- Kumar, R.; Qin, H.; Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 2015, 17, 043027. [Google Scholar] [CrossRef] [Green Version]
- Patel, K.A.; Dynes, J.F.; Lucamarini, M.; Choi, I.; Sharpe, A.W.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks. Appl. Phys. Lett. 2014, 104, 051123. [Google Scholar] [CrossRef] [Green Version]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103042. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Continuous Variable Quantum Cryptography using Two-Way Quantum Communication. Nat. Phys. 2006, 4, 726–730. [Google Scholar] [CrossRef]
- García-Patrón Sánchez, R.; Cerf, N. Quantum Information With Optical Continuous Variables: From Bell Tests to Key Distribution. Available online: http://difusion.ulb.ac.be/vufind/Record/ULB-DIPOT:oai:dipot.ulb.ac.be:2013/210655/TOC (accessed on 12 October 2007).



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhong, H.; Wang, Y.; Kang, Y.; Huang, D.; Guo, Y. Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber. Appl. Sci. 2018, 8, 1951. https://doi.org/10.3390/app8101951
Li F, Zhong H, Wang Y, Kang Y, Huang D, Guo Y. Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber. Applied Sciences. 2018; 8(10):1951. https://doi.org/10.3390/app8101951
Chicago/Turabian StyleLi, Fei, Hai Zhong, Yijun Wang, Ye Kang, Duan Huang, and Ying Guo. 2018. "Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber" Applied Sciences 8, no. 10: 1951. https://doi.org/10.3390/app8101951
APA StyleLi, F., Zhong, H., Wang, Y., Kang, Y., Huang, D., & Guo, Y. (2018). Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber. Applied Sciences, 8(10), 1951. https://doi.org/10.3390/app8101951





