The Evolutionary Game Theoretic Analysis for Emission Reduction and Promotion in Low-Carbon Supply Chains
Abstract
:1. Introduction
2. Literature Review
3. Evolutionary Game Model for Carbon Emission Reduction
3.1. Preliminaries and Notations
| Notation/Description |
|
3.2. Mathematical Models
3.3. Stability Analysis on System Equilibrium Point
- (1)
- is the evolution stability strategy (ESS) of dynamic replicator system, if (i) , and , , or (ii) and , or (iii) , and ;
- (2)
- is the ESS of dynamic replicator system, if (i) , and , , or (ii) , and or (iii) and , ;
- (3)
- is the ESS of dynamic replicator system, if (i) , and , , or (ii) and , , or (iii) , and ;
- (4)
- is the ESS of dynamic replicator system, if (i) and , , or (ii) , and , or (iii) , and , ;
- (5)
- and are the ESS of the dynamic replicator system, if and ;
- (6)
- and are the ESS of the dynamic replicator system, if and .
3.4. Managerial Insights
4. Computational Study and Analysis
4.1. Parameter Setting
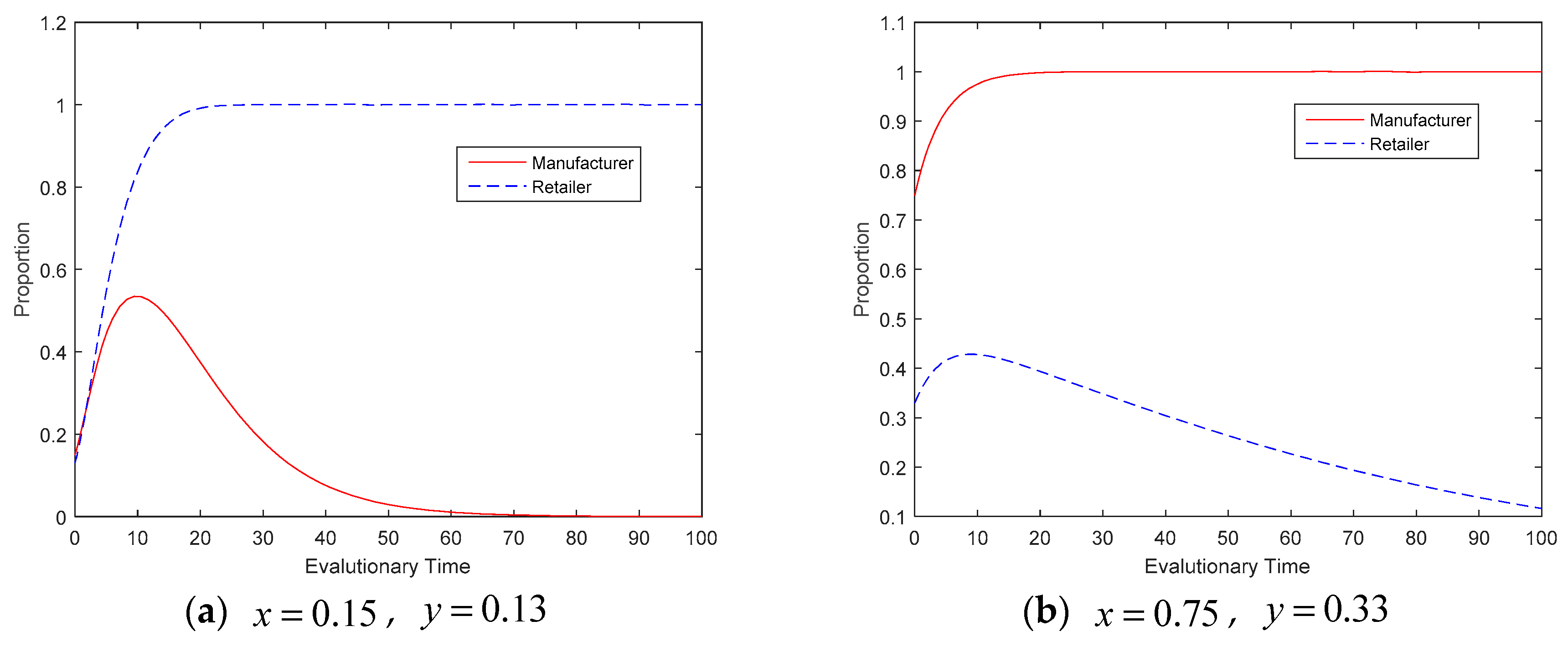
4.2. Evolution Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Equilibrium Point | ||
|---|---|---|
| 0 |
| Condition | Determinant | Equilibrium Point | |||||
|---|---|---|---|---|---|---|---|
| 1 | Non-existent | ||||||
| ? | ? | ||||||
| result | ESS | saddle point | saddle point | instability point | |||
| 2 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | ESS | saddle point | instability point | |||
| 3 | Non-existent | ||||||
| ? | ? | ||||||
| result | ESS | saddle point | instability point | saddle point | |||
| 4 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | ESS | instability point | saddle point | |||
| 5 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | saddle point | ESS | instability point | |||
| 6 | |||||||
| ? | |||||||
| result | instability point | ESS | ESS | instability point | saddle point | ||
| 7 | Non-existent | ||||||
| ? | ? | ||||||
| result | instability point | ESS | saddle point | saddle point | |||
| 8 | Non-existent | ||||||
| ? | ? | ? | ? | ||||
| result | saddle point | saddle point | saddle point | saddle point | |||
| 9 | Non-existent | ||||||
| ? | ? | ||||||
| result | ESS | instability point | saddle point | saddle point | |||
| 10 | Non-existent | ||||||
| ? | ? | ? | ? | ||||
| result | saddle point | saddle point | saddle point | saddle point | |||
| 11 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | saddle point | instability point | ESS | |||
| 12 | |||||||
| ? | |||||||
| result | ESS | instability point | instability point | ESS | saddle point | ||
| 13 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | instability point | ESS | saddle point | |||
| 14 | Non-existent | ||||||
| ? | ? | ||||||
| result | saddle point | instability point | saddle point | ESS | |||
| 15 | Non-existent | ||||||
| ? | ? | ||||||
| result | instability point | saddle point | ESS | saddle point | |||
| 16 | Non-existent | ||||||
| ? | ? | ||||||
| result | instability point | saddle point | saddle point | ESS | |||
References
- Laroche, M.; Bergeron, J.; Barbaro-Forleo, G. Targeting consumers who are willing to pay more for environmentally friendly products. J. Consum. Mark. 2001, 18, 503–520. [Google Scholar] [CrossRef]
- Brecard, D.; Hlaimi, B.; Lucas, S.; Perraudeau, Y.; Salladarre, F. Determinants of demand for green products: An application to eco-label demand for fish in Europe. Ecol. Econ. 2009, 69, 115–125. [Google Scholar] [CrossRef]
- Bai, Y.; Liu, Y. An exploration of residents’ low-carbon awareness and behavior in Tianjin, China. Energy Policy 2013, 61, 1261–1270. [Google Scholar] [CrossRef]
- Cachon, G.P. Supply Chain Coordination with Contracts. Handb. Oper. Res. Manag. Sci. 2003, 11, 227–339. [Google Scholar] [Green Version]
- Cachon, G.P.; Zipkin, P.H. Competitive and Cooperative Inventory Policies in a Two-Stage Supply Chain. Manag. Sci. 1999, 45, 936–953. [Google Scholar] [CrossRef] [Green Version]
- Chen, F. Information Sharing and Supply Chain Coordination. Handb. Oper. Res. Manag. Sci. 2003, 11, 341–421. [Google Scholar] [Green Version]
- Berger, P.D. Vertical Cooperative Advertising Ventures. J. Mark. Res. 1972, 9, 309–312. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Hoseinpour, P. On a cooperative advertising model for a supply chain with one manufacturer and one retailer. Eur. J. Oper. Res. 2012, 219, 458–466. [Google Scholar] [CrossRef]
- Aust, G.; Buscher, U. Vertical cooperative advertising and pricing decisions in a manufacturer-retailer supply chain: A game-theoretic approach. Eur. J. Oper. Res. 2012, 223, 473–482. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Li, J.C.; Zhong, Y.G. Cooperative advertising and ordering policies in a two-echelon supply chain with risk-averse agents. Omega-Int. J. Manag. Sci. 2018, 75, 97–117. [Google Scholar] [CrossRef]
- He, X.L.; Prasad, A.; Sethi, S.P. Cooperative Advertising and Pricing in a Dynamic Stochastic Supply Chain: Feedback Stackelberg Strategies. Prod. Oper. Manag. 2009, 18, 78–94. [Google Scholar] [CrossRef]
- Jørgensen, S.; Sigué, S.P.; Zaccour, G. Dynamic cooperative advertising in a channel. J. Retail. 2000, 76, 71–92. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, Q.; Liang, L.; Huang, Z. Supply chain coordination through cooperative advertising with reference price effect. Omega-Int. J. Manag. Sci. 2013, 41, 345–353. [Google Scholar] [CrossRef]
- Inkmann, J. Horizontal and Vertical R&D Cooperation. CoFE Working Paper. 2000. Available online: http://hdl.handle.net/10419/85237 on September 2018 (accessed on 17 October 2018).
- Arranz, N.; Arroyabe, J.C.F.D. The choice of partners in R&D cooperation: An empirical analysis of Spanish firms. Technovation 2008, 28, 88–100. [Google Scholar]
- Ge, Z.; Hu, Q.; Xia, Y. Firms’ R&D Cooperation Behavior in a Supply Chain. Prod. Oper. Manag. 2014, 23, 599–609. [Google Scholar]
- Belderbos, R.; Carree, M.; Lokshin, B. Cooperative R&D and firm performance. Res. Policy 2004, 33, 1477–1492. [Google Scholar] [Green Version]
- Lee, C.; Bae, Z.T.; Lee, J. Strategies for Linking Vertical Cooperative R&D to Commercialization in Korea. J. Prod. Innov. Manag. 1994, 11, 325–335. [Google Scholar]
- Ishii, A. Cooperative R&D between vertically related firms with spillovers. Int. J. Ind. Organ. 2004, 22, 1213–1235. [Google Scholar]
- Zeng, D.M.; Xu, L.Y.; Bi, X.A. Effects of asymmetric knowledge spillovers on the stability of horizontal and vertical R&D cooperation. Comput. Math. Organ. Theory 2017, 23, 32–60. [Google Scholar]
- Cachon, G.P. Retail Store Density and the Cost of Greenhouse Gas Emissions. Manag. Sci. 2014, 60, 1907–1925. [Google Scholar] [CrossRef] [Green Version]
- Sundarakani, B.; Souza, R.D.; Goh, M.; Wagner, S.M.; Manikandan, S. Modeling carbon footprints across the supply chain. Int. J. Prod. Econ. 2010, 128, 43–50. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.Z.; Daskin, M. Carbon Footprint and the Management of Supply Chains: Insights From Simple Models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Chen, X.; Hao, G. Sustainable pricing and production policies for two competing firms with carbon emissions tax. Int. J. Prod. Res. 2015, 53, 6408–6420. [Google Scholar] [CrossRef]
- Du, S.; Hu, L.; Song, M. Production optimization considering environmental performance and preference in the cap-and-trade system. J. Clean. Prod. 2016, 112, 1600–1607. [Google Scholar] [CrossRef]
- Xia, L.J.; He, L.F. Game Theoretic Analysis of Carbon Emission Reduction and Sales Promotion in Dyadic Supply Chain in Presence of Consumers’ Low-Carbon Awareness. Discret. Dyn. Nat. Soc. 2014, 2014, 837376. [Google Scholar] [CrossRef]
- Du, S.F.; Zhu, J.; Jiao, H.F.; Ye, W.Y. Game-theoretical analysis for supply chain with consumer preference to low carbon. Int. J. Prod. Res. 2015, 53, 3753–3768. [Google Scholar] [CrossRef]
- Wang, Q.P.; Zhao, D.Z.; He, L.F. Contracting emission reduction for supply chains considering market low-carbon preference. J. Clean. Prod. 2016, 120, 72–84. [Google Scholar] [CrossRef]
- Liu, Z.G.; Anderson, T.D.; Cruz, J.M. Consumer environmental awareness and competition in two-stage supply chains. Eur. J. Oper. Res. 2012, 218, 602–613. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Bao, M.J.; Chen, X.H.; Xu, X.H. Co-op advertising and emission reduction cost sharing contracts and coordination in low-carbon supply chain based on fairness concerns. J. Clean. Prod. 2016, 133, 402–413. [Google Scholar] [CrossRef]
- Ji, J.N.; Zhang, Z.Y.; Yang, L. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Smith, J.M. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory. Curr. Biol. Cb 1995, 9, 503–505. [Google Scholar]
- Friedman, D. On economic applications of evolutionary game theory. J. Evol. Econ. 1998, 8, 15–43. [Google Scholar] [CrossRef] [Green Version]
- Xiao, T.J.; Yu, G. Supply chain disruption management and evolutionarily stable strategies of retailers in the quantity-setting duopoly situation with homogeneous goods. Eur. J. Oper. Res. 2006, 173, 648–668. [Google Scholar] [CrossRef]
- Yi, Y.Y.; Yang, H.S. Wholesale pricing and evolutionary stable strategies of retailers under network externality. Eur. J. Oper. Res. 2017, 259, 37–47. [Google Scholar] [CrossRef]
- Yu, H.S.; Zeng, A.Z.; Zhao, L.D. Analyzing the evolutionary stability of the vendor-managed inventory supply chains. Comput. Ind. Eng. 2009, 56, 274–282. [Google Scholar] [CrossRef]
- Barari, S.; Agarwal, G.; Zhang, W.J.; Mahanty, B.; Tiwari, M.K. A decision framework for the analysis of green supply chain contracts: An evolutionary game approach. Expert Syst. Appl. 2012, 39, 2965–2976. [Google Scholar] [CrossRef]
- Ji, P.; Ma, X.; Li, G. Developing green purchasing relationships for the manufacturing industry: An evolutionary game theory perspective. Int. J. Prod. Econ. 2015, 166, 155–162. [Google Scholar] [CrossRef]
- Esmaeili, M.; Allameh, G.; Tajvidi, T. Using game theory for analysing pricing models in closed-loop supply chain from short- and long-term perspectives. Int. J. Prod. Res. 2016, 54, 2152–2169. [Google Scholar] [CrossRef]
- Bhatia, N.P.; Szegö, G.P. Stability Theory of Dynamical Systems; Springer: Berlin, Germany, 2002. [Google Scholar]
- Liu, B.; Tang, W. Modern Control Theory, 3rd ed.; China Machine Press: Beijing, China, 2006. [Google Scholar]

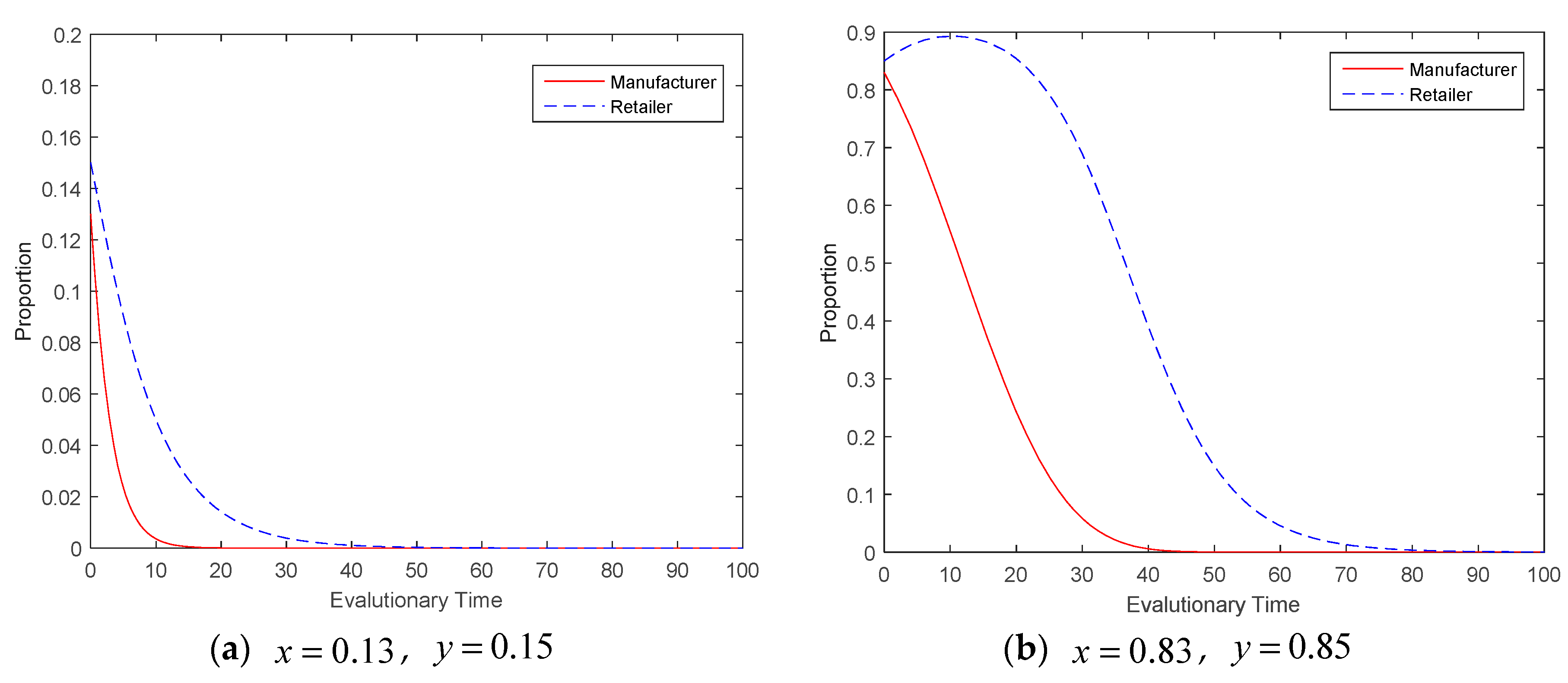
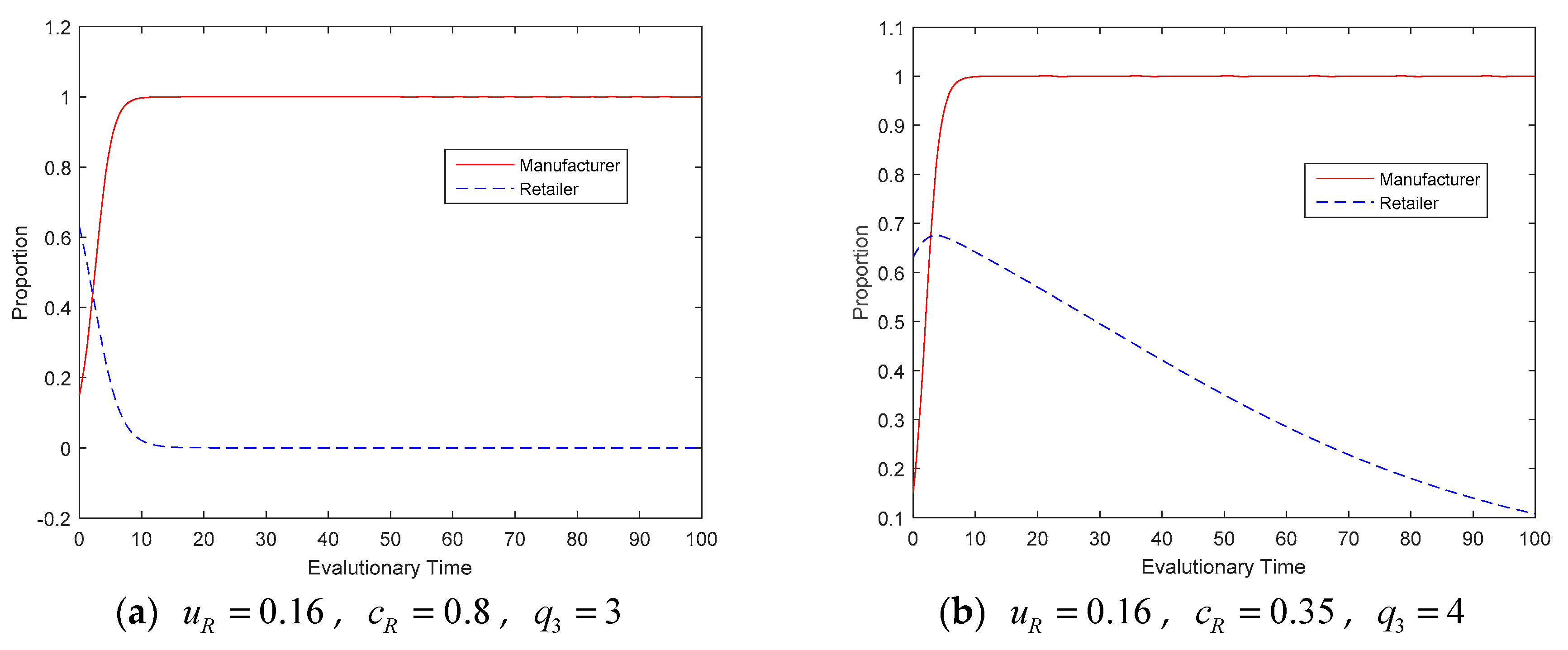
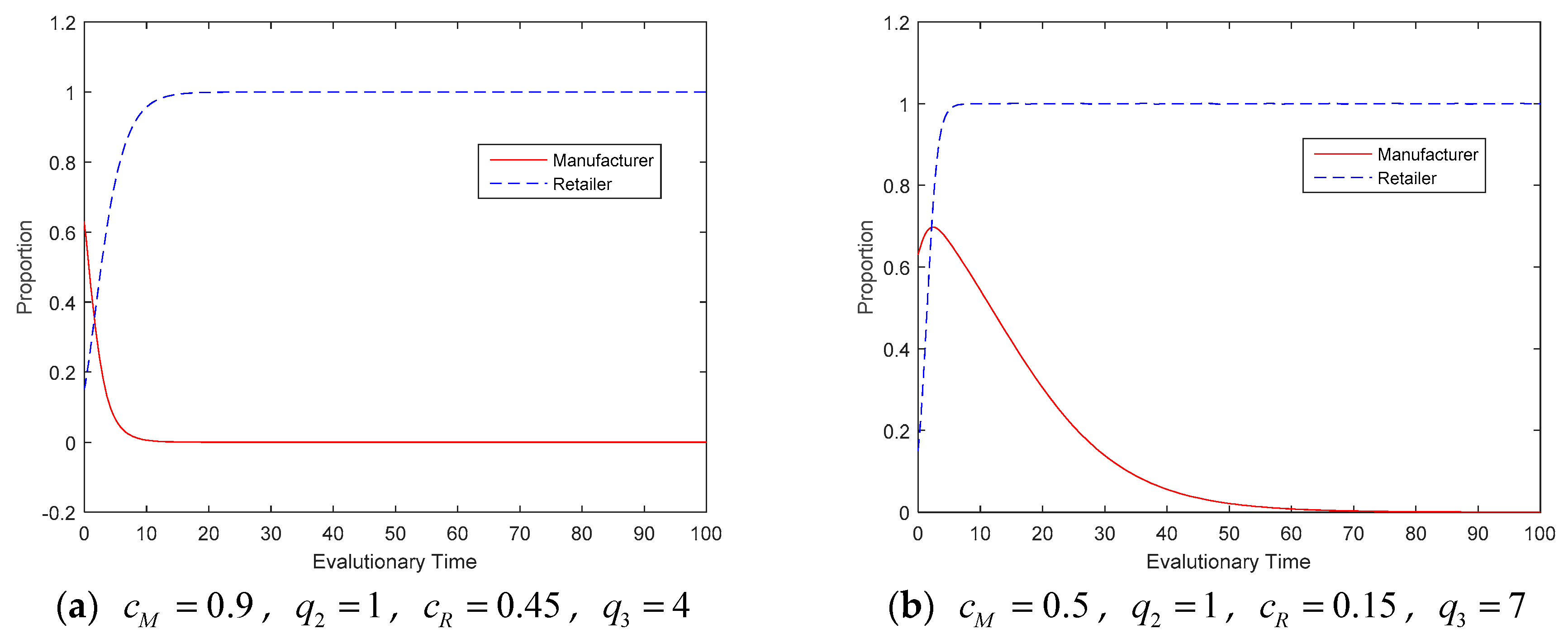

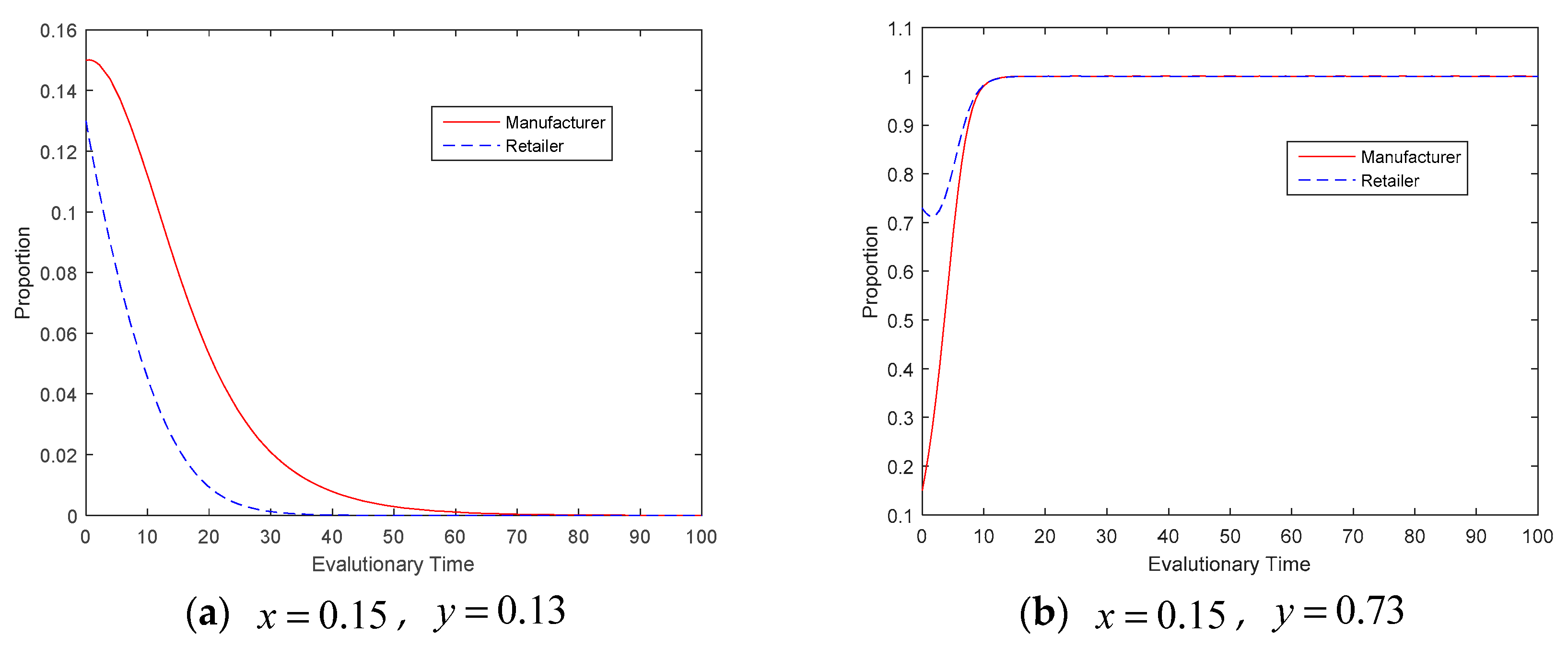
| Manufacturers | Retailers | |
|---|---|---|
| High-Level Promotion on Low Carbon (H) | Low-Level Promotion on Low Carbon (L) | |
| High-level emission reduction investment (H) | ||
| Low-level emission reduction investment (L) | ||
| Production | uM | uR | cM | cR | q1 | q2 | q3 |
|---|---|---|---|---|---|---|---|
| A1 | 0.1 | 0.08 | 0.5 | 0.45 | 8 | 1 | 4 |
| A2 | 0.2 | 0.16 | 0.2 | 0.8 | 7 | 5 | 3 |
| A3 | 0.2 | 0.16 | 0.2 | 0.35 | 8 | 6 | 4 |
| A4 | 0.11 | 0.21 | 0.9 | 0.45 | 8 | 1 | 4 |
| A5 | 0.4 | 0.21 | 0.5 | 0.15 | 8 | 2 | 7 |
| A6 | 0.2 | 0.21 | 0.5 | 0.65 | 8 | 4 | 2 |
| A7 | 0.2 | 0.21 | 0.5 | 0.65 | 8 | 2 | 2 |
| A8 | 0.2 | 0.21 | 0.5 | 0.65 | 8 | 5 | 6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, B.; He, L.; Gu, B.; Zhang, Y. The Evolutionary Game Theoretic Analysis for Emission Reduction and Promotion in Low-Carbon Supply Chains. Appl. Sci. 2018, 8, 1965. https://doi.org/10.3390/app8101965
Yuan B, He L, Gu B, Zhang Y. The Evolutionary Game Theoretic Analysis for Emission Reduction and Promotion in Low-Carbon Supply Chains. Applied Sciences. 2018; 8(10):1965. https://doi.org/10.3390/app8101965
Chicago/Turabian StyleYuan, Baiyun, Longfei He, Bingmei Gu, and Yi Zhang. 2018. "The Evolutionary Game Theoretic Analysis for Emission Reduction and Promotion in Low-Carbon Supply Chains" Applied Sciences 8, no. 10: 1965. https://doi.org/10.3390/app8101965
APA StyleYuan, B., He, L., Gu, B., & Zhang, Y. (2018). The Evolutionary Game Theoretic Analysis for Emission Reduction and Promotion in Low-Carbon Supply Chains. Applied Sciences, 8(10), 1965. https://doi.org/10.3390/app8101965




