A Unified Approach to Design Robust Controllers for Nonlinear Uncertain Engineering Systems
Abstract
:Featured Application
Abstract
1. Introduction
2. Problem Formulation and Preliminaries
- (a)
- a possible appropriate changing of variable and/or;
- (b)
- the use of a possible appropriate compensation signal dependent on and/or;
- (c)
- possible appropriate mathematical steps by using the derivative of Lie, are of type (1). In the following five significant classes of the above systems are reported.
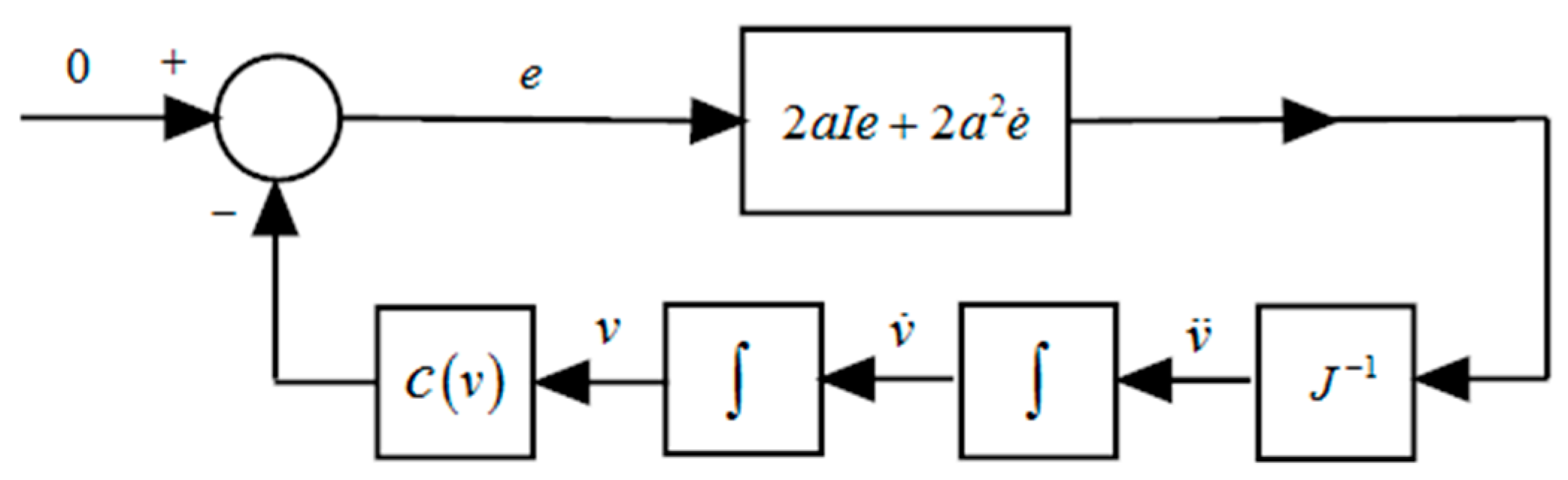
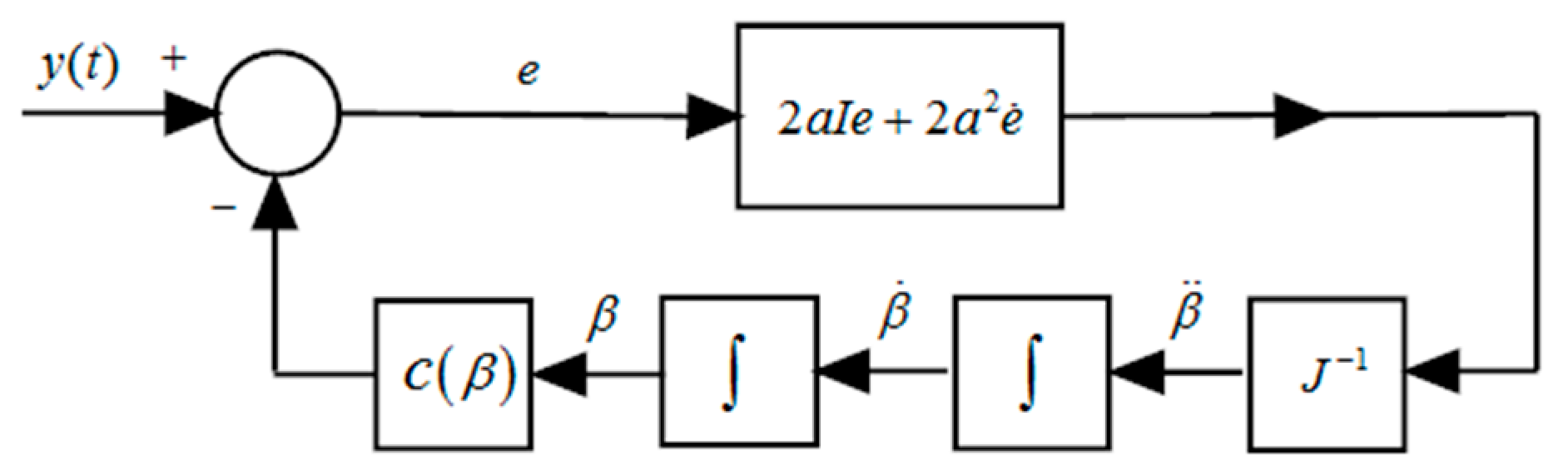
3. Main Results
- (a)
- if
- -
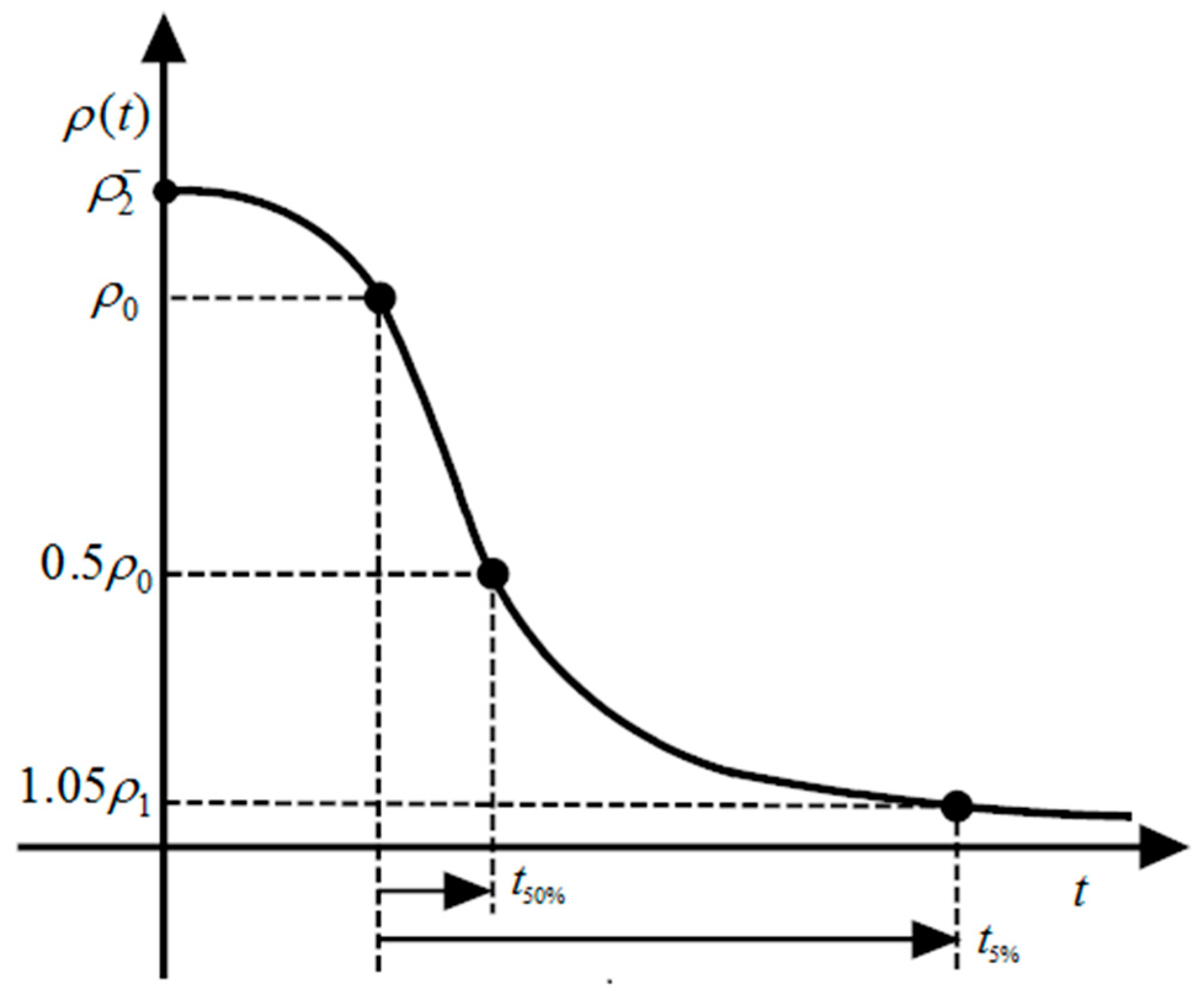
- behavior of a Butterworth filter with angular frequency ;
- -
- time constant ;
- -
- overshoot equal to 4.32%;
- -
- damping ratio ;
- -
- forced responses:
- (b)
- if :
- -
- cutoff angular frequency ;
- -
- max time constant ;
- -
- overshoot 4.32%;
- -
- damping ratio ;
- -
- forced responses:
- (i)
- in the hypothesis thatis a p.d. matrix (in the case of (4) and (9));
- (ii)
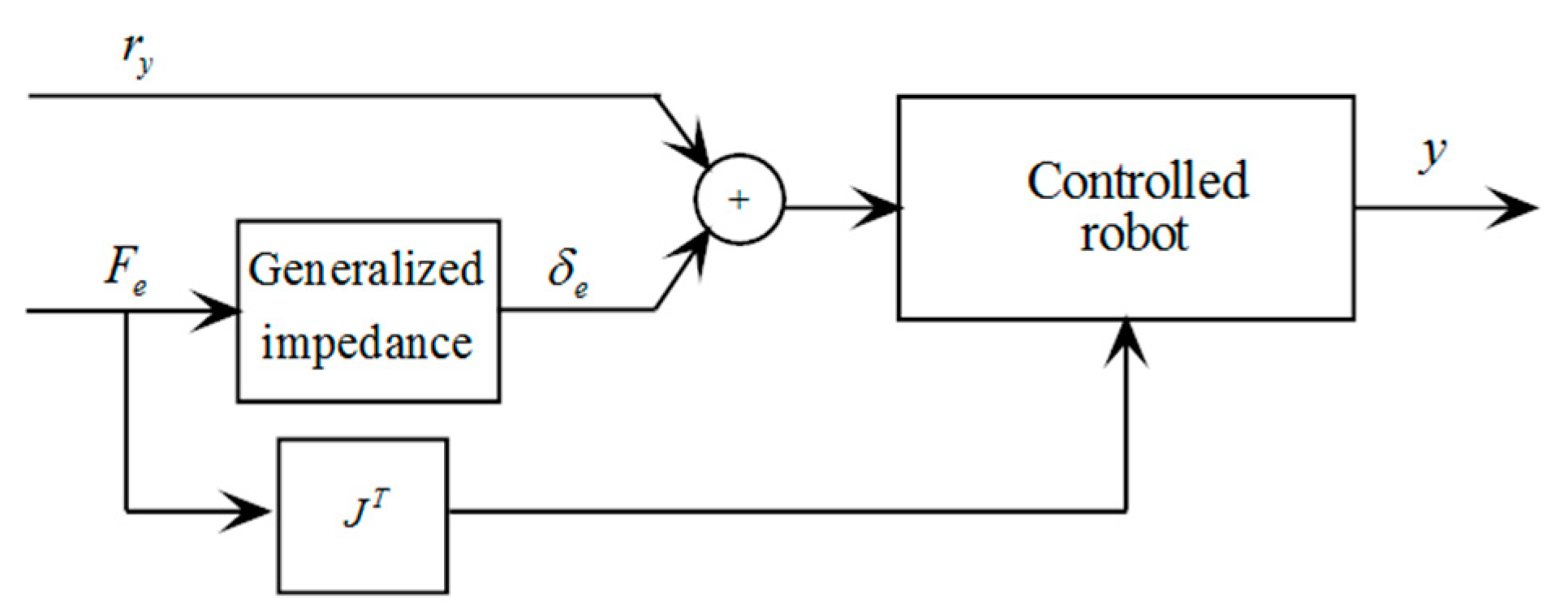
- whereis the Jacobian matrix of a suitable coordinate transformation (e.g., the case of robots in their workspace or equipped with cameras used as sensors, in the cases of ships, drones, or satellites);
- (iii)
- ifis independent of(e.g., in the case of kinematic inversion) or, by evaluatingin correspondence of the nominal valueof, in the hypothesis that the variations ofare sufficiently bounded;
- (iv)
- other more suitable matrices(see Application 3).
- 1.
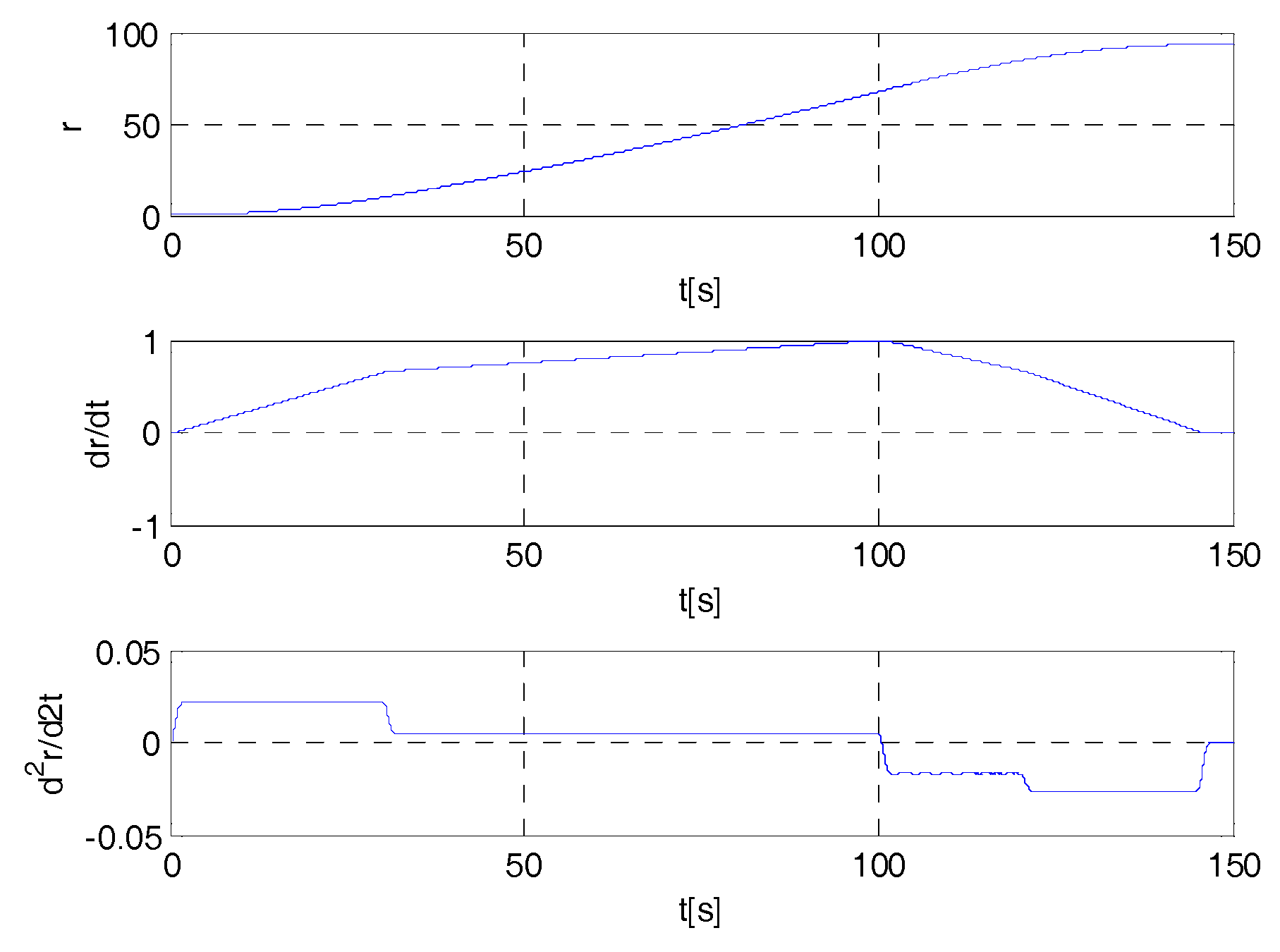
- smooth the trajectories with appropriate filters and suitable initial conditions;
- 2.
- better identify the process parameters and the disturbances, and use a compensation signalto reduce the norm of;
- 3.
- use a connection trajectory if the initial error is excessive [35];
- 4.
- slow down, i.e., replace the reference signalby.
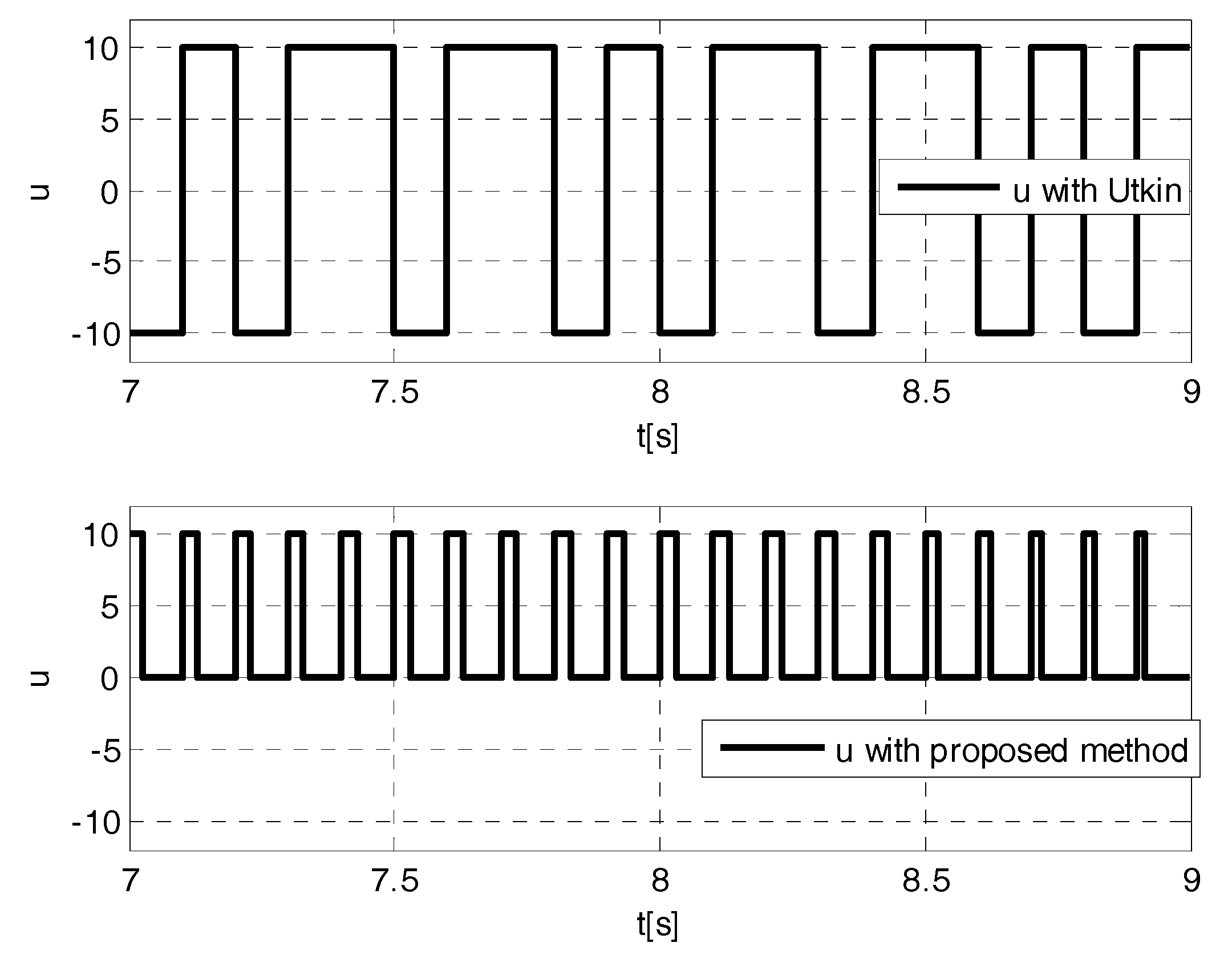
- the control signals are without the chattering phenomenon, since the proposed control law does not present discontinuities and does not have high gains,
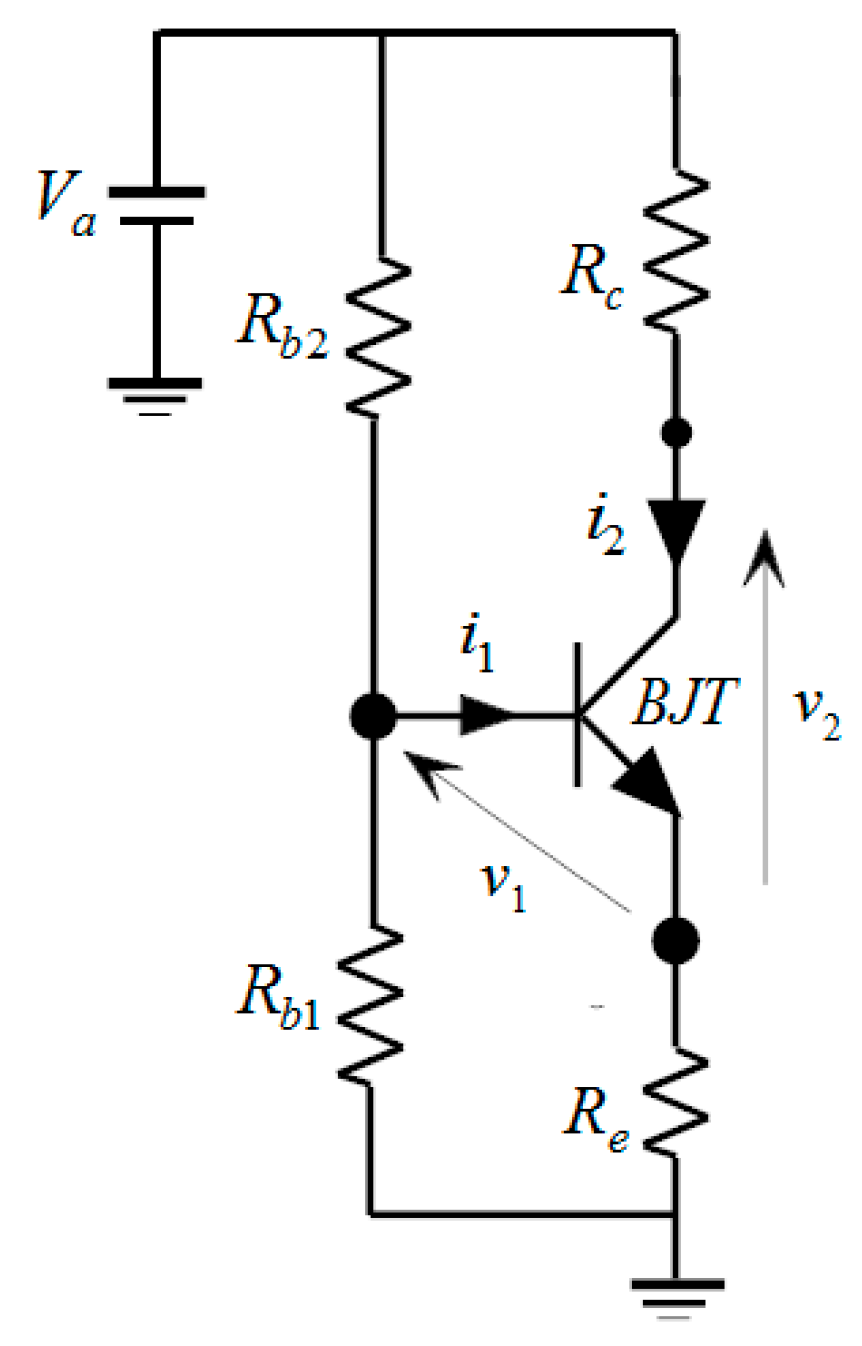
- the proposed control laws can be also realized by using simple analogical circuits,
- the stated theoretical results are useful to obtain other analytical and synthetic results, significant both from a theoretical and practical point of view, and to analyze complex systems with parametric and structural uncertainties.
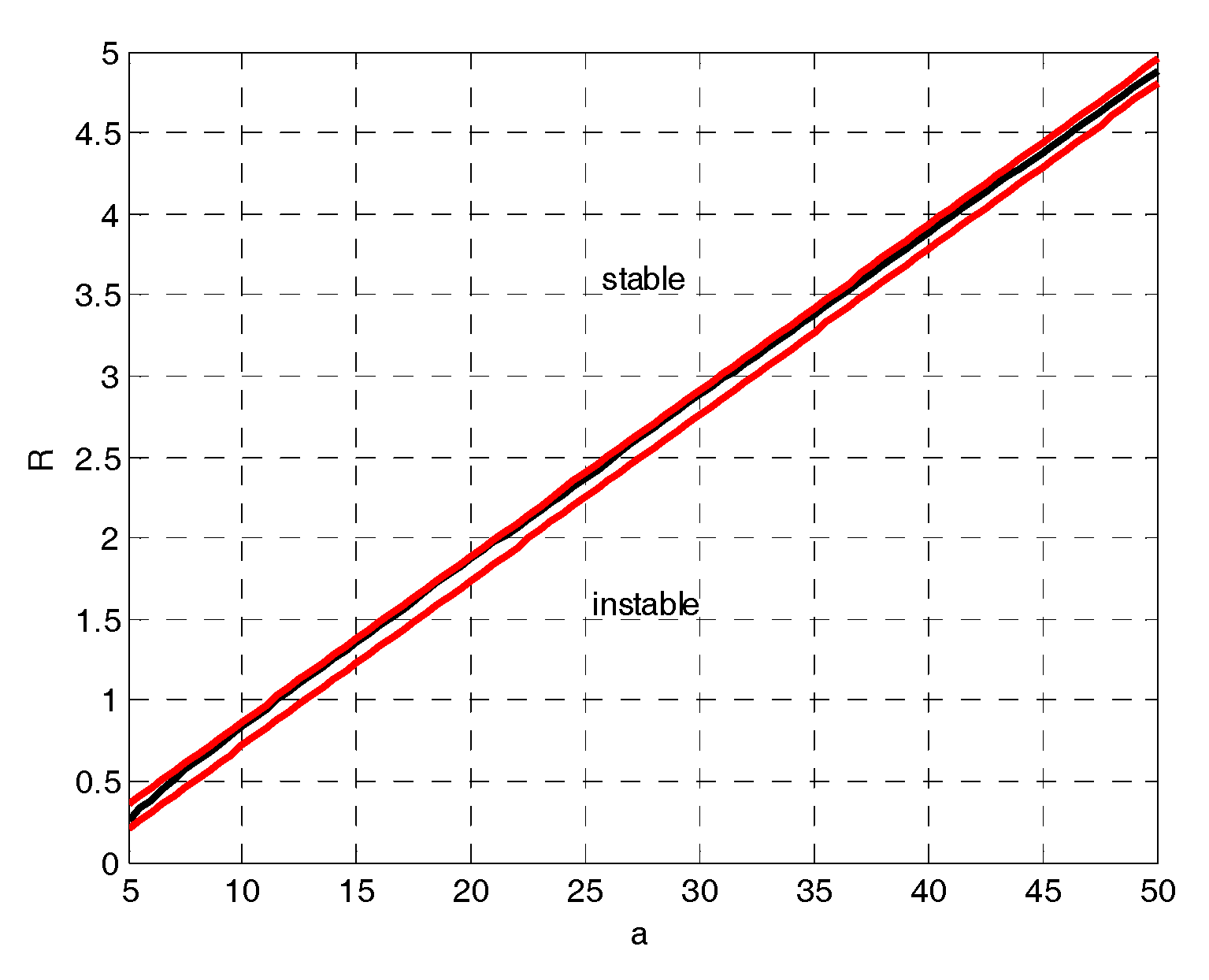
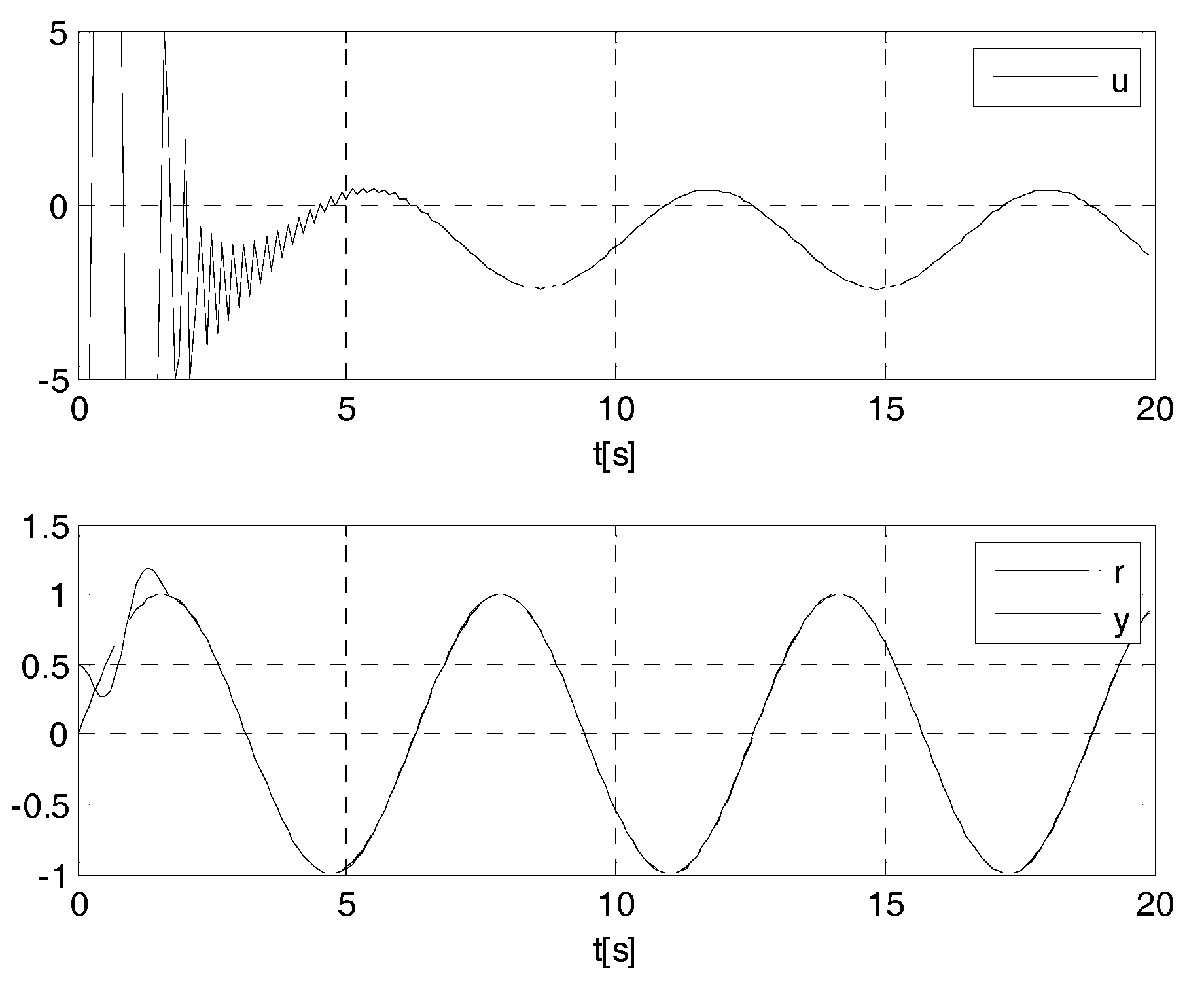
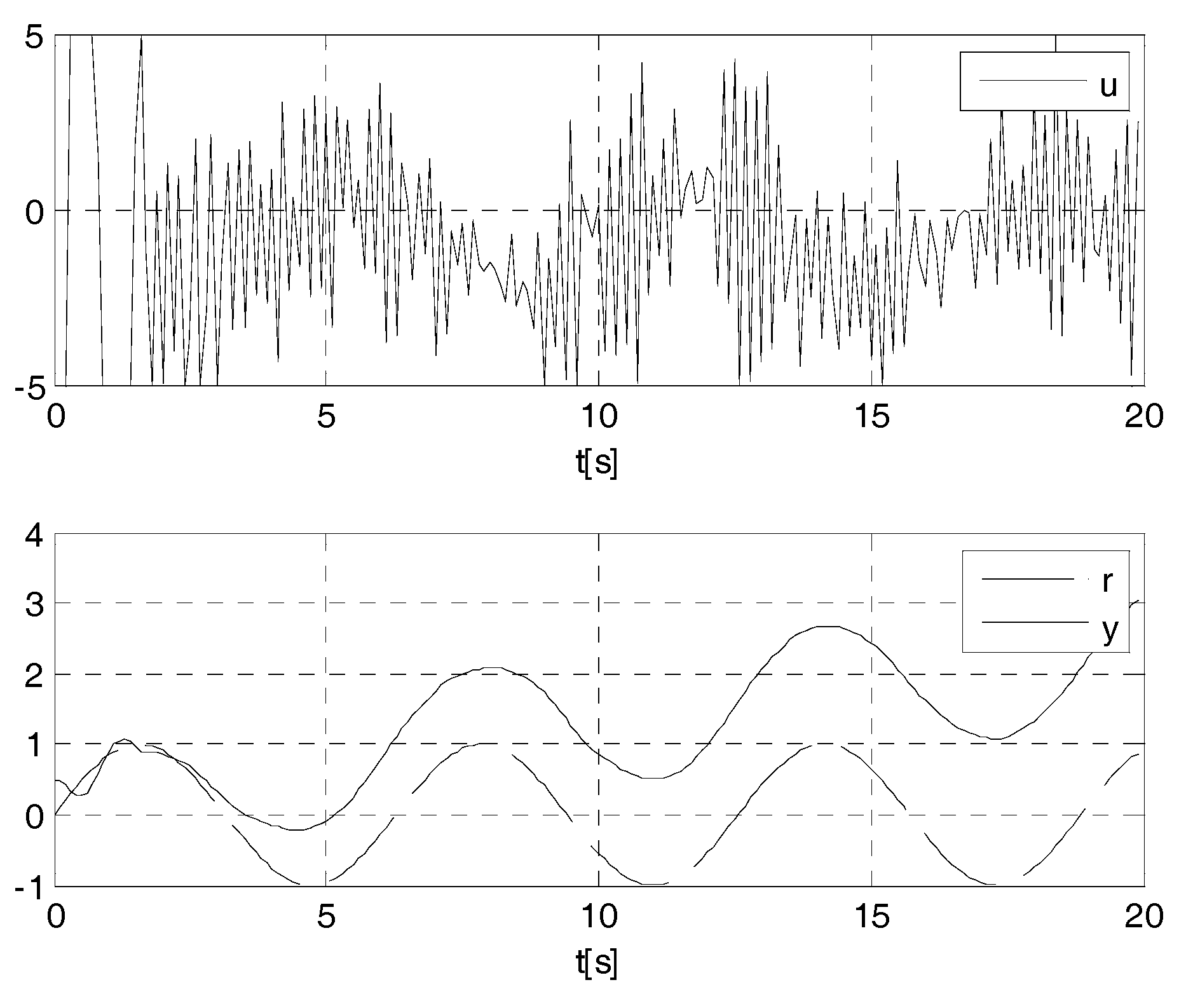
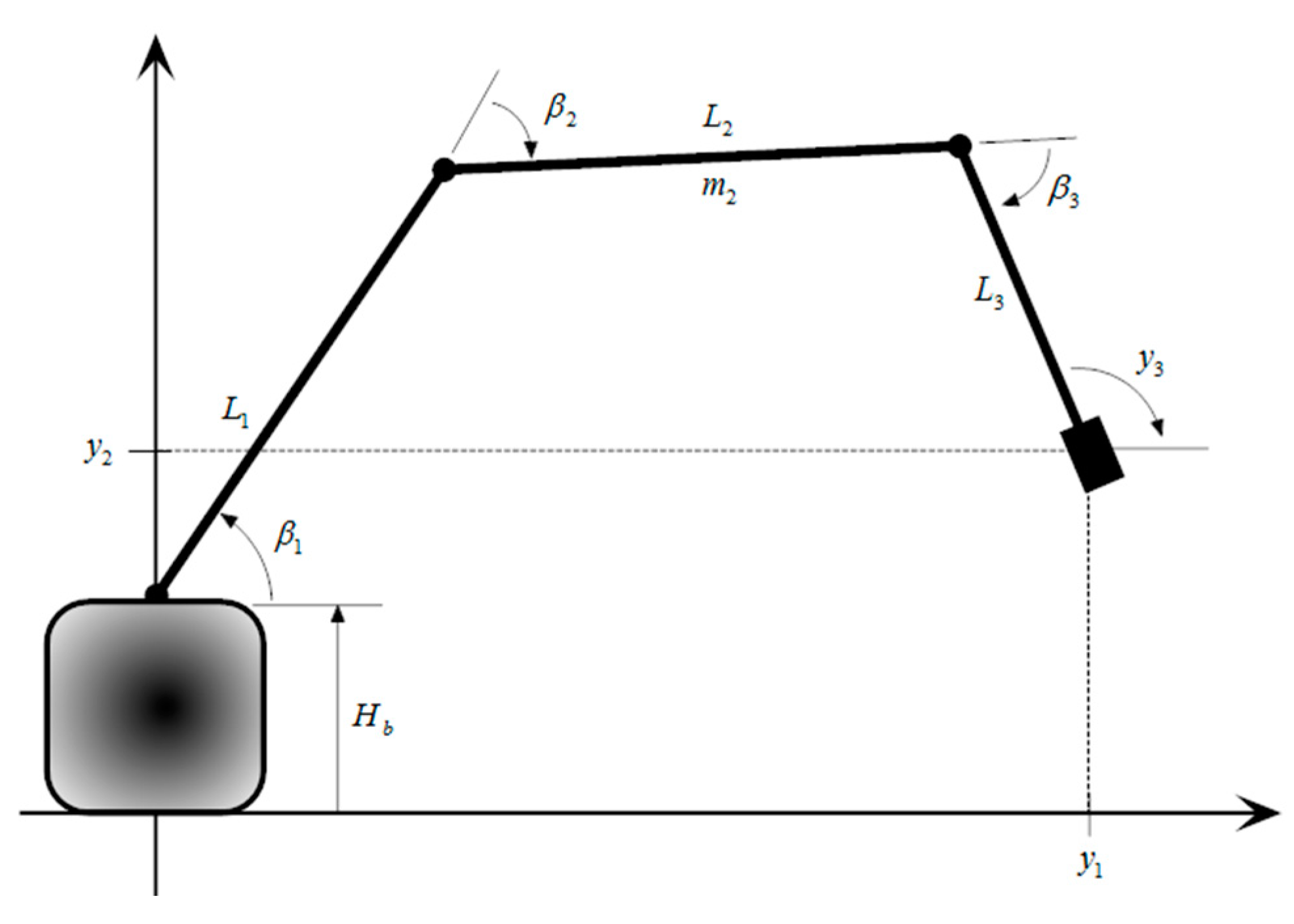
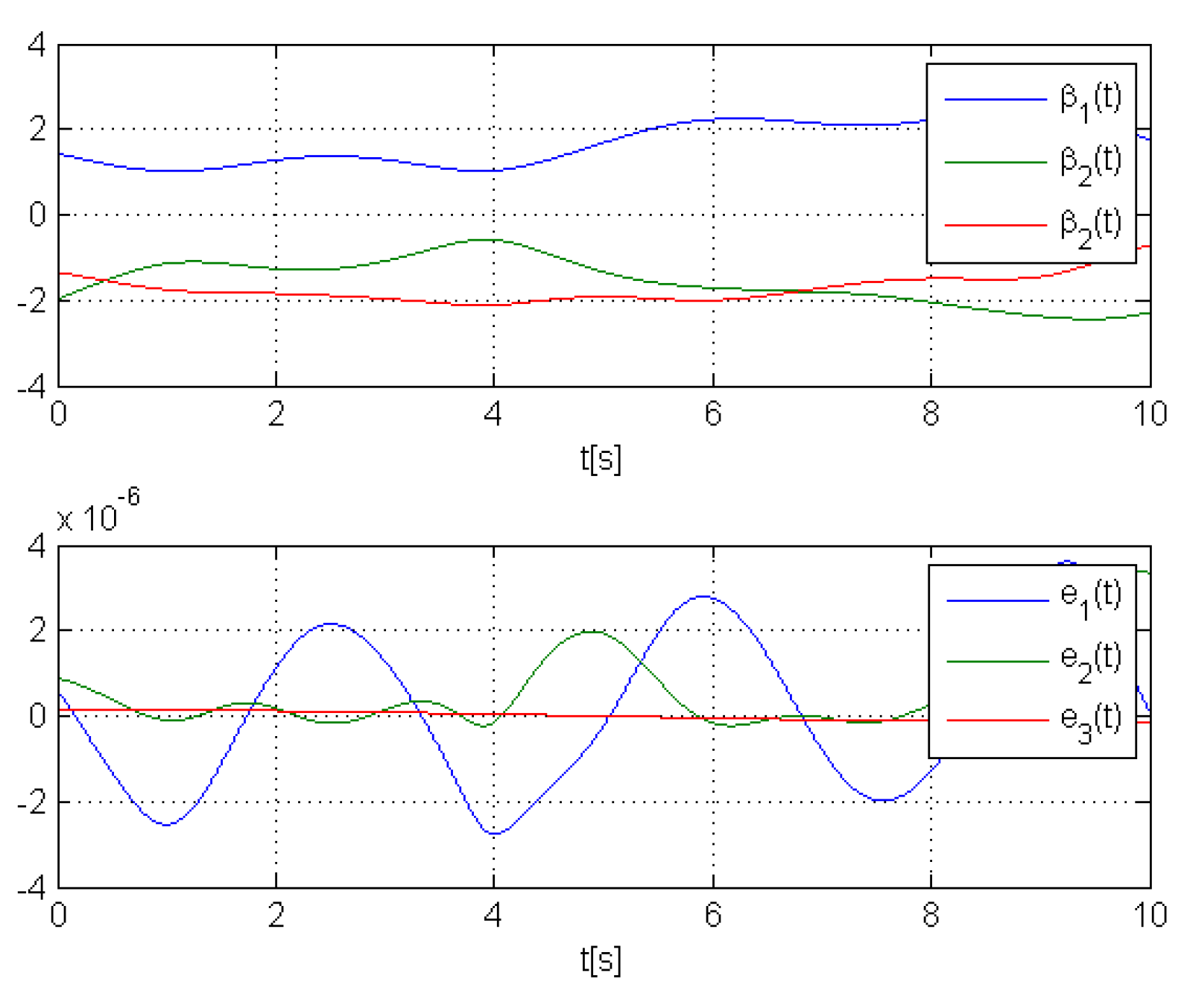
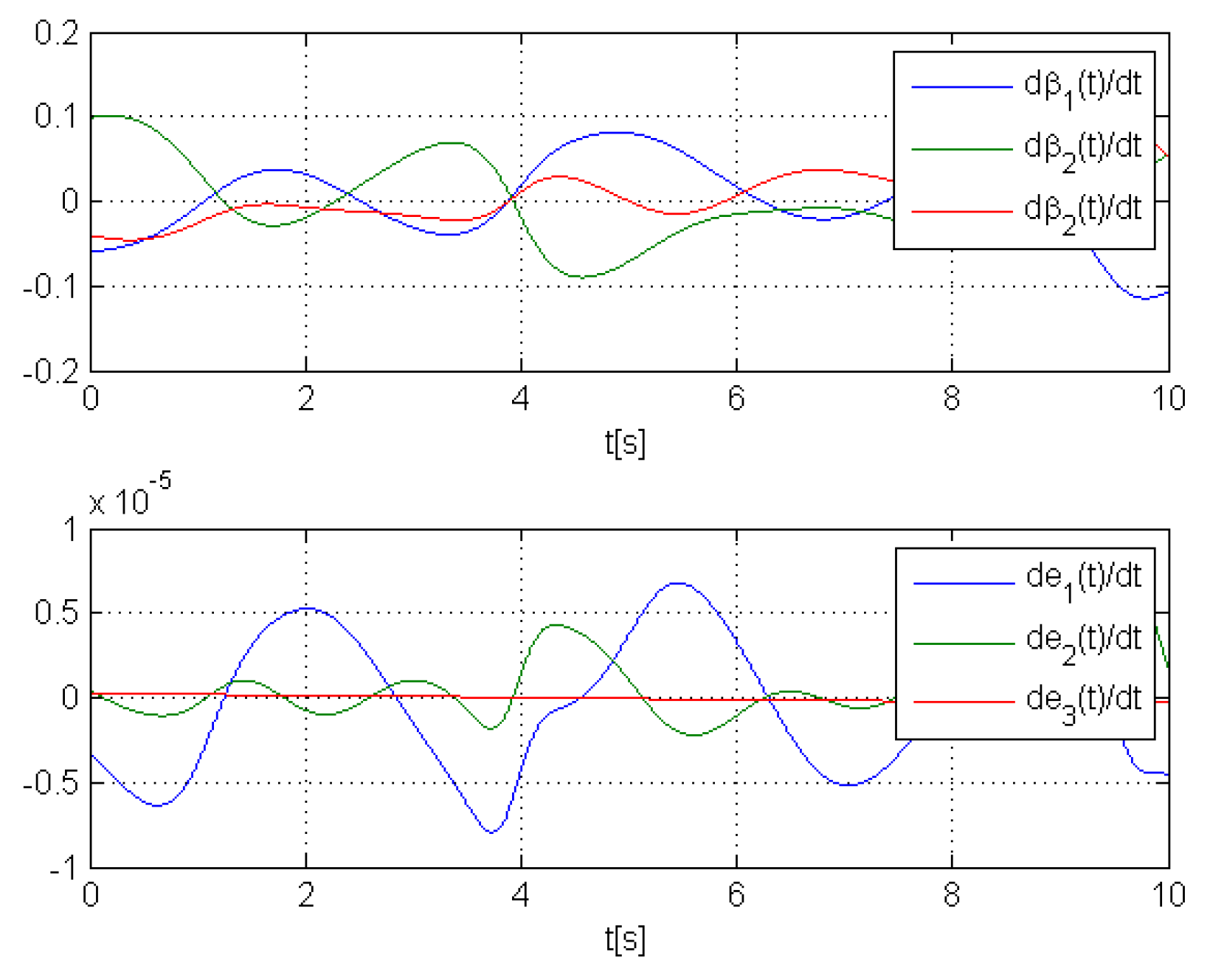
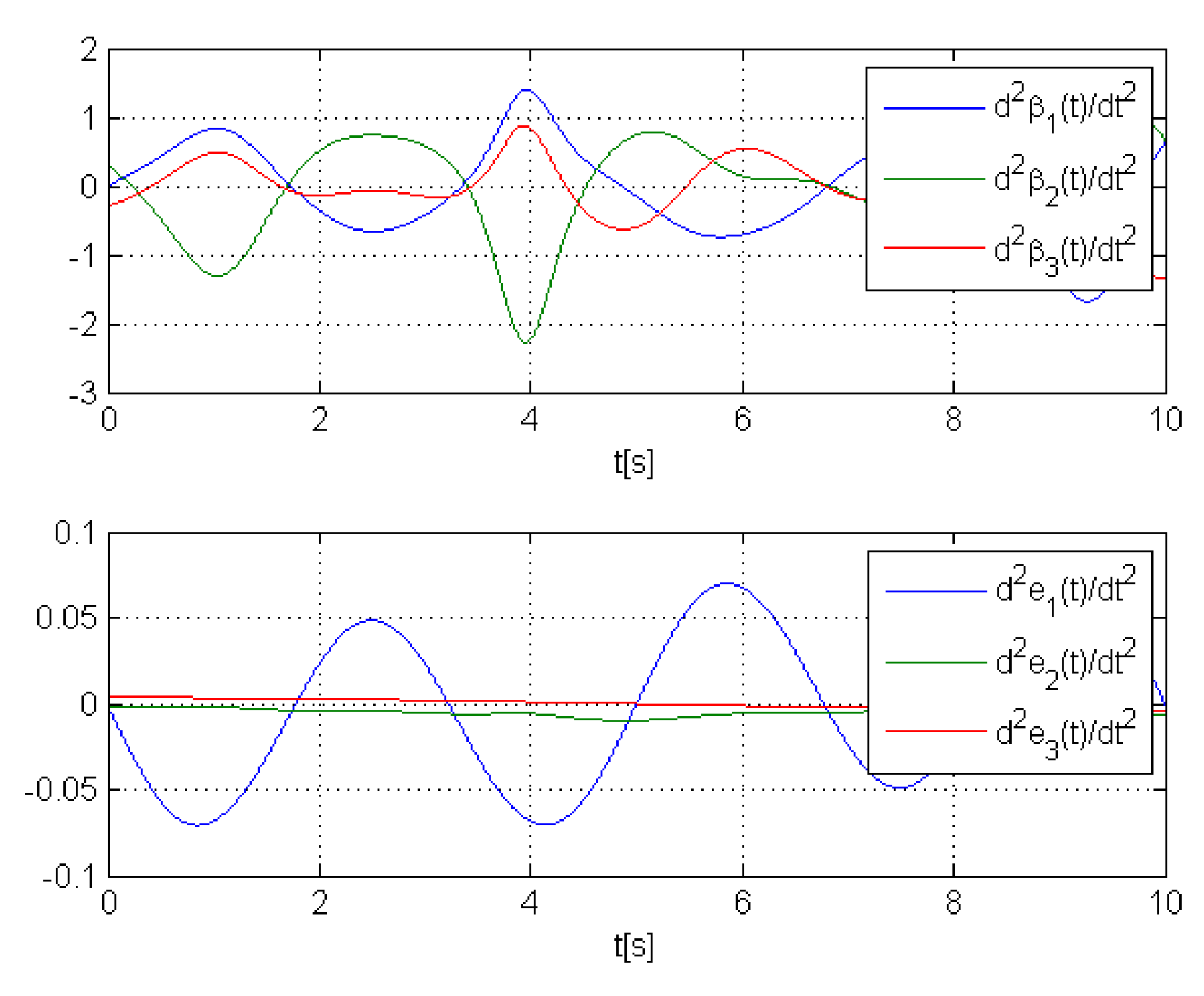
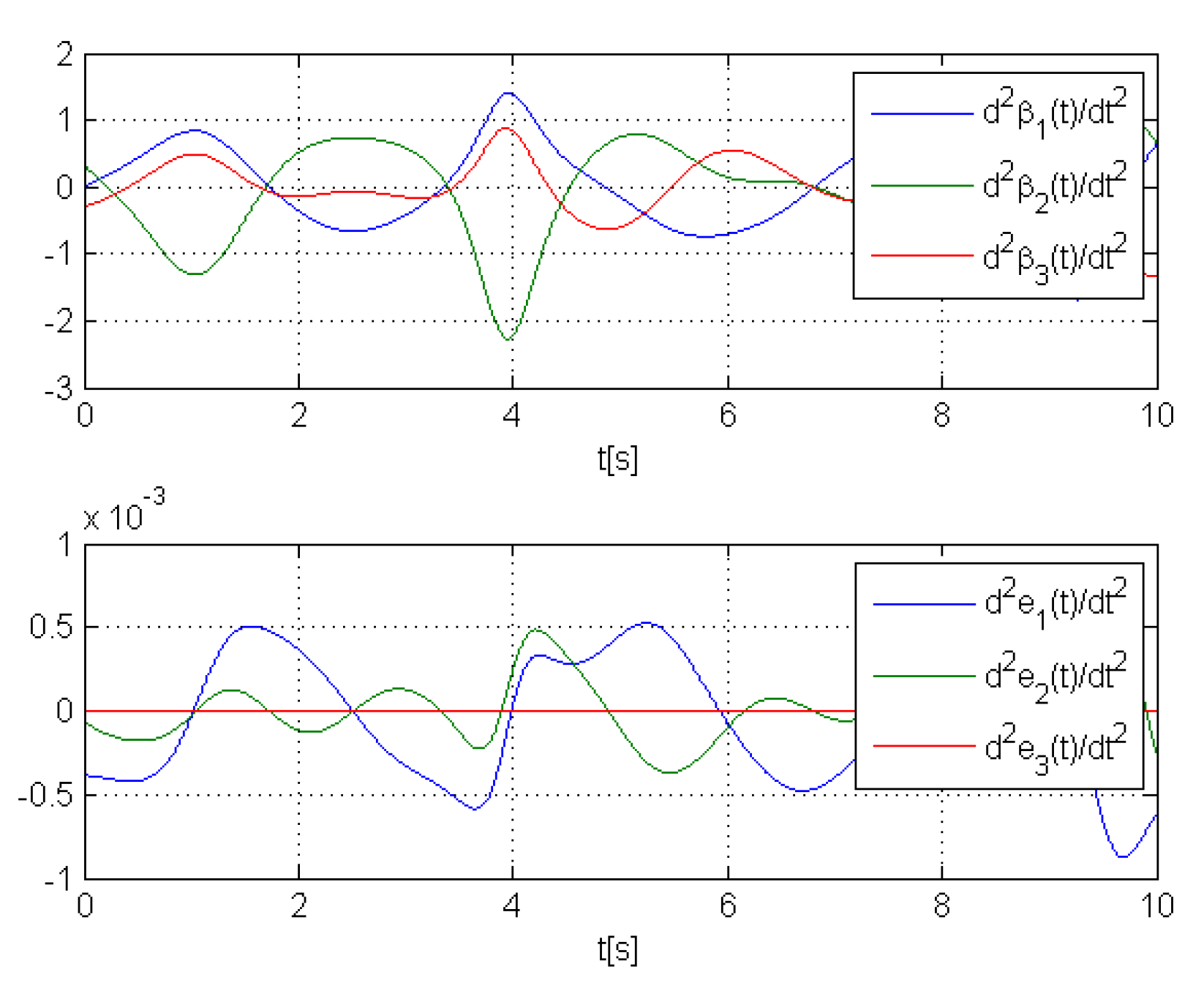
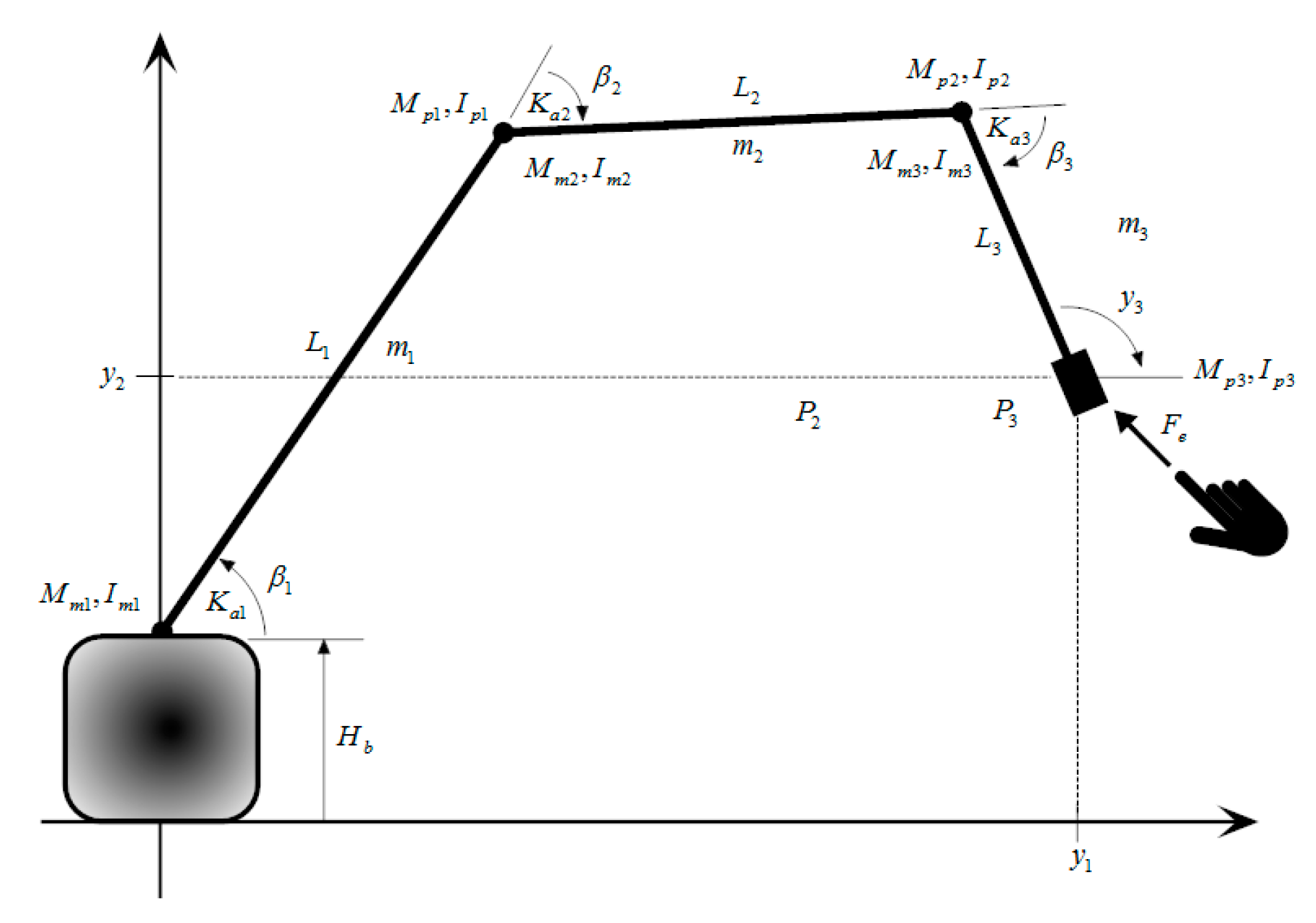
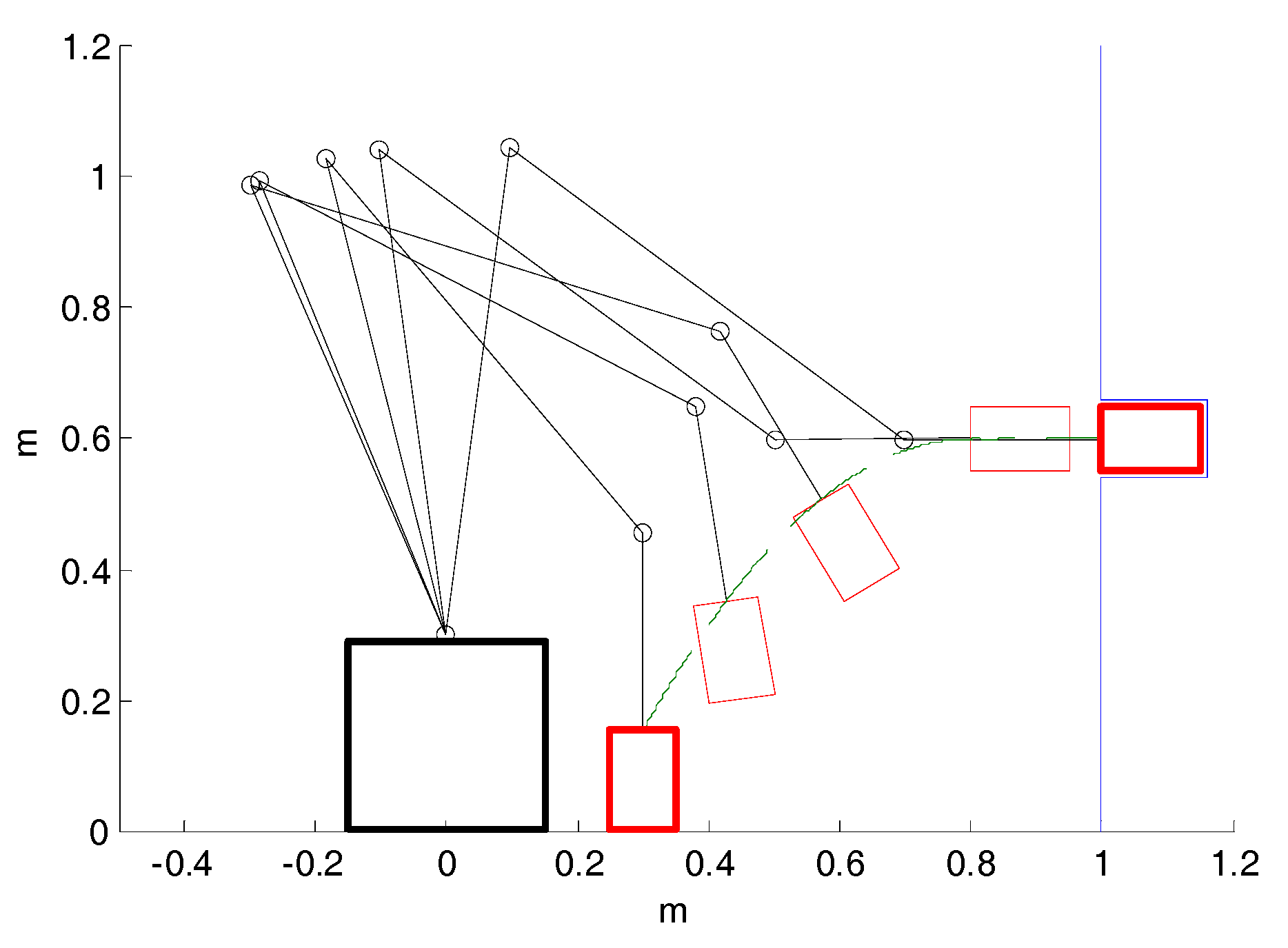
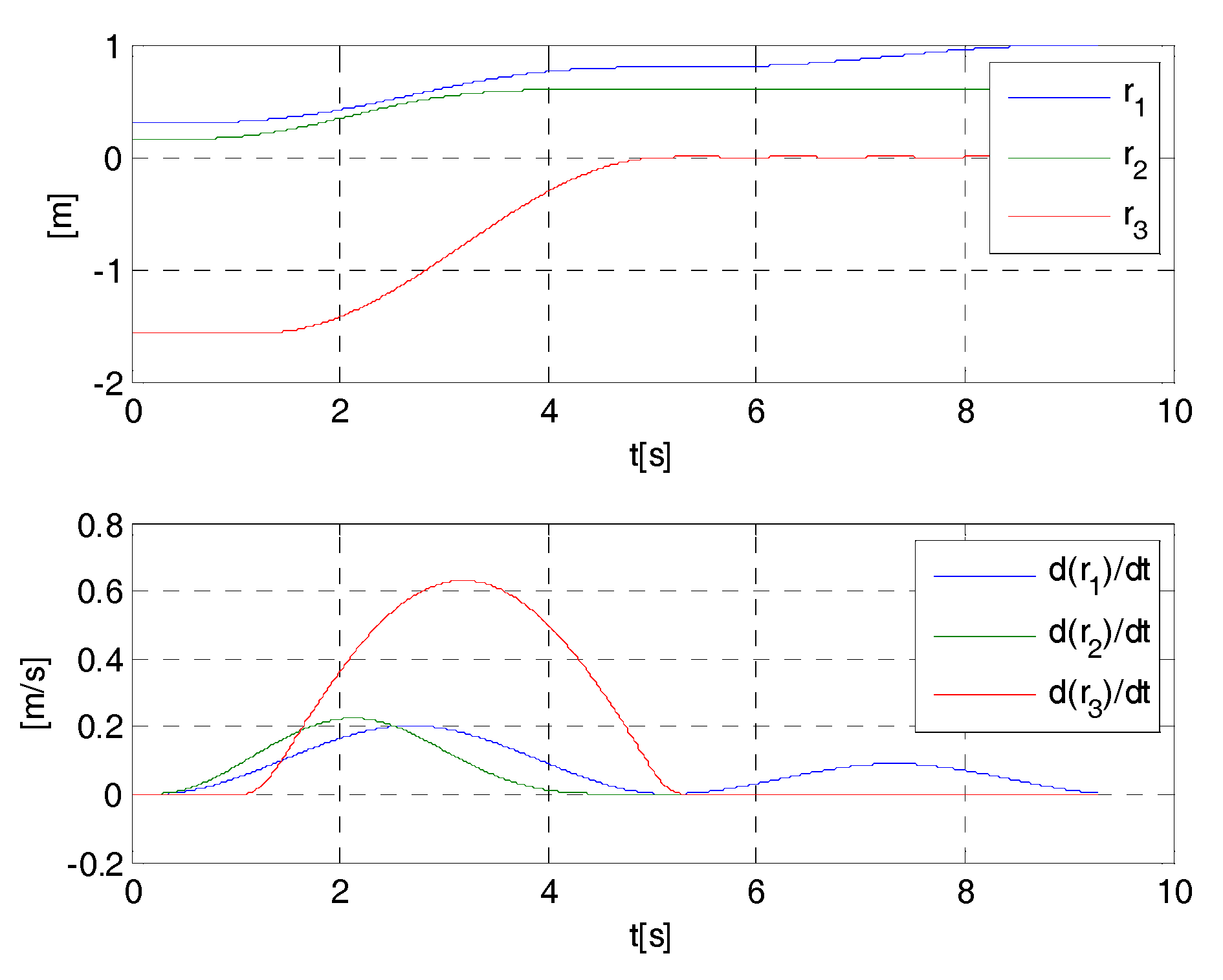
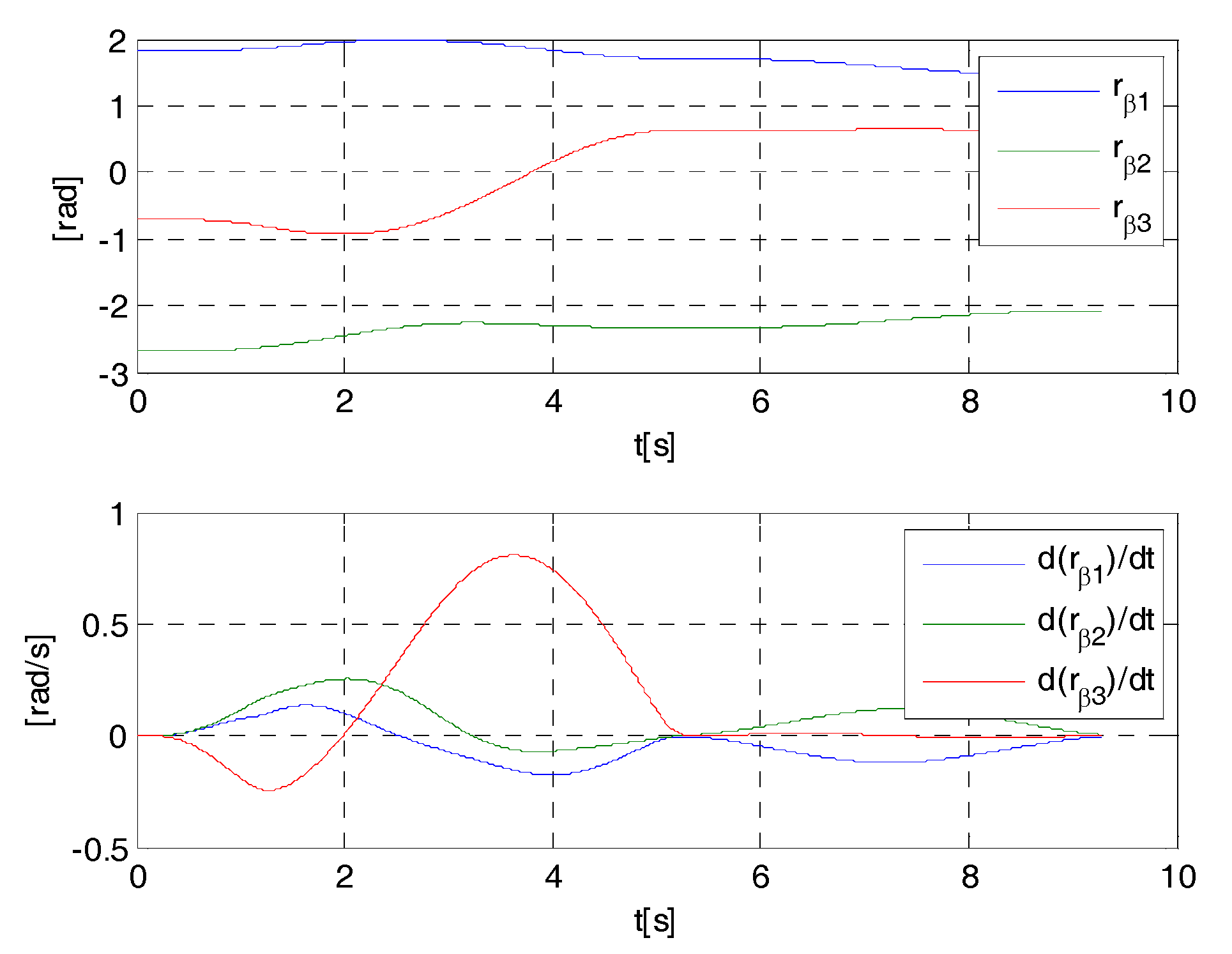
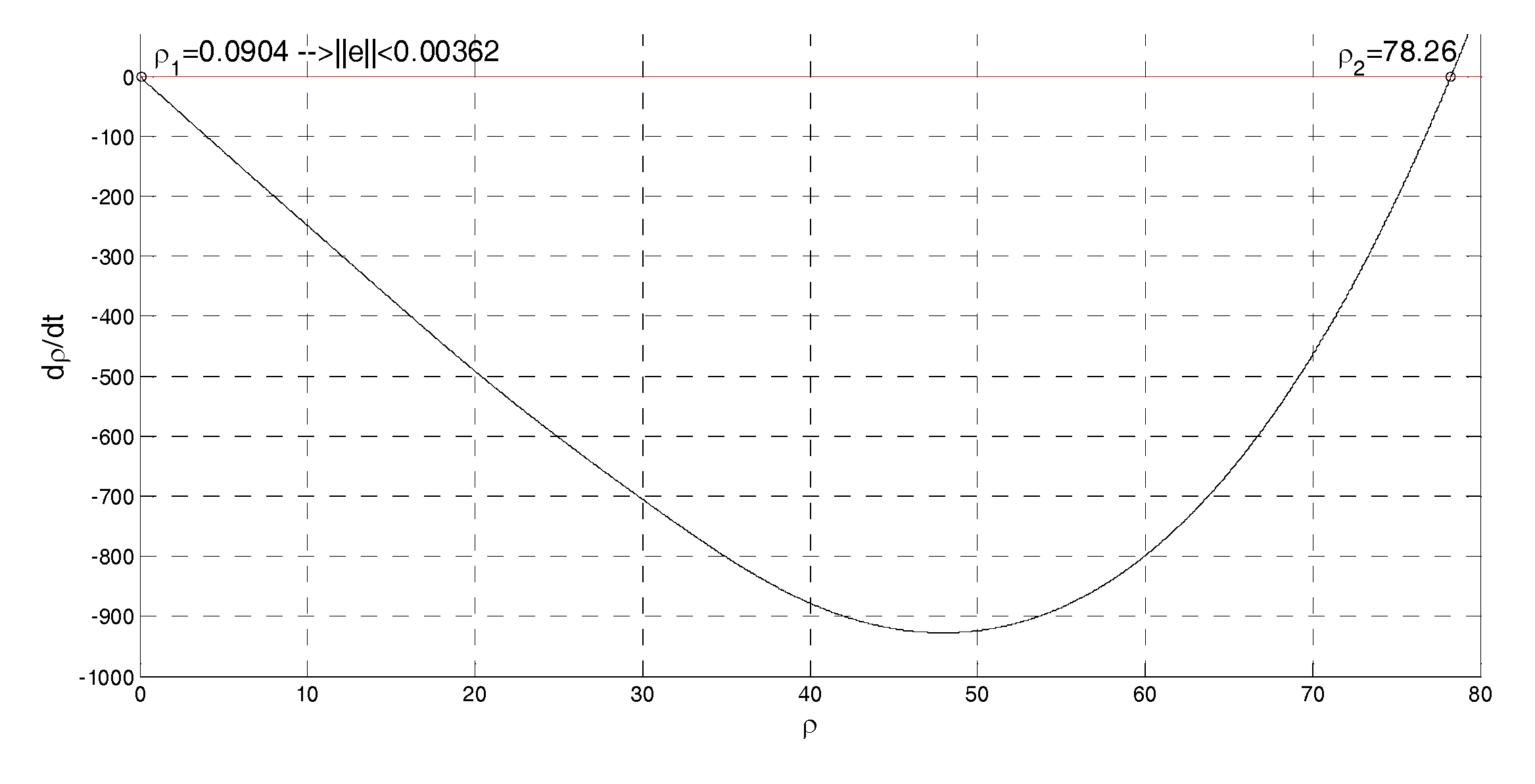
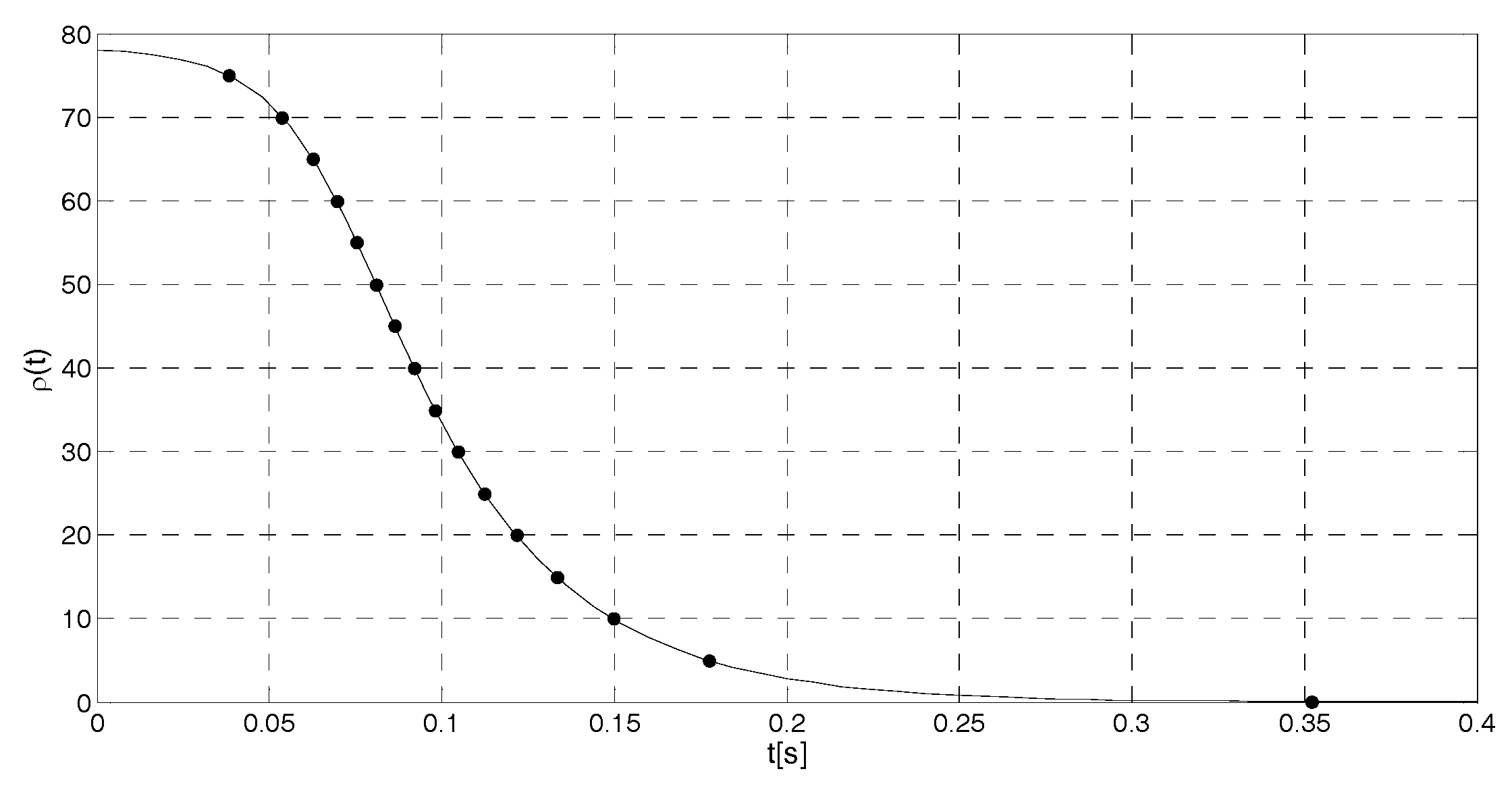
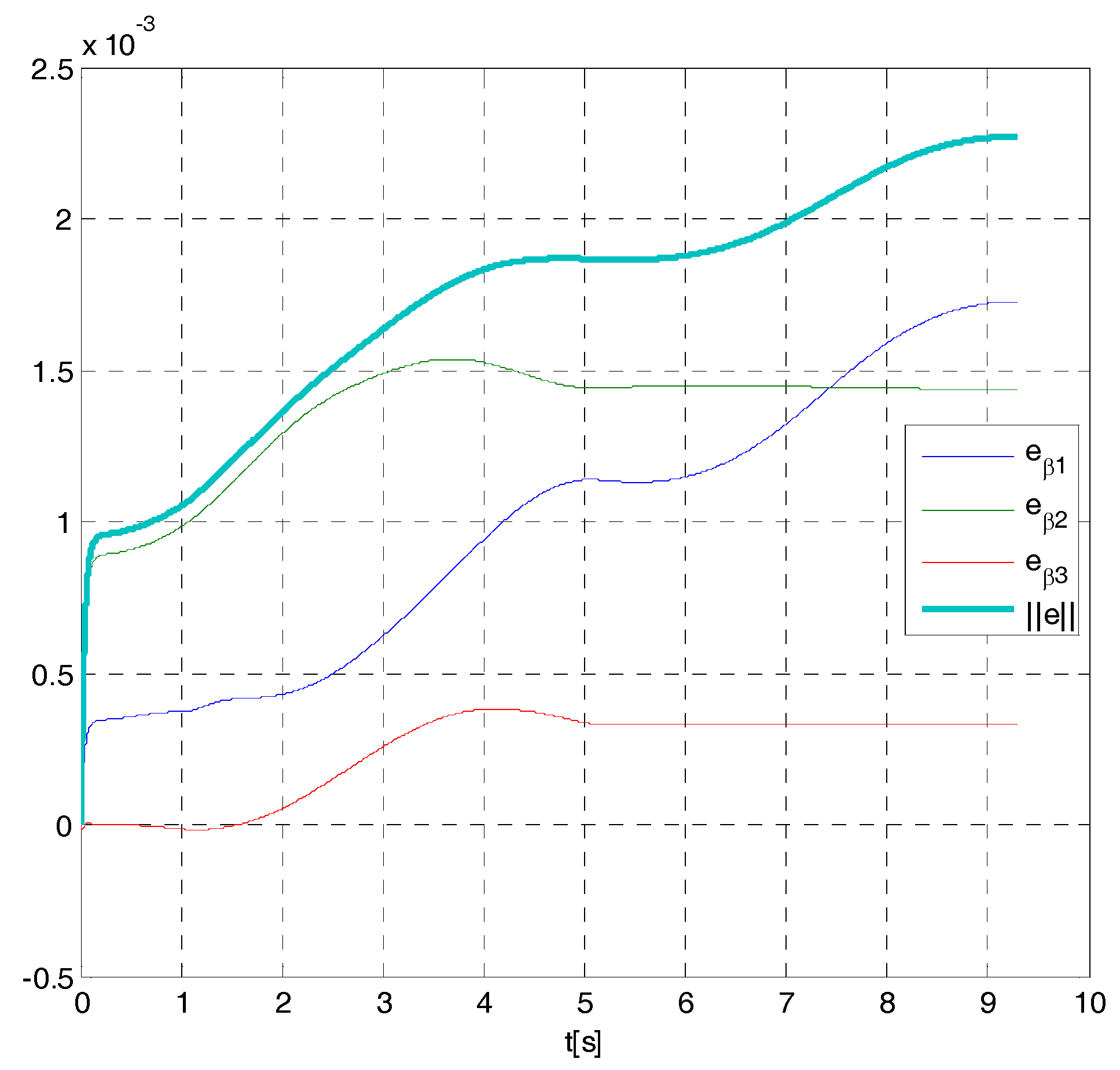
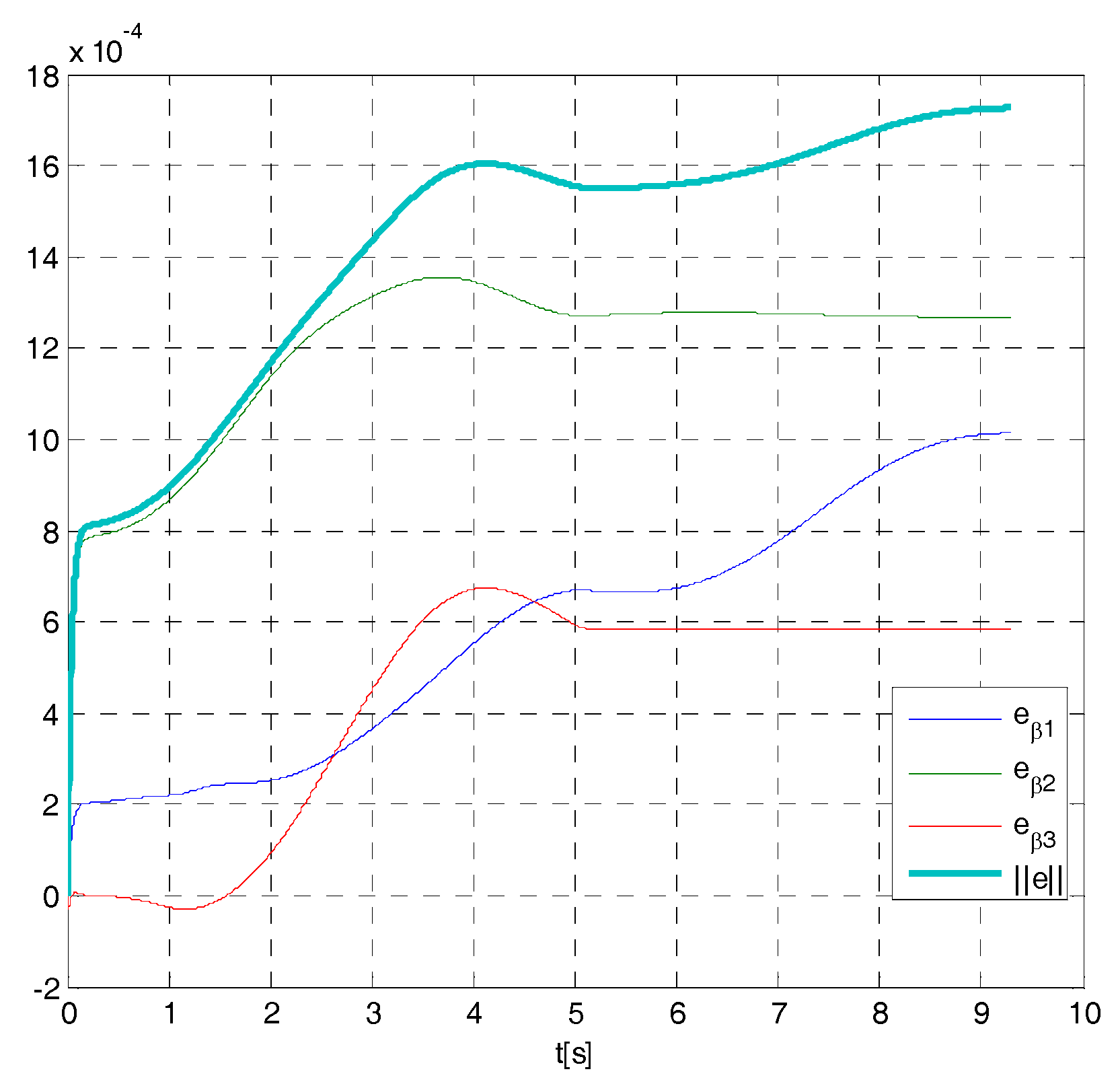
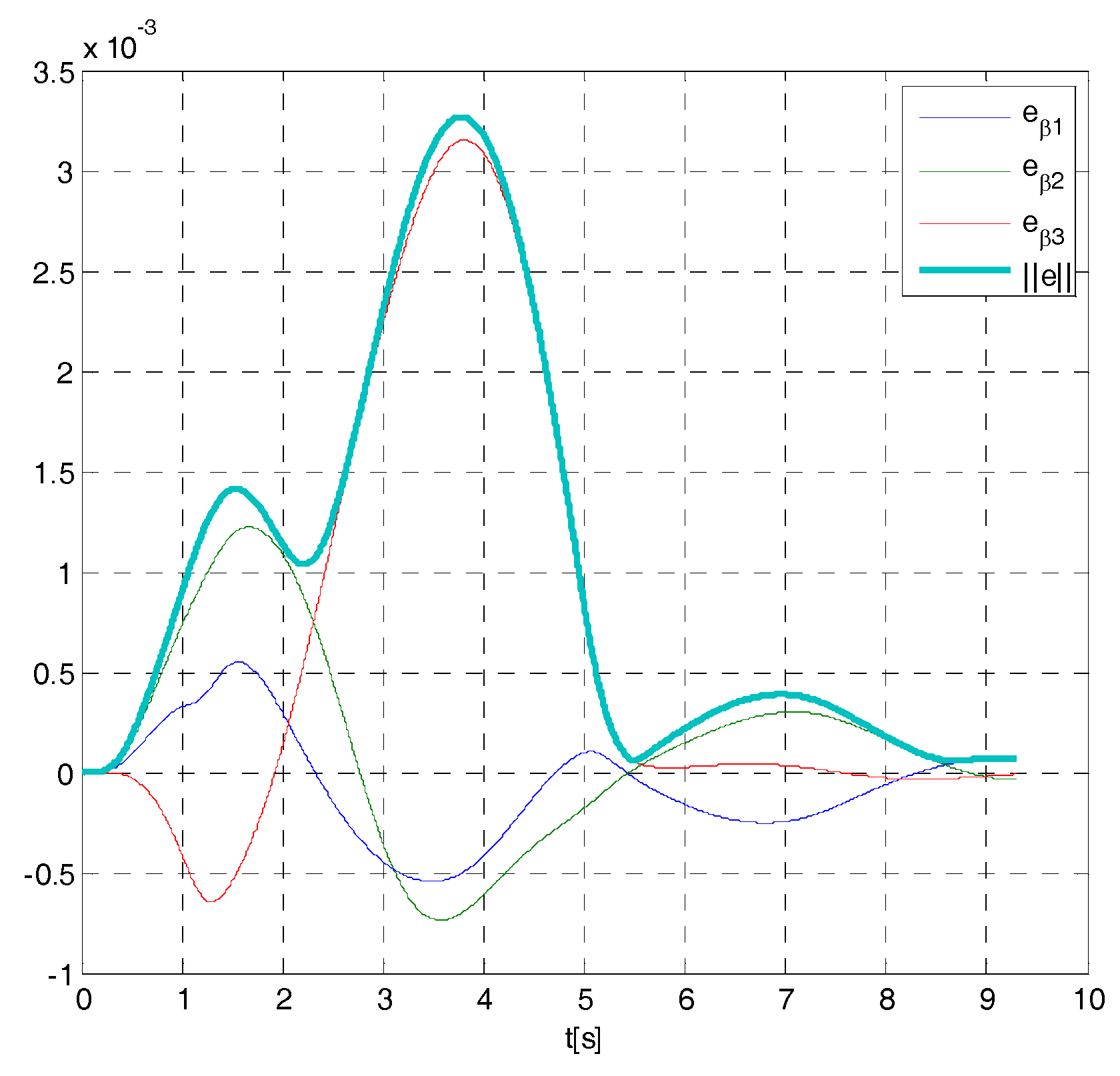
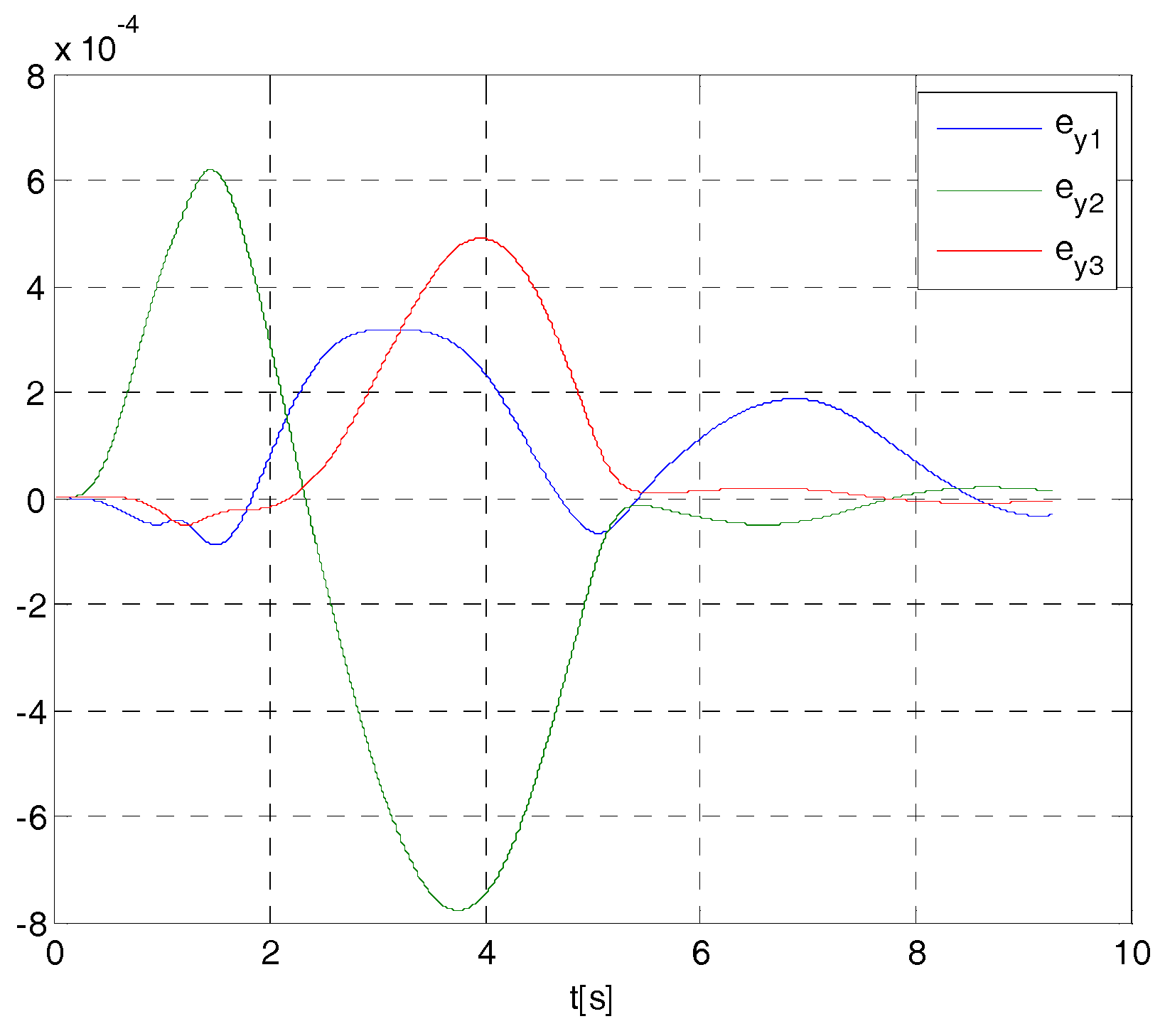
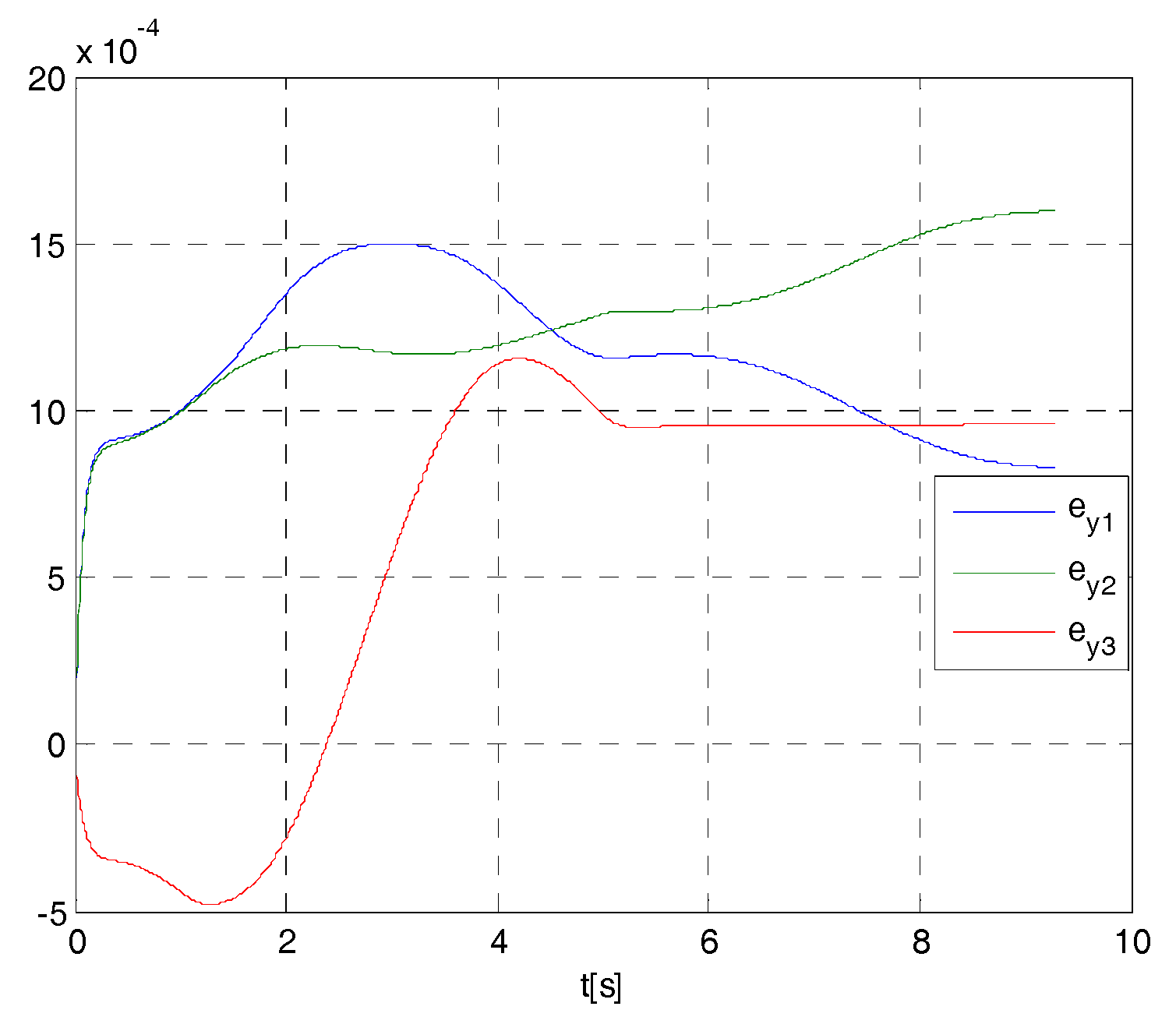
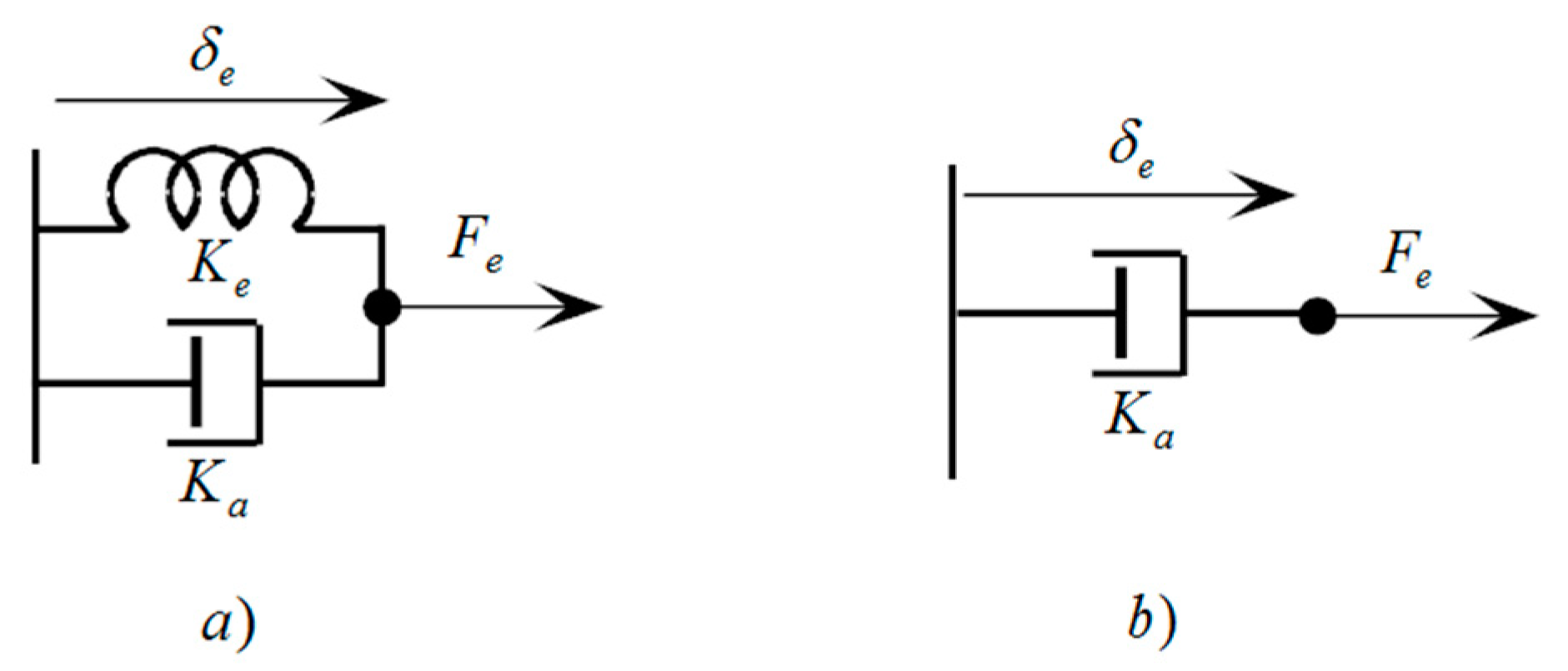
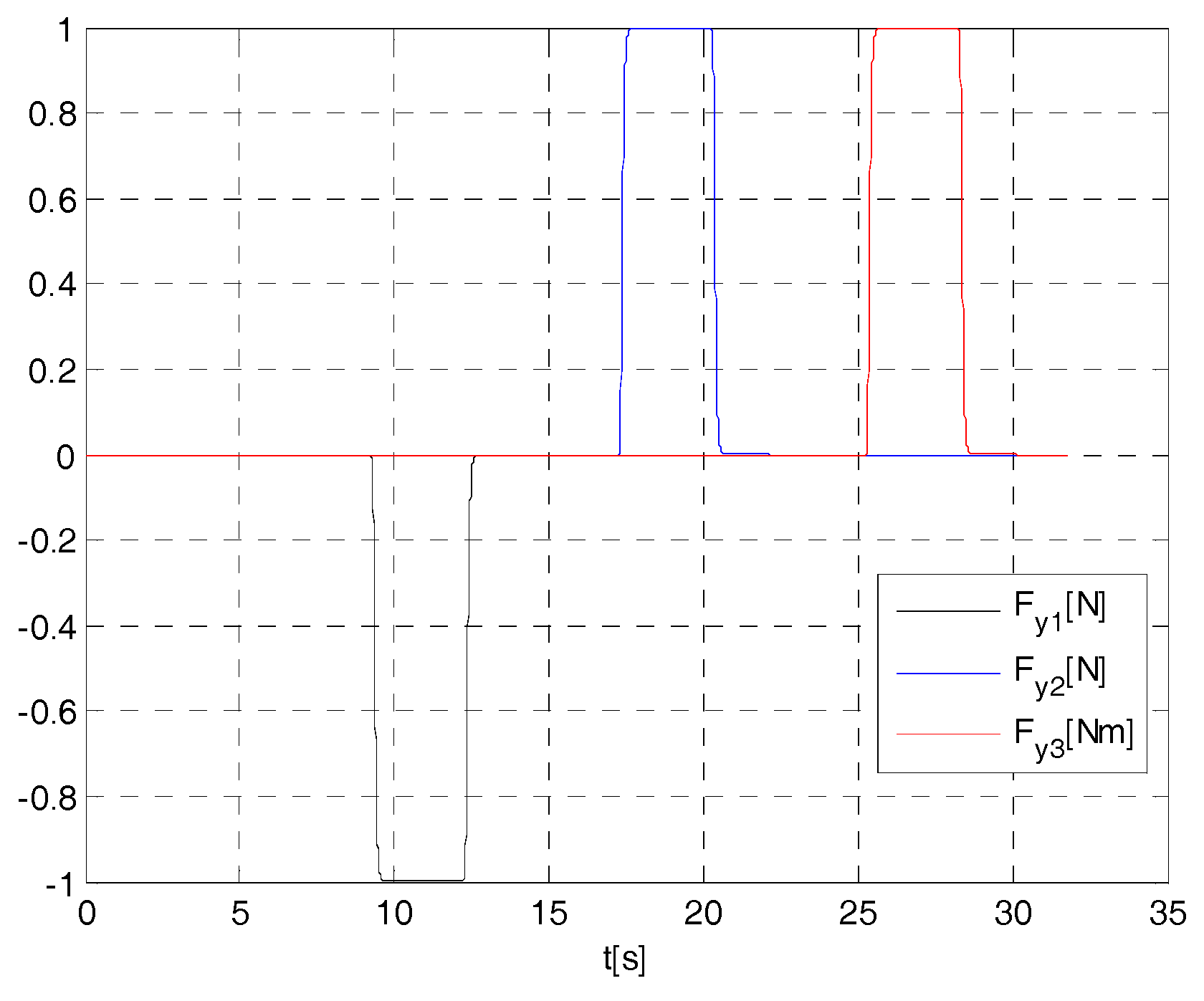
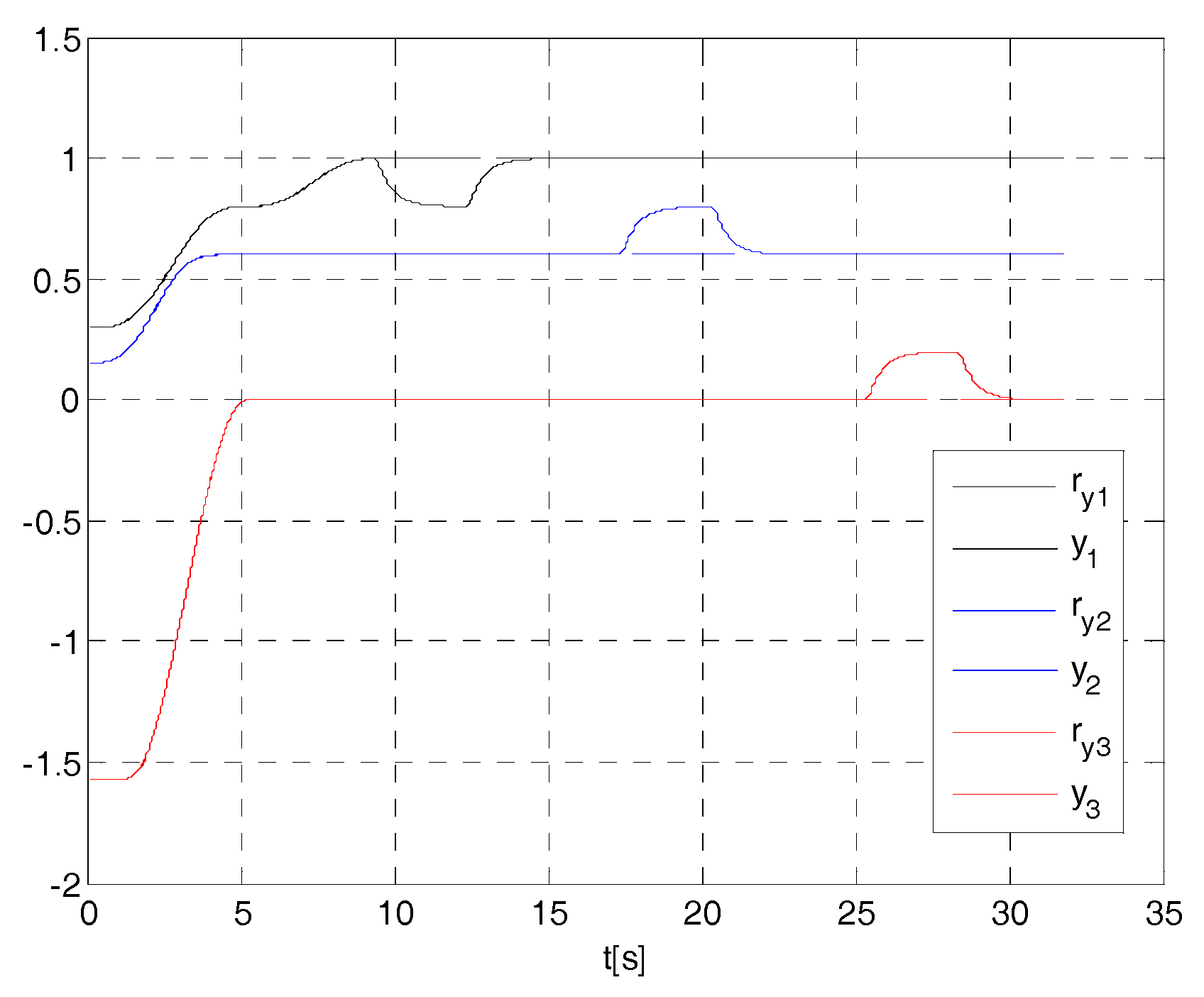
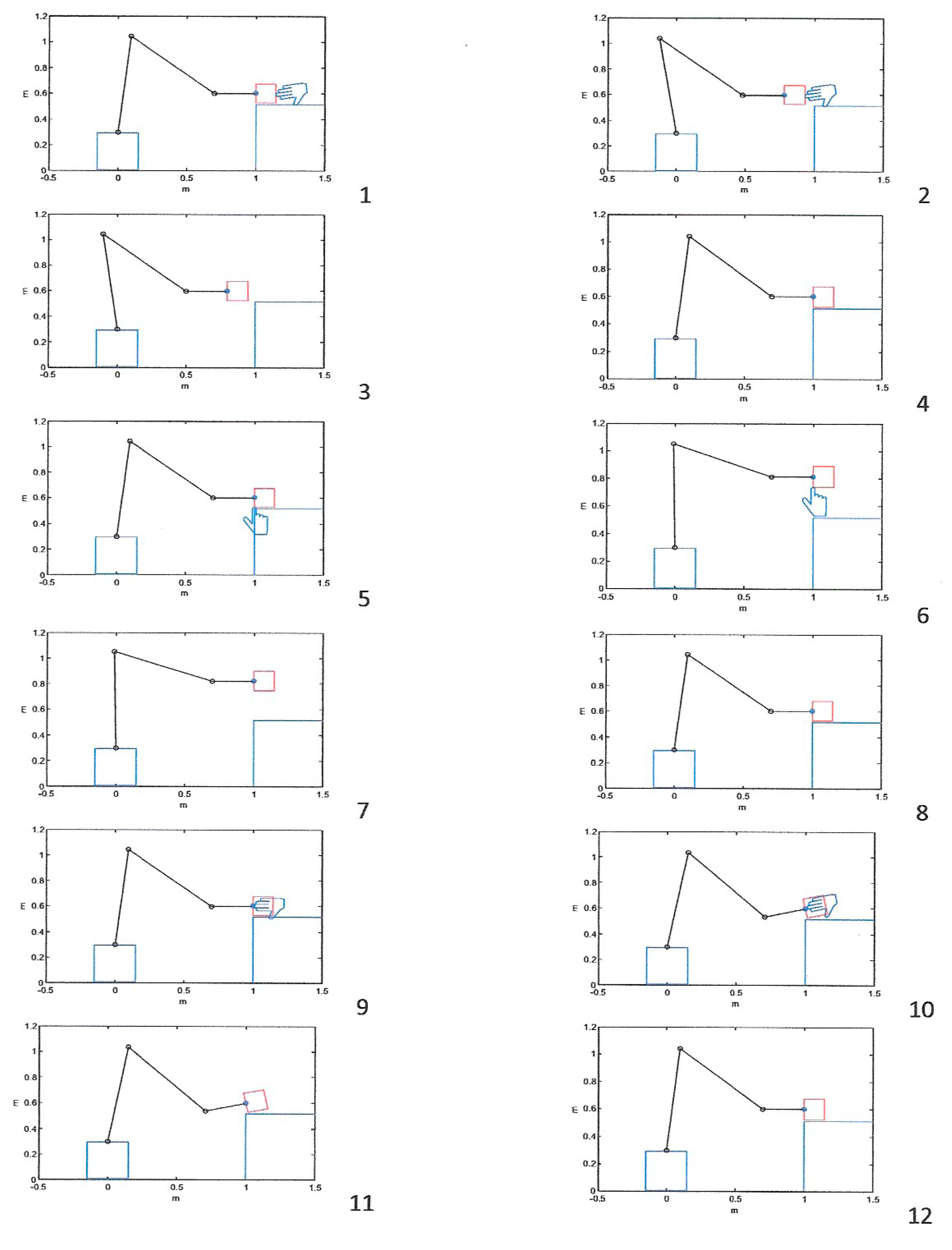
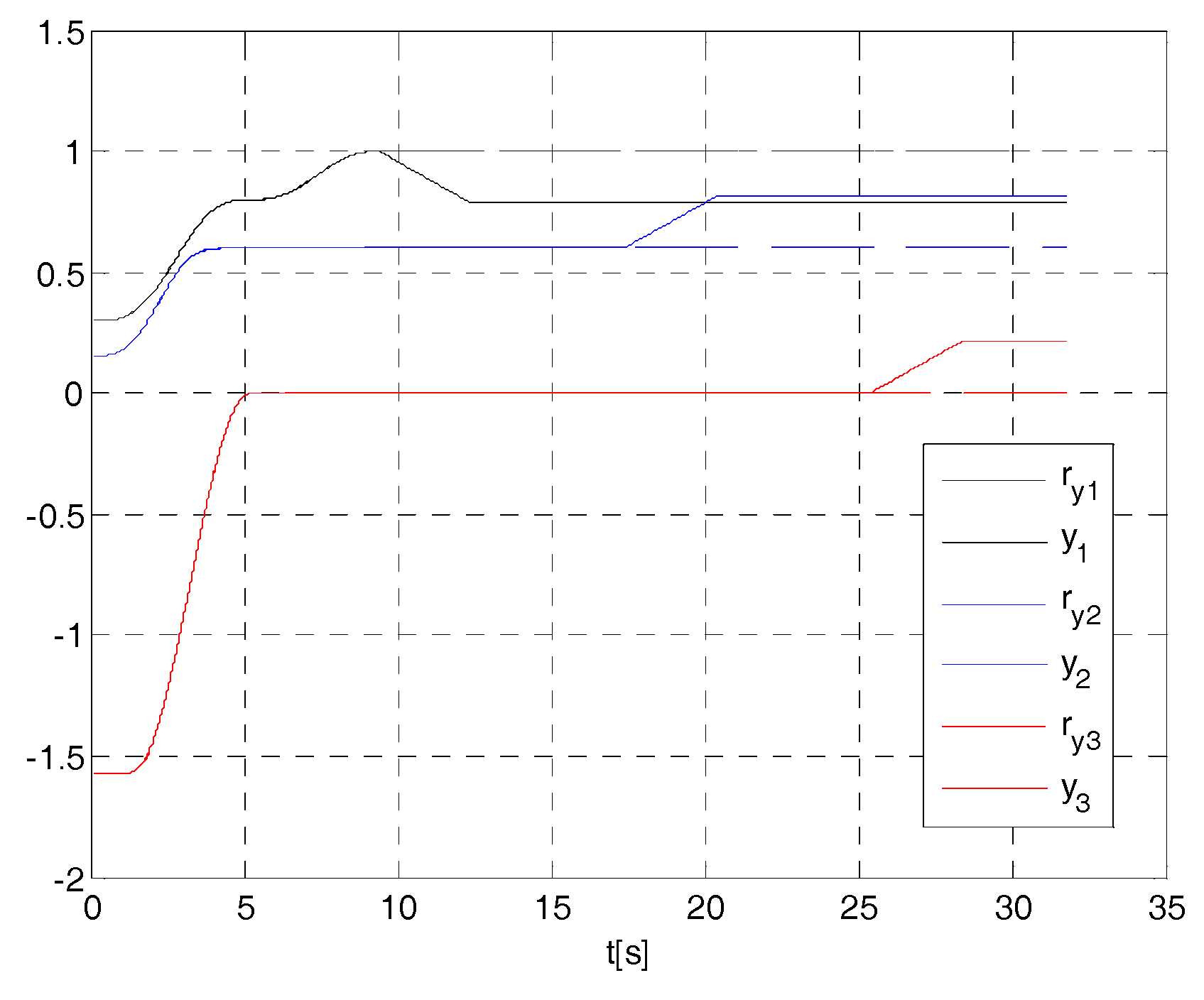
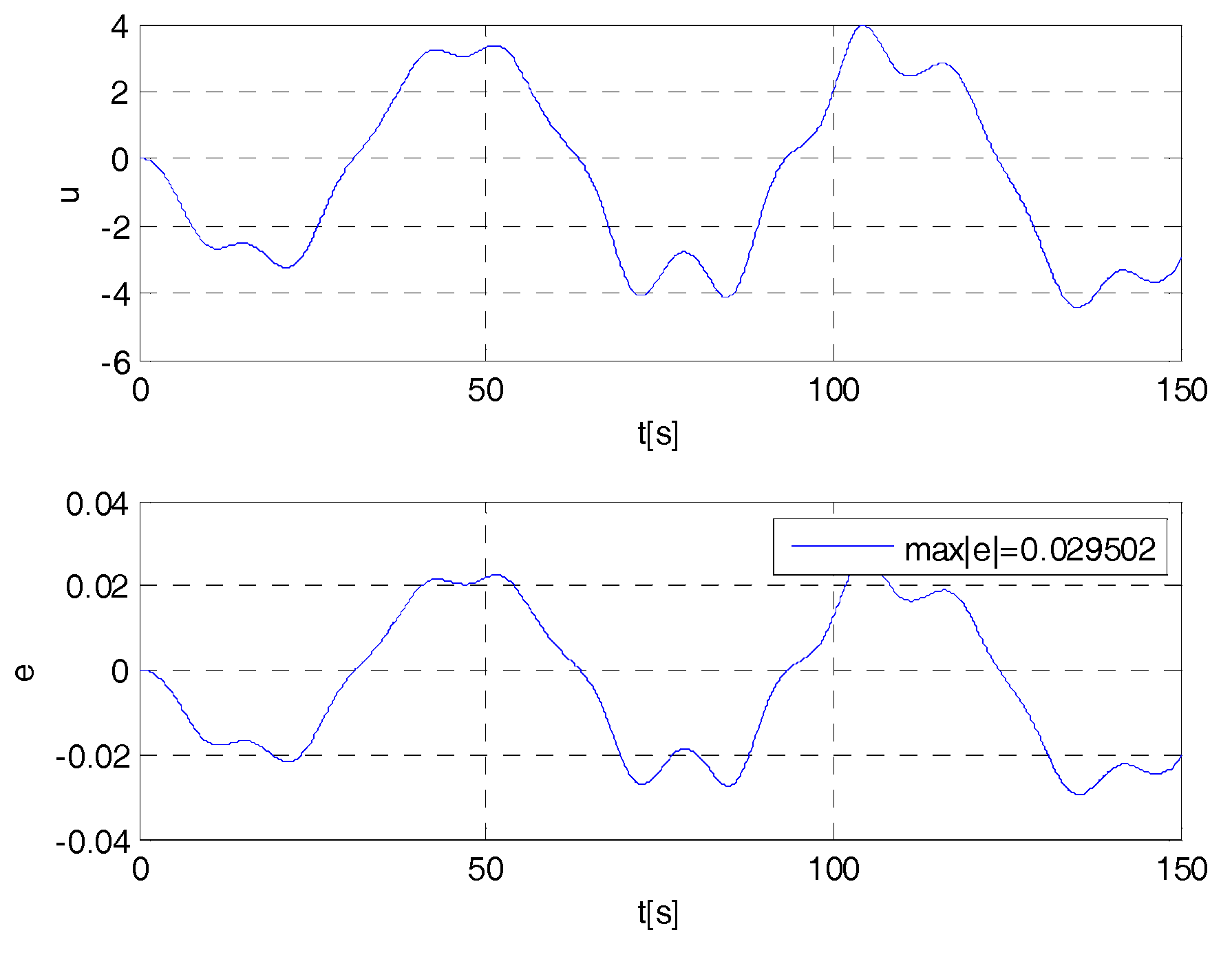
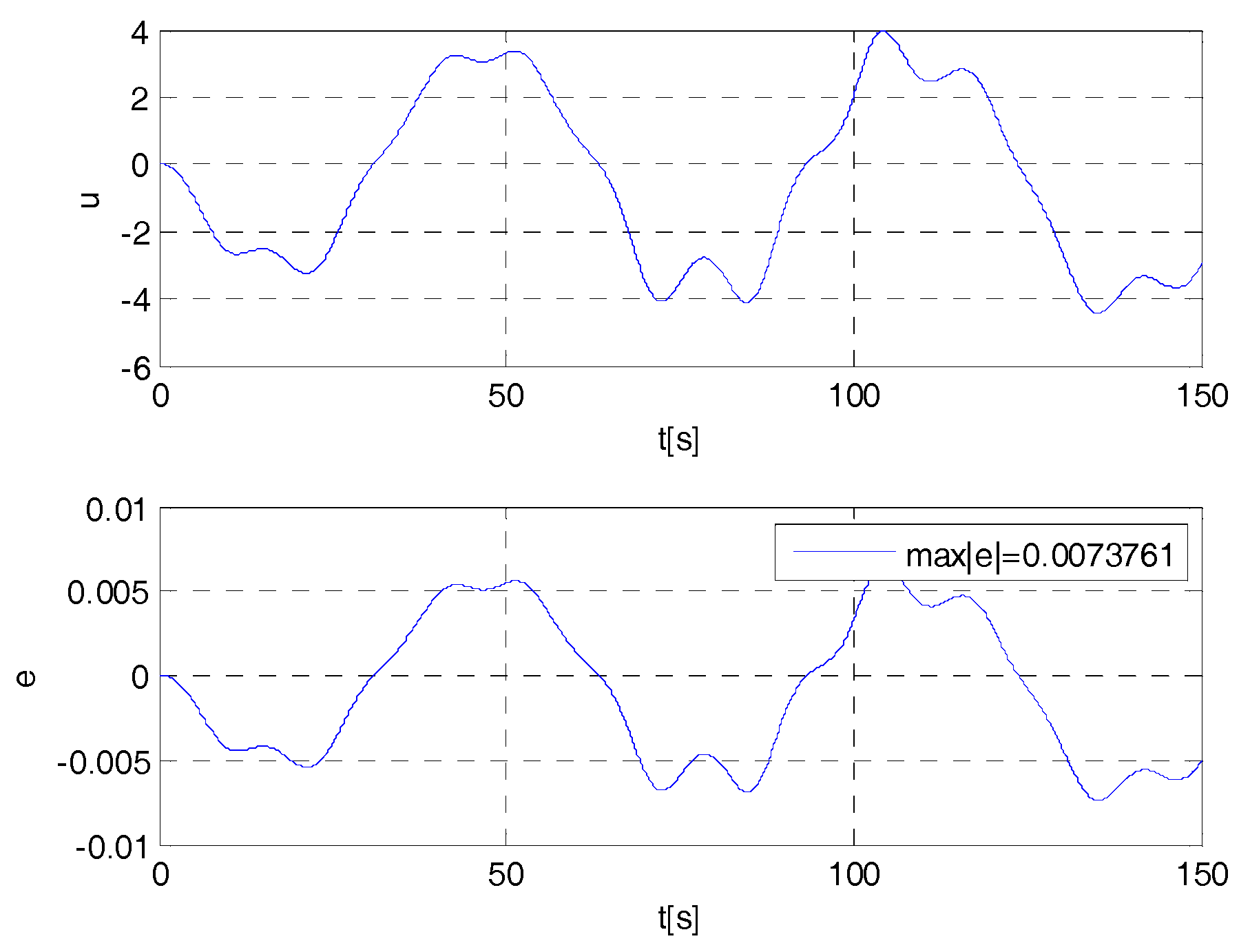
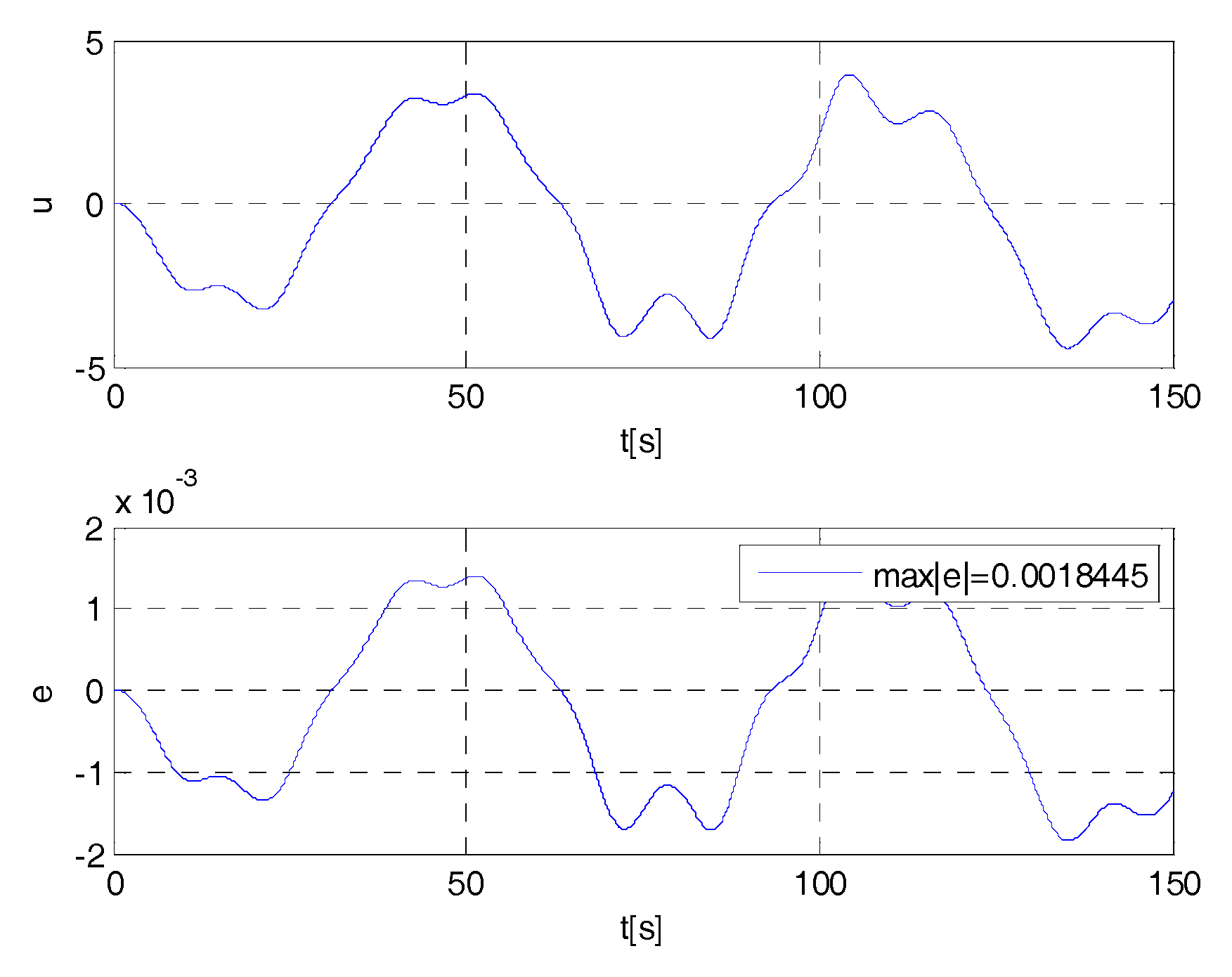
4. Cases Study
- if , then ;
- if , then (e.g., if , at less ,
5. Conclusions and Future Developments
- The considered class of nonlinear uncertain MIMO systems is broad and includes an important class of uncertain linear systems.
- A comprehensive approach based on the concept of majorant systems is provided to design smooth robust controllers. They have been used to track a generic reference signal with bounded second derivative with a tracking error norm smaller than a prescribed value.
- The obtained control laws are easy to design and implement. These laws have no high gains and are free from discontinuities.
- Suitable filtering laws are proposed for tracked trajectories to facilitate the implementation of the control laws and reduce the control magnitude, particularly during the transient phase.
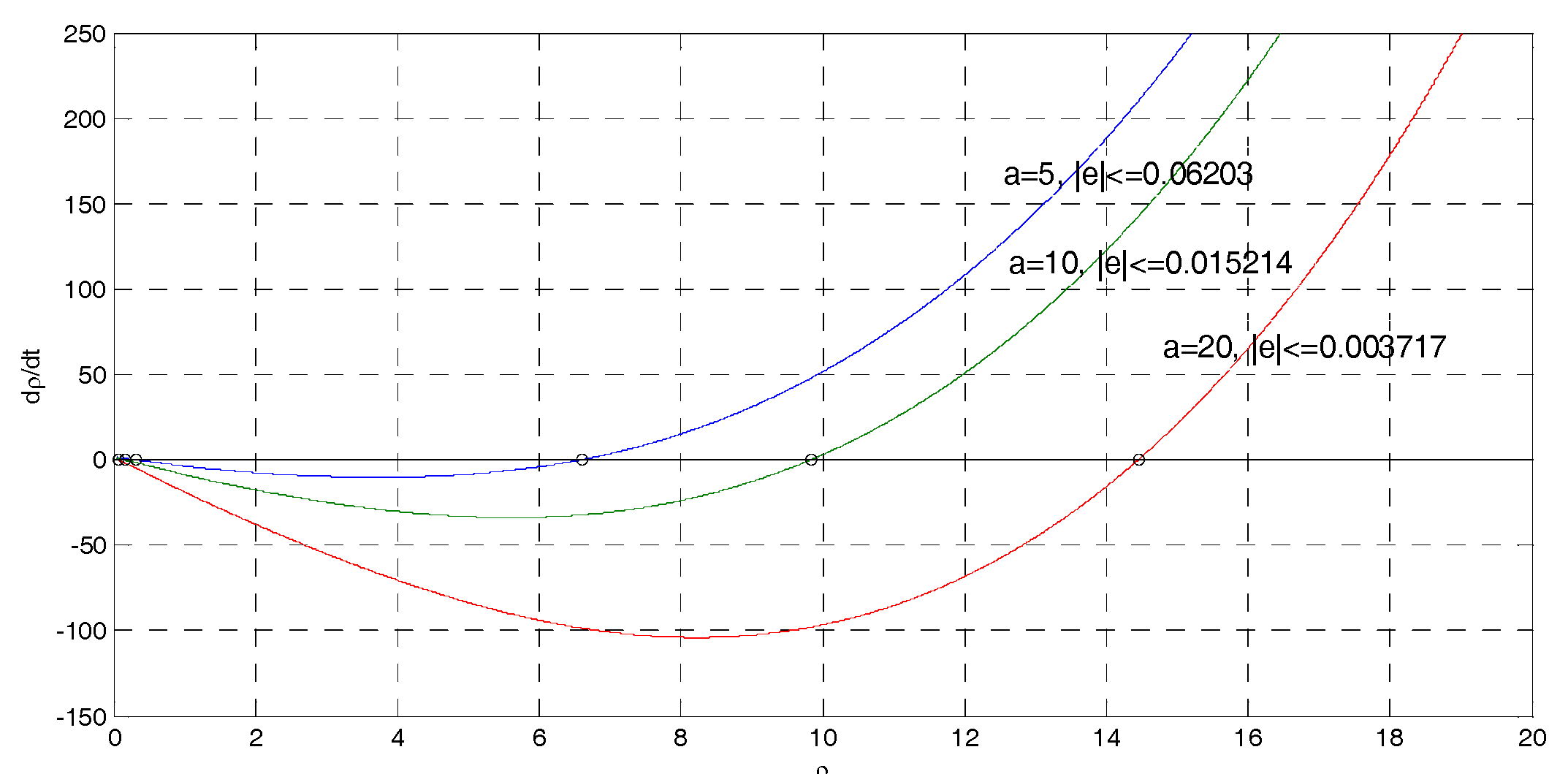
- The maximum tracking error can be fixed a priori despite bounded parametric uncertainties, disturbances, and velocity measurement noise.
- A simple relation exists between a single design parameter of the controller and the maximum tracking error, which is useful for obtaining the desired tracking precision.
- The proposed control laws are robust with respect to bounded measurement noises.
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- (1)
- parametric uncertainties;
- (2)
- real actuators;
- (3)
- measurement noise;
- (4)
- finite online computation time of the control signal.


- (1)
- for more complex nonlinear systems with parametric uncertainties the MPC controller requires a high online computational burden,
- (2)
- in general, the properties of asymptotic stability depend in a complex way on the model chosen to predict the evolution and on other parameters of the controller,

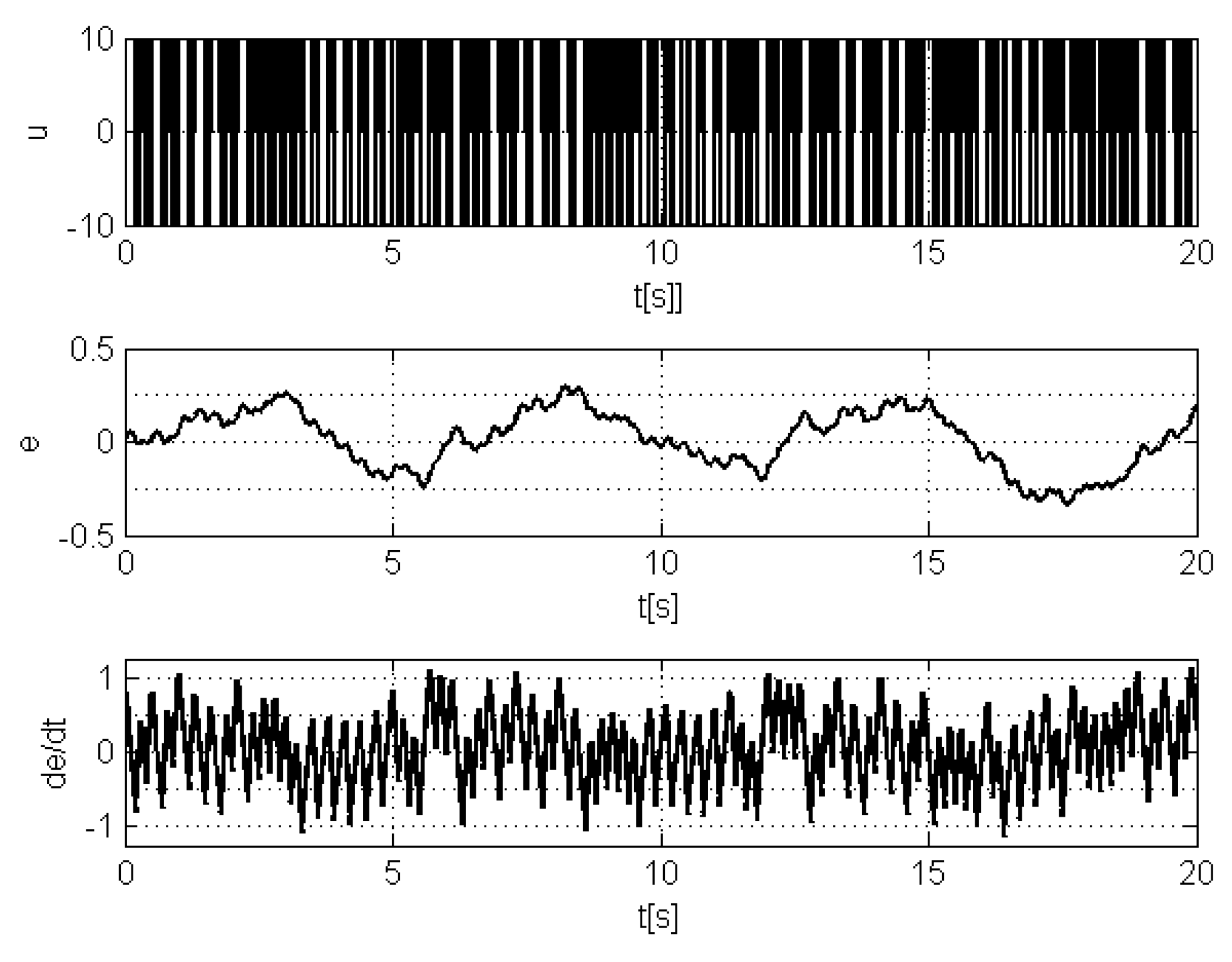
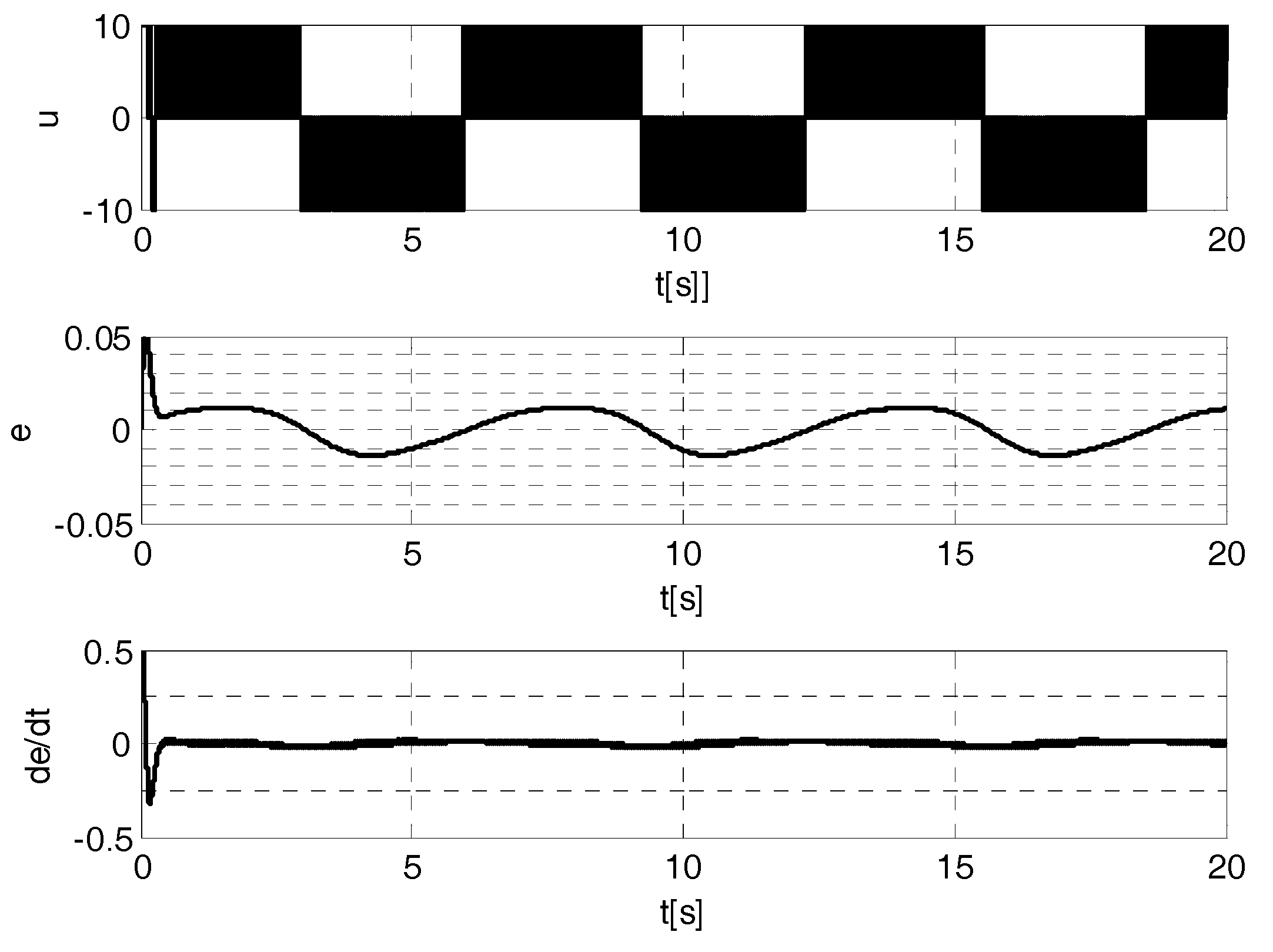
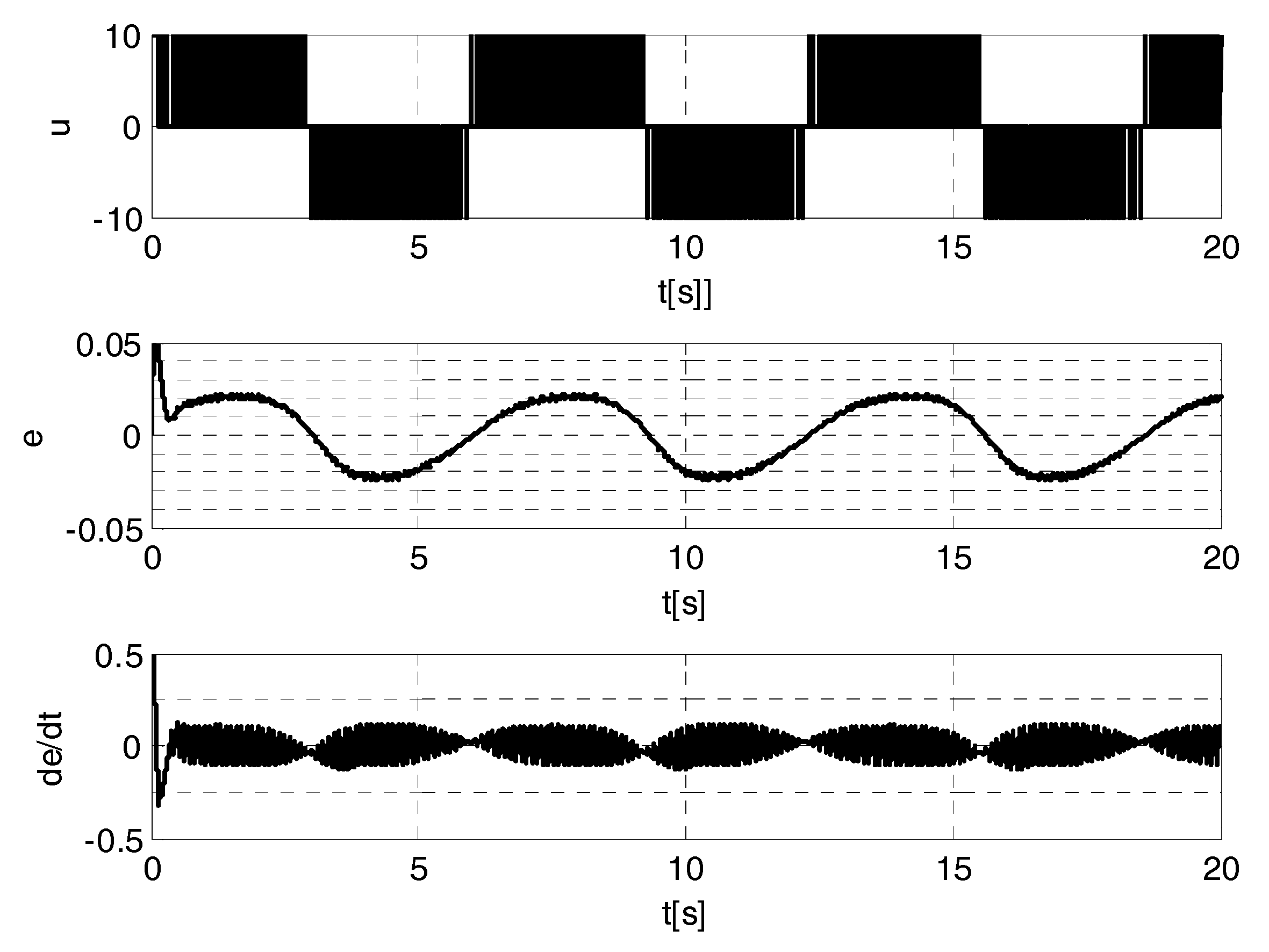
- (1)
- (2)
- that the articulated mechanical systems are very complex (see [6]) and that, hence, techniques using their online models are difficult to be implemented without delays; therefore, the delays due to the online computation times can make unstable the control system.
References
- Dorato, P. (Ed.) Robust Control; IEEE Press: New York, NY, USA, 1987. [Google Scholar]
- Abdallah, C.T.; Dawson, D.; Dorato, P.; Jamshidi, M. Survey of robust control for rigid robots. IEEE Control Syst. 1991, 11, 24–30. [Google Scholar] [Green Version]
- Ackermann, J. Robust Control: Systems with Uncertain Physical Parameters; Springer: New York, NY, USA, 1993. [Google Scholar]
- Jafarov, E.M.; Tasaltin, R. Robust sliding-mode control for the uncertain MIMO aircraft model F-18. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1127–1141. [Google Scholar]
- Adams, R.J.; Buffington, J.M.; Sparks, A.G.; Banda, S.S. Robust Multivariable Flight Control; Springer: London, UK, 1994. [Google Scholar]
- Wu, C.-J.; Huang, C.-H. A neural network controller with PID compensation for trajectory tracking of robotic manipulators. J. Frankl. Inst. 1996, 333, 523–537. [Google Scholar] [CrossRef]
- Yoshikawa, T. Force Control—Foundations of Robotics: Analysis and Control; The MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Tsuji, T.; Tanaka, Y. Tracking control properties of human-robotic systems based on impedance control. IEEE Trans. Syst. Man Cybern. A 2005, 35, 523–535. [Google Scholar] [CrossRef]
- Celentano, L.; Iervolino, R. New results on robot modeling and simulation. ASME J. Dyn. Syst. Meas. Control 2006, 128, 128–811. [Google Scholar] [CrossRef]
- Chung, W.; Fu, L.-C.; Hsu, S.-H. Motion control. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot. Modeling and Control; John Wiley & Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Chang, Y.-C.; Yen, H.-M. Robust tracking control for a class of uncertain electrically driven robots. IET Control Theory Appl. 2009, 3, 519–532. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer: London, UK, 2009. [Google Scholar]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sabanovic, A.; Ohnishi, K. Motion Control Systems, Chapters: Interactions in Operational Space and Interactions and Constraints; Wiley-IEEE Press: Hoboken, NJ, USA, 2011. [Google Scholar]
- Celentano, L.; Coppola, A. A wavelet based method to modeling realistic flexible robots. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 929–937. [Google Scholar]
- Tamura, K.; Ohmori, H. Adaptive PID control for asymptotic tracking problem of MIMO systems. In PID Control, Implementation and Tuning; Mansour, T., Ed.; InTech Educ.: London, UK, 2011; pp. 187–200. [Google Scholar]
- Celentano, L. Robust Tracking Controllers Design with Generic References for Continuous and Discrete Uncertain Linear SISO Systems; LAP LAMBERT Academic Publishing: Saarbrücken, Germany, 2012. [Google Scholar]
- Celentano, L. An innovative method to modeling realistic flexible robots. Appl. Math. Sci. 2012, 6, 3623–3659. [Google Scholar]
- Piltan, F.; Yarmahmoudi, M.H.; Shamsodini, V.; Mazlomian, E.; Hosainpour, A. PUMA-560 Robot Manipulator Position Computed Torque Control Methods Using MATLAB/SIMULINK and Their Integration into Graduate Nonlinear Control and MATLAB Courses. Int. J. Robot. Autom. 2012, 3, 167–191. [Google Scholar]
- Celentano, L. Robust tracking method for uncertain MIMO systems of realistic trajectories. J. Frankl. Inst. 2013, 350, 437–451. [Google Scholar] [CrossRef]
- Tempo, R.; Calafiore, G.; Dabbene, F. Randomized Algorithms for Analysis and Control of Uncertain Systems: With Applications, 2nd ed.; Springer: London, UK, 2013. [Google Scholar]
- Liu, H.; Xi, J.; Zhong, Y. Robust motion of quadrotors. J. Frankl. Inst. 2014, 351, 5494–5510. [Google Scholar] [CrossRef]
- Leban, F.A.; Díaz-Gonzalez, J.; Parker, G.G.; Zhao, W. Inverse kinematic control of a dual crane system experiencing base motion. IEEE Trans. Control Syst. Technol. 2015, 23, 331–339. [Google Scholar] [CrossRef]
- Jang, J.T.; Gong, H.C.; Lyou, J. Computed torque control of an aerospace craft using nonlinear inverse model and rotation matrix. In Proceedings of the 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 1743–1746. [Google Scholar]
- Rastogi, E.; Prasad, L.B. Comparative performance analysis of PD/PID computed torque control, filtered error approximation based control and NN control for a robot manipulator. In Proceedings of the 2015 IEEE UP Section Conference on Electrical Computer and Electronics (UPCON), Allahabad, India, 4–6 December 2015; pp. 1–6. [Google Scholar]
- Zhou, Y.; Chen, M.; Jiang, C. Robust tracking control of uncertain MIMO nonlinear systems with application to UAVs. IEEE/CAA J. Autom. Sin. 2015, 2, 25–32. [Google Scholar]
- Labrecque, P.D.; Haché, J.-M.; Abdallah, M.; Gosselin, C. Low-Impedance Physical Human Robot Interaction Using an Active–Passive Dynamics Decoupling. IEEE Robot. Autom. Lett. 2016, 1, 938–945. [Google Scholar] [CrossRef]
- Yoon, Y.; Sun, Z. Robust motion control for tracking time-varying reference signals and its application to a camless engine valve actuator. IEEE Trans. Ind. Electron. 2016, 63, 5724–5732. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, J.; Fu, Z.; Wu, C.; Huo, X. A proportional-derivative-type attitude tracking control of satellite. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 10858–10863. [Google Scholar]
- Li, P.; Ma, J.; Zheng, Z. Robust adaptive sliding mode control for uncertain nonlinear MIMO system with guaranteed steady state tracking error bounds. J. Frankl. Inst. 2016, 353, 303–321. [Google Scholar] [CrossRef]
- Kumar, V.; Rana, K.P.S.; Mishra, P. Robust speed control of hybrid electric vehicle using fractional order fuzzy PD and PI controllers in cascade control loop. J. Frankl. Inst. 2016, 353, 1713–1741. [Google Scholar] [CrossRef]
- Brahmi, B.; Saad, M.; Rahman, M.H.; Ochoa-Luna, C. Cartesian trajectory tracking of a 7-dof exoskeleton robot based on human inverse kinematics. IEEE Trans. Syst. Man Cybern. Syst. 2017, 99, 1–12. [Google Scholar] [CrossRef]
- Celentano, L. Design of a pseudo-PD or PI robust controller to track C2 trajectories for a class of uncertain nonlinear MIMO system. J. Frankl. Inst. 2017, 354, 5026–5055. [Google Scholar] [CrossRef]
- Celentano, L. Pseudo-PID robust tracking method for a class of mechanical uncertain MIMO systems. In Proceedings of the 20th IFAC World Congress, Toulouse, France, 9–14 July 2017; Volume 50, pp. 1545–1552. [Google Scholar]
- Wang, H.; Shi, P.; Li, H.; Zhou, Q. Adaptive Neural Tracking Control for a Class of Nonlinear Systems with Dynamic Uncertainties. IEEE Trans. Cybern. 2017, 47, 3075–3087. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Xia, Y.; Dai, L.; Liu, K.; Ma, D. Disturbance Rejection MPC for Tracking of Wheeled Mobile Robot. IEEE/ASME Trans. Mechatron. 2017, 22, 2576–2587. [Google Scholar] [CrossRef]
- Celentano, L.; Basin, M. An Approach to Design Robust Tracking Controllers for Nonlinear Uncertain Systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, in press. [Google Scholar] [CrossRef]
- Ha, W.; Back, J. A disturbance observer-based robust tracking controller for uncertain robot manipulators. Int. J. Control Autom. Syst. 2018, 16, 417–425. [Google Scholar] [CrossRef]
- Chen, L.-H.; Peng, C.-C. Extended backstepping sliding controller design for chattering attenuation and its application for servo motor control. Appl. Sci. 2017, 7, 220. [Google Scholar] [CrossRef]
- Wu, K.; Cai, Z.; Zhao, J.; Wang, Y. Target tracking based on a nonsingular fast terminal sliding mode guidance law by fixed-wing UAV. Appl. Sci. 2017, 7, 333. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Jiang, D.; Wang, Q.; Xiong, W.; Liu, J.; Li, X. Prescribed performance constraint regulation of electrohydraulic control based on backstepping with dynamic surface. Appl. Sci. 2018, 8, 76. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Yang, X.; Hu, F.; Jiang, A.; Yang, C. Trajectory tracking of an omni-directional wheeled mobile robot using a model predictive control strategy. Appl. Sci. 2018, 8, 231. [Google Scholar] [CrossRef]
- Celentano, L.; Basin, M. New results on robust stability analysis and synthesis for MIMO uncertain systems. IET Control Theory Appl. 2018, 12, 1421–1430. [Google Scholar] [CrossRef]









© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celentano, L. A Unified Approach to Design Robust Controllers for Nonlinear Uncertain Engineering Systems. Appl. Sci. 2018, 8, 2236. https://doi.org/10.3390/app8112236
Celentano L. A Unified Approach to Design Robust Controllers for Nonlinear Uncertain Engineering Systems. Applied Sciences. 2018; 8(11):2236. https://doi.org/10.3390/app8112236
Chicago/Turabian StyleCelentano, Laura. 2018. "A Unified Approach to Design Robust Controllers for Nonlinear Uncertain Engineering Systems" Applied Sciences 8, no. 11: 2236. https://doi.org/10.3390/app8112236