Stress Concentration and Optimized Analysis of an Arbitrarily Shaped Hole with a Graded Layer under Anti-Plane Shear
Abstract
:1. Introduction
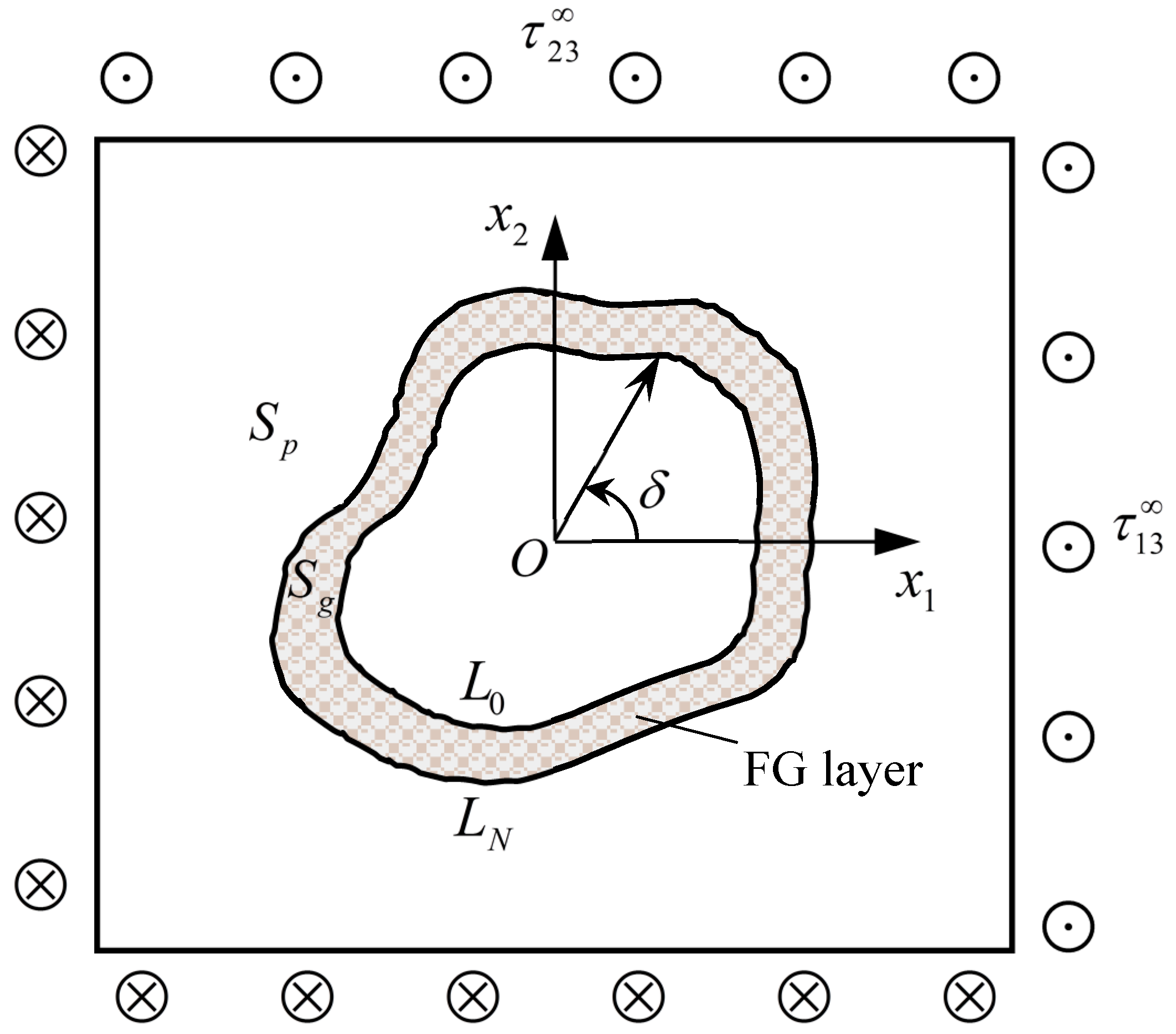
2. Theoretical Analysis
3. Numerical Examples
4. Optimized Analysis
5. Conclusions
- (1)
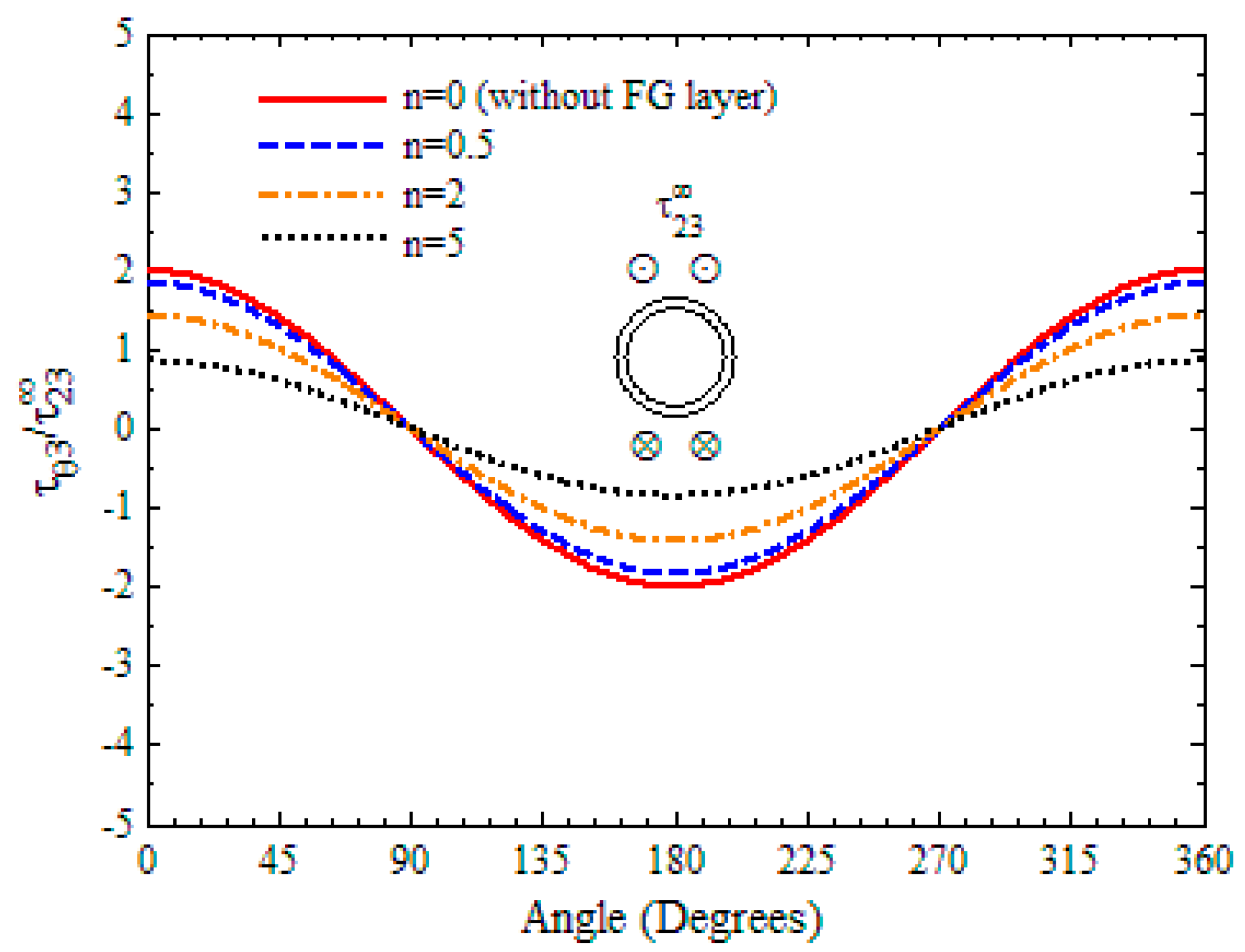
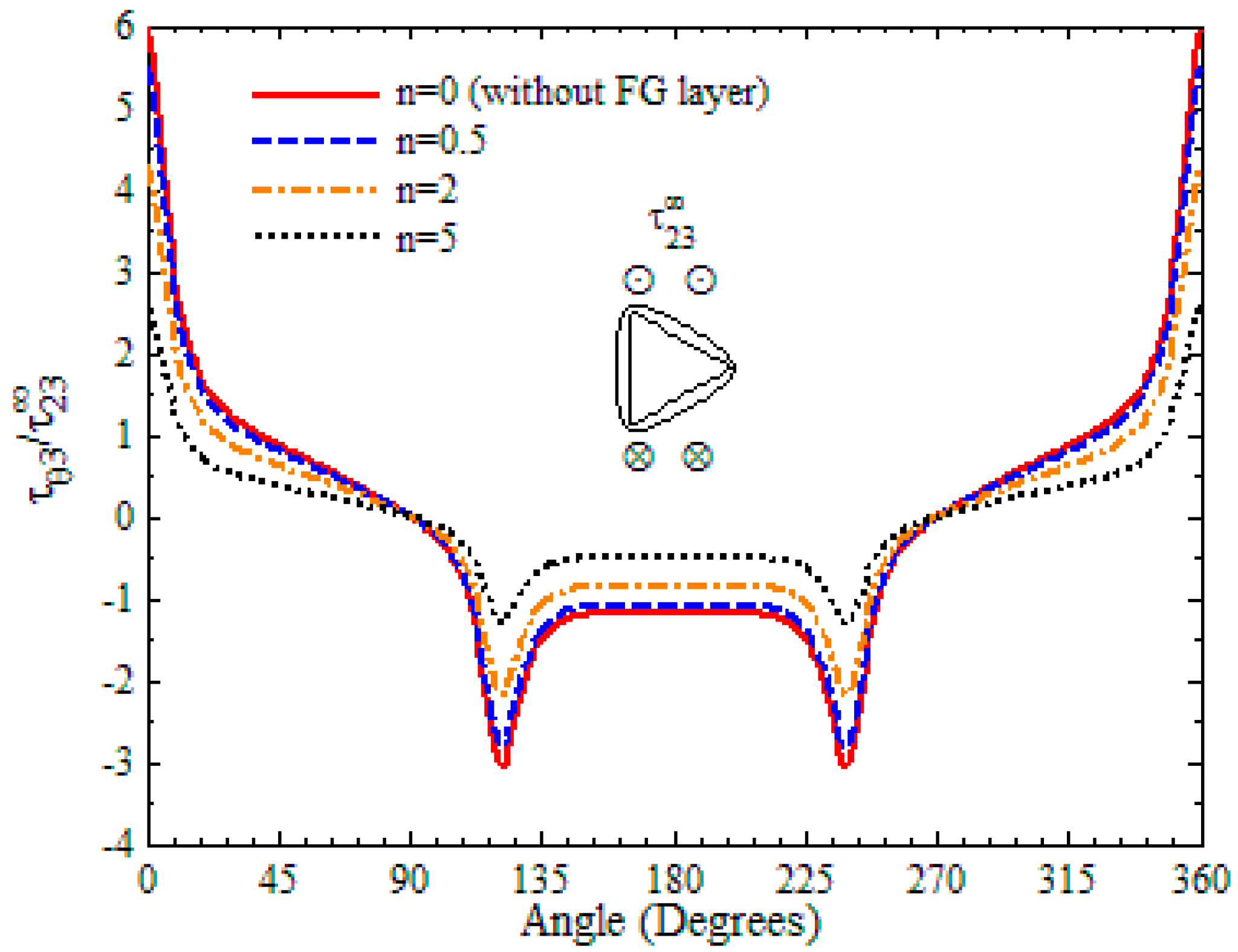
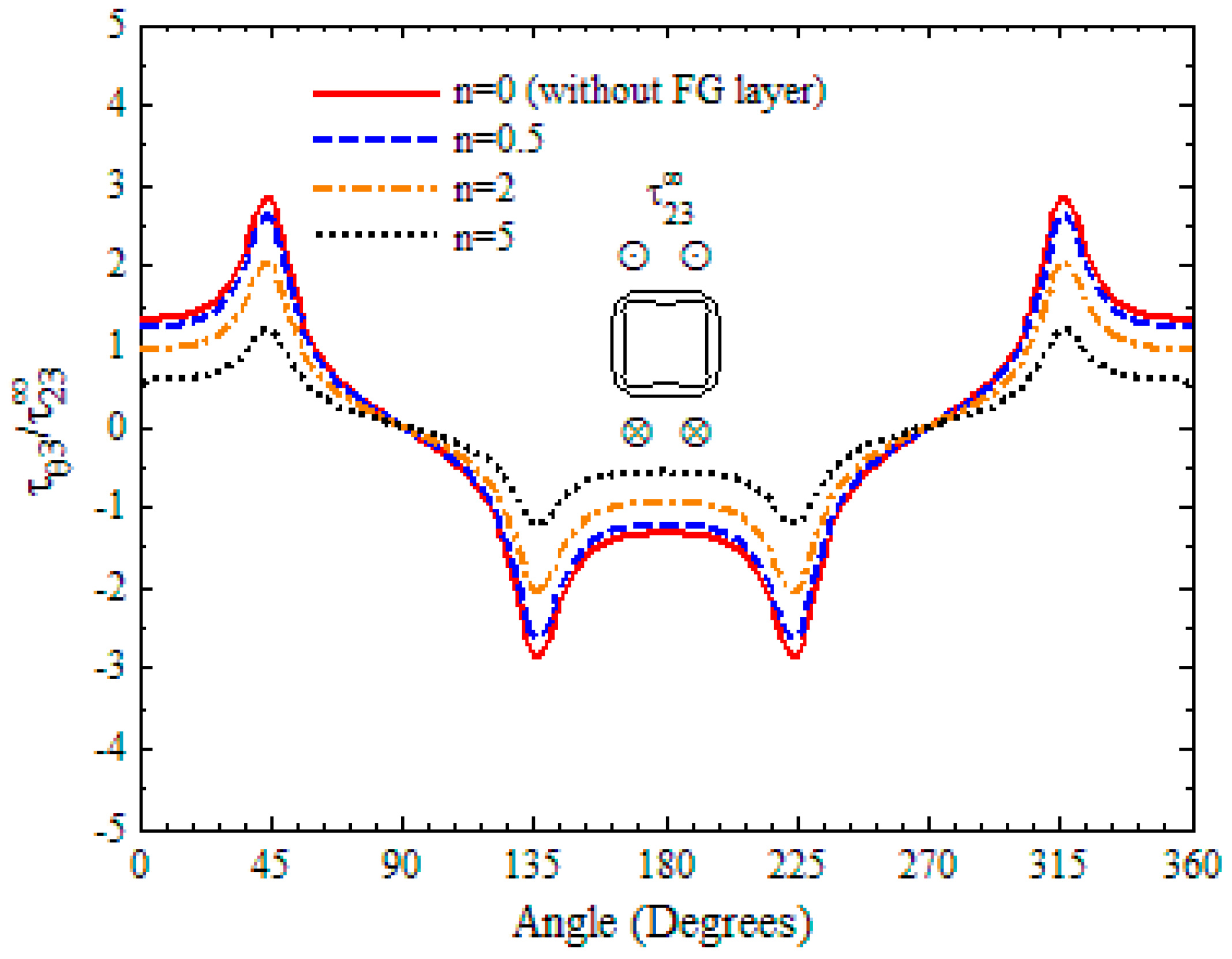
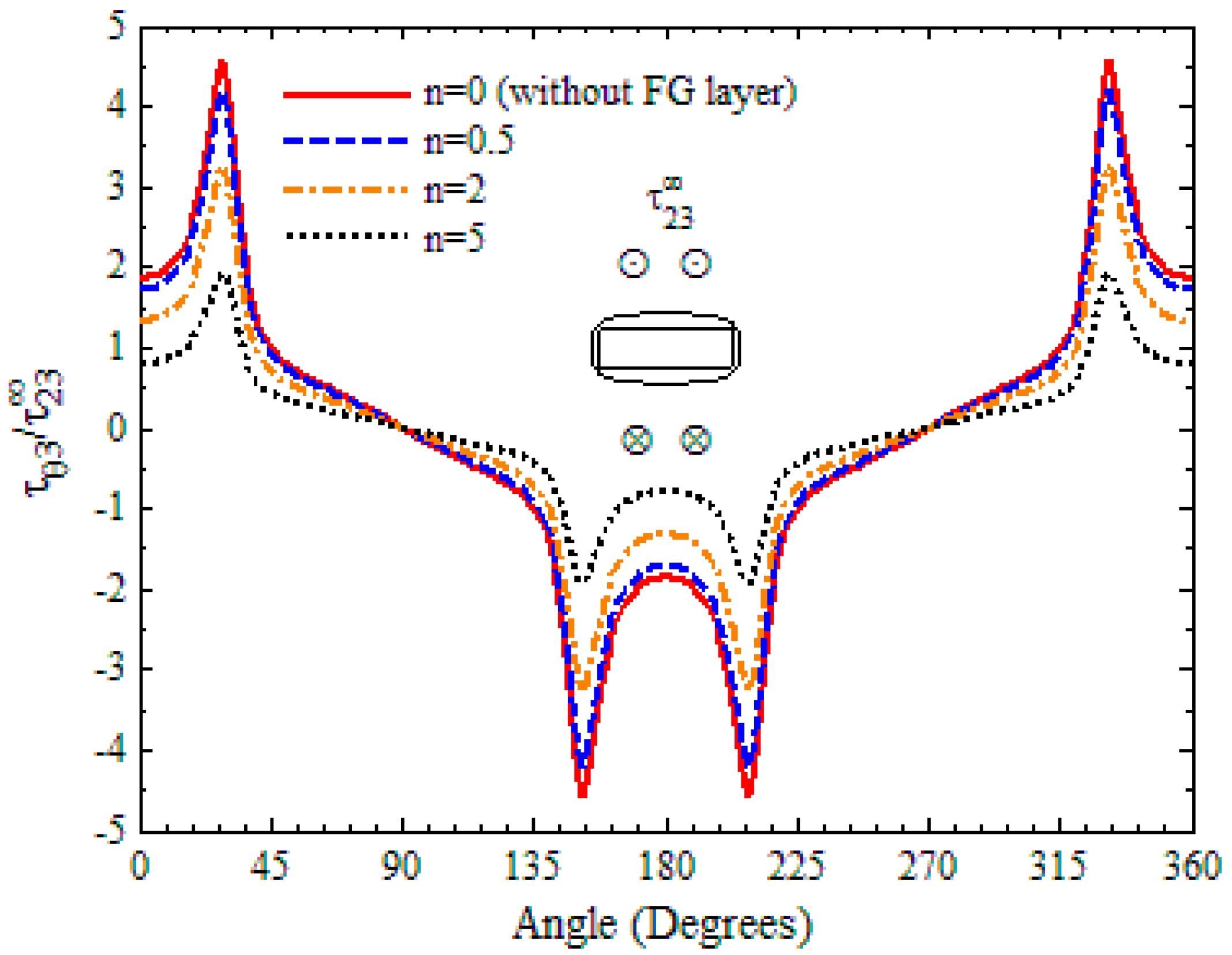
- The maximum shear stress of ellipse and rectangle shaped holes is usually larger than that of circular and square shaped holes, respectively, and the FG layer around the triangular hole has the largest magnitude of concentrations of all the five different shaped holes.
- (2)
- When the hole is reinforced by an FG layer, the maximum shear stresses at the hole surface get smaller, and they decrease further for all shaped holes when the gradient exponent of Young’s modulus increases.
- (3)
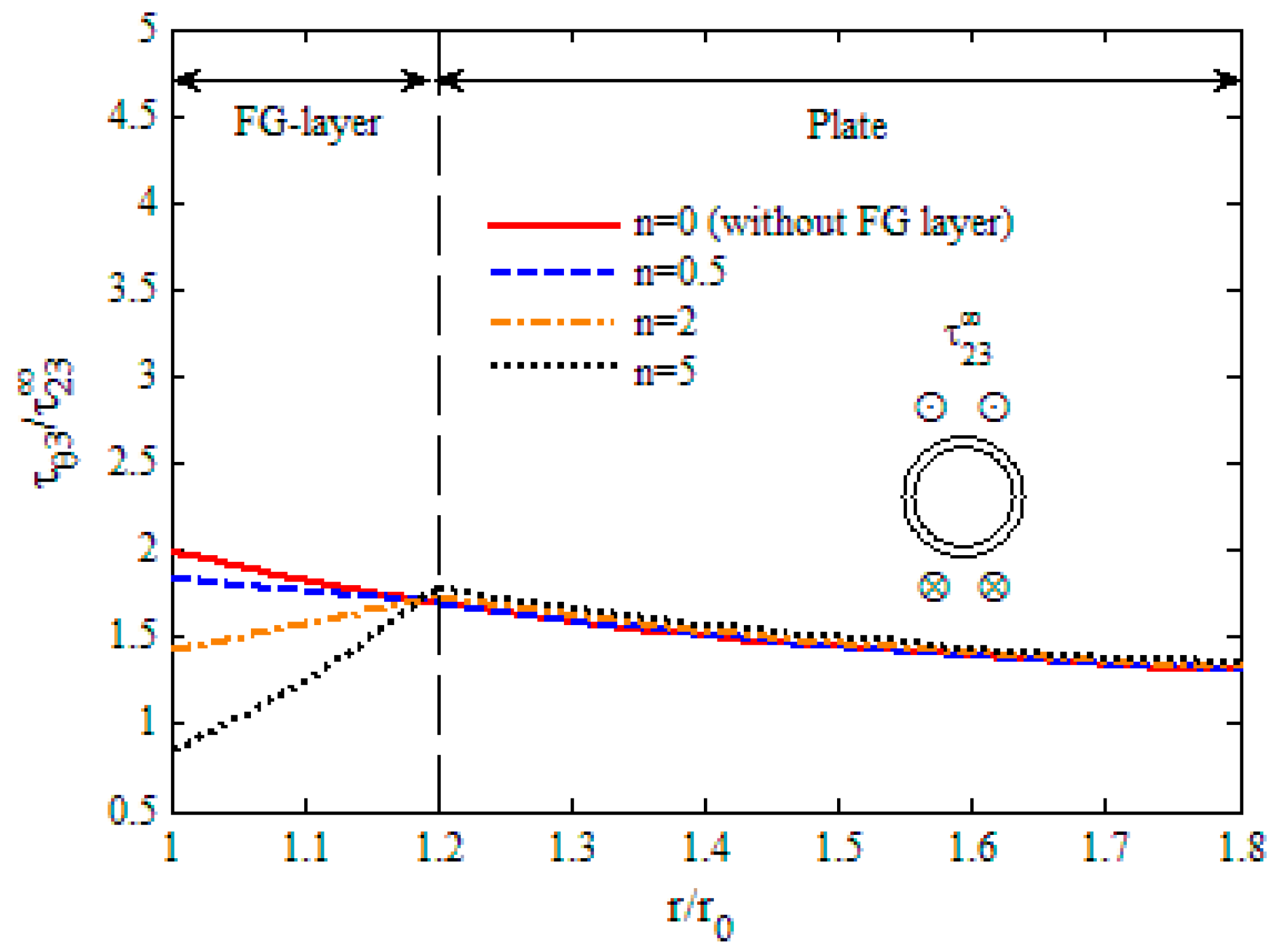
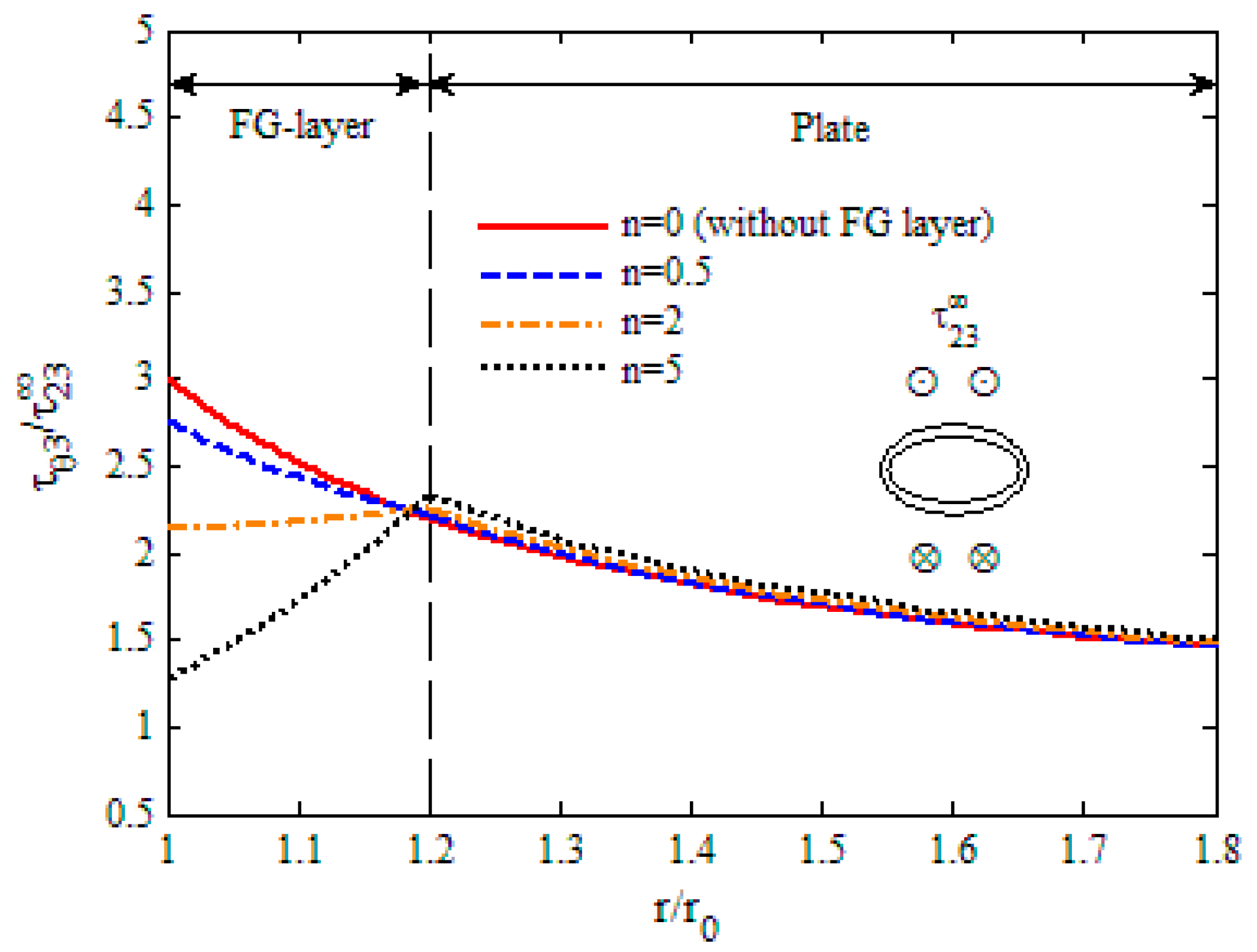
- As the gradient exponent increases, the shear stresses decrease obviously in the FG layer, while they increase slightly in the plate. So, the position of maximum stress changes from the hole to the interface after increases to some value.
- (4)
- The SCF of various shaped holes can be reduced significantly by using the optimum design of the material variations in the layer, and the most obvious one is the triangular hole whose SCF can be decreased by more than 50%.
Author Contributions
Funding
Conflicts of Interest
References
- Udupa, G.; Rao, S.S.; Gangadharan, K.V. Functionally graded composite materials: An overview. Procedia Mater. Sci. 2014, 5, 1291–1299. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Mudunuru, M.K.; Nakshatrala, K.B. A framework for coupled deformation–diffusion analysis with application to degradation/healing. Int. J. Numer. Meth. Eng. 2012, 89, 1144–1170. [Google Scholar] [CrossRef]
- Xu, C.; Mudunuru, M.K.; Nakshatrala, K.B. Material degradation due to moisture and temperature. Part 1: Mathematical model, analysis, and analytical solutions. Contin. Mech. Therm. 2016, 28, 1847–1885. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Sburlati, R.; Atashipour, S.R.; Atashipour, S.A. Reduction of the stress concentration factor in a homogeneous panel with hole by using a functionally graded layer. Compos. Part B 2014, 61, 99–109. [Google Scholar] [CrossRef]
- Gouasmi, S.; Megueni, A.; Bouthikhi, A.S. On the reduction of stress concentration factor around a notch using a functionally graded layer. Mater. Res. 2015, 18, 971–977. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.F. Reduction of the stress concentration around an elliptic hole by using a functionally graded layer. Acta Mech. 2016, 227, 2427–2437. [Google Scholar] [CrossRef]
- Cardenas-Garcia, J.F.; Shabana, Y.M.; Medina, R.A. Thermal loading and material property characterization of a functionally graded plate with a hole using an inverse problem methodology. J. Therm. Stress. 2006, 29, 1–20. [Google Scholar] [CrossRef]
- Fang, X.Q.; Hu, C.; Du, S.Y. Dynamic stress of a circular cavity buried in a semi-infinite functionally graded material subjected to shear waves. ASME J. Appl. Mech. 2007, 74, 916–922. [Google Scholar] [CrossRef]
- Ashrafi, H.; Asemi, K.; Shariyat, M. A three-dimensional boundary element stress and bending analysis of transversely/longitudinally graded plates with circular cutouts under biaxial loading. Eur. J. Mech. A Solids 2013, 42, 344–357. [Google Scholar] [CrossRef]
- Ohmichi, M.; Noda, N. Steady thermal stresses in functionally graded eccentric polygonal cylinder with circular hole. Arch. Appl. Mech. 2016, 86, 1163–1177. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Kitipornchai, S.; Liew, K.M.; Lim, C.W.; Peng, L.X. Thermal stresses around a circular hole in a functionally graded plate. J. Therm. Stress. 2003, 26, 379–390. [Google Scholar] [CrossRef]
- Huang, J.; Venkataraman, S.; Rapoff, A.J.; Haftka, R.T. Optimization of axisymmetric elastic modulus distributions around a hole for increased strength. Struct. Multidiscip. Optim. 2003, 25, 225–236. [Google Scholar] [CrossRef]
- Theotokoglou, E.E.; Stampouloglou, I.H. The radially nonhomogeneous elastic axisymmentric problem. Int. J. Solids Struct. 2008, 45, 6535–6552. [Google Scholar] [CrossRef]
- Kubair, D.V.; Bhanu-Chandar, B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension. Int. J. Mech. Sci. 2008, 50, 732–742. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.F.; Chen, W.T. Stress analysis of a functional graded material plate with a circular hole. Arch. Appl. Mech. 2010, 80, 895–907. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.F. Non-axisymmetric thermal stress around a circular hole in a functionally graded infinite plate. J. Therm. Stress. 2010, 33, 318–334. [Google Scholar] [CrossRef]
- Mohammadi, M.; Dryden, J.R.; Jiang, L.Y. Stress concentration around a hole in a radially inhomogeneous plate. Int. J. Solids Struct. 2011, 48, 483–491. [Google Scholar] [CrossRef]
- Sburlati, R. Stress concentration factor due to a functionally graded ring around a hole in an isotropic plate. Int. J. Solids Struct. 2013, 50, 3649–3658. [Google Scholar] [CrossRef]
- Kubair, D.V. Stress concentration factors and stress-gradients due to circular holes in radially functionally graded panels subjected to anti-plane shear loading. Acta Mech. 2013, 224, 2845–2862. [Google Scholar] [CrossRef]
- Kubair, D.V. Stress concentration factor in functionally graded plates with circular holes subjected to anti-plane shear loading. J. Elast. 2014, 114, 179–196. [Google Scholar] [CrossRef]
- Dave, J.M.; Sharma, D.S. Stresses and moments in through-thickness functionally graded plate weakened by circular/elliptical cut-out. Int. J. Mech. Sci. 2016, 105, 146–157. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. On the reduction of stress concentration factor in an infinite panel using different radial functionally graded materials. Int. J. Mater. Prod. Technol. 2018, 57, 109–131. [Google Scholar] [CrossRef]
- Batista, M. On the stress concentration around a hole in an infinite plate subject to a uniform load at infinity. Int. J. Mech. Sci. 2011, 53, 254–261. [Google Scholar] [CrossRef]
- Louhghalam, A.; Igusa, T.; Park, C. Analysis of stress concentrations in plates with rectangular openings by a combined conformal mapping-finite element approach. Int. J. Solids Struct. 2011, 48, 1991–2004. [Google Scholar] [CrossRef]
- Ukadgaonker, V.G.; Kakhandki, V. Stress analysis for an orthotropic plate with an irregular shaped hole for different in-plane loading conditions—Part 1. Compos. Struct. 2005, 70, 255–274. [Google Scholar] [CrossRef]
- Shen, M.H.; Chen, F.M.; Chen, S.N. Piezoelectric study for a coated hole of quasi-polygonal shape in an infinite plate. Int. J. Eng. Sci. 2009, 47, 475–486. [Google Scholar] [CrossRef]
- Ping, X.C.; Chen, M.C.; Leng, L. Singular stress analysis of an anisotropic elastic medium containing polygonal holes using a novel hybrid finite element method. Int. J. Mech. Mater. Des. 2012, 8, 219–236. [Google Scholar] [CrossRef]
- Pan, Z.; Cheng, Y.; Liu, J. Stress analysis of a finite plate with a rectangular hole subjected to uniaxial tension using modified stress functions. Int. J. Mech. Sci. 2013, 75, 265–277. [Google Scholar] [CrossRef]
- Savin, G.N. Stress Concentration around Holes; Pergamon Press: New York, NY, USA, 1961. [Google Scholar]
- Theocaris, P.S.; Petrou, L. Stress distributions and intensities at corners of equilateral triangular holes. Int. J. Fract. 1986, 31, 271–289. [Google Scholar] [CrossRef]
- Daoust, J.; Hoa, S.V. An analytical solution for anisotropic plates containing triangular holes. Compos. Struct. 1991, 19, 107–130. [Google Scholar] [CrossRef]
- Simha, K.R.Y.; Mohapatra, S.S. Stress concentration around irregular holes using complex variable method. Sadhana 1998, 23, 393–412. [Google Scholar] [CrossRef]
- Lei, G.; Ng, C.; Rigby, D. Stress and displacement around an elastic artificial rectangular hole. J. Eng. Mech. 2001, 127, 880–890. [Google Scholar] [CrossRef]
- Sharma, D.S.; Dave, J.M. Stress intensity factors for hypocycloidal hole with cusps in infinite anisotropic plate. Theor. Appl. Fract. Mech. 2015, 75, 44–52. [Google Scholar] [CrossRef]
- Sharma, D.S. Stresses around hypotrochoidal hole in infinite isotropic plate. Int. J. Mech. Sci. 2016, 105, 32–40. [Google Scholar] [CrossRef]
- Jafari, M.; Ardalani, E. Stress concentration in finite metallic plates with regular holes. Int. J. Mech. Sci. 2016, 106, 220–230. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problem of Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1953. [Google Scholar]
- Yang, Q.; Zhu, W.; Li, Y.; Zhang, H. Stress field of a functionally graded coated inclusion of arbitrary shape. Acta Mech. 2018, 229, 1687–1701. [Google Scholar] [CrossRef]
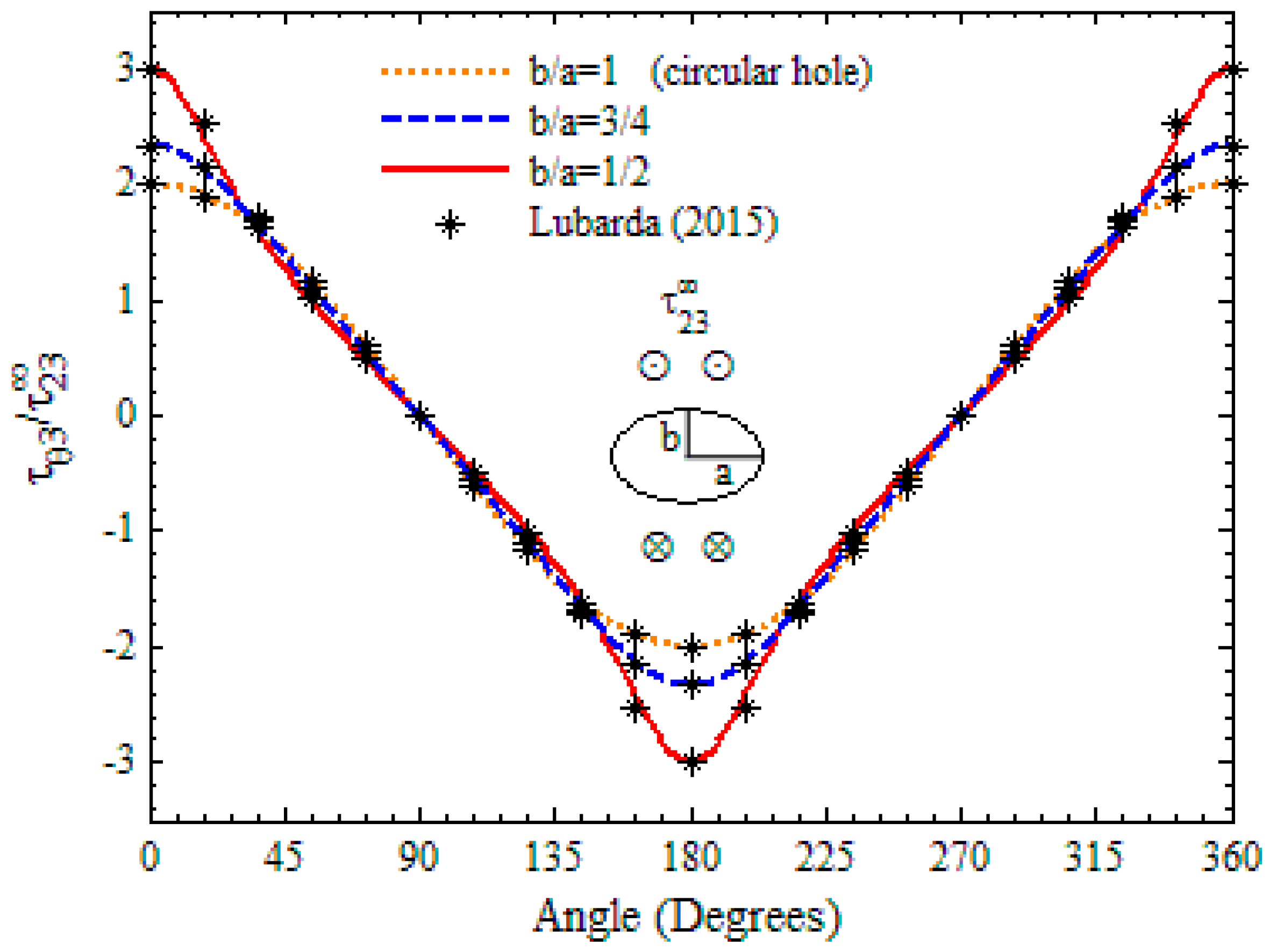
- Lubarda, V.A. On the circumferential shear stress around circular and elliptical holes. Arch. Appl. Mech. 2015, 85, 223–235. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. Reduction in stress concentration around a pair of circular holes with functionally graded material layer. Acta Mech. 2018, 229, 1045–1060. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Q.; Yang, B. Localized stress recoveries in hierarchical aligned porous materials with the influence of surface effects or interphases. Mater. Des. 2018, 155, 8–18. [Google Scholar] [CrossRef]

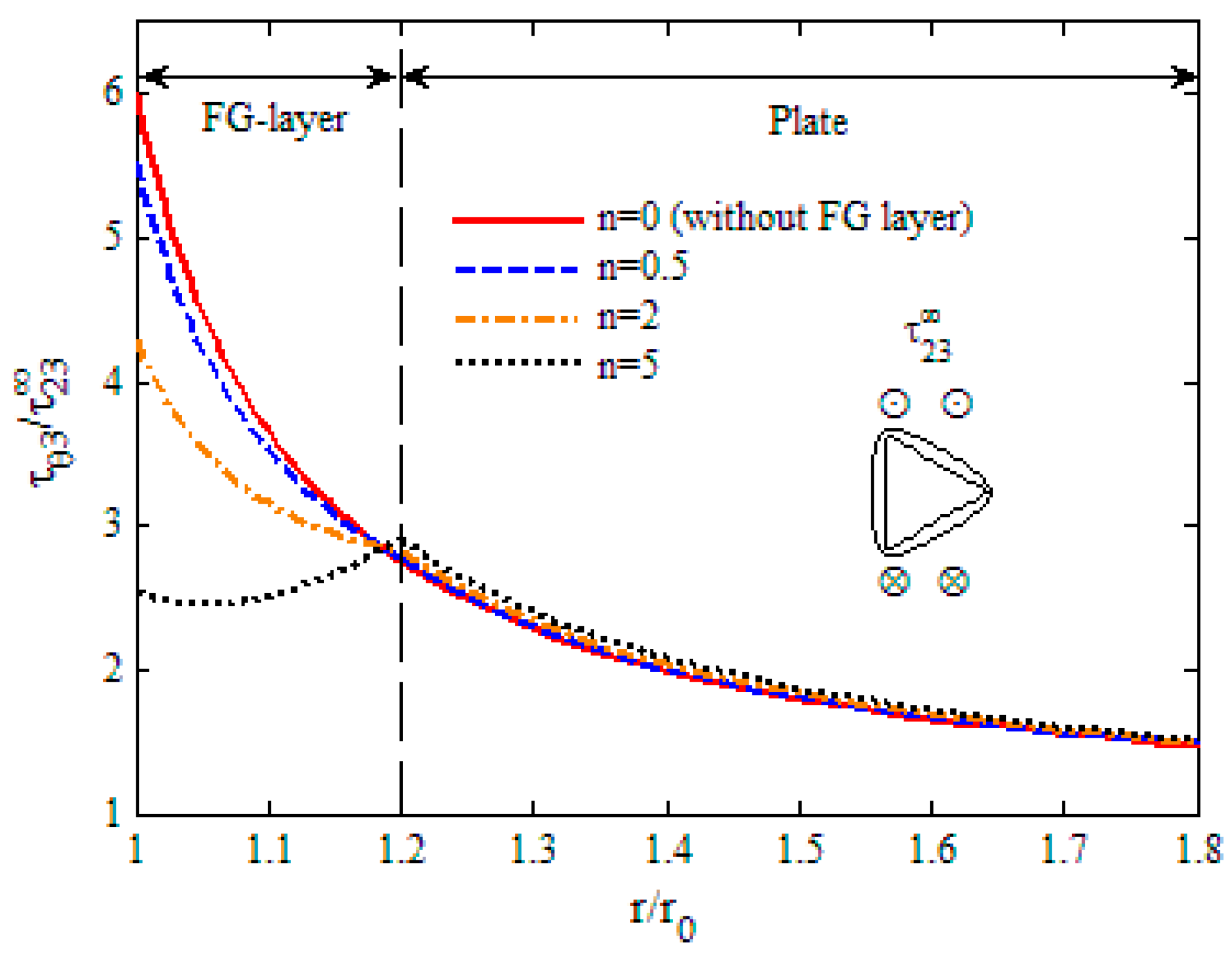
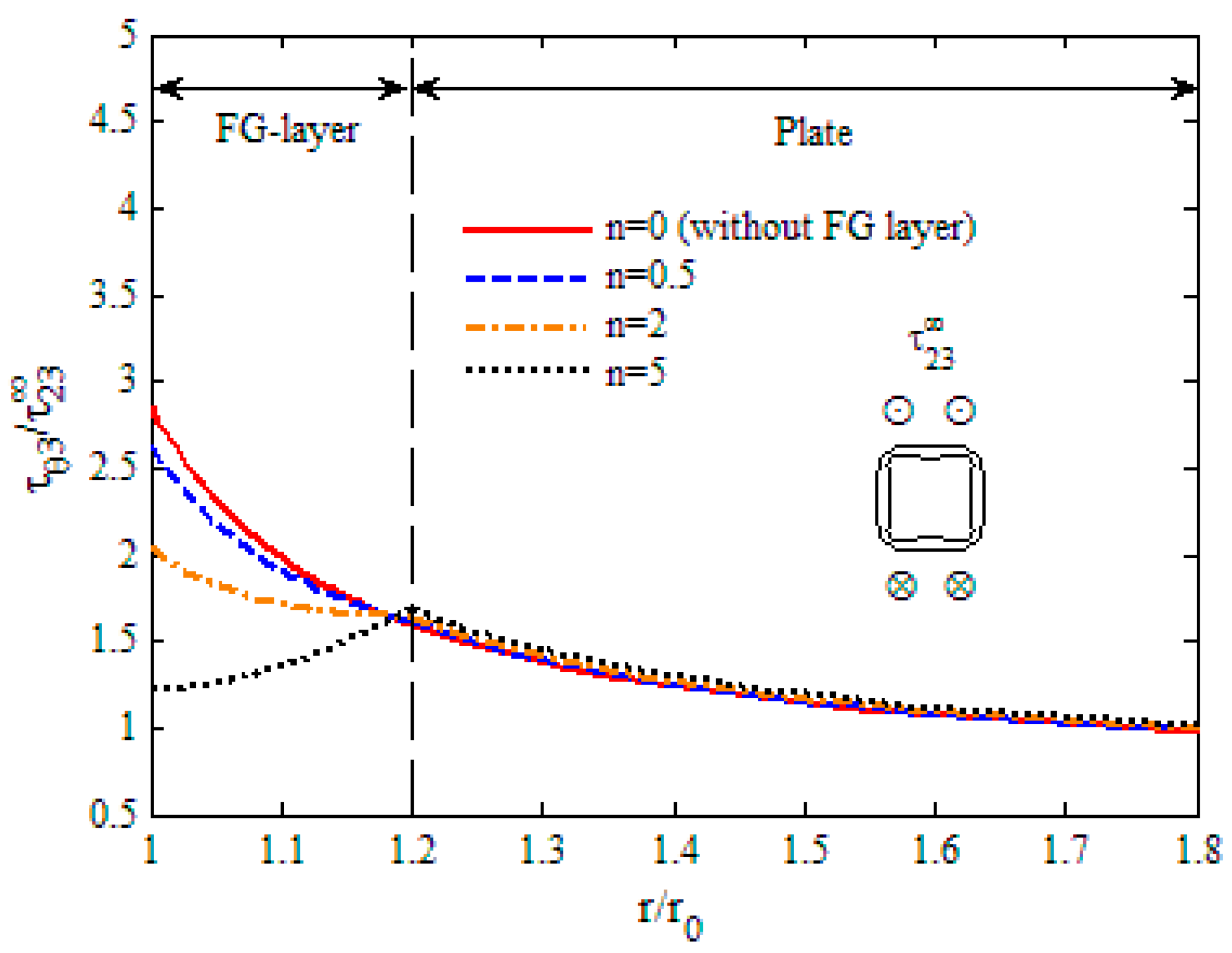
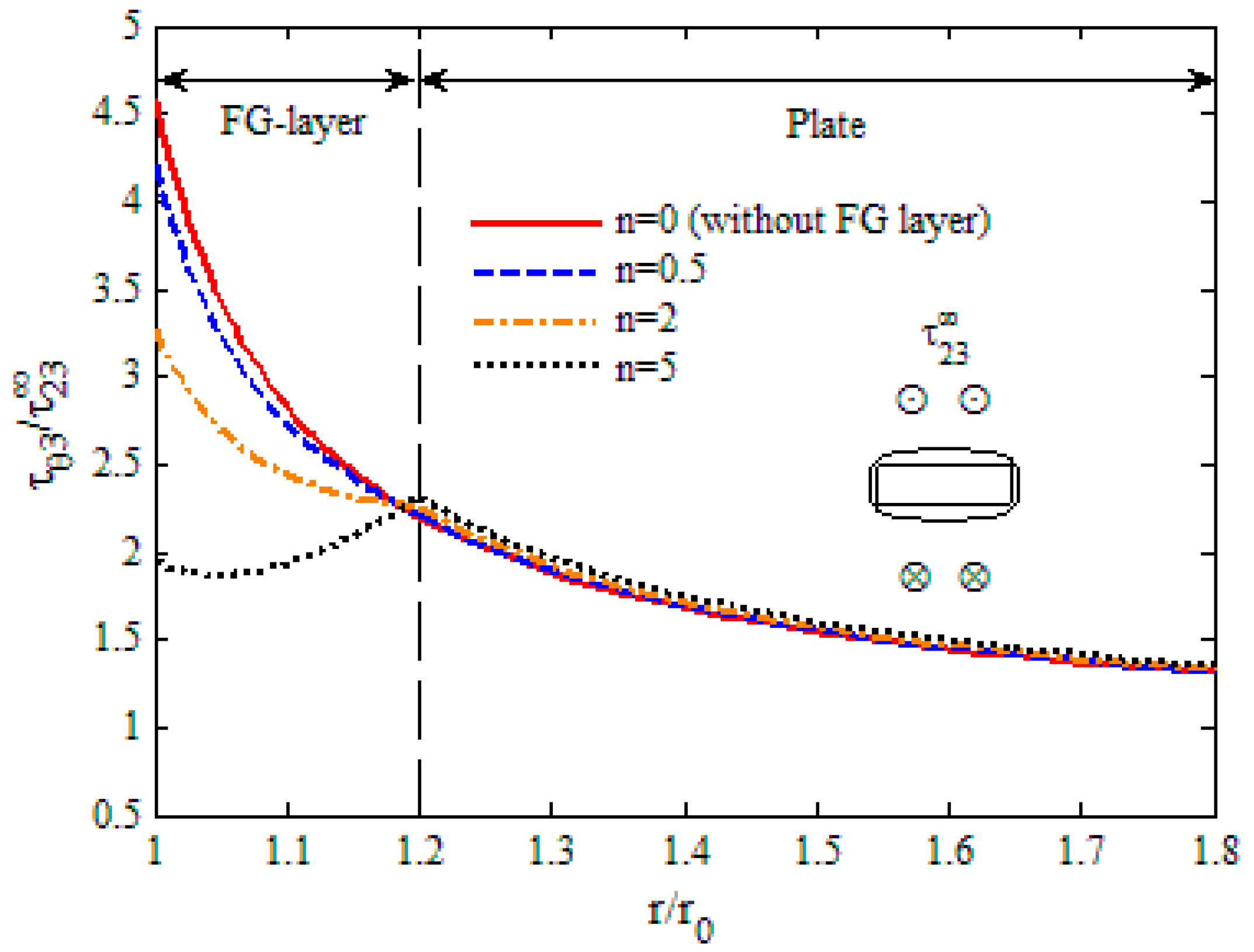

| Shape of Hole | Without FG Layer | With FG Layer | The Decreasing Percentage of SCF | ||
|---|---|---|---|---|---|
| Exponent | SCF | Exponent | Minimum SCF | ||
| Circle | = 0 | 2.000 | = 0.932 | 1.716 | 14.2% |
| Ellipse | = 0 | 3.000 | = 1.695 | 2.255 | 24.8% |
| Triangle | = 0 | 6.000 | = 4.237 | 2.919 | 51.4% |
| Square | = 0 | 2.856 | = 3.220 | 1.663 | 41.8% |
| Rectangle | = 0 | 4.575 | = 4.068 | 2.299 | 49.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Li, Y. Stress Concentration and Optimized Analysis of an Arbitrarily Shaped Hole with a Graded Layer under Anti-Plane Shear. Appl. Sci. 2018, 8, 2619. https://doi.org/10.3390/app8122619
Guan Y, Li Y. Stress Concentration and Optimized Analysis of an Arbitrarily Shaped Hole with a Graded Layer under Anti-Plane Shear. Applied Sciences. 2018; 8(12):2619. https://doi.org/10.3390/app8122619
Chicago/Turabian StyleGuan, Yonggang, and Yun Li. 2018. "Stress Concentration and Optimized Analysis of an Arbitrarily Shaped Hole with a Graded Layer under Anti-Plane Shear" Applied Sciences 8, no. 12: 2619. https://doi.org/10.3390/app8122619




